Cycle-by-cycle assembly of respiratory network activity is dynamic and stochastic

Abstract

Rhythmically active networks are typically composed of neurons that can be classified as silent, tonic spiking, or rhythmic bursting based on their intrinsic activity patterns. Within these networks, neurons are thought to discharge in distinct phase relationships with their overall network output, and it has been hypothesized that bursting pacemaker neurons may lead and potentially trigger cycle onsets. We used multielectrode recording from 72 experiments to test these ideas in rhythmically active slices containing the pre-Bötzinger complex, a region critical for breathing. Following synaptic blockade, respiratory neurons exhibited a gradient of intrinsic spiking to rhythmic bursting activities and thus defied an easy classification into bursting pacemaker and nonbursting categories. Features of their firing activity within the functional network were analyzed for correlation with subsequent rhythmic bursting in synaptic isolation. Higher firing rates through all phases of fictive respiration statistically predicted bursting pacemaker behavior. However, a cycle-by-cycle analysis indicated that respiratory neurons were stochastically activated with each burst. Intrinsically bursting pacemakers led some population bursts and followed others. This variability was not reproduced in traditional fully interconnected computational models, while sparsely connected network models reproduced these results both qualitatively and quantitatively. We hypothesize that pacemaker neurons do not act as clock-like drivers of the respiratory rhythm but rather play a flexible and dynamic role in the initiation and stabilization of each burst. Thus, at the behavioral level, each breath can be thought of as de novo assembly of a stochastic collaboration of network topology and intrinsic properties.

common among many models of neural rhythmogenesis is the incorporation of autonomously rhythmic neurons (bursting pacemakers) as potential contributors to network oscillations (Ramirez et al. 2011; Koch et al. 2011; Garcia et al. 2011). These pacemakers have been elemental in descriptions of a variety of rhythmic neural circuits underlying a range of motor behaviors in invertebrates (Kristan et al. 2005; Selverston 2010; Zhao et al. 2010) and mammals (Ramirez et al. 2004; Brocard et al. 2010; Harris-Warrick 2010) as well as both physiological and pathophysiological cortical rhythms (Chagnac-Amitai and Connors 1989; van Drongelen et al. 2006; de Kock and Sakmann 2008; Higgs and Spain 2009; Marcuccilli et al. 2010; Wang 2010). In the pre-Bötzinger complex (pre-BötC), a rhythmically active network that is essential for breathing (Smith et al. 1991; Tan et al. 2008; Ramirez et al. 1998), pacemakers have figured prominently, although often controversially, in causal explanations for the generation of the breathing rhythm.

While it has been suggested that pacemaker behavior in individual neurons might be a discrete epiphenomenon of a continuous distribution of intrinsic currents (Butera et al. 1999a; Del Negro et al. 2002a), the distinction between pacemakers and nonpacemakers has typically been treated as unproblematically categorical, although conditional and weak pacemaking has sometimes been invoked for borderline cases (Smith et al. 1991; Stil et al. 2009; Viemari and Tryba 2009). The hypothesis that pacemakers are critical for rhythmogenesis has led to two interrelated predictions about the cycle-by-cycle behavior of these cells within the network: 1) The capability of such neurons to exhibit ectopic bursts might allow them to kindle global activity on some cycles (Ramirez et al. 2004), or their intrinsically generated ramping preinspiratory activity may trigger individual population events (Rekling et al. 1996); and 2) Their firing sequence within each population burst cycle is invariably determined by each cell's endowment of intrinsic currents as illustrated in some modeling studies (Butera et al. 1999a; Rybak et al. 2003).

Nonetheless, a precise characterization of how these neurons participate in ongoing activity under baseline conditions has not been published. In this study, we used multichannel simultaneous extracellular recordings to analyze combined single-spike and population activity in the in vitro respiratory slice including the pre-BötC. We find that synaptically isolated neurons exhibit a range of rhythmic behavior that defies easy classification into pacemaker and nonpacemaker categories. In addition, although some features of average firing behavior in control conditions are predictive of such intrinsic rhythmicity, other hypothesized features were not found to correlate with pacemaker behavior. Analysis of the cycle-by-cycle firing pattern of cells within the network did show some tendency for intrinsically rhythmic cells to lead some burst cycles, but variability in burst onset was dramatic. Network models using full cell-to-cell connectivity were unable to reproduce this variability under reasonable physiological assumptions, but sparsely connected networks were. In light of these results, we propose a novel model of rhythmogenesis in which intrinsically bursting neurons play a stochastic, dynamic, and flexible role in the assembly of respiratory rhythms on a cycle-by-cycle basis within a sparse network topology.

MATERIALS AND METHODS

Transverse medullary brain stem slices were taken from CD1 mice, P6–9, as described previously (Ramirez et al. 1996; Viemari and Ramirez 2006). In accordance with protocols approved by the Institutional Animal Care and Use Committee at the University of Chicago, animals were deeply anesthetized with ether and rapidly decapitated. The brainstem was isolated in ice-cold, oxygenated (95% O₂-5% CO₂) artificial cerebrospinal fluid (aCSF) containing (in mM): 128 NaCl, 3 KCl, 1.5 CaCl₂, 1 MgCl₂, 24 NaHCO₃, 0.5 NaH₂PO₄, and 30 d-glucose (pH 7.4). The brainstem was then glued to an agar block on the mounting plate of a Leica Vibratome with the rostral end up and the ventral face toward the blade. Serial slices proceeded until visual landmarks became clear. The cut of the rostral face of the experimental slice was typically 530 μm caudal to the opening of the fourth ventricle. From this position, slices of between 600 and 620 μm were taken and presumed to contain the pre-BötC. This slice was transferred directly to the recording chamber, where it was superfused with aCSF at a typical rate of 10 ml/min and allowed to equilibrate to experimental temperature (33–35°C). Robust population activity was initiated by raising the extracellular potassium concentration from 3 to 8 mM in two steps over 60 min.

In some experiments, fast chemical synaptic transmission was blocked using 20 μM 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX) for non-N-methyl-d-aspartic acid-mediated glutamatergic synapses; 10 μM 4-(3-phosphonopropyl)piperazine-2-carboxylic acid (CPP) for N-methyl-d-aspartic acid-mediated transmission; 1 μM strychnine for glycinergic synapses; and 50 μM picrotoxin for γ-aminobutyric acid-mediated synapses.

Extracellular recording.

Extracellular neural activity from the transverse medullary slice was recorded on up to 16 channels using custom-made microwire gold-plated multielectrodes (25-μm inner diameter, Formvar-insulated Nichrome; A-M Systems). Microwire bundles were twisted together using an electric drill and then sealed into a solid shank with epoxy and clear nail polish. The bundle was then cut flush with microscissors, producing an arbitrary, but roughly circular configuration of wires within the electrode tip, typically ∼300 μm in diameter. Neural signals were amplified 1,000× and band-pass filtered from 250 to 7,500 Hz with a custom analog amplifier. The signals were then sampled at 20 kHz, digitized, and saved using a Digidata 1322A and AxoScope (Molecular Devices). To reduce superimposition of waveforms from presumptive single units on multiple channels, resulting signals were preprocessed using independent component analysis (FastICA, http://www.cis.hut.fi/projects/ica/fastica/). After preprocessing, action potential waveforms from distinct neurons were typically present on from one to three channels. These waveforms were detected and sorted using Offline Sorter (Plexon) with manual cluster cutting in tetrode-based feature spaces. Care was taken to follow nonstationarities in waveform shapes in assigning spikes to separate units, and auto- and cross-correlation histograms were examined as a check on sorting results (Lewicki 1998). To generate an integrated population activity waveform, signals from multiple channels were averaged, rectified, and digitally low-pass filtered at 30 Hz. With the exception of spike detection and sorting, all signal processing and statistical analyses were done in MATLAB (The MathWorks) using custom applications.

Quantitative analysis.

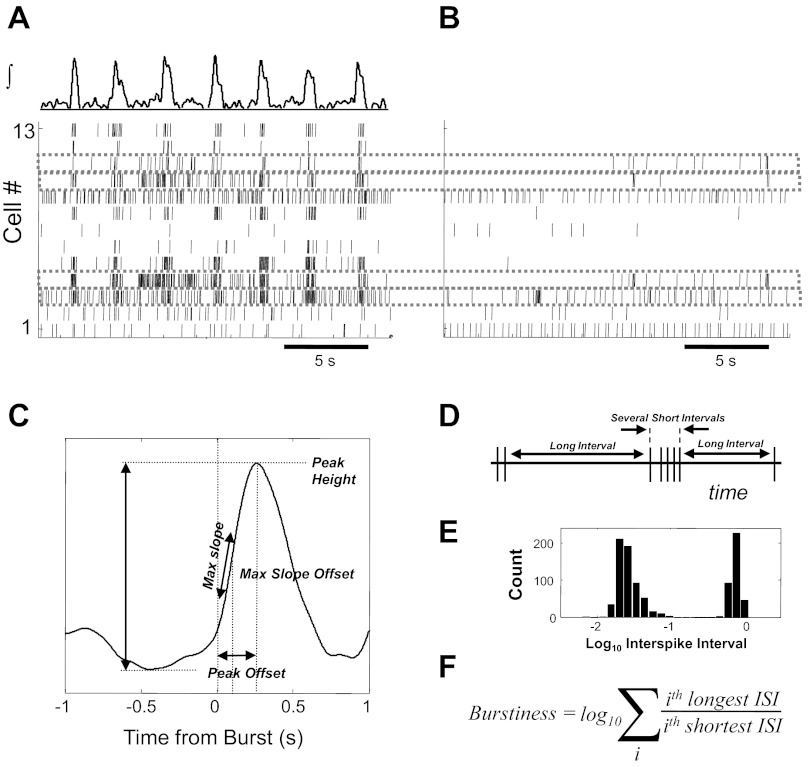
Some of the key methods for assessing the relationship between single cell firing behavior within the intact respiratory network and after synaptic isolation are schematized in Fig. 1. Simultaneously recorded single-cell activity (Fig. 1A) was associated with spiking activity after synaptic blockade (Fig. 1B). The integrated population activity waveform (Fig. 1A, top) for each experiment was characterized by a combination of four metrics of burst shape and timing variability: variance of interburst intervals, variance of burst peak amplitudes, burst shape variability, and signal-to-noise ratio. Slow baseline nonstationarity was eliminated by subtracting off a highly smoothed version of the signal, estimated by low-order polynomial regression. A threshold was set interactively for each recording based on the signal noise power during intraburst intervals. The resulting detected bursts were screened for artifacts and false detections, and the burst onset time was defined from the remaining waveforms as the time of threshold crossing. For the purposes of this study, no effort was made to distinguish high amplitude bursts (fictive sighs; Lieske et al. 2000) from other bursts, although such bursts were observed in many recordings.

Fig. 1.

Schematic of multielectrode recording and analysis of in vitro rhythmic activity. Example spike time raster of 13 neurons recorded during several inspiratory population bursts under baseline conditions (A) and after synaptic isolation (B). Average population burst phase-dependent firing activity is parameterized on multiple features (C), which are tested for correlation with endogenous activity after synaptic block. For this comparison, a burstiness metric based on a characteristic pattern of long and short interspike intervals (D), and exemplified in a bimodal interspike interval histogram (E), is comprised of a log₁₀ sum of the ratio of longest to shortest intervals (F). ISI, interspike interval.

The relationship between the activity of individual neurons and the phase of the fictive inspiratory rhythm was determined by various analyses of the firing times of action potentials relative to the onset of each population burst (as defined above). Peri-burst firing rate histograms, for example, were generated by counting the number of occurrences of spikes from a given cell within small time bins relative to burst onset. These counts were then normalized by the bin width, and the number of bursts were recorded to provide a measure of the average firing rate for a given cell relative to the fictive inspiratory phase. These histograms were categorized according to their most prominent feature of phase-dependent firing (as described in the companion paper, Carroll et al. 2012) into nonrespiratory, inspiratory, expiratory, and postinspiratory (one cell was silent during control conditions). Manual scoring was done blind to subsequent behavior of the cell under isolated conditions. For other types of analysis, the behavior of each cell relative to the population activity was characterized by the estimation of instantaneous firing rate functions. A single vector of burst-relative spike times was created, and the instantaneous firing rate was generated by a summation of Gaussian kernel functions, each centered on the time of one action potential. Compared with histogram estimation, which imposes arbitrary boundaries based on the selection of the number of time bins and produces a discontinuous function, kernel rate estimation can generate a function of arbitrarily fine smoothness, avoiding the imposition of ad hoc boundaries within the data. Instead, kernel estimation requires the specification of a smoothing parameter (in the Gaussian case, the sigma width parameter of the kernel function), which determines the level of temporal detail discernable in the rate estimate. The nominal smoothing width for most analyses was 0.03 s.

The phase-dependent firing rate functions and histograms were estimated under baseline conditions and parameterized for waveform features expected to predict subsequent behavior after synaptic isolation. Spike rate parameters included the following: overall spike rate (Mean Spike Rate), spike rate during expiration (between population bursts; Exp. Spike Count), mean spike rate during inspiratory burst phases (Insp. Spike Count), spike rate during the postinspiratory phase (Post Spike Count), and spike rate modulation by the inspiratory burst (the difference in spike rate between the peak/trough of inspiration and that during the expiratory phase; Insp. Modulation). Spike rate variability (across fictive respiration cycles) was assessed as spike count standard deviation during expiratory, inspiratory, and postinspiratory phases (Exp./Insp./Post Count Std.). Spike rate change over time was evaluated as the slope of the estimated firing rate function during the preinspiratory phase, inspiratory onset, and offset (Preinsp./Insp./Post Slope). Additionally, timing of inspiratory burst onset and offset was evaluated at two threshold-crossing events (quarter-amplitude and half-amplitude; Quart. Over Time and Half Over Time). Phase-dependent firing rate functions were also parameterized by principal component analysis (as described in the companion paper, Carroll et al. 2012) by projecting the dataset into the vector space defined to capture the most variance in a single dimension.

The behavior of the recorded cells after synaptic isolation was assessed by two methods designed to characterize intrinsic rhythmicity. Based on the idea that bursting behavior consists of relatively long interspike intervals (ISIs) interspersed with groups of relatively short intervals (Fig. 1D), producing a bimodal ISI histogram (often more easily visualized on a logarithmic scale; Fig. 1E), a burstiness metric was calculated using the set of ISIs from each cell during synaptic isolation (Fig. 1E). This activity was also characterized by manual inspection of each spike raster and log₁₀ transformed ISI histogram, assigning each cell heuristically to one of five burstiness classes: weakly active or with regular tonic activity (Weak/Tonic), irregularly tonic activity and no high-frequency bursts (Tonic/Irregular), irregularly tonic activity with some bursts (Tonic w/Bursts), frequent bursts over tonic background activity (Bursting), and high frequency bursts with little interburst activity (Strongly Bursting). These categories were chosen to reflect the largely descriptive classification of intrinsic behavior that is common in previous studies.

Simulations.

Networks of point-conductance neurons were simulated using single-cell parameters taken without modification from a series of influential studies by Butera et al. (1999a) and Rybak et al. (2003). As in those studies, each cell is a represented by a single-compartment conductance model with the standard fast sodium and delayed rectifier potassium currents for spike generation as well as a persistent sodium current and a passive leak current. Synaptic connections (all excitatory in this model) are generated by a single exponential time course current source against a 0-mV reversal potential. Details of the single-cell model are presented in the appendix. Sparse random networks were generated by iterating through all possible neuron pairs in either direction and creating a synaptic connection if a uniform pseudorandom number was generated that was less than or equal to a threshold value representing the mean proportion of connectedness for each cell. Neither the spatial location nor the specific size of individual neurons was modeled in this study. All the cells within this network are assumed to lie within a roughly 350-μm spheroid where all cells are at least theoretically mutually accessible with comparatively short axonal projections; therefore, axo-dendritic conduction delays were also not a part of this model.

The network simulation was custom-written in C++ with standard libraries (GNU gcc 3.4.4 on a Pentium class laptop running Windows XP). Integration was performed with a custom implementation of the fourth order Runge-Kutta method with a fixed time step of 0.01 ms. Typical simulations included 300 cells and ran for 90 s of model time, of which the first 30 s of activity was discarded as reflecting transient initial dynamics. The C++ code was neither particularly inefficient nor specifically optimized for execution speed, and computational demands were rather high, with typical run times for a single simulation of around 24 h.

Statistical methods.

The distributions of study variables were often non-Gaussian and therefore characterized by median (for central tendency) and half the interquartile range (for variability). Linear relationships between raw variables were typically assessed with Kendall's tau, a nonparametric measure of correlation. This statistic was considered significant for P < 0.001 (without any further correction for multiple comparisons). The Kruskal-Wallis test was used for a nonparametric comparison of group medians with a Bonferroni correction for post hoc analysis (significant for an uncorrected P < 0.05).

RESULTS

Intrinsic rhythmicity and burst-triggered firing rate functions.

The ability to generate intrinsic bursting was assessed in 892 cells from 72 experiments by bath application of a cocktail of antagonists that block chemical glutamatergic and GABAergic synaptic transmission (CNQX, CPP, strychnine, and picrotoxin, for more details on synaptically isolating respiratory neurons, see Tryba et al. 2003, 2008; Tryba and Ramirez 2003, 2004). Intrinsic rhythmic bursting under these conditions was evaluated using two distinct methods: calculation of a metric based on the ISI distribution and manual inspection of the ISI histogram and spike raster plots.

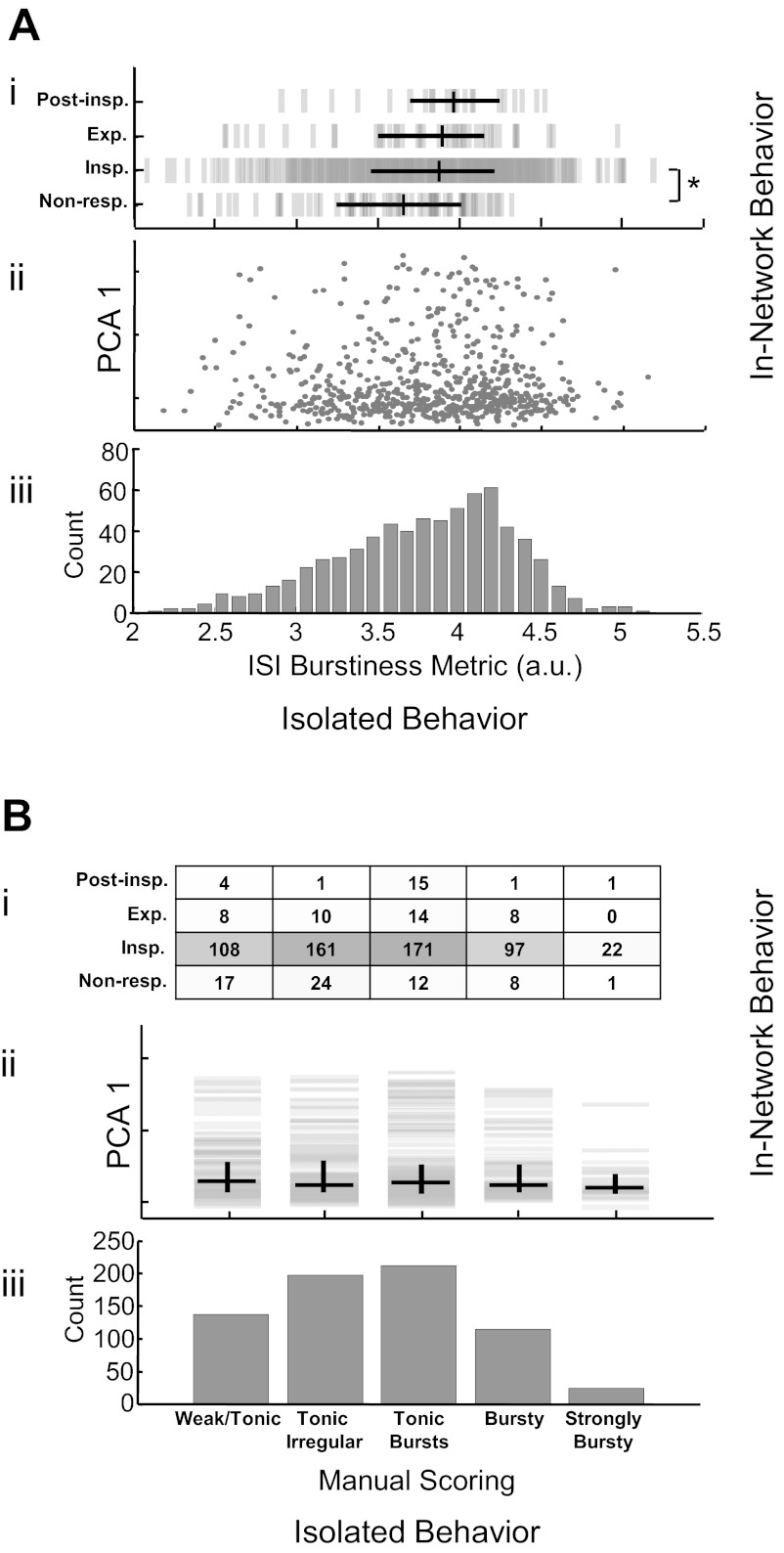
The ISI metric stratified cocktail spiking behavior along a unimodal distribution with no clear divisions (Fig. 2Aiii). Classifications of the phase-dependent behavior of individual cells in control conditions did not clearly predict subsequent burstiness during synaptic isolation (Fig. 2Ai), although those identified as nonrespiratory had a significantly lower median burstiness score than those classified as inspiratory (3.6 ± 0.4 vs. 3.9 ± 0.4; median ± half interquartile range; P < 0.05). Further, no clear relationship was seen between phase-dependent control behavior, as parameterized by principal component analysis (Fig. 2Aii), and the ISI burstiness metric.

Fig. 2.

Comparison of in-network firing patterns with two characterizations of intrinsic rhythmicity derived from recordings made in synaptic isolation. An intrinsic burstiness metric produces a broad unimodal distribution (Aiii) that is uncorrelated with the first principle component decomposition of in-network firing behavior (Aii) and only weakly related to manual categorization of control activity (Ai; *P < 0.05 for nonrespiratory vs. inspiratory). Manual score of intrinsic behavior also produces a unimodal distribution (Biii) that is not clearly related to in-network behavior as defined by manual classification (Bi) or principal component analysis (PCA; Bii). Non-resp., nonrespiratory; Insp., inspiratory; Exp., expiratory; Post-Insp., postinspiratory; a.u., arbitrary units.

Manual scoring separated spiking activity into five categories: weak or tonic firing (20.0%), irregular tonic (with no high frequency spiking; 28.8%), tonic with some high frequency bursts (30.9%), bursting with tonic spiking between bursts (16.7%), and strongly bursting without spiking between bursts (3.5%) as shown in Fig. 2Biii. There was no clear relationship between manually classified control behavior and manually scored behavior in synaptic isolation (Fig. 2Bi). Similarly, these categories did not correlate with control behavior defined by the first principle component of the set of firing patterns (Fig. 2Bii).

To evaluate potential relationships between phasic activity patterns under control conditions (characterized by burst-triggered firing rate functions), several dimensions of control activity were parameterized for all active cells (i.e., >50 spikes in both control and cocktail conditions: n = 683) and these variables were compared with the two intrinsic bursting metrics by nonparametric correlation analysis (Kendall's tau). Measured correlations were positive and significant against both burstiness metrics (P < 0.001) for all variables except those related to burst timing (Fig. 3, A and B). The uniformity of correlations suggested a high degree of collinearity in the data, probably dominated by the influence of overall spike rate in the metrics of control and cocktail spiking behavior. Indeed, mean spike rate during control epochs (log₁₀ transformed) was significantly correlated with mean spike rate during cocktail epochs (Kendall's tau = 0.32; P < 0.0001; data not shown).

Fig. 3.

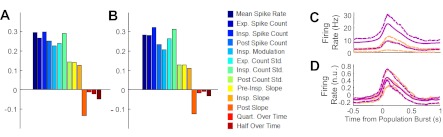
Correlations between features of firing patterns during control epochs and subsequent behavior during synaptic blockade. Kendall tau shows prominent correlations between an algorithmic metric of burstiness (A) and manually scored burstiness classes (B) for features related to spike rate and variability, although not for features associated with the timing of burst-triggered single unit activity. A and B: Mean Spike Rate, average spike rate across all phases of population burst activity; Exp. Spike Count, spike count during expiratory phases of population activity; Insp. Spike Count, count during inspiratory phases; Post Spike Count, count during post-inspiratory period; Insp. Modulation, difference between inspiratory and expiratory phase spike counts; Exp./Insp./Post Count Std., standard deviations of spike counts during indicated phases; Pre-insp. Slope, slope of the firing rate function during the preinspiratory phase; Insp. Slope, slope during the inspiratory burst onset; Post Slope, slope during the inspiratory burst offset; Quart. Over Time, relative timing of the quarter-amplitude threshold crossing during the inspiratory phase; Half Over Time, relative timing of the half-amplitude threshold crossing. C: mean (solid lines) and quartile bounds (dashed) of firing rate function for the most (purple) and least (orange) bursty 25% of cells. Means and interquartile bounds are shown after amplitude normalization and detrending in D.

As an alternate evaluation of the relationship between burst-triggered firing rate functions and subsequent intrinsic bursting (during synaptic blockade), firing rate functions corresponding to the most and least intrinsically rhythmic quartile (in the ISI metric) were extracted and averaged, producing an illustration of the characteristic firing rate function of the control behavior for those groups of cells. Although variability is high, the higher mean firing rates in most rhythmic cells are apparent through all phases (Fig. 3C). To highlight possible differences in shape and timing of these average waveforms independent of mean and peak rate differences, the rate functions were normalized to unit amplitude and zero mean before being averaged again (Fig. 3D). While the mean and interquartile bounds are nearly overlapping in these two populations, a sharper and more pronounced burst onset is evident in the group that proves later to have intrinsic rhythm capability (Fig. 3D).

Cycle-by-cycle variability.

While the mean phase-dependent spiking behavior of cells during control conditions did not show a tendency for intrinsically bursting neurons to fire earlier in the inspiratory phase than other cells (see above), it is possible that this analysis of mean spiking behavior obscured important timing relationships between population bursts and the firing of cells found subsequently to be intrinsically rhythmic in synaptic blockade. To address this possibility, multicellular data were analyzed cycle-by-cycle to determine the identity of units that anticipate the population burst. As illustrated in a representative raster plot (Fig. 4B), in which the firing of 18 simultaneously recording neurons is indicated with an instantaneous frequency color code, considerable variability in the cycle-by-cycle firing pattern of each cell is obvious. Some bursts (indicated by the population activity shown in gray) seem to be led by spiking in cell 17 while in other cycles, cell 14 or cell 13 leads. To quantify these timing relationships, a score representing the probability of a cell anticipating a population burst based on a range of definitions of “anticipate” (i.e., firing the earliest 1st, 2nd, 3rd, etc. spike). These probabilities (Fig. 4A) indicate that while some cells (cell 14 and cell 17, for example) often anticipate the population burst, none is invariantly ahead of all others. By sorting the cells in ascending order of their tendency to burst in a subsequent epoch of synaptic block, it can be seen that neurons that prove to have intrinsic bursting capabilities do not necessarily lead the population rhythm. Cell 18, for example, despite its score as the most intrinsically rhythmic, always follows the spiking of other cells, while cell 3 occasionally leads despite a lack of rhythmicity during synaptic block. Since the lead probability calculation is at least partially dependent on the mean spike rate, the relationship between these variables was assessed with correlation analysis (Fig. 4C). Burst lead probability is strongly correlated with mean spike rate during control epochs (Kendall tau = 0.60; P < 0.0001) and more weakly correlated with rhythmicity in synaptic block (Fig. 4D; Kendall tau = 0.24; P < 0.0001).

Fig. 4.

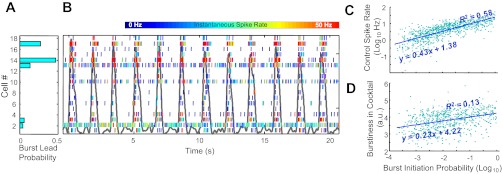
Cycle-by-cycle activation of individual units in relation to population activity is stochastic. Spike rasters for 18 simultaneously recorded neurons (B), ordered along the ordinate axis by degree of burstiness exhibited in synaptic block, and color-coded for instantaneous firing rate (shown against population burst activity, background line in gray), and probability of anticipating population burst activity for each recorded cell calculated over entire control epoch (A). C: burst initiation probability (log₁₀ transformed) of 688 cells is strongly related (Kendall tau = 0.60; P < 0.0001) to overall spike rate in control epochs and more weakly (although significantly; tau = 0.24; P < 0.0001) correlated with interspike interval metric of burstiness in synaptic block (D).

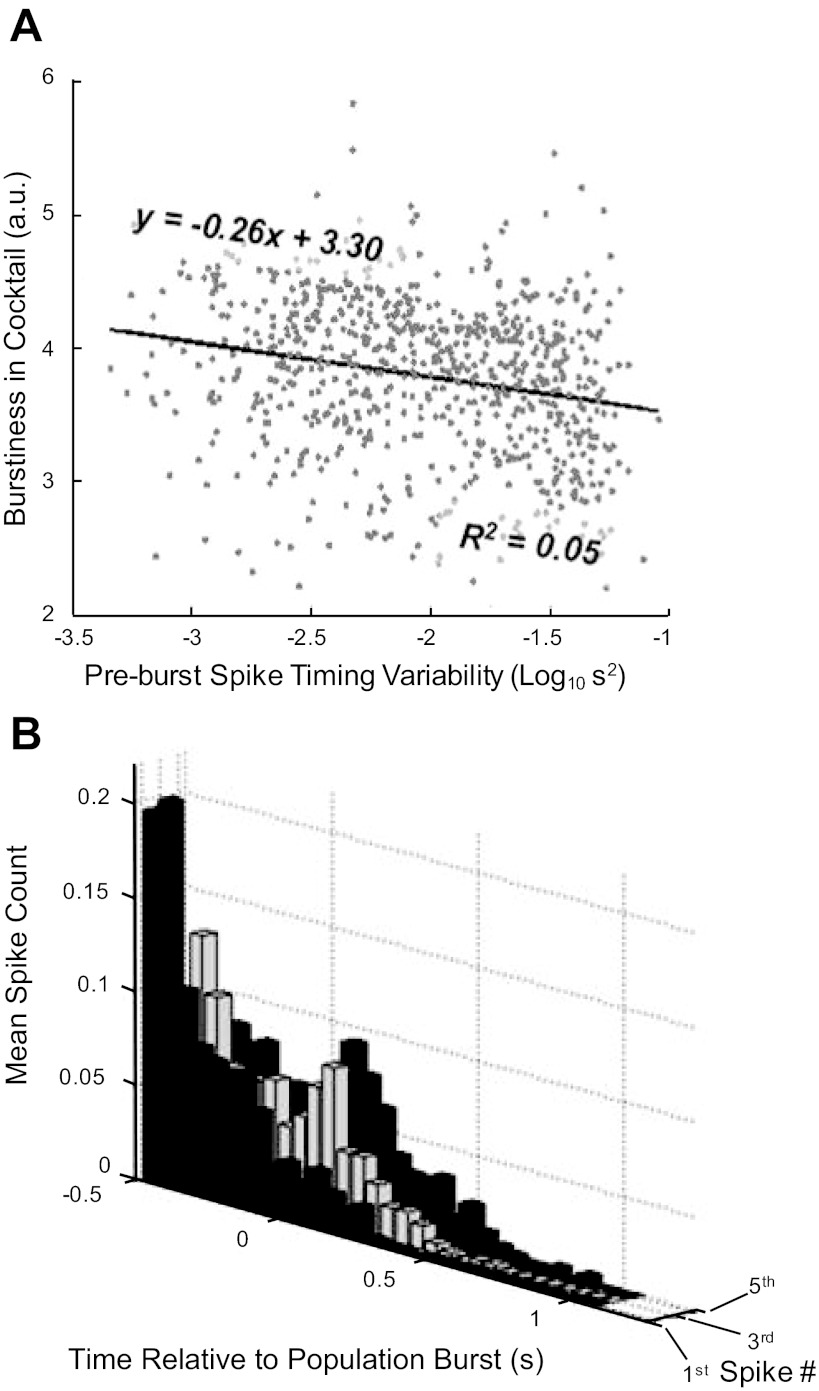
An alternative perspective on the variability in the identity of cells that spike in anticipation of the population burst is to look at the variability (jitter) of the mean spike time of each cell over all cycles. The variance in this timing (log₁₀ s²) showed a wide range of values and was very weakly (although significantly) and negatively correlated with the tendency of the cell to show intrinsic rhythmicity in subsequent synaptic block (Fig. 5A; Kendall tau = −0.16; P < 0.0001). As suggested above (Fig. 4B), even those cells that prove to be intrinsically rhythmic can show significant variability on a cycle-by-cycle basis. Figure 5B shows frequency histograms for periburst spike times for a randomly selected set of 10 cells which subsequently proved to be rhythmic in synaptic block. The first row shows the first spike times relative to the population burst onset, while the third and fifth spike times are shown in subsequent rows (Fig. 5B). From Fig. 5, it can be seen that even intrinsically rhythmic cells may fire their first spike in a cycle 200–300 ms after the onset of the population burst.

Fig. 5.

Burst onset timing is variable in individual neurons. Burst onset timing variability (A) is weakly, although significantly, anticorrelated with subsequent endogenous bursting (Kendall tau = −0,16; P < 0.0001). B: periburst first nth (for n = 1, 3, and 5; second axis) spike times for 10 randomly selected strong pacemakers confirms that burst onset in individual bursters can follow the population burst onset on many cycles.

Possible sources of cycle-by-cycle variability: simulation experiments.

Conductance-based network simulations were conducted to determine if connectivity profiles might account for the cycle-by-cycle variability seen in the in vitro experiments. Network simulations using a standard model with full connectivity failed to reproduce variability in population activity seen experimentally (Fig. 6A), but by increasing the size of the network while decreasing the probability of connections between cells (with a proportional increase in synaptic weight), population activity that mimicked experimental variability on several metrics could be generated (Fig. 6B). These sparsely connected networks also generated cycle-by-cycle variability at the single cell level that was similar in scale to that recorded in vitro (Fig. 6C). Other plausible sources of variability such as weak synaptic connections or membrane noise were simulated but either failed to generate the observed statistics or did so only at the expense of realistic constraints on other parameters (data not shown).

Fig. 6.

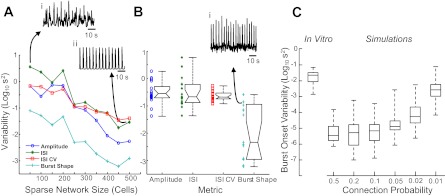
Population activity and single cell onset variability are dependent on network sparsity. A: 4 measures of variability in simulated population activity from sparsely connected (1% connection probability) networks of different sizes illustrate importance of larger networks in simulating physiological variability. Networks with only 50 cells produce overly irregular population rhythms (i) while networks with 500 units are unphysiologically regular (ii). B: same metrics applied to population recordings from 21 in vitro experiments (example in i) indicate that the simulation experiments shown in A reach similar levels of irregularity at population sizes of 200–300 cells. In 300-cell models, variability in single cell burst onset timing (C) with respect to the population burst varies with network sparsity and approaches mean levels from 21 in vitro experiments (left) only when the connection probability is near 1%.

DISCUSSION

In characterizing the role of intrinsically bursting pacemaker neurons in network oscillations, the simplistic opposition between network and pacemaker theories of rhythmogenesis has given way to more nuanced models that incorporate essential elements from both camps (Ramirez et al. 2004; Selverston 2010; Wang 2010). These models are well exemplified in the pre-BötC, a neuronal network critical for breathing (Ramirez et al. 2004; Feldman and Del Negro 2006). The data presented here indicate that the intrinsic rhythmic bursting of neurons in the pre-BötC can be predicted by the behavior of these cells during baseline conditions. Specifically, cells with higher mean firing rates in all phases of fictive respiration, with higher spike count variability across cycles and with more rapid burst onsets, are also likely to spike more in synaptic block conditions. However, other commonly assumed aspects of burst timing or shape were not predictive of pacemaker activity. Thus, contrary to the most straightforward model of pacemaker rhythmogenesis, the data presented here do not support an invariant role for preinspiratory activity on average or on a cycle-by-cycle basis in initiation network bursts (Rekling et al. 1996). Instead, preinspiratory spiking activity is profoundly variable for all neurons within the network, including those that prove to be capable of generating bursting pacemaker activity.

Indeed, approaching the question of burst onset from the point of view of simultaneously recorded neurons revealed a surprising degree of cycle-by-cycle variability both in the identity of neurons leading successive population bursts and in the timing jitter of spike patterns of individual neurons followed across many cycles. Together with the results of the above analysis of average burst-triggered firing rate functions, several conclusions are suggested. Neurons that fire robustly under control conditions are more likely to fire robustly during synaptic isolation. Neurons with more robust firing under these conditions will also be more likely to exhibit spiking behavior that is clustered into bursts, although this distinction is quantitative rather than categorical.

Although it is impossible to make mechanistic claims based on this extracellular evidence, this behavior is consistent with the hypothesis that neurons in this network are endowed with generally continuous distributions of membrane conductances that result in qualitatively graded firing behavior (Del Negro et al. 2002b; Purvis and Butera 2005; Koizumi and Smith 2008). The question of how conductance ratios are established is of considerable interest not only for the respiratory network but for neuronal networks in general (Hudson and Prinz 2010; Zhao et al. 2010; Temporal et al. 2012; Khorkova and Golowasch 2007; Brookings et al. 2012). Although particular combinations of conductances may interact in ways that produce dramatically discontinuous behavioral phenotypes, such discontinuities were not detected in our data. This may be a result of the limitations of the experimental approach used here, as other electrophysiological, immunohistochemical, and anatomical evidence may be more sensitive to such distinctions. Intracellular recording, for example, can reveal the membrane potential trajectory that underlies spiking behavior, revealing depolarization envelopes that help distinguish phasic bursting behavior from clusters of spikes riding on more placid membrane potential waveforms. On the other hand, intracellular recordings can be characterized by a strong selection bias (as discussed for example in Peña et al. 2004), perhaps leading to overly rigid categorical distinctions. Therefore, the detail of an intracellular recording comes at the expense of limiting the number of cells that can be recorded simultaneously (especially for long periods) as well as the types of neurons that can be directly compared in a simultaneous recording. Additionally, intracellular whole cell recording may also reduce the diversity of cellular behavior through dialysis of second messenger molecules and clamping of the intracellular calcium concentration.

The present finding of a high degree of burst onset timing variability, even among those cells subsequently confirmed as pacemakers, was in fact confirmed with intracellular data, suggesting that this phenomenon is not an artifact of the experimental methods used here. These data are inconsistent with models that have suggested that the onset timing of individual cells in each cycle is determined by their complement of intrinsic conductances and synaptic contacts, functioning as literal “pacemakers” on a cycle-by-cycle basis in rhythmically active networks. In contrast to that model, the stochastic assembly of rhythms from only sparsely synchronized individual neurons has also been recently emphasized as a more robust model for rhythmogenesis in the cortex (Wang 2010). The considerable cycle-by-cycle variability found in the pre-BötC is also consistent with the notion that excitatory synaptic interactions play a critical role in establishing the respiratory rhythm (Feldman and Del Negro 2006; Del Negro et al. 2010).

It must be emphasized that our findings are also consistent with recent results in invertebrate neuronal networks in which neurons are well identified. A large cycle-to-cycle variability was described, for example, in the well-defined Aplysia feeding network (Brezina et al. 2006; Horn et al. 2004; Lum et al. 2005). Indeed this variability caused a mismatch in some cycles between the animal's movement and the requirements of the feeding behavior, but it was found that this strategy was optimal in an uncertain and changing feeding environment (Brezina et al. 2006). Clearly, mammalian breathing is very similar, as it needs to have the flexibility to adjust to changes in metabolic, environmental, and behavioral conditions, including even the extremely complex demands of vocalization. Nonetheless, the Aplysia studies characterized variability at the behavioral level while our results point to variability at the level of component neurons in a network with a relatively regular output. Thus we conclude that it is the rhythm-generating mechanism that functions with a large onset variability, which may or may not result in an irregular behavioral output. As for breathing per se, we would expect that this behavior will not only be determined by the pre-BötC itself but in addition also by other central and peripheral components of the wider respiratory network.

Our data suggest that each population burst is a dynamic and stochastic assembly of diverse neurons, rather than an orderly recruitment beginning with the most intrinsically excitable and finally arousing the most recalcitrant. These data in fact suggest a more fluid role even for pacemakers, which here have been shown to anticipate (perhaps kindle) some population bursts, but also follow the onset of many others, possibly contributing to stability or providing nonlinear amplification. This is not to suggest that some cells might not participate more frequently in one of these roles than the other based on intrinsic or synaptic properties. In fact, previous research has established the existence in this network of two classes of pacemakers with distinct conductances and responses to neuromodulators that differentially affect the frequency, stability, and amplitude of network activity (Tryba and Ramirez 2003; Viemari and Ramirez 2006; Thoby-Brisson and Ramirez 2001; Peña et al. 2004). It is important to note that, in contrast to these earlier studies, the current experiments were performed at slightly higher (and presumably more physiological temperatures). The effect of temperature on the respiratory network containing the pre-BötC has been well characterized in two studies (Tryba and Ramirez 2003, 2004), where the network was found to be very sensitive to changes in temperature but not to differences in absolute steady-state temperature (Tryba and Ramirez 2003). This is very similar to the situation in response to hypoxia, where the network responds very sensitively to changes in oxygen levels but less robustly to absolute differences in the steady-state oxygen levels (Hill et al. 2011). Thus it is not very likely that the difference in steady-state temperature of 3–5° had a dramatic effect on the frequency of the overall network output. Interestingly, at the cellular level it was also demonstrated that transient increases in temperature resulted in increased burst frequency of bursting pacemaker neurons, while the discharge of tonically firing neurons was not affected as much (Tryba and Ramirez 2003, 2004). These studies also demonstrated that at more physiological temperatures some nonbursting, tonically spiking neurons turned into bursting neurons. Thus, while it is conceivable that the number of bursting pacemaker neurons may be somewhat higher in our study compared with in vitro studies performed at lower temperature, it must be emphasized that none of these differences would be considered to be less physiological than our prior in vitro studies. Also, while a 3–5° difference in steady-state temperature may have some minor network affects, it seems very unlikely that our principle findings would be different. We thus conclude that the emerging picture of respiratory rhythm generation indicated by our data is suggestive of the dynamic and flexible role bursting neurons are thought to also play in cortical networks (Wang 2010).

Indeed, the single-cell and network variability seen in these in vitro data is difficult to reconcile with previous computational models of this network (Rybak et al. 1997a,b,c; Butera et al. 1999a,b; Del Negro et al. 2001; Shevtsova et al. 2003). While these models have generated population behavior with a high fidelity to many experimental results, as well as generating a rich diversity of new hypotheses, they have tended to produce activity that is much more rigidly deterministic and regular than that from the multicellular in vitro recordings presented here. We hypothesized that activity with more physiological variability could be generated with such models if the connectivity profile were modified. Thus while previous models have typically used networks with full cell-to-cell connectivity (although some have mentioned similar findings in more sparsely coupled network, these have not been presented in detail), we simulated networks with decidedly sparse interconnectivity, where each cell only had a 1% chance of connecting with another cell in the network. To generate stable global rhythms, larger populations of cells were required for these networks, and by comparing the variability of population activity seen in simulated sparse networks of varied sizes with that of in vitro networks, a Goldilocks network size of 300 cells was found to produce population rhythms with a just right level of variability by comparison with in vitro data. This population size is surprisingly consistent with estimates of the population size of the rhythmogenic network in situ (Rekling et al. 2000; Gray et al. 2001; Hayes and Del Negro 2007). Indeed, a recent study demonstrated that not only the frequency but also the regularity of the respiratory rhythm was directly related to the number of active respiratory neurons within the pre-BötC (Hayes et al. 2012). This study estimated that the pre-BötC was comprised of 650 neurons. The authors also assumed that half of these neurons were inhibitory, which would suggest 325 excitatory neurons, which is very consistent with our computer model. Furthermore, simulations that attempt to reproduce the observed variability in fully connected networks fail to do so under physiologically reasonable assumptions.

Our simulation results therefore suggests that sparse network connectivity is a plausible architecture to produce the dynamic and stochastic assemblies of cells seen in the multicellular data presented here. These networks not only qualitatively reproduced the patterns seen in spike rasters from in vitro networks; quantitative analysis of burst onset variability in these networks shows that variability increases monotonically with increased sparseness until it reaches experimental levels at 1% connectivity. The degree of sparseness necessary in our simulations is indeed dramatically smaller than that reported (3/23; 13%) in what we believe is the only published paired whole-cell data from the pre-BötC (Rekling et al. 2000). However, there is some evidence that, in our hands at least, the pre-BötC is far less densely interconnected. Cross-correlation analysis from pairs of 10,778 cells in the multicellular experiments described here produced a connectivity probability of only 1.0%. The reason for the discrepancy between this and previous findings remains unclear but, considering the distinctness of the methods and preparations, is not all that surprising. It may also be that more moderate degrees of sparsity could exist in vivo but interact with other intrinsic or topological features to produce the variability described here. Alternatively, recent anatomical evidence from a slice culture preparation has been presented suggesting that the pre-BötC may be connected in a relatively complex topology that combines clusters of more densely coupled neurons with sparse intercluster connections (Hartelt et al. 2008). It remains unclear whether such a topology is functionally active in other preparations, or whether such a connectivity structure could produce the features of population activity identified in the current study.

The suggestion that the dynamics of rhythmical active networks might be nontrivially influenced by network topology will not come as a surprise to those familiar with recent interest in a broad range of complex networks (Watts and Strogatz 1998; Barabási and Albert 1999). The findings presented here indicate a view of breath-to-breath respiratory rhythm generation that is dynamic and stochastic, involving the interaction of neurons with active membrane conductances embedded within networks of neurons connected by nontrivial topologies. Additional research will be required to determine whether these characteristics are present in more diverse rhythm generating circuits and how such characteristics may contribute to network robustness and flexibility.

GRANTS

This study was supported by grants from National Institutes of Health Grants R01HL-107084-01, RO1-HL/NS-60120, and P01-HL090544 Project 3.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: M.S.C. and J.-M.R. conception and design of research; M.S.C. performed experiments; M.S.C. analyzed data; M.S.C. and J.-M.R. interpreted results of experiments; M.S.C. prepared figures; M.S.C. drafted manuscript; M.S.C. and J.-M.R. edited and revised manuscript; M.S.C. and J.-M.R. approved final version of manuscript.

APPENDIX

Network model description.

The pre-BötC network in this study was simulated using single-cell models based on the Hodgkin-Huxley formalism. Each single-compartment cell included the following conductances: fast sodium (NaT), persistent sodium current (NaP), delayed rectifier potassium current (K), leak (L), and an excitatory synaptic (syn) conductance. Membrane potential was integrated over time (t) for each cell from the standard current-balance equation:

$$C\frac{dV}{dt}=-I_{NaT}-I_{NaP}-I_K-I_L-I_{syn}$$ (1)

where I_x, with x ∈ {NaT, NaP, K, L, syn} denote the whole cell current for each channel type and C is the cell capacitance. For these simulations, C = 36.2 pF. These ionic currents are determined as follows:

$$\begin{array}{c}{I}_{NaT}={\overline{g}}_{NaT}{m}_{NaT}^3{h}_{NaT}\left(V-E_{Na}\right)\\ I_{NaP}={\overline{g}}_{NaP}{m}_{NaP}{h}_{NaP}\left(V-E_{Na}\right)\\ I_K={\overline{g}}_K{m}^4\left(V-E_K\right)\\ I_L=g_L\left(V-E_L\right)\\ I_{syn}=g_{syn}\left(V-E_{syn}\right),\end{array}$$ (2)

where m_x (with x∈ {NaT, NaP, K}) are activation variables, h_x (with x∈ {NaT, NaP}) are inactivation variables, and maximal conductances are denoted ḡ_x for x∈ {NaT, NaP, K}, and whole cell leak and synaptic conductances are g_L and g_syn. Conductance values used in the present simulations included deterministic and Gaussian distributed values (in nS; means ± SD): ḡ_NaT = 150, ḡ_NaP = 4.0 ± 0.4, ḡ_K = 50.0 ± 5.0, and ḡ_L = 2.0 ± 0.2 (calculation of ḡ_syn is described below). The reversal potential values are as follows (in mV): E_Na = 60, E_K = −96, E_L = −76, and E_syn = 0. The kinetics of the in/activation variables were modeled in the traditional formalism based on voltage dependent functions for the steady-state and time constant in the dynamics equations:

$$\begin{array}{c}\frac{d{m}_x}{dt}=\frac{\left(m_{\infty x}\left(V\right)-m_x\right)}{{\tau }_{mx}\left(V\right)}\\ \frac{d{h}_x}{dt}=\frac{\left(h_{\infty x}\left(V\right)-h_x\right)}{{\tau }_{hx}\left(V\right)}\end{array}$$ (3)

where m_∞x(V) and h_∞x(V) denote the steady-state activation functions and τ_mx(V) and τ_hx(V) are the voltage dependent reaction rate functions. The steady-state activation sigmoid functions are parameterized by half-activation (V_1/2) and slope terms (σ) for the respective kinetic variables:

$$\begin{array}{c}{m}_{\infty x}\left(V\right)=\frac{1}{1+e^{-\left(V-V_{1/2mx}\right)/{\sigma }_{mx}}}\\ h_{\infty x}\left(V\right)=\frac{1}{1+e^{-\left(V-V_{1/2hx}\right)/{\sigma }_{hx}}}.\end{array}$$ (4)

For the current simulations, the fast sodium conductance defined (in mV) as: V_½mNaT = −43.8, V_½hNaT = −67.5, σ_mNaT = 6.0, and σ_hNaT = 10.8. Persistent sodium was modeled as: V_½mNaP = −47.1, V_½hNaP = −57.0, σ_mNaP = 3.1, and σ_hNaP = 3.0. The delayed rectifier potassium current was described by V_½mK = −44.5 and σ_mK = 5.0. Rate functions are similarly defined:

$$\begin{array}{c}{\tau }_{mx}\left(V\right)=\frac{{\overline{\tau }}_{mx}}{\cosh \left(\left(V-V_{1/2mx}\right)/{\sigma }_{\tau mx}\right)}\\ {\tau }_{hx}\left(V\right)=\frac{{\overline{\tau }}_{hx}}{\cosh \left(\left(V-V_{1/2hx}\right)/{\sigma }_{hx}\right)},\end{array}$$ (5)

with values: fast sodium, τ̄_mNaT = 0.9 ms, V_½mNaT = −43.8 mV, σ_τmNaT = 14.0, τ̄_hNaT = 35.2, V_½hNaT = −67.5, and σ_τhNaT = 12.8; persistent sodium, τ̄_mNaP = 0.9 ms, V_½mNaP = −47.1, σ_τmNaP = 6.2 mV, τ̄_hNaP = 20,000, V_½mNaP = −57.0 mV, and σ_τhNaP = 6 m V; potassium, τ̄_mK = 40.0 ms, V_½mK = −44.5, and σ_τmK = 10.0 mV. The reversal potential for the leak current was defined as E_L = −76.0 mV, derived from the standard Goldman equation with parameters [Na⁺]_in = 15 mM, [Na⁺]_out = 145 mM, [K⁺]_in = 140 mM, and [K⁺]_out = 9 mM, a Na⁺/K⁺ permeability ratio of 0.03, and a temperature of 308° Kelvin.

Network sizes of between 50 and 500 with either all-to-all or random sparse connectivity were simulated. The total synaptic conductance g_syn was calculated as a sum of a stochastically initialized tonic drive (0.12 ± 0.012 nS; means ± SD) with connections from other cells in the network. For fully connected 50-cell networks, these connections were modeled as a product of Gaussian distributed synaptic weights (0.2 ± 0.02) and a scaling parameter of 0.1 nS. For simulation with larger networks and sparser connectivity, synaptic parameters were adjusted to maintain the same mean synaptic conductance to each cell.