On Efficient Assessment of Image-Quality Metrics Based on Linear Model Observers

Abstract

This paper is motivated by the problem of image-quality assessment using model observers for the purpose of development and optimization of medical imaging systems. Specifically, we present a study regarding the estimation of the receiver operating characteristic (ROC) curve for the observer and associated summary measures. This study evaluates the statistical advantage that may be gained in ROC estimates of observer performance by assuming that the difference of the class means for the observer ratings is known. Such knowledge is frequently available in image-quality studies employing known-location lesion detection tasks together with linear model observers. The study is carried out by introducing parametric point and confidence interval estimators that incorporate a known difference of class means. An evaluation of the new estimators for the area under the ROC curve establishes that a large reduction in statistical variability can be achieved through incorporation of knowledge of the difference of class means. Namely, the mean 95% AUC confidence interval length can be as much as seven times smaller in some cases. We also examine how knowledge of the difference of class means can be advantageously used to compare the areas under two correlated ROC curves, and observe similar gains.

I. Introduction

OBJECTIVE, rigorous evaluations of image quality are a critical component of imaging system development and optimization. For this purpose, engineers have traditionally relied on image fidelity metrics that quantify resolution and noise, such as the modulation transfer function (MTF), noise power spectrum (NPS), pixel signal-to-noise ratio (pSNR), or noise equivalent quanta (NEQ). However, because such metrics require the restrictive assumptions of a shift-invariant imaging system and stationary noise [1], they do not reflect the full complexity of real medical scanners. Furthermore, the interpretation of image fidelity metrics can be problematic because they are not necessarily correlated with the ability of an observer to perform a task with the image. For these reasons, a task-based approach to image-quality assessment has been advocated in which image quality is measured by specifying 1) a task, 2) an observer, and 3) an objective figure of merit for observer performance [1]. Either human observers or numerical (computerized) observers, which are typically called model observers, may be considered. There is value in each, and the choice for a specific observer depends on the goal at hand [1]. As discussed in [2], model observers are valuable for system development and optimization, whereas human observers are suitable for final clinical validation. The results presented in this paper are motivated by the problem of system development and performance optimization with model observers; they are not applicable to image-quality assessment using human observers.

Observer performance for a binary classification task can be described by the receiver operating characteristic (ROC) curve and by associated ROC summary measures [1], [3], [4]. Since only a finite number of images is available for testing the observer, estimates of ROC figures of merit suffer from statistical variability. Of course, this variability decreases as more images are used, but there are few situations where the number of images is large enough to allow variability to be neglected. In particular, creating images with modern 3-D reconstruction algorithms requires significant computational effort, so that the number of images that can be reasonably produced (typically around 200) for an ROC study necessitates careful control of statistical variability. This issue becomes particularly prominent when there are many parameters for the reconstruction algorithm, since any change in these parameters requires reconstruction of new images. Hence, even for model observers, there is strong motivation to control and reduce statistical variability so that sufficient statistical power may be achieved in image-quality evaluations.

In many types of image-quality evaluations, knowledge of the difference of image class means is available. In particular, when simulated tomographic data is used, which is generally the case for early-stage evaluations, the image means can often be well-estimated by reconstructing the data means. This is clearly the case for linear reconstruction methods, such as those of the filtered backprojection (FBP) type. Furthermore, this is often a very good assumption for nonlinear iterative reconstruction methods such as expectation maximization (EM) [5], [6] and penalized-likelihood [7]. (In general, the accuracy with which image means can be estimated from the data means depends on the reconstruction algorithm, signals, and backgrounds of interest, e.g., strong signals are typically more difficult to estimate.) In addition to simulated-data scenarios, good estimates of the image means can also be obtained for some types of real-data experiments; see, e.g., [2], [8].

For linear model observers, knowledge of the difference of image class means translates into knowledge of the difference of class means for the rating data. Note that current approaches to ROC estimation from observer ratings do not take advantage of this information and are not readily modified to include it. For excellent overviews of the ROC estimation literature, the reader is referred to the books by Pepe [3], Krzanowski and Hand [4], Zhou et al. [9], and Zou et al. [10].

By contrast, the ROC estimators that we propose in this work take knowledge of the difference of class means for the observer ratings into account. We demonstrate that knowledge of this difference can be used to greatly reduce statistical variability in estimates of observer performance¹ and that confidence intervals with exactly-known coverage probabilities can be constructed.

To construct our new estimators, we assume that 1) the difference in class means for the observer ratings is known, 2) the observer ratings are normally distributed for each class of images, and 3) the variance of the observer ratings is the same for each class of images. The first assumption is the central hypothesis of this work, while the other two assumptions are made primarily to facilitate our investigation. From a practical perspective, these conditions are generally satisfied for linear model observers applied to the detection of small, low-contrast lesions at a known-location. Specifically, the first assumption is well-justified in many settings for linear observers, as discussed earlier. In addition, the second assumption is a good approximation for linear observers since reconstructed tomographic images are often approximately multivariate normal; see [11, Sec. 2.5] and references therein for a nice discussion of this issue in the context of nuclear medicine, and see [12, Appendix] for the case of X-ray CT. Furthermore, even for images that are not normally-distributed, the normality of ratings for a linear observer is often justified by the central limit theorem. The third assumption is well-justified, since the absence or presence of a small, low-contrast lesion has little impact on the image covariance matrix. As a consequence, the variance of ratings produced by a linear model observer at a fixed location is practically the same for each class of images; this observation has been made by Barrett and Myers [1, p. 1209] in the context of nuclear medicine and it was quantitatively analyzed in [13] for X-ray CT.

The present work can be viewed as an extension of the study in [14], which pertained to the estimation of ideal (perfectly trained) channelized Hotelling observer (CHO) performance with known difference of class means in channel space. Although powerful, the results in [14] have the limitation that they are not applicable to the assessment of non-prewhitening matched filter (NPMF) observers or to general finitely-trained linear observers with a fixed template. These important cases are addressed here by suitably generalizing the approach of [14] to deal directly with observer ratings.

The paper is organized as follows. After reviewing ROC curves and ROC figures of merit, we present our new point and confidence interval estimators. Subsequently, the new point and interval estimators for the area under the ROC curve (AUC) with known difference of class means are compared to two estimators that do not incorporate this knowledge. Specifically, the comparison is with a simple parametric estimator that is closely related to the maximum likelihood estimator (MLE), and with the nonparametric Mann-Whitney U estimator. Finally, we present an approximate confidence interval for a difference of AUC values. Our results consistently show that knowledge of the difference of class means offers a large advantage for statistical inference.

II. Image-Quality Metrics Based on Linear Observers

Recall that a task-based approach to image quality requires three ingredients: a task, an observer, and an objective figure of merit for observer performance [1]. The approach presented in this work pertains to any binary discrimination task at a fixed location in the image. Here, each image is to be classified as belonging to one of two image classes, denoted as class 1 and class 2. In a medical context, these image classes could correspond to normal and diseased conditions, respectively.

We assume that the observer is a linear model observer, defined by a fixed (nonrandom) template, w. For each image, p, the observer computes a rating statistic, t, defined as t=w^Tp, where p and w are written as N × 1 column vectors. To classify each image, the model observer compares t to a threshold, c. If t > c, then the observer concludes that the image is from class 2. Otherwise, the image is classified as belonging to class 1. Throughout this paper, we will denote the values of the rating statistic, t, for class-1 images as X and the values of the rating statistic for class-2 images as Y.

Flexibility in the choice of the observer template, w, represents an important aspect of image-quality metrics based on the performance of linear observers. Typical choices for the template, w, include both non-prewhitening and prewhitening matched filters, possibly with the use of channels [1]. However, because there are many possible ways to define the template, and because we wish to keep our discussion general, the question of how to choose w will not be addressed here.

For each threshold, c, the observer’s performance is fully characterized by two quantities, called the true positive fraction (TPF) and the false positive fraction (FPF) [1], [3]. The TPF is the probability that the observer correctly classifies a class-2 image as belonging to class 2, whereas the FPF is the probability that the observer incorrectly classifies a class-1 image as belonging to class 2. Since each value of results in a different TPF and FPF, observer performance over all thresholds is completely described by the curve of (FPF, TPF) values parameterized by . This curve is called the receiver operating characteristic (ROC) curve [1], [3]. To denote the TPF as a function of the FPF, we will write TPF(FPF).

As explained in the introduction, we assume that X and Y are normally distributed with equal variances, i.e., $X~\mathcal{N}(\mu ,{\sigma }^2)$ and $Y~\mathcal{N}(\nu ,{\sigma }^2)$. (If a random variable, U, follows a normal distribution with mean, μ, and variance, σ², we write $U~\mathcal{N}(\mu ,{\sigma }^2)$.) In this case, the ROC curve takes the form [3, Result 4.7, p. 82]

$$\text{TPF}\left(\text{FPF}\right)=\Phi (\text{SNR}+{\Phi }^{-1}\left(\text{FPF}\right))$$ (1)

where Φ(x) and Φ⁻¹(p) are the cumulative distribution function (cdf) and the inverse cdf, respectively, for the standard normal distribution, $\mathcal{N}(0,1)$, and

$$\text{SNR}=\frac{\delta }{\sigma }$$ (2)

is the observer signal-to-noise ratio with δ=ν–μ. For normally distributed ratings, SNR is a meaningful measure of the distance between the distributions of X and Y and is therefore a suitable metric for observer performance [1, p. 819]. (Note that the notion of observer SNR should not be confused with that of pixel SNR, which is not directly connected with observer performance.)

A widely-used figure of merit for observer performance is the area under the ROC curve, denoted as AUC. The AUC may be interpreted as the average TPF, averaged over the entire range of FPF values [3]. Under our distributional assumptions, the AUC takes the form [1, p. 819], [3, p. 84]

$$\text{AUC}=\Phi \left(\frac{\text{SNR}}{\sqrt{2}}\right).$$ (3)

In this work, we will always assume that δ=ν −μ > 0, so that SNR > 0 and 0.5 < AUC ≤ 1.

When only a restricted range of FPF values is considered relevant for observer performance, then the partial area under the ROC curve, defined as

$$\text{pAUC}({\text{FPF}}_a,{\text{FPF}}_b)={\int }_{{\text{FPF}}_a}^{{\text{FPF}}_b}\text{TPF}\left(\text{FPF}\right)d\left(\text{FPF}\right)$$ (4)

can be used as a summary measure [3]. The pAUC may be interpreted as the TPF averaged over the FPF values between FPF_a and FPF_b. Observe that under our assumptions for the ratings, TPF at fixed FPF, AUC, and pAUC are strictly increasing functions of SNR only. Later, we will take advantage of this property to construct our confidence interval estimators for TPF, AUC, and pAUC.

III. Point Estimation of SNR

Suppose that continuous-valued observer ratings are available for m class 1 images and n class 2 images, where either m or n can be zero. Denote these ratings for classes X₁, X₂, … X_m and Y₁, Y₂, … Y_n as and , respectively, and suppose that the observer ratings are independent and normally distributed with equal variances for each class, i.e., $X_i~\mathcal{N}(\mu ,{\sigma }^2)$ and $Y_j~\mathcal{N}(\nu ,{\sigma }^2)$. In this section, we introduce and characterize a point estimator for SNR for the case when δ is known and μ, ν, and σ² are unknown.²

Below, the sampling distribution for the SNR estimator will be described using the inverted gamma distribution, which is reviewed in Appendix A. If a random variable, X, follows an inverted gamma distribution with parameters α and β, we write X ~ IG(α, β). Also, we use the notational convention that if the upper limit on a summation is zero, then the summation is zero.

We start by defining unbiased estimators of μ and ν as

$$\tilde{X}=\frac{1}{m+n}\left[\sum _{i=1}^m{X}_i+\sum _{j=1}^n{Y}_j-n\delta \right]$$ (5)

and

$$\tilde{Y}=\frac{1}{m+n}\left[\sum _{i=1}^m{X}_i+\sum _{j=1}^n{Y}_j+m\delta \right].$$ (6)

Observe that when m and n are both nonzero, X̃ and Ỹ have lower variance than the conventional unbiased sample mean estimators, $\stackrel{‒}{X}=(1∕m){\sum }_{i=1}^m{X}_i$ and $\stackrel{‒}{Y}=(1∕n){\sum }_{j=1}^n{Y}_j$, respectively. This advantage is gained through the incorporation of δ. The above mean estimates can then be used to define the pooled variance estimator

$${\tilde{S}}^2=\frac{1}{m+n-1}\left[\sum _{i=1}^m{(X_i-\tilde{X})}^2+\sum _{j=1}^n{(Y_j-\tilde{Y})}^2\right].$$ (7)

Now, for m + n > 2, define the SNR estimator

$$\widehat{\text{SNR}}=\frac{\gamma \delta }{\tilde{S}}$$ (8)

with

$$\gamma =\frac{\sqrt{\frac{2\pi }{q}}}{B\left(\frac{q-1}{2},\frac{1}{2}\right)}$$ (9)

where q=m + n−1 and B(a, b) is the Euler Beta function. The multiplicative factor, γ, is chosen so that $\widehat{\text{SNR}}$ is unbiased. The sampling distribution and optimality of $\widehat{\text{SNR}}$ are characterized by the following theorem, which is proved in Appendix B.

Theorem 1: Let q=m + n−1 and suppose that δ is known and that μ, ν, and σ² are unknown. If $\widehat{\text{SNR}}$ is computed from independent samples $X_i~\mathcal{N}(\mu ,{\sigma }^2)$ and $Y_j~\mathcal{N}(\nu ,{\sigma }^2)$, where i=1,2, …, n with m ≥0, n ≥0, and q > 1, then

1. ${\left(\widehat{\text{SNR}}\right)}^2~IG(\alpha ,\beta )$ with α= q/2 and β=ηSNR², where η = qγ²/2

2. $\widehat{\text{SNR}}$ is the uniformly minimum variance unbiased (UMVU) estimator for SNR.

Hence, the sampling distribution of $\widehat{\text{SNR}}$ is simply related to the inverted gamma distribution, and $\widehat{\text{SNR}}$ is the minimum variance estimator among all unbiased estimators of SNR. Below, we state a corollary to Theorem 1, which is also proved in Appendix B.

Corollary 1: Let q=m + n−1, η=qγ²/2, and suppose that the hypotheses of the previous theorem are satisfied. If q > 2, then

$$\frac{\text{E}\left[\widehat{\text{SNR}}\right]}{\sqrt{\text{Var}\left[\widehat{\text{SNR}}\right]}}=\frac{1}{\sqrt{\frac{2\eta }{(q-2)}-1}}.$$

Corollary 1 shows that the ratio of the mean of $\widehat{\text{SNR}}$ to its standard deviation only depends on m and n. This property can be used to select sample sizes, without requiring the nominal SNR value.

Note that instead of assuming that δ is known, both μ and ν could be assumed to be known. From a practical viewpoint, requiring knowledge of μ and ν is significantly more constraining. Nevertheless, we have investigated the advantage that results from assuming that both and are known, as opposed to only knowing δ. Specifically, the properties of the following SNR estimator that incorporates both μ and ν were studied:

$$\widehat{\theta }=\frac{\gamma \delta }{\widehat{S}}$$ (10)

where γ is defined by (9) with q=m + n and

$${\widehat{S}}^2=\frac{1}{m+n}\left[\sum _{i=1}^m{(X_i-\mu )}^2+\sum _{j=1}^n{(Y_i-\nu )}^2\right].$$ (11)

It turns out that $\widehat{\theta }$ obeys a theorem identical to that given for $\widehat{\text{SNR}}$, except that the value of q must be replaced by m + n. Given the behavior of the inverted Gamma distribution (q plays a role similar to that of degrees of freedom for a χ² distribution), the statistical advantage resulting from incorporating knowledge of both μ and ν, as opposed to only δ, is very small. For this reason, we focus the development in this paper to the less constraining case of known δ.

IV. Confidence Intervals

Our knowledge of the sampling distribution for $\widehat{\text{SNR}}$ implies the next theorem, which enables us to compute confidence intervals for SNR, TPF(FPF), AUC, and pAUC with exact coverage probabilities; see Appendix C for a proof.

Theorem 2: Let q = m + n−1 and suppose that δ is known and that μ, ν, and σ² are unknown. Let ω₁, ω₂ ∈ (0, 1) be such that ω₁ + ω₂ = ω for some ω ∈ (0, 1), and let $V={\left(\widehat{\text{SNR}}\right)}^2$. If $\widehat{\text{SNR}}$ is computed from independent samples $X_i~\mathcal{N}(\mu ,{\sigma }^2)$ and $Y_j~\mathcal{N}(\nu ,{\sigma }^2)$, where i=1, 2, …, m, j=1, 2, …, n with m ≥ 0, n ≥ 0, and q > 1, then

1. For each observation v of V, there exist unique values β_L(v) and β_U(v) in (0, ∞) satisfying F_V(v; α, β_L(v))=1−ω₁ and F_V(v; α, β_U(v))=1−ω₂, where F_V(v; α, β) is the cumulative distribution function (cdf) of the inverted gamma distribution with α=q/2.

2. Let ${\text{SNR}}_L\left(V\right)=\sqrt{{\beta }_L\left(V\right)∕\eta }$ and ${\text{SNR}}_U\left(V\right)=\sqrt{{\beta }_U\left(V\right)∕\eta }$. Then the random intervals

   $$\begin{array}{cc}\hfill & [{\text{SNR}}_L\left(V\right),{\text{SNR}}_U\left(V\right)],\hfill \\ \hfill & [\text{TPF}(\text{FPF};{\text{SNR}}_L\left(V\right)),\text{TPF}(\text{FPF};{\text{SNR}}_U\left(V\right))],\hfill \\ \hfill & [\text{AUC}\left({\text{SNR}}_L\left(V\right)\right),\text{AUC}\left({\text{SNR}}_U\left(V\right)\right)],\text{and}\hfill \\ \hfill & [\text{pAUC}({\text{FPF}}_a,{\text{FPF}}_b;{\text{SNR}}_L\left(V\right)),\text{pAUC}({\text{FPF}}_a,{\text{FPF}}_b;{\text{SNR}}_U\left(V\right))]\hfill \end{array}$$

where the last three intervals are defined by substituting SNR_L(V) and SNR_U(V) for SNR in (1), (3), and (4), are exact 1 − ω confidence intervals for SNR, TPF(FPF), AUC, and pAUC(FPF_a FPF_b), respectively.

Hence, we can calculate a 1 − ω confidence interval for SNR and any strictly increasing transformation of it from a realization of $\widehat{\text{SNR}}$ by numerically solving the equations in Theorem 2(a) for β_L and β_U. Note that if ω₁=0, then β_L(v)=0 and if ω₂=0, then β_U(v)=∞. In either of these cases, the confidence interval defined is said to be one-sided. Otherwise, the interval is said to be two-sided [15].

We close this section by restating a theorem that we proved in [13], which is also applicable here. When our assumptions for the observer ratings are satisfied, it shows that a simultaneous 1−ω confidence band for the entire ROC curve can be constructed from a 1−ω confidence interval for SNR. Below, we denote the collection of points on the ROC curve as Ω_ROC={(FPF, TPF) : FPF ∈ [0, 1]}.

Theorem 3: Suppose that $X~\mathcal{N}(\mu ,{\sigma }^2)$ and that $Y~\mathcal{N}(\nu ,{\sigma }^2)$. Let [SNR_L, SNR_U] be a 1−ω confidence interval for SNR, and define the set

$${\widehat{\Omega }}_{\text{ROC}}=\{(\text{FPF},T):\text{FPF}\in [0,1]\text{and}T\in \mathcal{I}\}$$

where

$$\mathcal{I}=[\text{TPF}\left({\text{FPF SNR}}_L\right),\text{TPF}\left({\text{FPF SNR}}_U\right)].$$

Then ${\widehat{\Omega }}_{\text{ROC}}$ is a 1−ω confidence band for the ROC curve in the sense that, for any value of SNR, Ω_ROC is contained in ${\widehat{\Omega }}_{\text{ROC}}$ with probability 1−ω, i.e., $P({\Omega }_{\text{ROC}}\subset {\widehat{\Omega }}_{\text{ROC}})=1-\omega$.

The 1−ω confidence band defined in Theorem 3 is equivalent to the union over all FPF values of 1−ω confidence intervals for TPF. Such a construction of an exact confidence band is possible because the ROC curve is parameterized by only SNR when our assumptions are satisfied [13].

V. AUC Estimator Evaluations

To assess the performance of the estimators introduced in the previous section, we now present an evaluation of our new point and interval AUC estimators. For this evaluation, we do not consider any specific imaging scenario, but rather compute all quantities from exact theoretical expressions, presuming that our assumptions for the ratings are satisfied. Hence, no Monte Carlo simulation of ratings was necessary. Such an approach allows us to cover a wide number of scenarios, and is enabled by the fact that the distributions of all estimators considered in this section only depend on SNR, m and n.

A. AUC Point Estimators

We compared our new parametric AUC point estimator, $\widehat{\text{AUC}}=\Phi (\widehat{\text{SNR}}∕\sqrt{2})$, to two other AUC estimators that do not incorporate prior knowledge of δ. The first is the parametric plug-in estimator ${\widehat{\text{AUC}}}_p=\Phi ({\widehat{\text{SNR}}}_p∕\sqrt{2})$ with ${\widehat{\text{SNR}}}_p=(\stackrel{‒}{Y}-\stackrel{‒}{X})∕S$. Here, $\stackrel{‒}{X}=(1∕m){\sum }_{i=1}^m{X}_i$ and $\stackrel{‒}{Y}=(1∕n){\sum }_{j=1}^n{Y}_j$ are the usual sample means and $S^2=[{\sum }_{i=1}^m{(X_i-\stackrel{‒}{X})}^2+{\sum }_{j=1}^n{(Y_j-\stackrel{‒}{Y})}^2]∕(m+n-2)$ is the usual pooled sample variance. Hence, ${\widehat{\text{AUC}}}_p$ is closely related to the MLE for AUC when δ is unknown,³ and only differs from it by the normalization factor in the expression of S², as the MLE would use m + n instead of m + n−2. The second AUC estimator is the normalized Mann-Whitney U statistic, defined as

$${\widehat{\text{AUC}}}_{\text{MW}}=\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^{n}I(Y_j>X_i)$$ (12)

where $I\left(\mathcal{S}\right)=1$ if $\mathcal{S}$ is true and $I\left(\mathcal{S}\right)=0$ otherwise. The normalized Mann-Whitney U statistic is a widely-used, nonparametric, unbiased estimator of AUC [3], [4].

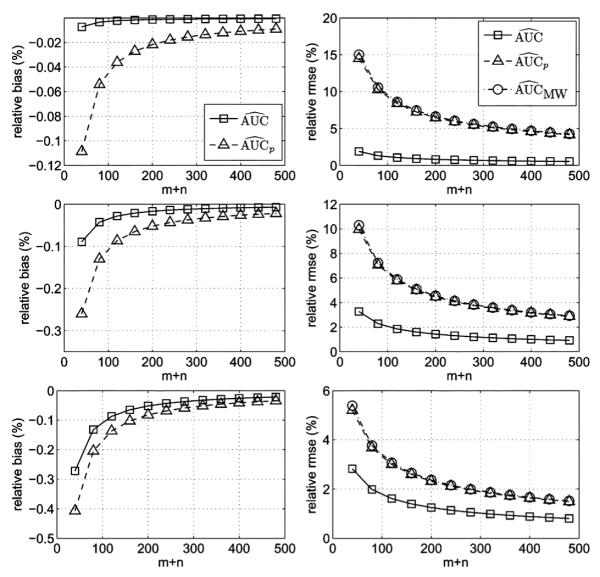
For our evaluations, we compared the relative bias and relative root-mean-square-error for true AUC values of 0.6, 0.75, and 0.9 with m=n. For each estimator, we computed the relative bias as $((\text{E}\left[\widehat{\text{AUC}}\right]-\text{AUC})∕\text{AUC})\times 100$ and the relative root-mean-square-error (rmse) as $(\sqrt{\text{mse}}∕\text{AUC})\times 100$, where mse is the estimator’s mean-square-error. All quantities were calculated numerically from exact analytical expressions, where the calculations for ${\widehat{\text{AUC}}}_p$ and ${\widehat{\text{AUC}}}_{\text{MW}}$ utilized observations made in [13] and [17], respectively. The results of our evaluations are shown in Fig. 1. Note that because ${\widehat{\text{AUC}}}_{\text{MW}}$ is unbiased, it is not included in the bias plots. From these plots, we see that our new AUC estimator, $\widehat{\text{AUC}}$, has a very small negative bias (less than 0.3%) and significantly better relative rmse than the estimators that do not incorporate knowledge of δ.

Fig. 1.

Plots of relative bias (left) and relative error (right) for AUC point estimators as a function of the total number of images, m + n, with m = n. The plots correspond to true AUC values of 0.6 (top), 0.75 (middle), and 0.9 (bottom).

B. AUC Confidence Intervals

Next, we compared the new AUC confidence interval based on $\widehat{\text{SNR}}$ to AUC confidence intervals based on ${\widehat{\text{SNR}}}_p$ and ${\widehat{\text{AUC}}}_{\text{MW}}$, respectively. The confidence intervals based on ${\widehat{\text{SNR}}}_p$ were computed as described in [13], and the confidence intervals based on ${\widehat{\text{AUC}}}_{\text{MW}}$ were calculated using method 5 of Newcombe, which was identified as a preferred approach [18].

The figure of merit for the AUC confidence interval comparison was the mean 95% confidence interval length (MCIL). For the intervals based on $\widehat{\text{SNR}}$ and ${\widehat{\text{SNR}}}_p$, we calculated the MCIL by numerically evaluating exact analytical expressions involving the sampling distributions. On the other hand, the MCIL for the intervals based on ${\widehat{\text{AUC}}}_{\text{MW}}$ was estimated from 50 000 Monte Carlo trials for each choice of the parameters, which gives an accuracy of ±0.0004.

The MCIL for the three AUC confidence interval estimators is plotted versus m + n in Fig. 2 with for m=n for AUC = 0.6, 0.75, and 0.9. The plots indicate that the $\widehat{\text{SNR}}-\text{based}$ estimator yields, on average, substantially shorter intervals than the estimators that do not incorporate knowledge of δ. For example, the plot for shows that with 100 images, the MCIL for the $\widehat{\text{SNR}}-\text{based}$ estimator is roughly 0.03, compared to approximately 0.21 for the other estimators. Fig. 2 (bottom right) contains plots of the ratio of the 95% MCIL for the ${\widehat{\text{SNR}}}_p-\text{based}$ intervals to the 95% MCIL for the $\widehat{\text{SNR}}-\text{based}$ intervals for AUC values of 0.6, 0.75, and 0.9. It can be seen that as the AUC value increases, the reduction in length realized by the $\widehat{\text{SNR}}-\text{based}$ intervals decreases. Nevertheless, even for , the MCIL for the $\widehat{\text{SNR}}-\text{based}$ intervals is smaller by a factor of almost two.

Fig. 2.

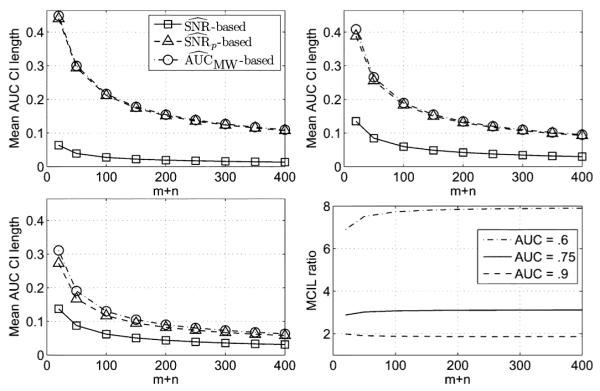
Mean 95% AUC confidence interval length plotted versus m + n with m = n and ω₁ = ω₂ = 0.025. The plots correspond to true AUC values of 0.6 (top left), 0.75 (top right), and 0.9 (bottom left). (bottom right) The ratio of the ${\widehat{\text{SNR}}}_p-\text{based}$ MCIL to the $\widehat{\text{SNR}}-\text{based}$ MCIL plotted versus m + n for AUC = 0.6, 0.75, and 0.9.

VI. Confidence Intervals for a Difference of auc Values

Typically, ROC analysis is used to compare two (or more) different imaging scenarios, whereas the confidence intervals discussed in the previous section only apply to the evaluation of a single imaging scenario. A simple approach to enable such a comparison is to invoke the Bonferroni inequality [19, p. 13] to build a rectangular confidence region for all involved AUC estimates. However, this approach is not optimal when a paired study design is considered, because it does not account for the possible reduction in variability when there is a positive correlation between AUC estimates. In this section, we discuss how to construct a confidence interval for a difference of two AUC values in a paired study design in the case where the difference between class means is known for the two underlying ROC curves. This confidence interval is approximate, but it is shown to be highly robust in terms of coverage probability, and to yield, like the intervals in the previous section, a strong statistical advantage.

A. Theory

Below, subscripts A and B will be used to denote quantities corresponding to scenarios A and B, respectively. For example, the AUC point estimator for scenario A will be written as ${\widehat{\text{AUC}}}_A$.

The difference in AUC values can be estimated as ${\widehat{\text{AUC}}}_A-{\widehat{\text{AUC}}}_B$. Assuming asymptotic normality of this difference, we can construct a 1 − ω Wald-style confidence interval for AUC_A – AUC_B as

$$\Delta \widehat{\text{AUC}}\pm {\Phi }^{-1}\left(1-\frac{\omega }{2}\right)\sqrt{\text{Var}\left(\Delta \widehat{\text{AUC}}\right)}$$ (13)

where $\Delta \widehat{\text{AUC}}={\widehat{\text{AUC}}}_A-{\widehat{\text{AUC}}}_B$.

Now, it is necessary to estimate

$$\text{Var}\left(\Delta \widehat{AUC}\right)=\text{Var}\left({\widehat{\text{AUC}}}_A\right)+\text{Var}\left({\widehat{\text{AUC}}}_B\right)-2\text{Cov}({\widehat{\text{AUC}}}_A,{\widehat{\text{AUC}}}_B).$$ (14)

As shown in Appendix E, the delta method (first-order Taylor approximations) can be used to derive the approximate expressions

$$\text{Var}\left({\widehat{\text{AUC}}}_A\right)\approx \left(\frac{1}{2}\right){\left[\varphi \left(\frac{{\text{SNR}}_A}{\sqrt{2}}\right)\right]}^2\text{Var}\left({\widehat{\text{SNR}}}_A\right)$$ (15)

$$\text{Var}\left({\widehat{\text{AUC}}}_B\right)\approx \left(\frac{1}{2}\right){\left[\varphi \left(\frac{{\text{SNR}}_B}{\sqrt{2}}\right)\right]}^2\text{Var}\left({\widehat{\text{SNR}}}_B\right)$$ (16)

$$\text{Cov}({\widehat{\text{AUC}}}_A,{\widehat{\text{AUC}}}_B)\approx \left(\frac{1}{2}\right)\varphi \left(\frac{{\text{SNR}}_A}{\sqrt{2}}\right)\times \varphi \left(\frac{{\text{SNR}}_B}{\sqrt{2}}\right)\text{Cov}({\widehat{\text{SNR}}}_A,{\widehat{\text{SNR}}}_B)$$ (17)

where ϕ(z)denotes the standard normal, $\mathcal{N}(0,1)$, probability density function (pdf). The coefficients in these expressions can be estimated by substituting ${\widehat{\text{SNR}}}_A$ and ${\widehat{\text{SNR}}}_B$ for SNR_A and SNR_B, respectively. Estimators for $\text{Var}\left({\widehat{\text{SNR}}}_A\right)$, $\text{Var}\left({\widehat{\text{SNR}}}_B\right)$, and $\text{Var}({\widehat{\text{SNR}}}_A,{\widehat{\text{SNR}}}_B)$ are discussed next.

Denote the class 1 and class 2 observer ratings for scenarios A and B with the vectors X = [X_A, X_B]^T and Y = [Y_A, Y_B]^T, respectively. Suppose that these ratings each follow bivariate normal distributions, i.e., $\mathbf{X}~{\mathcal{N}}_2(\mu ,\Sigma )$ and $\mathbf{Y}~{\mathcal{N}}_2(\nu ,\Sigma )$ with mean vectors $\mu ={[{\mu }_A,{\mu }_B]}^T$ and $\nu ={[{\nu }_A,{\nu }_B]}^T$, and common covariance matrix

$$\Sigma =\left[\begin{array}{cc}\hfill {\sigma }_A^2\hfill & \hfill \rho {\sigma }_A{\sigma }_B\hfill \\ \hfill \rho {\sigma }_A{\sigma }_B\hfill & \hfill {\sigma }_B^2\hfill \end{array}\right].$$ (18)

For each scenario, suppose that the observer rates m class 1 and n class 2 images. From the above distributional assumptions, it follows that (see Appendix E)

$$\text{Var}\left({\widehat{\text{SNR}}}_A\right)=\left[\frac{2\eta }{(q-2)}-1\right]{\text{SNR}}_A^2$$ (19)

$$\text{Var}\left({\widehat{\text{SNR}}}_B\right)=\left[\frac{2\eta }{(q-2)}-1\right]{\text{SNR}}_B^2$$ (20)

$$\text{Cov}({\widehat{\text{SNR}}}_A,{\widehat{\text{SNR}}}_B)=\left[{}_{2}F_1\left(\frac{1}{2},\frac{1}{2},\frac{q}{2};{\rho }^2\right)-1\right]\times {\text{SNR}}_A{\text{SNR}}_B$$ (21)

where q=m + n−1 is the degrees of freedom and ${}_{2}F_1$ is the Gaussian hypergeometric function. A MATLAB® function for ${}_{2}F_1(1∕2,1∕2;q∕2;{\rho }^2)$ is provided in Appendix E. The expressions in (19)–(21) are exact. We can estimate these quantities by substituting ${\widehat{\text{SNR}}}_A$ and ${\widehat{\text{SNR}}}_B$ for SNR_A and SNR_B, respectively, and by estimating ρ. To estimate the correlation coefficient, ρ, we define an unbiased covariance estimator, similar to S̃, as

$${\tilde{S}}_{AB}=\frac{1}{m+n-1}\left[\sum _{i=1}^m(X_{A,i}-{\tilde{X}}_A)(X_{B,i}-{\tilde{X}}_B)+\sum _{j=1}^n(Y_{A,j}-{\tilde{Y}}_A)(Y_{B,j}-{\tilde{Y}}_B)\right].$$ (22)

The correlation coefficient can then be estimated with

$$r=\frac{{\tilde{S}}_{AB}}{{\tilde{S}}_A{\tilde{S}}_B}.$$ (23)

B. Evaluations

We carried out Monte Carlo simulations to evaluate the coverage probability and mean confidence interval length (MCIL) for the approximate confidence intervals introduced in the last subsection. For purposes of comparison, we also assessed these metrics for Wald-style confidence intervals based on the Mann-Whitney U statistic employing the variance-covariance estimators of DeLong et al. [20]; see [3, p. 108] for further details on these intervals.

The results of our evaluation for several choices of the parameters m, n, AUC_A, AUC_B, and ρ are listed in Table I for the case of 95% confidence intervals (ω = 0.05). The coverage probabilities and MCILs in this table were estimated from 10 million Monte Carlo trials for each combination of parameters. Conservative 95% confidence bounds for each coverage probability can be obtained by adding and subtracting 0.014 to/from each point estimate (expressed in %), respectively. The estimates in Table I indicate that the coverage probability of the known-δ approach is more reliable than the Mann-Whitney-based intervals for small values of m and n. Moreover, a significant advantage in MCIL is observed for the known-δ estimator in all cases.

TABLE I.

Coverage Probabilities and Mean Confidence Interval Lengths Corresponding to 95% Confidence Intervals for AUC_A – AUC_B.The Table Compares Confidence Intervals Based on the Mann-Whitney Statistic (MW) to Intervals Based on $\widehat{\text{SNR}}$. All Coverage Probabilities are Expressed in %

m	n	AUCA	AUCB	ρ	CPmw	${\text{CP}}_{\widehat{\text{SNR}}}$	MCILmw	${\text{MCIL}}_{\widehat{\text{SNR}}}$	${\text{MCIL}}_{\text{MW}}∕{\text{MCIl}}_{\widehat{\text{SNR}}}$
10	10	0.80	0.90	0.90	90.56	95.60	0.248	0.100	2.48
20	20	0.60	0.55	0.90	96.02	94.96	0.187	0.030	6.21
25	15	0.80	0.90	0.90	92.90	95.31	0.168	0.066	2.54
50	50	0.55	0.60	0.80	95.27	94.99	0.151	0.022	6.99
50	50	0.90	0.80	0.70	94.67	95.02	0.136	0.066	2.07
50	50	0.80	0.90	0.99	95.22	95.52	0.073	0.014	5.26
50	50	0.90	0.95	0.90	93.43	94.92	0.070	0.037	1.87
50	100	0.80	0.70	0.70	94.96	95.01	0.138	0.050	2.78
100	100	0.70	0.80	0.70	95.05	95.02	0.112	0.043	2.62
100	100	0.55	0.60	0.90	95.28	94.99	0.076	0.013	5.96
100	100	0.80	0.90	0.80	94.77	95.02	0.083	0.039	2.14
125	75	0.90	0.95	0.70	94.50	95.01	0.070	0.041	1.72

The results of a more comprehensive evaluation of the coverage probability for the known-δ intervals are shown in Fig. 3 for m = n= 50 with ω = 0.05. This figure illustrates how the coverage probabilities change as ρ varies. Namely, for ρ = 0.55, 0.65, 0.75, 0.85, and 0.95, box plots are given to summarize the estimated coverage probabilities for 81 combinations of AUC values, with AUC_A, AUC_B ∈ {0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90, 0.95}. Each coverage probability was estimated from 1 million Monte Carlo trials to obtain an accuracy of ±0.05%. The box plots were each generated with the MATLAB® command boxplot. To interpret the plots, note that the edges of each box are the 25% and 75% percentiles, and the horizontal line inside the box is the median. The length of each whisker is 1.5 times the distance between the 75% and 25% percentiles, and data points outside this range are plotted individually.

Fig. 3.

Box plots displaying the estimated coverage probability of approximate 95% confidence intervals for AUC_A – AUC_B with m = n = 50. Each box plot corresponds to one value of ρ, and summarizes the coverage probability for 81 combinations of AUC values, with AUC_A, AUC_B ∈ {0.55, 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90, 0.95}.

From these plots, we see that the coverage probabilities for the known-δ intervals are generally very reliable. The most extreme outliers in each plot correspond to cases for which either AUC_A = 0.95 or AUC_B = 0.95. In these situations, the normality assumption on the difference of AUC estimates is likely not well-satisfied.

VII. Discussion and Conclusions

In this work, we investigated the reduction in statistical variability that may be gained in ROC estimates by using knowledge of δ, the difference of the class means for the observer ratings. To execute our investigation, we introduced parametric point and confidence interval ROC estimators that incorporate knowledge of δ. For the case of AUC estimation, we compared the performance of our known-δ point and interval estimators to parametric and nonparametric estimators that do not utilize knowledge of δ. This evaluation demonstrated that the known-δ estimators introduced here are much more powerful than estimators that do not incorporate knowledge of δ. For example, the mean length of the known-δ 95% AUC confidence intervals can be as much as seven times smaller than it is for approaches that do not use knowledge of δ; see Fig. 2 (bottom right).

In the definition of our point estimator for SNR, we included a multiplicative factor, γ, to make it unbiased (and hence, a UMVU estimator). Although it is not immediately obvious from our expressions, it is easy to show that our confidence interval estimators do not depend on γ. Also, it can be seen that as m and n increase, γ rapidly approaches one. Therefore, for large m and n, our SNR point estimator is essentially the same as the maximum likelihood estimator (MLE) for SNR when δ is known. As a consequence of the invariance property of MLEs [19, p. 320], our point estimators for TPF, AUC, and pAUC are therefore asymptotically equivalent to the MLEs for these quantities. Hence, because MLEs are asymptotically efficient [19, p. 472], our point estimators for TPF, AUC, and pAUC will also be asymptotically efficient.

After evaluating the known-δ confidence intervals for a single AUC value, we introduced an approximate confidence interval for the difference of two AUC values that utilizes knowledge of δ. An evaluation of this interval estimator demonstrated robustness as well as much better coverage probability and mean confidence interval length than intervals based on the Mann-Whitney U statistic employing the DeLong variance-covariance estimator.

The known-δ estimators introduced here rely on three assumptions. Namely, they require that 1) the difference in class means for the observer ratings is known, 2) the observer ratings are normally distributed for each class of images, and 3) the variance of the observer ratings is the same for each class of images. As discussed in the introduction, these assumptions are well-satisfied in many imaging contexts for linear observers applied to known-location discrimination tasks. Examples of such tasks include those with variable background [2], [21]–[23]. In addition to lesion detection tasks, detection of contrast/tracer uptake variations [24] also appears amenable to our assumptions. In a future work, we will report on the robustness of our estimation theory for application to X-ray CT image-quality evaluation.

We have demonstrated that large statistical advantages can be realized by parametric ROC estimators that incorporate knowledge of δ. Extension of the known-δ concept to more complex image-quality studies and to more general ROC estimators does not appear to be trivial. Nonetheless, any such extension could potentially be of great value for image-quality assessment.

Appendix A

In this appendix, we review the inverted gamma distribution and some of its properties that are needed in the paper.

The inverted gamma distribution originates as the distribution of the reciprocal of a gamma random variable. It has two positive parameters, α and β, called the shape and the scale parameters, respectively. A random variable U is said to have an inverted gamma distribution if its pdf takes the form [25]

$$f_U\left(u\right)=\frac{{\beta }^{\alpha }{e}^{-\beta ∕u}}{\Gamma \left(\alpha \right)u^{\alpha +1}}$$ (24)

when u > 0, and f_U(u) otherwise. Above, Γ(x) is the Gamma function. If U is an inverted gamma random variable with parameters α and β, we write U ~ IG(α, β). The mean of such an inverted gamma random variable is easily shown to be [25]

$$E\left[U\right]=\frac{\beta }{\alpha -1},\text{for}\alpha >1.$$ (25)

An important special case of the inverted gamma distribution is the inverted χ² distribution. Specifically, it can be shown that the reciprocal of a χ² random variable with ν degrees of freedom is an inverted gamma random variable with α=ν/2 and β=1/2.

Our proof of Theorem 1 in Appendix B requires the next two results regarding the inverted gamma distribution.

Lemma 1: Let c > 0 be an arbitrary constant. If U ~ IG(α, β) and V = cU, then V ~ IG(α, cβ).

Proof: See [14, Lemma 7].

Lemma 2: Suppose that U ~ IF(α, β) with α > 1/2 and let $V=\sqrt{U}$. Then $\text{E}\left[V\right]=\sqrt{\beta ∕\pi }B(\alpha -1∕2,1∕2)$, where B(a, b) is the Euler Beta function.

Proof: Since $V=\sqrt{U}$ is a strictly increasing function, we can use the monotonic transformation theorem for random variables [19, p. 51, Theorem 2.1.5] together with (24) to write the pdf of V as

$$f_V\left(v\right)=\frac{2{\beta }^{\alpha }{e}^{-\beta ∕v^2}}{\Gamma \left(\alpha \right)v^{2\alpha +1}}$$ (26)

when v > 0 and f_V(v) = 0 otherwise. Hence, the expected value of V is

$$E\left[V\right]={\int }_0^{\infty }v\frac{2{\beta }^{\alpha }{e}^{-\beta ∕v^2}}{\Gamma \left(\alpha \right)v^{2\alpha +1}}dv.$$ (27)

Performing the change of variable z=1/v, (27) becomes

$$E\left[V\right]=\frac{2{\beta }^{\alpha }}{\Gamma \left(\alpha \right)}{\int }_0^{\infty }{z}^{2\alpha -2}{e}^{-\beta z^2}dz$$ (28)

$$=\frac{{\beta }^{1∕2}\Gamma (\alpha -\frac{1}{2})}{\Gamma \left(\alpha \right)}$$ (29)

where we applied a standard formula [26, 18.76, p. 109], in the last step.

Using the relation B(a, b) = Γ(a)Γ(b)/Γ(a+b) between the Euler Beta function and the Gamma function and the fact that $\Gamma (1∕2)=\sqrt{\pi }$, (29) may be rewritten as $\text{E}\left[V\right]=\sqrt{\beta ∕\pi }B(\alpha -1∕2,1∕2)$.

It is straightforward to show that the cdf for the inverted gamma distribution is

$$F_U(u;\alpha ,\beta )=\frac{\Gamma \left(\alpha ,\frac{\beta }{u}\right)}{\Gamma \left(\alpha \right)}$$ (30)

where Γ(x, y) is the upper incomplete gamma function. In MATLAB®, the function gammainc can be used to evaluate the inverted gamma cdf as F_U(u; α, β) = gammainc(β/u, α, “upper”).

For our proof of Theorem 2 in Appendix C, we will need the following lemma, which expresses a useful property of the inverted gamma cdf.

Lemma 3: Suppose that U ~ IG(α, β). Then at arbitrary fixed values of u and α, the cdf of U, F_U(u; α, β), is a continuous, strictly decreasing function of β.

Proof: Although this property seems like it should be well-known, we could not find any proof of it in the literature. One way to prove it is as follows.

Suppose that and are fixed quantities, and define g(β) = F_U(u; α, β). By (30), g(β) may be written as

$$g\left(\beta \right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_{\beta ∕u}^{\infty }{t}^{\alpha -1}{e}^{-t}dt.$$ (31)

It follows from (31) and the theorem on absolute continuity for the Lebesgue integral [27, p. 141], that g(β) is continuous. In addition, since β > 0 and u > 0, the integrand in (31) is strictly positive. Hence, (31) implies that g(β) is a strictly decreasing function of β.

Appendix B

Now, we prove Theorem 1 and Corollary 1, which characterize $\widehat{\text{SNR}}$. We use the notational convention that a summation is zero if its upper limit is zero. Also, recall that q = m + n − 1.

Proof of Theorem 1(a): Let $\stackrel{‒}{X}=(1∕m){\sum }_{i=1}^m{X}_i$ and $\stackrel{‒}{Y}=(1∕n){\sum }_{j=1}^n{Y}_j$ be the sample means for class 1 and class 2, respectively. Here, we use the convention that X̄ = 0 if m = 0 and Ȳ = 0 if n = 0 .

From the definition of S̃², we have

$$q{\tilde{S}}^2=\sum _{i=1}^m{(X_i-\tilde{X})}^2+\sum _{j=1}^n{(Y_i-\tilde{Y})}^2.$$ (32)

Substituting (X_i − X̄ + X̄ − X̃) for (X_i − X̃) and (Y_i − Ȳ + Ȳ − Ỹ) for (Y_j − Ỹ) in (32) and rearranging yields

$$q{\tilde{S}}^2=\sum _{i=1}^m{(X_i-\stackrel{‒}{X})}^2+\sum _{j=1}^n{(Y_j-\stackrel{‒}{Y})}^2+m{(\stackrel{‒}{X}-\tilde{X})}^2+n{(\stackrel{‒}{Y}-\tilde{Y})}^2.$$ (33)

Inserting the definitions of X̃ and Ỹ into (33), simplifying, and dividing by σ² on both sides, we get

$$\frac{q{\tilde{S}}^2}{{\sigma }^2}=\left(\frac{1}{{\sigma }^2}\right)\sum _{i=1}^m{(X_i-\stackrel{‒}{X})}^2+\left(\frac{1}{{\sigma }^2}\right)\sum _{j=1}^n{(Y_j-\stackrel{‒}{Y})}^2+\left(\frac{mn}{m+n}\right)\left(\frac{1}{{\sigma }^2}\right){(\stackrel{‒}{Y}-\stackrel{‒}{X}-\delta )}^2.$$ (34)

By a standard result [19, Theorem 5.3.1(c), p. 218] for the distribution of the sample variance, the first and second terms on the right side of (34) are distributed as ${\chi }_{m-1}^2$ and ${\chi }_{n-1}^2$ random variables, respectively. In addition, it is easy to see that $\sqrt{mn∕(m+n)}(\stackrel{‒}{Y}-\stackrel{‒}{X}-\delta )∕\sigma ~\mathcal{N}(0,1)$. Hence, the third term in (34) is distributed as a ${\chi }_1^2$ random variable. Since the class-1 samples are independent of the class-2 samples, and since X̄ and Ȳ are independent of the first and second terms, respectively [19, Theorem 5.3.1(a), p. 218], it follows that all three terms in (34) are independent. Thus, $q{\tilde{S}}^2∕{\sigma }^2~{\chi }_q^2$. Applying the relationship between the inverted distribution and the inverted gamma distribution (see Appendix A), we have $1∕[q{\tilde{S}}^2∕{\sigma }^2]~IG(q∕2,1∕2)$. Next, observe that

$${\left(\widehat{\text{SNR}}\right)}^2=q{\gamma }^2\frac{{\delta }^2}{q{\tilde{S}}^2}\frac{{\sigma }^2}{{\sigma }^2}=\frac{2\eta {\text{SNR}}^2}{q{\tilde{S}}^2∕{\sigma }^2}$$ (35)

where η=qγ²/2. Thus, Lemma 1 implies that ${\left({\widehat{\text{SNR}}}_2\right)}^2~IG(\alpha ,\beta )$ with α=q/2 and β = ηSNR².

Proof of Theorem 1(b): For notational simplicity, denote the class-1 and class-2 samples with the (random) vectors X = [X₁, X₂, … X_m]^T and Y = [Y₁, Y₂, … Y_n]^T. Also, write realizations of these vectors as x = [x₁, x₂, … x_m]^T and y = [y₁, y₂, … y_n]^T, respectively. Below, we denote the statistics X̃, Ỹ, and as defined by (5)–(7) with x̃, ỹ, and s̃, respectively, when evaluated at x and y.

From Theorem 1(a), Lemma 2, and (9), it follows that $E\left[\widehat{\text{SNR}}\right]=\text{SNR}$, i.e., $\widehat{\text{SNR}}$ is an unbiased estimator of SNR. The joint pdf of the sample is

$$f(\mathbf{x},\mathbf{y})={\left(2\pi \right)}^{-(m+n)∕2}{\sigma }^{-(m+n)}\exp \left[-\frac{1}{2{\sigma }^2}\times \left(\sum _{i=1}^m{(x_i-\mu )}^2+\sum _{j=1}^n{(y_j-\nu )}^2\right)\right].$$ (36)

After lengthy algebra, (36) can be rewritten as

$$f(\mathbf{x},\mathbf{y})={\left(2\pi \right)}^{-(m+n)∕2}{\sigma }^{-(m+n)}\exp \left[-\frac{1}{2{\sigma }^2(m+n)}\times ({\mu }^2-2\mu \tilde{x}+(m+n)(m+n-1){\tilde{s}}^2+{\tilde{x}}^2)\right].$$ (37)

Define the vector

$$T(\mathbf{x},\mathbf{y})=\left[\begin{array}{c}\hfill \tilde{x}\hfill \\ \hfill (m+n)(m+n-1){\tilde{s}}^2+{\tilde{x}}^2\hfill \end{array}\right].$$ (38)

So (37) can be written in the form

$$f(\mathbf{x},\mathbf{y})={\left(2\pi \right)}^{-(m+n)∕2}{\sigma }^{-(m+n)}\times \exp \left[-\frac{{\mu }^2-\left(2\mu \right)T\left(1\right)+T\left(2\right)}{2{\sigma }^2(m+n)}\right].$$ (39)

By the Fisher-Neyman factorization theorem [28, Thm. 6.5, p. 35], [29, Prop. IV.C.1, p. 159], T(X, Y) is a sufficient statistic. Moreover, because the expression in (39) has the form of a full rank exponential family [28, pp. 23-24], T(X, Y) is a complete statistic [28, Thm. 6.22, p. 42]. Since 1) T(X, Y) is a complete sufficient statistic, 2) $\widehat{\text{SNR}}$ is an unbiased estimator of SNR, and 3) $\widehat{\text{SNR}}=\text{E}[\widehat{\text{SNR}}\mid T(\mathbf{X},\mathbf{Y})]$, i.e., $\widehat{\text{SNR}}$ is a function of T(X, Y) only, the Lehmann-Scheffé Theorem [28, Thm. 1.11, p. 88] [29, p. 164] implies that $\widehat{\text{SNR}}$ is the unique UMVU estimator of .

Proof of Corollary 1: From Theorem 1(b), we have $\text{E}\left(\widehat{\text{SNR}}\right)=\text{SNR}$. Also, from Theorem 1(a), and (25), we have

$$\text{E}\left[{\left(\widehat{\text{SNR}}\right)}^2\right]=\frac{2\eta {\text{SNR}}^2}{q-2}.$$ (40)

The identity $\text{Var}\left[\widehat{\text{SNR}}\right]=\text{E}\left[{\left(\widehat{\text{SNR}}\right)}^2\right]-\text{E}{\left[\widehat{\text{SNR}}\right]}^2$ then yields

$$\text{Var}\left[\widehat{\text{SNR}}\right]=\left[\frac{2\eta }{q-2}-1\right]{\text{SNR}}^2.$$ (41)

The stated ratio of mean to standard deviation thus follows.

Appendix C

Next, we prove Theorem 2, which enables us to calculate our ROC confidence intervals. For this task, we need the following lemmas.

Lemma 4: Let V be a continuous random variable with cdf, F_V(v; θ), that is a strictly decreasing function of the parameter θ for each v. Also, let ω₁, ω₂ ∈ (0, 1), be such that ω₁ + ω₂ = ω for some ω ∈ (0, 1). Suppose that, for each v in the sample space of V, the relations

$$F_V(v;{\theta }_L\left(v\right))=1-{\omega }_1\text{and}{\text{F}}_V(v;{\theta }_U\left(v\right))={\omega }_2$$

may be solved for θ_L(u) and θ_U(v). Then the functions θ_L(v) and θ_U(v) are uniquely defined and the random interval [θ_L(V), θ_U(V)] is an exact 1 − ω confidence interval for θ.

Proof: See [19, Theorem 9.2.12, p. 432] for a proof, and [15, Section 11.4] for a complementary discussion.

Lemma 5: Let g(θ) be a continuous, strictly increasing function of θ. If [θ_L, θ_U] is a 1 − ω confidence interval for θ, then [g(θ_L), g(θ_U)] is a 1 − ω confidence interval for g(θ).

Proof: See [13, Lemma 3].

Theorem 2 follows from Theorem 1(a) together with Lemmas 3, 4, and 5. Note that under our distributional assumptions, TPF, AUC, and pAUC are strictly increasing functions of SNR.

Appendix D

In this appendix, we give a MATLAB® function that computes the ROC confidence intervals that are discussed in this paper. Note that this code requires the Statistics Toolbox™ for MATLAB®.

% find_CIs.m

%---for the case when delta is known----

% Returns 1-omega confidence intervals for SNR, AUC,

% TPF, and pAUC, where omega = omegal + omega2

% inputs: oraegal, omega2, m (number of images from

% class 1), n (number of images from class 2)

% FPF (a column vector of fixed FPF values for TPF

% CIs), FPFa, FPFb (lower and upper FPF limits for

% pAUC), snr (estimated value of SNR)

% outputs: CI (a structure array with the fields

% CI.SNR, CI.AUC, CI.TPF, and CI.pAUC, each

% containing confidence intervals for the associated

% ROC metric)

function [CI] = find_CIs(omegal, omega2, m, n, FPF, … FPFa, FPFb, snr)

alpha = (m+n-l)/2; % inv-gamma parameter

eta = pi/(beta((m+n-2)*.5,.5)^2);

if m+n < 2,

disp(‘error: m+n too small!’)

return

end

snr_sq = snr^2;

% find confidence interval for second parameter

% of inverted gamma

% Note: The user may wish to check EXITFLA6 and

% add appropriate error messages, or they may

% wish to modify the tolerances of the fzero

% function with the OPTIONS argument.

beta0 = [le-6 le6]; % search interval

if (omegal ~= 0 && omega2 ~= 0),

[bet a_L, FVAL, EXITFLAG] = fzero(®(beta) …

gammainc(beta/snr_sq, alpha, ‘upper’) …

-(1-omegal),beta0);

[beta_U, FVAL, EXITFLAG] = fzero(®(beta) …

gammainc(beta/snr_sq, alpha, ‘upper’)…

-omega2,beta0);

elseif (omegal ~= 0 && omega2 == 0),

beta_L = 0;

[beta_U,FVAL,EXITFLAG] = fzero(®(beta) …

gammainc(beta/snr.sq, alpha, ‘upper’) …

-omega2,betaO);

elseif (omegal ~=0 && omega2 == 0),

[beta_L, FVAL, EXITFLAG] = fzero(®(beta) …

gammainc(beta/snr_sq,alpha,‘upper’) …

-(1-omegal)sbetaO);

beta_U = Inf;

else

disp([‘Warning: Both omegal and ’…

‘omega2 are zero!’])

beta_L = 0;

beta_U = Inf;

end

% find confidence intervals for summary measures

SNR_L = sqrt(beta_L/eta);

SNR_U = sqrt(beta_U/eta);

AUC_L = normcdf(SNR_L/sqrt(2));

AUC_U = normcdf(SNR_U/sqrt(2));

TPF_L = normcdf(SNR_L + norminv(FPF));

TPF_U = normcdf(SNR_U + norminv(FPF));

pAUC_L = quadgk(®(fpf) normcdf(SNR_L … + norminv(fpf)),FPFa,FPFb);

pAUC_U = quadgk(®(fpf) normcdf(SNR_U … + norminv(fpf)),FPFa,FPFb);

CI = struct(‘SNR’, [SNR_L SNR_U], ‘AUC‘,… [AUC_L AUC_U], ‘TPF’, [TPF_L TPF_U], ‘pAUC‘,… [pAUC_L pAUC_U]);

Appendix E

Here, we derive the expressions given in Section VI for the confidence interval estimator of AUC_A – AUC_B. Since $\widehat{\text{AUC}}=\Phi (\widehat{\text{SNR}}∕\sqrt{2})$, $\widehat{\text{AUC}}$ can be approximated with a first-order Taylor expansion around the point $\widehat{\text{SNR}}=\text{SNR}$, i.e., for scenarios A and B, ${\widehat{\text{AUC}}}_A\approx {\text{AUC}}_A+\varphi ({\text{SNR}}_A∕\sqrt{2})(1∕\sqrt{2})({\widehat{\text{SNR}}}_A-{\text{SNR}}_A)$ and ${\widehat{\text{AUC}}}_B\approx {\text{AUC}}_B+\varphi ({\text{SNR}}_B∕\sqrt{2})(1∕\sqrt{2})({\widehat{\text{SNR}}}_B-{\text{SNR}}_B)$, where ϕ(z) is the pdf for the standard normal distribution. The approximations (15)–(17) follow immediately from these expansions.

Next, note that (19) and (20) are simply restatements of (41). Now, it remains to derive (21). We start by using the unbiasedness of ${\widehat{\text{SNR}}}_A$ and ${\widehat{\text{SNR}}}_B$ to write

$$\text{Cov}({\widehat{\text{SNR}}}_A,{\widehat{\text{SNR}}}_B)=\text{E}\left[{\widehat{\text{SNR}}}_A{\widehat{\text{SNR}}}_B\right]-{\text{SNR}}_A{\text{SNR}}_B.$$ (42)

Employing subscripts A and B to denote scenario A and B quantities, respectively, the first term can be rewritten as

$$\text{E}\left[{\widehat{\text{SNR}}}_A{\widehat{\text{SNR}}}_B\right]={\gamma }^2{\delta }_A{\delta }_B\text{E}\left[\frac{1}{{\tilde{S}}_A{\tilde{S}}_B}\right]$$ (43)

$$={\gamma }^{2}q{\text{SNR}}_A{\text{SNR}}_B\times \text{E}\left[\left(\frac{{\sigma }_A}{\sqrt{q}{\tilde{S}}_A}\right)\left(\frac{{\sigma }_B}{\sqrt{q}{\tilde{S}}_B}\right)\right]$$ (44)

$$={\gamma }^{2}q{\text{SNR}}_A{\text{SNR}}_B\text{E}\left[U_A^{-1∕2}{U}_B^{-1∕2}\right]$$ (45)

where $U_A=q{\tilde{S}}_A^2∕{\sigma }_A^2~{\chi }_q^2$ and $U_B=q{\tilde{S}}_B^2∕{\sigma }_B^2~{\chi }_q^2$. Now, applying [30, Theorem 3.2] together with the identity B(a, b) = Γ(a)γ(b)/Γ(a+b) and the fact that $\Gamma (1∕2)=\sqrt{\pi }$, we get

$$\text{E}\left[U_A^{-1∕2}{U}_B^{-1∕2}\right]={}_{2}F_1\left(\frac{q-1}{2},\frac{q-1}{2};\frac{q}{2};{\rho }^2\right)\times {\left[B\left(\frac{q-1}{2},\frac{1}{2}\right)\right]}^2\frac{{(1-{\rho }^2)}^{q∕2-1}}{2\pi }$$ (46)

where ${}_{2}F_1(a,b,;c;z)$ is the Gaussian hypergeometric function. Inserting (46) into (45), recalling the definition of γ, and simplifying, yields

$$\text{E}\left({\widehat{\text{SNR}}}_A{\widehat{\text{SNR}}}_B\right)={(1-{\rho }^2)}^{q∕2-1}{\text{SNR}}_A{\text{SNR}}_B\times {}_{2}F_1\left(\frac{q-1}{2},\frac{q-1}{2};\frac{q}{2};{\rho }^2\right).$$ (47)

We can simplify further by using [31, identity (9.5.3), p. 248] to obtain

$$\text{E}\left[{\widehat{\text{SNR}}}_A{\widehat{SNR}}_B\right]={}_{2}F_1\left(\frac{1}{2},\frac{1}{2};\frac{q}{2};{\rho }^2\right){\text{SNR}}_A{\text{SNR}}_B.$$ (48)

Finally, (21) follows from (42) and (48).

The MATLAB® function below can be used to numerically approximate ${}_{2}F_2(1∕2,1∕2,;q∕2;{\rho }^2)$ with a series expansion. In our experience, 50 terms is generally sufficient to obtain high accuracy.

% hypergeom.m

% approximate the Gaussian hypergeometric function

% 2Fl(l/2,l/2,q/2,z) using an nterra series

% approximation

function F = hypergeom(q,z,nterm)

u=zeros(nterm);

u(l)=l; % k=0 term

for j=l:(nterm-1),

k-j-i;

% get (k+l)th term from kth term

u(j+l)=u(j)*(z/(k+l))*((l/2+k)-2)/Cq/2+k);

end

% sun terms from smallest to largest to get best

% numerical accuracy

F=0;

for j=nterm:-l:l,

F=F+u(j);

end