Modeling Nicotine Dependence: An Application of a Longitudinal IRT Model for the Analysis of Adolescent Nicotine Dependence Syndrome Scale

Abstract

Introduction:

Measures of nicotine dependence typically use the item average or total score from rating scales, such as the Nicotine Dependence Syndrome Scale (NDSS). Alternatively, item response theory (IRT) methods can provide useful item-specific information. IRT methods developed for longitudinal data can additionally provide information about item-specific changes over time.

Methods:

We describe a longitudinal 2-parameter ordinal IRT model, and compare the results from this model with those from an IRT model for only the baseline item responses, and a conventional longitudinal analysis of the item-average NDSS score. We examined a 10-item, adolescent version of the NDSS at baseline, 6, 15, and 24 months for 1,097 9th or 10th graders.

Results:

IRT analysis of the baseline data revealed that the items “willing to go out of the house in a storm to find a cigarette,” “choose to spend money on cigarettes than lunch,” “function better after morning cigarette,” and “worth smoking in cold or rain,” were good items at distinguishing individuals’ levels of nicotine dependency. While the analysis of the averaged NDSS score indicated linear growth over time, the longitudinal IRT method revealed that only 5 out of the 10 items showed statistical increase over time.

Conclusions:

Infrequently endorsed NDSS items were generally better able to distinguish higher levels of dependency. The endorsement of such items increased over time. Items that changed significantly over time reflected the general drive concept of dependence, as well as the total first overarching dimension of dependence.

Introduction

In studying nicotine dependence, rating scales like the Fagerström (Fagerström, 1978; Haddock, Lando, Klesges, Talcott, & Renaud, 1999; Heatherton, Kozlowski, Frecker, & Fagerström 1991) and Nicotine Dependence Syndrome Scale (NDSS; Shiffman, Waters, & Hickcox, 2004) are often used, and an item average or total score is typically used as the subject’s scale score. The underlying assumptions for using such scores are that each item on the scale represents an equal level of smoking dependency and is equally related to an individual’s overall level of nicotine dependence. Sometimes, an overall score for an individual cannot be formed due to missing information on one or more items from that individual. Alternatively, item response theory (IRT; Lord, 1980) methods can be used to model the underlying individual nicotine dependence from multiple items comprising the scale. Such methods have the advantage of simultaneously accounting for the characteristics of the individual and providing particular properties of each item. In addition, the underlying dependency for an individual can be estimated even when the individual has missing information on one or more items.

In addictions research, Panter and Reeve (2002) analyzed adolescents’ tobacco beliefs data using the IRT method to demonstrate how item properties can be established and be used for instrument construction. Kirisci, Vanyukov, Dunn, and Tarter (2002) found IRT methods useful in revealing the factor structure of the psychometric characteristics of substance use. Strong, Brown, Ramsey, and Myers (2003) examined adolescent nicotine dependency measurements, and concluded that the IRT method provided insights in terms of the relative severity of the instrument items, as well as each item’s ability to discriminate individual levels of nicotine involvement.

Originated as improvements over the classical test theory (Novick, 1966; Spearman, 1904), IRT models are typically developed for cross-sectional data. Researchers now are increasingly facing the challenge of modeling repeatedly measured rating scales in longitudinal designs. One popular approach for modeling repeatedly measured items is subsumed under the General Latent Variable Modeling framework in the context of structural equation modeling. Such models estimate the development of a single latent construct over time, with the latent construct at each time point estimated from multiple observed indicators (Curran & Muthén, 1999; Duncan & Duncan, 1995; McArdle, 1988; Muthén, 1991; Muthén & Muthén, 1998–2003). Using a different approach that falls in the area of mixed-effects regression models, Liu and Hedeker (2006) incorporated a two-parameter IRT method into a mixed-effects regression model that allows for differential change of the items, in addition to the typical focus on item characteristics in IRT methods.

In this study, we employed a cross-sectional IRT model and the longitudinal IRT method by Liu and Hedeker (2006) to data from a longitudinal study of the natural history of smoking among adolescents, focusing on the NDSS. The aims addressed in this study are: (a) to examine the baseline pattern of endorsement of the NDSS items among these adolescents, and each item’s ability to discriminate individual levels of nicotine dependence and (b) to examine the development of the items over time. With the employment of a two-parameter IRT method, we hypothesized that those hard-to-endorse NDSS items were better items at discriminating individual nicotine dependence and that the 10 items would have differential change patterns over time.

Methods

Subjects

The data for this paper come from a longitudinal study of the natural history of smoking among adolescents. The study uses a multimethod approach to assess adolescents at multiple time points (baseline, 6, 15, and 24 months). The data collection modalities include paper-and-pencil questionnaires, in-person interviews, and for subsets of participants, more intensive measurement modalities including family observations, psychophysiological assessments, and week-long time/event ecological momentary assessment sampling via hand-held palmtop computers (referred to as “Electronic Diary”). The NDSS instrument examined in this study was collected from questionnaires.

Out of the 1,263 baseline adolescents who had smoked and were eligible to respond to the NDSS items, 1,034 responded to at least 1 out of the 10 NDSS items and are included in the baseline analysis (Model I in the analysis and result sections). An averaged NDSS score was created for subjects who responded to at least five NDSS items at a given wave of data collection, resulting in a sample of 1,032 adolescents for the longitudinal NDSS score analysis (Model II). Those subjects who responded to at least one NDSS item at one or more time points are included in the longitudinal analysis of item responses (Model III), resulting in the largest sample size among the three sets of analyses, N = 1,097. Of the 1,097, the adolescents were either in Grade 9 (n = 545, 49.7%) or Grade 10 (n = 552, 50.3%), and 612 (55.8%) were female students. The ethnicity groups include Non-Hispanic White (618, 56.3%), Non-Hispanic Black (172, 15.7%), Hispanic (204, 18.6%), Asian/Pacific Island (39, 3.6%), and other (64, 5.8%).

Measures

The 10 NDSS items were rated on a four-category ordinal scale (1 = not at all true; 2 = not very true; 3 = fairly true; 4 = very true). About one-fifth of the subjects missed information on at least one item at each wave. An average NDSS score was obtained for those individuals who responded to at least five items at a given time point. Descriptions and summary statistics for the items and the averaged score across waves are listed in Table 1. The subjects had a consistently high rating to Item 2, Since I started smoking, I have increased how much I smoke. Two other relatively highly rated items were: Item 1, Compared with when I first started smoking, I need to smoke a lot more now in order to be satisfied, and Item 3, After not smoking for awhile, I need to smoke to relieve feelings of restlessness and irritability. Items with relatively low ratings include: Item 5, I can function much better in the morning after I’ve had a cigarette, Item 7, When I’m craving a cigarette, it feels like I’m in the grip of some unknown force that I can’t control, Item 8, If there were no cigarettes in the house and there was a big rainstorm, I would still go out of the house and find a cigarette, and Item 10, If I’m low on money, I’ll spend it on buying cigarettes instead of buying lunch. The ratings of most items, as well as the averaged NDSS score, appeared to increase over time.

Table 1.

Observed Means (SD) and Sample Sizes for Nicotine Dependence Syndrome Scale (NDSS) by Wave

Item	Baseline	6 Month	15 Month	24 Month
1. Compared with when I first started smoking, I need to smoke a lot more now in order to be satisfied.	1.53 (0.85), n = 1,031	1.55 (0.90), n = 938	1.61 (0.90), n = 920	1.66 (0.94), n = 951
2. Since I started smoking, I have increased how much I smoke.	1.79 (1.06), n = 1,030	1.85 (1.12), n = 937	1.93 (1.12), n = 918	1.98 (1.17), n = 951
3. After not smoking for awhile, I need to smoke to relieve feelings of restlessness and irritability.	1.63 (0.93), n = 1,031	1.58 (0.91), n = 942	1.63 (0.91), n = 926	1.66 (0.95), n = 946
4. After not smoking for awhile, I need to smoke in order to keep myself from experiencing any discomfort.	1.42 (0.79), n=1029	1.43 (0.81), n = 939	1.44 (0.81), n = 923	1.48 (0.80), n = 943
5. I can function much better in the morning after I’ve had a cigarette.	1.22 (0.67), n = 1029	1.31 (0.77), n = 938	1.37 (0.77), n = 923	1.44 (0.87), n = 943
6. Whenever I go without a smoke for a few hours, I experience craving.	1.32 (0.73), n = 1,004	1.41 (0.81), n = 924	1.48 (0.81), n = 899	1.50 (0.90), n=914
7. When I’m craving a cigarette, it feels like I’m in the grip of some unknown force that I can’t control.	1.28 (0.65), n = 1,027	1.29 (0.68), n = 941	1.31 (0.68), n = 925	1.34 (0.73), n = 944
8. If there were no cigarettes in the house and there was a big rainstorm, I would still go out of the house and find a cigarette.	1.23 (0.63), n = 1,028	1.28 (0.70), n = 940	1.34 (0.70), n = 925	1.36 (0.76), n = 943
9. In situations where I need to go outside to smoke (e.g., home if your parents don’t know you smoke, at school during lunch), it’s worth it to be able to smoke a cigarette, even in cold or rainy weather.	1.44 (0.84), n = 1,027	1.48 (0.88), n = 942	1.50 (0.88), n = 923	1.54 (0.92), n = 943
10. If I’m low on money, I’ll spend it on buying cigarettes instead of buying lunch	1.28 (0.72), n = 1,028	1.32 (0.78), n = 941	1.40 (0.78), n = 924	1.41 (0.84), n = 943
Average NDSS Score (if responded to ≥five items)	1.30 (0.67), n = 1,032	1.33 (0.73), n = 942	1.39 (0.73), n = 926	1.43 (0.79), n = 945

Data Analysis

Model I—IRT Model for Baseline NDSS Items

As described by several authors (e.g., Bock & Aitkin, 1981; Lord, 1980), a popular IRT model for dichotomous responses is the two-parameter logistic (2-PL) model that specifies the probability of a subject endorsing an item, conditional on the subject’s “ability,” using two-item parameters, item difficulty and item discrimination. Suppose a total of N subjects, with subject i responding to all m items or a subset of size n _i. Let Y_ik denote the 0/1 response of individual i to item k, with Y_ik = 1 representing endorsement of the item. The 2-PL model of Bock and Aitkin (1981) specifies the probability of endorsement of item k by subject i, conditional on the latent subject “ability,” or latent trait of subject i (θ_i) as

$$P_r(Y_{ik}=1|{\theta }_i)=\frac{1}{1+\exp (-a_k[{\theta }_i-b_k\left]\right)},$$ (1)

or in terms of the log odds (logit) as

$$\log i{t}_{ik}=\log \left(\frac{P_r[Y_{ik}=1|{\theta }_i]}{1-P_r[Y_{ik}=1|{\theta }_i]}\right)=a_k({\theta }_i-b_k)$$ (2)

The parameter θ_i denotes the level of the latent trait for subject i, usually assumed to be standard normal in the population of subjects. The parameter b_k is the item difficulty, which indicates the trait level needed to have a 50% chance of endorsing an item. The parameter a_k is the discriminating parameter for item k, with higher value a_k indicating the associated item being better able to discriminate the latent trait levels.

The above 2-PL model can also be written in a mixed-effects regression representation, commonly seen in models for repeatedly measured data. Let X_ik (k = 1, 2, … . m) denote the set of item response indicators by subject i. The 2-PL model can be written as

$$\log i{t}_{ik}={\chi }_{ik}{\beta }_k+{\chi }_{ik}{a}_k{\theta }_i$$ (3)

where β _k = − a _k b _k (k = 1, 2, … m) are the item intercepts, and the item discrimination parameters a _k correspond to random-effect SDs associated with the items, akin to the factor loadings in a factor analysis model. The random subject “ability” θ _i is assumed to follow a standard normal distribution N(0, 1). Essentially, this 2-PL model is a random intercept logistic regression model that allows the random-effect variance terms to vary across items. In such a mixed-effects model, the item indicator variables X_ik’s are specified as both fixed- and random-effects covariates.

In Model I of this study, we applied the 2-PL model for the baseline NDSS items. The results were obtained using the MIXOR (Hedeker & Gibbons, 1996) program for items measured on an ordinal scale with C categories. The ordinal model extends the binary logistic regression model by specifying C-1 cumulative logits for the C ordered response categories. Thus, in the ordinal model, in addition to the set of item intercept parameters (β _k) and item discrimination parameters (a _k), a set of C-2 thresholds γ_c (c = 2, … ., C − 1) with γ₁ = 0 are estimated for the cumulative logits. As a result, γ _c − β _k compares the relative frequency in categories c and lower (Y_ik ≤ c) with that in categories higher than c (Y_ik > c). With γ₁ = 0, the item intercept parameters (β _k’s) represent the probability of response in categories two or higher versus the probability of Y_ik = 1.

Model II—Mixed-Effects Regression Model for NDSS Score Over Time

Consider the following linear mixed model (LMM) for the continuous NDSS average score y _ij for subject i at time point j, regressed on the time value T _ij :

$$y_{ij}=({\beta }_0+{\upsilon }_{0i})+({\beta }_1+{\upsilon }_{1i})T_{ij}+{ϵ}_{ij}$$ (4)

where β ₀ is the overall population intercept, indicating population mean NDSS score at baseline; υ _0i is the intercept deviation for subject i; β ₁ is the overall population slope, that is, change in mean NDSS score per unit change in time; υ _1i is the slope deviation for subject i; and ϵ _ij is an independent error term distributed normally with mean 0 and variance . The errors are independent conditional on both υ _0i and υ _1i. With two random subject-specific effects, the population distribution of intercept and slope deviations is assumed to be a bivariate normal N(0,Σ _υ), where S _υ is the 2×2 variance–covariance matrix given as:

$${\Sigma }_{\upsilon }=\left[\begin{array}{cc}{\sigma }_{{\upsilon }_0}^2& {\sigma }_{{\upsilon }_0{\upsilon }_1}\\ {\sigma }_{{\upsilon }_0{\upsilon }_1}& {\sigma }_{{\upsilon }_1}^2\end{array}\right]$$

This model indicates the linear effect of time both at the individual (υ _0i and υ _1i) and population (β ₀ and β ₁) levels. For this study, the LMM in equation (4) was implemented in SAS PROC MIXED for the analysis of the averaged NDSS score over time.

Model III—Longitudinal 2-PL IRT Model for NDSS Items Over Time

When a total of m items are repeatedly measured across time for N subjects, the observed binary response to item k for subject i at time point j is denoted as Y_ijk. For the analysis of such data at the item level, Liu and Hedeker (2006) incorporated the random subject effect components (υ _0i and υ _1i in Equation 4), a crucial feature for longitudinal models, into the 2-PL Model (Equation 3) as

$$\log i{t}_{ijk}=({\chi }_{ijk}{\beta }_{0k}+{\upsilon }_{0i})+({\chi }_{ijk}{\beta }_{1k}+{\upsilon }_{1i})T_{ij}+{\chi }_{ijk}{a}_k{\theta }_{ij},$$ (5)

Here, X_ijk denotes the indicator variable for the kth item for subject i at time point j, T_ij denotes the time value associated with the item response, β _0k and β _1k are the population intercept and linear trend for the kth item (both are fixed-effect parameters), and υ _0i and υ _1i are the same random subject effects as defined in Model II, reflecting individual deviations from the population intercepts and linear trends. Similar to the 2-PL model in Equation (3), the item discrimination parameters a _k correspond to the SDs (or factor loadings) for the items. These discrimination parameters are constrained to be invariant over time. The random subject “ability,” θ _ij assumed to have distribution N(0, 1), reflects the deviation of individual i’s ability at time point j relative to the linear growth of that individual (X _ijk β _0k + υ _0i) + (X _ijk β _1k + υ _1i)T _ij. As indicated by Liu and Hedeker (2006), the advantages of incorporating the IRT component into a mixed-effects model representation include that the number of items observed at each time point can vary across different time points, and the number of time points from which the subject-provided data can vary across subjects. In addition, covariates can be at any level (item, time point, or subject level covariates). For this study, we only included 10 item indicators (X_ijk) (design vector for 10 item intercepts) and 10 item-by-time interaction terms (design vector for 10 item slopes) as fixed-effects covariates. The NDSS items in this study were measured on an ordinal scale with four categories, and so a cumulative logit model was estimated, with the same interpretations as described previously in the section relating to Model I. As in Liu and Hedeker (2006), maximum marginal likelihood estimation was employed utilizing multidimensional Gauss–Hermite quadrature for integration over the random effects distribution. The procedure was implemented using the GAUSS programming language (GAUSS 3.6, 2001).

Results

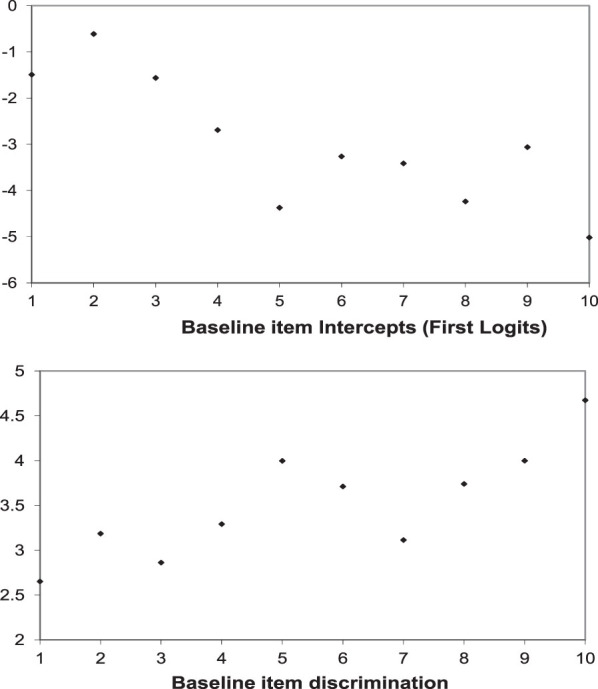
Table 2 lists the analysis results for Models I, II, and III. In Model I, the baseline 2-PL ordinal IRT model, the 10 estimates of item intercepts represent the estimated first logits, comparing the relative frequency in categories 2, 3, and 4 together to that in Category 1. The negative estimates indicate that, at baseline, subjects are less likely to endorse the higher categories (i.e., categories that indicate higher level of nicotine dependence). The larger the negative value of the estimate the smaller the relative frequencies for the higher categories, indicating lower levels of nicotine dependence. The baseline item intercept estimates are plotted in Figure 1, top panel.

Table 2.

Parameter Estimates (SE) of Analysis Results

	Model I. Two-parameter IRT: Baseline items	Model II. Mixed model: Score over time	Model III. Longitudinal IRT: Items over time
Intercepts β0		1.29 (0.02)**
Item
1 β01	−1.49 (0.15)**		−2.12 (0.15)**
2 β02	−0.61 (0.13)**		−0.97 (0.13)**
3 β03	−1.56 (0.16)**		−1.85 (0.16)**
4 β04	−2.69 (0.23)**		−3.00 (0.23)**
5 β05	−4.37 (0.35)**		−5.06 (0.35)**
6 β06	−3.26 (0.26)**		−3.83 (0.26)**
7 β07	−3.41 (0.26)**		−4.22 (0.26)**
8 β08	−4.24 (0.35)**		−5.26 (0.35)**
9 β09	−3.06 (0.28)**		−3.21 (0.28)**
10 β0_10	−5.02 (0.40)**		−4.81 (0.40)**
Slopes β1		0.04 (0.01)**
Item
1 β11			0.02 (0.04)
2 β12			0.09 (0.04)**
3 β13			−0.07 (0.04)
4 β14			−0.04 (0.05)
5 β15			0.31 (0.06)**
6 β16			0.14 (0.05)**
7 β17			−0.04 (0.05)
8 β18			0.17 (0.05)**
9 β19			0.02 (0.05)
10 β1_10			0.18 (0.06)**
Item discriminations
a1	2.65 (0.15)**		1.10 (0.07)**
a2	3.19 (0.16)**		1.24 (0.06)**
a3	2.86 (0.17)**		1.27 (0.07)**
a4	3.29 (0.21)**		1.63 (0.07)**
a5	4.00 (0.28)**		2.44 (0.10)**
a6	3.71 (0.22)**		2.17 (0.08)**
a7	3.11 (0.22)**		1.99 (0.08)**
a8	3.74 (0.28)**		2.82 (0.10)**
a9	4.00 (0.28)**		2.35 (0.09)**
a10	4.67 (0.32)**		2.72 (0.10)**
Random subject effects
συ1 2		0.35 (0.02)**	2.91 (0.08)**
συ1 υ2		−0.009 (0.004)**	−0.14 (0.03)**
συ2 2		0.02 (0.002)**	0.73 (0.03)**
Thresholds
γ2	1.57 (0.04)**		1.73 (0.02)**
γ3	3.74 (0.07)**		4.10 (0.03)**

Note. IRT = item response theory.

*p < .05. **p < .05.

Figure 1.

Two-parameter IRT model results for baseline NDSS items.

Notice that Item 2 was the most endorsed item: Since I started smoking, I have increased how much I smoke. In the baseline sample, the response percentages for this item were: 58.5% (not at all true), 14.2% (not very true), 17.1% (fairly true), and 10.3% (very true). Conversely, Item 10 was the least endorsed item: If I’m low on money, I’ll spend it on buying cigarettes instead of buying lunch, with response percentages 84.5%, 6.9%, 4.8%, and 3.8%, respectively. Other less endorsed items included: Item 5 (I can function much better in the morning after I’ve had a cigarette), and Item 8 (If there were no cigarettes in the house and there was a big rainstorm, I would still go out of the house and find a cigarette). The estimated item discrimination parameters (Figure 1, bottom panel) indicate the loading of the item on the latent nicotine dependency. Items with higher discrimination values are better at separating individuals of different dependency levels. Notice that Item 10 (choose to spend money on cigarettes than lunch) is the most discriminating item at baseline. Other relatively discriminating items included Item 5 (function better after morning cigarette), Item 8 (find cigarette in rainstorm) and Item 9 (In situations where I need to go outside to smoke, it’s worth it to be able to smoke a cigarette, even in cold or rainy weather). Items 1 (Compared with when I first started smoking, I need to smoke a lot more now in order to be satisfied) and 3 (After not smoking for awhile, I need to smoke to relieve feelings or restlessness and irritability) are the least discriminating.

Results of the mixed-effects linear growth model for the item-average NDSS score over time are listed in the second column in Table 2. While the mean linear growth over time was significant and positive (${\overline{\beta }}_1$ = 0.04 per 6 months, p value < 0.001), indicating increased dependency over time, there was a significant amount of variation in both the intercept and slope in the population of subjects. Thus, subjects vary considerably in their initial levels of dependency and its change over time.

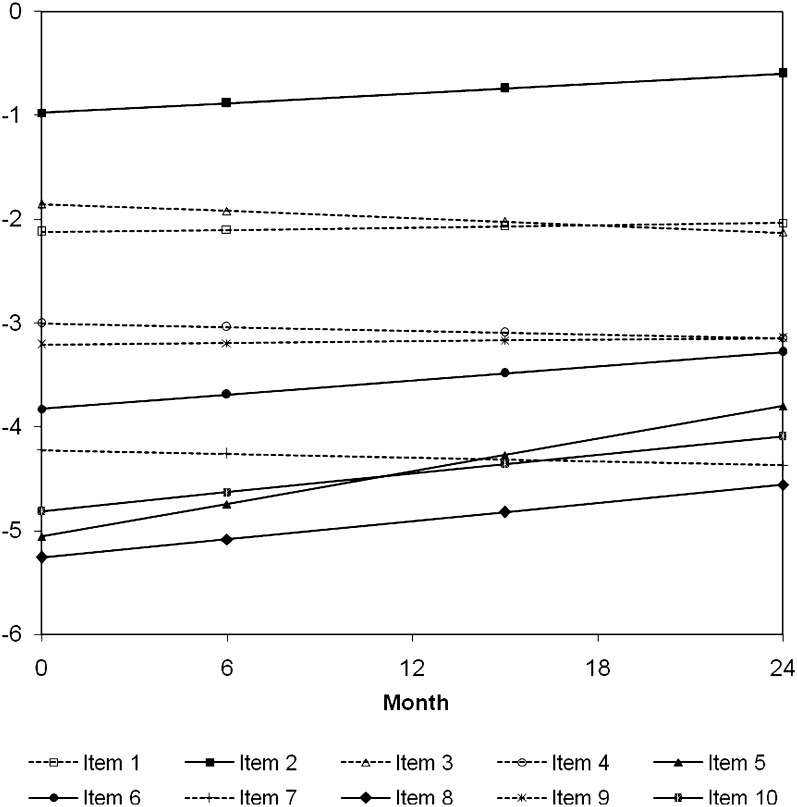
Analysis results from the longitudinal IRT model are listed in the third column of Table 2. Compared with a longitudinal IRT model in which all item discrimination parameters (a_k) were constrained to be equal (not shown), Model III provided much better fit of the data (χ² ₉ = 240.3, p value < .000), indicating that the item discrimination parameters were significantly different. By and large, the estimates of item-intercept and discrimination parameters in Model III agred with those from Model I. Items 5 (function better after morning cigarette), 8 (find cigarette in rainstorm), and 10 (choose to spend money on cigarettes than lunch) were still the least endorsed items, and items 5, 8, 9 (worth smoking in cold or rain), and 10 were again the most discriminating ones. The only difference from Model I was that Item 8 (find cigarette in rainstorm), rather than Item 10, became the least endorsed and most discriminating item. Notice that the scale for the discrimination parameters from Model III was smaller than that from Model I (baseline model); this is because these parameters were estimated from four waves of data in Model III, which included random subject trend parameters for the longitudinal data. The mean trends of the 10 items (first cumulative logits comparing relative frequencies in higher categories with Category 1) are illustrated in Figure 2. Statistically significant increases in only 5 out of the 10 items over time were detected (solid lines in Figure 2): items 2 (increased smoking), 5 (function better after morning cigarette), 6 (craving), 8 (find cigarette in rainstorm), and 10 (choose to spend money on cigarettes than lunch). Notice that the least endorsed items (items 5, 8, and 10) had the most profound increases. The most endorsed item, Item 2, also exhibited significant increase over time. The five items that did not exhibit increased endorsements are (dotted lines in Figure 2): need more to be satisfied; smoke to relieve feelings; smoke to keep from discomfort; grip of unknown force when craving; worth smoking in cold or rain.

Figure 2.

NDSS item change (first logits) over time.

Discussion

In this article, we described IRT and mixed models in the examination of the characteristics and development of the 10 items of the NDSS scale among a sample of adolescents. While a typical mixed-effects regression model applied to the item-averaged NDSS score revealed linear increase in nicotine dependence among adolescents, the IRT models with item intercept and discrimination parameters revealed more item-level information. By and large, the item discrimination values were inversely related to the intercepts (which are minus the product of discriminations and difficulties in the IRT parameterization), indicating that the less frequently endorsed items were better able to distinguish higher levels of dependency. We found that items 5 (function better after morning cigarette), 8 (find cigarette in rainstorm), and 10 (choose to spend money on cigarettes than lunch) fell into this category. In addition, these three items had the most profound increases over time. Two of these items reflect the total score dimension of the original NDSS (Shiffman, Waters, & Hickcox, 2004), and the third reflects more of a priority dimension, with adolescents who endorse this item indicating that they are choosing cigarettes over other behavioral reinforcers.

What is perhaps more interesting are items that are relatively frequently endorsed (less negative intercepts), but also more discriminating. Such items would be better able to distinguish relatively low and high levels of dependency. Here, the item, “It is worth smoking even in cold or rainy weather,” is best for this purpose. Notice, however, the endorsement level of this item remained stable over time, that is, there was no significant change over time for this item. An item that did exhibit significant increase over time was an “easy,” or frequently endorsed item, Item 2 (increased smoking). There was also an increase in the endorsement of Item 6 over time (Whenever I go without a smoke for a few hours, I experience craving), whose difficulty and discrimination values were both in the middle range. Together, the items that changed significantly over time reflected the general drive concept of dependence, as well as the total first overarching dimension of dependence (c.f., Costello, Dierker, Sledjeski, Flaherty, Flay, & Shiffman, 2007). The drive dimension reflects the individual’s compulsion to smoke or subjective need for nicotine, often in response to the need to relieve withdrawal symptoms (Shiffman, Waters, & Hickcox, 2004). The total first dimension is still the best summary representation of nicotine dependence, often showing the highest correlations with other validators (Shiffman et al., 2004). The other five items in the NDSS scales did not exhibit significant change over time.

As illustrated by Liu (2008), another advantage of applying the longitudinal IRT model is that it is not necessary that every subject responds to the complete set of items at each wave. In the analyses of an average score, the results are often based on the sample of subjects who respond to some minimum number of items (e.g., 50% or 75%). In this case, the degree of certainty/uncertainty in calculation of this average varies (because it is based on different numbers of item response), but is ignored in the analysis. However, the longitudinal IRT model employed in this study allows for different number of item responses at different time points and/or for different subjects, and accounts for these differences in terms of the model standard errors.

The present study also adds to our understanding of the development of nicotine dependence among adolescents. Most prior work has focused on examining the dimensional structure of nicotine dependence in adolescents (e.g., Clark, Wood, Martin, Cornelius, Lynch, & Shiffman, 2005) or examining how symptoms may change over time following treatment (e.g., Strong et al., 2007). One prior study has also examined the predictive validity of specific symptoms of nicotine dependence among very light, infrequent adolescent smokers (Dierker & Mermelstein, 2010). We found a fair amount of heterogeneity in level of symptoms over time, but our results suggest that some symptoms may be especially important to track to help with the early identification of adolescents who are vulnerable to developing higher levels of dependency. These symptoms include ones that reflect more drive toward smoking, compared with those focused on relief of withdrawal. The drive dimension, among these adolescent very light smokers, may reflect a vulnerability to escalate and to develop further dependence. The examination of nicotine dependence and changes in patterns of dependency over time helps to increase our understanding of the development of dependence and to identify potential screening items for adolescents at high risk for escalation.

Funding

This work was supported by National Cancer Institute grant 5PO1 CA98262.

Declaration of Interests

None.