Abstract
To gauge the relative importance of contingency and determinism in evolution is a fundamental problem that continues to motivate much theoretical and empirical research. In recent evolution experiments with microbes, this question has been explored by monitoring the repeatability of adaptive changes in replicate populations. Here, we present the results of an extensive computational study of evolutionary predictability based on an experimentally measured eight-locus fitness landscape for the filamentous fungus Aspergillus niger. To quantify predictability, we define entropy measures on observed mutational trajectories and endpoints. In contrast to the common expectation of increasingly deterministic evolution in large populations, we find that these entropies display an initial decrease and a subsequent increase with population size N, governed, respectively, by the scales Nμ and Nμ2, corresponding to the supply rates of single and double mutations, where μ denotes the mutation rate. The amplitude of this pattern is determined by μ. We show that these observations are generic by comparing our findings for the experimental fitness landscape to simulations on simple model landscapes.
Keywords: clonal interference, epistasis, experimental evolution
Evolutionary adaptations arise from an intricate interplay of deterministic selective forces and random reproductive or mutational events, and the relative roles of these two types of influences on the outcome of evolution has been subject to long-standing controversy with significant philosophical implications (1, 2). Although the vision of “replaying the tape of life” on Earth or on some extrasolar planet remains confined to the realm of imagination (3, 4), evolution experiments with microbial populations have begun to address predictability of adaptation on a microevolutionary scale (5–9). In particular, strong signatures of parallel evolution have been observed in the context of the evolution of antibiotic resistance in pathogens, a finding that is of direct relevance to strategies of drug design and deployment (10–14). As lack of knowledge of crucial parameters (e.g., the frequency of beneficial mutations) in such experiments prevents forward predictions, predictability is used in a weaker, a posteriori sense implying repeatability of evolutionary trajectories in replicate populations. For this reason, the two terms will often be used interchangeably in the following (15).
The repeatability of adaptive trajectories is expected to depend on the genetic constraints imposed by epistatic interactions as well as on parameters such as population size N, mutation rate μ, and the typical scale s of selection coefficients (16–18). To be specific, consider a population evolving in the regime of strong selection and weak mutation (SSWM), where mutations are so rare that normally not more than one mutant is present simultaneously and the population can be represented as a single entity that performs an adaptive walk in the space of genotypes (19–21). Such walks are constrained to move uphill in fitness (strong selection, Ns ≫ 1) in single mutational steps (weak mutation, Nμ ≪ 1). As a consequence, a mutational pathway connecting two genotypes is selectively accessible in the SSWM regime only if fitness increases in each step (22). A number of recent studies of empirical fitness landscapes have shown that, in most cases, only a small fraction of possible adaptive pathways are accessible in this sense, which implies a dramatic enhancement of evolutionary predictability (10, 11, 15, 23–27). Moreover, the statistical weights of different accessible trajectories often vary widely, further narrowing the range of possibilities to a small number of dominant evolutionary pathways (10, 11, 15). In the SSWM regime, the likelihood of a given trajectory can be quantified straightforwardly in terms of the product of the relative fixation probabilities for individual mutational steps (10).
With increasing N, the simultaneous presence of several mutant clones becomes likely and clonal interference sets in (28–31). Clonal interference introduces a bias favoring mutations of large effect (32, 33), thus bringing the dynamics closer to the “greedy” limit, in which the mutation of largest effect is fixed deterministically in each step (34, 35). Although this in itself tends to reduce the heterogeneity of evolutionary trajectories (12, 35–37) and thus increases predictability, it is counteracted by the increasing availability of genotypes carrying multiple mutations. For sufficiently large populations, the crossing of small fitness valleys (which is completely suppressed in the SSWM limit) becomes relatively facile (38–40), opening up a host of previously inaccessible pathways and leading to a greater degree of randomness in the dynamics. The resulting overall effect on evolutionary repeatability in large populations is hard to assess without detailed analysis, and is expected to depend significantly on the structure of the underlying fitness landscape.
The objective of this article is to explore how the predictability of evolutionary dynamics depends on population parameters, primarily population size and mutation rate, in the presence of realistic epistatic interactions. To this end, we performed extensive simulations of standard asexual population dynamics of Wright–Fisher type on an empirical eight-locus fitness landscape obtained experimentally for the asexual filamentous fungus Aspergillus niger (26). We provide two definitions of adaptive pathways, which can be applied across all evolutionary regimes of interest, and reduce to the familiar adaptive walks in the SSWM regime. Probabilities of pathways and endpoints are then accumulated in a large number of independent runs, and their repeatability is quantified through the entropies of these empirical probability distributions. As usual, high predictability is signaled by low values of the entropies.
Our central result is that the entropies of evolutionary trajectories and endpoints vary nonmonotonically with population size and mutation rate. The variation with population size is governed by the parameters Nμ and Nμ2, which describe the supply of single and double mutants, respectively, and it becomes more pronounced with decreasing μ. Simulations on the empirical A. niger landscape are complemented by a study using a class of model landscapes with tunable roughness (26, 41), which display the same type of behavior.
Results
Path Types and Arrow Plots.
There are different ways of defining the path taken by an adapting population in a genotypic fitness landscape, which are generally not equivalent but may yield complementary information. Here, we focus primarily on lines of descent (LODs), which represent the lineages that arrive at the most populated genotype at the final time (see below for a precise definition). Similar definitions of paths have been introduced previously (see, e.g., refs. 42 and 43). In addition, we will make use of the information supplied by the paths defined as the time ordered sets of genotypes that at some time contain the largest subpopulation. We will call such a path the path of the maximum (POM). The POMs have been studied extensively in the context of deterministic mutation-selection models (44). Note that single steps in POMs, in contrast to those in LODs, can connect states that are separated by an arbitrary number of point mutations.
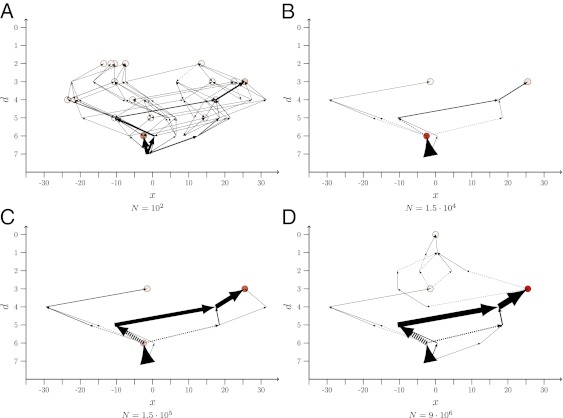
To gain a better understanding of the factors that determine the shape of the paths, we find it convenient to introduce arrow plots representing ensembles of paths realized up to time T (Fig. 1). Details of the construction are explained in the caption. Note that the choice of the final time T is, up to a certain point, arbitrary, as the population dynamics will never terminate completely. Here, we generally choose T such that the population has time to find at least some local fitness maximum. Only for the smallest population sizes, where the dynamics become very slow, do we observe trajectories that do not terminate at a local maximum.
Fig. 1.
Arrow plots of LODs obtained from an ensemble of 1,000 runs over T = 215 = 32,768 generations, starting from genotype 250 of the empirical A. niger dataset. Population size N varies from 102 in A to 9⋅106 in D, and the mutation rate is μ = 10−5. The possible states (genotypes) are ordered such that the abscissa provides the Hamming distance, d, of a genotype to the global optimum (GO), which is located at the origin. The Hamming distance is the number of single mutational steps separating two genotypes. States with the same d are distributed equidistantly along the horizontal direction. The circles represent endpoints of paths; the darker their filling, the more often the corresponding state was the most populated one at final time T. The thicknesses of the arrows are directly proportional to the fraction of times a certain step has been taken when the numerical experiment was repeated. The arrows always point from the ancestor to the descendant. The lines with arrows at both ends mean that the step was taken in both directions, although not necessarily in the same realization. The dashed arrows indicate that the descendant’s fitness is lower than that of the ancestor.
The LODs are obtained as follows: After a fixed time T, the most populated state is determined. The last step of the path is then defined as the connection between this state and the state from which it arose for the last time by mutation. By “arose,” we mean that the target state was unpopulated before the mutation occurred. A given genotype may undergo several episodes of “colonization” and extinction that are stored by the algorithm, and the last episode before the colonization of the final state is used to construct the step. Subsequent steps of the path are constructed analogously, starting from the latest ancestor state determined, i.e., we search for the state from which the latest ancestor arose for the last time before giving rise to the next genotype. The protocol is repeated until the starting point of the simulations is reached.
Note that the paths generated in this way do not include all paths explored by the population, nor all of the paths that contribute to the production of the final state. Rather, they represent the “stepwise fastest” paths through which the final state may have been accessed. The assumption made here is that this path should normally be the one responsible for creating the first mutants on the final state. Once these mutants have been created, selection will dominate the further evolution. Thus, the supply of additional mutants through other paths should play a minor role. If there are several paths with similar probabilities for being the fastest in this sense, they should all show up when the numerical experiment is repeated many times.
The POMs, however, are constructed by keeping track of the most populated genotype at every generation (Fig. S1). Note that maxima do not need to move between adjacent genotypes but can jump to states at Hamming distance larger than unity. Such events have sometimes been referred to as leapfrog events (28) (for experimentally observed examples, see, e.g., refs. 45 and 46). We depict them by wavy lines. By comparing LODs and POMs, we can thus obtain information about whether fitness valleys have been crossed by sequential fixation or by “stochastic tunneling” (38, 39). In the latter case, the deleterious mutation is not fixed, but the population on the deleterious state survives long enough for a secondary mutant of higher fitness to arise. As we will see later, tunneling is negligible as long as N is small compared with a threshold scaling as 1/μ2, but becomes dominant for larger N.
Population Size Dependence of Typical Paths.
Although the main focus of this article is on the statistical analysis of repeatability, it is instructive to first elucidate the effects of population size on the shape of evolutionary trajectories by means of a few typical examples. For this purpose, we refer to Fig. 1, where ensembles of LODs are shown that start from one of the four viable states at Hamming distance d = 7 from the global optimum (GO) in the A. niger landscape (see Materials and Methods for details on the landscape, Fig. S1 for the corresponding representation in terms of POMs, and Figs. S2–S4 for LODs starting from different initial genotypes). The figure was generated with a mutation rate of μ = 10−5, and the data were accumulated over 1,000 realizations of the process. Note that, in the A. niger landscape, the wild type is the fittest state (the GO) and that, on average, the mutants are less fit the more mutations they have incorporated (26, 47). This is why most observed steps run in the direction of decreasing d.
For the population parameters used in Fig. 1A and Fig. S1A, SSWM behavior is expected. The population is mainly monomorphic, i.e., only single mutants appear on the background of the presently dominant genotype and fix with probabilities that are proportional to their selection coefficient but independent of N (19–21). Hence all steps that lead to fitter states are realized with comparable probabilities, provided their fitness values are not too different. At the same time, the fixation probability for deleterious mutations is exponentially small in N (48), making transitions to less fit states very unlikely (Fig. S5B). This leads to a large number of realized paths and endpoints and highly unpredictable dynamics.
As the population size increases, several nearest neighbor mutants of the currently most populated genotype are present simultaneously, leading to competition between different mutants. Fitter mutations will be more commonly selected. Thus, in this regime, the dynamics becomes greedier and more deterministic (17, 35). The corresponding pronounced increase in predictability results in a dramatic thinning of the graph of adaptive pathways when going from Fig. 1A and Fig. S1A (with N = 102) to Fig. 1B and Fig. S1B (with N = 1.5 ⋅ 104). Direct evidence for the increasingly greedy nature of the dynamics is provided in Fig. S5A, which shows how the fraction of mutational steps that go to the fittest neighbor grows from fgs ≃ 0.63 for N = 210 to fgs ≃ 0.88 for N = 220.
As N is increased further, the number of first step mutants, including deleterious ones, becomes larger and therefore second step mutants are created more frequently. If these second step mutants are sufficiently fit, they can eventually take over the population, effectively tunneling through (38) (or leaping over) the intermediate state. Such events yield a mechanism for crossing fitness valleys that becomes increasingly important for increasing N, as can be verified in Fig. 1 and Figs. S1–S4 and S5B. As long as only a few second step mutants are produced by this mechanism, the dynamics becomes again less deterministic, as it depends sensitively on which mutants are randomly created and the number of possible second step mutations is enormous. Although some indication of this effect can be seen in the comparison between Fig. 1C and Fig. 1D, it is brought out more clearly by the quantitative analysis that we turn to next.
Entropy Analysis.
When quantifying the degree of determinism of the evolutionary dynamics, it is important to distinguish between the repeatability of endpoints and of the paths taken, as well as between different types of paths. That this distinction matters is easily understood in the context of infinite population sizes. In that limit, the population always finds the GO and this optimal state always takes over the population. Thus, with respect to endpoints, the dynamics becomes totally deterministic. However, in the same limit, all possible paths (in the sense of LODs) to the GO will be taken, and the predictability of LODs should be low for very large N. In contrast, the most populated genotype follows a unique path (POM) in the infinite population limit (44).
To study the determinism of the dynamics on more quantitative grounds, it is convenient to define entropies with respect to the endpoints and the paths taken, respectively. The standard choice for the entropy function is 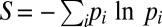 , where the sum runs over all endpoints (paths) and pi is the probability to observe a certain endpoint (path). The pi values are approximated by the fraction of times an endpoint (path) was observed among replicate simulation runs. The entropy is more appropriate to quantify determinism than just counting the number of endpoints or paths observed as it includes information about how often each outcome occurs. Note that the findings to be presented in the following do not depend strongly on the specific choice of the entropy function. Largely equivalent results are obtained for similar observables such as the repeatability measure
, where the sum runs over all endpoints (paths) and pi is the probability to observe a certain endpoint (path). The pi values are approximated by the fraction of times an endpoint (path) was observed among replicate simulation runs. The entropy is more appropriate to quantify determinism than just counting the number of endpoints or paths observed as it includes information about how often each outcome occurs. Note that the findings to be presented in the following do not depend strongly on the specific choice of the entropy function. Largely equivalent results are obtained for similar observables such as the repeatability measure 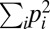 used in refs. 49 and 15.
used in refs. 49 and 15.
It is important to notice that the observed ensemble of pathways generally depends strongly on the initial state, as is apparent when comparing the arrow plots in Fig. 1 to Figs. S2–S4 (the corresponding entropies are shown in Fig. S6 A and B). Although this effect is interesting in itself, here we focus on investigating how entropies behave on average when considering ensembles of equivalent starting points. To maximize the number of possible starting points on the A. niger landscape, we consider all paths that start at one of the 46 viable genotypes at Hamming distance d = 4 from the GO. To illustrate the role of the scales Nμ and Nμ2, we calculate the entropies for a broad range of mutation rates.
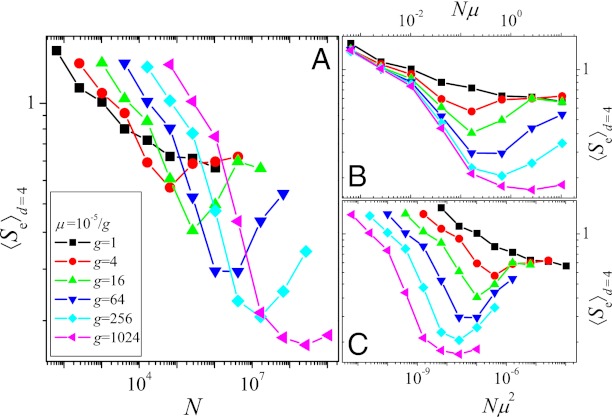
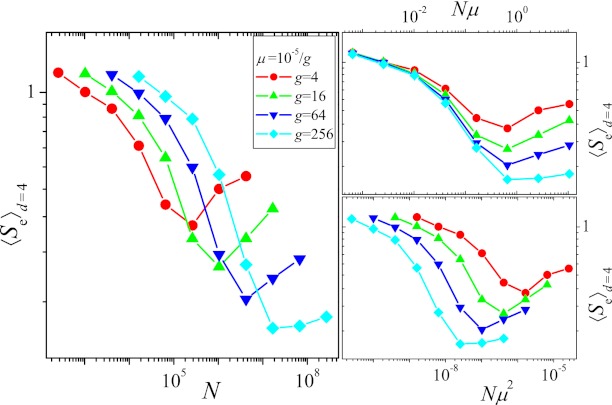
In Fig. 2, we plot the average endpoint entropy for starting points at Hamming distance d = 4, 〈Se〉d=4, obtained in the following way: First, the entropy was determined separately for each starting point by carrying out 100 independent evolutionary runs up to time T = 215. Subsequently, the entropies were averaged over the different starting points, and the procedure was repeated for different values of μ and N. Apart from the case with the largest mutation rate (μ = 10−5), one observes an initial decrease of the entropy followed by a subsequent rise with increasing N (Fig. 2A). This can be explained by means of the qualitative arguments given in the last section: The initial decrease of the entropy, i.e., increase of determinism of the dynamics, is due to the competition between single mutants causing the dynamics to become greedier, whereas the subsequent increase is a consequence of the increased appearance of double mutants. Fig. S5A shows that the fraction fgs of greedy steps goes through a maximum around the same value of N at which the entropy is minimal.
Fig. 2.
(A) Entropy with respect to endpoints, 〈Se〉d=4, vs. population size. (B and C) Same as A but entropy is plotted vs. Nμ and Nμ2, respectively. Each curve was obtained from simulations covering T = 215 generations and averaged over the 46 different possible starting points with Hamming distance d = 4 from the GO, with 100 independent runs from each starting point. Mutation rates vary between μ = 10−5 and 10−5/210 ∼ 10−8.
The initial transition toward greedier dynamics depends on the production of nearest neighbor mutants, the supply rate of which is proportional to Nμ. In contrast, the subsequent increase of the entropy due to the appearance of double mutants is linked to their production rate ∼ Nμ2. The separation between these two scales becomes more pronounced the smaller the mutation rate μ, and correspondingly the minimum value reached by the entropy decreases with decreasing μ, as is clearly seen in Fig. 2. To make apparent the importance of the scales Nμ and Nμ2, in Fig. 2 B and C we plot the entropy as a function of Nμ and Nμ2, respectively. The approximate collapse of the decreasing parts of the curves in Fig. 2B and of the increasing parts in Fig. 2C immediately affirms the roles played by the two scales. The lack of an increase of the entropy for the largest mutation rate considered here is most likely due to the lack of clear separation of the two scales.
We also calculated the averaged entropy with respect to the paths, 〈Sp〉d=4, for the same ensemble of pathways (Fig. S7). Despite the expected distinct behaviors of the two quantities in the limit N → ∞, we find essentially the same N dependence as for 〈Se〉d=4. This reflects the fact that, even for the largest values of N and μ used here, populations are likely to get trapped at local fitness maxima. New paths that open when increasing N often lead to formerly unexplored local maxima, which implies that an increase of the number of explored paths is strongly correlated with the number of endpoints.
Finding the Fittest State.
In the SSWM regime, adaptation proceeds through single mutational steps moving uphill in fitness, and the fixation probability is independent of N or μ (19–21). As a consequence, the statistical weights of different evolutionary trajectories are also independent of N, and the SSWM regime should therefore appear as a plateau at small population sizes in the graphs showing pathway or endpoint entropies as a function of N. The fact that no such plateau is observed in Fig. 2 and Fig. S7 shows that clonal interference already plays an appreciable role in the considered range of parameters, and that smaller populations or mutation rates would be needed to fully realize the SSWM regime.
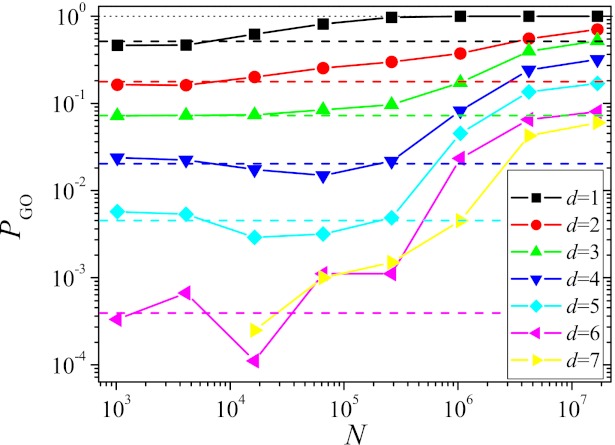
Other quantities, however, seem to be more robust with respect to a certain level of clonal interference. As an example, we show in Fig. 3 the probability PGO for the largest subpopulation to end up on the GO. The figure shows PGO as a function of N averaged over starting points at a given Hamming distance d from the GO. The averaging is necessary, as the probability strongly depends on the specific starting point (Fig. S6C). For each starting point, 100–1,000 runs were carried out over T = 217 generations.
Fig. 3.
Probability PGO for the largest subpopulation to end up at the GO within T = 217 generations vs. population size, for all Hamming distances d for which viable starting genotypes exist. The horizontal dashed lines show the SSWM predictions. The mutation rate was μ = 10−5/16.
The probability of finding the fittest state has a plateau for small N that coincides rather well with the SSWM value indicated by the horizontal dashed lines. The deviations that are particularly pronounced for d = 4 and 5 are most likely due to valley crossings that happen with a low probability for small populations but are prohibited within the SSWM approximation. When PGO is small, these valley crossings, albeit very rare, may open up additional mutational pathways that are not accessible to SSWM dynamics because they contain at least one fitness decreasing step, thus increasing PGO over the SSWM value. With increasing N, clonal interference sets in, making the dynamics more greedy and thus more deterministic. As this implies a decrease in the number of different paths that are explored, the probability to find the GO decreases below the SSWM level. This effect is more pronounced the further away the starting point is from the GO, as the probability for the greedy dynamics to miss the GO by leading the population to a suboptimal local fitness maximum increases. Only when N is increased further to such large values that double mutants are regularly produced, the dynamics becomes again more stochastic, leading to a higher number of explored paths and thus to a higher PGO exceeding the SSWM value. As for the entropy measures discussed previously, the variation of PGO with population size is distinctly nonmonotonic.
Apart from the probability for finding the fittest state, it is also of interest to study through which mutational pathways this state is reached. Here, we are particularly interested in the role played by paths along which fitness increases monotonically [monotonically increasing pathways (MIPs)]. These are the only paths that are accessible to adaptation in the SSWM regime and have therefore been at the focus of much recent theoretical and empirical work on fitness landscapes (10, 11, 22–27). What we would like to clarify is whether (or when) such paths are actually the dominating ones when it comes to finding the fittest state, and to what extent they are realized by the dynamics.
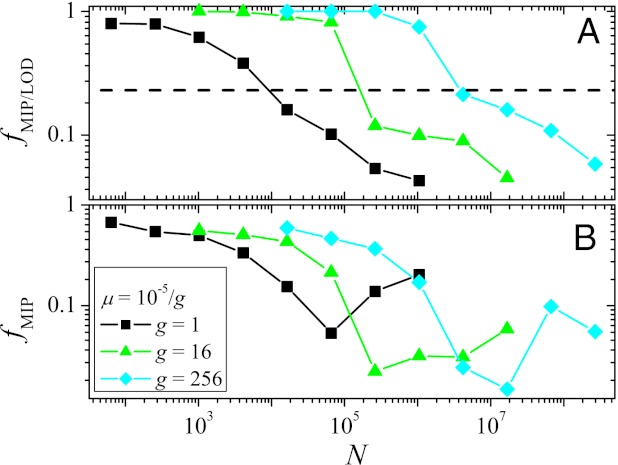
To address these questions, we identified all MIPs that start at Hamming distance d = 4 from the GO, restricting ourselves to direct paths along which the distance to the GO decreases at every step. As a first measure, we computed the fraction of MIPs among all observed LODs that reach the GO, fMIP/LOD. This quantity was averaged over 100 realizations from each starting point with Hamming distance 4 from the GO from which at least one such path exists (Fig. 4A). One finds that at small N, almost all successful paths are monotonically increasing in fitness. However, as N increases, fMIP/LOD decreases rapidly, showing that the MIPs become increasingly less relevant for adaptation. The dashed line in Fig. 4A represents the ratio of the number of MIPs to the total number of direct paths, equal to d!, averaged over all starting points at d = 4. Values of fMIP/LOD below this line indicate that MIPs are selected even less frequently than would be expected if all direct paths were equally likely.
Fig. 4.
(A) The fraction of MIPs among all paths observed in 100 runs from each of the 46 viable starting genotypes at distance d = 4 from the GO that reach the GO within T = 215 generations is plotted vs. N. The horizontal dashed line shows the expected fraction if all paths occurred with equal probability. (B) Fraction of observed MIPs among all possible MIPs as a function of N. In both panels, averages are taken over starting points for which at least one MIP exists. The poor statistics are due to the fact that, in general, only a few MIPs are observed.
Furthermore, we have measured the fraction fMIP of MIPs that are actually observed within the 100 simulational runs (Fig. 4B). This quantity displays a nonmonotonic dependence on N that can be explained in similar terms as for the entropies. It should, however, be noticed that, even at small N, less than 70% of all existing MIPs are observed. Thus, the sheer existence of, in principle, easily accessible paths leading to high fitness genotypes does not guarantee that they are actually realized by the dynamics. This can also be concluded from the low values of PGO observed in Fig. 3 for small N.
Comparison with Model Landscapes.
To demonstrate that the results described so far are not caused by the idiosyncrasies of the specific empirical landscape used in this work, we carried out simulations on a family of random model landscapes tuned to reproduce the overall features of the A. niger fitness data set. The model we consider is a slight variation of the rough Mount Fuji (RMF) model (26, 27) originally introduced in ref. 41. Within the RMF model, the fitness value wi of a genotype i is determined according to the following:
where di is the Hamming distance of i to a reference state whose fitness is set to 1 and will be the GO, c1 and c2 are constants, and ξi is a Gaussian random variable with mean zero and SD σ. The constants c1 and c2 were obtained from the A. niger fitness data as follows: First, we averaged over all fitness values at a given Hamming distance di ≥ 1 from the GO, including the states with zero fitness corresponding to nonviable genotypes (26). Then a straight line was fitted to the averaged values plotted against Hamming distance. The slope yields c1 ≈ 0.064, and for the intercept we obtain the estimate c2 ≈ 0.730. The variance of the fitness values yields the estimate σ2 ≈ 0.091 for the variance of the ξi. Only values wi < 1 are accepted, to ensure that the GO is located at the reference genotype. In cases when Eq. 1 yields a negative value, the corresponding fitness is set to zero. In principle the nonviable genotypes in the landscape could be modeled explicitly, e.g., along the lines of ref. 26. However, we prefer to keep the model simple and do not include a separate treatment of nonviable states.
The observed qualitative features have been reproduced by simulations of the RMF model over a broad range of parameters, but here we focus on the specific “A. niger” parameter set described above, which optimally matches the empirical landscape (see Fig. S8 for results covering a broader range of parameters). In Fig. 5 and Fig. S9, we plot the quantities obtained from simulations of adaptation on this model landscape. We considered 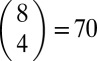 different starting points at Hamming distance d = 4 from the GO, and 100 independent runs from each of them were carried out. For each of the starting points, a new fitness landscape was created using Eq. 1.
different starting points at Hamming distance d = 4 from the GO, and 100 independent runs from each of them were carried out. For each of the starting points, a new fitness landscape was created using Eq. 1.
Fig. 5.
Endpoint entropy vs. population size N obtained from simulations on the RMF fitness landscapes with A. niger parameters, to be compared with Fig. 2.
Fig. 5 and Fig. S9A show that the entropies obtained for the model landscapes display a similar nonmonotonic dependence on N and μ as the empirical landscape. Again, rescaling N by μ and μ2, respectively, leads to an approximate data collapse of the decreasing and increasing parts of the entropy curves, respectively. Although comparison with Fig. 2 and Fig. S7 reveals that the values of the entropies and the positions of the respective minima are not quantitatively recovered by the model, the qualitative behavior is well reproduced.
Fig. S9B depicts a similar comparison for the probability to reach the state with the highest fitness. Because PGO ≪ 1 in most cases, this quantity is strongly affected by rare events and displays massive fluctuations between different realizations of the RMF model landscape. Averaging over realizations is therefore not appropriate for the comparison with the A. niger landscape. Instead, in Fig. S9B, we display data obtained for individual landscape realizations, which show that the overall shape of the variation of PGO with N is reproduced by the model. Moreover, the supplementary results in Fig. S8 show that the nonmonotonic variation of the entropy with population size persists whenever the fitness landscape is sufficiently rugged, and disappears only when the limiting case of a smooth, additive landscape is approached.
Discussion
The repeatability of evolutionary trajectories in replicate populations is determined jointly by the distribution of the fitness effects of beneficial mutations, by their epistatic interactions, and by the rate at which they appear in the population. Whereas previous work has addressed primarily the first two determinants of evolutionary predictability (14, 18, 22, 26, 49, 50), here we focused on the effect of mutation supply mediated by the population size N and the mutation rate μ. By performing simulations on an experimentally measured fitness landscape, we ensured a realistic representation of the distribution of mutational effects and their epistatic interactions.
Our key observation is that, because of the distinct roles played by the supply rate of single (∼Nμ) and double (∼Nμ2) mutations, evolutionary predictability as quantified by the entropy measures Se and Sp varies nonmonotonically with population size. Simulation results for the RMF model suggest that this behavior is generic whenever the underlying fitness landscape is rugged with many local optima, as is often the case for empirically determined fitness landscapes (27, 51). Similar to earlier observations of an evolutionary advantage of small populations in complex fitness landscapes (35–37), the phenomenon depends crucially on the clonal interference among beneficial mutations and cannot be captured within the commonly used SSWM approximation. This also implies that the restriction of evolutionary accessibility to pathways with monotonically increasing fitness (MIPs) assumed in a number of recent studies (10, 22, 24, 26) may be of limited relevance to adaptation.
Although the endpoint entropy Se is easier to access experimentally than the path entropy Sp, at least partial information about adaptive pathways can be inferred from microbial evolution experiments (12, 13, 45). Parallel evolution has been observed on several occasions, but very few studies explicitly addressed the effect of population size on repeatability. Among those, one found an increase of genotypic diversity with increasing population size (45). Other experiments have addressed the population size dependence of phenotypic diversity on the level of fitness trajectories. One study using Escherichia coli found a pronounced reduction of the variability of fitness trajectories with increasing population size (36), but another study using Aspergillus nidulans found no effect (52). More experimental work under precisely controlled conditions is clearly needed to test the predictions of the present article.
Materials and Methods
Empirical Fitness Landscape.
The construction of the A. niger strains and the measurement of their fitness values has been explained in detail elsewhere (47). The fitness landscape consists of the wild-type strain and combinations of eight marker mutations: fwnA1 (fawn-colored conidiospores), argH12 (arginine deficiency), pyrA5 (pyrimidine deficiency), leuA1 (leucine deficiency), pheA1 (phenyl-alanine deficiency), lysD25 (leucine deficiency), oliC2 (oligomycin resistance), and crnB12 (chlorate resistance). Of the 28 = 256 possible combinations, a total of 186 were found to be viable and assigned nonzero Wrightian fitness (26). Among these, there are four mutants with seven mutations each, i.e., incorporating all but one mutation. In the order in which the genotypes were presented in table S1 of ref. 26, these are genotypes 250 (all but pyrA5), 251 (all but leuA1), 252 (all but pheA1), and 253 (all but lysD25).
Evolutionary Dynamics.
The simulations presented here were performed using standard Wright–Fisher dynamics according to the following algorithm:
i) Draw the number nμ of mutation events in a generation from an exponential distribution with mean λ = NLμ, where N is the population size, L is the number of loci, and μ is the mutation rate.
ii) The nμ mutations are distributed among the present mutations with probabilities corresponding to their frequencies. The possibility of individuals accumulating several mutations in a single time step is neglected. Mutations at all loci are chosen with equal probability.
iii) Selection is carried out in two steps. First, frequencies are evolved analytically according to
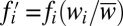 , where fi denotes the frequency of the ith state before selection, i.e., at generation t, the wi denote the respective fitnesses, and
, where fi denotes the frequency of the ith state before selection, i.e., at generation t, the wi denote the respective fitnesses, and 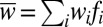 denotes the mean fitness of the population.
denotes the mean fitness of the population.iv) Finally, the frequencies at time step t + 1 are obtained by drawing N individuals from a multinomial distribution with probabilities
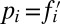 .
.
Supplementary Material
Acknowledgments
We thank J.-M. Park for useful discussions. This work was supported by Deutsche Forschungsgemeinschaft within Sonderforschungsbereich 680.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1213613110/-/DCSupplemental.
References
- 1.Beatty J. Replaying life’s tape. J Philos. 2006;7:336–362. [Google Scholar]
- 2.Conway Morris S. Evolution: Like any other science it is predictable. Philos Trans R Soc Lond B Biol Sci. 2010;365(1537):133–145. doi: 10.1098/rstb.2009.0154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gould SJ. Wonderful Life. New York: Norton; 1989. [Google Scholar]
- 4.Conway Morris S. Life’s Solution: Inevitable Humans in a Lonely Universe. Cambridge, UK: Cambridge Univ Press; 2003. [Google Scholar]
- 5.Travisano M, Mongold JA, Bennett AF, Lenski RE. Experimental tests of the roles of adaptation, chance, and history in evolution. Science. 1995;267(5194):87–90. doi: 10.1126/science.7809610. [DOI] [PubMed] [Google Scholar]
- 6.Cooper TF, Rozen DE, Lenski RE. Parallel changes in gene expression after 20,000 generations of evolution in Escherichia coli. Proc Natl Acad Sci USA. 2003;100(3):1072–1077. doi: 10.1073/pnas.0334340100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Blount ZD, Borland CZ, Lenski RE. Historical contingency and the evolution of a key innovation in an experimental population of Escherichia coli. Proc Natl Acad Sci USA. 2008;105(23):7899–7906. doi: 10.1073/pnas.0803151105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Saxer G, Doebeli M, Travisano M. The repeatability of adaptive radiation during long-term experimental evolution of Escherichia coli in a multiple nutrient environment. PLoS One. 2010;5(12):e14184. doi: 10.1371/journal.pone.0014184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wichman HA, Brown CJ. Experimental evolution of viruses: Microviridae as a model system. Philos Trans R Soc Lond B Biol Sci. 2010;365(1552):2495–2501. doi: 10.1098/rstb.2010.0053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Weinreich DM, Delaney NF, Depristo MA, Hartl DL. Darwinian evolution can follow only very few mutational paths to fitter proteins. Science. 2006;312(5770):111–114. doi: 10.1126/science.1123539. [DOI] [PubMed] [Google Scholar]
- 11.Lozovsky ER, et al. Stepwise acquisition of pyrimethamine resistance in the malaria parasite. Proc Natl Acad Sci USA. 2009;106(29):12025–12030. doi: 10.1073/pnas.0905922106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Salverda MLM, et al. Initial mutations direct alternative pathways of protein evolution. PLoS Genet. 2011;7(3):e1001321. doi: 10.1371/journal.pgen.1001321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Toprak E, et al. Evolutionary paths to antibiotic resistance under dynamically sustained drug selection. Nat Genet. 2012;44(1):101–105. doi: 10.1038/ng.1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schenk MF, Szendro IG, Krug J, de Visser JAGM. Quantifying the adaptive potential of an antibiotic resistance enzyme. PLoS Genet. 2012;8(6):e1002783. doi: 10.1371/journal.pgen.1002783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Roy SW. Probing evolutionary repeatability: Neutral and double changes and the predictability of evolutionary adaptation. PLoS One. 2009;4(2):e4500. doi: 10.1371/journal.pone.0004500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wahl LM, Krakauer DC. Models of experimental evolution: The role of genetic chance and selective necessity. Genetics. 2000;156(3):1437–1448. doi: 10.1093/genetics/156.3.1437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jain K, Krug J. Deterministic and stochastic regimes of asexual evolution on rugged fitness landscapes. Genetics. 2007;175(3):1275–1288. doi: 10.1534/genetics.106.067165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lobkovsky AE, Wolf YI, Koonin EV. Predictability of evolutionary trajectories in fitness landscapes. PLoS Comput Biol. 2011;7(12):e1002302. doi: 10.1371/journal.pcbi.1002302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gillespie JH. A simple stochastic gene substitution model. Theor Popul Biol. 1983;23(2):202–215. doi: 10.1016/0040-5809(83)90014-x. [DOI] [PubMed] [Google Scholar]
- 20.Gillespie JH. Molecular evolution over the mutational landscape. Evolution. 1984;38:1116–1129. doi: 10.1111/j.1558-5646.1984.tb00380.x. [DOI] [PubMed] [Google Scholar]
- 21.Orr HA. The population genetics of adaptation: The adaptation of DNA sequences. Evolution. 2002;56(7):1317–1330. doi: 10.1111/j.0014-3820.2002.tb01446.x. [DOI] [PubMed] [Google Scholar]
- 22.Weinreich DM, Watson RA, Chao L. Perspective: Sign epistasis and genetic constraint on evolutionary trajectories. Evolution. 2005;59(6):1165–1174. [PubMed] [Google Scholar]
- 23.Poelwijk FJ, Kiviet DJ, Weinreich DM, Tans SJ. Empirical fitness landscapes reveal accessible evolutionary paths. Nature. 2007;445(7126):383–386. doi: 10.1038/nature05451. [DOI] [PubMed] [Google Scholar]
- 24.Carneiro M, Hartl DL. Colloquium papers: Adaptive landscapes and protein evolution. Proc Natl Acad Sci USA. 2010;107(Suppl 1):1747–1751. doi: 10.1073/pnas.0906192106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.da Silva J, Coetzer M, Nedellec R, Pastore C, Mosier DE. Fitness epistasis and constraints on adaptation in a human immunodeficiency virus type 1 protein region. Genetics. 2010;185(1):293–303. doi: 10.1534/genetics.109.112458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Franke J, Klözer A, de Visser JAGM, Krug J. Evolutionary accessibility of mutational pathways. PLoS Comput Biol. 2011;7(8):e1002134. doi: 10.1371/journal.pcbi.1002134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Szendro IG, Schenk MF, Franke J, Krug J, de Visser JAGM. 2012. Quantitative analyses of empirical fitness landscapes. arXiv:1202.4378.
- 28.Gerrish PJ, Lenski RE. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102–103(1–6):127–144. [PubMed] [Google Scholar]
- 29.Wilke CO. The speed of adaptation in large asexual populations. Genetics. 2004;167(4):2045–2053. doi: 10.1534/genetics.104.027136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Park SC, Krug J. Clonal interference in large populations. Proc Natl Acad Sci USA. 2007;104(46):18135–18140. doi: 10.1073/pnas.0705778104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Park SC, Simon D, Krug J. The speed of evolution in large asexual populations. J Stat Phys. 2010;138:381–410. [Google Scholar]
- 32.Rozen DE, de Visser JAGM, Gerrish PJ. Fitness effects of fixed beneficial mutations in microbial populations. Curr Biol. 2002;12(12):1040–1045. doi: 10.1016/s0960-9822(02)00896-5. [DOI] [PubMed] [Google Scholar]
- 33.Schiffels S, Szöllosi GJ, Mustonen V, Lässig M. Emergent neutrality in adaptive asexual evolution. Genetics. 2011;189(4):1361–1375. doi: 10.1534/genetics.111.132027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Orr HA. A minimum on the mean number of steps taken in adaptive walks. J Theor Biol. 2003;220(2):241–247. doi: 10.1006/jtbi.2003.3161. [DOI] [PubMed] [Google Scholar]
- 35.Jain K, Krug J, Park SC. Evolutionary advantage of small populations on complex fitness landscapes. Evolution. 2011;65(7):1945–1955. doi: 10.1111/j.1558-5646.2011.01280.x. [DOI] [PubMed] [Google Scholar]
- 36.Rozen DE, Habets MGJL, Handel A, de Visser JAGM. 2008. Heterogeneous adaptive trajectories of small populations on complex fitness landscapes. PLoS One 3:e1715.
- 37.Handel A, Rozen DE. The impact of population size on the evolution of asexual microbes on smooth versus rugged fitness landscapes. BMC Evol Biol. 2009;9:236. doi: 10.1186/1471-2148-9-236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Iwasa Y, Michor F, Nowak MA. Stochastic tunnels in evolutionary dynamics. Genetics. 2004;166(3):1571–1579. doi: 10.1534/genetics.166.3.1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Weinreich DM, Chao L. Rapid evolutionary escape by large populations from local fitness peaks is likely in nature. Evolution. 2005;59(6):1175–1182. [PubMed] [Google Scholar]
- 40.Weissman DB, Desai MM, Fisher DS, Feldman MW. The rate at which asexual populations cross fitness valleys. Theor Popul Biol. 2009;75(4):286–300. doi: 10.1016/j.tpb.2009.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Aita T, et al. Analysis of a local fitness landscape with a model of the rough Mt. Fuji-type landscape: Application to prolyl endopeptidase and thermolysin. Biopolymers. 2000;54(1):64–79. doi: 10.1002/(SICI)1097-0282(200007)54:1<64::AID-BIP70>3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
- 42.Lenski RE, Ofria C, Pennock RT, Adami C. The evolutionary origin of complex features. Nature. 2003;423(6936):139–144. doi: 10.1038/nature01568. [DOI] [PubMed] [Google Scholar]
- 43.Østman B, Hintze A, Adami C. Impact of epistasis and pleiotropy on evolutionary adaptation. Proc R Soc B Biol Sci. 2012;279(1727):247–256. doi: 10.1098/rspb.2011.0870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jain K, Krug J. Evolutionary trajectories in rugged fitness landscapes. J Stat Mech. 2005;2005:P04008. [Google Scholar]
- 45.Miller CR, Joyce P, Wichman HA. Mutational effects and population dynamics during viral adaptation challenge current models. Genetics. 2011;187(1):185–202. doi: 10.1534/genetics.110.121400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Woods RJ, et al. Second-order selection for evolvability in a large Escherichia coli population. Science. 2011;331(6023):1433–1436. doi: 10.1126/science.1198914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.de Visser JAGM, Hoekstra RF, van den Ende H. Test of interaction between genetic markers that affect fitness in Aspergillus niger. Evolution. 1997;51:1499–1505. doi: 10.1111/j.1558-5646.1997.tb01473.x. [DOI] [PubMed] [Google Scholar]
- 48.Kimura M. On the probability of fixation of mutant genes in a population. Genetics. 1962;47:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Orr HA. The probability of parallel evolution. Evolution. 2005;59(1):216–220. [PubMed] [Google Scholar]
- 50.Joyce P, Rokyta DR, Beisel CJ, Orr HA. A general extreme value theory model for the adaptation of DNA sequences under strong selection and weak mutation. Genetics. 2008;180(3):1627–1643. doi: 10.1534/genetics.108.088716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kouyos RD, et al. Exploring the complexity of the HIV-1 fitness landscape. PLoS Genet. 2012;8(3):e1002551. doi: 10.1371/journal.pgen.1002551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Schoustra SE, Bataillon T, Gifford DR, Kassen R. The properties of adaptive walks in evolving populations of fungus. PLoS Biol. 2009;7(11):e1000250. doi: 10.1371/journal.pbio.1000250. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.