Measuring collective transport by defined numbers of processive and nonprocessive kinesin motors

Abstract

Intracellular transport is thought to be achieved by teams of motor proteins bound to a cargo. However, the coordination within a team remains poorly understood as a result of the experimental difficulty in controlling the number and composition of motors. Here, we developed an experimental system that links together defined numbers of motors with defined spacing on a DNA scaffold. By using this system, we linked multiple molecules of two different types of kinesin motors, processive kinesin-1 or nonprocessive Ncd (kinesin-14), in vitro. Both types of kinesins markedly increased their processivities with motor number. Remarkably, despite the poor processivity of individual Ncd motors, the coupling of two Ncd motors enables processive movement for more than 1 μm along microtubules (MTs). This improvement was further enhanced with decreasing spacing between motors. Force measurements revealed that the force generated by groups of Ncd is additive when two to four Ncd motors work together, which is much larger than that generated by single motors. By contrast, the force of multiple kinesin-1s depends only weakly on motor number. Numerical simulations and single-molecule unbinding measurements suggest that this additive nature of the force exerted by Ncd relies on fast MT binding kinetics and the large drag force of individual Ncd motors. These features would enable small groups of Ncd motors to crosslink MTs while rapidly modulating their force by forming clusters. Thus, our experimental system may provide a platform to study the collective behavior of motor proteins from the bottom up.

The active intracellular transport of a large variety of cargos is fundamental for many cellular processes. In such transport, molecular motors bound to the cargo usually work together in teams (1–3). These teams can consist of one or several types of motor, with varying mechanical properties, including velocity, directionality, and processivity (2–5). Whereas processive motors take hundreds of steps before they detach from a track, nonprocessive motors detach after a single step. Some motors such as kinesin-5, kinesin-14, and cytoplasmic dynein exhibit low or variable processivity depending on the local environment, including modified microtubule (MT) lattice and the arrangement of MT tracks (6–9). All types of motors have been shown to increase the force or run length of cargos, which are generally larger than can be achieved by single motors (10–12), and many studies have suggested that the number of motors in these teams regulates the transport (3, 5, 10). However, a recent in vivo study has shown that the copy number of highly processive kinesin-1 had little influence on the velocity and run length of cargos (1). These observations raise the question of how the mechanical properties of individual motors contribute to the collective function and the regulation of the transport.

To address this issue, one must identify the numbers and types of motor proteins present on a cargo. The practical problem associated with the study of collective transport is that it is extremely difficult to determine the number of motors on a cargo. Nonetheless, the exact number (not the average number) of motors is critical, because the typical number of motors on subcellular cargos is so small (1, 3, 5, 13) that stochastic effects would dominate rather than be averaged (14). Despite the remarkable progress of single-molecule techniques, controlling the motor number remains challenging for technical reasons. A pioneering investigation that used two coupled kinesin-1 dimers linked by a DNA duplex has opened up the possibility of studying collective transport (15). However, the motor number is limited to two molecules as a result of the DNA duplex formation.

Here, we present the systematic study of the impact of motor number on collective transport. Previous studies on collective transport have mainly focused on processive motors, and our results for processive kinesin-1 at low load are generally consistent with previously proposed theories (14, 16–18). However, we made unexpected observations when a load was imposed, and report the distinct properties of nonprocessive motors that might be required for efficient collective transport.

Results and Discussion

Self-Assembly of DNA–Motor Assemblies.

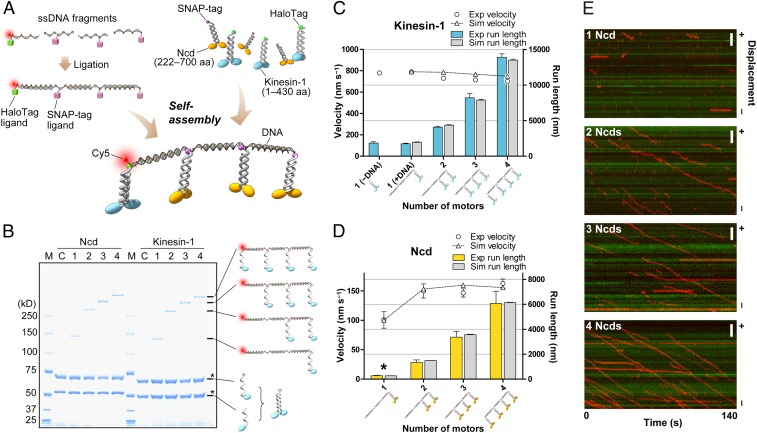
Our approach was based on the site-specific linkage between DNA and an enzyme tag fused to a motor protein (Fig. 1A and SI Appendix, Fig. S1E). Following the modification of DNA with an enzyme tag ligand, motor proteins can easily bind DNA via a highly stable covalent bond that allows quantitative determination of motor number by SDS/PAGE (Fig. 1B). To construct the DNA scaffolds, each of four DNA fragments was separately modified with the ligand of the desired enzyme tag or left unmodified, and ligated into a single DNA scaffold (SI Appendix, Fig. S1F). The DNA–motor assemblies were then self-assembled by simply mixing the DNA scaffold with motor proteins, each carrying a single enzyme tag. Fig. 1B shows that this technique can precisely control the number of motors connected to the individual DNA scaffolds.

Fig. 1.

Self-assembly and collective motility of kinesins. (A) Schematic representation of DNA–motor construction (not drawn to scale). The typical spacing between motors is 22.7 nm, and the lengths of kinesin, SNAP-tag, and HaloTag are ∼17, 4.3, and 4.8 nm, respectively. (B) SDS/PAGE analysis of the DNA–motor assemblies. SDS/PAGE was performed on a 3% to 10% polyacrylamide gel. The numbers at the top of each lane represent the number of molecules engaged to the DNA scaffolds. Bands with asterisks denote an excessive amount of unreacted dimers. Note that the dimers consist of two different polypeptides, one of which carries a single enzyme tag. Unreacted dimers are not visible by fluorescence microscopy. M, markers; C, control lanes without DNA scaffold. (C) Velocities and run lengths of the assemblies including one, two, three, or four kinesin-1 dimer(s) linked by flexible DNA scaffolds (22.7-nm spacing). Open circles and blue bars show experimental data. Run lengths are corrected for photobleaching. The velocity distributions of the two groups (single and four kinesin-1 motors) differed significantly (Mann–Whitney test, P < 0.0001, two-tailed). Triangles connected by the dashed line and bars in gray show the simulated data. Error bar represents SEM. The simulated data were obtained by averaging the three data sets, each consisting of 1,000 traces. (D) Velocities and run lengths of the Ncd assemblies. The DNA scaffolds and the legend are the same as in C. Note that the scored run length for single Ncd (asterisk) is an overestimation (see text). (E) Kymographs showing the motion of the assemblies including (from top to bottom) one, two, three, or four Ncd dimer(s) linked by flexible DNA scaffolds with 22.7-nm spacing (red) on Cy3-labeled MTs (green). Plus and minus symbols at right refer to the polarity of the MT. (Scale bars, 3 μm.)

To reconstitute collective transport in vitro, we purified two different types of kinesin motor proteins. First, we used the best-studied kinesin motor, kinesin-1, which moves processively toward the MT plus end. Second, we chose the kinesin-14 family member Ncd, which moves in a nonprocessive manner toward the MT minus end, although it can move short distances when its tail interacts with MTs (6). To quantify the movement of multiple-motor assemblies along MTs, we tracked the single Cy5 dyes attached to the DNA scaffold by using total internal reflection fluorescence microscopy (Fig. 1 A and E). The photobleaching behavior and intensity profiles of fluorescent spots indicated that we were observing single DNA scaffolds, excluding the possibility of DNA aggregation (SI Appendix, Fig. S2). We also confirmed that the free motors present in the assay solution did not lead to traffic jams on MTs or the aggregation of motors (SI Appendix, Fig. S5).

Collective Motility of Processive Kinesin-1.

We first examined the collective motility of processive kinesin-1. The kinesin-1 motors were linked together by flexible DNA scaffolds with a spacing of 22.7 nm (SI Appendix, Fig. S3). The length of each kinesin including the SNAP-tag is approximately 21 nm. Fig. 1C shows the average velocities and run lengths of the multiple-kinesin assemblies vs. the number of kinesin-1 molecules (SI Appendix, Fig. S6 and Table S1, and Movies S1 and S2). Whereas the run length markedly increased with the number of motors, the velocity decreased slightly, suggesting that processive kinesin-1 motors in the assemblies slightly interfere with each other.

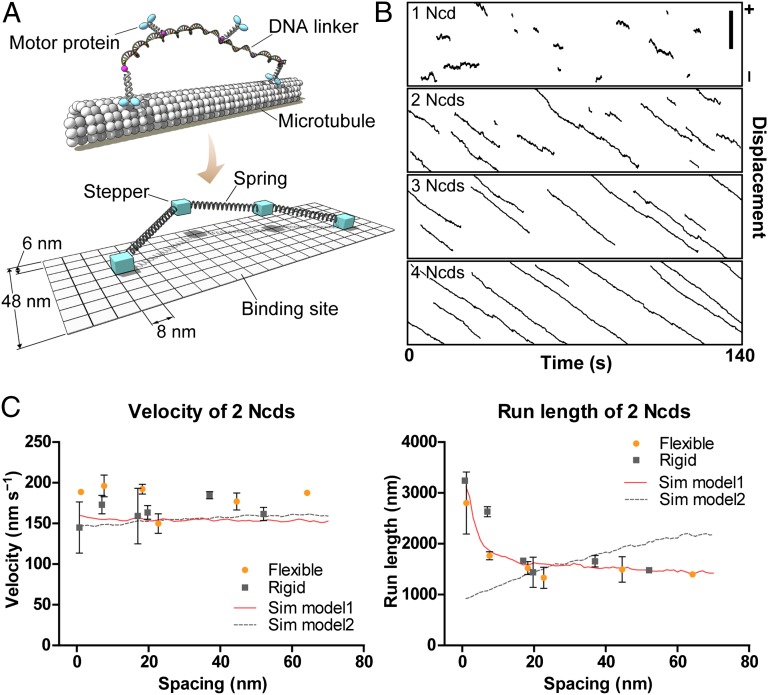
To compare experimental observations with simulations, data obtained from both approaches should be analyzed identically. However, experimentally obtained trajectories are limited by MT length and the microscope field of view. Conversely, very short runs cannot be reliably measured. To obtain individual simulated trajectories for identical analysis with experimental data, we used a Monte Carlo simulation rather than solving the master equation of mean-field theory. Another advantage of the simulation approach was that we could take account of the stochastic effects that would govern the transient motion of multiple-molecule assemblies in the small number limit. For simulation, we built a mechanical model based on earlier theoretical studies (14, 16). The details of the model are provided in the SI Appendix. Briefly, each motor is a stochastic stepper that binds to discrete binding sites on a MT. The linkage between motor domains was modeled as a special spring that exerts Hookean restoring force only when stretched beyond its rest length (Fig. 2A). Simulated runs were detected with the same criteria and analyzed in the same manner as for actual experimental data. To compare experiment and theory, the experimental data were fitted to a simulation model by automated scanning of the parameter space. Note that the kinesin-1 model was severely constrained by the experimentally obtained parameters; the free parameters were on-rate and linker stiffness alone. Fig. 1C shows that the simulation successfully reproduced the experimental data. Without the limitation of track length, the simulated run length reached tens of micrometers with four kinesins (SI Appendix, Fig. S8), which is consistent with previous theoretical studies. However, our data are not consistent with the subadditive run length reported from a previous study that used two coupled kinesin-1s linked by a 50-nm DNA duplex (12). The difference is most likely caused by the difference in the elastic components of the two constructs (SI Appendix, p. 16).

Fig. 2.

Monte Carlo simulations of collective motility. (A) Schematic of the in vitro experiment (Upper) and the simulation model (Lower). (B) Kymographs showing simulated motion of assemblies including (from top to bottom) one, two, three, or four Ncd dimer(s) linked by flexible DNA scaffolds (22.7-nm spacing). Plus and minus symbols at right refer to the polarity of the MT. (Scale bar, 3 μm.) (C) Velocities (Left) and run lengths (Right) of two coupled dimers of Ncd. The experimental data for flexible (orange circles) and rigid (gray squares) DNA scaffolds are plotted vs. intermotor spacing. Red solid line represents the model in which on-rate depends on intermotor spacing (on-rate = 68.0 × L^−0.7, where L is intermotor spacing; model 1). Gray dashed line shows the model with constant on-rate (model 2). Each simulated plot was calculated from 1,000 traces at intervals of 1 nm.

Processive Movement by Multiple Dimers of Ncd.

Next, we linked together multiple dimers of nonprocessive Ncd by flexible DNA scaffolds with a spacing of 22.7 nm. Fig. 1 D and E, SI Appendix, Fig. S9, and Movie S3 show the unexpected finding that assemblies composed of two coupled dimers of Ncd moved processively along MTs for more than 1 μm, whereas single molecules of Ncd showed only short runs or diffusive movement along MTs (6, 19). It is of note that the scored run length for single Ncd in Fig. 1D and SI Appendix, Table S1, is obviously an overestimation, because 316 of 449 binding events were below the lower limit of reliable analysis (200 nm), and thus were not included in the analysis. Moreover, the speed was as fast as ∼150 nm⋅s⁻¹, a similar value to the average velocity of gliding MTs on an Ncd-coated surface (Fig. 1D and SI Appendix, Table S1) (6).

To describe the collective motility of Ncd, we first used the same model used for processive kinesin-1. Despite extensively scanning the parameter space, we could not determine the parameter set that explains the experimental observation of a gap between the velocities of single and two coupled motors. The most striking difference from the kinesin-1 traces was the diffusive component in the movement of Ncd. In the presence of ATP, the diffusion coefficient of single Ncd was measured as 2.2 × 10⁴ nm²⋅s⁻¹, which is much larger than that observed for single kinesin-1 (0.45 × 10⁴ nm²⋅s⁻¹; SI Appendix, Fig. S10), suggesting that the stepping of Ncd is frequently interrupted by unproductive random steps. These steps are probably driven by thermal agitation because single Ncds can also move bidirectionally in the absence of ATP with a similar diffusion coefficient (2.7 × 10⁴ nm²⋅s⁻¹) (6). Fig. 1E, SI Appendix, Fig. S10D, and Movies S3 and S4 clearly show that the diffusive component was decreased with the number of Ncds. To test the effect of random steps, we introduced a simple assumption into the model: when there is only one motor in the assembly that binds to a MT, the motor is prone to be driven by thermal “kick.” When there are multiple motors bound to a MT, the motors can avoid the thermal kick and are likely to take a unidirectional step. In the modified model, the free parameters were (i) on-rate, (ii) critical detachment force, and (iii) lower limit of random steps (SI Appendix, p. 13). The linker stiffness was taken from the kinesin-1 model described earlier, and the stall force was set to 0.2 pN, assuming that Ncd can take at most one step in the optical trap (k = 0.015 pN⋅nm⁻¹) (20). The force–velocity relationship was assumed to be linear, as measured for mitotic kinesin-5 (21). Figs. 1 D and E and 2B show that the experimental data were successfully reproduced by the modified model.

We made two unexpected observations. First, when two Ncd dimers were linked together, the average velocity was increased to ∼150 nm⋅s⁻¹, and remained unchanged with up to four motors. There are two opposing effects that determine the velocity when increasing the motor number: (i) a decreased diffusive component in the movement and (ii) increased interference between motors. The simulations suggest that, in the range of two to four molecules, these two effects are balanced (SI Appendix, Fig. S11). Second, the stepping rate was suggested to be ∼22 s⁻¹, indicating that the ATPase rate of each Ncd dimer must be accelerated approximately 10-fold from the previously reported values of approximately 2.0 s⁻¹ (6, 22–24). How do two coupled Ncd dimers achieve this high stepping rate? Previous studies have reported that the ATPase rate of individual Ncd dimers is limited by ADP release (22, 25). We speculate that, when kept close to an MT, Ncd can find binding sites on the MT much more rapidly than can freely diffusing molecules, leading to a high ADP release rate. Consequently, the hydrolysis rate of 20 to 23 s⁻¹ (23, 24) would in turn limit the stepping rate of each motor. Thus, the distinct coordination of multiple motors may allow Ncd to become active only upon accumulation, which may be advantageous to the regulation of transport.

Effects of Arrangement of Two Coupled Motors.

To investigate the effect of coupling on motility, we systematically determined the effects of the spacing and rigidity of the DNA linker between two coupled motors (SI Appendix, Fig. S3). The results for Ncd and kinesin-1 are summarized in Fig. 2C and SI Appendix, Fig. S12, respectively (see also SI Appendix, Tables S2 and S3). Numerical simulations have predicted that, with closer spacing, the run length of two coupled motors decreases because of the pulling forces between motors (Fig. 2C, Right, dashed line, and SI Appendix, Fig. S12B). However, the in vitro experiment showed, rather, that run length increased with closer spacing, particularly for nonprocessive Ncd. To understand this discrepancy, one possible explanation is that the on-rate depends on the spacing between motors. It seems plausible to suppose that, when a motor is tethered to a MT via a linker, one with a shorter linker would find the binding sites more quickly, thereby increasing the binding time. Most recently, Erickson et al. have predicted that the on-rate of cargo-bound motors is strongly affected by the motor organization on a cargo and that the on-rate is inversely proportional to a power of the motor length (18). We therefore assumed that the on-rate was similarly dependent on the intermotor spacing, which successfully reproduced the experimental observations for two coupled Ncds (Fig. 2C, Right, red solid line). The data led us to predict that the motor organization, for example, whether the motors are clustered at a single site or randomly distributed, is crucial to the performance of multiple motor-based transport. This also leads to the expectation that, when multiple motors are closely coupled in a small space, the interaction between motors and a MT would be dramatically activated. This view could be extended to large assemblies, including the spindle, myofibrils, and the axoneme in cilia and flagella, which are primarily driven by nonprocessive motors.

Collective Force Production by Multiple Motors.

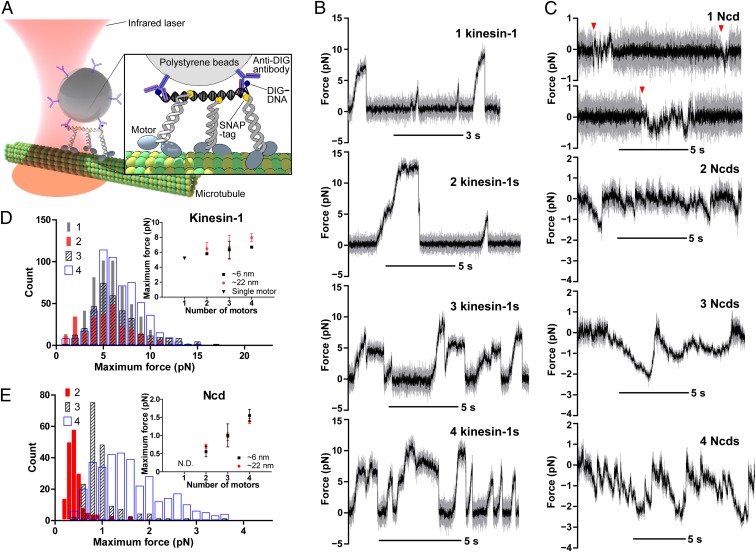
In the cell, molecular motors work in a crowded environment and experience drag forces as they transport a cargo along MTs. To compare and understand how the different types of motors cooperate to transport a cargo against these forces, we used an optical trap to directly measure the forces they generate. The average maximum force of single kinesin-1 motors was measured to be 5.2 pN, and the stall force to be 6.8 pN, consistent with previous reports (Fig. 3 B and D and SI Appendix, Table S4). The average maximum forces are determined by averaging the force corresponding to the maximum height of each peak. The stall force was determined by averaging the force of plateaus that lasts for more than 200 ms just before detachment. To our surprise, the maximum force of two kinesin-1 dimers (5.8 pN) was only slightly larger than that of a single kinesin-1 (5.2 pN), which is consistent with the findings of a previous study (26). Further, we observed only a slight increase in the maximum force with an increasing number of motors of as many as four, and all profiles contained a peak at ∼5.5 pN. It is possible that some of the kinesins are damaged when adsorbed to the surface of a bead; however, we ruled out this possibility by determining the additive run length of the two-kinesin bead in the absence of the trapping force (SI Appendix, Fig. S14). We also ruled out the possibility that one of the linkages in the bead–motor assembly breaks before the motors unbind from MTs (SI Appendix, Fig. S15). Thus, the result implies that just one kinesin in the assemblies bears the load most of the time. This is in line with the model that kinesin-1 provides constant force irrespective of its copy number (1), whereas opposing motors such as cytoplasmic dynein regulate the transport of cargos by motor number (3, 11). Nonetheless, intracellular transport should be more complex. For example, obstacles are present on MTs, cargos exhibit elasticity, and motors are activated/inactivated by various regulators. Further investigations using simplified assays that explicitly include these factors are required to better understand the regulation of intracellular transport.

Fig. 3.

Optical trapping assays. (A) Schematic of the typical experimental setup for optical trapping assays (not drawn to scale). (B) Time traces of optical trapping assays for (from top to bottom) one, two, three, or four kinesin-1 dimer(s) linked by rigid DNA scaffolds (∼6-nm spacing). Traces were acquired at 10 kHz (gray) and median-filtered to 25 Hz (black). The positive value corresponds to the force toward the MT plus-end (bead diameter, 0.45 μm; trap stiffness, 0.05–0.182 pN⋅nm⁻¹). (C) Time traces of optical trapping assays for Ncd linked by rigid DNA scaffolds (∼6-nm spacing). Arrowheads show examples of binding events (bead diameter, 0.21 μm; trap stiffness, 0.014–0.027 pN⋅nm⁻¹). (D) Histogram of the average maximum force generated by kinesin-1. The motors are linked by rigid DNA scaffolds (∼6-nm spacing). The numbers in the legend represent the number of motors in the assemblies. Inset: Average maximum forces (mean ± SEM) are plotted vs. motor number. Black and red colors represent intermotor spacings of 6.1 to 7.0 nm and 22.1 to 22.7 nm, respectively (SI Appendix, Fig. S4). The spacing between motors did not appear to affect the on-rate unlike in the low load condition, probably because of the difference in the arrangement of the motors on the trapped bead. (E) Histogram of the average maximum force generated by Ncd. The motors are linked by rigid DNA scaffolds (∼6-nm spacing). The color scheme and symbol are the same as in D. N.D., not determined.

We next measured the force of multiple Ncd assemblies. By contrast, the average maximum force of multiple Ncds increased additively with the motor number (Fig. 3 C and E). Although the force of single Ncd motors was too weak to be measured reliably, the binding and unbinding events were clearly observed when using a 0.21-μm bead (Fig. 3C). The force of two coupled Ncds was frequently observed beyond the level of thermal noise. Three and four Ncds showed repeated force production before they completely detached from the MT. The striking difference in the maximum force histogram compared with kinesin-1 is that the peak clearly shifts with an increasing number of motors (Fig. 3E).

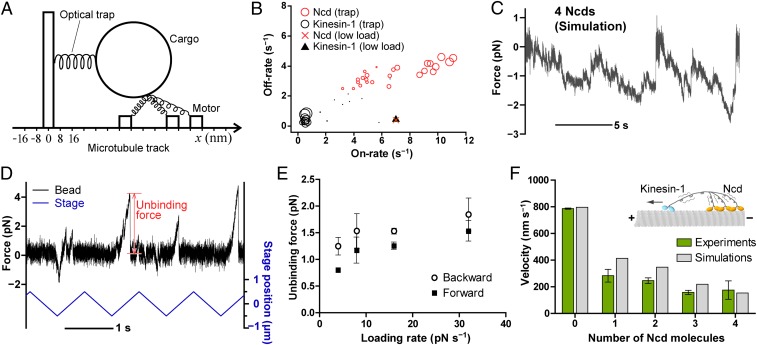
To understand the underlying mechanisms, we used numerical simulations (Fig. 4A and SI Appendix, p. 14). The models are identical for kinesin-1 and Ncd; we omitted the diffusive component in the low-load model for Ncd, assuming that the diffusion takes place in the weakly bound states (6) and thus is negligible when a load is imposed. The global fitting of kinesin-1’s force vs. motor number suggested that the on-rate is dramatically decreased compared with that in low-load conditions (Fig. 4B, black circles, and SI Appendix, Fig. S16). Note that the on-rate here is defined as the binding rate of a motor that is tethered to a MT, but not of a freely diffusing motor. The small on-rate of kinesin-1 means that a second (or third, fourth, etc.) kinesin cannot effectively bind to the MT. Given the additive run length of the two-kinesin bead in the absence of the trap (SI Appendix, Fig. S14), it is likely that a load imposed on a cargo somehow lowers the on-rate of a second kinesin. The inhibition is most likely caused by upward (i.e., perpendicular to the MT axis) or backward force as a result of the binding arrangement of motors on the MT, as proposed by Jamison et al. (26). However, a model including 3D forces requires parameters that have not been accurately measured. These possibilities should be addressed in a future study by using high-resolution measurement of upward forces.

Fig. 4.

Ratchet-like mechanism of Ncd. (A) Schematic of the simulation model for optical trapping assays. (B) Fitted parameters for optical trapping assays determined by an automated scanning algorithm (SI Appendix, p. 15). Each plot represents the parameter set obtained from each trial of the simulated annealing optimization. The free parameters were on-rate, off-rate, and critical detachment rate (SI Appendix, Table S7). The size of the circles represents the goodness of fit, which is inversely proportional to the sum of residuals between experimental and simulated data. Triangles and crosses denote the parameters in low load conditions (SI Appendix, Figs. S16 and S18). (C) Typical simulated traces of the force generated by four Ncds. Parameters are as follows: bead diameter, 0.21 μm; trap stiffness, 0.015 pN⋅nm⁻¹. The other parameters are listed in SI Appendix, Table S7. (D) Typical time trace of the unbinding force of single Ncd (black) and displacement of the stage (blue). The positive value of force corresponds to the applied force toward the MT plus-end. The trapped beads were dragged back and forth over MTs in the presence of 1 mM ATP (trap stiffness, 0.018 pN⋅nm⁻¹). (E) Unbinding force of single Ncd as a function of loading rate (1 mM ATP). Values represent mean ± SEM. The total number of unbinding events and the number of MTs for each plot was 242 to 518 and 7 to 11, respectively. Because we measured the impulse rather than the force, the unbinding force here is dependent on the loading rate. Thus, the actual force that unbinds Ncd from the MT would be larger than the plotted values. (F) Velocities for the tug-of-war between single kinesin-1 and several Ncds. The motors are linked by a flexible DNA scaffold (22.7-nm spacing). Green and gray bars correspond to experimental and simulated data, respectively. The parameter sets are shown in SI Appendix, Table S6. Each bar represents the mean velocity ± SEM toward the MT plus-ends.

In contrast to kinesin-1, the global fitting of Ncd’s maximum force vs. motor number suggests that the on- and off-rates are larger than those of kinesin-1 (Fig. 4B, red circles, and SI Appendix, Fig. S18). Strikingly, the off-rate is much larger than that observed at low load (0.45 s⁻¹). This trend is consistent with the high off-rate (7.8 s⁻¹) directly measured by an optical trap (SI Appendix, Fig. S17). One possibility is that Ncd can bind MTs in the weak binding state at low load, thus simply extending the binding time on MTs. Further, it is possible that Ncd is sensitive to an upward force, similarly to kinesin-1. The fast binding kinetics are also consistent with the observation that multiple-Ncd assemblies showed repeated force production before they completely detached from the MT (Figs. 3C and 4C). Another important observation is that the critical detachment force is required to be at least 2.0 pN, which is much larger than the force that individual motors can generate (SI Appendix, Fig. S18 C and D).

Ratchet-Like Mechanism of Ncd.

To test whether Ncd actually exhibits a large detachment force, the external load was imposed by moving the microscope stage at constant speed in the presence of ATP (Fig. 4D) (27). Fig. 4E shows that the unbinding force was always larger when loaded in the backward direction. The result leads us to further predict that even single Ncd can slow down opposing kinesin-1 despite its small active force.

To test this, we linked together Ncd dimers with a single kinesin-1 dimer to a DNA scaffold and observed their “tug-of-war” (Fig. 4F and SI Appendix, Figs. S21 and S22 and Table S5). As expected, kinesin-1 generally wins against as many as four Ncd motors; however, the average velocity of kinesin-1 was dramatically decreased when linked with Ncd. This may be explained by the drag force that arises from protein friction between Ncd and the MT. This ratchet-like mechanism has also been reported for myosin II (28) and would allow small groups of Ncd to antagonize the opposing force. It is of note that much larger numbers of Ncd molecules would be required to slide and lock together MTs in vivo because of the diffusive nature of the nonmotor MT binding site in Ncd’s tail (29, 30). However, the direction-dependency of the drag force and fast MT binding/unbinding rate is likely to be important for motors that work in teams. Given the much higher affinity for MTs when the motors accumulate (Fig. 2C, Right) and the diffusive nature of Ncd, we propose that the fast MT binding kinetics allow continuous reorganization of motors to reach a stable load-bearing arrangement in between MT bundles. This process would generate clusters of motors, each of which can act as a virtual processive motor. The number of motors in each cluster can fluctuate in time and space in response to load (31), which may contribute to cooperative phenomena on a large scale such as dynamic assembly and disassembly of the spindle. Thus, individual Ncd motors have to be poorly processive to rapidly affect the dynamics of MT organization.

In the present study, we have shown that nonprocessive Ncd motors can be highly activated when closely coupled, unlike kinesin-1. Overall, the simulations generally reproduced the experimental observations. However, we noticed that the force of single Ncd motors is much smaller than the simulated force; we never observed clear force production by single Ncd motors, unlike in the simulations (SI Appendix, Fig. S23). One possibility is that the stepping of single Ncd could be interrupted by thermal diffusion, as seen in assays at low load. In fact, the diffusive movement was frequently observed when a single Ncd motor binds to a MT even in the presence of a trapping force (Fig. 3C). However, we favor the other possibility that the load can induce the synchronization of Ncd stepping, which would make coupled motors much stronger than can be expected from weak single molecules. This might be possible if some rate constants are load-dependent, and may result in cooperative collective behavior. Currently, single-molecule measurements of low-processivity motors are still very difficult. Measuring the response of small ensembles of such motors will therefore be particularly helpful for investigating these possibilities.

After this paper was submitted, another study coupling a known number of motors via DNA origami scaffolds reported on the tug-of-war between yeast cytoplasmic dynein and human kinesin-1 (32). The authors showed that the dynein tended to win the “game” despite the fact that the stall force of dynein is smaller than that of kinesin. This demonstrates that stall force was not the only determinant of multiple-motor dynamics. Likewise, we have shown here that single Ncd can effectively slow down kinesin-1, suggesting that factors other than the stall force, such as MT binding kinetics and detachment force, also play critical roles in determining the behavior of motor ensembles.

To conclude, we have presented a model system that enables the study of collective motor functions from the bottom up. Moreover, our approach is not restricted to the motor field but can be readily extended to the rich variety of molecular machines that work collectively in the cell.

Methods

Single fluorescence tracking (6) and optical trapping assays (33) were performed essentially as described previously. Theoretical modeling was performed as described previously (14, 16). Further details are provided in SI Appendix.