A continuous climatic impact on Holocene human population in the Rocky Mountains

Abstract

Ancient cultural changes have often been linked to abrupt climatic events, but the potential that climate can exert a persistent influence on human populations has been debated. Here, independent population, temperature, and moisture history reconstructions from the Bighorn Basin in Wyoming (United States) show a clear quantitative relationship spanning 13 ka, which explains five major periods of population growth/decline and ∼45% of the population variance. A persistent ∼300-y lag in the human demographic response conforms with either slow (∼0.3%) intrinsic annual population growth rates or a lag in the environmental carrying capacity, but in either case, the population continuously adjusted to changing environmental conditions.

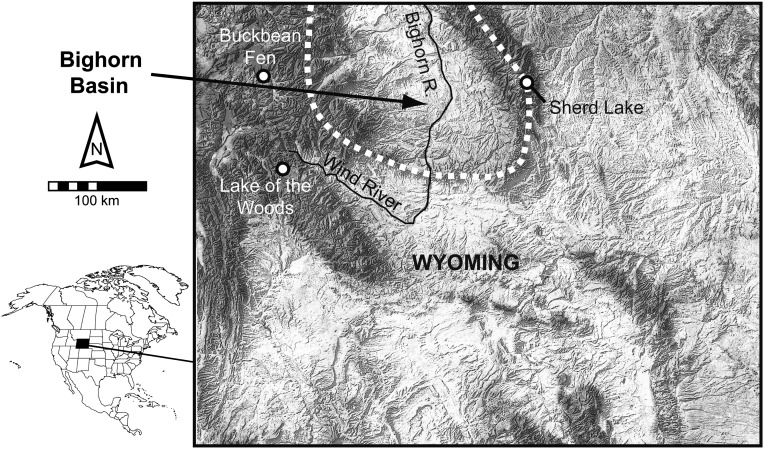
Many cultural changes have been linked to climate change, from the collapse of civilizations (1) to the frequency of civil conflict (2). However, tests of the relationship between climate and population size have been hampered by the lack of long-term, high-resolution records that are collaboratively interpreted by archaeologists and paleoclimatologists (3). One consequence is that many archaeological examples emphasize the impact of severe events and have not resolved the importance of continuous climate change in shaping cultural history. Here, we report on high-resolution approaches to paleoclimate and population reconstructions that permit us to ask how human population size responds to moisture and temperature dynamics over long timescales. We examine the hunter-gatherer population history of the Bighorn Basin (Fig. 1) in Wyoming (United States) over the past 13,000 y and test whether that history is associated with changes in moisture and temperature.

Fig. 1.

Location of Bighorn Basin and sites of paleohydrologic and paleotemperature records.

Changes in the relative size of prehistoric human populations can be reconstructed using the frequency of radiocarbon dates (4, 5) if one accounts for discovery bias and taphonomic factors. The radiocarbon dataset (Dataset S1) includes 421 dates from open-air archaeological sites and 158 dates from closed sites (caves and rock shelters); all dates have SEs ≤ 100 y and come from anthropogenic contexts. The open- and closed-site dates were separately calibrated and the summed probability values (SPVs) generated by CALPAL (6); open-site values were then corrected for taphonomic loss (7). Relative basin-wide population changes derive from an average of the open- and closed-site SPVs, which was then smoothed and standardized (Fig. 2C). We note that our analysis assumes that the ratio of summed probability to actual population remains constant throughout time, and that the open and closed sites should be weighted equally. These assumptions might deserve investigation in the future.

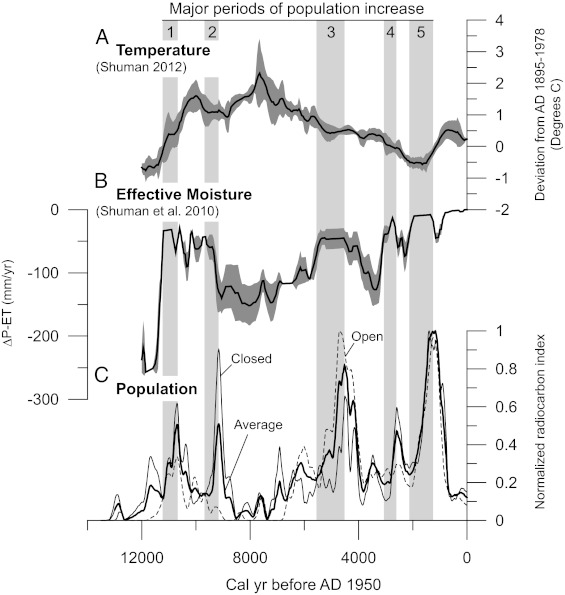
Fig. 2.

Graphs of radiocarbon, paleohydrologic, and paleotemperature records: (A) temperature changes reconstructed from Yellowstone and Bighorn Mountains pollen cores (10); (B) moisture deficit changes reconstructed from Lake of the Woods paleohydrologic record (12); (C) summed probability values, open- and closed-site curves, and averaged values, in 50-y intervals.

Two independent paleoclimate datasets test whether the observed demographic changes were driven by climate change. A temperature reconstruction for the region derives from representative pollen profiles from Yellowstone National Park (Buckbean Fen, 44.30 N, 110.26 W, 2,363 m elevation) (8) and the Bighorn Mountains (Sherd Lake, 44.27 N, 107.01 W, 2,665 m) (9), on the west and east sides of the Bighorn Basin, respectively, and was generated using the modern analog technique, which matches fossil pollen samples to their best modern equivalents (10) (Figs. 1 and 2A). Both records are among the best resolved from Wyoming in the North American Pollen Database (11) with one to two pollen samples per 500-y interval. The reconstruction of effective moisture derives from temporal changes in lake volume at Lake of the Woods (LOW) (43.48 N, 109.9 W, 2,819 m) (12) in the Wind River Mountains, at the headwaters of the Wind-Bighorn River, which flows through the Bighorn Basin (Fig. 2B). The LOW record uses the elevation of shallow water sediment facies to constrain the past position of the lake shoreline, and thus provides a basis for quantitatively estimating the watershed balance of precipitation and evapotranspiration, which we refer to as effective moisture (12). The LOW record agrees with other reconstructions (13) and thus reflects regional rather than local climate. We compare the population, moisture, and temperature records to evaluate potential linkages between change in climate and past human populations.

Results

The data indicate five significant increases in population coinciding with periods of high effective moisture and moderate temperatures (Fig. 2C). The human population entered the region at ∼13.0 ka and grew to reach the first population peak at ∼10.7 ka during a period of high water at LOW from 11.3 to 10.4 ka. The population then declined after 10.6 ka, but increased to a second peak at ∼9.15 ka, which is only recorded in closed sites (and may represent movement of people out of the basin into higher-elevation sites) (SI Text). Human population was extremely low at ∼9.0–6.77 ka, with some intervals returning an SPV of 0 (e.g., 8.14–7.97 ka), when LOW reached its lowest levels (12) (Fig. 2B) and regional temperatures reached their Holocene maximum (10) (Fig. 2A).

Population began a third period of growth at ∼7.0 ka, reaching one minor peak at ∼6.1 ka. After a short decline, the population then increased to a third major peak at ∼4.5 ka at the end of a period of high water at LOW from ∼5.7 to 4.4 ka (Fig. 2); much of the growth occurred during the wettest interval, between 5.5 and 4.5 ka.

A low-elevation paleoshoreline deposit at LOW bracketed by calibrated radiocarbon ages of 4.8–4.3 and 3.5–3.1 ka (12) marks the onset of renewed aridity and a 75–80% population decline from 4.5 to ∼3.8 ka (Fig. 2). The population then remained low, except for a brief fourth increase at ∼2.6 ka between episodes of low water at LOW (Fig. 2). Population began a fifth period of growth at ∼1.9 ka, and continued until ∼1.17 ka when water levels at LOW fell and regional temperatures increased (Fig. 2). The population then appears to have declined rapidly until ∼0.56 ka. The five major periods of population growth (when SPVs grew to >0.35), from earliest to latest, suggest mean annual growth rates of 0.31%, 0.30%, 0.19%, 0.30%, and 0.16%. The positive rates of change over the entire record have a mean of 0.27%, and a maximum of 1.9%.

To examine the relationship between relative human population size and climate, we first use multiple linear regression to establish statistical significance. We then apply a mathematical model of dynamic equilibrium. This model assumes exponential population growth consistent with the observed growth rates, which are substantially slower than the rates of climate change (10, 12) and thus produce lags in the population response (14).

We find that both the temperature (T) and effective moisture (M) records correlate individually and significantly with the (logged) SPVs at 50-y intervals (M: r = 0.52, P = 2.3 × 10⁻¹³, n = 241; T: r = −0.49, P = 3.7 × 10⁻¹¹, n = 241). Low effective moisture and high temperatures are both associated with low population levels. The correlation is strengthened when moisture and temperature are considered jointly through multiple regression (adjusted R² = 0.43, P < 2.2 × 10⁻¹⁶, n = 241); this also reveals a clear lag in the actual SPVs (Fig. 3A). We used Granger causality analysis in R (15) using the function, grangertest, to evaluate the magnitude of the lag while also accounting for the effects of autocorrelation. The analysis showed no significant lag for temperature, but revealed significant lags at 100 and 300 y for moisture (100 y: r = 0.46, P = 0.02, n = 241; 300 y: r = 0.52, P = 0.03, n = 241). When moisture is lagged 300 y, the strength of the multiple regression improves (adjusted R² = 0.48, n = 235, P < 2.2 × 10⁻⁶); the revised best fit equation is the following: ln(SPV) = 0.006 * M_lagged − 0.593 * T − 0.696. This suggests that a 1 °C increase in temperature resulted in a 45% decline in population, whereas a 50-mm increase in the moisture deficit resulted in a 26% decline in population after 300 y.

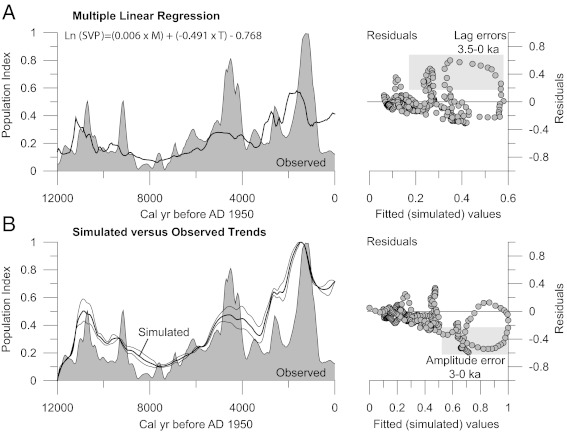
Fig. 3.

Comparison of actual and predicted radiocarbon records: (A) radiocarbon SPVs, in 50-y intervals and values predicted based on multilinear regression equation (solid line); (B) radiocarbon SPVs with predicted values based on a model of dynamic equilibrium (Eq. 4) based on lagged population responses to changes in the exponential population carrying capacity determined by the moisture and temperature time series (Fig. 2 A and B).

Discussion

One explanation for the 300-y lag is that either the population or the ecological carrying capacity responds slowly to changes in climate. We use a dynamic equilibrium model (14) to evaluate this possibility. The model has been used to show how vegetation can track shifting equilibrium states as climatic conditions change, in much the same way as a thermometer dynamically equilibrates to changing temperatures (14). In the model, population response to climate change depends upon (i) the difference between the current population size (P) and the equilibrium population (P*) possible under the current climatic carrying capacity (K), and (ii) the population response (“1/e-folding”) time (λ).

The basic model (Eq. 1) encompasses these essential concepts and can be integrated from time 0 to time t to produce a form (Eq. 2) that is similar to the familiar equation for exponential population growth as follows:

The population response time (λ) equals the time required for exponential population growth to reduce the difference between P_t and P* to (P_t − P*)/e (or by ∼63.2%). The population response time depends upon the population growth rate (r) as required by Eq. 2:

For t = 1 y, the difference between P_t and P₀ (and between their deviations from P*) equals r/100.

If P* equals K, which is a function of moisture and temperature, then Eq. 2 can be rewritten for each 50-y time step to predict the subsequent value of P_t as a deviation from K as follows:

In Eq. 4, P_t replaces P₀ from Eq. 2 as time progresses in the model. The ratio 50/λ also represents the fraction of the response (“1/e-folding”) time passed in each 50-y step [e.g., if λ = t = 50 y, then exp(−50/λ) = 1/e]. K can be estimated for each time step most simply by adding normalized time series of moisture and temperature together, but here we use our initial multiple regression (Fig. 3A) to provide the relative contributions of moisture and temperature to K. We calculate λ from the mean observed population growth rate (0.27%).

Applying the model demonstrates that the population lag could reflect an equilibration process consistent with the observed climate trends and population growth rates (Fig. 3B). The model produces lags that shift the predicted peaks in population size to their observed timing, and thus demonstrates that the offset could be expected from equilibration processes and population dynamics. Model adjustments may allow for a closer fit to the data during some intervals (SI Text), but our simulation shows a strong correlation (r = 0.65) between the predicted and observed population trends, particularly when the most recent portion (<0.85 ka) of the population curve is excluded (r = 0.74).

Using a range of inputs equal to the range of uncertainty in the paleoclimate reconstructions (Fig. 2) produces an envelope of predicted relative population sizes that explains a large fraction of the variance in the observations (R² = 0.38–0.44 for the entire record; 0.52–0.55 for the record before 0.85 ka). The most important differences between the observed and predicted trends result from the low amplitude of some predicted versus observed changes, such as at ∼9.15 ka and <0.85 ka; the model does not predict a clear second population peak at ∼9.15 ka (possibly due to a geographic redistribution of population) (SI Text) or a continued decline in the population after 0.85 ka (which may be due to researcher bias in date sample selection, introduced diseases, and/or the use of other dating methods for this time interval) (SI Text). Varying the relative weights of temperature and moisture in the model, the exponential transformation of the data, and the population growth rate can produce larger amplitude changes, however.

The foraging population that inhabited the Bighorn Basin responded to climate change in expected ways: major periods of growth are associated with cooler/wetter intervals, during which population grew at a mean overall annual rate of ∼0.27%, but sometimes with annual rates as high as 1.9%; likewise, declines are associated with aridity. Moisture was crucial here, which is expected for an arid landscape, but so was temperature. Intrinsic factors may drive the responses, but we do not know if changes in the human population were also affected by immigration or emigration. The role of such extrinsic factors could be tested by comparing the Bighorn Basin radiocarbon date frequency against that of neighboring regions. Our study produced higher growth rates than a study of >25,000 radiocarbon dates from continental North America (5), where the mean reconstructed growth rate was 0.05% with a maximum of 0.25% (5). That study, however, used bins of 200 y and thus might have missed shorter-term instances of higher growth, and averaged growth rates from regions with subsistence economies that, unlike the current geographically restricted study, were not always and everywhere the same and that may have been differently affected by changing climate.

These data are instructive for two issues. First, they suggest that prehistoric population size was held in check by periodic declines that appear to be linked to climate-induced changes in the environmental carrying capacity. During the five growth periods, the average growth rate of 0.27% is below those known for living foragers, which average about 1.4% (16–20). Annual growth rates were >1.0%, and closer to those of living foragers, only three times, and for only 50–250 y; these three instances fall between 8.5 and 7.25 ka, when regional population was at its lowest and small absolute changes in population size could have a relatively large effect. Modern foragers might also have consistently high growth rates because of access to Western medicine, food supplements from agricultural neighbors, government-provided rations, and government-linked reductions in murder (21), although when these factors were tested on the demography of the African Hadza, they did not appear to be significant (22). Instead, it may be that prehistoric growth rates were held in check by higher rates of accidents and, especially, homicide than are recorded for most living foragers (21). However, our study suggests that (i) long-term growth rates slower than those documented ethnographically can be attributed solely to periodic climatically induced reductions in environmental carrying capacity, and (ii) that relatively high growth rates among living foragers might reflect populations in a recovery stage.

Second, today’s climate in the Bighorn Basin has become as warm and dry as it was 6,000–9,000 y ago (10) when the region was depopulated through mortality and/or emigration. Modern populations with sophisticated technology can adapt in ways other than regional abandonment or death, but as with ancient foragers, we are unlikely to maintain the status quo as climate continues to change. The Bighorn Basin record indicates that climate may well impact cultures not only through episodic severe events, but also as a slowly varying control on the regional resources that can determine population size and trajectory.

Materials and Methods

The radiocarbon dates were generated by many archaeological projects over the past several decades with various research agendas; many were generated by compliance projects with no temporally biased agenda. The initial dataset consisted of 555 dates from open sites and 281 from closed sites. We removed dates of questionable anthropogenic origin, duplicate dates from the same anthropogenic feature, and any dates with a SE of >100 y. Only one date is on bone. Thirty-one dates are listed as “carbon?” as the report failed to list the source; they are most likely carbon (Dataset S1). Following Williams’ (23) recommendation, we note that the mean SE for the entire sample was 64.4 (closed sites, 52.6; open sites, 69.0). The sample of 579 dates exceeds Williams’ suggested minimum of 500, and encompasses a far smaller area and shorter time interval than was the basis of that recommendation (Australia’s 40,000-y prehistory). Williams uses a modified version of the taphonomic correction used here, but there is no difference between the summed probability distributions [r = 0.99, n (pairs) = 1,201, P « 0.001]. The resulting SPVs were smoothed with a 200-y moving average, the average of 200 y centered on X_i. Williams (23) recommended a 500- to 800-y smoothing, but we prefer a 200-y smoothing since the temporal range in this case (∼13,000 calendar years) is about one-quarter that of Williams’ case study. In any case, a 500-y smoothing produced very similar results [r = 0.97, n (pairs) = 1,331, P « 0.001]. After smoothing, the data were standardized by X_i/X_max. The dates were calibrated using CALPAL’s HULU 2007 and checked against IntCal04; there is no significant difference between the SPVs [r = 0.99, P « 0.001, n (pairs) = 1,204]; although IntCal has been updated, IntCal09 has only minimal differences from IntCal04 for the time range here (24).