Extended polarization in 3rd order SCC-DFTB from chemical potential equilization

Abstract

In this work we augment the approximate density functional method SCC-DFTB (DFTB3) with the chemical potential equilization (CPE) approach in order to improve the performance for molecular electronic polarizabilities. The CPE method, originally implemented for NDDO type methods by Giese and York, has been shown to emend minimal basis methods wrt response properties significantly, and has been applied to SCC-DFTB recently. CPE allows to overcome this inherent limitation of minimal basis methods by supplying an additional response density. The systematic underestimation is thereby corrected quantitatively without the need to extend the atomic orbital basis, i.e. without increasing the overall computational cost significantly. Especially the dependency of polarizability as a function of molecular charge state was significantly improved from the CPE extension of DFTB3. The empirical parameters introduced by the CPE approach were optimized for 172 organic molecules in order to match the results from density functional methods (DFT) methods using large basis sets. However, the first order derivatives of molecular polarizabilities, as e.g. required to compute Raman activities, are not improved by the current CPE implementation, i.e. Raman spectra are not improved.

Introduction

Semi-empirical theory has made a huge progress in the last decades.^1–4,19 Starting from successful models of the early days like MNDO, AM1 and PM3,^6–8 many improvements in the formalism and parametrization have led to a new generation of SE methods,^9–13,37 being all derived from Hartree-Fock (HF) theory, however, treating the important effects of electron correlation implicitly. A second route to SE methods starts from Density functional theory^20,21 (DFT), introducing several approximations which lead to a speedup of of 2–3 orders of magnitude wrt to DFT methods with medium sized basis sets.

The approximations are threefold: (i) the expansion of the DFT total energy around a suitably chosen reference density in first²⁴ (DFTB), second²⁵ (DFTB2) and third order^31,32,36 (DFTB3). While the second order terms are crucial for polar molecules, the third order expansion becomes indispensable for charged molecular species. In DFTB, this expansion is truncated after the monopole term at every order. At second order, this allows to include the effect of charge transfer between atoms in the energy expression, in third order the change of atomic hardness with charge state. However, the non-sperical charge-redistribution around the atoms are neglected. This expansion has been analyzed in more detail recently by York and coworkers.³⁴

(ii) The neglect and approximation of interaction integrals. In particular, this concerns the neglect of 2-center integrals for the diagonal terms and three-center integrals for the off-diagonal contributions.²⁴ Further, the DFT ’double counting’ contributions are grouped into a pairwise potential, which is either determined by comparison with DFT calculations²⁴ or fitted to empirical data.³³

(iii) The use of a minimal basis, which is part of the computational efficiency since it reduces the size of the eigenvalue problem to be solved significantly. However, this approximation is also the core of the problems when it comes to the calculations of response properties.

Among the multitude of molecular properties SE models were applied to evaluate, molecular electronic polarizability remains a challenging one, since SE models mostly work with a minimal molecular orbital basis to gain efficiency. It has been shown,²⁹ however, that the size of the ao-basis is a crucial aspect for the accuracy of polarization, which is underestimated by an average of 25% from SE methods⁴⁴ compared to experimental results. To overcome this limitation with-out increasing the ao-basis itself, which would lower the efficiency of SE methods significantly, empirical models were proposed, e.g. for neglect of differential overlap (NDDO) based SE methods,^16–19 originated from perturbation theory.^14–16 Another approach which has been shown to be promising is the chemical potential equilization (CPE) method, founded by Sanderson²⁶ as an electronegativity equalization approach, which was later modified and improved.^27,28 In the framework of CPE extended MNDO³⁹ and 2nd order SCC-DFT³⁴ (DFTB2), Giese and York were able to accurately reproduce polarizabilities compared to DFT with a large ao-basis. Concerning SCC-DFTB the accuracy is limited not only by the minimal ao-basis approach but also by the monopole basis representation of charge density fluctuations in second order.³²

In the present work, we discuss the implementation, parametrization and performance of the CPE extended 3rd order SCC-DFTB (DFTB3) for polarizability calculations. Although the 3rd order expansion denotes a clear step ahead over the DFTB2 formalism,36 DFTB3 suffers from the same basic limitations as DFTB2 for polarizability calculations, i.e. the minimal basis and the monopole representation of charge fluctuations. For the treatment of phosphorus containing molecules, e.g. which can not be properly described by DFTB2, DFTB3 is an important step ahead. In this respect, a DFTB3/CPE approach would be especially beneficial for studies on DNA, in which the polarization effect of the highly negatively charged phosphate backbone would be significantly underestimated by standard DFTB3.

As a step ahead, we will also evaluate in this work the potential of the current CPE formalism to accurately reproduce Raman intensities, since they depend on first order polarizability derivatives with respect to normal mode vibrations. Concerning Raman intensities, we will have to have a closer look on the polarizability tensor as a whole, while most of the previous studies^{17,18,34,37,39} focused just on the mean polarizability, i.e. the average of the tensors diagonal elements.

Theoretical Approach

Theory of 3rd order SCC-DFTB

The extension of the DFTB2 approach to the third order (DFTB3) has been introduced recently^32,36 and will be briefely summarized in the following. The starting point to derive the DFTB3 total energy is the energy expression of the Kohn-Sham density functional theory.²¹ Instead of finding the electron density ρ( r) that minimizes the energy a reference density ρ⁰ is assumed which is perturbed by some density fluctuation, ρ( r) = ρ⁰( r)+δρ( r). The exchange-correlation energy functional is then expanded in a Taylor series up to third order and the total energy can be written as

$$E^{\text{dftb}3}[{\rho }^0+\delta \rho ]={\displaystyle \sum _i{n}_i}\langle {\psi }_i|\widehat{H}[{\rho }^0]|{\psi }_i\rangle -\frac{1}{2}{\displaystyle \iint \frac{{\rho }^0(\mathit{r}){\rho }^0(\mathit{r}\prime )}{|\mathit{r}-\mathit{r}\prime |}}\mathrm{d}\mathit{r}\mathrm{d}\mathit{r}\prime -{\displaystyle \int V^{\text{xc}}[{\rho }^0]{\rho }^0(\mathit{r})\mathrm{d}\mathit{r}+E^{\text{xc}}[{\rho }^0]+E^{\text{nn}}+\frac{1}{2}{\displaystyle \iint \left(\frac{1}{|\mathit{r}-\mathit{r}\prime |}+\frac{{\delta }^2{E}^{\text{xc}}[\rho ]}{\delta \rho (\mathit{r})\delta \rho (\mathit{r}\prime )}{|}_{{\rho }^0}\right)\delta p(\mathit{r})\delta \rho (\mathit{r}\prime )\mathrm{d}\mathit{r}\mathrm{d}\mathit{r}\prime +\frac{1}{6}{\displaystyle \int {\displaystyle \iint \frac{{\delta }^3{E}^{\text{xc}}[\rho ]}{\delta \rho (\mathit{r})\delta \rho (\mathit{r}\prime )\delta \rho (\mathit{r}″)}{|}_{{\rho }^0}\delta \rho (\mathit{r})\delta \rho (\mathit{r}\prime )\delta \rho (\mathit{r}″)\mathrm{d}\mathit{r}\mathrm{d}\mathit{r}\prime \mathrm{d}\mathit{r}″.}}}}$$ (1)

Several approximations follow: First, the Kohn-Sham orbitals ψ_i are represented in a minimal basis of pseudoatomic orbitals, ψ_i = Σ_µ c_µiϕ_µ. The diagonal elements of the resulting Hamiltonian matrix$H_{\mu \nu }^0$ (first term of Eq. (1)) are chosen to be atomic DFT eigenvalues evaluated with the PBE²³ exchange correlation functional, the off-diagonal elements are calculated in a two-center approximation.³⁵ Second, the double counting terms (2nd to 5th term of Eq. (1)), the exchange-correlation energy at the reference density E^xc[ρ⁰], and the nucleus-nucleus interaction Eⁿⁿ are approximated as two-center pair-potentials$V_{ab}^{\text{rep}}$. Third, the charge density fluctuation δρ is written as a superposition of atomic contributions δρ = Σ_a δρ_a, where the atomic contributions are approximated as spherical charge distributions by a simple Slater function with the magnitude of the Mulliken charge q_a of that atom centered around coordinate R_a:

$$\delta {\rho }_a\approx q_a\frac{{\tau }_a^3}{8\pi }{e}^{-{\tau }_a|\mathit{r}-{\mathit{R}}_a|}$$ (2)

Using this approximation the Coulomb interaction of the second order term with respect to δρ can be expressed analytically and is abbreviated as γ_ab in the following. The exponent τ_a is chosen such that the on-site value of the γ-function properly describes the atomic chemical hardness (or alternatively the Hubbard parameter as calculated from DFT) and thus, implicitly takes into account the exchange-correlation contribution to the second order term. For improving this interpolation between long-range Coulomb interaction and the onsite term further refinements on the γ-function have been applied.³⁶ For the third order term a Γ-function is defined which results as the derivative of the γ-function with respect to charge by introducing the Hubbard derivative parameter expressing the change of the Hubbard parameter with respect to the charge state of that atom in a linear way. It has been shown, that a third order term from a more rigorous density-functional expansion does not contribute significantly to the accuracy of the method.³⁴ In that way the third order terms within SCC-DFTB can be rather seen as a robust way to introduce the charge dependence capturing some deficiencies of problematic approximations within the second order formalism, namely, the small size of the pseudoatomic orbital basis as well as the very simplified density fluctuation scheme. With all these approximations the SCC-DFTB total energy in 3rd order is given by

$$E^{\text{dftb}3}={\displaystyle \sum _{iab}{\displaystyle \sum _{\mu \in a}{\displaystyle \sum _{\nu \in b}{n}_i{c}_{\mu i}{c}_{\nu i}{H}_{\mu \nu }^0+\frac{1}{2}{\displaystyle \sum _{ab}{q}_a{q}_b{\gamma }_{ab}+\frac{1}{3}{\displaystyle \sum _{ab}{q}_a^2{q}_b{\mathrm{\Gamma }}_{ab}+\frac{1}{2}{\displaystyle \sum _{ab}{V}_{ab}^{\text{rep}}}}}}}}.$$ (3)

The derivative of this expression with respect to the molecular orbital coefficients lead to the corresponding Kohn-Sham equations

$${\displaystyle \sum _{\nu }{c}_{\nu i}(H_{\mu \nu }-{\epsilon }_i{S}_{\mu \nu })=0\text{\hspace{1em}with }\nu \in b\text{}}\text{\hspace{1em}and }\forall a,\mu \in a,$$ (4)

$$H_{\mu \nu }=H_{\mu \nu }^0+S_{\mu \nu }{\displaystyle \sum _c{q}_c}\left(\frac{1}{2}({\gamma }_{ac}+{\gamma }_{bc})+\frac{1}{3}(q_a{\mathrm{\Gamma }}_{ac}+q_b{\mathrm{\Gamma }}_{bc})+\frac{q_c}{6}({\mathrm{\Gamma }}_{ca}+{\mathrm{\Gamma }}_{cb})\right),$$ (5)

where S_µν is the overlap matrix. The Hamilton matrix elements depend on the Mulliken charges which in turn depend on the molecular orbital coefficients c_µi, thus, these equations have to be solved self-consistently.

For DFTB3, molecular electronic polarizabilities were evaluated via the finite electric field approach as

$${\alpha }_{ij}=\left(\frac{\delta {\mu }_i}{\delta F_j}\right)i,j=x,y,z,$$ (6)

where F_j is the Cartesian component of an external applied electric field. To capture the effect of the field perturbing the system, an extra term³⁰ is added to the DFTB3 energy expression, describing the interaction of the field with the induced Mulliken charges of the system, as

$$E^{\text{field}}=E-{\displaystyle \sum _A{q}_A{\displaystyle \sum _{j=1}^3{F}_j{x}_{jA}.}}$$ (7)

Here, x_jA denotes the Cartesian coordinate of atom A in direction j. The charge self-consistent Hamiltonian becomes

$$H_{\mu \nu }^{\text{field}}=H_{\mu \nu }-\frac{1}{2}{S}_{\mu \nu }{\displaystyle \sum _{j=1}^3{D}_j{x}_{jA}.}$$ (8)

The CPE approach and its implementation into DFTB3

In the framework of extending DFTB3 by the chemical potential equilization method, we follow the ideas of York and Giese.^37–39 The total energy of the system can be written as

$$E_{\text{tot}}[\rho ]=E_{\text{dftb}3}[\rho ]+E_{\text{cpe}}[\rho ],$$ (9)

where E_dftb3[ρ] is the DFTB3 energy and E_cpe[ρ] a self-consistent CPE response correction. CPE uses the DFTB3 charge density as a reference in a second order Taylor series expansion of an approximate density functional. To derive the expression for E_cpe[ρ], we define the density functional generically as

$$E[\rho ]={\displaystyle \int \nu (\mathit{r})\rho (\mathit{r})d^{3}r+F[\rho ],}$$ (10)

and the Taylor expansion becomes

$$E[{\rho }^{\text{ref}}+\delta {\rho }^{\text{cpe}}]-E[{\rho }^{\text{ref}}]={{\displaystyle \int \left[\frac{\delta E[\rho ]}{\delta \rho (\mathit{r})}\right]}}_{\rho ={\rho }^{\text{ref}}}\delta {\rho }^{\text{cpe}}(\mathit{r})d^{3}r+\frac{1}{2}{\displaystyle \int {{\displaystyle \int \left[\frac{{\delta }^{2}F[\rho ]}{\delta \rho (\mathit{r})\delta \rho (\mathit{r}\prime )}\right]}}_{\rho ={\rho }^{\text{ref}}}\delta {\rho }^{\text{cpe}}(\mathit{r})}\delta {\rho }^{\text{cpe}}(\mathit{r}\prime )d^{3}r{d}^{3}r\prime .$$ (11)

In the framework of the current CPE implementation, the response density δρ^cpe is expressed in a basis of functions φ^cpe as

$$\delta {\rho }^{\text{cpe}}(\mathbf{r})={\displaystyle \sum _i{c}_i{\phi }_i^{\text{cpe}}(\mathbf{r}),}$$ (12)

where the response coefficients c_i are unknown and have to be evaluated throughout a variational approach. Inserting the basis representation for δρ^cpe(r)Eq. (11) is transformed into

$$E_{\text{cpe}}[\rho ]=E[{\rho }^{\text{ref}}+\delta {\rho }^{\text{cpe}}]-E[{\rho }^{\text{ref}}]=E_{\text{cpe}}[\mathbf{q},\mathbf{c}],$$ (13)

which leads to an algebraic set of equations of the following form:

$$E_{\text{cpe}}[\mathbf{q},\mathbf{c}]={\mathbf{c}}^T\cdot \mathbf{M}\cdot \mathbf{q}+\frac{1}{2}{\mathbf{c}}^T\cdot \mathbf{N}\cdot \mathbf{c},$$ (14)

where q denotes the vector of atomic Mulliken charges from DFTB3. In Eq. (14), the first and second functional derivatives appearing in Eq. (11) are approximated by Coulomb interactions between basis functions:

$$M_{ij}=f(R_{ij}){\displaystyle \int {\displaystyle \int \frac{{\phi }_i^{\text{cpe}}(\mathbf{r}){\phi }_j^{\text{dftb}3}(\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}}{d}^{3}r{d}^{3}r\prime ,}$$ (15)

$$N_{ij}=\int {\displaystyle \int \frac{{\phi }_i^{\text{cpe}}(\mathbf{r}){\phi }_j^{\text{cpe}}(\mathbf{r}\prime )}{|\mathbf{r}-\mathbf{r}\prime |}}{d}^{3}r{d}^{3}r\prime .$$ (16)

Here, Gaussian dipolar basis functions describe the CPE response density as

$${\phi }_i^{\mathit{\text{cpe}}}(\mathbf{r})=-2\zeta {(q_i)}^2{\left(\frac{{\zeta }^2}{\pi }\right)}^{3/2}(k-k_i)e^{{\zeta }^2|\mathbf{r}-{\mathbf{R}}_i{|}^2},$$ (17)

in which k is either x, y, or z, and K_i is either X_i, Y_i, or Z_i a component of the atomic position of atom i. The exponential factor ζ denotes an empirical parameter. To be able to account for the strong dependency of molecular polarizability as a function of the number of electrons in a system, i.e. its charge state, a monoexponential relation was asumed for ζ equal to the one proposed in the former work of Giese et al.³⁸ as

$$\zeta (q_i)=Z_i\cdot e^{B_i\cdot q_i},$$ (18)

where the value of ζ depends exponentially on the partial charge q_i of atom i as derived from DFTB3. In contast to the CPE dipolar Gaussian basis, charge density fluctuations in DFTB3 are described by monopolar Slater functions as

$${\phi }^{dftb3}(\mathbf{r})=\frac{{\tau }_i^3}{8\pi }{e}^{-{\tau }_i|\mathbf{r}-{\mathbf{R}}_i|}\text{ with }{\tau }_i=\frac{16}{5}(U_i+\frac{\partial U_i}{\partial q_i}\cdot q_i).$$ (19)

It should be noted that the expression for τ is rather empirically chosen for the purpose of including charge dependency. As already mentioned in the introductory part, in the framework of these monopoles, only radial but no angular dependent changes in the charge density can be captured.

The screening function f in Eq. (15), introduced earlier by Giese et al.,³⁸ has shown to be a useful empirical tool to capture the balancing effect of the kinetic energy that has been neglected by the Coulomb approximation of the first and second functional derivatives in Eq. (11). The screening function used here is

$$f(R_{ij})=\{\begin{array}{cc}1,\hfill & {\text{if }R}_{ij}>R_u\hfill \\ 0,\hfill & {\text{if }R}_{ij}<R_l\hfill \\ 1-10x^3+15x^4-6x^5,\hfill & \text{otherwise,}\hfill \end{array}$$ (20)

where

$$R_u=R_{i,u}+R_{j,u},$$ (21)

$$R_l=R_{j,l}+R_{j,l}.$$ (22)

Here, R_i,u and R_i,l are empirical parameters associated with atom i, which define interatomic distances in which the screening function is turned on. The variable x is defined as

$$x=\frac{R_u-R_{ij}}{R_u-R_l}.$$ (23)

The CPE response coefficients that minimize Eq. (14) are

$$\mathbf{c}=-{\mathbf{N}}^{-1}\cdot \mathbf{M}\cdot \mathbf{q}.$$ (24)

Because of the alteration of atomic charges q_i as a function of the DFTB3 SCF cycle and since the CPE energy expression depends on these charges, the CPE solution must enter back into the DFTB3 Hamilton matrix H_µν. Just as DFTB3 maps the density matrix into a basis of atomic charges, so too must the atom potentials be mapped into the Hamilton matrix.

These atom potentials p_i, i.e. the derivatives of the CPE energy (Eq. (14)) with respect to the charges q_i can be written as

$$p_i=\frac{\partial E_{\mathit{\text{cpe}}}[\mathbf{q},\mathbf{c}]}{\partial q_i}=\mathbf{c}\cdot \mathbf{M}+\mathbf{q}\cdot (d\mathbf{M}/d{q}_i)\cdot \mathbf{c}+\frac{1}{2}{\mathbf{c}}^T\cdot (d\mathbf{N}/d{q}_i)\cdot \mathbf{c}.$$ (25)

Finally, the Hamilton matrix correction Δ H_µν can be written as

$$\mathrm{\Delta }{H}_{\mu \nu }={\displaystyle \sum _i{p}_i\cdot \frac{{\partial }_{q_i}}{\partial {\rho }_{\mu \nu }}}$$ (26)

where ρ_µν is the single-particle DFTB3 density matrix.

From the set of coefficients c_j for the CPE basis functions and dipole moment of the standard DFTB3 reference method, a new molecular dipole moment ${\mu }_i^{\mathit{\text{cpe}}}$ can be defined as

$${\mu }_i^{\mathit{\text{cpe}}}={\mu }_i^{\mathit{\text{dftb}}3}+{\displaystyle \sum _j^N{c}_j},\text{\hspace{1em}with\hspace{1em}}i=x,y,z.$$ (27)

In analogy to equation Eq. (6), the finite electric field approach is used again for the evaluation of the polarizability tensor α utilizing the CPE corrected dipole moment ${\mu }_i^{\mathit{\text{cpe}}}$ as

$${\alpha }_{\mathit{\text{ij}}}^{\mathit{\text{cpe}}}=\left(\frac{\partial {\mu }_{\mathit{i}}^{\mathit{\text{cpe}}}}{\partial F_j}\right)\text{\hspace{1em}with\hspace{1em}}i,j=x,y,z.$$ (28)

Raman intensities

For the calculation of Raman spectra, the Normal Mode Analysis (NMA) method as implemented in the GAUSSIAN 03⁴⁵ program were used to generate the reference data on the DFT level. Concerning SCC-DFTB, spectra were calculated from an in-house NMA approach. At this point we will just briefly present the equations for the calculation of Raman activities. For a comprehensive treatment of the Raman effect, please refer to the literature (e.g. Long⁴⁰). By default, the Raman activity A_k for each individual normal mode of vibration Q_k in the system is evaluated via

$$A_k=\frac{1}{45}(45{\overline{\alpha }}_{\mathit{\text{iso}}}^2+13{\overline{\alpha }}_{\mathit{\text{aniso}}}^2),$$ (29)

where ᾱ_iso and ᾱ_iso denote the normal coordinate derivatives of the two rotational invariants of the polarizability tensor, α_iso and α_aniso. Those are calculated as

$${\overline{\alpha }}_{\mathit{\text{iso}}}^2=\frac{1}{9}{\left(\frac{\partial {\alpha }_{\mathit{\text{xx}}}}{\partial Q_k}+\frac{\partial {\alpha }_{\mathit{\text{yy}}}}{\partial Q_k}+\frac{\partial {\alpha }_{\mathit{\text{zz}}}}{\partial Q_k}\right)}^2,$$ (30)

$${\overline{\alpha }}_{\mathit{\text{aniso}}}^2=\frac{1}{2}[{\left(\frac{\partial {\alpha }_{\mathit{\text{xx}}}}{\partial Q_k}-\frac{\partial {\alpha }_{\mathit{\text{yy}}}}{\partial Q_k}\right)}^2+{\left(\frac{\partial {\alpha }_{\mathit{\text{xx}}}}{\partial Q_k}-\frac{\partial {\alpha }_{\mathit{\text{zz}}}}{\partial Q_k}\right)}^2+{\left(\frac{\partial {\alpha }_{\mathit{\text{yy}}}}{\partial Q_k}-\frac{\partial {\alpha }_{\mathit{\text{zz}}}}{\partial Q_k}\right)}^2++6\left({\left(\frac{\partial {\alpha }_{\mathit{\text{xy}}}}{\partial Q_k}\right)}^2+{\left(\frac{\partial {\alpha }_{\mathit{\text{yz}}}}{\partial Q_k}\right)}^2+{\left(\frac{\partial {\alpha }_{\mathit{\text{xz}}}}{\partial Q_k}\right)}^2\right)].$$ (31)

Parametrization and Performance of DFTB3/CPE

For the CPE parametrization of DFTB3, the structures of 172 small organic molecules ranging from 3–14 atoms and containing elements H,S,N,O,S,P were taken from the QCRNA⁴¹ database as well as their molecular properties of interest. The set contains overall 112 neutral, 37 monoanionic and 23 monocationic model compounds for which dipole moments (using a 6-311G++(3df,2p) triple zeta basis) and polarizabilities (using a 6-31G++(p,d) double zeta basis) were generated with density functional theory (DFT) together with Becke’s B3LYP²² exchange-corrrelation functional, as implemented in GAUSSIAN 03.

For the current CPE implementation an overall number 24 empirical fit parameters (for H,S,N,O,S,P) were required, i.e. 2 distance parameters R_i,u and R_i,1 for the switching function (Eq. (20)), as well as 2 parameters, Z_i and B_i, for the CPE ζ -exponent (Eq. 18). The empirical parameters where chosen to minimize the discrepancy between the norm of molecular dipole moments µ and isotropic polarizabilities α^iso, evaluated as

$$\mu =\sqrt{{({\mu }_x)}^2+{({\mu }_y)}^2+{({\mu }_z)}^2},$$ (32)

$${\alpha }^{\mathit{\text{iso}}}=\frac{1}{3}({\alpha }_{\mathit{\text{xx}}}+{\alpha }_{\mathit{\text{yy}}}+{\alpha }_{\mathit{\text{zz}}}),$$ (33)

from DFTB3 calculations with respect to target data from full density functional calculations.

The merit function Θ to be minimized during the parametrization process can be written as

$$\mathrm{\Theta }={\displaystyle \sum _i^{172}({\mu }_i-{\mu }_{\mathit{\text{ref}},i})+}{\displaystyle \sum _i^{172}({\alpha }_i^{\mathit{\text{iso}}}-{\alpha }_{\mathit{\text{ref}},i}^{\mathit{\text{iso}}}).}$$ (34)

Results and Discussion

The optimized set of empirical parameters for the switching function f and Slater exponents ζ in the CPE basis functions are listed in Table 1.

Table 1.

Optimized set of empirical CPE fit parameters for DFTB3.

	Z (a.u.)	B (a.u.)	Ri,l (a.u.)	Ri,u (a.u.)
H	4.10743330	4.37992780	0.65017096	0.89976532
C	2.12941380	0.46271552	1.58230960	2.60816630
O	4.59123620	1.05271210	4.14445140	4.50938330
N	2.58954660	0.50147210	2.99983790	3.12407570
S	2.26117890	0.74985889	3.40497140	624.334400
P	36.9483900	105.240460	74.7108830	1998.27850

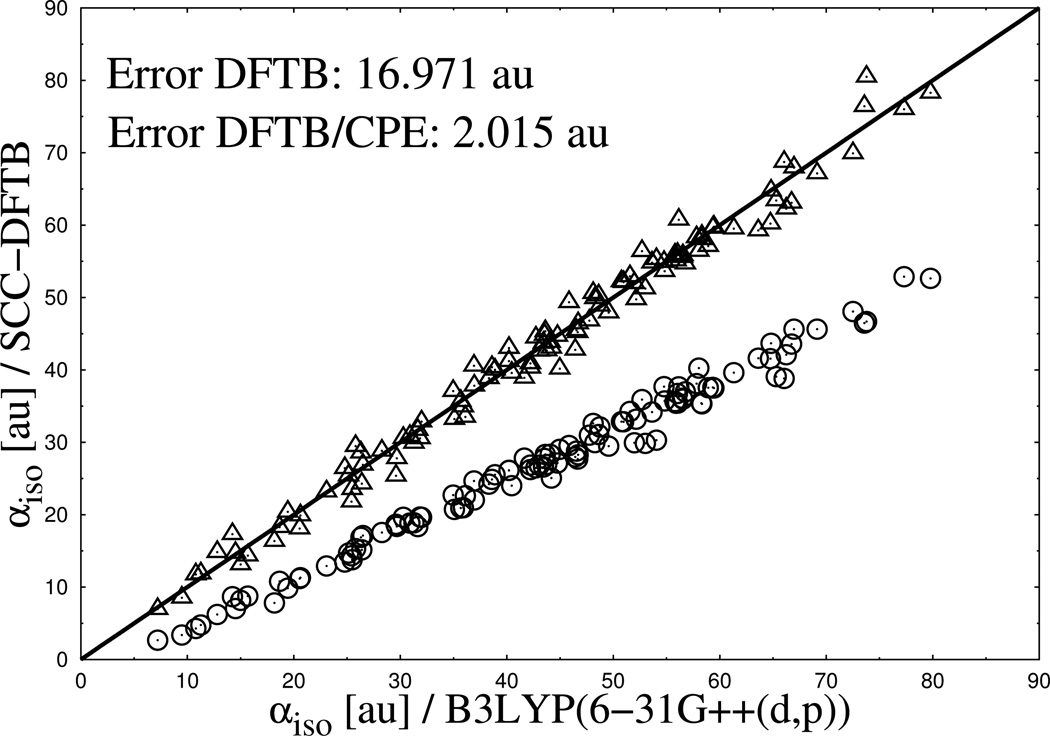
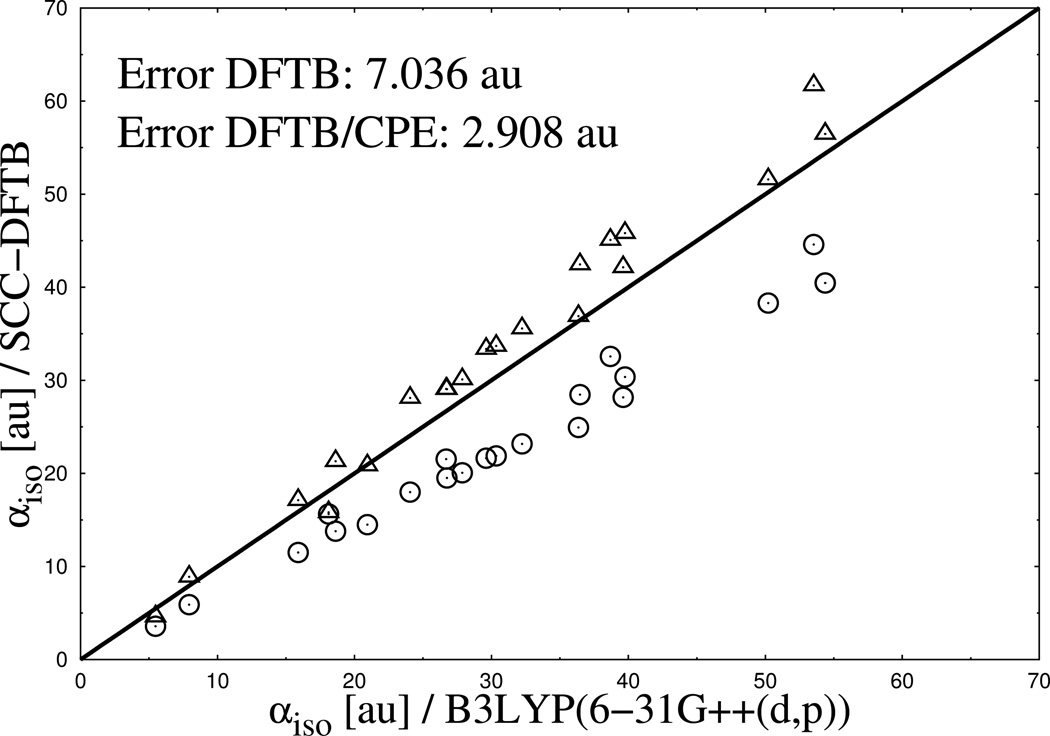
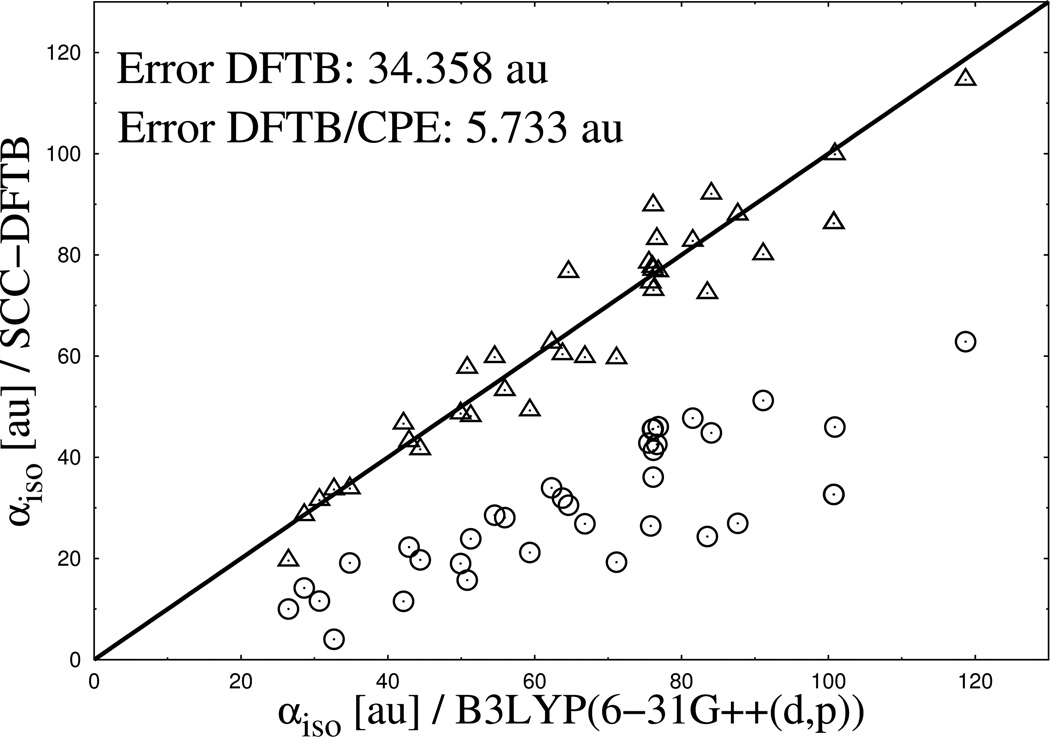
In Figure 2 to Figure 4 the performance of DFTB3/CPE for the calculation of the mean molecular polarizability is shown and compared with the reference data from DFT and results form standard DFTB3. Generally, the results show several clear tendencies. Most striking is the systematic underestimation of molecular polarizability from standard DFTB3 compared to DFT reference data for neutral, cationic and monoanionic compounds, an observation in line with previous studies. ³⁹

Figure 2.

Calculated isotropic molecular polarizabilities for a set of 112 neutral organic molecules. Results from DFTB3 (spheres) and DFTB3/CPE (triangles) calculations are compared with DFTB/B3LYP reference data (diagonal line).

Figure 4.

Calculated isotropic molecular polarizabilities for a set of 23 monocationic organic molecules. Results from DFTB3 (spheres) and DFTB3/CPE (triangles) calculations are compared with DFTB/B3LYP reference data (diagonal line).

Furthermore, an increasing deviation of the DFTB3 results from the reference with an increasing number of electrons (charge state) in the system can be observed. The error in mean polarizability (see Figure 2 to Figure 4) approximately doubles when going from cationic (7.036 au error) to neutral (16.971 au error) compounds and again when going to anionic (34.358 au error) molecules. Apart from that, the deviation between DFTB3 and DFT reference also increases with increasing absolute polarizability of the system, illustrated by increasing differences from the left to the right side of the graphs in Figure 2 to Figure 4. The results from parametrized DFTB3/CPE approach, as also shown in Figure 2 to Figure 4, reveal a significant improvement for the the calculated isotropic polarizabilities. Most notably, an almost equally good agreement is achieved along the different charge states of molecules, due to the fact that the current CPE implementation accounts for charge dependency of molecular polarization.

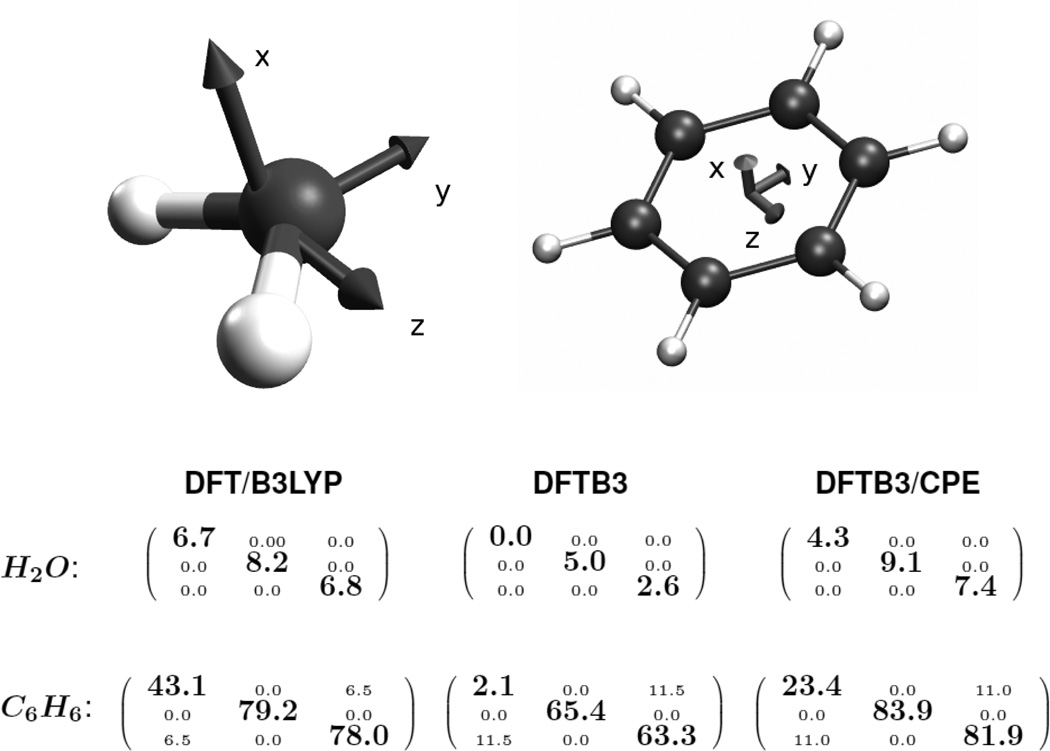
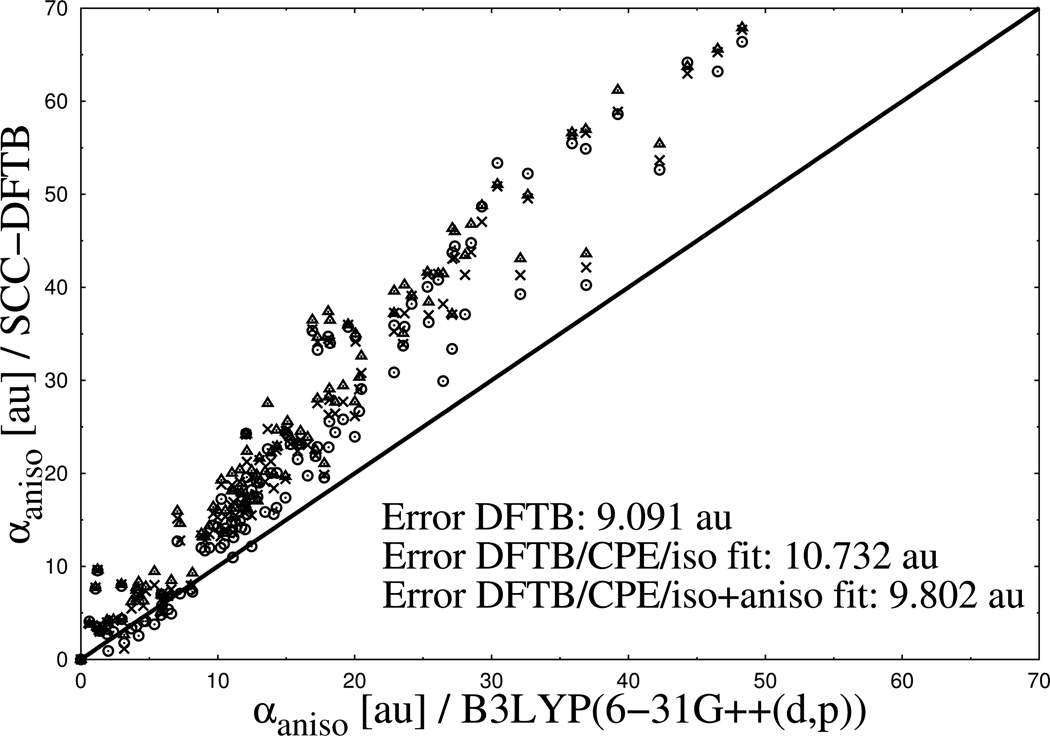
To emphasize the progress the current CPE extension delivers in this respect, the molecular polarizability of a glycine residue as a function of its charge state is presented in Table 2. As shown in the table, DFTB3 not only underestimates values for the polarizabilities itself but, more severely, shows the wrong tendency, a decreasing polarizability with increasing number of electrons in the system. For both of these errors the currently implemented DFTB3/CPE approach denotes a dramatic improvement. Besides polarizability calculations on single molecules, we’ve also tested the CPE parameters on a water dimer to figure out its performance for molecular complexes. In Figure 5, the polarisability of the dimer is plotted against the intermolecular distance of the monomers. As observed for single molecules, the polarizability of the dimer is underestimated by DFTB3 by a factor of ~ 2.5 compared to full DFT over the entire range of distances. This deviation to the reference data is again significantly reduced within the DFTB3/CPE approach. To analyze the inherent problems in electronic polarizability calculations of DFTB3 in more detail, the complete tensors of two molecules, water and benzene, are shown in Figure 6. For water, only the diagonal elements are nonzero from both the reference data (DFT) and DFTB3. Although all three diagonal elements from DFTB3 are smaller compared to the DFT ones, the deviation is especially large for the xx-component of the tensor where DFTB3 predicts zero polarizability out of plane. As mentioned in the theory section, the monopole Slater representation of charge fluctuations (see Eq. (18) is insufficient to describe polarization out of a molecular plane. This systematic shortcoming is largely removed by the current CPE extension, as shown in Figure 6. From DFTB3/CPE, all diagonal elements are in closer agreement with the DFT reference. The same observation holds for benzene concerning the diagonal tensor elements. Here again, very little out of plane polarzability (xx-component) is observed from DFTB3 calculations, a situation significantly improved with DFTB3/CPE. The off-diagonal elements (xz/zx-components) for benzene, however, show a clear overestimation from DFTB3 compared to the reference by a factor of ~ 2, which also holds for the DFTB3/CPE approach. That this observation, overestimation of off-diagonal elements, is a tendency also holding for the majority of test molecules is shown in Figure 7. Here, the anisotropic component of the polarizability tensor

$${\alpha }_{\mathit{\text{aniso}}}=\frac{1}{2}[{({\alpha }_{\mathit{\text{xx}}}-{\alpha }_{\mathit{\text{yy}}})}^2+{({\alpha }_{\mathit{\text{yy}}}-{\alpha }_{\mathit{\text{zz}}})}^2+{({\alpha }_{\mathit{\text{zz}}}-{\alpha }_{\mathit{\text{xx}}})}^2+{({\alpha }_{\mathit{\text{yy}}}-{\alpha }_{\mathit{\text{zz}}})}^2+6({\alpha }_{\mathit{\text{xy}}}^2-{\alpha }_{\mathit{\text{yz}}}^2+{\alpha }_{\mathit{\text{yz}}}^2)],$$ (35)

is plotted. Since all elements of the tensor appear in α_aniso, and not only diagonal ones as in α_iso and because of the first 3 difference terms, which are more prone to error, α_aniso is more complicate to evaluate accurately. The plot shows 3 different graphs which all show the same basic pattern, i.e. a clear overestimation of the anisotropic component compared to full DFT over the entire range of 112 neutral test molecules. From the deviations of anisotropic polarizability as given in Figure 7, it can also be seen that DFTB3/CPE/iso-fit (10.732 au), does not give any improvement over the standard DFTB3 method (9.091 au). Here, the extension ’iso-fit’ shall clarify that the CPE parameters have only been optimized for isotropic components (α_iso) of the tensor so far. Therefore, a re-parametrization has been performed, where also the anisotropic components were included in the merit function Θ as

$$\mathrm{\Theta }={\displaystyle \sum _i^{172}({\mu }_i-{\mu }_{\mathit{\text{ref}},i}})+{\displaystyle \sum _i^{172}({\alpha }_i^{\mathit{\text{iso}}}-{\alpha }_{\mathit{\text{ref}},i}^{\mathit{\text{iso}}}})+{\displaystyle \sum _i^{172}({\alpha }_i^{\mathit{\text{aniso}}}-{\alpha }_{\mathit{\text{ref}},i}^{\mathit{\text{aniso}}}}).$$

Table 2.

Comparison of calculated mean molecular polarizabilities (given in au) as a function of charge state for the amino acid glycine.

Charge state	DFT/B3LYP	DFTB3	DFTB3/CPE
+1	36.4	24.9	36.9
0	40.5	24.0	39.6
−1	51.3	23.9	48.1

Figure 5.

Comparison of calculated isotropic molecular polarizabilities as a function of intermolecular distance for a water dimer.

Figure 6.

Comparison of polarizability tensors for water and benzene (both oriented in the yz-plane) as calculated from DFT/B3LYP and DFTB3 levels of theory. Diagonal elements are emphasized.

Figure 7.

Calculated anisotropic molecular polarizabilities for a set of 112 neutral organic molecules. Results from DFTB3 (spheres), DFTB3/CPE/iso (triangles) and DFTB/CPE/aniso (crosses) calculations are compared with DFTB/B3LYP reference data (diagonal line).

The results from the re-parametrization, also presented in Figure 7 and denoted with DFTB3/CPE/iso+aniso fit, show no notable improvement for α_aniso. With the current CPE implementation, no parameter set were found to reproduce equally well both rotational invariants,α_iso and α_aniso, of the polarzability tensor.

Raman intensities from DFTB3/CPE

So far, we’ve focused on absolute electronic polarzabilities. The ability of an accurate description of polarizability changes as a function of normal mode vibrations, however, opens the way to the prediction of Raman vibrational spectra. As already discussed in the theory section, Raman intensities (or activities) are connected to first order polarizability derivatives with respect to normal mode vibrations Q_k. As a first test on how CPE performs for those derivatives we replaced them by finite differences as

$$A_k\propto {\left(\frac{\partial \alpha }{\partial Q_k}\right)}^2\approx {\left(\frac{\mathrm{\Delta }\alpha }{\mathrm{\Delta }{Q}_k}\right)}^2.$$ (36)

For a subset of the test molecules we took the optimized DFT structure and its polarizability as a reference (α_opt), which was subsequently subtracted by the resulting polarizability from the molecule in a distorted structure (α_dist) along a certain normal mode of vibration, so that Δα in Eq. (36) becomes

$$\mathrm{\Delta }{\alpha }_{\mathit{\text{iso}}}={\alpha }_{\mathit{\text{iso}}}^{\mathit{\text{opt}}}-{\alpha }_{\mathit{\text{iso}}}^{\mathit{\text{dist}}},$$ (37)

$$\mathrm{\Delta }{\alpha }_{\mathit{\text{aniso}}}={\alpha }_{\mathit{\text{aniso}}}^{\mathit{\text{opt}}}-{\alpha }_{\mathit{\text{aniso}}}^{\mathit{\text{dist}}}.$$ (38)

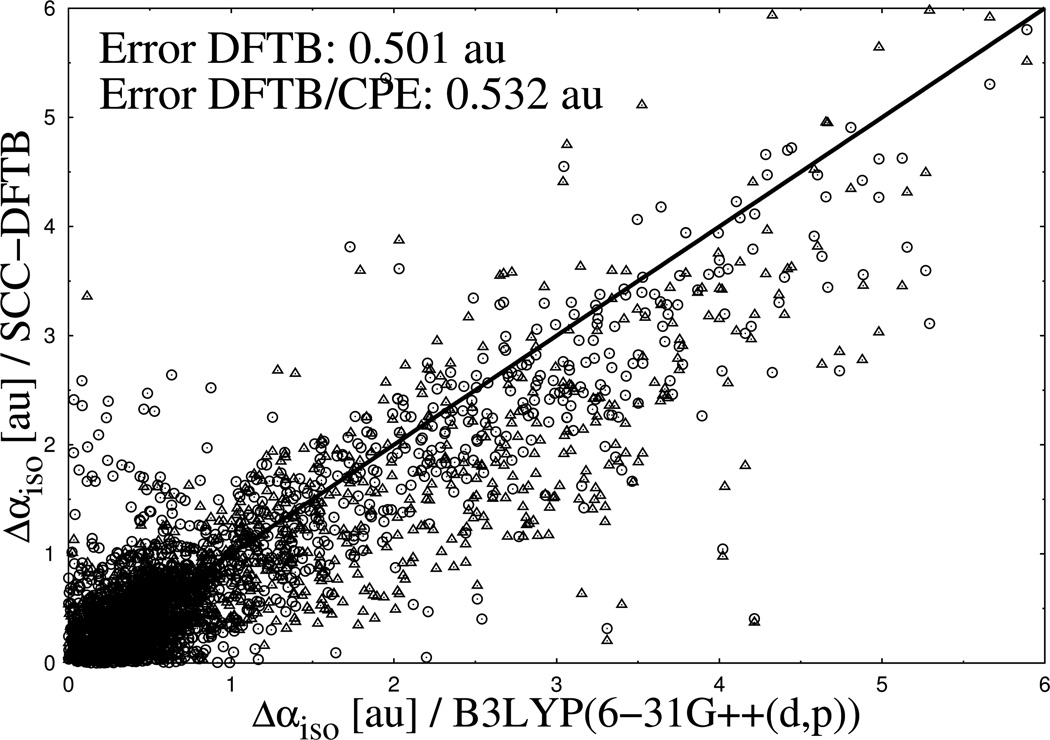
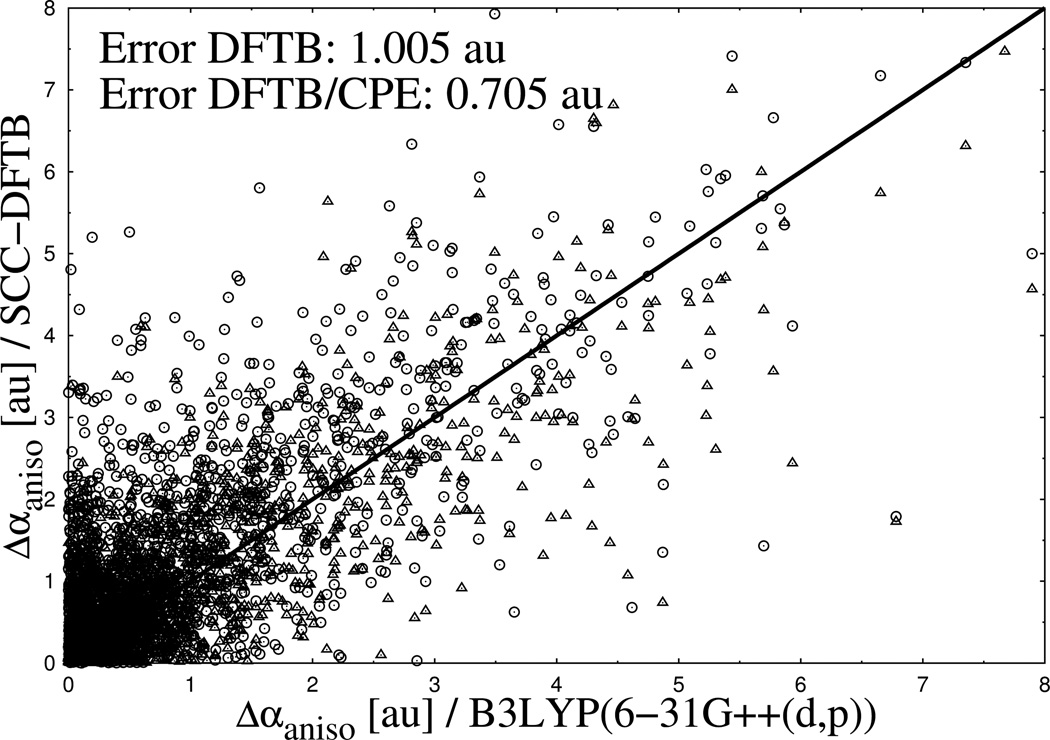
The same molecular structures were used for calculations with DFTB3 for comparison. In Figure 8 and Figure 9, the results are shown for Δα_iso and Δα_aniso for a set of overall 1847 normal modes of vibration. By comparing the scatter plots from both figures, the same tendency appears for the polarizability differences as for the absolute values. While most of the data points for Δα_iso from DFTB3 are below the reference diagonal line from full DFT, meaning an underestimation of polarizability change, the data points of Δα_iso spread more homogenous around the reference with small tendency of overestimation. As pointed out in Figure 8 and Figure 9, the average deviation of DFTB3 from the reference is twice as large for Δα_iso 0.501 au) compared to Δα_aniso (1.005 au), reflecting that the latter is more difficult to evaluate accurately. In this respect it is remarkable that with the CPE extension of DFTB3 the average deviation of Δα_aniso from the reference could be reduced by ~ 30 % (1.05 vs. 0.705 au), while CPE has no notable effect on Δα_iso (0.501 vs. 0.532 au).

Figure 8.

Calculated differences of isotropic molecular polarizabilities for a subset of test molecules. Results from DFTB3 (spheres) and DFTB3/CPE (triangles) calculations are compared with DFTB/B3LYP reference data (diagonal line).

Figure 9.

Calculated differences of isotropic molecular polarizabilities for a subset of test moleculess. Results from DFTB3 (spheres) and DFTB3/CPE (triangles) calculations are compared with DFTB/B3LYP reference data (diagonal line).

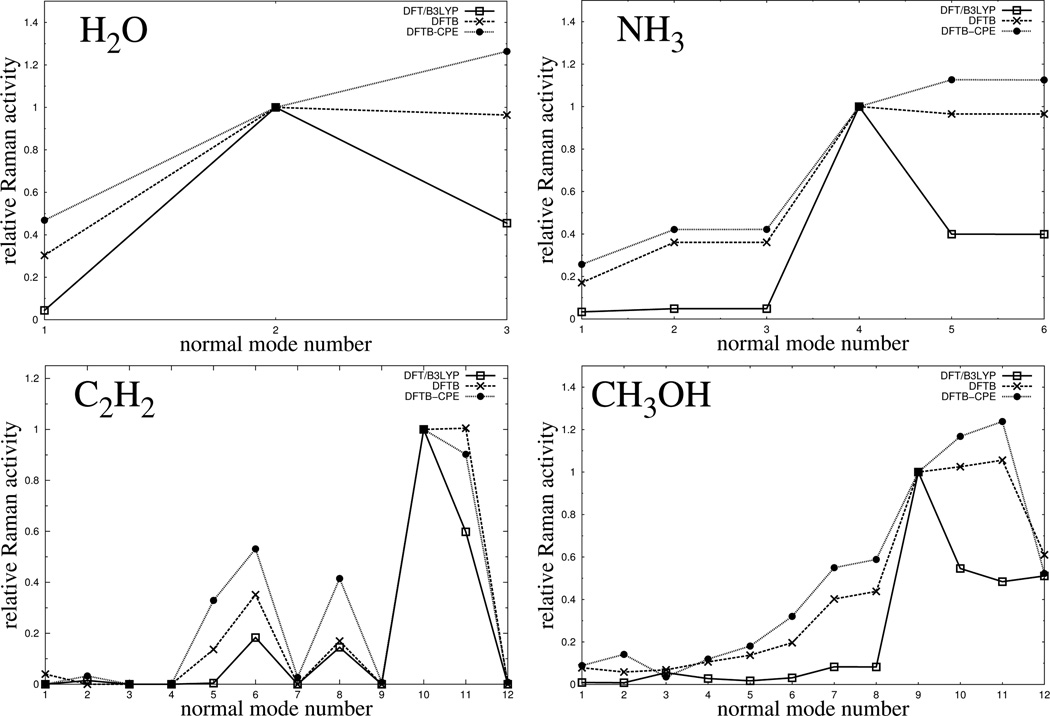
As a final test in which we go from finite differences for electronic polarizabilities to first order derivatives, Raman activities were calculated for a small subset of test molecules. In Figure 10, the results are shown for 4 molecules. We restricted the analysis to very small molecules to achieve a low density of states (DOS) in the interesting mid-infrared region, in order to keep the assignment of vibrational modes simple. For each molecule, three graphs (DFT vs. DFTB3 vs. DFTB3/CPE) are presented, where Raman activities are plotted against the vibrational mode number. For better comparison of the relative activities (we are not interested in absolute activities), all the graphs are normalized to unity against the mode with highest activity from the DFT reference. From the graphs in Figure 10, two tendencies can be observed. For all molecules, the relative activities are systematically overestimated by DFTB3 compared to the reference over the entire spectral range. This effect is even more pronounced for DFTB3/CPE, which leads to a stronger overestimation for the activities. Further, modes in the high frequency region (frequency increases with mode number), tend to be more overestimated as modes in the region of lower frequencies, which is especially true for H₂O, NH₃ and CH₃OH.

Figure 10.

Comparison of calculated Raman activities, plotted against the normal mode number, for 4 small sized molecules and different levels of theory. Here, the normal mode number denotes a vibrational mode being of the same character for both levels of theory (DFT and DFTB3), increasing from low to high energies (vibrational frequencies). All graphs for a specfic molecule are normalized to unity with respect to the activity of a certain vibrational mode. In particular, mode 2 for H₂O, mode 4 for NH₃, mode 10 for C₂H₂ and mode number 9 for CH₃OH.

Summary and Conclusions

In the present work, we successfully implemented and parametrized the chemical potential equalization method (CPE) into the DFTB3 program, in order to calculate accurate electronic polarizabilities. The improvements of DFTB3 over DFTB2 and DFTB for molecular properties has been discussed in detail recently.³⁶ The main improvements found for DFTB3 are basically related to a better description of charged molecules, particularly relevant for this work.

We were encouraged add CPE to DFTB3 because of significant improvements York and Giese achieved with an MNDO/CPE code for polarizabilitiy calculations when compared to standard MNDO. As for semi empirical methods in general, also SCC-DFTB works with a minimal atomic orbital basis, which is critical, since the accuracy of electronic polarizability depends strongly on the size of the ao-basis. In the current CPE formalism response density is added to the system without increasing the ao-basis, which keeps the computational cost fairly low. Besides the minimal ao basis, also the restriction of the second order terms to monopole contributions may limit SCC-DFTB’s ability to describe density response properties severely. This is also confirmed by further results presented in the supplementary information where the performance of CPE implemented into DFTB2 is shown. Since both DFTB2 and DFTB3 are characterized by the same approximations, i.e. minimal basis and monopole representation of charge fluctuations, either the errors for polarizabilities in the standard implementations as well as the improvements when CPE is employed are very similar (see supplementary information). In fact, DFTB3 does not perform notably better in polarizability calculations of neutral molecules than DFTB2 because of the same basic limitations.

For charged molecules, however, there is a drastic improvement due to the charge dependent exponent of the CPE basis functions. Note, that this can be added also to the DFTB2 formalism in an ad hoc fashion, but its formal justifications comes from the DFTB3 extension, where a charge dependent Hubbard is derived from the third order expansion of the DFT total energy. Therefore, a formally consistent application of charged dependent CPE is only possible at the DFTB3 level, leading to a significantly improved description of charged molecules³⁶ and their polarizabilities, as shown in this work.

With an overall number of 24 optimized empirical parameters for elements H,S,N,O,S,P, the DFTB3/CPE approach has shown to correct for these shortcomings of the original SCC-DTB to give very accurate mean (isotropic) polarzabilities, in comparison to full DFT reference data, for a large set of small to medium sized organic molecules. This accuracy, however, comes at a considerable lower computational cost, with SCC-DFTB being 3 orders of magnitude faster than DFT. Another shortcoming of SCC-DFTB, the inability to predict the strong charge dependence of electronic polarizability could also be removed by the present DFTB3/CPE approach. While DFTB3/CPE can be successfully applied for the calculation of isotropic polarizabilities (average of diagonal tensor elements) alone, the entire polarizability tensor remains a challenging task. It seems that off-diagonal elements tend to be overestimated while diagonal elements are underestimated by SCC-DFTB. In fact, no single parameter set could be found within the current framework of DFTB3/CPE to predict both rotational invariants of the polarizability tensor accurately.

The observation that the CPE correction largely improves the isotropic polarizability is consistent with previous observations, and primarily due to the fact that the CPE dipole functions have an isotropic self-energy; i.e., the diagonal elements of the N-matrix are the same for the x-, y-, and z-directions. In this way, the model itself is a superposition of loosely coupled isotropic dipolar response functions, and therefore largely isotropic.

Besides the absolute values of polarizability, also their changes along vibrational modes were investigated to estimate the ability of the DFTB3/CPE approach for Raman activity calculations. In this respect, only changes in anisotropic polarizability were improved from DFTB3/CPE compared to full DFT, which remains rather questionable to us, since the anisotropic component is the more complex value compared to the isotropic one.

As a matter of fact, the current implementation of DFTB3/CPE can also not contribute to the improvement of Raman activities, i.e polarizability derivatives, instead the agreement with the reference DFT is worse compared to plain DFTB3. Here, the damping function in the first Coulomb integral expression, maybe responsible for that. Since the function screens out the Coulombic interactions for atoms which are close in distance and because molecular vibrations elongate bonds for approximately 0.1 Å, normal mode vibrations may cause to little structural and therefore polarizability changes to be captured by the current CPE implementation.

As future work, one could think of a modified CPE approach capable of "fine-tuning" the polarizability as a function of bond length, which could be helpful for parametrically reproducing Raman spectra.

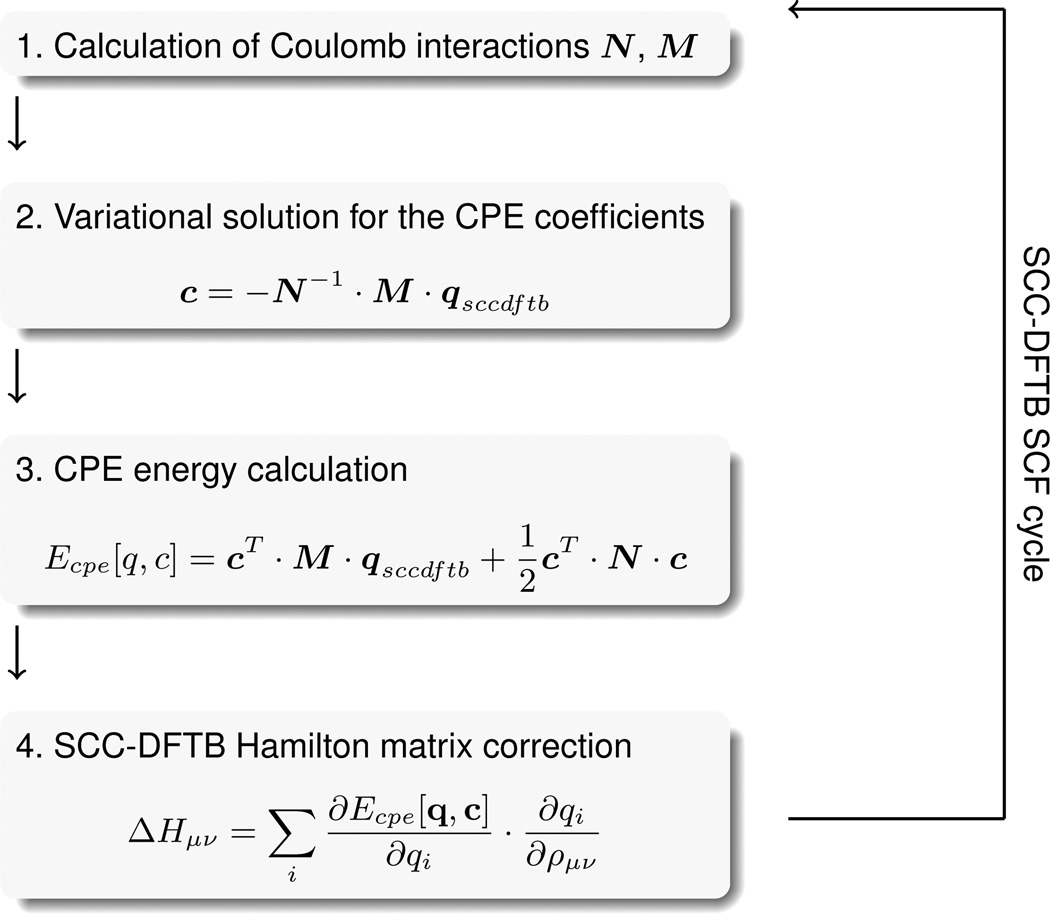
Figure 1.

Schematic representation of the CPE framework as imbedded into DFTB3.

Figure 3.

Calculated isotropic molecular polarizabilities for a set of 37 monoanionic organic molecules. Results from DFTB3 (spheres) and DFTB3/CPE (triangles) calculations are compared with DFTB/B3LYP reference data (diagonal line).