In silico study of Aquaporin V: Effects and affinity of the central pore-occluding lipid

Abstract

Because of its roles in human physiology, Aquaporin V (AQP5), a major intrinsic protein, has been a subject of many in vitro studies. In particular, a 2008 experiment produced its crystal structure at 2.0 Å resolution, which is in a tetrameric conformation consisting of four protomers. Each protomer forms an amphipathic pore that is fit for water permeation. The tetramer has a pore along its quasi-symmetry axis formed by quadruplets of hydrophobic residues (every protomer contributes equally to the quadruplets). A lipid, phosphatidylserine (PS6), is bound to AQP5 in the central pore, totally occluding it. A 2009 experiment showed that AQP5 facilitates not only permeation of water but also permeation of hydrophobic gas molecules across the cell membrane. In this article, we present an in silico study of AQP5 to elucidate the effects of PS6’s binding to and dissociating from AQP5’s the central pore. Computing the lipid’s chemical-potential along its dissociation path, we find that PS6 inhibits the function of the central pore with an IC₅₀ in the micromolar range. Examining the central pore and the interstices between two adjacent protomers, we propose that nonpolar gas molecules (O₂) permeate through AQP5’s hydrophobic central pore when un-occluded.

INTRODUCTION

Aquaporin V (AQP5) has been implicated in Sjogren’s disease and in cancers of the lung, pancreas, colon, and more. Therefore, a great many efforts have been invested on this major intrinsic membrane protein [1-11]. High-resolution x-ray structure of AQP5 was determined by Horsefield et al [12] in 2008. They found that AQP5 resembles other aquaporins in its tetrameric conformation consisting of four protomers, each of which forms an amphipathic pore that selectively conducts water and solutes. However, it lacks the four-fold quasi-symmetry among its four protomers and it contains a lipid, phosphatidylserine (C₂₆H₅₀NO₁₀P, PS6), in its central pore. PS6 totally occludes the central pore and thus was hypothesized to inhibit gas permeation through AQP5. Meanwhile, the 2009 in vitro experiment by Musa-Aziz et al [13] showed that AQP5 facilitates permeation of gas as well as water. In light of the existent in vitro studies of AQP5’s functions and its crystal structure, several questions of functional relevance can be answered by conducting in silico studies. First, does the presence or absence of PS6 cause any changes to AQP5’s functions? Second, while it is expected that water permeates through the four conducting pores of an AQP5 tetramer, what is the passageway for gas permeation? Is the hydrophobic central pore the only possibility? Is there enough interstitial space between two adjacent protomers to allow gas permeation through there? Or is there any space between the protein and the membrane lipids for that purpose? Third, the x-ray structure clearly tells us that PS6 occludes the central pore. What is the dissociation constant of PS6 from AQP5 and what is the binding mechanics? In this article, we answer these fundamental questions by conducting extensive molecular-dynamics (MD) simulations of two model membrane systems consisting of an AQP5 tetramer embedded in a lipid bilayer: the first system (SysI) with the lipid, PS6, in AQP5’s central pore and the second system (SysII) without the lipid.

We conducted equilibrium MD runs (100 ns for SysI and 100 ns for SysII) and computed the water permeabilities and the root-mean-square-deviations (RMSD) of the protein in both systems. We compare the results between the two systems to elucidate the effects of PS6 on AQP5’s structure and its water conducting mechanics. We analyze the equilibrated structures to search for possible passageways of gas permeation. We conducted non-equilibrium steered molecular-dynamics (SMD) runs (164 ns for SysI) to compute the free-energy profile of PS6 along its dissociation path. In this way, we determine the dissociation constant and the binding mechanics. We also conducted 68 ns SMD runs for SysII to determine the free-energy profile of O₂ along its permeation path.

METHODS

System setup

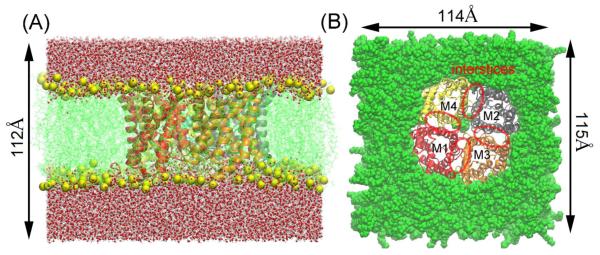
This study was based on the following all-atom model of AQP5 in the cell membrane: The AQP5 tetramer with PS6 (PDB: 3D9S) is embedded in a patch of fully hydrated palmitoyloleylphosphatidyl-ethanolamine (POPE) bilayer. The AQP5-POPE complex is sandwiched by two layers of water, each of which is approximately 40Å in thickness. The system is ionized and neutralized with Na⁺ and Cl⁻ ions at a concentration of 111mM. The entire system, consisting of 143,310 atoms, is 114Å×115Å×112Å in dimension when fully equilibrated. This is SysI (illustrated in Fig. 1). The second system (SysII) was derived from SysI by deleting the lipid, PS6, and adding one additional Cl⁻ ion so that the entire system remains neutral. It has 143,224 atoms in all and dimensions approximately equal to those of SysI. The Cartesian coordinates are chosen such that the xy-plane is parallel to the lipid-water interface and the z–axis is pointing from the cytoplasm to the periplasm.

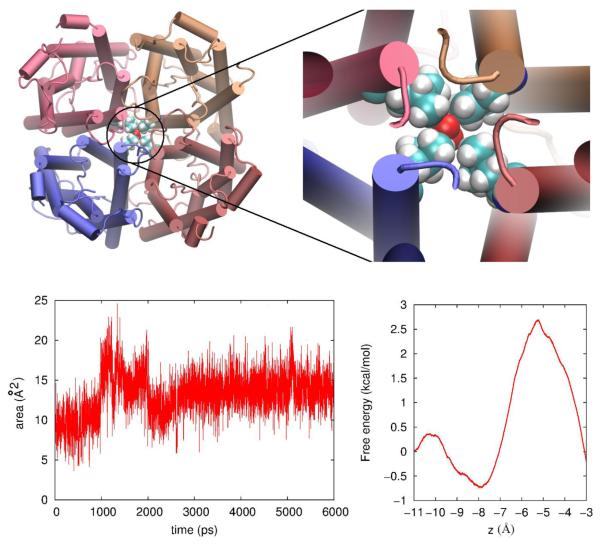
Fig. 1.

System setup: side view (A) and top view (B) of the model membrane patch. The AQP5 tetramer is embedded in a POPE lipid bilayer. M1, M2, M3 and M4 represent the four protomers. Interstitial spaces between adjacent protomers are circled. The system dimensions are noted. Shown in (A) are the protein in Ribbons representation, the POPE lipids in Lines representation with phosphorus atoms in yellow balls, and waters in CPK representation. Shown in B are the protein, the POPE lipids and central-pore occluding lipid (both in VDW representation, colored green). Rendered with VMD[33].

All the simulations of this work were performed using NAMD 2.8 [14]. The all-atom CHARMM36 parameters [15, 16] were adopted for all the inter- and intra-molecular interactions (including O₂ gas). Water was represented explicitly with the TIP3 model[17]. The pressure and the temperature were maintained at 1 bar and 300 K, respectively. The Langevin damping coefficient was chosen to be 5/ps. The periodic boundary conditions were applied to all three dimensions, and the particle mesh Ewald[18] was used for the long-range electrostatic interactions. The PMEGrideSizeX,Y,Z parameters are all set to 128. Covalent bonds of hydrogen atoms were fixed to their equilibrium length. The time step of 2 fs was used for short-range interactions in equilibrium simulations but 1 fs was used for nonequilibrium runs. The same time step of 4 fs was used for long-range forces in both equilibrium and nonequilibrium simulations. The cut-off for long-range interactions was set to 12 Å with a switching distance of 10 Å. all SMD runs, the alpha carbons on the transmembrane helices of AQP5 (−10Å < z <10Å) were fixed to the corresponding crystal coordinates to fully respect the crystal structure.

Equilibrium MD

Two MD runs of 100 ns each in length were conducted, one for SysI and one for SysII. The structures of the two systems were compared to elucidate the structural consequences of the central-pore occluding lipid, PS6. Using the theoretical formulation of Ref. [19], we computed the mean square displacements (MSD) of the water molecules in the water-conducting pores. From the slope of the MSD vs time curves, we can compute the osmotic permeability: The slope is equal to 2D_n (D_n being the collective diffusion constant of the waters in the pore) and the osmotic permeability p_f = v_WD_n where v_W is the average volume occupied by one water molecule.

Nonequilibrium SMD with BD-FDT

In an SMD study [20-28], we pull (steer) a group of atoms with appropriate forces so that they go along a desired direction to explore a certain manifold of the system’s phase space. In the present study, we pull the center-of-mass of PS6 or O₂ along the z-axis to sample transition paths between States A and B. Along each forward pulling path from A to B, the work done to system was recorded as W_A→Z when a molecule was pulled from A to Z. Along each reverse pulling path from B to A, the work done to system was recorded as W_B→Z when the molecule was pulled from B to Z. Here Z represents a state of the system when the center-of-mass z-coordinate of the pulled molecule is z. A and B represent, respectively, the two ends of a given section that was 1 Å each in width. The chemical potential of the pulled molecule, G⁰ (z), when its center of mass is at a given coordinate z, can be computed through the Brownian dynamics fluctuation-dissipation theorem (BD-FDT)[29, 30] as follows:

$$G^0\left(z\right)-G^0\left(z_A\right)=-k_{B}T\ln \left(\frac{{\langle \exp [-W_{A\to Z}∕2k_{B}T]\rangle }_F}{{\langle \exp [-W_{Z\to A}∕2k_{B}T]\rangle }_R}\right).$$ (1)

Here the brackets in the numerator and the denominator represent, respectively, the statistical means along the forward and the reverse paths. W_Z→A = W_B→A−W_B→Z is the work done to the system for the part of a reverse path when the molecule was pulled from Z to A. k_B is the Boltzmann constant and T is the absolute temperature. z_A and z_B are the z-coordinates of the center of mass of the pulled molecule at the end states, A and B. Long (4 ns) equilibrations were done at each end state (A or B) and the pulling speed was v = 2.5Å / ns for both PS6 and O₂. In each set, five forward and five reverse paths were sampled. It should be noted that the free-energy barriers computed in this manner is approximate and they can be higher than the actual barriers of the system in equilibrium state because the entire system is not fully relaxed.

RESULTS AND DISCUSSION

Structural consequences of PS6

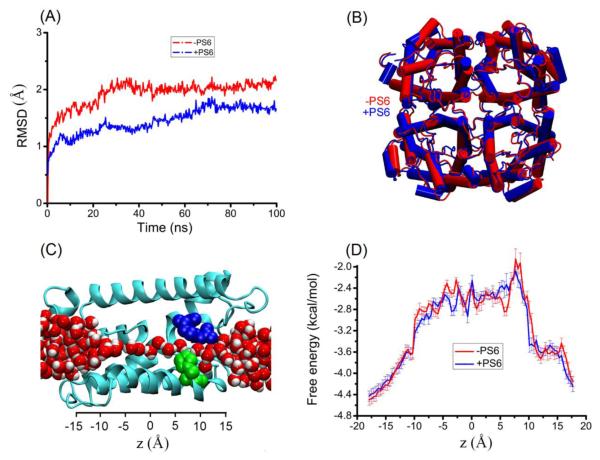
In contrast to other tetrameric conformation of aquaporins that do not have a lipid occluding the central pore along the four-fold quasi-symmetry axis, the crystal structure of AQP5 was found to have a lipid, PS6, residing in there. So far, however, there is no direct experimental evidence for the lipid’s functional role. It is still unknown whether or not the presence of PS6 is necessary to stabilize the tetrameric conformation of AQP5, which is the first question we aim to answer. In order to elucidate the structural consequences of the central pore-occluding lipid, we computed AQP5’s root mean square deviations (RMSD) from its crystallographic form (PDB code: 3D9S) during the equilibrium MD runs of SysI (with PS6) and SysII (without PS6). The RMSDs, shown in Fig. 2(A), are approximately within the X-ray structure resolution of 2.0 Å. After 100 ns equilibrium MD runs, the structure of the AQP5 tetramer does not differ significantly between SysI and SysII (Fig. 2(B)). Therefore, we found no evidence against the hypothesis that the lipid found in the central pore of the AQP5 tetramer is not necessary to stabilize the functional tetrameric conformation of AQP5.

Fig. 2.

SysI vs SysII. Shown in (A) are the RMSDs of AQP5 from the X-ray structure during equilibrium MD runs, in the presence and in the absence of PS6 in the central pore, respectively. Shown in (B) are the superimposed structures of AQP5 in SysI and SysII after 100 ns equilibration. Proteins are shown in the Cartoon representation. Shown in (C) is one of the four water-conducting pores with waters lining up in single file throughout the channel. The protein is in the NewRibbons representation (colored in cyan), the SF forming residues in VDW (R188 in blue and H173 in green), and the waters in VDW (oxygen in red and hydrogen in white). Plotted in (D) are the free-energy profiles of water permeating through AQP5 in SysI and SysII.

It is known that water permeates through aquaporins including AQP5 in concerted diffusion, lining up in single file, through every one of the four amphipathic pores formed individually by the four protomers of a tetrameric protein[12] (Fig. 2(C)). The next question we aim to answer is: Does the presence of PS6 alter or regulate AQP5’s water permeability? Examining the atomistic structures from the equilibrium MD simulations of SysI and SysII, we found that the presence or absence of PS6 in the central pore does not significantly alter the conducting pore structure or the hydrogen bondings among the single-file waters and between those waters and the lumen residues. Quantitatively, we computed the free-energy profiles of water along the conducting channel (Fig. 2(D)). In the presence of PS6, the free-energy curve along the AQP5 channel shows multiple barriers, one around the NPA motifs (z~1Å) and another in the SF region (around z=8Å). The free energy reaches its maximum at the SF region with a peak value of 2.2 kcal/mol. The second highest free-energy barrier is in the region of the NPA motifs with a value of 1.7 kcal/mol. In the absence of PS6, the free-energy profile closely resembles that in the presence of PS6, meaning that PS6 does not alter the water permeability of AQP5. Furthermore, we computed the osmotic coefficients p_f of water permeation for both SysI and SysII by determining the mean square displacements (MSD) of the single-file waters as a function of time [19] (shown in Fig. 3). For SysI, we found p_f = 7.1± 0.6×10⁻¹⁴ cm³/s per channel and, for SysII, p_f = 6.0 ± 0.8×10⁻¹⁴ cm³/s per channel, of which the difference is within the margin of error. This confirms that PS6 does not significantly alter AQP5’s water permeability.

Fig. 3.

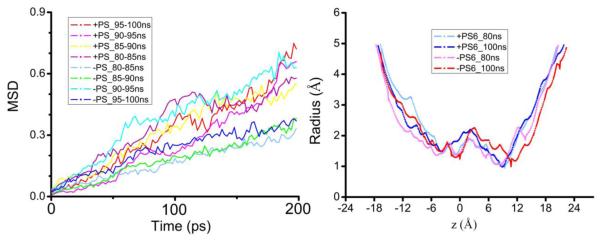
MSD of waters in the conducting pore and the pore radius: SysI vs SysII. Shown in the left panel are the MSD as a function of time for the waters in AQP5’s four conducting pore in SysI and SysII. Shown in the right panel is the pore radius along the channel axis at 80 ns and 100 ns of the two systems.

Affinity of PS6

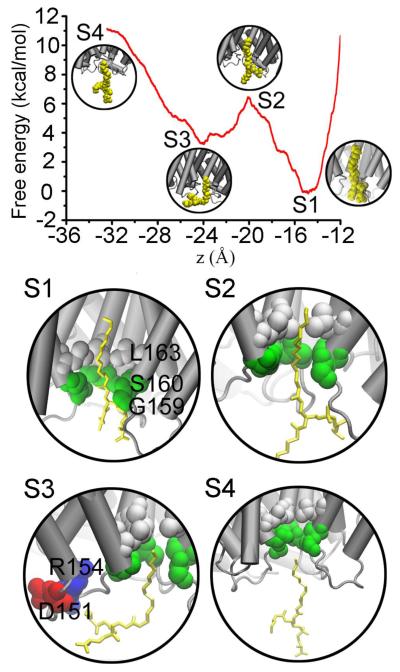
Even though the lipid in the central pore of AQP5 does not alter its overall structure or its function of transporting water through the amphipathic conducting pores, the question about the mechanics of binding PS6 to AQP5 is still relevant because PS6 totally occludes the central pore of AQP5 that may facilitate permeation of nonpolar gas molecules. To pursue this question, we determine the chemical-potential profile of PS6 along its dissociation path out of AQP5’s central pore by the means of SMD with BD-FDT. The results are shown in Fig. 4 where the standard free energy of PS6, G⁰ (z), is plotted as a function of its center-of-mass z-coordinate. Along the dissociation path, there are four states worth noting. State S1 is at the lowest minimum of the free energy. It is the bound state where the center-of-mass z-coordinate of PS6 is approximately z_B≃−15Å. State S4 is at the juncture when PS6 leaves from the central pore of the AQP5, close to but is not yet the dissociated state. In the dissociated state (aqueous state), z_D < −32Å, PS6 is free from any restrictions on its rotation around its center of mass but in State S4 that freedom of rotation is restricted as the tail end of the lipid still resides within the mouth of the central pore. The absolute binding energy, the free-energy difference between the bound state and the dissociated state, can be split in the following way,

$$\Delta G^0=G^0\left(z_B\right)-G^0\left(z_{S4}\right)+G^0\left(z_{S4}\right)-G^0\left(z_D\right).$$ (2)

Our estimate of the free-energy difference between States S4 and S1 was, as shown in Fig. 4, G⁰(z_B)−G⁰(z_S4) = −11.1±1.6 kcal/mol. The free-energy difference between State S4 and thedissociated state,

$$G_0\left(z_{S4}\right)-G^0\left(z_D\right)\simeq -k_{B}T\ln (A_{\text{c}.\text{p}.}∕4\pi R^2)=3.9\pm 0.3\mathrm{kcal}∕\mathrm{mol},$$ (3)

which represents the entropic penalty due to the restriction on the tail end of the lipid in State S4. The tail only has the mouth area, A_c.p.≃17Ų, of the central pore to occupy when the lipid’s center of mass is fixed (z_S4 = −32Å). The distance from the tail end to the center of mass of PS6 is approximately, R≃30Å. All these estimates together lead to an estimate of the absolute binding energy of G⁰(z_B)−G⁰(z_D) = −7.2±1.6 kcal/mol. Correspondingly, the dissociation constant k_D is around 6.1μM that is also equal to the half maximal inhibitory concentration (IC₅₀) because the binding of PS6 to AQP5 is not competitive in nature.[31] Therefore, PS6 is predicted to inhibit the biophysical functions of AQP5 facilitated by its central pore in the concentration range of micromolars. It should be pointed out that the constant for dissociation from the central pore into the membrane is equal to the k_D computed in this study divided by the constant for dissociation from the membrane into the aqueous state. Namely,

$$k_D{\mid }_{cp\to m}=k_D∕k_D{\mid }_{m\to aq}.$$ (4)

While the latter is not quantitatively known, we expect that it makes the dissociation constant between being bound in the central-pore and being in the membrane much higher than what we computed, k_D, between the central-pore bound state and the aqueous state.

Fig. 4.

Free-energy profile for binding PS6 to the central pore of AQP5. Plotted in the top panel is the system’s free energy as a function of the PS6’s center-of-mass z-coordinate. Illustrated in S1 through S4 are four states of interest showing the PS6-AQP5 interactions.

Examining States S1 to S4 illustrated in Fig. 4, we can identify the interactions responsible for binding PS6 to AQP5 in the central pore. In the bound state (S1), the hydrophilic head of the PS6 was positioned between two residues G159 and S160. The hydrogen bonds between these two residues and the hydrophilic head of PS6 compensate the reduction in hydrogen bonds with waters in the dissociated state when the head is fully surrounded by waters. The hydrophobic tail of PS6 is completely inside the central pore lined up with hydrophobic residues. The hydrocarbon groups of PS6 are all at or near optimal distances from the hydrophobic side chains of the central pore and, therefore, the VDW interactions between PS6’s tail and the central pore-forming residues are all attractive. These attractions give rise to the free-energy minimum in State S1. Going from State S1 to State S2, the attractive VDW interactions are reduced in proportion to the portion of PS6’s tail coming out of the central pore while its head loses hydrogen bonding with G159 and S160 but forms new hydrogen bonding with waters. These two factors combine to be responsible for the rise in free energy from S1 to S2. From S2 to S3, we observe a drop in free energy, which is caused by the strong attraction between PS6’s head and the charged residues R154 and D151. From S3 to S4, the free-energy increase comes from two factors: (1) the further reduction in the VDW interactions between the tail and the central pore and (2) the lipid head breaking away from the charged R154 and D151. Finally, going from S4 to the dissociated state, PS6 loses the final touch of VDW interactions with the central pore but gains the entire freedom of rotating around its center of mass. Note that the center of mass of PS6 is controlled (fixed) at every step along the dissociation path. Overall, going from the dissociated state to the bound state, PS6 is subjected to significant entropic penalty and VDW attractions. These two factors combine to give the binding energy of PS6 in the central pore.

Now, what is the specificity of binding PS6 to AQP5? PS6 is peculiar in comparison with the typical membrane lipids. Membrane lipids such as POPC and POPE all have two long hydrocarbon tails that are approximately equally long. There is significant VDW attraction between the two long tails. In contrast, PS6’s two hydrocarbon tails are not equally long and they are easily separable. In fact, the long tail of PS6 resides completely inside the central pore while the short tail remains outside the central pore in the company of the lipid head. The space available in the central pore is fit for one hydrocarbon tail but not for two long tails sticking together or for a bulky one such as that of a cholesterol. Based on this, we believe that the central pore of AQP5 only binds PS6 or another lipid that has only one long hydrocarbon tail. PS6 concentration must have been much higher than k_D during the crystallization process of Ref. 12. And PS6 concentration must have been much lower than k_D in the functional experiment of Ref. 13.

Possible passageways of gas permeation

In Ref. [13], Musa-Aziz et al demonstrated that AQP5 facilitates permeation of nonpolar gas molecules. We examine the equilibrated structure of SysII (shown in Fig. 5) to look for possible passageways for gas permeation. We suggest that the central pore is the permeation passageway of nonpolar gas molecules for the following reasons:

1. The four water-conducting pores are amphipathic, in which waters and some polar solutes (if present) line up in single-file and form hydrogen bonds between neighbors and with the lumen atoms. These amphipathic pores do not facilitate gas permeation because the presence of a nonpolar gas molecule would interrupt the hydrogen-bonding network. They are not favorable for nonpolar molecules to go through or to stay in. In contrast. the central pore is not amphipathic. Its walls are lined with the sidechains of hydrophobic residues. Even in the absence of PS6, when the central pore is not occluded, it is only favorable for nonpolar molecules to go in but not for waters or polar solutes.

2. The interstices have some gap spaces formed between two adjacent protomers and they are hydrophobic. However, they do not constitute transmembrane holes (channels) as indicated in Fig. 5(B). Therefore, they cannot conduct even nonpolar gas molecules.

3. The spacing, if existed, between the protein and the membrane would be effective for conducting nonpolar gas molecule. We searched for possible holes between the AQP5 tetramer and the membrane lipids but found none.

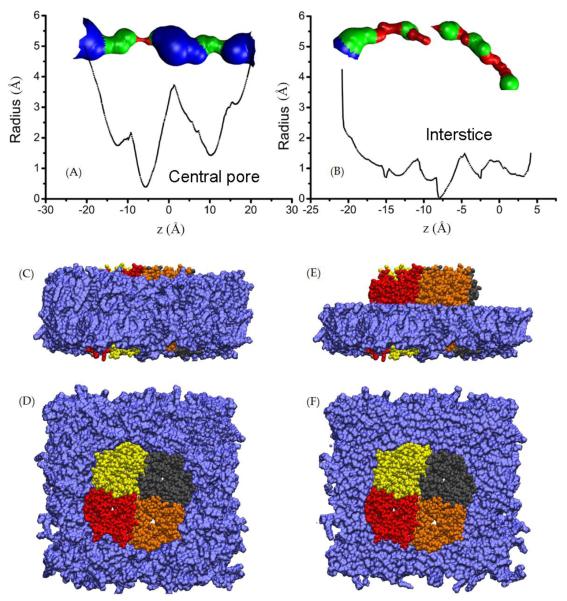
4. The only possible passageway left is the central pore formed by quadruplets of hydrophobic residues, which would be very efficient if it is wide enough. We computed the cross-sectional radius of the central pore shown in Fig. 5(A). The narrowest part of the central pore (the red part around z = −6Å in Fig. 5(A), having a radius of approximately 0.5Å) seems to be a bottleneck not wide enough for passage of a gas molecule. However, the cross-section of the pore is not circular (Fig. 6) and the radius computed with HOLE2[32] is a measure of the narrowest dimension. Moreover, the quadruplet of hydrophobic residues (L163) forming the bottleneck are flexible. Thermal fluctuations of their side-chains are sufficient to open up the bottleneck for a gas molecule’s passage (see Fig. 6, bottom left panel). This point is also confirmed by the free-energy profile (Fig. 6, bottom right panel) which shows that the free-energy barrier for gas permeation is only about 3 kcal/mol. Putting all these analyses together, we can conclude that O₂ permeates through the central pore of AQP5 when not occluded by PS6.

Fig. 5.

Possible passageways of gas permeation through the AQP5-POPE system. Graphics rendered with VMD.[33] (A) Pore radius of the central pore of AQP5. (B) Pore radius of an interstice space between two adjacent protomers. (In both (A) and (B), the pore radius was measured with HOLE2.[32]) (C) Side view of the AQP5-POPE system with all POPE lipids (in VDW, colored in mauve) shown along with the protein (in VDW, colored by Segname). (D) Top view of the same as in (C). (E) Side view of the AQP5-POPE system with only half of the POPE lipids (in VDW, colored in mauve) shown along with the protein (in VDW, colored by Segname).

Fig. 6.

The bottleneck part of the central pore (top), the cross-sectional area of the bottleneck (bottom, left), and the chemical-potential profile (bottom, right) for O₂ permeation through there. Graphics rendered with VMD.[33]: Protein in the Cartoon representation (colored by Segname), Oxygen, VDW (colored in red), and the L163 quadruplet, VDW (colored by Element).

CONCLUSION

Based on extensive equilibrium MD and nonequilibrium SMD simulations, we make the following predictions: The lipid, PS6, bound to the central pore of AQP5 tetramer does not have significant effects on the overall structure of the protein in the cell membrane. And it does not alter the protein’s ability of transporting water through its amphipathic pores. However, it does occlude the central pore and the central pore is the transport passageway of nonpolar gas (O₂, in particular). PS6 inhibits gas permeation through AQP5 with an IC₅₀ in the micromolar range, confirming the hypothesis of Ref. 12.

Highlights.

• The dissociation constant of PS6 is in the concentration range of micromolars.

• The van der Waals attractions are responsible for binding PS6 to Aquaporin V.

• Oxygen permeates through the central pore of Aquaporin V inhibitable by PS6.

ABBREVIATIONS

AQP

Aquaporin

BD-FDT

Brownian dynamics fluctuation dissipation theorem

IC₅₀

Half maximal inhibitory concentration

MD

Molecular dynamics

MSD

Mean square displacement

NPA

Asparagine-Proline-Alanine

PDB

Protein Data Bank

POPE

Palmitoyloleylphosphatidyl-ethanolamine

PS

Phosphatidylserine

RMSD

Root mean square deviation

SF

Selectivity filter

SMD

Steered molecular dynamics