Abstract
We propose a complete methodology to find the full set of feasible grasp wrenches and the corresponding wrench-direction-independent grasp quality for a tendon-driven hand with arbitrary design parameters. Monte Carlo simulations on two representative designs combined with multiple linear regression identified the parameters with the greatest potential to increase this grasp metric. This synthesis of computational approaches now enables the systematic design, evaluation, and optimization of tendon-driven hands.
Keywords: Biologically inspired robots, grasping, mechanism design, multifingered hands
I. Introduction
Tendon-driven hands have been designed for the purposes of grasping and manipulation [1]–[6]. While their shortcomings can include friction and tendon compliance [7], in certain applications (such as dexterous hands), they have distinct advantages over torque-driven systems including lightweight, low backlash, small size, high speed, and remote actuation [8], [9]. They can also offer significant design flexibility in setting moment arms and maximal tendon tensions [8], which allows optimization of system output capabilities for a particular task while minimizing size and weight.
Several studies have addressed the problem of designing the topology, tendon routing, or link design of tendon-driven manipulators (or fingers) [2], [9]–[16]. According to [15], for example, “the knowledge of maximum twist and wrench capabilities is an important tool for achieving the optimum design of manipulators.” Optimization of kinematic hand parameters, such as finger placements, link lengths, and joint limits is addressed in [2], but we still lack comprehensive methodologies to do large-scale optimization in these high-dimensional parameter spaces. In addition, special attention has been given to the design of manipulators with isotropic transmission characteristics (i.e., ability to transmit forces equally in all directions at the end effector) [2], [10]–[14]. Advantages of this isotropy include more uniform tendon force distribution and minimization of the dispersion of noise through the system [2], [12]. However, it may be advantageous to design a finger with nonisotropic characteristics [9], as in the human hand [17]. In addition, prior work on isotropic transmission does not consider limits on tendon tensions, which is critical when designing small, dexterous hands.
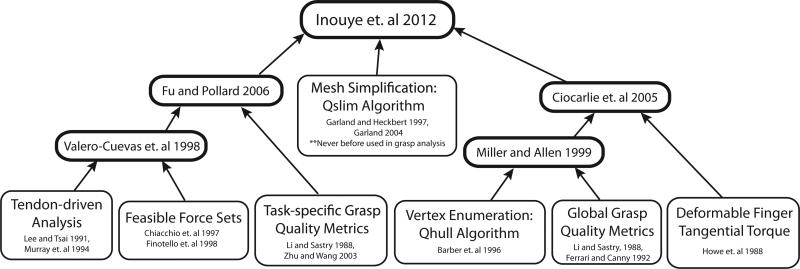
While there has been progress in designing and controlling tendon-driven robotic hands, a complete methodology for the evaluation and refinement of alternative topologies based on general-purpose grasp quality (i.e., wrench-direction-independent) has not yet been synthesized or implemented. Our novel synthesis of computational approaches now allows us to integrate and expand prior work to eliminate the following shortcomings of using previous techniques in isolation for optimization of wrench-direction-independent grasp quality of tendon-driven hands. The previously isolated computational approaches and the integration we have accomplished are illustrated graphically in Fig. 1:
optimization intractability;
not considering tendon-driven architecture;
inability to calculate wrench-direction-independent grasp quality.
Fig. 1.
Integration of techniques that were previously isolated.
The first shortcoming has been previously circumvented by using an approximation of the full grasp wrench set itself using mathematically convenient operations [18], [19]. If desired, our method can make computations more efficient by a different method: mesh simplification of the full grasp wrench set. This allows more accurate grasp quality calculations than prior approximations. The second shortcoming has not been addressed in several studies that only consider independent and identical contact points for grasp planning or analysis [18]–[24]. We have incorporated complete characterization of the force production capabilities of arbitrary tendon-driven hands. The third shortcoming was encountered in [25]. They used an efficient linear programming approach to calculate a grasp quality metric for tendon-driven hands based on a very specific, predefined task wrench space, in which a finite number of required wrench magnitudes and directions was specified. They note that their methodology does not generalize to the full set of feasible grasp wrenches. Our integrated method does generalize to the full set of feasible grasp wrenches and allows efficient calculation of wrench-direction-independent grasp quality for tendon-driven hands.
Many other studies have addressed multifingered grasp [26]–[31]. Several other grasp quality metrics can be computed based on other criteria, but their application to the design of tendon-driven mechanisms is extremely limited [27]. Compliances are included in grasp analysis for statically indeterminate grasps in [26] and for grasp stiffness analysis in [29], [30]. We calculate the boundaries of the grasp wrench set, where the forces are deterministic. A software environment for grasp synthesis is presented in [31], but it does not consider tendon-driven architecture.
We demonstrate this novel synthesis of techniques and compare grasp quality among two tendon-driven finger topologies, two grasp configurations, and thousands of parameter combinations. We then use Monte Carlo simulations to demonstrate how this computationally efficient method can be used to optimize grasp quality metrics by tuning specific design parameters.
II. Procedure
A. Finding the Set of Feasible Grasp Wrenches and Computing Grasp Quality
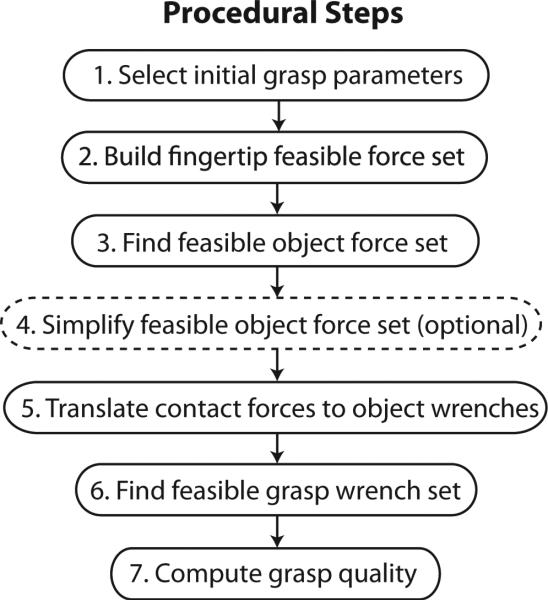
Assessing the quality of a specific grasp with a specific hand/manipulator topology requires computing the feasible grasp wrench set and its associated grasp quality. A flowchart is shown in Fig. 2.
Fig. 2.
Flowchart of steps for finding feasible grasp wrench set and computing grasp quality.
1) Select Initial Grasp Parameters
The calculation of grasp quality involves a few preliminary parameters to be specified, based on the finger geometry, number of fingers, and placement of grasping points. Grasp qualities will differ when these parameters are altered (although not substantially if they are not greatly altered, in general). Therefore, the finger geometry (i.e., D–H parameters of the finger), finger placements, finger postures, and object size and shape must all be specified before the rest of the steps of the procedure are carried out. Finger geometry is used to find the analytical manipulator Jacobian (see Appendix A for further details) and the finger postures are determined from the finger geometry and choice of finger placements (which is based on object size and shape) on the object.
2) Build Fingertip Feasible Force Set
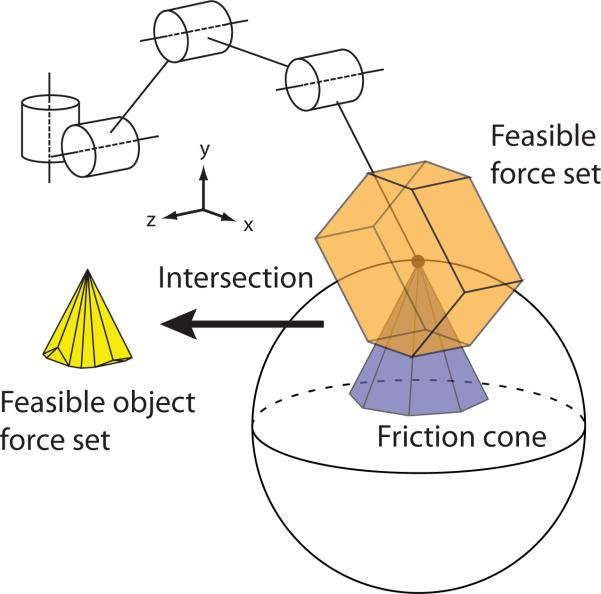
The next step is to build the set of 3-D forces that each finger can produce while maintaining a static posture. This set has been called the feasible force set [17], [32], or force manipulability set in the strong sense (i.e., zero endpoint torque) using the language of [33], [34].1 The user must specify the finger input parameters of topology (i.e., tendon routing), maximal tendon tensions, moment arm values, finger posture, and link lengths. Then the feasible force set can be calculated using the method described in detail in the Appendix. A visual example of a feasible force set is in Fig. 3.
Fig. 3.
Example of a fingertip feasible force set and its intersection with a friction cone to produce a feasible object force set.
3) Find Feasible Object Force Set
The fingertip feasible force set does not represent the actual forces that can be applied to the surface of an object by the finger because fingertips can generally only push against surfaces. To find these feasible object forces, we must find the portion of the feasible force set that also lies inside a Coulomb friction cone. We approximate this cone by using the convex hull of eight vectors around the perimeter of the base of the cone, plus the origin, as in [19], [26]. We intersect this cone with the feasible force set to find the convex hull of feasible forces that may be applied to the object. We call this set the feasible object force set, and an example is in Fig. 3.
The inputs required for this step are the static coefficient of friction and the angle of finger contact (which is determined by object shape and finger placement). We use the Qhull vertex enumeration algorithm to complete the intersection of these convex sets.
4) Simplify Feasible Object Force Set
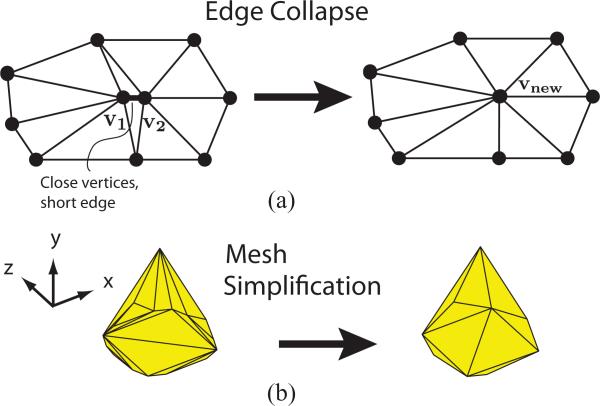
Due to the complexity and high number of vertices that may define the feasible object force set for each contact point, we may wish to simplify the set to make the analysis more computationally efficient.2 The analysis presented in this paper can still be completed without this step, but for thousands or millions of calculations, this step can be very beneficial with minimal loss in accuracy. To this end, we use edge collapse operations to perform 3-D mesh simplification, see Fig. 4(a). Due to the nature of tendon-driven feasible force sets, there may be many vertices that are very near to each other. The edge collapse operations, in effect, combine these very close points into a few points or one point, as can be seen in Fig. 4. This procedure was developed in computer graphics to reduce the processing and display time for 3-D objects [35].
Fig. 4.
(a) Example of an edge collapse operation. The vertices v1 and v2 are collapsed into a new vertex vnew . Adapted from [35]. (b) Example of using edge collapse operations to simplify the feasible object force set from 19 vertices down to 10 vertices. Note that this view is of the underside of the feasible object force set in Fig. 3.
While some of the finer details of the feasible object force set are eliminated after this process, this algorithm accomplishes the simplification in a theoretically optimal manner (when considering the minimization of quadric error). Because of this, the algorithm automatically selects close vertices for edge collapse operations. Fig. 4(b) shows a feasible object force set before and after simplification. We find that it reduces computation time considerably with minimal effect on the results (see Section III).
When the routing of the tendons is complex, such as in the human hand or in robotic hands with complex interconnections among tendons such as in the ACT Hand [36], the mesh simplification will improve performance even more drastically than with simple routings. For example, simplification of the human finger feasible object force sets in [37] from approximately 60 down to 12 vertices reduced computation time from 50 to 1.37 s, a 97% reduction.
The single parameter input for this step is the number of desired vertices for the simplified feasible object force set. Qslim is the program used to implement the edge collapse operations for mesh simplification [38].
5) Translate Contact Forces to Object Wrenches
The combined forces of the fingertips produce a resultant wrench on the object. An object wrench vector wi,j produced statically by a point-contact force with friction fi,j at fingertip location i is given by the following equation [13]:
| (1) |
where λ is the scaling factor that converts units of torque to comparable units of force, di is the vector from the torque origin to the ith contact point, i = 1, . . . , n, where n is the number of fingertip contact locations, and j = 1, . . . , mi, where mi refers to the number of points defining the convex hull of the feasible object force set at fingertip location i. Each mi may be unique, in contrast with analyses that treat all contact points equally and for which all mi are equal. A reasonable choice for λ is 1/r, where r is the distance from the torque origin to the furthest point on the object from that origin. As noted in this choice of λ guarantees that the feasible object wrench, and hence grasp quality metrics, are independent of object scale.
We use a soft finger model for two-finger grasp so that the grasp can produce force closure by withstanding tangential torque [39]. The finger model assumes a certain contact area for the calculation of a rotational coefficient of friction, but the contact is still considered to be a point contact that can withstand tangential torque, which is described in [26]. Past work has shown that an approximately elliptical friction limit suffices to enclose all combinations of tangential torque and shear force that the fingertip can withstand without slipping or rotating. However, a linear approximation of the friction limit surface is a valid conservative way to model a soft finger [39], which we use to make calculations more efficient: all we need to do is add and subtract the tangential torque limit to the appropriate object wrench torque component for each vertex of the feasible object force set. This process is similar to that used in [40], but they do not consider any feasible force set (only a simple friction cone). We assume that the fingertip can resist any combination of tangential torque and tangential force for a constant normal force underneath the boundary of the linear approximation.
The inputs to this step are the finger placements (for an arbitrary grasp), and coefficient of rotational friction (which can be specified directly or calculated from the soft-finger contact radius) if the grasp is with two fingers, and linearization of the tangential torque capabilities is utilized for two-finger grasp.
6) Find Feasible Grasp Wrench Set
After computing all the feasible object wrenches that can be applied by each finger, these wrench vectors in 6-D are combined to form the set of all wrenches in 6-D space that can be applied to the object which the grasp can resist. This set is a convex polytope found by taking the convex hull of the Minkowski sum of the sets of feasible object wrench vectors, where each set corresponds to a fingertip contact location. This operation is given by the following equation [22]:
| (2) |
where FGWS is the feasible grasp wrench set, ⊕ is the Minkowski sum operator, n is the number of contact points, and {wi, 1, . . . , wi,mi} denotes the mi wrench vectors defining the feasible forces at the ith contact point. It should be noted that often the union and not the Minkowski sum is used in grasp quality calculations to greatly reduce computation time [18], [19].3
7) Compute Grasp Quality
Once we have calculated the feasible object wrench set, we can compute a grasp quality based on that set. The user can specify their own grasp quality metric of choice. We chose as an example the wrench-direction-independent grasp quality metric known as the radius of the largest ball. It was originally proposed in [22]. Determination of this grasp quality metric involves calculating the minimum offset (from the origin) of the halfspaces that define the convex hull of feasible grasp wrenches. The minimum of these offsets is equal to the radius of the largest ball, centered at the origin, that the hull can contain. The metric, in effect, is equal to the maximal magnitude of a wrench that can be applied to the object in all directions in wrench space without it losing force closure (i.e., causing the grasp to fail). A wrench vector whose magnitude is less than the grasp quality can be applied to the object in any direction in 6-D wrench space without losing force closure. These calculations have been completed for independent and identical contact points in [18].
We use the Qhull vertex enumeration algorithm for the calculation of grasp quality and it can also be easily implemented for 2-D or 3-D visualizations of the feasible object wrench set [19].
B. Computing Grasp Quality Metrics for Specific Manipulator Designs
Here, we describe the specifications of the designs we analyzed and the parameters that we used in the computations and Monte Carlo simulations presented in the results section.
1) Finger Topology
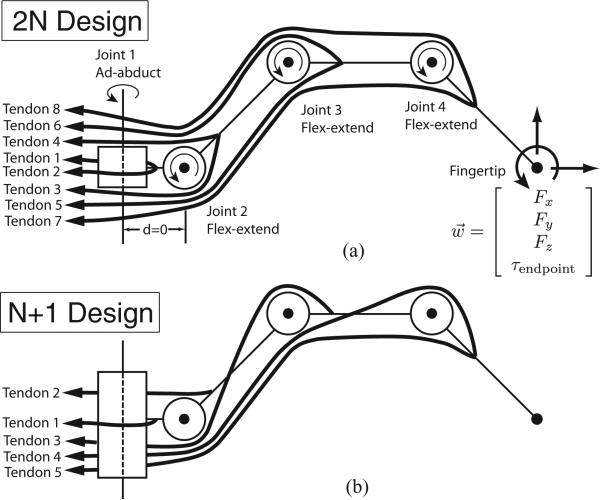
We performed this analysis on the two different finger topologies in Fig. 5(a) and (b). Both of them had four kinematic degrees of freedom (DOFs): one universal joint at the base of the finger and two parallel hinge joints distally. For the purposes of kinematic clarity, the finger ad-abduction (i.e., side-to-side) axis was considered to be immediately proximal to the perpendicular axis of the first flexor-extensor joint, which is demonstrated in Fig. 5(a). The first finger topology had a “2N” tendon arrangement, in which there are two opposing (or antagonistic) tendons for each DOF, Fig. 5(a). This topology is similar to that in the Utah/MIT, DLR, and Shadow Hands [1], [3], [4].4 The second finger topology had an “N + 1” tendon arrangement, which has one more tendon than DOF, and it is the minimum number of tendons that can be used to fully control the finger [10].5N + 1 topologies are analyzed for isotropic transmission in [11], [13] and analyzed for implementation in the Stanford-JPL hand [2]. The particular N + 1 topology we analyzed (there are many possible N + 1 topologies) is in Fig. 5(b).
Fig. 5.
Grasp configurations analyzed. (a) 4-DOF robotic finger, 2N tendon arrangement, with endpoint wrench description. (b) 4-DOF robotic finger, N + 1 tendon arrangement.
For the baseline results, each of the three links of each finger had length of 2 cm. The posture of the finger was 0° ad-abduction, 45° extension on joint 2, and 45° flexion on both joints 3 and 4. This is the posture in Fig. 5. The link lengths and the posture were used to calculate the Jacobian matrix for these fingers. All of the moment arms for both topologies and all joints were given a value of 5 mm, which, along with the tendon configuration, defined the R matrix. This matrix was either 4 × 8 (2N design) or 4 × 5 (N + 1 design). The sum of the maximal tendon tensions was 1000 N and divided up evenly among the tendons. This defined the F0 matrix, which was a diagonal 8 × 8 (2N topology) or 5 × 5 (N + 1 topology) matrix. The J, R, and F0 matrices were then used to calculate the feasible force sets of the fingers.
The sum of maximal tendon tensions being equal is an important constraint due to the size, weight, and motor torque (and therefore tendon tension) limitations inherent in dextrous hands. For example, the torque capacity of motors is roughly proportional to motor weight, and minimization of weight was an important consideration in the design of the DLR Hand II [42]. In addition, the maximal force production capabilities of the McKibben-style muscles are roughly proportional to cross-sectional area [43]. Since the actuators, typically, will be located in the forearm, then the total cross-sectional area will be limited to the forearm cross-sectional area. In this first presentation of the methodology, we do not consider alternative constraints on the actuation system (e.g., electrical current capacity, tendon velocities, etc.).
2) Grasp Configuration
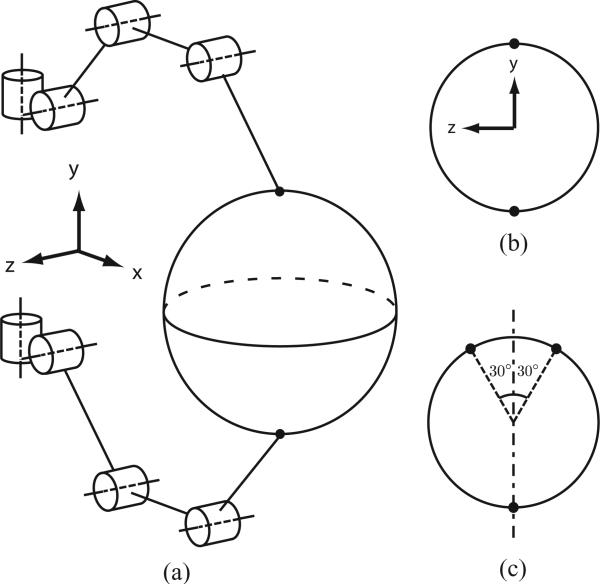
Both two- and three-finger grasps were analyzed for each of the two topologies, and the finger placements are in Fig. 6. The two-finger grasp simply had both fingertips on opposite sides of a sphere of radius 6 cm. The two-finger configuration is in Fig. 6(a) and (b). The three-finger grasp had one fingertip at the bottom and the other two fingers were placed so that they were 30° from a vertical line going through the bottom finger [see Fig. 6(c)].
Fig. 6.
Grasp configurations analyzed. (a) Isometric view of two-finger grasp. (b) Front view of two-finger grasp. (c) Side view of three-finger grasp.
3) Calculating Grasp Quality
For the two-finger grasps, the linear coefficient of friction was set to 0.5. The rotational coefficient of friction was set to 2.5 times the linear coefficient of friction (in millimeter). This corresponds to a very soft-finger contact radius of 5 mm [14].
The grasp analysis was performed in MATLAB (R2010a, The MathWorks) on an Apple desktop computer (2 x 2.66 GHz Dual-Core Intel Xeon) running OS X Version 10.6.4. The programs Qhull (floating-point arithmetic vertex enumeration), LRS (lexicographic reverse search algorithm), and Qslim (edge collapse operations) were used as compiled binaries for Mac OS X and were called through the MATLAB “system” command [38], [44], [45]. The rest of the computations were completed using custom MATLAB code.
4) Monte Carlo Simulations
To demonstrate the computational utility of our method, the baseline parameters of moment arms, maximal tendon tensions, and link lengths were perturbed simultaneously and independently [46]. To do so, we drew from uniform distributions with the lower bound being 20% below each particular baseline parameter value and the upper bound being 20% above the baseline parameter value, for a total range of 40% variation (see Fig. 7). For each finger, there are 14 nonzero moment arm values, three link lengths and eight (for 2N topology) or five (for N + 1 topology) maximal tendon tensions, for a total of 25 (2N topology) or 22 (N + 1 topology) total independent parameters that were perturbed for each iteration. We performed 1000 iterations (each having their own set of parameters) for each of the two topologies and each of the two grasp configurations. This number of iterations was found to be sufficient for convergence, as in [47] (discussed further in Section III).
Fig. 7.
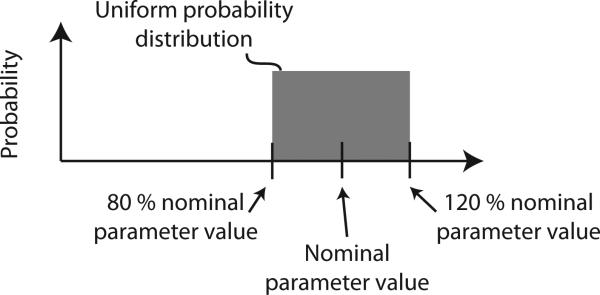
Uniform sampling distribution used for each independent parameter value perturbation in Monte Carlo simulations.
5) Regression Analysis
To demonstrate the utility of these Monte Carlo simulations for design and analysis purposes, the grasp quality was regressed on the independent parameters that were varied during the simulations. Stepwise regression on only the linear terms was performed (i.e., no interaction or higher order terms were used) using an initial model with no predictors, and predictors were added to the model with a cutoff p-value of 0.05. This was performed in MATLAB. Prior to the regression analysis, the independent parameters were normalized so that the baseline value was equal to 1. In addition, the dependent parameters were normalized so that their average was also 1. Therefore, the regression coefficients represent the expected percentage increase in the grasp quality with a 1% increase in the independent parameter.
III. Results
A. Baseline Results
Table I shows the grasp quality results for the two “baseline” topologies (i.e., those with the nominal values for each design parameter) for the two- and three-finger grasps. Despite the fact that both topologies have the same sum of maximal tendon tensions (i.e., system input), the 2N topology is clearly superior to the N + 1 topology (using the nominal parameters) in grasp quality, and hence can resist wrenches of higher magnitude in all directions.
TABLE I.
Baseline Grasp Quality Results
| 2N Topology (N) | N+1 Design (N) | |
|---|---|---|
| 2-finger | 2.59 | 1.71 |
| 3-finger | 8.66 | 5.60 |
Coefficient of static friction μs = 0.5. Units of gArasp quality are in newtons.
In addition, as expected, the grasp quality is higher for the three-finger grasp than the two-finger grasp for both topologies. These baseline results were verified using the exact arithmetic vertex enumeration code LRS [44], where the evaluation time was around 100 times greater than the Quickhull algorithm [45].
B. Monte Carlo Simulations
Given that computation times for the baseline cases were fairly long (about 30 s), especially for the three-finger grasp, we simplified the feasible object force sets to make Monte Carlo simulations feasible. We found that simplifying the feasible object force set down to 12 vertices reduced computation time by a minimum of 46% (reduction from 23.7 to 12.7 s for N + 1, three-finger case) and a maximum of 77% (reduction from 39.9 to 9.10 s for 2N, three-finger case) out of the four baseline cases, and resulted in less than 2% error in grasp quality.
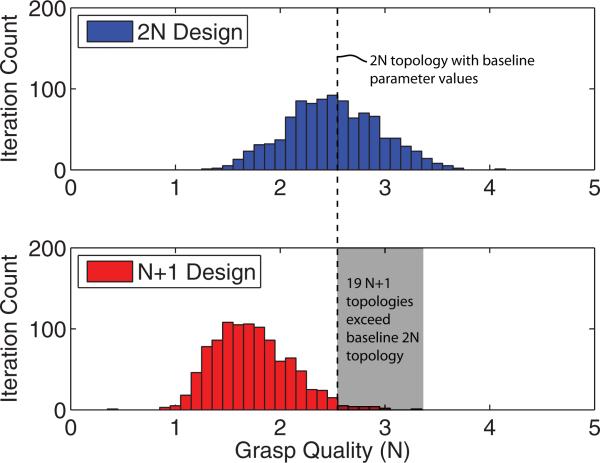
The 1000 Monte Carlo simulations reached “convergence” in the sense that the running mean and coefficient of variation varied less than 2% in the last 20% of iterations, similar to the criteria used in [22]. Average evaluation time for each of the four configurations is shown in Table II. Fig. 8 shows histograms of the Monte Carlo grasp quality results for two-finger grasp. The different finger topologies for this grasp certainly have different mean characteristic lengths (p < 0.00001) when the parameter values are perturbed by 20%. However, for the N + 1 topology, we find that 19 parameter combinations exceed the grasp quality of the 2N topology with baseline parameter values.
TABLE II.
Average Evaluation Times (Standard Deviations) During Monte Carlo Simulations, in Seconds
| 2N Topology (s) | N+1 Topology (s) | |
|---|---|---|
| 2-finger | 1.46 (0.30) | 1.29 (0.42) |
| 3-finger | 9.79 (1.98) | 9.77 (2.66) |
Fig. 8.
Histogram of grasp quality values from Monte Carlo simulations for two-finger grasp, 2N and N + 1 designs. The N + 1 topologies exceeding the baseline 2N topology are shaded gray.
C. Regression Analysis
The significant regression coefficients at a cutoff p-value of 0.05 for grasp quality for the N + 1, two-finger case are shown in Table III, grouped by parameter type. The coefficient of determination R2 is 0.930, signifying a good fit for the linear model. Link lengths, maximal tendon tensions, and moment arms should be adjusted according to Table III to produce the N + 1 topologies that exceed the baseline 2N topology. We find that decreasing the link lengths understandably increases grasp quality (because it improves the moment-arm:lever-arm ratio of the tendons), and decreasing the length of link 2 has the greatest predicted effect on grasp quality. As would be expected, the one significant regression coefficient for maximal tendon tension is positive (i.e., grasp quality can never be worsened by increasing one of the maximal tensions). However, not all maximal tendon tensions improve this grasp quality metric, if increased. While all maximal tendon tensions change the size and shape of the feasible grasp wrench set, some have insignificant effects on grasp quality because increasing them increases the size of the feasible grasp wrench set in directions that do not increase the weakest wrench capability of the grasp. That is, they do not push out the boundary of the feasible grasp wrench set that is closest to the origin. However, the maximal tension of tendon 1 does affect that boundary and increasing it enhances this metric of grasp quality. Therefore, one of the “weak links” in this topology is the maximal tension of tendon 1, which if increased leads to better performance. Moment arms exhibit both positive and negative regression coefficients in their effect on grasp quality, as they affect the direction and magnitude of the wrench basis vectors [17]. The best N + 1 topology from the Monte Carlo simulations (grasp quality of 3.31–94% greater than the N + 1 baseline) has maximal tension of tendon 1 15% higher than the baseline and the moment arm of tendon 1 across the ad-abduction axis is 16% above baseline. These parameters have the greatest effect on grasp quality, as can be seen in Table III.
TABLE III.
Significant Normalized Regression Coefficients for Grasp Quality With 95% Confidence Intervals on N + 1 Topology. Two-Finger Grasp
| Parameter | Expected Percentage Increase in Quality for a 1% Increase in Parameter Value | 95% Confidence Interval | |
|---|---|---|---|
| Link length | Link 2 | -0.436 | (-0.466, -0.406) |
| Link 1 | -0.333 | (-0.363, -0.302) | |
| Link 3 | -0.290 | (-0.320, -0.260) | |
| Max tension | Tendon 1 | 0.995 | (0.265, 1.03) |
| Tendon 2 | – | – | |
| Tendon 3 | – | – | |
| Tendon 4 | – | – | |
| Tendon 5 | – | – | |
| Moment arm | 1,1 | 1.01 | (0.975, 1.04) |
| 1,5 | -0.593 | (-0.623, -0.564) | |
| 2,5 | 0.553 | (0.522, 0.583) | |
| 2,4 | 0.272 | (0.243, 0.302) | |
| 1,4 | -0.259 | (-0.289, -0.228) | |
| 2,3 | 0.159 | (0.128, 0.190) | |
| 1,3 | -0.143 | (-0.174, -0.112) | |
| 1,2 | – | – | |
| 2,2 | – | – | |
| 3,3 | – | – | |
| 3,4 | – | – | |
| 3,5 | – | – | |
| 4,4 | – | – | |
| 4,5 | – | – | |
‘–’ Denotes not significant at the cutoff p-value of 0.05. Moment arms expressed as (joint number, tendon number). R2 = 0.930.
Table IV shows the effects of adjusting the significant moment arm parameters individually by 10% in the direction that increases grasp quality while keeping all the other parameters at baseline levels. We see that the predictions from even a simple linear regression are validated.
TABLE IV.
Expected (From Linear Regression on Monte Carlo Iterations) and Actual (From Computational Method Implementation) Effects of Moment Arm Adjustments by 10% on Grasp Quality of N + 1 Design. Two-Finger Grasp
| Grasp Quality | Normalized Coefficient | Expected Increase | Actual Increase | |
|---|---|---|---|---|
| Baseline | 1.709 | – | – | – |
| Moment arm 1,1 (+10%) | 1.880 | 1.01 | 10.1% | 10.0% |
| Moment arm 1,5 (-10%) | 1.812 | -0.593 | 5.93% | 6.03% |
| Moment arm 2,5 (+10%) | 1.809 | 0.553 | 5.53% | 5.88% |
| Moment arm 2,4 (+10%) | 1.756 | 0.272 | 2.72% | 2.79% |
| Moment arm 1,4 (-10%) | 1.758 | -0.259 | 2.59% | 2.86% |
| Moment arm 2,3 (+10%) | 1.733 | 0.159 | 1.59% | 1.40% |
| Moment arm 1,3 (-10%) | 1.734 | -0.143 | 1.43% | 1.47% |
Moment arms expressed as (Joint number, tendon number).
IV. Discussion
In this paper, we have demonstrated a novel synthesis of computational approaches to evaluate the grasp quality of arbitrary tendon-driven hand designs. Our formulation is efficient enough to consider all finger design parameters (number and routing of tendons, tension limits, and posture) and grasp (number and configuration of fingers, friction characteristics, and object shape and size) and computes the full feasible grasp wrench set, from which a variety of grasp quality metrics can be obtained. In this first demonstration of our methodology, we compared the wrench-direction-independent grasp quality for two topologies, two grasp configurations, and thousands of parameter combinations when grasping a sphere, and we present the steps for extending this methodology to completely arbitrary hand designs, objects, and finger placements.
Our Monte Carlo exploration of the design space demonstrates the computational efficiency and utility of our method and shows that, as expected, the 2N topology is generally superior to the N + 1 topology in grasp quality and hence can resist wrenches of higher magnitude in all directions. This is because this 2N topology can exert a wider range of forces on the object than the N + 1 topology, resulting in higher grasp quality. Importantly, however, our parameter exploration found certain designs (within the allowed ±20% variability) for which the N + 1 topology can outperform the nominal 2N topology. If a designer favors the N + 1 topology due to actuator/space/weight constraints, there are N + 1 topologies that can meet or exceed the performance of a nominal 2N topology (which may have less design flexibility because of more tendons). These results would apply to most objects of similar size since the main difference would be a small change in finger contact angle.
In addition, the extensive exploration of the high-dimensional parameter spaces (i.e., 22 or 25 dimensions) allows us to identify some critical design parameters for grasp quality (i.e., with a high R2 value of 0.930, noted in Table III). Regressions for our N + 1, two-finger case (see Table III), for example, it is clear that one tendon and one moment arm are, from among 22 parameters, the most critical individual parameters in the design; altering them in isolation has the greatest effect on grasp quality. Exploring second- and third-order parameter sensitivities is likely intractable with this or most other techniques because of the geometric growth of iterations needed. Second-order terms in a regression would bring the number of regressed independent variables to over 400, and third-order terms would raise that number to over 8000.
Nevertheless, our approach demonstrates sufficient computational efficiency to enable, for the first time, exploring large-dimensional design spaces. Optional adjustments in mesh simplification procedures or friction cone approximations can and do bring improvements to speed with minimal loss in accuracy, but they are not central to our methodology. Additionally, other techniques, such as hull approximation or the Voronoi filtering, could be used to simplify the grasp wrench set. Importantly, we tested and found that our computationally streamlined floating-point computations produced results equivalent to the 100 times slower exact arithmetic calculations.
This approach is innovative because it now enables optimizing the design of dexterous tendon-driven hands by testing hundreds or thousands of alternative hand topologies quickly. For anthropomorphic hands or prosthetic hands, link geometry is relatively fixed, but all tendon routing and moment arm values can be varied. For general-purpose manipulators, everything from number and arrangement of fingers, to DOFs and link lengths of each finger, to number, routing and strength of tendons may be varied and evaluated. Any number of optimization algorithms, including gradient-descent, genetic, or random search algorithms, could be employed with this methodology to explore the design space and optimize the topology of dexterous hands. The efficacy and efficiency of random search algorithms are being explored in current research.
This method can also be used to determine the optimal grasping points of a particular object for a particular set of tendon-driven hand design parameters. If this is desired, then many finger placements can be tested to determine the one with the optimal grasp quality.
We calculate the grasp quality for precision grasp (i.e., grasp by the fingertips) in this study. This is the grasp that is necessary to manipulate an object. Power grasp capabilities (where the fingers are wrapped completely around an object) could be calculated with a modified version of this algorithm. However, in general, power grasp quality and precision grasp quality will tend to be highly correlated due to the fact that a high flexion force in the fingers is desirable for both grasps.
The shaping of the feasible output of a robotic system via variation of mechanical design parameters has been of interest for several decades [2], [10]–[14]. Our novel synthesis of computational approaches now enables its pursuit for large dimensional, tendon-driven systems. Grasp quality, manipulability metrics, and hand complexity metrics such as number of fingers, number of joints per finger, and number of tendons could also be integrated into a multiobjective optimization algorithm.
Many other grasp quality metrics are easily computed using the basic procedure we have described. One example is the volume of the feasible wrench set [18]. Qhull can be easily queried to calculate this volume at the same time it is calculating the weakest wrench metric we analyzed in this study. Another example is task-specific grasp quality metrics such as those used in [25], [48], and [49]. Once the grasp wrench set is calculated, the straightforward linear programming technique used in [25] can be used to calculate this metric for polytopes or using singular value decomposition [49] for ellipsoids.
Future work will use this methodology to design dexterous, tendon-driven hands with higher grasp capabilities than are currently available, and simpler hands with specific capabilities. Furthermore, this work on static grasp can be extended to manipulability sets or feasible acceleration sets, which quantify the velocities or accelerations with which an object can be manipulated. This methodology could also be used in grasp planning, where an optimal or near-optimal grasp found for a specific tendon-driven hand may actually be a bad grasp for another tendon-driven hand. This methodology also enables the quantitative analysis of biological hands and grasps (including human [37]) and can help to answer questions about its anatomical structure; so we can perhaps draw inspiration from it for novel robotic designs. Finally, this analysis can also be applied to design and optimize arbitrary tendon-driven and reconfigurable robots, such as tensegrity structures, to perform complex manipulation and locomotion tasks [50], [51].
Acknowledgment
The authors would like to acknowledge the useful comments by M. Kurse, B. Holt, and C. Raths.
This work was supported by the National Science Foundation under Grant 0836042, by the National Institute on Disability and Rehabilitation Research under Grant 84-133E2008-8, and by the National Institutes of Health under Grant AR050520 and Grant AR052345 to F. J. Valero-Cuevas.
Appendix
Calculation of the Feasible Force Sets of Tendon-Driven Manipulators
Fundamental to feasible force set analysis is the calculation of the posture-dependent manipulator Jacobian J(q). q is the vector of joint angles (i.e., finger posture). The Jacobian represents a linear mapping from angular velocities of the joints to endpoint velocity, as shown in the following:
| (3) |
where ẋ is the endpoint velocity vector (it can include both translational and rotational components and therefore can be up to 6-D; see [34] for more details), J(q) is the manipulator Jacobian, q is the vector of joint angles (i.e., finger posture), and q̇ is the vector of joint angle velocities.
If an underactuated finger is being analyzed, then the Jacobian is only constructed with columns that correspond with joint angles that can be independently actuated, and the analytical expressions for each entry of the Jacobian matrix, which would normally include all joint angles, will only include the actuated joint angles. If the last two joints are coupled such as in the human hand or shadow hand [3], [52], then the last joint angle q4 would be a (presumably) linear function of q3 (e.g., q4 = q3/2). The Jacobian could be reduced from four to three columns, and the analytical expressions for each entry of the Jacobian matrix could be constructed as a function of three joint angles by substituting in for the last joint angle (e.g., substituting q3/2 in for q4). The Jacobian would then be 3 × 3 (instead of 3 × 4), even though there are four joint angles. Advanced kinetostatic analysis of under-actuated fingers is performed in [53], although the simple procedure just described should be sufficient for the calculation of feasible force sets for most robotic applications. Furthermore, minimally underactuated hands with, for example, one tendon for flexion and springs for extension could be analyzed in the torque domain and appropriate dimensionality reduction of the Jacobian matrix.
Once the Jacobian is calculated, using the principle of virtual work, we can find the linear mapping between endpoint wrench (i.e., generalized forces which can include force and torque components and, therefore, can be up to 6-D, depending on the formulation of the Jacobian used) w and joint torques τ as shown in the following:
| (4) |
Since we are analyzing tendon-driven systems, we also need the moment arm matrix R which contains the values of the moment arms for each of the tendons across each of the joints. It is a matrix, where n is the number of joints, and ℓ is the number of tendons of the manipulator. The entries are ri,j, which is a signed moment arm value (positive values indicate positive torque generated at a joint when tension is applied to the tendon, and v-v), i is the joint number and ranges from 1 to n, and j is the tendon number, which ranges from 1 to ℓ. The moment arm matrix can be used to transform tendon tensions T to joint torques using the following:
| (5) |
We can use an activation vector a to represent the degree to which a tendon is activated. Each element of a ranges between 0 (no activation) and 1 (full activation). Further discussion may be found in [17]. If we define F0 as a diagonal matrix of maximal tendon tensions, then we get the following relation between activations and tendon tensions:
| (6) |
The first step to calculate the feasible force set is to find the feasible torque set by taking the convex hull of points generated by mapping each vertex of the feasible activation set to joint torque space by combining (5) and (6):
| (7) |
The feasible 3-D force set can be found from this feasible torque set by intersecting the feasible torque set with the linear subspace spanned by the columns of JT [25], [54]. This can be accomplished with any vertex enumeration algorithm. The vertices of this reduced-dimensionality set can then be transformed to endpoint force space using the Moore–Penrose pseudoinverse so that
| (8) |
where J+T denotes the Moore–Penrose pseudoinverse of JT.6
If the 3-D feasible force set is being calculated (as in this study), then the wrench vector in (8) will be of length 3 and will have components of Fx , Fy, and Fz.
Footnotes
The force manipulability set in the weak sense is the set of all Cartesian forces that can be exerted by a manipulator with no constraints on endpoint torque. The strong sense force manipulability set is a subset of weak sense set with the added constraint of zero endpoint torque.
The number of vertices of the grasp wrench set is on the order of mn , where n is the number of feasible object force set vertices, and m is the number of fingers [19]. Therefore, the computation time can become intractable for high numbers of vertices.
The union limits the sum of finger forces (i.e., if one finger exerts more force at a given time, then the other cannot produce as much force), while the Minkowski sum limits each finger force (i.e., the feasible object force sets are independent). While the union is computationally easier and still can provide important information about a grasp, for this study, we concentrated on the more realistic Minkowski sum. For more discussion, see [8].
These hands are not all fully actuated, and some have coupled joints. However, they are 2N designs in the sense that they use two antagonistic, symmetrically routed tendons to actuate each independent joint. It should also be noted that there are many possible 2N, symmetric, antagonistic designs, and that we simply chose this particular one for demonstration purposes.
Any more than N + 1 tendons is considered tendon redundancy, and typically not more than 2N tendons are used in dexterous robotic fingers. Manipulators or fingers with more than 2N tendons can have very interesting redundancy properties, as in [16], and can be analyzed using our method as well.
If the Jacobian is square and invertible, the inverse J–T can be taken, and the feasible torque set subspace intersections are unnecessary.
Contributor Information
Joshua M. Inouye, Department of Biomedical Engineering, University of Southern California, CA 90089 USA (jinouye@usc.edu).
Jason J. Kutch, Department of Biomedical Engineering, University of Southern California, CA 90089 USA (kutch@usc.edu).
Francisco J. Valero-Cuevas, Department of Biomedical Engineering and the Division of Biokinesiology and Physical Therapy, University of Southern California, CA 90089 USA (valero@usc.edu).
REFERENCES
- 1.Jacobsen S, Iversen E, Knutti D, Johnson R, Biggers K. Design of the utah/mit dextrous hand. Proc. IEEE Int. Conf. Robot. Autom. 1986:1520–1532. [Google Scholar]
- 2.Salisbury JK, Craig JJ. Articulated hands: Force control and kinematic issues. Int. J. Robot. Res. 1982;1(1):4–17. [Google Scholar]
- 3.Shadow Dexterous Hand, Shadow Robot Company 2012 May 15; [Online]. Available: http://www.shadowrobot.com/hand.
- 4.Grebenstein M, Albu-Schffer A, Bahls T, Chalon M, Eiberger O, Friedl W, Gruber R, Hagn U, Haslinger R, Hppner H. The DLR hand arm system. Proc. IEEE Int. Conf. Robot. Autom. (ICRA) 2011:3175–3182. [Google Scholar]
- 5.Ambrose RO, Aldridge H, Askew RS, Burridge RR, Bluethmann W, Diftler M, Lovchik C, Magruder D, Rehnmark F. Robonaut: Nasa's space humanoid. IEEE Intell. Syst. Appl. 2000 Jul-Aug;15(4):57–63. [Google Scholar]
- 6.Jau BM. Dexterous telemanipulation with four fingered hand system. Proc. IEEE Conf. Robot. Autom. 1995;1:338–343. [Google Scholar]
- 7.Chang SL, Lee JJ, Yen HC. Kinematic and compliance analysis for tendon-driven robotic mechanisms with flexible tendons. Mech. Mach. Theory. 2005;40(6):728–739. [Google Scholar]
- 8.Pons JL, Ceres R, Pfeiffer F. Multifingered dextrous robotics hand design and control: A review. Robotica. 1999;17(6) [Google Scholar]
- 9.Tsai LW. Design of tendon-driven manipulators. J. Mech. Des. 1995;117:80. [Google Scholar]
- 10.Lee JJ, Tsai LW. The structural synthesis of tendon-driven manipulators having a pseudotriangular structure matrix. Int. J. Robot. Res. 1991;10(3):255. [Google Scholar]
- 11.Chen DZ, Su JC, Yao KL. A decomposition approach for the kinematic synthesis of tendon-driven manipulators. J. Robot. Syst. 1999;16(8):433–443. [Google Scholar]
- 12.Ou YJ, Tsai LW. Isotropic design of tendon-driven manipulators. J. Mech. Des. 1996;118(3):360–366. [Google Scholar]
- 13.Ou YJ, Tsai LW. Kinematic synthesis of tendon-driven manipulators with isotropic transmission characteristics. J. Mech. Des. 1993;115:884. [Google Scholar]
- 14.Sheu JB, Huang JJ, Lee JJ. Kinematic synthesis of tendon-driven robotic manipulators using singular value decomposition. Robotica. 2009;28(1):1–10. [Google Scholar]
- 15.Firmani F, Zibil A, Nokleby SB, Podhorodeski RP. Wrench capabilities of planar parallel manipulators. part I: Wrench polytopes and performance indices. Robotica. 2008;26(06):791–802. [Google Scholar]
- 16.Tsai LW, Lee JJ. Inst. Syst. Res. Univ. Maryland, Baltimore, Tech. Rep. ISR; TR: 1988. Kinematic analysis of tendon-driven robotic mechanisms using graph theory; pp. 1988–20. [Google Scholar]
- 17.Valero-Cuevas FJ. A mathematical approach to the mechanical capabilities of limbs and fingers. Progr. Motor Control. 2005;629:619–633. doi: 10.1007/978-0-387-77064-2_33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Miller AT, Allen PK. Examples of 3d grasp quality computations. Proc. IEEE Int. Conf. Robot. Autom. 1999;2:1240–1246. [Google Scholar]
- 19.Miller AT, Allen PK. Graspit! A versatile simulator for robotic grasping. IEEE Robot. Autom. Mag. 2004 Dec.11(4):110–122. [Google Scholar]
- 20.Markcnscoff X, Yapadimitriou CH. Dept. Comput. Sci. Stanford Univ.; CA: 1987. Optimum grip of a polygon. Rep. STAN-CS-87-1153. [Google Scholar]
- 21.Kirkpatrick D, Mishra B, Yap CK. Quantitative steinitz's theorems with applications to multifingered grasping. Discr. Comput. Geometry. 1992;7(1):295–318. [Google Scholar]
- 22.Ferrari C, Canny J. Planning optimal grasps. Proc. IEEE Int. Conf. Robot. Autom. 1992:2290–2295. [Google Scholar]
- 23.Lin Q, Burdick JW, Rimon E. A stiffness-based quality measure for compliant grasps and fixtures. IEEE Trans. Robot. Autom. 2000 Dec.16(6):675–688. [Google Scholar]
- 24.Mishra B. Robotics Manuf. Lab. New York: 1995. Grasp metrics: Optimality and complexity. Tech. Rep. TR1995-680. [Google Scholar]
- 25.Fu JL, Pollard NS. On the importance of asymmetries in grasp quality metrics for tendon driven hands. Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst. 2006:1068–1075. [Google Scholar]
- 26.Murray RM, Li Z, Sastry SS. A Mathematical Introduction to Robotic Manipulation. CRC; Boca Raton, FL: 1994. [Google Scholar]
- 27.Suárez Feijóo R, Cornellá J, Roa Garzón M. Grasp quality measures. 2006 [Google Scholar]
- 28.Dai JS, Kerr DR. Analysis of force distribution in grasps using augmentation. Proc. Inst. Mech. Eng. C, Mech. Eng. Sci. 1996;210(13):15–22. [Google Scholar]
- 29.Ghafoor A, Dai JS, Duffy J. Stiffness modeling of the soft-finger contact in robotic grasping. J. Mech. Des. 2004;126:646. [Google Scholar]
- 30.Dai JS, Kerr DR. A six-component contact force measurement device based on the stewart platform. Proc. Inst. Mech. Eng. C, Mech. Eng. Sci. 2000;214(5):687. [Google Scholar]
- 31.Dai JS, Kerr DR. A computation environment for restraint analysis and synthesis in robotic grasping. Int. J. Eng. Simul. 2002;3(2):16–25. [Google Scholar]
- 32.Valero-Cuevas FJ, Zajac FE, Burgar CG. Large index-fingertip forces are produced by subject-independent patterns of muscle excitation. J. Biomech. 1998;31(8):693–704. doi: 10.1016/s0021-9290(98)00082-7. [DOI] [PubMed] [Google Scholar]
- 33.Finotello R, Grasso T, Rossi G, Terribile A. Computation of kinetostatic performances of robot manipulators with polytopes. Proc. IEEE Int. Conf. Robot. Autom. 1998;4:3241–3246. [Google Scholar]
- 34.Yoshikawa T. Translational and rotational manipulability of robotic manipulators. Proc. IEEE Int. Conf. Ind. Electron., Control Instrum. 2002:1170–1175. [Google Scholar]
- 35.Garland M, Heckbert PS. Surface simplification using quadric error metrics. Proc. 24th Annu. Conf. Comput. Graph. Interactive Tech. 1997:216. [Google Scholar]
- 36.Deshpande AD, Balasubramanian R, Lin R, Dellon B, Matsuoka Y. Understanding variable moment arms for the index finger mcp joints through the act hand. Proc. IEEE RAS EMBS Int. Conf. Biomed. Robot. Biomechatron. 2008:776–782. [Google Scholar]
- 37.Inouye JM, Kutch JJ, Valero-Cuevas F. Quantitative prediction of grasp impairment following peripheral neuropathies of the hand. presented at the 35th Annu. Meet. Amer. Soc. Biomech.; Long Beach, CA. 2011. [Google Scholar]
- 38.Garland M. Qslim software package. Carnegie Mellon Univ. 2004 Available: http://www.cs.cmu.edu/~garland/quadrics/qslim.html.
- 39.Howe RD, Kao I, Cutkosky MR. The sliding of robot fingers under combined torsion and shear loading. Proc. IEEE Int. Conf. Robot. Autom. 1988:103–105. [Google Scholar]
- 40.Ciocarlie M, Miller A, Allen P. Grasp analysis using deformable fingers. Proc. IEEE/RSJ Int. Conf. Intell. Robots Syst. 2005:4122–4128. [Google Scholar]
- 41.Kobayashi H, Hyodo K, Ogane D. On tendon-driven robotic mechanisms with redundant tendons. Int. J. Robot. Res. 1998;17(5):561. [Google Scholar]
- 42.Butterfass J, Grebenstein M, Liu H, Hirzinger G. DLR-hand II: Next generation of a dextrous robot hand. Proc. IEEE Int. Conf. Robot. Autom. 2001;1:109–114. [Google Scholar]
- 43.Pollard NS, Gilbert RC. Tendon arrangement and muscle force requirements for humanlike force capabilities in a robotic finger. Environment. 2002;17:14. [Google Scholar]
- 44.Avis D. A revised implementation of the reverse search vertex enumeration algorithm. In: Kalai G, Ziegler G, editors. Polytopes—Combinatorics and Computation. Birkhauser-Verlag; Cambridge, MA: 2000. pp. 177–198. [Google Scholar]
- 45.Barber CB, Dobkin DP, Huhdanpaa H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996;22(4):469–483. [Google Scholar]
- 46.Valero-Cuevas FJ, Hoffmann H, Kurse MU, Kutch JJ, Theodorou EA. Computational models for neuromuscular function. IEEE Rev. Biomed. Eng. 2009;2:110–135. doi: 10.1109/RBME.2009.2034981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Santos VJ, Valero-Cuevas FJ. Reported anatomical variability naturally leads to multimodal distributions of denavit-hartenberg parameters for the human thumb. IEEE Trans. Biomed. Eng. 2006 Feb.53(2):155–163. doi: 10.1109/TBME.2005.862537. [DOI] [PubMed] [Google Scholar]
- 48.Zhu X, Wang J. Synthesis of force-closure grasps on 3-d objects based on the q distance. IEEE Trans. Robot. Autom. 2003 Aug.19(4):669–679. [Google Scholar]
- 49.Li Z, Sastry SS. Task-oriented optimal grasping by multifingered robot hands. IEEE J. Robot. Autom. 1988 Feb.4(1):32–44. [Google Scholar]
- 50.Paul C, Valero-Cuevas FJ, Lipson H. Design and control of tensegrity robots for locomotion. IEEE Trans. Robot. 2006 Oct.22(5):944–957. [Google Scholar]
- 51.Rieffel J, Valero-Cuevas F, Lipson H. Automated discovery and optimization of large irregular tensegrity structures. Comput. Struct. 2009;87(5/6):368–379. [Google Scholar]
- 52.Leijnse J, Quesada PM, Spoor CW. Kinematic evaluation of the finger's interphalangeal joints coupling mechanism–variability, flexion-extension differences, triggers, locking swanneck deformities, anthropometric correlations. J. Biomech. 2010;43(12):2381–2393. doi: 10.1016/j.jbiomech.2010.04.021. [DOI] [PubMed] [Google Scholar]
- 53.Birglen L, Gosselin CM. Kinetostatic analysis of underactuated fingers. IEEE Trans. Robot. Autom. 2004 Apr.20(2):211–221. [Google Scholar]
- 54.Chiacchio P, Bouffard-Vercelli Y, Pierrot F. Force polytope and force ellipsoid for redundant manipulators. J. Robot. Syst. 1997;14(8):613–620. [Google Scholar]
- 55.Fukuda K, Prodon A. Double description method revisited. Combinatorics Comput. Sci. 1996;1120:91–111. [Google Scholar]