Abstract
This paper investigates the precision of parameters estimated from local samples of time dependent functions. We find that time delay embedding, i.e. structuring data prior to analysis by constructing a data matrix of overlapping samples, increases the precision of parameter estimates and in turn statistical power compared to standard independent rows of panel data. We show that the reason for this effect is that the sign of estimation bias depends on the position of a misplaced data point if there is no a priori knowledge about initial conditions of the time dependent function. Hence, we reason that the advantage of time delayed embedding is likely to hold true for a wide variety of functions. We support these conclusions both by mathematical analysis and two simulations.
Keywords: Time Delay Embedding, Dynamical Systems Models, Intraindividual Variability, Oscillatory Data
Introduction
Many phenomena of interest in psychology exhibit intraindividual variability (Baltes, Reese, & Nesselroade, 1977; Nesselroade & Ram, 2004). That is to say, when variables that indicate a phenomenon are observed on multiple occasions, their values are likely to exhibit fluctuations — at some occasions the variables values will be higher and at other occasions lower. If one wishes to model this variability, it is necessary to measure each individual sufficiently often to capture the fluctuations and for a sufficient number of occasions in order to be able to estimate interindividual differences in this intraindividual variability. The required density of measurement in time is dependent on how rapidly the phenomenon is fluctuating (Shannon & Weaver, 1949). The required number of occasions per individual is a function of the statistical power required to detect the effects of interest (Cohen, 1988). In addition, one may wish to predict individual differences in coefficients of models intraindividual variability.
Experimental designs for longitudinal studies range from very short time series (e.g., 3 or 4 observations per individual) with many individuals to long time series (e.g. hundreds of observations per person) and fewer individuals. Such designs are frequently employed to understand how a trait–like characteristic of a person (e.g., sex) predicts a within–person coefficient representing the time–dependent behavior of the individual. Such models are sometimes expressed as multilevel models where the repeated observations are grouped by individual (Bisconti, Bergeman, & Boker, 2006; Pinheiro & Bates, 2000).
When only a few observations per individual (e.g., 5) are collected on many individuals (e.g., 200), there is reduced power to estimate the within–person time series coefficients. However, this design has the advantage of a large sample of individuals, and thus the standard error of the mean within–person time series coefficient may be small. In this example design, 1000 observations were made: 5 observations on each of 200 individuals.
When many observations per individual are collected, the estimates of within–person time series coefficients are more precise. But if a study has a fixed budget and a fixed cost of obtaining an observation, this means that fewer individuals can be recruited if a greater number of observations per person are obtained. If the budget allows 1000 observations, another plausible design might be 50 observations on 20 individuals. In this case, improved within–person precision comes at the cost of decreased between–persons sample size. But a more precise within–person measure requires fewer individuals in order to estimate its mean and variance. Thus, there is a trade–off between within–person precision and between–persons precision for a fixed budget.
Others have explored trade–offs between number of individuals and number of observations per individual in multilevel designs (see e.g., Hox, 2002; Snijders & Bosker, 1999), finding that the variance and sample size at each level of a multilevel model determines power and thus impacts optimal design. The current article presents a method for improving power at the within–person level when the objective is to fit models to account for intraindividual fluctuations. This improvement can, for instance, substantially change the optimal balance between the number of observations per individual and number of individuals in any given experimental design.
Time delay embedding (sometimes called state space embedding) has been used for the estimation of coefficients in models of intraindividual fluctuations (e.g., Bisconti et al., 2006; Butner, Amazeen, & Mulvey, 2005; Chow, Ram, Boker, Fujita, & Clore, 2005; Deboeck, Boker, & Bergeman, in press). Time delay embedding has also been widely used for the estimation of invariants of nonlinear time series in physics (see e.g., Abarbanel, 1996; Grassberger & Procaccia, 1983; Kantz & Schreiber, 1997; Sauer, Yorke, & Casdagli, 1991). Due to theorems of Whitney (1936) and Takens (1985), the dynamics of a time series can be estimated from a time delay embedding as long as the embedding delay is not poorly chosen. However, standard errors for models estimated from an overlapping samples time delay embedding may not be correct when calculated using methods that either assume independence of rows in the data matrix or only account for within–person dependency. The current article explores how overlapping samples time delay embedding affects the precision of estimates of within–person fluctuations relative to an independent samples design.
We will begin by describing what we mean by overlapping samples time delay embedding. We will next derive a reason why overlapping samples time delay embedding method can improve precision of coefficient estimates of intraindividual fluctuations. We will then use two simulations to compare the precision of coefficients obtained when a model is estimated using either (a) many short independent longitudinal bursts (essentially a panel design with 5 waves) or (b) an overlapping samples time delay embedding of a longer longitudinal sample.
Overlapping Samples Time Delay Embedding
Time delay embedding is a method for transforming a time series into a matrix of time–dependent chunks of data. By transforming a long sequence of data into a set of short time–dependent chunks, the time–dependence itself becomes the focus of the analysis rather than the prediction of any particular value at any particular moment in time. That is to say, each row in a time delay embedded data matrix encapsulates the time–dependence of a short chunk of the time series.
We will adopt the terminology “burst” (after Nesselroade, 1991) to describe short, independent, time–sequential samples from a longer time series. We will use the term “overlapping samples” to describe overlapping time–dependent samples created using time delay embedding. Finally, we will use the term “samples” when we are referring to both “bursts” and “overlapping samples”.
In this article we are concerned with the effect of time delay embedding on within–person precision. In order to simplify the exposition we will assume that there are no between–persons differences and then compare two extremes of experimental design. Of course, a real world design would also be interested in between–person differences and thus an optimum design would include estimates of between–persons variance and fall somewhere between the two extremes examined here. But, by setting between–persons differences to zero, we can isolate the within–person portion of the problem and focus our discussion only on issues that have to do with overlapping samples. Although our exposition makes the assumption of no between–persons differences, the logic we use also applies to a multilevel case where coefficients can vary by individual.
At one end of the spectrum of design, one might observe many individuals a few times. For instance, suppose we observe 200 individuals each on 5 occasions separated by equal intervals of time, Δt. In such a design, each row in a data matrix corresponds to one individuals’s data and can be considered to be independent. If between-person differences are zero, each row is an independent sample in which the covariances between the observations and their time derivatives within each row have the same true scores. Any observed between–row differences in covariances are thus assumed to be due to error of measurement.
While this experimental design may seem to be assuming a great deal, analyses such as these are remarkably common in the literature. Consider a panel design with 5 waves that assumes stationarity and only analyzes mean point estimates and standard errors for coefficients of time dependence. We argue that this type of design makes the same assumptions that we are making in the following simplified examples.
Consider how the data might be arranged to analyze this experimental design. A 200 × 5 data matrix, X, can be expressed as
| (1) |
where x(i,j) is the value of the variable x for the ith individual on the jth occasion of measurement. Each of 200 individuals was measured 5 times, so the total number of measurements was 1000.
At the other extreme, suppose that we observe a single individual on 1000 occasions separated by the same interval of time, Δt, as in the previous design. According to our assumptions of stationarity and no between–persons differences, the expectation of the point estimates for covariances between observations and their derivatives is the same as in the previous example if we arrange the 1000 observations into a 200 × 5 data matrix as
| (2) |
where x(i,j) is the value of the variable x for the ith individual on the jth occasion of measurement. Since there is only one individual in this design, i = 1 for all observations.
The data matrices in Equations 1 and 2 are of the same order, 200 × 5. But note that there is time dependence between the last column in each row, x(1,p), and the first column in the next row, x(1,p+1), that is being ignored. Since estimating within–person time dependence is the objective of our analysis, we are losing information that could be used to help improve precision of parameter estimates.
Suppose now that we change how the data matrix is constructed and use overlapping samples time–delay embedding to create a 200 × 5 data matrix X(5),
| (3) |
where x(i,j) is the value of the variable x for the ith individual on the jth occasion of measurement. Again, there is only one individual in this design, so i = 1 for all observations. Note that in contrast to the 1000 observations required in the first two designs, we now only require 204 observations to construct the 200 × 5 data matrix.
The two data matrices X and X(5) in Equations 1 and 3 are of the same order, 200× 5. But the overlapping samples time delay embedded matrix, X(5), has two characteristics that appear to be problematic. First, there are only 204 measurements in X(5) and there are 1000 measurements in X. So, we would expect that the time delay embedded matrix, X(5), would provide model parameter point estimates that would tend to vary more from sample to sample than would estimates using X. Second, the rows of X(5) are not independent of one another; in fact the data is being reused from one row to the next. Thus, the assumption of independence of rows is not met.
Intuition would suggest that the lower number of observations and violation of standard assumptions in the time delay embedded matrix would lead to parameter point estimates for models of intraindividual variability that are less precise than those from the data matrix constructed from independent rows and to standard errors estimates that are smaller than the empirical variability in the parameter point estimates. In fact, we find that each of these intuitions are incorrect both in the case of linear and for the case of a linear oscillator. The remainder of this article demonstrates why this counter–intuitive result holds, first by deriving sources of imprecision in the case of linear change and the case of a linear oscillator, and then by presenting two simulations that show that the advantage derived algebraically does hold in practice.
Effects of Overlapping Time Delayed Samples
Assume a long data series that follows a known model with one parameter θ that describes the behavior of the model. Many local samples of this series are given to estimate θ. If a normally distributed unbiased measurement error is introduced on any data point xt, then θ for all samples that include xt and subsequently the total estimator θ̂ will decrease in precision.
In a specific situation, the error constitutes a displacement of xt from its true value, and θ̂ will consequently be displaced, too. If xt is included in two samples, though, the displacement of θ̂ will not necessarily be twice as high, as the error in xt may have less influence in the second sample. Even more, if the displacement of θ̂ caused by a erroneous xt has different signs in two different samples, the overall error on θ̂ may be smaller than if xt would only be included in one sample, or even cancel out completely.
In the following, we show a situation where such a reduction of the displacement of θ̂ holds true for every fixed displacement of xt. As these displacement are caused by unbiased measurement error, the effect will manifest in a higher precision (and not lower bias) of θ̂. So, assume in the following that all samples from the data series are accurate, with exception of a single data point xt, which is displaced by a small error.
Linear Functions
Consider for example that the original data series is a line, and three local overlapping samples are taken from it as shown in the three panels of Figure 1. Assume the data point given are perfect, but the data point marked with an arrow (which is a member of all three samples) is a little bit too high. In the first panel of Figure 1, where xt is at the end of the sample, the line that fits the data best has a positively biased slope (dotted line). In the middle panel, xt is at the center of the panel, and the best fitting line has a positively biased intercept, but no bias in the slope. In the third panel, where xt is at the beginning of the sample, the situation is inverted: Here, the slope is underestimated.
Figure 1.
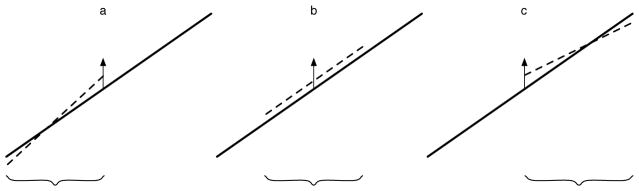
Change of estimated slope with unknown intercept. When in a perfect data set a positive error at the end of a sample is introduced, the slope estimate increases. If the positive error is introduced in the middle of the sample, the estimate of slope does not change, and if the error is introduced at the beginning of the sample, the slope estimate decreases. Thus, in a time delay embedding, a small error introduced in a perfect data set cancels out; indeed, if the estimate is made for each sample separately and the average is taken as overall estimator, the canceling is perfect.
This situation is typical for time delay embedding, where each data points (except the first and last few data points) will be at each possible position in one sample. So we can expect that errors in the data set are partially canceling out.
Suppose that intercept and mean are separately estimated by a maximum likelihood estimation and then averaged over the overlapping samples. In practice the slope would likely be fixed over the samples, and all samples estimated simultaneously, but arguably the behavior of the estimator would be very similar. Assume the data set is based on a model given by a linear curve with added normally distributed error
| (4) |
where et is normally distributed with zero mean, no covariances and variance . To support the intuition evoked by Figure 1, it will be shown in the following that the biases in a time delay embedding in fact cancel out perfectly for a small error.
For a given sample x0, …, xT −1 of length T from the data set, the likelihood of the sample is
| (5) |
and hence the minus two log likelihood, denoted by
 (I, S, x), is
(I, S, x), is
| (6) |
the gradient of
 with respect to S and I is given by
with respect to S and I is given by
| (7) |
To find the maximum likelihood estimator of I and S in the sample, the gradient is set equal to zero. The constant factor does hence not influence the estimator and will be omitted from here on, i.e. we define as
| (8) |
Analogously, we define H as the Hessian of
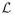 divided by the same constant factor, i.e.
. H is then
divided by the same constant factor, i.e.
. H is then
| (9) |
We want to investigate the change of the maximum likelihood estimator Ŝ and Î on an infinitesimally small increase of one of the data points xτ. The change of the gradient on this small increase will be the derivative of g w.r.t. xτ, which is
| (10) |
To have the gradient return to zero, a change m in S and I has to be made such that the change of g on this is the negative of the above value. The change of g with respect to I and S is described by H, i.e. we have to choose m such that
| (11) |
| (12) |
The inverse of H is , so we have
| (13) |
| (14) |
| (15) |
This vector describes the change of the estimators Ŝ and Î on a small positive error on xτ.
Now assume we have picked some overlapping samples from the model in a time delay embedding, i.e. in a way that the first sample contains the time points 0…T −1, the second 1…T, and so forth. Assume that the (T − 1)th data point is biased; then, for the ith sequence, the derivative of the estimators is
| (16) |
where τi = T − 1 − i, hence
| (17) |
Taking the average of the first column (the one corresponding to S) for all T overlapping samples, we get
| (18) |
We express the double sum as a single sum that runs over all values j of (T − 1 − (i + t)), i.e. j runs from −(T − 1) to T − 1; each j appears (T − |j|) in the sum, i.e. the above term is equal to
| (19) |
| (20) |
This means that the averaged estimator of S does not change on a small error introduced in one data point of a linear curve if time delay embedding is applied. The biases of the overlapping samples cancel out each other perfectly.
If part of the global information is given, though, the effect vanishes; consider for example that we know the position of the first data point in each sample, and the estimate the slope only. Figure 2 illustrates this situation; as can be seen, the estimated slope now would change to higher values, and only the absolute value of the slope bias is dependent on the position of the error in the sample.
Figure 2.
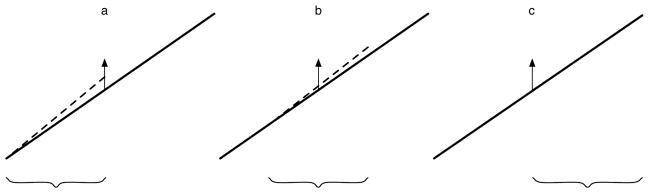
Change of estimated slope with known first point. When in a perfect data set a positive error is introduced while assuming a known first point, the slope estimate will increase, no matter where the error is introduced in the sample.
Oscillatory Functions
The reasons for a local sampling are usually even more pronounced in oscillatory functions like sine curves. So a natural question is whether the canceling effect of bias for time delay embedding as can be found for linear functions can be found here, too. Figure 3 illustrates the situation of overlapping samples for a sine curve; again, we assume that perfect data is given, and a single measurement xt is misplaced by a small positive error, indicated by the arrow. In the first Panel of Figure 3, the error is at the end of the sample (which in this examples is the end of the first half cycle). The dotted line gives the best fitting sine approximation to the curve, with freely estimated phase and frequency. We can see that the begin of the cycle is shifted to the left (out of the left end of the panel), while the frequency is decreased.
Figure 3.
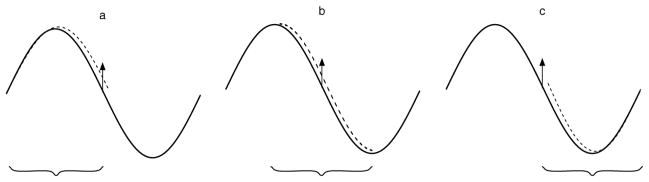
Change of estimated frequency with unknown phase. When in a perfect data set a positive error at the end of a sample (with a half cycle and phase zero) is introduced, the frequency estimate decreases. If the positive error is introduced in the middle of a sample with phases , the estimate of frequency does not change, and if the error is introduced at the beginning of a sample with phases π, the frequency estimate increases. Thus, in a time delay embedding, a small error introduced in a perfect data set cancels out. If the error is introduced at a phase which is a integer multiple and the estimate is made for each sample separately and then averaged, the canceling is perfect.
In the middle panel, the sample is taken from a quarter of the cycle to three quarters of the cycle, and the same error is introduced at the middle of the sample. Here, the best fitting sine curve is the same curve shifted slightly to the right; so the frequency estimate in this sample does not change.
In the last panel, finally, the frequency is increased to counter the effect of the error. So it is reasonable to assume that on average, the biases cancel out, at least partly. To show this, the following is an analogue development of the one given for linear curves. Here, we will concentrate on the change of the average frequency estimator for a small deviation of an otherwise perfect sample of the sine curve.
So assume the model is now given by a sine curve with added normally distributed error
| (21) |
where et is normally distributed with zero mean, no covariances and variance . Again, the likelihood for a given sample x0, …, xT −1 is
| (22) |
and hence the minus two log likelihood
 (θ, f, x)
(θ, f, x)
| (23) |
We again consider the gradient with respect to the two model parameters f and θ
| (24) |
again, since the gradient is set to zero to find the maximum likelihood estimators of f and θ, we omit the constant factor and define g(θ, f, x) with as
| (25) |
Let H again be the Hessian of
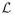 divided by the same constant, i.e.
, which is
divided by the same constant, i.e.
, which is
| (26) |
Assume a situation where the data set x is perfect. To investigate the change of the maximum likelihood estimators f̂ and θ̂ on an infinitesimally small increase of one of the data points xτ, consider again the change of g
| (27) |
Let m again be the vector of changes in f and θ such that the gradient returns to zero after a change in xτ. Since , we get . Since we assumed a perfect data set, we have xt = sin(θ + f t), which simplifies the expansion of this term to
| (28) |
| (29) |
| (30) |
As before in the linear case, m describes the change of the estimator f̂ and θ̂ on a small positive error in xτ. If we compare to the linear case, we have two differences: The cosine in front of the sum, which is merely a factor out of the sum and not important, and the squared cosine in the sum.
Now assume T samples taken in a time delay embedding from 2T − 1 data points, again with the (T − 1)th data point biased. This bias will change the estimates in the ith sample to
| (31) |
where τi = T − 1 − i, hence
| (32) |
Taking the average estimate of f for all T samples, we obtain
| (33) |
again, we express the double sum as a single one running over all values j of T −1 −(i + t). The jth summand appears T − |j| times, so the above term becomes
| (34) |
| (35) |
As the cosine square is in [0, 1], we see that the effect of the error at least partially cancels out. An easy bound from above shows that the average bias of the error in this way is at most half as much as the bias would be if just one sample was taken with the error in it. Perfect cancelation occurs if the cosine square is symmetric around θ + (T − 1)f, i.e. symmetric around the position at which the error was introduced. That is the case if θ + (T − 1)f is an integer multiple of .
So we see that for the sine curve the same effect as for the linear case occurs when a small error is introduced and samples are taken in a time delay embedding. Cancelation for the sine is not necessarily perfect, but as the cosine square has even more symmetry points than the sine curve, it still happens at many positions.
As in the linear case, the effect vanishes when a global embedding is known, for example if the phase is known (which fixes the first data point). Figure 4 illustrates this situation: In the first two panels, the estimated frequency decreases, and stays constant in the last (as the error is introduced at a data point which was assumed to be known).
Figure 4.
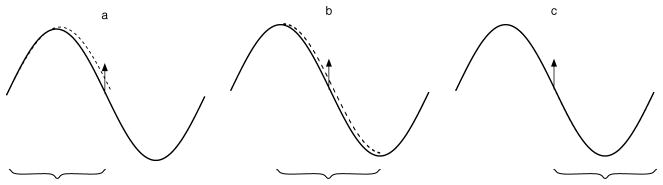
Change of estimated slope with known first point. When in a perfect data set a positive error is introduced while assuming a known phase (as is approximately the case if the phases of the samples are linked in a known way), the frequency estimate will change in the same direction if the samples are made in a time delay embedding.
Simulation Fitting Sine Curves
To illustrate the effect of overlapping samples time delay embedding, we simulated data to conform to (a) the independent samples case and (b) the overlapping samples time delay embedding case. We simulated the data as an undamped linear oscillator (i.e., a pure sine curve) with amplitude equal to one and wavelength equal to 100 observations, i.e. we simulated 100 data points per cycle. In these units, this corresponds to a frequency of 0.01. To this latent score, we added a homogeneous fixed measurement error for each single data point. The measurement error was normally distributed with variance 0.01 or 0.05. From this data, we sampled 40, 200 or 1000 samples of length five each. For the independent sample case, we simulated each burst separately. Starting with a uniformly distributed phase between 0 and 2π, we simulated five consecutive measurements with frequency and amplitude described above. For the overlapping time delay sampling, we simulated N + 4 (i.e., 44, 204, or 1004, respectively) consecutive points with one uniformly distributed starting phase, and then sampled N overlapping samples of length five.
In both the independent and the overlapping cases, the same method was used to estimate the frequency. A sine curve was fit to all samples simultaneously, each with an individual starting phase but the same frequency parameters (so N +1 parameters in total), using maximum likelihood estimation. For each cell, the simulation was repeated until the standard deviation of the estimated frequency was no longer changing significantly, but using at least 200 repetitions per cell.
For a frequency of 0.01, the error variance of 0.01 corresponds to a signal to noise ratio in the range of 0.000905 (for samples close to the inflexion point of the sine) to 0.72 (for samples close to the intercept of the sine with the x axis). The average signal to noise ratio is 0.35. Expressed in reliabilities (i.e. latent variance over total variance), these values correspond to a range from 0.000904 to 0.42, with a mean of 0.26. For an error variance of 0.05, the signal to noise range is 0.00018 to 0.144, with a mean of 0.07. Thus, the simulated time series were of markedly low reliability, i.e., were contaminated with a great deal of noise. We set the frequency parameter to be equal in all samples, while estimating a separate phase parameter for each sample.
The assumption of homogenous error can make the data difficult to fit, since some samples will always be close to the inflexion point and suffer from an extremely bad signal to noise ratio. The problem becomes more emphasized the lower the frequency is because with low frequencies, each single data point in a sample close to the inflexion will have the low signal to noise ratio. We chose the low frequency and the homogeneous error to show that nevertheless the frequency parameter can be estimated, and the estimation can be improved drastically by constructing an overlapping samples time delay embedding.
Table 1 gives the results of our simulation. The first two columns give the error variance and the number of bursts simulated in each simulation cell. Column three to five report the results from the overlapping samples time delay embedding, while columns six to eight report the results of the independent sampling.
Table 1.
Standard deviation of estimated frequency, f̂, for different homogenous error variance and sample size. “Rows” refers to the number of rows in the data matrix as described in Equations 1 and 3 (i.e., number of samples) and “Obs” refers to the total number of observations required to build a data matrix of the given type (overlapping time delay embedding or independent bursts). In no cell was the proportion of bias of the mean estimated frequency more than 0.005 of the true value.
| Condition | Time Delay Embedding | Independent Bursts | |||||
|---|---|---|---|---|---|---|---|
| Error | Rows | Obs | mean(f̂) | SD | Obs | mean(f̂) | Stdv |
| 0.01 | 40 | 44 | 0.00999 | 0.000053 | 200 | 0.01001 | 0.000126 |
| 0.01 | 200 | 204 | 0.01000 | 0.000019 | 1000 | 0.01000 | 0.000052 |
| 0.01 | 1000 | 1004 | 0.01000 | 0.000009 | 5000 | 0.01000 | 0.000024 |
| 0.05 | 40 | 44 | 0.01003 | 0.000296 | 200 | 0.00998 | 0.000553 |
| 0.05 | 200 | 204 | 0.01003 | 0.000105 | 1000 | 0.01004 | 0.000254 |
| 0.05 | 1000 | 1004 | 0.01003 | 0.000037 | 5000 | 0.01001 | 0.000106 |
In column three and six, the overall number of simulated data points (respectively the total number of observations) are calculated for both sampling methods. For the time delay embedding, this is the number of overlapping samples plus four. For the independent bursts, this is the number of bursts multiplied by five. In all cells with both sampling methods, frequency was estimated within half a percent of the true value (see column four and seven, respectively).
The most important information of Table 1 can be found in columns five and eight, which report the standard deviations of the estimated frequency for both methods of sampling. Note that estimation precision was relatively high despite the high error. Nevertheless, precision was always higher for a time delay embedding, usually more than twice as precise. Note in addition that roughly only a fifth of the data points were needed to create the same number of samples in the time delay embedding, since four of the five data points were reused from the sample before. To compare the methods assuming equally many data points, time delay embedding with 200 samples (line two and five, respectively) must be compared to random sampling with 40 samples (line one and four, respectively), and 1000 samples to 200 samples. The advantage of the time delay embedding then becomes even more pronounced.
Simulation using Latent Differential Equations
Time delay embedding is simply a method for setting up a data matrix prior to analysis. To illustrate that this method can be used with other estimation techniques, we next fit a Latent Differential Equations model (see Boker, Neale, & Rausch, 2004, for a more complete description of this model) to simulated data and show that the advantage holds for estimation of frequency and damping parameters for a damped linear oscillator. Each row in the data matrices in Equations 1 and 3 can be used to estimate the displacement and derivatives at a time t by filter basis functions similar to quadratic growth curve model. The covariances between these estimated displacements and the derivatives can then estimate the coefficients η and ζ in a second order differential equation model for the damped linear oscillator expressed as
| (36) |
where xt is the displacement of the variable from its equilibrium value at time t and ẋt and ẍt are its first and second derivatives at time t.
The data for the simulation were generated to conform to a factor model as shown in Figure 5, but with four indicator variables rather than three. The indicator variables were generated for a damped linear oscillator latent process and time–independent normally distributed error was added to each indicator variable. The latent process variable was created by numerically integrating Equation 36 using Mathematica. Values for each of the coefficients was chosen from the sets ζ = {0.0, −0.02} and η = {−0.6}. Thus we generated two oscillators: one with no damping and one with mildly negative damping. All indicator variables were simulated with communalities of 0.8, and the four factor loadings were selected as 1.0, 0.9, 0.8, and 0.7 respectively. We drew samples either using the randomized initial condition method (bursts of 5) or using the time delayed embedding method so that the resulting data matrices either had 200 or 400 rows. Thus, we created a 2 × 2 × 2 design with 2 levels of damping, 2 levels of matrix rows, and 2 types of sampling. For each cell in the simulation design we simulated 1000 data sets and fit an LDE model to each data set.
Figure 5.
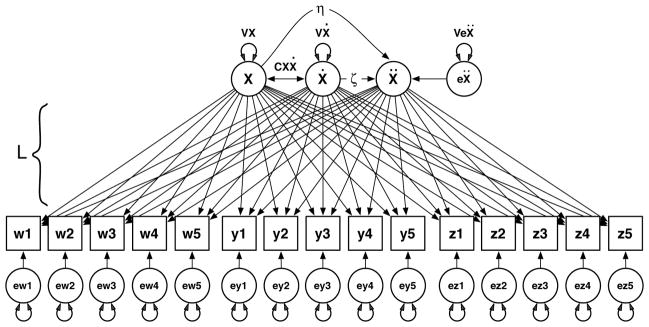
Multivariate Latent Differential Equation structural model with three indicators for a damped linear oscillator latent process.
The LDE factor model was specified as follows. First a loading matrix, L, was constructed to conform to the four indicators by 5 occasions of measurement per row in the data matrices (Boker et al., 2004)
| (37) |
where s is the sampling interval between successive samples, and a, b, and c are free parameters accounting for the factor loadings of the indicators for the latent process. Next, the structural part of the model is specified according to the RAM notation (McArdle & McDonald, 1984)
| (38) |
| (39) |
Finally, a 20 × 20 diagonal matrix U is constructed for the residual variances and then the expected covariances of the model can be calculated as
| (40) |
The structural equation modeling software Mx (Neale, Boker, Xie, & Maes, 2003) was then used to fit the LDE model to all data sets using full information maximum likelihood as the objective function.
LDE Simulation Results
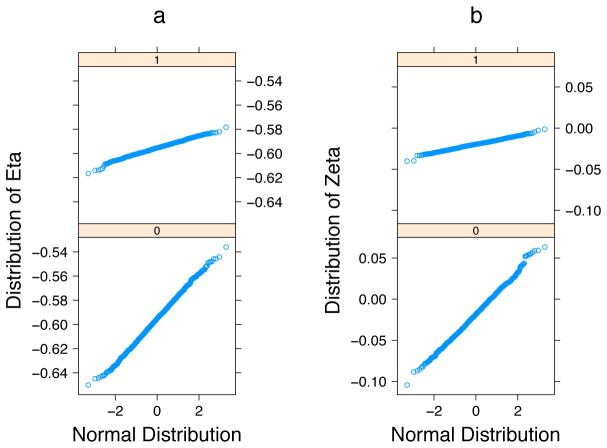
The distributions of η and ζ for the conditions ζ = −0.02 and N = 500 are plotted against the normal distribution as a QQ plot in Figures 6–a and 6–b respectively. Since each of these plots approximates a straight line, the distributions of estimates of η and ζ are approximately normal. The greater the slope of the line, the wider the distribution of the parameters — thus it is evident that the distributions of η and ζ for time delay embedding in the top two plots are much more precise than those of the independent rows sampled cases in the bottom two plots. Note also that the mean of the distributions for all four plots are approximately the true values of η = −0.6 and ζ = −0.02. The pattern of results in these plots are representative of all of the other cells in the simulation. In all cases, the time delay embedding estimates were considerably more precise than the independent rows sampled estimates, there was no appreciable bias, and the parameter estimates approximated a normal distribution.
Figure 6.
QQ plots of coefficient distributions of (a) η and (b) ζ versus normal distribution for ζ = −0.02 and N = 500. The top row of plots in (a) and (b) are the overlapping time delay embedded data and the bottom row of plots are the independent rows sampled data.
Table 2 displays the results of predicting the standard deviations of the parameter values from two of the simulation conditions: number of rows in the data matrix and whether or not the matrix was constructed as a time delayed embedding. Note that the effect on the standard deviation of the parameters of adding one hundred rows to the data matrix is about one fifth the effect of using time delayed embedding.
Table 2.
Standard deviations of η and ζ predicted as a multiple regression from simulation conditions. N is the number of rows in the matrix in hundreds (i.e., 2 or 5). Embedded is coded 0 for the independent rows data and 1 for the overlapping samples time delay embedded data.
| η | Value | SE | t | p |
|---|---|---|---|---|
| (Intercept) | 0.0369 | 0.00255 | 14.480 | < 0.0001 |
| N (in hundreds) | −0.0032 | 0.00062 | −5.082 | 0.00383 |
| Embedded | −0.0181 | 0.00187 | −9.665 | 0.00020 |
| Multiple R-Squared: 0.960, Adjusted R-squared: 0.943
| ||||
| ζ | Value | SE | t | p |
|---|---|---|---|---|
| (Intercept) | 0.0520 | 0.00354 | 14.693 | < 0.0001 |
| N (in hundreds) | −0.0047 | 0.00086 | −5.421 | 0.00289 |
| Embedded | −0.0263 | 0.00259 | −10.121 | 0.00016 |
| Multiple R-Squared: 0.964, Adjusted R-squared: 0.949
| ||||
The bias of η and ζ was also modeled and the results are shown in Table 3. Overall, there was a small, but statistically significant bias for η (bias = 0.005, p < 0.001) and the bias for ζ was not significantly different from zero. However, there was not a significant effect on the bias of η or ζ from whether the matrix was constructed as a time delay embedding.
Table 3.
Bias for η and ζ predicted as a multiple regression from simulation conditions. N is the number of rows in the matrix in hundreds (i.e., 2 or 5). Embedded is coded 0 for the burst sample matrix and 1 for the embedded matrix.
| η | Value | SE | t | p |
|---|---|---|---|---|
| Intercept | 0.00560 | 0.00065 | 8.562 | < 0.001 |
| N (in hundreds) | −0.00006 | 0.00016 | −0.402 | 0.704 |
| Embedded | −0.00083 | 0.00048 | −1.737 | 0.143 |
| Multiple R-Squared: 0.389, Adjusted R-squared: 0.144
| ||||
| ζ | Value | SE | t | p |
|---|---|---|---|---|
| Intercept | 0.00057 | 0.00233 | 0.244 | 0.817 |
| N (in hundreds) | 0.00004 | 0.00057 | 0.077 | 0.941 |
| Embedded | −0.00066 | 0.00171 | −0.388 | 0.714 |
| multiple R-Squared: 0.030, Adjusted R-squared: −0.358
| ||||
Discussion
Overlapping samples time delay embedding of a time series improves precision of parameter estimates in comparison to sampling short independent rows when the assumptions made in this article are met. There is a surprisingly large benefit to using the time delay embedding method, but there is a mathematical reason why this benefit appears. If one is interested in modeling intraindividual variability as a time dependent process then it appears to be a much better strategy to put effort into gathering a few more samples for a single longer time series than into gathering another independent row of data.
We expect that one beneficiary of this method will be models of intraindividual processes that are formulated as differential equations. Differential equations have long been considered as appropriate for social science data (Hotelling, 1927), but only recently have sufficient data and methods for estimation been available. There are now several ways to estimate the parameters of differential equations such as Equation 36. We expect that the result presented in the current article may improve power in some of these methods. For instance, functional data analysis (Ramsay, Hooker, Campbell, & Cao, 2007) and the approximate discrete method (Oud & Jansen, 2000) are candidate estimation methods that might exhibit improved power when using overlapping samples time delay data matrices.
We caution that overlapping samples time delay embedding is a tool that, like any statistical tool, could lead to poor results when assumptions are violated. In our simulations we assumed that (a) we are interested in modeling fluctuations about an equilibrium and not growth from a known zero point, (b) the model parameters were invariant over time, (c) the error was homogeneous and uncorrelated over time, and (d) the models were linear change and linear oscillators. Our results show that the time delay embedding method has no advantage when the initial conditions are known and do not need to be estimated. However, more work needs to be done in order to find out whether the other three assumptions are actually necessary and how robust the advantage of overlapping samples time delay might be if the assumptions are violated.
Furthermore, we caution that one should not assume that it is always a better strategy to put one’s money and effort into sampling a longer time series than to gather more independent rows of data. For instance, suppose one is interested in how short–term regulation changes over the long term, e.g., how emotional regulation changes as we age. In this case, one must carefully weigh the power requirements for detecting time–related change in the short–term regulatory coefficients. More reliable estimates of the coefficients will help, indicating more observations within a independent row; but longer intervals between independent rows will also improve ones chance of detecting time–related change in the regulatory coefficients. Additional work needs to be done in order to integrate multilevel power calculations (e.g., Snijders & Bosker, 1999) with power calculations for overlapping samples time delay embedding.
In conclusion, we found much to recommend overlapping samples time delay embedding as a method for improving precision of parameter estimates for models of intraindividual processes in relatively short and noisy time series such as are commonly seen in social science data. We have found that this advantage holds in the case of linear change and for a linear oscillator. Other models for intraindividual process may also benefit from this method, but we have not yet shown that the advantage holds in general. The advantage of time delay embedding does not appear to depend on the estimation method used, thus many methods for estimation may be able to take advantage of this data structuring technique. When applied in situations where the assumptions made in the present article are satisfied, we recommend considering time delay embedding prior to estimation of parameters.
Acknowledgments
Funding for this work was provided in part by NSF Grant BCS–0527485 and NIH Grant 1R21DA024304–01. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation or the National Institutes of Health.
Contributor Information
Timo von Oertzen, Center for Lifespan Psychology, Max Planck Institute for Human Development Berlin, Germany.
Steven M. Boker, Department of Psychology, The University of Virginia, Charlottesville, VA 22903
References
- Abarbanel HDI. Analysis of observed chaotic data. New York: Springer–Verlag; 1996. [Google Scholar]
- Baltes PB, Reese HW, Nesselroade JR. Life–span developmental psychology: Introduction to research methods. Monterey, CA: Brooks/Cole; 1977. [Google Scholar]
- Bisconti TL, Bergeman CS, Boker SM. Social support as a predictor of variability: An examination of the adjustment trajectories of recent widows. Psychology and Aging. 2006;21(3):590–599. doi: 10.1037/0882-7974.21.3.590. [DOI] [PubMed] [Google Scholar]
- Boker SM, Neale MC, Rausch J. Latent differential equation modeling with multivariate multi-occasion indicators. In: van Montfort K, Oud H, Satorra A, editors. Recent developments on structural equation models: Theory and applications. Dordrecht, Netherlands: Kluwer Academic Publishers; 2004. pp. 151–174. [Google Scholar]
- Butner J, Amazeen PG, Mulvey GM. Multilevel modeling to two cyclical processes: Extending differential structural equation modeling to nonlinear coupled systems. Psychological Methods. 2005;10(2):159–177. doi: 10.1037/1082-989X.10.2.159. [DOI] [PubMed] [Google Scholar]
- Chow SM, Ram N, Boker SM, Fujita F, Clore G. Capturing weekly fluctuation in emotion using a latent differential structural approach. Emotion. 2005;5(2):208–225. doi: 10.1037/1528-3542.5.2.208. [DOI] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum; 1988. [Google Scholar]
- Deboeck PR, Boker SM, Bergeman CS. Modeling individual damped linear oscillator processes with differential equations: Using surrogate data analysis to estimate the smoothing parameter. Multivariate Behavioral Research doi: 10.1080/00273170802490616. in press. ??(??), ?? [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grassberger P, Procaccia I. Measuring the strangeness of strange attractors. Physica D. 1983;9:189–208. [Google Scholar]
- Hotelling H. Differential equations subject to error, and population estimates. Journal of the American Statistical Association. 1927;22(159):283–314. [Google Scholar]
- Hox JJ. Multilevel analysis: Techniques and applications. Mahwah, NJ: Lawrence Erlbaum Associates; 2002. [Google Scholar]
- Kantz H, Schreiber T. Nonlinear time series analysis. Cambridge: Cambridge University Press; 1997. [Google Scholar]
- McArdle JJ, McDonald RP. Some algebraic properties of the Reticular Action Model for moment structures. British Journal of Mathematical and Statistical Psychology. 1984;87:234–251. doi: 10.1111/j.2044-8317.1984.tb00802.x. [DOI] [PubMed] [Google Scholar]
- Neale MC, Boker SM, Xie G, Maes HH. Mx: Statistical modeling. 6 VCU Box 900126, Richmond, VA 23298: Department of Psychiatry; 2003. [Google Scholar]
- Nesselroade JR. The warp and woof of the developmental fabric. In: Downs R, Liben L, Palermo DS, editors. Visions of aesthetics, the environment, and development: The legacy of Joachim F Wohlwill. Hillsdale, NJ: Lawrence Erlbaum Associates; 1991. pp. 213–240. [Google Scholar]
- Nesselroade JR, Ram N. Studying intraindividual variability: What we have learned that will help us understand lives in context. Research in Human Development. 2004;1(1 & 2):9–29. [Google Scholar]
- Oud JHL, Jansen RARG. Continuous time state space modeling of panel data by means of SEM. Psychometrica. 2000;65(2):199–215. [Google Scholar]
- Pinheiro JC, Bates DM. Mixed–Effects Models in S and S–Plus. New York: Springer–Verlag; 2000. [Google Scholar]
- Ramsay JO, Hooker G, Campbell D, Cao J. Parameter estimation for differential equations: A generalized smoothing approach. Journal of the Royal Statistical Society B. 2007;69(5):774–796. [Google Scholar]
- Sauer T, Yorke J, Casdagli M. Embedology. Journal of Statistical Physics. 1991;65(3,4):95–116. [Google Scholar]
- Shannon CE, Weaver W. The mathematical theory of communication. Urbana: The University of Illinois Press; 1949. [Google Scholar]
- Snijders TAB, Bosker RJ. Multilevel analysis : an introduction to basic and advanced multilevel modeling. Newbury Park, CA: Sage Publications; 1999. [Google Scholar]
- Takens F. Detecting strange attractors in turbulence. In: Dold A, Eckman B, editors. Lecture notes in mathematics 1125: Dynamical systems and bifurcations. Berlin: Springer–Verlag; 1985. pp. 99–106. [Google Scholar]
- Whitney H. Differentiable manifolds. Annals of Mathematics. 1936;37:645–680. [Google Scholar]