Broad Conditions Favor the Evolution of Phase-Variable Loci

ABSTRACT

Simple sequence repeat (SSR) tracts produce stochastic on-off switching, or phase variation, in the expression of a panoply of surface molecules in many bacterial commensals and pathogens. A change to the number of repeats in a tract may alter the phase of the translational reading frame, which toggles the on-off state of the switch. Here, we construct an in silico SSR locus with mutational dynamics calibrated to those of the Haemophilus influenzae mod locus. We simulate its evolution in a regimen of two alternating environments, simultaneously varying the selection coefficient, s, and the epoch length, T. Some recent work in a simpler (two-locus) model suggested that stochastic switching in a regimen of two alternating environments may be evolutionarily favored only if the selection coefficients in the two environments are nearly equal (“symmetric”) or selection is very strong. This finding was puzzling, as it greatly restricted the conditions under which stochastic switching might evolve. Instead, we find agreement with other recent theoretical work, observing selective utility for stochastic switching if the product sT is large enough for the favored state to nearly fix in both environments. Symmetry is required neither in s nor in sT. Because we simulate finite populations and use a detailed model of the SSR locus, we are also able to examine the impact of population size and of several SSR locus parameters. Our results indicate that conditions favoring evolution and maintenance of SSR loci in bacteria are quite broad.

IMPORTANCE

Bacteria experience frequent changes of environment during the infection cycle. One means to rapidly adapt is stochastic switching: a bacterial lineage will stochastically produce a variety of genotypes, so that some descendants will survive if the environment changes. Stochastic switching mediated by simple sequence repeat (SSR) loci is widespread among bacterial commensals and pathogens and influences critical interactions with host surfaces or immune effectors, thereby affecting host persistence, transmission, and virulence. Here, we use the most detailed in silico model of an SSR locus to date, with its phase variation calibrated to match the mod locus of Haemophilus influenzae. The type III restriction-modification system encoded by mod participates in the regulation of multiple other genes; thus, SSR-mediated phase variation of mod has far-reaching cis-regulatory effects. This coupling of phase-variable switching to complex phenotypic effects has been described as the “phasevarion” and is central to understanding the infection cycle of bacterial commensals and pathogens.

Introduction

Simple sequence repeat (SSR) loci in bacteria. During the infection cycle, as bacteria migrate between hosts and within a single host, they experience changes of environment. Bacterial surface molecules influence many interactions between the bacterium and the host environment. Selection for and against the production of such molecules can be strong and can vary in time depending on many factors, including the state of the host immune system, the location of the bacterium within the host, the prevalence and specificity of bacteriophages, and whether the bacterium is transitioning between two hosts.

One means for a bacterium to produce a suitable phenotype in a changing environment is to maintain a sensory apparatus and to regulate the phenotype within the lifespan of one bacterial individual. However, sensing and regulation can be expensive and complex. An alternatively evolutionary strategy is to eschew sensing and to blindly generate a variety of descendant genotypes; the descendants as a whole will thereby be prepared to survive in a variety of contingent environments. This strategy is called stochastic switching or phase variation.

Simple sequence repeat (SSR) tracts are a major mechanism of stochastic switching in bacterial commensals and pathogens such as Escherichia coli, Salmonella enterica, Campylobacter pylori, Neisseria meningitidis, Mycoplasma pneumoniae, and Bacteroides fragilis (1–3). In an SSR tract, a short unit of several (e.g., 4) nucleotides is repeated multiple times in the DNA sequence. During DNA replication, the process of slipped-strand mispairing can change the number of repeated units at a particular locus; this, in turn, can cause a shift of the downstream reading frame, resulting in incorrect translation, and effectively “switching off” the downstream gene. Mutations of this type are frequent and reversible, leading to rapid, stochastic on-off switching of expression of the gene and the associated phenotype. Such loci may produce, as standing variation, high frequencies (10⁻² to 10⁻⁵) of mutants/variants prior to the appearance of the selective pressure; such populations may thus be “primed” for rapid adaptation (4).

Measurements of mutation rates for the tetranucleotide repeat tracts of Haemophilus influenzae indicate that mutability increases proportionally with tract length (5); this has also been shown in Neisseria (6, 7). Thus, the length of the tract simultaneously encodes not only the switch state (on or off) but also its rate of switching. This suggests that SSR loci may serve as a mechanism by which bacteria can effect a genetic stochastic switch with an evolvable switching rate.

Most of the genes subject to SSR-mediated phase variation encode surface molecules, enzymes for biosynthesis or modification of surface molecules, or restriction-modification systems. They are, therefore, possible candidates for fluctuating selection as bacteria move between hosts, or within a host, during the infection cycle. Here, we calibrate our computational model of an SSR locus to the mod gene of H. influenzae. mod is an interesting family of genes because it is involved in type III restriction-modification systems, and its phase variation is now known to control the expression of multiple other genes associated with virulence, transport surface-exposed proteins, and heat shock proteins in H. influenzae and other pathogens (8). Some authors have called this novel genetic regulation system the “phase-variable regulon” or the “phasevarion” (8).

Theoretical work on stochastic switching. How are SSR loci expected to evolve? Most theoretical work on stochastic switching in asexual clonal populations has not considered the full complexity of the SSR locus, in which alleles of many tract lengths may coexist in a population. Instead, a simpler switching mechanism has been studied: a two-locus mechanism, comprising a major locus with two alleles, A and a, and a mutator locus that controls the rate of mutation at the major locus. Typically, the environment is assumed to alternate, at period T, between two states, one favoring allele A and the other favoring a. The mutator locus is not directly selected, but its alleles may be selected indirectly via their linkage to alleles of the major locus.

Assuming symmetry in the mutation rates from A to a and back, Leigh (9) and Ishii et al. (10) found via analytical methods that the optimal mutation rate (μ_ess) was approximately equal to 1/T. Palmer and Lipsitch (11) used computer models to show that the selection coefficient (s) must be strong enough, and the epochs (of length T) long enough, for a sufficiently complete reversal of the frequencies of A and a (i.e., near-fixation of the favored allele) to occur during each environmental epoch: a nonminimal (far from zero) mutation rate could evolve only if the product sT was above a certain threshold.

Kussell and Leibler (12) generalized from the case of two environments to multiple environments. They assumed that the environmental epochs were long enough to reach mutation-selection balance; this produces near-fixation of the favored allele before the end of each epoch. (As we discuss below, this is equivalent to assuming that sT is large in each environment.) In this case, they found the optimal switching rate from phenotype j to i to be proportional to the probability that the environment changes from environment j to i and inversely proportional to the average duration of environment j.

Salathé et al. (13) studied the two-locus model with computer methods but allowed the selection coefficients associated with each environment (s₀ and s₁, respectively) to be unequal. If the selection coefficients were unequal enough (which they called “asymmetric fitness”), they reported that a mutation rate approaching zero was favored, unless selection was very strong. In the case of asymmetry and weak selection, the genotype that is favored over the long term consists of, at the mutator locus, the available allele with the lowest mutation rate and, at the major locus, the allele associated with the higher selection coefficient (s₀ or s₁). Switching essentially stops, and the population essentially fixes for a constant phenotype. Notably, this finding made it difficult to envision how nonzero mutation rates could evolve in SSR loci in bacteria, since close symmetry between s₀ and s₁ could not be expected to be common in nature (and very strong selection would be required otherwise).

So far, we have discussed the two-locus model; this simple abstraction of the molecular mechanics of real genetic loci was designed to enable easy analysis and simulation. More mechanistically accurate versions of SSR loci have also been studied. Zhivotovsky and Feldman (14) analyzed the dynamics of variation of SSR loci with stepwise mutations, but they were concerned with neutral variation and therefore did not include selection in their model. Saunders et al. (15) considered an SSR locus with differential on-to-off and off-to-on switching rates and did include selection but did not explicitly model the lengths of the repeat tracts.

In this article, we present computer simulations of the evolution of a realistic model of SSR loci. An individual in our model possesses one SSR locus, and we explicitly follow the tract length of each individual in a finite population, evolving under various selective regimens. We use a realistic model of the transitions from one tract length to another, calibrating them to in vitro measurements of mutation rates and mutational patterns of the mod gene of H. influenzae (5). The realism of our model, and its inclusion of experimentally derived mutational parameters, is unique. It is also adaptable to other SSR loci for which the mutational parameters are known.

By simultaneously varying the selection coefficients (s₀ and s₁) and the mean epoch durations (T₀ and T₁), we determine that the result of Salathé et al. (13) was incomplete: the statement of Salathé et al. that switching (a nonzero mutation rate) may evolve when s₀ and s₁ are both large is actually a reflection of the more general requirement that s₀T₀ and s₁T₁ both be large. Gaál et al. (16), using analytical methods, independently arrived at a similar result for the two-locus model. Neither symmetry in s₀ and s₁ nor symmetry in T₀ and T₁ is required. This finding significantly broadens the opportunity for stochastic switching to evolve: selection (s₀ or s₁) need not be extremely strong; it can instead be applied for a longer time (higher T₀ and/or T₁), as long as the products s₀T₀ and s₁T₁ are both large. These products must each be large enough for the favored state (on or off) to nearly fix in each epoch. (If symmetry in s₀T₀ and s₁T₁ does happen to be present, it lowers the required threshold for switching to evolve.)

In addition, our results demonstrate that, despite its significantly more complex internal mechanics, a realistically modeled SSR locus shows evolutionary behavior similar to that of the simpler, classically studied, two-locus model.

RESULTS

SSR locus model.

Our population-genetic computer simulation models individual bacteria possessing a single SSR locus. The genotype of an individual is fully described by L, the number of tetranucleotide repeats present at this locus. Because DNA codons are triplets, the addition or deletion of tetranucleotide units upstream of a reading frame may change its “phase”; out-of-phase reading frames are incorrectly translated, which effectively switches them off. We compute the phase of a locus of length L as P = (4 × L) % 3 (where “%” indicates the modulo operator). In order to match the mod locus of H. influenzae, we assumed that if P = 2, the presumptive downstream gene is in phase and is correctly translated, or on; otherwise, it is out of phase and thus incorrectly translated, or off. There are twice as many off states as on states: for example, L = 17 is on, L = 18 and L = 19 are off, L = 20 is on, L = 21 and L = 22 are off, etc. We permitted L to take values between 11 and 61 inclusive (51 possible values).

Calibration of the SSR locus model to data from the H. influenzae mod locus.

In nature, slipped-strand mispairing during DNA replication can cause the number of a repeats at a locus to decrease or increase, at a certain rate and in a certain pattern. We calibrated our simulated SSR locus model to match the length change patterns observed in living bacteria, from experimental analysis by De Bolle et al. (5, 17) of the H. influenzae mod gene. These studies used reporter constructs and constructs containing tracts of between 17 and 38 5′ AGTC repeats. The mod gene contains a single functional initiation codon with high-level expression resulting in switching between one on frame and two off frames. An approximately linear relationship was observed between the mutation rate (chance of any length change) and the tract length at this locus. The mutation rate was well approximated by μ = aL + b with linear fit parameters determined to be a = 2 × 10⁻⁵ and b = −2 × 10⁻⁴ (17), where L is the tract length.

De Bolle et al. (5) also reported the distribution of length change events of different sizes. Table 1 reproduces a portion of their data, showing counts of observed length changes of particular sizes, for on-to-off phenotypic switches. A total of 63 length change events of between +2 and −4 repeat units are shown. From these data, we derive the “mutation kernel” used in our simulated SSR model, which permits length changes from +2 units to −4 units to occur and is given in Table 2. See Materials and Methods for additional details on how Table 2 was derived from Table 1.

TABLE 1 .

Length changes observed in 5′-AGTC tetranucleotide repeat tracts in the mod locus of H. influenzae, on-to-off transitions only^a

Length change	No. of 5′-repeat units deleted or inserted
	Deletions			Insertions
	<−2	−2	−1	+1	+2	>+2
Length 38	1		4	2	1
Length 32		1	12	9
Length 23			9	4	1
Length 17	1	3	11	3	1
Total	2	4	36	18	3	0

^a Data reproduced from reference 5.

TABLE 2 .

Mutation kernel for our model specifying the distribution of length change events of different sizes, derived from the data in Table 1^a

Length change	No. of 5′-repeat units deleted or inserted
	Deletions				No change	Insertions
	−4	−3	−2	−1	0	+1	+2
Probability	μ × 2/66	μ × 3/66	μ × 4/66	μ × 36/66	1 − μ	μ × 18/66	μ × 3/66

^aThe chance of any mutation occurring is μ = aL + b. Length changes from −4 to +2 repeat units occur with the probabilities shown.

Selection model.

Most of the SSR loci of H. influenzae mediate switching between two states, on and off. Each of these states may engender a selective advantage in different environments, which may refer to conditions in different hosts, in different physical locations within one host, or in the same physical location in one host but at different times. Therefore, in the simulations shown here, we permit two possible environmental states: E₀ favors the on switch state, and E₁ favors the off switch state. The environments strictly alternate in time. Each E₀ “epoch” persists for T₀ generations, and each E₁ epoch persists for T₁ generations. (See also Fig. 1 at http://www.mepalmer.net/supplementary/mbio/palmer-mbio-supp.pdf, in which we explore the effect of geometrically distributed epoch lengths, with means of T₀ and T₁, respectively.) In environment E₀, the on state is favored: on genotypes receive a raw fitness of 1, and off genotypes receive a raw fitness of 1 − s₀. In environment E₁, off is favored: off genotypes receive a raw fitness of 1 and on genotypes receive a raw fitness of 1 − s₁. The parameters T₀, T₁, s₀, and s₁ are fixed during a simulation run.

FIG 1 .

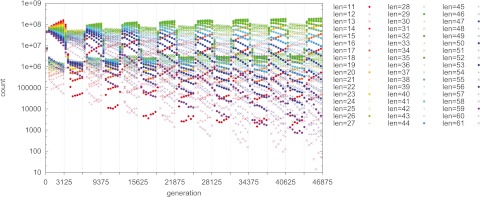
Counts of the 51 genotypes over 46,875 generations, with symmetric T and symmetric s. Environmental changes are marked by vertical lines; a period of T₀ = T₁ = 3,125 generations favors a length of 26 over the long term. Points are plotted every 400 generations. On state, filled circles (P = 2). Off state, plus (P = 0) or multiplication (P = 1) signs. Note that the on state (filled circles) successfully fixes in every E₀ (odd-numbered) epoch, whereas the off state (plus or multiplication sign) fixes in every E₁ (even-numbered) epoch. s₀ = s₁ = 0.01 (s₀T₀ = s₁T₁ = 31.25); n = 10⁹.

A simple case: symmetric selection and symmetric mean epoch length.

In the simulations shown here, we place n = 1 × 10⁹ individuals with a single SSR locus into one panmictic population. The simplest case possesses symmetric epoch lengths (T₀ = T₁) and symmetric selective advantage for the favored expression state in each environment (s₀ = s₁). Figure 1 shows a single simulation run of 46,875 generations for this simple case. We plot the counts of the 51 possible genotypes (tract lengths) at intervals of 400 generations, for clarity (although every generation is explicitly simulated). Filled circles indicate on genotypes; plus signs and multiplication signs indicate off genotypes. At generation 0, all 51 genotypes are present in equal numbers. In this example, T₀ = T₁ = 3,125 generations; thus, there is an environmental switch every 3,125 generations. Environment E₀ is imposed during the first epoch, and the environments strictly alternate. In the figure, on genotypes (filled circles) increase in number during the E₀ epochs (which favor on), and off genotypes (plus or multiplication signs) increase during the E₁ epochs (which favor off). After 15 environmental epochs, the first and last each being an E₀ epoch, the genotype with L = 26 has the highest count. This genotype has a “mutation rate” (frequency of length change) of μ = [(2 × 10⁻⁵) × 26] − (2 × 10⁻⁴) = 0.00032, which is approximately equal to 1/3,125. Thus, in this example, the winning strain has a mutation rate of approximately 1/T, matching the classical two-locus prediction (9, 10). (This simple prediction does not hold in all cases; see below.)

High sT in both environments favors a nonminimal mutation rate; symmetric selection is not required.

Because exactly symmetric fitness advantages for the on and off states are unlikely during the natural infection cycle, Salathé et al. (13) studied the case of “asymmetric” fitness in the simpler, “two-locus” model (comprising a mutator locus and a major locus possessing two alternative alleles, A and a). They concluded that if the selection coefficients associated with each environment (s₀ and s₁, respectively) were unequal (“asymmetric”) enough, and not very high, a minimal mutation rate (i.e., a mutation rate approaching zero) would be favored in the long term.

When epoch lengths are symmetric (T₀ = T₁ = T), for moderate values of T, we found agreement with the work of Salathé et al. in the SSR model: that the strain with the minimal (i.e., the lowest available) mutation rate will dominate in the long term, unless selection is symmetric (s₀ = s₁) or selection in both environments is very strong. However, upon further investigation, we found that the important condition, for more general T₀ and T₁, is not whether s₀ and s₁ are symmetric. Rather, the important condition is that both s₀T₀ and s₁T₁ be large enough for a fixation of the favored state (on or off) to occur in each epoch. This requirement has also been observed in exact analysis of the two-locus model (16).

For example, in Fig. 1, note that shortly after each environmental switch, a near-complete fixation of the favored switch state—on (filled circles) or off (plus or multiplication signs)—occurs. This is due to the fact that the product of s and T is high in each environment: selection is strong enough, and the epochs long enough, that fixation of the favored state is reached in every epoch.

If sT is low in a single environment, a minimal mutation rate is favored.

In contrast to Fig. 1, if we sufficiently decrease any one of s₀, s₁, T₀, or T₁, fixation of the favored state (on or off) will not complete in one type of epoch (E₀ or E₁), and this will cause a minimal mutation rate to evolve. Figure 2 replicates the conditions in Fig. 1, except that we reduce the value of s₁ from 0.01 to 0.001. This change makes s₁T₁ too weak for the off (plus and multiplication sign) strains to sufficiently gain on the on (filled circle) strains during the E₁ epochs. Therefore, strains that remain in the on state more of the time are favored overall; this favors a minimal mutation rate (along with fixation of the on state). The strain with L = 11 has the lowest mutation rate of all the on strains and is the numerical winner by the end of the run.

FIG 2 .

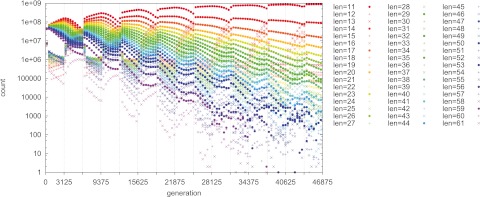
s₁T₁ is too small for the selective sweeps to complete in the E₁ (even-numbered) epochs. The strategy of remaining on without switching is optimal; this favors a minimal mutation rate. T₀ = T₁ = 3,125; s₀ = 0.01; s₁ = 0.001 (s₀T₀ = 31.25, s₁T₁ = 3.125); n = 10⁹.

Because the L = 12 and L = 13 strains are readily derived by mutation from the L = 11 strain, they are the most common two off strains. Moreover, other short-length on strains, e.g., L = 14 and L = 17, remain common. Thus, a “cloud” of lengths is maintained about the favored length. The distribution of lengths in this cloud is dictated by a mutation-selection-drift balance.

The reduction of s₁ from 0.01 (as in Fig. 1) to 0.001 (as in Fig. 2) causes s₁T₁ to decrease from 31.25 to 3.125. We show below that the critical threshold producing near-fixation in the favored allele in each epoch is approximately sT = 7 (measured empirically). Thus, since s₁T₁ is below the threshold in Fig. 2, a minimal mutation rate is favored.

The situation in Fig. 2 can be reversed so that off variants are dominant, by setting s₀, instead of s₁, too low (not shown). However, the qualitative result is similar: low-mutation-rate strains dominate because the population adapts fully to only one of the two alternating environments (E₁ in this case). Decreasing either T₀ or T₁ sufficiently (not shown) also leads to a similar result.

If sT is low but symmetric, a nonminimal mutation rate can still be favored.

When s₀T₀ and s₁T₁ are both low, fixations of the preferred state do not occur in either type of epoch (E₀ or E₁). Nonetheless, if there is symmetry in sT (i.e., if s₀T₀ = s₁T₁), then a nonminimal mutation rate can still be favored. (This is analogous to the effect at low but symmetric s found by Salathé et al. [13] in the two-locus model.) An example is shown in Fig. 3. In the figure, T₀ = T₁ = 3,125 and s₀ = s₁ = 0.001; thus, s₀T₀ = s₁T₁ = 3.125, which is below our empirically measured requirement of sT > 7 in both environments. The switching behavior in Fig. 3 is visibly sluggish compared to that in Fig. 1 (where selection is stronger, producing s₀T₀ = s₁T₁ = 31.25). Nonetheless, because s₀T₀ = s₁T₁, a nonminimal mutation rate is also favored in Fig. 3.

FIG 3 .

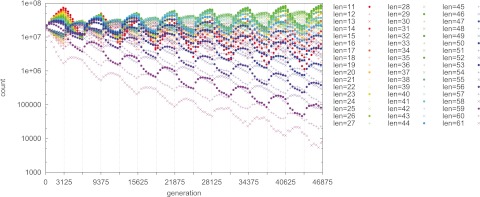
Even though s₀T₀ and s₁T₁ are both too low to produce a complete fixation (to equilibrium) of the favored state in each epoch, a nonminimal mutation rate is favored because of the exact symmetry in sT. T₀ = T₁ = 3,125; s₀ = s₁ = 0.001 (s₀T₀ = s₁T₁ = 3.125); n = 10⁹.

Figure 3 may also be compared to Fig. 2. In both figures, T₀ = T₁ = 3,125. However, in Fig. 2, s₀ is stronger than in Fig. 3; this asymmetry in s₀ and s₁ favors a minimal mutation rate in Fig. 2. When switches are incomplete (i.e., when sT is low) in one environment, as in the E₁ epochs of Fig. 2, there is nonergodicity (a “memory effect”) across epochs, producing a gradually accruing advantage to the on state (and therefore favoring a minimal mutation rate in the long term). However, in Fig. 3, although nonergodicity is possible, the fitness values and epoch lengths are exactly symmetric; thus, neither the on nor the off state accrues a long-term advantage, and a nonminimal mutation rate can still be favored.

A broad range of conditions favors nonminimal mutation rates.

As described above, there is a broad range of conditions in which nonminimal mutation rates are favored, and there are two distinct cases: (i) if sT is high enough in each environment and (ii) if sT is low but symmetric in the two environments. In order to illustrate the full range of such conditions, we conducted a large set of runs, varying all of s₀, s₁, T₀, and T₁. Specifically, we examined all combinations where s₀ and s₁ each assumed one of four possible values (0.0001, 0.001, 0.01, and 0.1) and T₀ and T₁ each assumed one of 10 possible values (12,500, 7,143, 5,000, 3,846, 3,125, 2,273, 1,786, 1,471, 1,250, and 1,163). This was a total of 4 × 4 × 10 × 10 = 1,600 combinations. (See Materials and Methods for how these T values were selected.)

For each combination of the parameters (s₀, s₁, T₀, and T), we conducted 20 replicate runs, each with a different random seed (which causes different stochastic mutation and selection events to be produced in each replicate). Each run was of 25 epochs in duration (13 epochs of E₀, alternating with 12 epochs of E₁). We determined L_win, the average long-term “winning” length (i.e., in one replicate, the “winner” is the length with the highest count at the end of the last epoch).

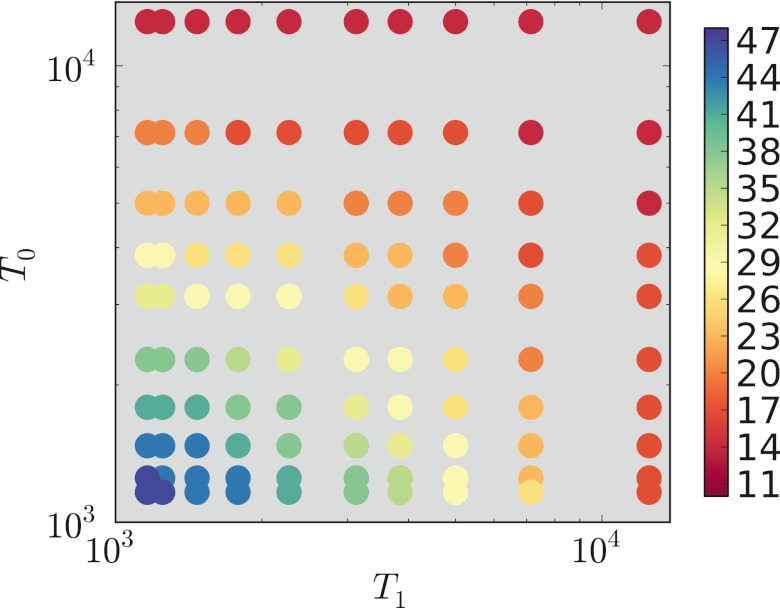
In Fig. 4, we plot L_win for the 100 (T₀, T₁) pairs for the symmetric selection case of s₀ = s₁ = 0.1. We make the qualitative remark that when both T₀ and T₁ are high, shorter lengths win, and when they are both low, longer lengths win. Note that selection is very strong, so we expect complete switching between the favored states for all T₀ and T₁; thus, Fig. 4 shows a subset of the parameter space in which switching is complete.

FIG 4 .

The color of each spot indicates the average (over 20 replicate runs) winning length, L_win, for the indicated T₀ and T₁. A subset of the runs with symmetric selection is shown: s₀ = s₁ = 0.1; n = 10⁹.

Comparison to the classical model: μ_ess = 1/T.

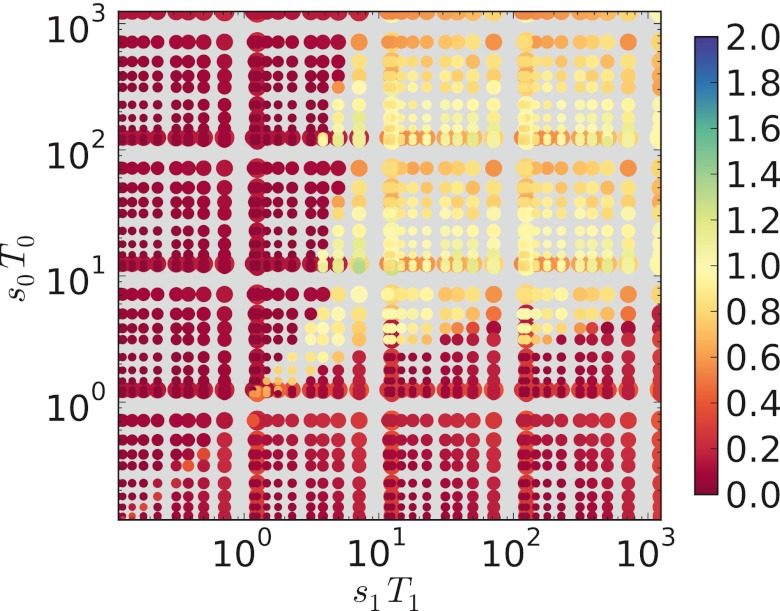
To show the behavior over the full range of parameters, we will compare the evolved mutation rate to the mutation rate predicted in the classical two-locus model, namely, μ_ess = 1/T, for symmetric T and strong selection (9, 10). We use this simple prediction to emphasize the importance of the product sT, by comparing how much the empirically evolved mutation rate is depressed or elevated from the classically predicted μ_ess. Call the average “winning” (i.e., the most frequent in the long term) length, L_win, as plotted in Fig. 4. The corresponding winning mutation rate is μ_win = aL_win + b. We take the value T_avg = (T₀ + T₁)/2 and compute the classically predicted mutation rate μ_avg = 1/T_avg, as if the (single) period length were equal to T_avg. In Fig. 5, we plot the ratio μ_win/μ_avg; this is a measure of how much the winning mutation rate is decreased or increased from what might be expected in the classical model with a period of T_avg, and in every case, this ratio turns out to be between 0 and 2. In Fig. 5, colors near the middle of the color bar (yellow) indicate a μ_win/μ_avg ratio near 1.0, indicating that μ_win is near μ_avg, the expectation from the classical model. Red and orange colors indicate a depressed mutation rate, while green and blue colors indicate an elevated mutation rate, relative to this prediction.

FIG 5 .

Each of the 1,600 combinations of s₀, s₁, T₀, and T is plotted as a circle centered at the point (s₀T₀, s₁T₁.) The ratio μ_win/μ_avg is indicated by the color of the circles, where μ_win = aL_win + b and μ_avg = 2/(T₀ + T₁). This ratio measures how much the “winning” mutation rate is increased/decreased from the classical expectation for T = T_avg = (T₀ + T₁)/2. The circle size is proportional to T_avg so that overlapping (s₀T₀, s₁T₁) points can be distinguished. μ_avg is a good estimate of μ_win (points are yellowish) when s₀T₀ > 7 and s₁T₁ > 7, conditions under which the favored state will proceed to fixation (to equilibrium) in each epoch. n = 10⁹.

Generally, if s₀T₀ and s₁T₁ are both large enough (greater than or equal to approximately 7), μ_win is near μ_avg (circle colors are near-yellow). Thus, symmetry in sT is not required, as long as sT is large enough in each type of epoch (E₀ and E₁). In every individual epoch in which sT is large enough, the favored allele at the major locus attains near-fixation. (An example of this was shown in Fig. 1, above.) If sT is at least this large in one epoch and (asymmetrically) much larger in another epoch, this essentially does not change the evolved mutation rate. In contrast, for slightly lower sT (e.g., between 1 and 7), μ_avg is a good predictor of μ_win (near-yellow points) only if sT is nearly symmetric (i.e., s₀T₀ = s₁T₁). In this case, the frequencies of on and off individuals do not fluctuate between near-fixation and near-absence; rather, more modest swings of frequency occur (an example of this was shown in Fig. 3, above), due to the shortness of the epochs and/or the weakness of selection. This gentle fluctuation in frequency is possible only if sT is symmetric; if not, then the state associated with higher sT gradually increases in frequency over many epochs, a nonergodic effect across epochs (as in Fig. 2, above), and a minimal mutation rate is favored. In a few regions of Fig. 5, the plotted values slightly exceed 1 (greenish points), indicating that μ_avg is an underestimate; we do not seek any particular explanation for this, since μ_avg reflects only a simple model of how we might expect μ_win to behave.

In summary, Fig. 5 shows that for a wide range of s and T values (all points that are not dark red), it will be evolutionarily favored to possess an SSR locus with a nonminimal, evolutionarily adjustable mutation rate. It is required that s₀T₀ and s₁T₁ both be large enough (greater than or equal to about 7, for the particular locus parameters defined in Materials and Methods) or that s₀T₀ and s₁T₁ be symmetric. Finally, the figure demonstrates empirically that μ_avg = 1/T_avg, where T_avg = (T₀ + T₁)/2, is a simple “rule-of-thumb” estimate of the favored mutation rate, in the complete-switching case, as has also been shown for the two-locus model by Gaál et al. (16).

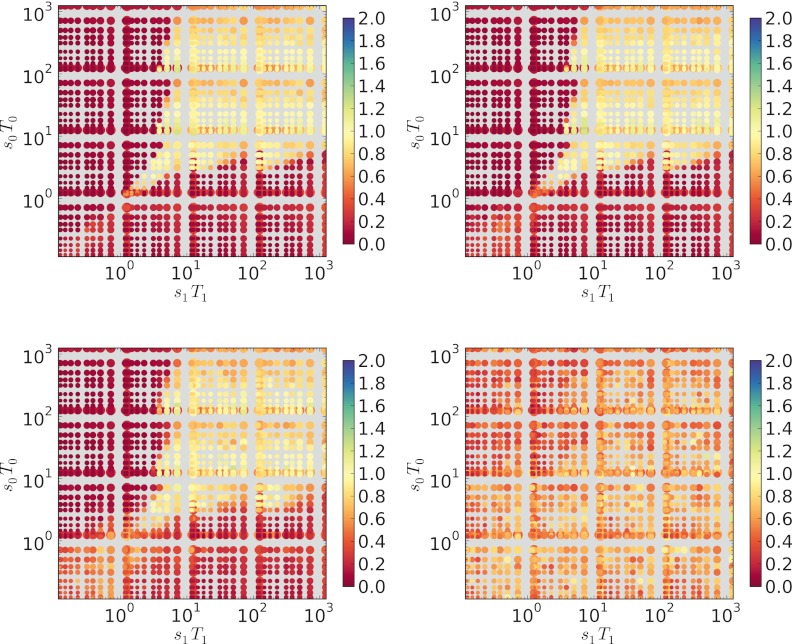
The sT threshold holds for a wide range of population sizes.

The analysis by Gaál et al. (16) assumed infinite populations. Here, we model finite populations and can examine the effect of population size on the evolved mutation rate. We conducted experiments similar to those shown in Fig. 5 but with lower population sizes. In Fig. 6, population sizes of 10⁷, 10⁶, 10⁵, and 10⁴ (from top left to bottom right) are plotted. Notably, population size does not affect the required threshold for sT (i.e., sT ≥ 7) until the population becomes quite low (~10⁴). At this point, drift becomes strong, and the standard deviation in the winning length (data not shown, but see Fig. 2 at http://www.mepalmer.net/supplementary/mbio/palmer-mbio-supp.pdf) becomes large. It is not clear how the effective population sizes of pathogenic bacteria may vary over time in vivo, but our simulations indicate that the population size, if held constant during each epoch, is not a strong determinant of the sT threshold value.

FIG 6 .

The threshold of sT > 7 does not vary with population size, until the population size becomes low (n ~ 10⁴), at which point drift becomes strong, and the standard deviation in the winning length (data not shown, but see Fig. 2 at http://www.mepalmer.net/supplementary/mbio/palmer-mbio-supp.pdf) becomes large. From top left to bottom right, n = 10⁷, n = 10⁶, n = 10⁵, and n = 10⁴.

See also Fig. 3 to 5 at http://www.mepalmer.net/supplementary/mbio/palmer-mbio-supp.pdf, where we examine the effect on the sT threshold of several changes to the mutation kernel: (i) halving all mutation rates, (ii) doubling all mutation rates, and (iii) constraining the mutation kernel such that only changes of −2 to +2 are permitted. The sT threshold is robust to all of these changes.

DISCUSSION

The rapid generation of genetic and phenotypic variation in bacterial populations is widely recognized as having major importance for enabling bacteria to adapt to fluctuating environments. Phase variation mediated by mutations in SSR tracts is of particular interest because of its prevalence in the genes of important pathogens such as Neisseria meningitidis, Campylobacter jejuni, Helicobacter pylori, and Haemophilus influenzae. While our model utilizes experimental values from one specific locus, the principles are applicable to other SSR loci and to a general understanding of the evolution of mutation rates.

Ours is the most realistic model of an SSR locus of which we are aware. We explicitly follow the tract lengths possessed by individuals in a finite population; we have tuned the mutation kernel to match empirical measurements of an actual bacterial SSR locus; and we include fluctuating selection in our model, simultaneously varying the selection strength and epoch duration.

Using this computational model of the SSR locus, we independently discovered several results analogous to those of Gaál et al. (16), who used analytical methods in the two-locus model. First, for the case of complete switching, we find that when epoch lengths are symmetric (T = T₀ = T₁), evolved mutation rates approximately follow the rule μ_win = 1/T. Second, if epoch lengths are not symmetric, but we define T_avg = (T₀ + T₁)/2, then evolved mutation rates approximately follow μ_win = 1/T_avg. This estimate holds as long as the product sT is high enough in both environments; this corrects an inaccurate conclusion of the work of Salathé et al. (13), which stated that symmetry in s was required unless selection was very strong. Third, as sT decreases in both environments, symmetry in sT permits nonminimal mutation rates to evolve at lower sT values than is possible in the asymmetric case; an analogous result was also found by Salathé et al. (13). Finally, our threshold for “complete switching” measured empirically at approximately sT > 7 is close to the value that Gaál et al. determined analytically for the two-locus model: approximately sT > 5.1.

These results suggest that the parameter ranges in which SSR loci can evolve and persist are broad. The darkest red points in Fig. 5 represent regions of parameter space in which SSR loci would not be expected to evolve: a minimal mutation rate (no switch at all) is favored here. All other points (besides dark red) are where an SSR locus, were it to arise, might have a selective advantage. In addition, if s, or T, varies gradually over time, or among local groups of hosts, it could be advantageous for a population of bacteria to have the ability to evolutionarily tune its rate of switching to better match local and contemporaneous conditions. An SSR locus provides the ability to explore a range of switching rates over the long term.

Do observed SSR lengths match typical epoch lengths in bacteria, according to our model? Examination of multiple isolates from an outbreak (n = 20) and sporadic cases (n = 10) of disease found modal numbers for five SSR loci of between 20 and 40 repeats (2). Lengths of 20 to 40 would correspond to epoch durations of between 1,667 (for length 40) and 5,000 (for length 20) generations. Measurements in vitro indicate a doubling time of less than 1 h for H. influenzae in rich media and around 90 min in minimal media (18). Assuming an average in vivo generation time of 1 h, epoch lengths of 1,667 to 5,000 generations would correspond to T = 1.2 to 3.5 months. A possible scenario is for epochs of alternating selection within a single host. H. influenzae can promote inflammatory immune responses, and induction of inflammation is influenced by phase-variable epitopes (19, 20), suggesting that this bacterial species may be subject to alternating periods of low and high inflammatory responses during persistence in the nasopharynx. These two very different environments would impose differential selection pressures, producing two environmental epochs within a single host, followed by transmission to a new host. Some H. influenzae clones are known to persist in each host for periods of 3 to 7 months (21, 22). Thus, if we take 2T to be 3 to 7 months, that is indeed consistent with the tract lengths observed in reference 2. Careful epidemiological and genomic studies may be able to identify the selective pressures contributing to the evolution of specific ranges of tract lengths at specific loci.

MATERIALS AND METHODS

Details of the derivation of the mutation kernel from in vitro data.

In the data reproduced in Table 1, De Bolle et al. (5) report two deletion events of more than 2 units in magnitude; we make the assumption that both events were changes of −4 units. (A change of −4 units is the next most likely change corresponding to an on-to-off switch.) In addition, because De Bolle et al. were screening phenotypically for on-to-off switches to produce the data in Table 1, no length changes of −3 units (corresponding to an on-to-on switch) could be observed. In our mutation kernel (Table 2), we extrapolate from their data, making the assumption that three changes of −3 units would have occurred, unobserved. Thus, we assume that a total of 66 events occurred (the 63 on-to-off switches observed by De Bolle et al., plus three presumed on-to-on switches). If we make the reasonable assumption that the distribution of length change magnitudes is independent of the on or off state of the switch, then the mutation kernel shown in Table 2 should be an equally accurate model of length change events starting from the off state.

Note that the on-to-off switching rate implied by Table 2 is almost equal to μ, because if a particular length is in the on state, and a length change occurs (at rate μ), then most permitted length changes alter the state to off, producing an on-to-off switch; only a length change of −3 (at a probability of 3/66 or 4.5%) maintains the on state. The off-to-on switching rate is more complex to compute, but for simplicity, one may consider the off-to-on rate to be ~0.5μ on average.

Population genetic model.

In the simulations shown here, the population size is fixed (n = 1 × 10⁹ for most simulations). It would be computationally expensive to track so many individuals explicitly. Instead, since there are only L_num = 51 possible alleles, we track, at different points in a generation, either counts or frequencies of the L_num genotypes. This is much more efficient and yields an equivalent result. The cycle to advance the counts of each genotype by a single generation proceeds as follows.

(i) Conversion to frequencies.

Each generation begins with an integer count of each genotype. These counts are converted to a set of genotype frequencies by dividing by the total number of individuals.

(ii) Selection step.

Raw fitness values of 1, 1 − s₀, or 1 − s₁ are assigned to each genotype, depending on its on or off state, and the environmental state E₀ or E₁. We normalize the raw fitness values so that the mean fitness of the population is 1, yielding the relative fitness of each genotype. Each genotype’s frequency is multiplied by its relative fitness. The frequencies now reflect the effects of selection.

(iii) Mutation step.

The mutation kernel specified in Table 2 describes the probabilities of changes in length of between −4 and +2 units to a genotype of length L. These mutation probabilities are applied to the genotype frequencies to generate a final set of frequencies, reflecting the effects of both selection and mutation. (Note that transitions to lengths less than L_min = 11 or greater than L_max = 61 are not permitted; thus, some of the shortest and longest lengths have disallowed transitions. For these lengths, the transition probabilities are normalized so that the probabilities of the remaining permitted transitions sum to one.)

(iv) Conversion back to counts.

New integer counts of the L_num genotypes, summing to the carrying capacity n, are drawn from the multinomial distribution using the final transition frequencies, and a generation is complete.

Selection of T values.

In Fig. 4 to 6, the epoch lengths T₀ and T₁ each assumed values of 1/(aL_opt + b), where L_opt took values from the set 14, 17, 20, 23, 26, 32, 38, 44, 50, and 53 and a and b were as defined above. These L_opt values are the ones expected to win for symmetric period T in the simple, classical analysis (9, 10). The classical analysis assumes separate mutator and major loci; two alleles, A and a, at the major locus; symmetric fitnesses; and symmetric period lengths. Our model breaks all these assumptions in general, but the classical analysis provides a useful baseline for comparison.