Defining and predicting structurally conserved regions in protein superfamilies

Abstract

Motivation: The structures of homologous proteins are generally better conserved than their sequences. This phenomenon is demonstrated by the prevalence of structurally conserved regions (SCRs) even in highly divergent protein families. Defining SCRs requires the comparison of two or more homologous structures and is affected by their availability and divergence, and our ability to deduce structurally equivalent positions among them. In the absence of multiple homologous structures, it is necessary to predict SCRs of a protein using information from only a set of homologous sequences and (if available) a single structure. Accurate SCR predictions can benefit homology modelling and sequence alignment.

Results: Using pairwise DaliLite alignments among a set of homologous structures, we devised a simple measure of structural conservation, termed structural conservation index (SCI). SCI was used to distinguish SCRs from non-SCRs. A database of SCRs was compiled from 386 SCOP superfamilies containing 6489 protein domains. Artificial neural networks were then trained to predict SCRs with various features deduced from a single structure and homologous sequences. Assessment of the predictions via a 5-fold cross-validation method revealed that predictions based on features derived from a single structure perform similarly to ones based on homologous sequences, while combining sequence and structural features was optimal in terms of accuracy (0.755) and Matthews correlation coefficient (0.476). These results suggest that even without information from multiple structures, it is still possible to effectively predict SCRs for a protein. Finally, inspection of the structures with the worst predictions pinpoints difficulties in SCR definitions.

Availability: The SCR database and the prediction server can be found at http://prodata.swmed.edu/SCR.

Contact: 91huangi@gmail.com or grishin@chop.swmed.edu

Supplementary information: Supplementary data are available at Bioinformatics Online

1 INTRODUCTION

Proteins descending from a common ancestor usually conserve certain features of sequence, structure or function. These features can often be used to assess evolutionary relationships. Although it is generally accepted that high sequence similarity implies protein homology, it is not uncommon for homologous proteins to exhibit significant sequence variability (Murzin et al., 1995), underscoring the need for additional ways to deduce homologous relationships. In these cases, the use of 3-dimensional structures can aid homology inference (Cheng et al., 2008; Dietmann and Holm, 2001), as structures tend to be more conserved than sequences (Chothia and Lesk, 1986). Distantly related proteins generally maintain similar structural folds, and as a result, a large fraction of regions (e.g. ≥50%) can be structurally aligned even given very low sequence identity (e.g. ≤20%) (Chothia and Lesk, 1986; Hilbert et al., 1993). Therefore, study of structurally conserved regions (SCRs) and structurally variable regions (SVRs) can help characterize protein families and is useful in applications that rely on homology, such as structure modelling and sequence alignment (Bates and Sternberg, 1999; Chakrabarti et al., 2006; Chivian and Baker, 2006; Greer, 1980).

SCRs are generally characterized by, but not limited to, a set of key secondary structures arranged in an overall topology shared by most members of a protein family. In practice, SCRs are usually deduced by aligning a set of two or more homologous structures and then inspecting which positions were alignable in the majority of the structures (Chothia and Lesk, 1986; Deane et al., 2001; Greer, 1980; Hilbert et al., 1993; Sandhya et al., 2008). The number and divergence of available homologous structures can affect SCR definition, as a positive correlation exists between the fraction of structurally alignable parts and sequence similarity (Hilbert et al., 1993). The exact methodology of aligning structures also affects SCR definition. SCR definitions have often relied on a structural superposition procedure that aims to optimize scoring functions (e.g. RMSD) based on intermolecular distances of structurally equivalent residues. A fixed distance cut-off is then selected to define all SCRs (Chothia and Lesk, 1986; Hilbert et al., 1993). However, rigid structural alignment methods based on minimizing intermolecular distances might be problematic, because proteins are fairly elastic in evolution and can exhibit significant secondary structure deformations, shifts and rotations when divergent structures are compared. Therefore, it has been noted that SCRs defined with a fixed cut-off of intermolecular distance tend to underestimate structurally equivalent positions for divergent homologues. Extensions of these SCRs with other geometric features such as backbone conformations have been shown to improve the performance of comparative modelling (Deane et al., 2001; Montalvao et al., 2005). More ‘elastic’ alignment methods, such as those based on comparison of intramolecular contacts, emphasize similarities in the local structural environment and allow deducing correspondences even for structural elements with larger deviations (Fong and Marchler-Bauer, 2009; Hasegawa and Holm, 2009; Holm and Sander, 1996).

Although the number of solved structures is growing rapidly, it still pales in comparison with the amount of available sequence data (Levitt, 2007). There are still quite a number of protein families with few or even no experimental structures. For these cases, it is necessary to rely on predictive methods to identify SCRs. A few methods have been developed to predict the conservation of various structural properties similar to SCRs with measured success. Hydrophobicity plots and wavelet analysis have been used to predict ‘hydrophobic cores’, hydrophobic regions that determine the ‘native-like’ structure of a protein (Hirakawa et al., 1999). However, hydrophobic cores do not comprise the entire set of SCRs, because not all structurally conserved residues are buried within a hydrophobic environment. In the MegaMotifBase database, conserved ‘structural motifs’ were defined based on multiple homologous structures as short isolated fragments that exhibit both high sequence and structural conservation (Pugalenthi et al., 2008). These structural motifs were subsequently predicted without information about multiple structural homologues by using a neural network ensemble (Pugalenthi et al., 2009). However, the structural motifs in MegaMotifBase are different from general SCRs, which harbour residues that are not necessarily highly conserved in terms of sequence. In fact, owing to the requirement of both sequence and structural conservation, the fraction of residues in the motifs defined in MegaMotifBase is quite low (∼20%), as compared with the fraction of structurally conserved residues (≥60%) in even highly divergent protein families (Hilbert et al., 1993). To our knowledge, methods for prediction of SCRs in absence of multiple structures are currently not available.

In this work, we approach the process of SCR delineation as two separate challenges. When a given protein family has multiple known structures, SCRs can be defined by accurate structural alignments. However, in the absence of structural homologues, SCRs can be predicted given information from a single structure and/or homologous sequences. Here, based on DaliLite (Holm and Sander, 1996) alignments of homologous structures, we introduce structural conservation index (SCI) as a simple measure of positional structural conservation. Using SCI, we constructed a database of SCRs found in SCOP (Murzin et al., 1995) superfamilies with five or more non-redundant members. This database was used to develop an SCR predictor based on artificial neural networks, with inputs of various features derived in each case from homologous sequences and at most a single structure. We further analysed the results of SCR predictions and identified common problems and difficulties in SCR definitions.

2 METHODS

2.1 Compilation of the SCR database

2.1.1 Selection of protein superfamilies 

Our dataset was based on the SCOP (version 1.75) database, which contains protein domain structures divided hierarchically into classes, folds, superfamilies, families, protein domains, species and PDB domains (from highest to lowest). We were particularly interested in the conservation at the superfamily level, which is the largest grouping of evolutionarily related proteins in SCOP that share common structural folds.

To define the dataset, we only considered the structures in the ASTRAL SCOP40 database (Chandonia et al., 2004). ASTRAL contains a subset of SCOP domains with a level of non-redundancy corresponding to at most 40% sequence identity. We excluded certain superfamilies that we anticipated to have poor alignments by the DaliLite algorithm. In particular, SCOP classes g–k (small proteins, coiled coil proteins, low resolution proteins, peptides and fragments, and designed proteins) were removed. A handful of individual folds and superfamilies in the remaining six classes (all alpha proteins, all beta proteins, a/b proteins, a+b proteins, multi-domain proteins, and membrane and cell surface proteins and peptides) were also omitted from the dataset as they exhibited either high structural variability or topologies, such as repeating or duplicated domains and circular permutations, that could pose problems for DaliLite (a.6.1, a.100.1, a.118, a.138.1, b.34.5, b.82.1, b.84.2, b.108.1, c.1.8, c.10.2, c.37.1, c.47.1, d.2.1, d.3.1, d.52.3, d.133, d.169.1, d.198.1, d.211.1, d.325.1, f.4.1). Finally, superfamilies with fewer than five domains were removed to ensure that there were enough members to provide meaningful structural conservation measurement. In total, 386 superfamilies with a total of 6489 protein domains were used.

2.1.2 Structure alignments and SCR definition 

Using the program DaliLite, all-against-all pairwise alignments were generated for the domains in every superfamily. For each domain, we combined the alignments in a master–slave fashion to obtain a multiple structure-based sequence alignment. From these alignments, a value called the SCI was assigned to each residue in every structure, measuring positional conservation of 3-dimensional structure within the superfamily. For a target residue, the SCI was defined as:

(1)

where N_aligned, N_unaligned, N_gap and N_total are, respectively, the number of residues alignable to the target residue (uppercase letters in DaliLite alignment), the number of unalignable residues (lowercase letters in DaliLite alignment), the number of gaps in the position containing the target residue and the total number of proteins in the superfamily (the target residue itself is counted as one aligned residue). Thus, SCI is a measure of the alignability of each amino acid by DaliLite, with a higher SCI suggesting more structural conservation among superfamily members. After manual inspection, the criterion of 80% conservation (SCI: ≥ 0.8) was used to define SCRs.

2.2 Prediction of SCRs

2.2.1 Neural network procedure 

We implemented a neural network prediction procedure that explores information from a window of positions centred at a target residue. Using Fast Artificial Neural Network (http://leenissen.dk/fann), a neural network package based on the feedforward/backpropagation training algorithm, we performed 5-fold cross validation experiments in which we predicted real-valued SCIs for individual residues based on a variety of sequence and structural features.

To generate the dataset for cross validation, we randomly selected a single representative from each protein superfamily in the SCR database. The 386 domains were then partitioned uniformly into 5 sets of 77 (one with 78) domains. Each set was used as a testing set, with the remaining four sets used for training the neural network. To prevent over-training, the members not included in the testing set were randomly divided into (i) a subset of 259 (258) domains that was fed into the neural network for training and (ii) a monitoring subset of 50 domains. The monitoring subset was used to find the training round that returned the lowest mean-squared error (MSE) between the predicted and calculated SCIs, at which point the training procedure was considered to be complete. We then reported the results on the testing set.

Inputs of neural networks were various positional features derived from one 3-dimensional structure and/or sequence homologues. To account for a residue in the context of its neighbours, we included a window of residue features, a technique popularized by secondary structure prediction algorithms (Qian and Sejnowski, 1988). We fixed a local window of size 2 × k + 1, centred on one residue, and containing features from k residues before and k residues after. We considered the case when windows near the start or end of the protein sequence would extend beyond the sequence itself by adding a binary tag as an input feature to indicate its occurrence.

We then monitored the MSE between the predicted and defined SCIs to determine the parameters to be used in the neural network. Varying parameters and monitoring the MSE suggested these best parameter settings: one hidden layer of 20 neurons, and both activation steepness and output steepness of 0.5.

2.2.2 Features derived from a 3-dimensional structure

The DSSP program (Kabsch and Sander, 1983) was used to calculate secondary structure (SS) and solvent accessibility for each residue. The SS values were categorized into three states: α-helices (H, G and I), β-strands (E and B) and loop regions (other letters reported by DSSP). The solvent accessibility, a measure of the number of water molecules in contact with a given residue, was normalized between 0 and 1 to give the relative solvent accessibility (RSA). The number of Cβ atoms in a 14 Å radius of the Cβ of the target residue (CB14) was also calculated and scaled by a constant of 0.01 to yield values approximately between 0 and 1.

2.2.3 Features derived from sequence 

We used four iterations of PSI-BLAST (Altschul et al., 1997) with an inclusion e-value of 1e-4 to generate multiple sequence alignments which were used to derive three positional features. The position-specific scoring matrix (PSSM), a measurement of the amino acid occurrences, was obtained from the PSI-BLAST checkpoint file. Conservation indices calculated by the AL2CO (Pei and Grishin, 2001) were used as a measure of sequence conservation between homologous sequences. The last alignment-derived feature was the fraction of gaps per residue position. The combination of features derived from PSI-BLAST alignment (PSSM, conservation value and gap fraction) is called PBL.

Local structure prediction results were also used as neural network inputs. PSIPRED (Jones, 1999) was used to obtain predicted secondary structures (SSP). Predicted RSA values (RSAP) were generated by using a simple neural network with the PSI-BLAST PSSM as inputs. The sequence length of the protein was also added as a feature and was scaled by dividing by 200.

2.2.4 Performance measures 

We considered a residue to be in an SCR when the SCI of that residue was at least 0.8. A cut-off value for the prediction values was also used to separate predicted SCRs (positives) from predicted non-SCRs (negatives). The results of our prediction methods were thus categorized in a 2 by 2 contingency table consisting of TP (true positives: correctly predicted SCRs), TN (true negatives: correctly predicted non-SCRs), FP (false positives: non-SCRs predicted to be SCRs) and FN (false negatives: SCRs predicted to be non-SCRs).

The cut-off value for the predicted SCI values was determined by scanning the space [0.5, 1] at increments of 0.01 and optimizing once on accuracy score (Q2) and again on Matthews correlation coefficient (MCC) given by equations (2) and (3), respectively.

(2)

(3)

Additionally, we performed receiver-operating characteristic (ROC) analysis, which plots the true positive rate (sensitivity, equation 4) versus false positive rate [1-specificity (equation 5)] of a prediction method when the cut-off value for SCR predictions was systematically varied:

(4)

(5)

The area under the ROC curve (AUC) gives an overall estimate of performance, with a higher AUC value implying better prediction results (Baldi et al., 2000).

2.2.5 SCR predictions compared with MegaMotifBase structural motif predictions 

We compared our work with another neural network predictor (Pugalenthi et al., 2009) based on the MegaMotifBase database (Pugalenthi et al., 2008). First, we tested their structural motif predictors on our data by running their neural network ensemble on our dataset of 386 proteins. Our neural network was then used to predict structural motifs defined in MegaMotifBase. Of the 1194 SCOP superfamilies listed on their server, 23 single-membered superfamilies (a.2.2, a.4.8, a.7.6, a.8.2, a.38.1, a.49.1, a.50.1, a.118.13, a.137.1, a.148.1, a.165.1, b.20.1, b.119.1, c.9.2, c.23.8, c.96.1, d.28.1, d.29.1, d.50.2, d.58.42, d.58.45, e.15.1, g.41.8) had proteins with sequences that did not match those listed in the SCOP version 1.75 files. These superfamilies were omitted from the testing set. With the remaining 1171 superfamilies, we selected a single protein structure at random as a representative of the superfamily and ran our neural network prediction. The SCI cut-offs in our prediction results were optimized both on the MCC and Q2.

3 RESULTS AND DISCUSSION

3.1 The database of SCRs

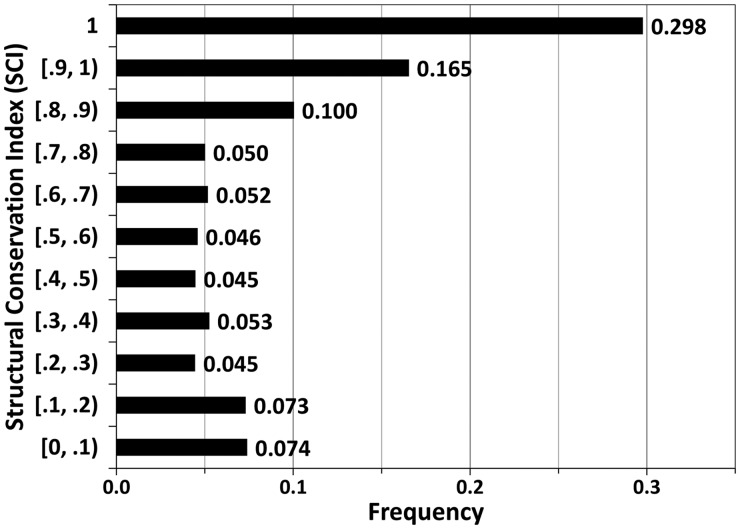
A database of protein structures was assembled from the 386 SCOP superfamilies with five or more nonredundant structures at the 40% sequence identity level (see Methods). For any structure, its DaliLite pairwise alignments to other members in the same superfamily were used to calculate the SCI, i.e. the fraction of alignable residues in each position (see Methods). An SCI cut-off of 80% (inclusive) was applied to determine SCRs. This definition resulted in a total of 653 362 residues in SCRs out of 1 172 507 residues, or a fraction of 55.72%. The distribution of SCIs (Fig. 1) shows that about 30% of the residues were structurally conserved in all members of a superfamily (SCI = 1), while the SCI values have a nearly uniform distribution between 0.2 and 0.8.

Fig. 1.

The distribution of SCI values in the SCR database. The range in the format of [a, b) suggests SCI values no less than a and less than b

The fraction of SCRs has a negative correlation with the number of structures in a superfamily. For superfamilies with eight or less members, the average fraction of SCRs is about 70%, while for superfamilies with 20 or more members, the average SCR fraction is about 52%. Structural diversity is also reflected in the number of SCOP families classified in a SCOP superfamily. While more than half of the superfamilies (223 out of 386) have three or more SCOP families, there are 89 and 74 superfamilies with only one and two SCOP families, respectively. SCOP families with three or more families have median SCR factions <62% (Supplementary Fig. S1). On the other hand, SCOP superfamilies with one family and two families have higher median SCR fractions of 77.8% and 72.5%, respectively (Supplementary Fig. S1). SCRs in some of these superfamilies could be overestimated. It has also been observed that the fraction of SCRs is correlated with the sequence similarity (Hilbert et al., 1993). As a crude measurement of sequence similarity, we calculated pairwise sequence identities of all domain pairs in each superfamily. For the majority of the superfamilies (362 out of 386), the average sequence identity among domain pairs is <25%. The median of the average sequence identity among the 386 SCOP superfamilies is only 17.1%. A positive correlation between SCR fraction and average sequence identity in a superfamily was observed (Supplementary Fig. S2).

Nine superfamilies have <30% residues defined as SCRs, suggesting high structural divergence between the superfamily members. The five superfamilies with the lowest SCR fractions (all <20%) are well known for their high structural divergence: His-Me finger endonucleases (d.4.1, SCR fraction 9.3%) (Friedhoff et al., 1999; Shub et al., 1994), DNA/RNA polymerases (e.8.1, SCR fraction 10.3%) (Majumdar et al., 2009), Restriction endonuclease-like (c.52.1, SCR fraction 17.2%) (Bujnicki, 2001; Roberts and Macelis, 1991), Ribonuclease H-like (c.55.3, SCR fraction 18.9%) (Nowotny, 2009), and Metalloproteases (‘zincins’), catalytic domain (d.92.1, SCR fraction 19.3%) (Gomis-Ruth, 2003). One common feature for these superfamilies is that they have a core consisting of several structural elements, while many members have diverse structural decorations that fall into unalignable regions. Conversely, there are 18 superfamilies with very high SCR fraction (i.e. >85%). These superfamilies have relatively few members (12 at most).

Our SCR definition relies on pairwise DaliLite structural alignments. For each target structure, a master–slave pseudo-multiple alignment was constructed from the pairwise alignments of that structure (master) to all the other structures (slaves) in the same superfamily (these alignments are available at the website of SCR database). SCRs were then deduced from this alignment. However, information in structural alignments among the slaves is not used in SCR definition. Structural equivalences deduced from pairwise structural alignments among three or more structures are not always consistent. For example, even if position i_A in a master structure A is aligned to position j_B in one slave structure B and aligned to position k_C in another slave structure C, positions j_B and k_C may not be aligned between the two slave structures B and C. Such inconsistency should compromise the structural conservation for position i_A of structure A. Multiple structural alignment methods that explore the consistency among pairwise structural alignments could lead to improved definitions of SCRs.

3.2 Predictions of SCRs using neural networks

We used artificial neural network to predict SCRs based on features derived from a single structure and/or homologous sequences. A 5-fold cross-validation procedure was conducted (see Methods) with input features derived from a window of positions centred at a target position. We varied window sizes starting from a size of one residue and increasing by increments of four residues. Plotting the MCC and Q2 of the neural networks as a function of window size for a variety of combinations of input features, we observed that the scores stopped increasing when the window size exceeded 13 (Supplementary Fig. S3). This suggests that a local window of 13 residues is optimal for neural network predictors in terms of accuracy and speed. We thus report results of neural network predictions with a fixed window size of 13 for all feature combinations to facilitate their comparisons. Neural networks were also trained with or without sequence length (scaled by a factor of 1/200) as a feature to determine its necessity in SCR prediction. We found that as an input feature, sequence length benefited both MCC and Q2 in every case (data not shown), so it was included in all experiments described below.

To evaluate the performance of SCR predictions, we applied a cut-off to predicted SCIs to distinguish predicted SCRs (residues with predicted SCIs no less than the cut-off) from predicted non-SCRs (residues with predicted SCIs less than the cut-off), which allows us to assign true/false positive or true/false negative for each residue (see Methods). For each neural network, such a cut-off of predictions was systematically varied to obtain the ROC curve, from which the AUC was calculated and served as a performance evaluation score (Fig. 2 and Supplementary Figs S4–S6). For each neural network, we also determined a cut-off of predicted SCIs that reported the best MCC and another cut-off that reported the optimal Q2. MCC, Q2, sensitivity (SE) and specificity (SP) given both cases are shown in Table 1.

Fig. 2.

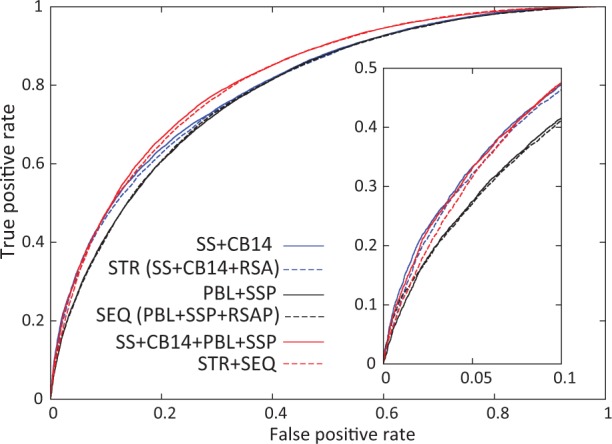
ROC curves of selected neural network predictions. Two best neural networks using structure features (blue lines), sequence features (black lines) and combined features (red lines) are shown

Table 1.

Evaluation of SCR predictions

Features used inneural network	Optimization on MCC				Optimization on Q2				AUC
	MCC	Q2	SE	SP	Q2	MCC	SE	SP
Structural features
SS	0.315	0.681	0.768	0.541	0.687	0.308	0.837	0.445	0.724
RSA	0.391	0.711	0.757	0.636	0.716	0.388	0.807	0.57	0.767
CB14	0.423	0.726	0.769	0.655	0.731	0.414	0.85	0.541	0.783
SS + RSA	0.414	0.719	0.751	0.668	0.728	0.406	0.853	0.527	0.784
SS + CB14	0.436	0.719	0.703	0.745	0.739	0.432	0.852	0.556	0.802
RSA + CB14	0.417	0.727	0.795	0.618	0.729	0.41	0.84	0.55	0.777
STR (SS + RSA + CB14)	0.433	0.726	0.747	0.692	0.735	0.429	0.824	0.592	0.797
Sequence features
PBL	0.408	0.721	0.783	0.623	0.728	0.404	0.861	0.513	0.777
SSP	0.364	0.698	0.746	0.621	0.707	0.354	0.854	0.469	0.749
RSAP	0.389	0.713	0.776	0.61	0.716	0.387	0.808	0.568	0.766
PBL + SSP	0.424	0.735	0.844	0.559	0.735	0.423	0.855	0.543	0.788
PBL + RSAP	0.405	0.727	0.842	0.541	0.727	0.402	0.868	0.501	0.775
SSP + RSAP	0.418	0.731	0.826	0.578	0.732	0.413	0.862	0.521	0.782
SEQ (PBL + SSP + RSAP)	0.423	0.725	0.765	0.661	0.733	0.417	0.865	0.522	0.788
Combined features
SS + CB14 + PBL	0.465	0.752	0.836	0.617	0.753	0.464	0.861	0.58	0.812
SS + CB14 + PBL + SSP	0.476	0.75	0.782	0.698	0.755	0.468	0.867	0.575	0.817
SS + CB14 + SEQ	0.467	0.753	0.841	0.512	0.753	0.467	0.841	0.512	0.814
STR + PBL	0.465	0.751	0.83	0.624	0.752	0.461	0.864	0.572	0.814
STR + PBL + SSP	0.468	0.751	0.815	0.647	0.752	0.461	0.853	0.589	0.814
STR + SEQ	0.474	0.753	0.809	0.662	0.755	0.471	0.846	0.61	0.814

SE and SP are sensitivity and specificity, respectively. The best two predictions in each category are shown in bold and underlined numbers.

3.2.1 SCR predictions using information derived from a single structure 

Conventionally, defining SCRs has required alignment of two or more homologous structures, and the result depends on the diversity of available structures. In contrast, we explored the prediction of SCRs using features derived from just one structure. The three structural features we tested were secondary structure (SS) and two residue burial properties: RSA and CB14 (Table 1). The single feature with the best predictive power was CB14 (MCC = 0.423, Q2 = 0.731, AUC = 0.783). It outperformed RSA (MCC = 0.391, Q2 = 0.716, AUC = 0.767; Table 1 and Supplementary Fig. S4), suggesting that the number of residue contacts and solvent accessibility are not interchangeable properties despite the strong correlation between them (Pollastri et al., 2001). Our result is consistent with previous finding that CB14 is one of the most effective residue burial properties, outperforming RSA in fold recognition and alignment experiments (Karchin et al., 2004). Both CB14 and RSA gave better results than SS (MCC = 0.315, Q2 = 0.687, AUC = 0.724), suggesting that residue burial properties are more important in determination of SCRs than secondary structure. When combining structural features, the best performance was achieved by the combination of SS and CB14 (MCC = 0.436, Q2 = 0.739, AUC = 0.802), which performs similarly to the combination of all three structural features (MCC = 0.433, Q2 = 0.735, AUC = 0.797; Table 1).

3.2.2 SCR predictions using sequence information 

For protein families without available structures, we explored information from homologous proteins to predict SCRs. For each family, we first tested the performance of a PSI-BLAST PSSM coupled with two additional alignment-derived positional properties, sequence conservation value and gap fraction (combination of the three features named PBL in Table 1). Two structural properties predicted from PSI-BLAST PSSMs were independently tested, SSP and RSAP. Of the three variables PBL, SSP and RSAP, PBL performed at the highest level (MCC = 0.408, Q2 = 0.728, AUC = 0.777). The features that performed the best when in combination were PBL and SSP (MCC = 0.424, Q2 = 0.735, AUC = 0.788), showing a similar performance to that of combining all the sequence-based features (MCC = 0.423, Q2 = 0.733, AUC = 0.788; Table 1 and Supplementary Fig. S5). The best performer using sequence information yielded slightly worse results compared with the best performer using information from a single structure (Table 1).

3.2.3 Combining information from both sequence and structure improves SCR predictions 

We varied the combinations of features from the structural category and the sequence category. Various combinations all gave similar performance (Table 1 and Supplementary Fig. S6). The best result (MCC = 0.476, Q2 = 0.755, AUC = 0.817) was achieved when combining the two features that gave the best performance in the structural category (SS + CB14) and the two features that gave the best performance in the sequence category (PBL + SSP). This result was similar to that of combining all structural and sequence features (STR + SEQ in Table 1). Given the input SS + CB14 + PBL + SSP, adding sequence information improved MCC by about 9%, Q2 by about 2% and AUC by about 2% when compared with the best performer that used structural information only (SS + CB14).

3.3 Comparison with the predictions of MegaMotifBase structural motifs

In a related study, neural network predictions of conserved structural motifs in the MegaMotifBase were reported (Pugalenthi et al., 2009). These MegaMotifBase motifs were defined as segments with both high sequence conservation and structural conservation, while our SCR definitions do not include sequence conservation. Our neural network did not accurately predict MegaMotifBase motifs (see Methods; best MCC was only 0.348), as compared with the reported performance of neural networks trained directly on these motifs (MCC = 0.845) (Pugalenthi et al., 2009). Likewise, the MegaMotifBase motif prediction program is inferior in predicting our definitions of SCRs (MCC = 0.192, Q2 = 0.476). The relatively inaccurate predictions of both our program on the MegaMotifBase dataset and Pugalenthi et al.’s program on our SCR dataset highlight how our SCR definitions differ from the MegaMotifBase motifs.

3.4 Structural analysis of SCR predictions

We compared prediction results (based on the feature combination of SS + CB14 + PBL + SSP) to SCR definitions for each individual protein to determine prediction sensitivity, specificity and accuracy (Supplementary Table S1). The prediction accuracies for individual domains ranged from 0.119 to 0.977, with a median value of 0.783 and an average value of 0.765.

Inspection of SCR definitions and predictions revealed two major reasons for the worst prediction accuracies. The first was unreasonable SCR definitions owing to the inconsistency in SCOP domain definitions in a superfamily. In particular, for some SCOP superfamilies, a domain definition comprised a single unit for some members, but duplicate units for other members. One example is the low prediction accuracy for the structure of a hypothetical protein (SCOP ID: d1u9da_, pdb code: 1U9D, chain A) from the Tautomerase/MIF superfamily (SCOP ID: d.80.1). This structure is characterized by a duplication of two beta-alpha-beta structural units (Fig. 3a). However, 4 out of 11 domains in this superfamily contain only one beta-alpha-beta unit, and they are all aligned to the C-terminal beta-alpha-beta unit of d1u9da_ (β-strands b3 and b4 and α-helix A2 in Fig. 3a). The N-terminal beta-alpha-beta unit of d1u9da_ (β-strands b1 and b2 and α-helix A1, Fig. 3a) is thus devoid of SCRs according to our SCR definition, as the SCI values for the residues in the N-terminal unit are no more than 7/11 and less than the SCR cut-off of 0.8 (see Supplementary Fig. S7a for the alignment). Our neural network predicted a similar fraction of SCRs in both the N- and C-terminal units of d1u9da_. However, the SCR predictions in the N-terminal unit were counted as false positives (green, Fig. 3a) according to the unreasonable SCR definitions, which resulted in the low prediction accuracy for d1u9da_ (Q2 = 0.500). Besides d1u9da_, we found low prediction accuracies for several other proteins with unreasonable SCR definitions owing to inconsistent SCOP domain definitions involving duplicated domains (such as d1s7ja_ and d1wwia1, Supplementary Table S1). A similar problem was found for a few cases where SCRs were not defined for regions corresponding to an inserted domain, while reasonable SCR predictions were made for the inserted domain (e.g., d1t3qc2 in the superfamily of d.145.1, Supplementary Table S1).

Fig. 3.

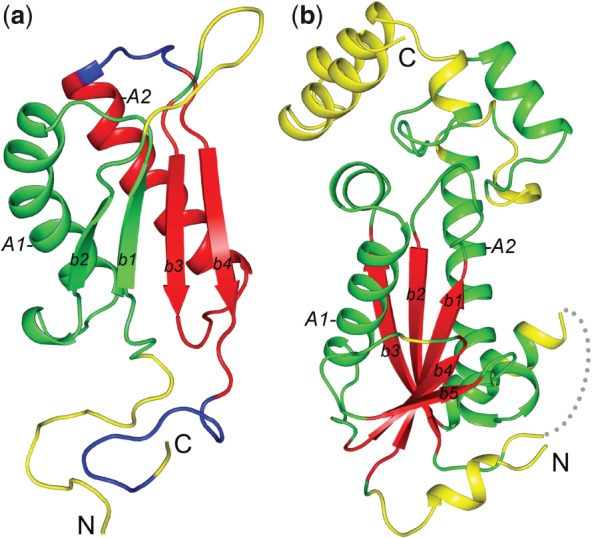
Structural mapping of SCR predictions for (a) d1u9da_ from the Tautomerase/MIF superfamily and (b) d2etja1 from the Ribonuclease H-like superfamily. True positives, false positives, true negatives and false negatives are coloured red, green, yellow and blue, respectively. N- and C-termini are marked. Major secondary structural elements are labelled ‘A’ for α-helices and ‘b’ for β-strands

A second cause of low prediction accuracy was found in several domains from SCOP superfamilies with high structural divergence and low fractions of defined SCRs. One example is the domain (SCOP ID: d2etja1) from the Ribonuclease H-like superfamily (SCOP ID: c.33.3, Fig. 3b). Our SCR definition procedure successfully identified the five central β-strands of this domain as its SCRs (b1–b5 in Fig. 3b), consistent with the SCOP description of the general ‘Ribonuclease H-motif’ fold. The neural network also predicted these five β-strands as SCRs (true positives, coloured red in Fig. 3b), resulting in high sensitivity of the prediction (SE = 1.0, all 35 defined SCRs were predicted as SCRs). However, the neural network predictor also included additional structural elements as predicted SCRs (a total of 44 residues were false positives), resulting in low prediction specificity (SP = 0.426) and a low Q2 score of 0.521. Most noticeably, two α-helices (A1 and A2 in Fig. 3b) sandwiching the central beta sheet were predicted as SCRs, while they were not defined as SCRs. In quite a number of members of the Ribonuclease H-like superfamily, these two α-helices are indeed present and could be structurally aligned to their counterparts in d2etja1 (Supplementary Fig. S7b). However, the SCI values for residues in these two α-helices were around 0.5, and so did not pass the SCR definition cut-off of 0.8.

High structural divergence among some superfamily members also resulted in incorrect DaliLite alignments, as observed for some members in the His-Me endonuclease superfamily (SCOP ID: d.4.1). Other structural changes that posed problems for DaliLite alignment program and SCR definitions included circular permutation (such as superfamily d1r5ba2 in the superfamily of b.44.1) and domain swap (such as d2gmya1 in the superfamily of a.152.1). Manual inspection of structures with the worst prediction results revealed 11 protein domains with SCR definition problems (gray lines in Supplementary Table S1). For the neural network (SS + CB14 + PBL + SSP) trained on 386 domains, removal of the 11 domains led to improved performance for the remaining 375 domains (MCC = 0.491, Q2 = 0.765, AUC = 0.826, Supplementary Table S2) compared with the performance averaged on the 386 domains (MCC = 0.476, Q2 = 0.755, AUC = 0.817). To investigate whether those cases of unreasonable SCR definitions negatively affected neural network training, we excluded them and did new cross-validation tests of neural networks using the remaining 375 domains (Supplementary Table S3). However, this procedure yielded no improvement over the procedure trained using the entire 386 domains (Supplementary Tables S2 and S3). This result suggests that our neural network procedure is robust and can tolerate a few cases of unreasonable SCR definitions.

4 CONCLUSION

We developed SCI, a measure of positional structural conservation based on pairwise DaliLite alignments among a set of homologous structures. A database of SCRs was defined for 386 SCOP superfamilies with five or more structures at the ≤40% sequence identity. We explored various structure-based and sequence-based features in SCR predictions using the artificial neural network technique. For features derived from a single structure, we observed that CB14 was a more informative residue burial property than relative solvent accessibility, and that CB14 coupled with SS achieved a prediction Q2 of 0.739 and MCC of 0.436. For features derived from homologous sequences, we observed that SSP contributed to prediction accuracy, and SSP coupled with PBL properties [PSI-BLAST position scoring matrix (PSSM), gap fraction and positional amino acid conservation score] gave Q2 of 0.735 and MCC of 0.424. Combination of features derived from a single structure and features derived from homologous sequences (SS + CB14 + PBL + SSP) resulted in the best predictor with Q2 of 0.755 and MCC of 0.476. Inspection of the discrepancies between the prediction results and SCR definitions for structures with low prediction accuracies highlights problems and difficulties in defining SCRs caused by inconsistency in domain definitions and high structural divergence.