A system for exact and approximate genetic linkage analysis of SNP data in large pedigrees

Abstract

Motivation: The use of dense single nucleotide polymorphism (SNP) data in genetic linkage analysis of large pedigrees is impeded by significant technical, methodological and computational challenges. Here we describe Superlink-Online SNP, a new powerful online system that streamlines the linkage analysis of SNP data. It features a fully integrated flexible processing workflow comprising both well-known and novel data analysis tools, including SNP clustering, erroneous data filtering, exact and approximate LOD calculations and maximum-likelihood haplotyping. The system draws its power from thousands of CPUs, performing data analysis tasks orders of magnitude faster than a single computer. By providing an intuitive interface to sophisticated state-of-the-art analysis tools coupled with high computing capacity, Superlink-Online SNP helps geneticists unleash the potential of SNP data for detecting disease genes.

Results: Computations performed by Superlink-Online SNP are automatically parallelized using novel paradigms, and executed on unlimited number of private or public CPUs. One novel service is large-scale approximate Markov Chain–Monte Carlo (MCMC) analysis. The accuracy of the results is reliably estimated by running the same computation on multiple CPUs and evaluating the Gelman–Rubin Score to set aside unreliable results. Another service within the workflow is a novel parallelized exact algorithm for inferring maximum-likelihood haplotyping. The reported system enables genetic analyses that were previously infeasible. We demonstrate the system capabilities through a study of a large complex pedigree affected with metabolic syndrome.

Availability: Superlink-Online SNP is freely available for researchers at http://cbl-hap.cs.technion.ac.il/superlink-snp. The system source code can also be downloaded from the system website.

Contact: omerw@cs.technion.ac.il

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Genetic linkage analysis is a statistical method for locating disease-susceptibility genes by finding patterns of excess co-segregation between a genetic marker and a phenotype of interest in a pedigree (Lin and Zhao, 2010; Ott, 1999). This method is recently gaining newfound interest, thanks to the rapidly growing availability of high-throughput sequencing data (Bailey-Wilson and Wilson, 2011; Bamshad et al., 2011; Vieland and Devoto, 2011). Namely, linkage analysis of large pedigrees can be better powered and more cost-effective than genome-wide association studies for discovering rare variants (Wijsman, 2012). It has recently been shown that genetic linkage analysis can be performed using single nucleotide polymorphism (SNP) genotypes extracted from sequencing data (Smith et al., 2011), demonstrating the necessity of efficient tools capable of analysing SNP data in large pedigrees.

Existing packages that perform exact linkage analysis, such as LIPED (Ott, 1974), LINKAGE (Lathrop et al., 1985), MENDEL (Lange et al., 1988), FASTLINK (Cottingham et al., 1993), GENEHUNTER (Kruglyak et al., 1996), VITESSE (O’Connell, 2000), Superlink (Fishelson and Geiger, 2002), Merlin (Abecasis et al., 2002) and Allegro (Gudbjartsson et al., 2005), use either the Elston–Stewart algorithm (Elston and Stewart, 1971), the Lander–Green algorithm (Lander and Green, 1987) or a combination thereof. While these packages have been successfully used for exact genetic linkage analysis of moderately sized families, they are not suitable for analysing dense SNP data in large pedigrees owing to the high computational complexity of the aforementioned algorithms.

Several approaches have been proposed to circumvent the high complexity of linkage analysis in large pedigrees. One approach is to split a large pedigree into several smaller easier to analyse pedigrees (Axenovich et al., 2008; Bellenguez et al., 2009b; Falchi and Fuchsberger, 2008; Falchi et al., 2004; Kirichenko et al., 2009; Liu et al., 2008; Pankratz and Iturria, 2001), but this can result in significant power loss (Dyer et al., 2001). Another well-established approach is the approximate analysis of large pedigrees through Markov Chain–Monte Carlo (MCMC), available in packages such as Loki (Heath, 1997), MORGAN (Tong and Thompson, 2008) and SimWalk2 (Sobel and Lange, 1996). The main drawback of MCMC methods is the lack of a reliable accuracy measure, for which there is no general analytical analysis. Other approaches include estimating identical by descent regions heuristically or by observing each marker separately (Abney, 2008; Leibon et al., 2008; Thomas et al., 2008), but an exact method for analysing dense SNP data in large pedigrees, using the full pedigree information, is still lacking.

The analysis of dense SNP data in large pedigrees also necessitates suitable interoperable software tools for manipulating bulky raw SNP data. While several SNP data manipulation packages have been developed in recent years [e.g. SNP HiTLink (Fukuda et al., 2009), easyLINKAGE-Plus (Hoffmann and Lindner, 2005), IGG (Li et al., 2007), Mega2 (Mukhopadhyay et al., 2005) and SNPP (Zhao et al., 2005)], none is tightly integrated with a software package capable of parallelizing linkage analysis tasks across a multitude of CPUs. Superlink-Online SNP provides a comprehensive and easy-to-use solution for both computational and technical challenges posed by linkage analysis of SNP data in large pedigrees.

First, the system makes extensive use of modern distributed computing technologies, which provide both performance and functional improvements impossible otherwise. The exact linkage analysis is sped up by using thousands of CPUs in parallel. Superlink-Online SNP uses novel methodologies to reduce the amount of computations required for a single analysis by up to a 100-fold (Silberstein, 2011) and uses a computer grid 10 times larger than we reported before (Silberstein et al., 2006a), resulting in up to three orders of magnitude faster analyses. Superlink-Online SNP also parallelizes the approximate linkage analysis of an arbitrary number of markers and pedigree members using the MORGAN software. Importantly, the parallel infrastructure enables us to improve the practical utility of this analysis by providing a reliable accuracy estimate through the well-established Gelman–Rubin (GR) statistic (Gelman and Rubin, 1992). Finally, the system uses DAOOPT, a novel parallel algorithm for maximum-likelihood haplotyping analysis, yielding two orders of magnitude faster analysis than previously reported for demanding pedigrees (Fishelson et al., 2005).

Second, the system presents a simple, intuitive and secure web interface, fully integrating these powerful data analysis services with a set of pre- and post-processing tools for preparation and filtering of SNP data, and presentation of the results. All the tools are designed to be used in succession, where one may invoke each tool on the output received from another tool. Notably, the system records the full history of every data artifact it produces, thus enabling users to reconstruct all the processing steps that led to a given result, and easily reproduce the results when necessary. All the input data as well as the analysis results can be readily downloaded and entirely removed from the Superlink-Online SNP web site.

By providing an intuitive interface to sophisticated state-of-the-art tools executed on thousands of CPUs, Superlink-Online SNP enables the computation of a variety of analyses that were infeasible before, and helps geneticists exploit the full potential of SNP data for detecting disease genes.

2 ANALYSIS WORKFLOW

Superlink-Online SNP promotes a workflow-oriented genetic analysis using its set of highly integrated tools. We first describe a typical analysis workflow, and then demonstrate a real usage scenario through an example study.

2.1 Workflow stages

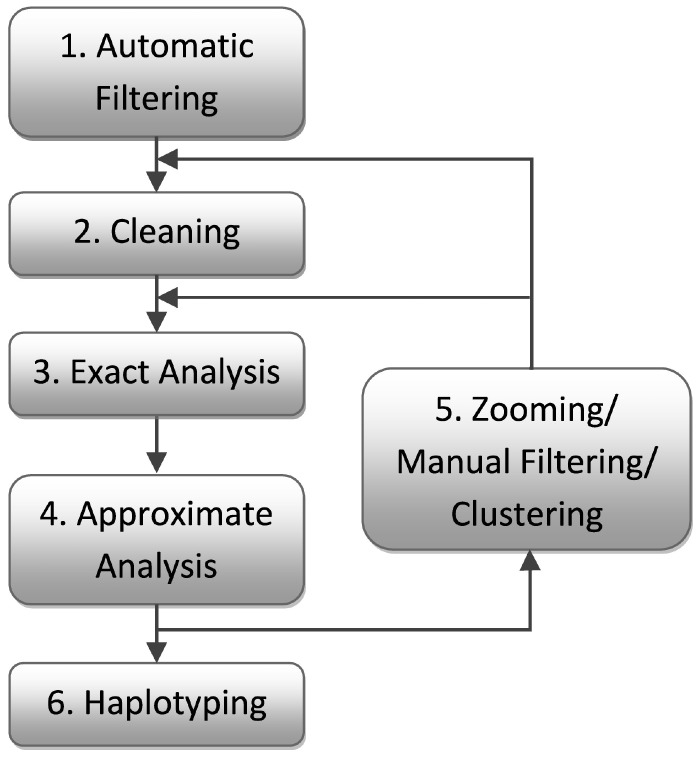
A typical genetic analysis workflow naturally supported in Superlink-Online SNP is depicted in Figure 1. The system is flexible and supports an arbitrary combination of the processing stages described below. However, we present a specific workflow based on the best practices for effective detection of a candidate genomic region using raw SNP data, to emphasize the suitability of the system for performing a complete end-to-end genetic analysis.

Fig. 1.

A typical analysis workflow in Superlink-Online SNP

Automatic Filtering randomly chooses up to 25 000 markers spanning the entire genome and sets the rest aside. This number of markers enables fast analyses and helps reduce the amount of linkage disequilibrium (LD), which can lead to misleading results (Schaid et al., 2002), while still providing sufficient genomic coverage. The markers are chosen so as to preserve the relative densities of the original marker maps. Removed markers can later be restored using the Zooming tool (see below).

Cleaning automatically removes erroneous markers, often introduced by genotyping errors, and uninformative markers. The tool prunes markers with Mendelian errors, markers with extreme allele frequencies and markers with likelihood (computed using the standard genetic model but without considering the phenotype) being higher when not conditioning on their surrounding markers (Tzemach, 2009). Markers in which the same pair of alleles is present in all genotyped individuals can also be removed.

Exact Analysis performs multipoint analyses. The system automatically chooses a computational algorithm most suitable for a given pedigree size. For smaller pedigrees, the system computes both a parametric multipoint LOD score and the non-parametric linkage scores S_pairs and S_all (Kruglyak et al., 1996; Whittemore and Halpern, 1994), using all markers jointly through the Lander–Green algorithm. If, however, the pedigree is too large, the number of markers in the multipoint analysis can be adjusted by defining the size of the analysis window. The system then automatically generates several multipoint runs by moving the analysis window over the entire set of markers and computes parametric multipoint LOD scores through Superlink-Online (Silberstein et al., 2006a).

Approximate Analysis approximates parametric LOD scores through MCMC, using MORGAN. The approximate analysis allows for multipoint analysis using larger windows that are infeasible to perform using exact analysis. An accuracy estimate is provided through the GR score of the analysis. We provide more details about MORGAN and the statistical aspects of the GR score in Section 3.2.

Zooming, Manual Filtering and Clustering enable users to focus on specific regions of interest that they wish to analyse more thoroughly. The Zooming tool creates a window of all the markers contained in a specific region, including the ones filtered out by the Automatic Filtering tool. The Manual Filtering tool randomly filters markers out of a specific region while controlling the average distance between adjacent markers. These tools can be used in conjunction to obtain a set of equidistant markers encompassing a specific region, which can help reduce LD (Evans and Cardon, 2004). Finally, the Clustering tool merges groups of SNP markers in close proximity into one multi-allelic marker (Tzemach, 2009), which can enable exact analysis of large genomic regions that are infeasible by using separate markers, as well as help eliminate LD (Abecasis and Wigginton, 2005).

Haplotyping computes a maximum-likelihood haplotype configuration that maximizes the probability of the given genotype data, taking into account intermarker recombination fractions. This serves to determine if a disease-associated haplotype segregating affected and unaffected individuals is found in a candidate region. More details are provided in Section 3.3.

Superlink-Online SNP also includes several services not shown in Figure 1. One service is a pedigree drawing tool, which uses the packages Haplopainter (Thiele and Nürnberg, 2005) and Madeline 2.0 (Trager et al., 2007) to provide two different drawings for each pedigree. Another service is a mode of inheritance (MOI) estimation tool, which computes the likelihood of the phenotypic data alone under several different values of the penetrance and disease allele frequency parameters, while ignoring the markers data, to estimate the most likely MOI. This tool considers models typical for Mendelian traits (i.e. dominant and recessive models with fairly high penetrances and fairly low phenocopy rates), but the system allows one to specify arbitrary models when performing subsequent analyses. The system also includes a Data Browser tool that graphically shows homozygous regions shared by different individuals, which is useful for analysing recessive traits. Superlink-Online SNP accepts input files in FASTLINK format, as well as an input format suitable for SNP data and a web-based input form. The system assumes that each input file corresponds to a different, unlinked, genomic region. Users can thus perform a genome-wide analysis by uploading several different input files, each one corresponding to a different chromosome or genomic region, and analysing them all simultaneously. More details are available at the system website.

2.2 An example study

We illustrate a typical analysis workflow through an example study of a complex Arab pedigree from the North of Israel with several individuals affected with metabolic syndrome (Alberti et al., 2006) and Familial Hypercholesterolemia, as shown in Figure 2. This pedigree is too difficult for analysis with programs using the Lander–Green algorithm, such as Merlin and Allegro, owing to its large size and high degree of consanguinity.

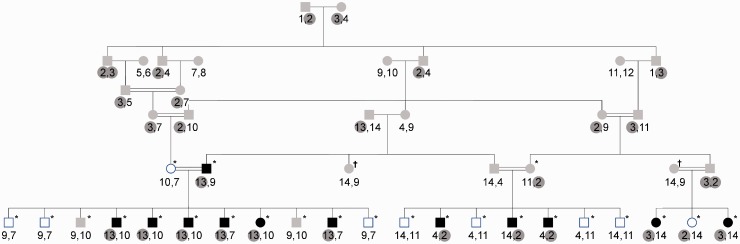
Fig. 2.

A large complex pedigree affected with high LDL levels. Unaffected, affected and individuals with an unknown affection status are shaded in white, black and gray, respectively. Individuals who have been genotyped are marked with an asterisk. The two individuals marked with a † symbol refer to the same individual, who is shown twice to simplify the drawing. The results of the Haplotyping analysis are shown in the two numbers below each individual. Each number corresponds to a different haplotype that originated from one of the founders, and each individual carries two different haplotypes. Haplotypes 2, 3 and 13, which are shaded in gray, are the haplotypes most likely to be causative

We tested for linkage between a genomic region and the LDL cholesterol levels. Initial analysis was done according to the known criteria, where individuals were marked as affected if their total cholesterol level exceeded 200 mg% or the LDL-cholesterol exceeded 130 mg%. Second level of analysis was made with strict arbitrary definition, where individuals were marked as affected if their LDL-cholesterol levels exceeded 300 mg% (before treatment was instituted) or above 200 mg% (while medication is undertaken on a daily basis). The clinical status of individuals whose LDL level has not been measured was marked as unknown. The individuals marked with an asterisk have been genotyped using the CytoSNP 300K arrays (HumanCytoSNP-12 v2.1, lllumina lnc.) panel.

In the following section, we omit the precise linkage location because this study is still in progress. Nevertheless, the example study demonstrates well the system power and capabilities. The exons of three genes [LDLR (OMIM 606945), APOB (OMIM 107730) and PCSK9 (OMIM 607786)], known to be involved in familial hypercholesterolemia, were sequenced and no mutations were detected.

Automatic filtering. The input files contained the readings of 298 199 SNPs. The Automatic Filtering tool randomly chose 25 000 SNPs out of those, while preserving the relative genome-wide density.

Cleaning. The Cleaning tool removed 8299 SNPs that were uninformative, and an additional 481 SNPs that contained Mendelian errors or were unlikely given their surrounding SNPs, leaving 16 220 markers for the initial analysis.

Exact analysis. We first used the MOI estimation tool to choose the disease allele prevalence f and the penetrance level p to use in the analysis. This tool showed that the studied trait is likely to follow a dominant MOI, and that the likelihood increases monotonically with f and p in the range of values examined (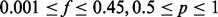), indicating that the trait is likely to follow a highly prevalent highly penetrant dominant MOI in this pedigree. This is consistent with the fact that a large proportion of the children in each nuclear family is affected. We chose the parameter values f = 0.1, p = 0.9 to account for the fact that the studied trait is complex and is thus not likely to have extreme disease allele frequency or penetrance levels. We next performed exact genome-wide linkage analysis using these parameters. Because of the pedigree complexity, the largest feasible window size for a genome-wide analysis is three (four-point analysis). The analysis revealed a 5 cM long region spanning 30 markers with LOD scores ≥2 on one of the chromosomes, indicating suggestive linkage.

Approximate analysis. We began the Approximate Analysis stage with an accuracy evaluation, conducted by repeating the same computations carried out in the Exact Analysis stage in the candidate region. We performed an approximate four-point analysis with exponentially increasing numbers of MCMC iterations, using the default parameter values specified in MORGAN. A LOD score and a GR score were reported for each tested locus in each analysis. We compared the obtained LOD scores with those obtained in the exact analysis. Direct comparison was not possible, as the exact analysis places the tested loci on the markers, whereas the approximate analysis places the tested loci halfway between every two adjacent markers owing to restrictions of the MCMC algorithm. Instead, we performed an approximate comparison by computing the average LOD score of every two adjacent markers obtained in the exact analysis with the LOD score obtained between these two markers in the approximate analysis. Table 1 shows the approximate root mean square error (RMSE*) of the LOD scores (compared with the exact analysis) and the average GR score obtained for all tested loci. As expected, the accuracy of the results increases with the number of MCMC iterations and the GR scores become closer to one, indicating convergence. Note that the RMSE* statistic overestimates the error term owing to the approximation.

Table 1.

The approximate Root Mean Square Error (RMSE*) of the LOD scores obtained using approximate analysis with 3-marker windows (compared with the exact analysis), the Root Mean Square Error (RMSE) of the LOD Scores using other window sizes (compared with those obtained in an analysis with 100 × 2¹³ iterations) and the average GR Scores obtained in these analyses

Window size		Number of MCMC iterations (×100)
		21	24	27	210	213
3	RMSE*	1.32	1.06	0.98	0.97	0.96
	Average GR	3.39	2.36	1.87	1.62	1.53
10	RMSE	0.4	0.27	0.15	0.06	0
	Average GR	7.49	4.78	3.92	2.8	1.54
25	RMSE	0.44	0.47	0.13	0.06	0
	Average GR	97.41	156.92	20.01	3.2	5.86
50	RMSE	0.18	0.17	0.03	0.18	0
	Average GR	7.32	7.34	3.66	167.4	7.4
100	RMSE	0.53	0.09	0.05	0.02	0
	Average GR	30.7	2.27	3.5	3.34	1.77

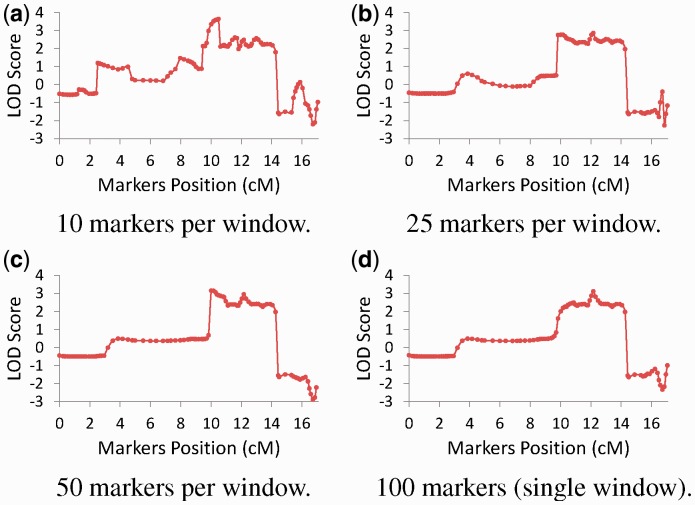
Zooming and filtering. We used the Zooming and Filtering tools to obtain a window of 100 markers 0.1 cM apart encompassing the candidate region. We performed approximate analysis in this region using windows of 10, 25, 50 and 100 markers with exponentially increasing numbers of iterations. Because exact analysis with such window sizes is infeasible, we estimated the accuracy by comparing the obtained LOD scores of each analysis with those obtained in the analysis with the largest number of iterations we performed (100 × 2¹³). The results, as well as the average GR score reported for each analysis, are shown in Table 1. Table 1 demonstrates that the RMSE tends to decrease with the number of iterations, although on rare occasions one or more of the concurrent analyses performed may fail to converge, causing the RMSE to increase. Table 1 also shows that the average GR score is a conservative measure of convergence. In our analyses, average GR scores ≤3.5 always indicate that the RMSE is smaller than 0.1, but higher GR scores do not necessarily indicate the converse. This demonstrates that the GR score is sensitive to small differences in the results of the concurrent MCMC runs. Thus, small GR scores indicate that the results obtained in an approximate analysis are reproducible. We therefore recommend performing approximate analysis by exponentially increasing the number of iterations until an average GR score ≤3.5 is obtained. The LOD scores obtained using the various analyses performed are shown in Figure 3, which demonstrates that analyses using larger windows are less fluctuant because each window is more informative, thus better pinpointing the disease gene location.

Fig. 3.

LOD scores of candidate region using approximate analyses with (a) 10 markers per window (b) 25 markers per window (c) 50 markers per window (d) a single 100 markers window (high resolution versions of graphs automatically produced by the system)

Haplotyping. We concluded the analysis by using the Haplotyping tool to determine if a disease-associated haplotype can be found in the candidate region. We ran several seven-point Haplotyping analyses encompassing the candidate region. For these analyses, we used markers with a high degree of heterozygosity among the genotyped individuals, as such markers are more informative and enable faster computations. Such markers can be readily found using the Data Browser tool. The analysis results are shown in Figure 2. Surprisingly, the analyses revealed that three different haplotypes, originating from three different founders, segregate in all affected individuals but in only one unaffected individual in the candidate region. A possible explanation is that two of the haplotypes originate from a common ancestor. This hypothesis is supported by the fact that haplotypes 2 and 3 share a 0.2 cM long common sequence. When analysing only this shared region, a LOD score of 3.48 is obtained (versus a maximum LOD score of 3.07 obtained in the 100-markers analysis shown in Fig. 3). The expected maximum LOD score for this pedigree, obtained when only one disease-associated locus segregates in all affected individuals, is 4.18 [evaluated by simulating 100 genotypes conditional on the trait using the MORGAN tool markerdrop (Basu et al., 2008)]. This is consistent with the fact that the three segregating haplotypes are less likely than a single segregating haplotype. Note that the results of the Haplotyping tool do not directly correspond to the computed LOD score, as the Haplotyping tool finds the most likely inheritance vector while the LOD score computation averages over all possible inheritance vectors. The two computations are equivalent only when all meioses are fully informative, which rarely happens when analysing SNP data with limited window sizes.

3 SYSTEM AND METHODS

3.1 System infrastructure

Superlink-Online SNP speeds up linkage analysis computations by using the aggregate power of thousands of CPUs scattered in computing clusters and home desktops around the world. The system automatically parallelizes the computations by splitting the problem into many independent subtasks, invokes these subtasks in parallel on many remote computers and finally combines all the partial results to be presented to the user as if they were executed on a single machine.

By design, Superlink-Online SNP does not rely on expensive supercomputing resources for operation. Instead, it leverages non-dedicated computers that are not allocated to be exclusively used by the system, but permit execution of tasks occasionally, only when allowed to do so by their owners.

Providing a dependable and fast service over such a best-effort distributed execution environment poses a number of unique challenges. Below we list the main such challenges and briefly describe the key techniques instrumental to the successful operation of the Superlink-Online SNP system.

Parallelization. The original computing task has to be split into multiple subtasks while satisfying a number of constraints.

Independence. The subtasks must be independent to ensure steady progress of the computations despite subtasks failures. Such failures are in fact common in reality. For example, they occur when a computer owner requests to regain the control of his/her machine. The running task must be then immediately and unconditionally vacated from that machine. Independence between subtasks enables them to be restarted on a different CPU without affecting the execution of other concurrently running subtasks.

Number of subtasks and their size. The number of subtasks generated for each linkage analysis task determines the maximum performance increase for that task versus its execution on a single CPU, and thus has to be maximized. However as the number of subtasks increases, the amount of computations per subtask shrinks, and the benefits of adding more CPUs become outweighed by the overheads owing to their execution in a distributed environment.

The parallelization in Superlink-Online SNP is based on the algorithm introduced and implemented in the previous generation of the system, Superlink-Online (Silberstein et al., 2006a,b). The algorithm splits the problem by assigning values to some variables in the underlying statistical model. The subtasks are recursively split further, until their estimated running time is within the system-dictated boundaries. The created subtasks are independent, and the final result is obtained by computing a simple sum of all partial results.

While designing Superlink-Online SNP, we analysed the performance of 15 000 real linkage analysis tasks previously submitted to Superlink-Online during 1 year of operation. We found that although the algorithm often allowed for scalable parallelization of real inputs, it was notoriously inefficient in many others, often misclassifying input tasks as infeasible. The reason for this inefficiency was hidden in the false assumption that the running times of all the subtasks were identical. In reality, in addition to the subtasks that were consistent with the estimate, there were a large number of very short subtasks, regardless of what was predicted by the algorithm. These short subtasks often constituted >95% of all the generated subtasks, and caused excessive network load and system slowdown.

We devised a pruning algorithm for fast detection of short subtasks, which is used to analyse all the generated subtasks before the full parallel execution. As a result, the short subtasks are eliminated and their contribution to the final result is quickly computed without actually running each subtask. The pruning algorithm itself is executed in parallel as well. More technical details can be found in (Silberstein, 2011).

Execution environment. Our goal to reach out as many CPUs as possible is realized through a system, called GridBot (Silberstein et al., 2009), which is capable of acquiring and efficiently using a variety of uncoordinated computing resources. These resources range from university computing clusters and large-scale computational grids and clouds, to desktop computers scattered all over the world.

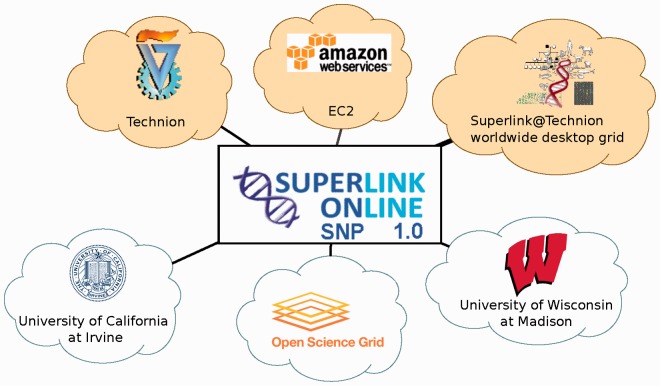
The current deployment of the Superlink-Online SNP system is depicted in Figure 4. During the period of 1 year, the system used about 50 000 computers in 130 countries, providing the total computing power equivalent to about 1000 CPU years.

Fig. 4.

Superlink-Online SNP production deployment. Each cloud represents a single independently managed system with hundreds to tens of thousands of CPUs

The GridBot system was designed with two primary goals: to dynamically establish a centrally managed cluster of CPUs in response to computing demand of linkage analysis tasks, and to provide mechanisms for prompt and correct execution of multiple parallel tasks on these CPUs.

To achieve the first goal, the system dynamically creates an overlay of execution clients across the diverse computing environments connected to the GridBot system. These clients, invoked on remote CPUs instead of actual subtasks, connect back to the central GridBot server to fetch the subtasks or report results. The system dynamically provisions the number of the CPUs from each connected environment, by considering the amount of subtasks in its queue, as well as the availability and local policies of the remote computers. This technique enables us to effectively lease CPUs from many different computing systems, simplifying their coordination and management. A CPU lease ends when GridBot completes its computations, or when the CPU owner requires it back.

After the leased CPUs become available, GridBot invokes the subtasks according to the following execution policy:

1. Less demanding linkage analysis requests are prioritized on more reliable CPUs, thereby reducing the chance of a subtask failure, and resulting in faster completion. Simpler runs are also prioritized over more demanding ones to allow interactive response.

2. Few subtasks that belong to a task toward its completion are invoked more than once on different CPUs. Then, the result of the first task is accepted. This technique, called replication, is known to facilitate prompt completion of large parallel runs, which would otherwise be significantly delayed by failures of the last few remaining subtasks.

GridBot dynamically learns the reliability of the CPUs participating in the computation by counting the number of subtasks successfully completed by each CPU. Similarly, other system characteristics are constantly gathered and analysed, allowing for automatic adjustment of the execution behavior to the rapid changes in the system conditions. We refer the interested reader to (Silberstein et al., 2009) for more details.

3.2 Approximate analysis via MCMC

MCMC is a class of algorithms for sampling from a distribution using a Markov chain whose stationary distribution is the target distribution (Andrieu et al., 2003). The main drawback of MCMC methods is the difficulty in determining the chain convergence rate, for which there is no general analytical analysis. A variety of statistical measures for convergence have been proposed, among which is the GR score. This statistic compares the sample variance of a certain quantity of interest between different MCMC chains with the average within-chains sample variance. The closer the GR score is to one, the closer the MCMC chains are to convergence. The GR scores calculation can be briefly described as follows. Denote m as the number of MCMC chains invoked and n as the number of MCMC iterations. Further denote B / n as the sample variance of the quantity of interest between different MCMC chains and W as the average within-chain sample variance. The GR score is defined as 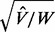, where 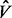is given by 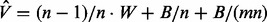[Superlink-Online SNP actually uses a slightly more refined measure, described in (Gelman and Rubin, 1992) and further refined in (Brooks and Gelman, 1998)]. Assuming that the starting points of the different MCMC chains are over-dispersed compared with the target distribution, is an overestimate of the true pooled variance, and thus the GR score is an overestimate of the sample variance ratio.

MORGAN is a collection of software, under the PANGAEA (pedigree analysis for genetics and epidemiological attributes) umbrella. These programs implement a number of methods for the analysis of data observed on members of a pedigree structure. lm_linkage is a program of the MORGAN package, which estimates multi point LOD scores using Monte Carlo sampling of latent autozygosity states conditional on multilocus marker data. Superlink-Online SNP performs approximate genetic linkage analysis using this program. Each analysis is repeated five times to refine the obtained LOD score and compute a GR score, and the reported LOD score is the average. Note that the actual MCMC algorithm is not parallelized, but several different MCMC runs of different genomic regions can run on several CPUs simultaneously, speeding up the analysis. Additional details about the MORGAN package are available elsewhere (Tong and Thompson, 2008).

3.3 Parallel haplotyping algorithm

Superlink-Online SNP uses the DAOOPT solver [Distributed AND/OR Optimization (Otten and Dechter, 2012a)] for efficient parallel exact maximum-likelihood haplotyping. Initially, the pre-processed pedigree is converted into a Bayesian network and a number of domain-specific optimizations are applied (Allen and Darwiche, 2008; Fishelson et al., 2005). The subsequent execution of DAOOPT is based on sequential AND/OR branch-and-bound (Marinescu and Dechter, 2009a,b), a state-of-the-art algorithm that explores the AND/OR context minimal search space of the pedigree-based Bayesian network in a depth-first manner by exploiting the following key methods:

• decomposition of independent subproblems, enabling exponential time savings;

• full caching of intermediate solutions, further reducing computation time at the expense of additional memory usage;

• mini-bucket heuristics whose strength, controlled by an i-bound, is dynamically adjusted based on the amount of memory available. The required memory is exponential in the i-bound (Kask and Dechter, 2001).

This general framework has been highly competitive in recent algorithmic competitions; for instance, it won first places in all three optimization tracks of the PASCAL 2011 Probabilistic Inference Challenge (results at http://www.cs.huji.ac.il/project/PASCAL/). Furthermore, already in non-distributed execution, it has proven to be far more efficient than earlier haplotyping schemes in Superlink-Online.

The distributed implementation of DAOOPT follows the paradigm of parallel tree search, where a space of partially assigned (conditioned) subproblems are solved by different CPUs. These subproblems are managed through a central search scheme (Otten and Dechter, 2012a). The complexity and number of these subproblems is a central factor that governs the overall performance; sufficiently many subproblems are required to allow for efficient parallelization on a large number of parallel resources, but overhead and structural redundancies dictate that the individual work units do not become too small.

The most important task of the distributed algorithm and primary research challenge is then to maintain efficient load balancing, meaning that the parallel subproblems have similar solution complexity and computational resources are thus used equally; in particular, no single subproblem should dominate the overall runtime. In practice, however, this is made highly difficult by the pruning power of the branch-and-bound algorithm, which can have vastly diverging impact in different parts of the search space.

We have therefore developed a number of novel schemes that estimate subproblem size ahead of time based on different subproblem parameters (Otten and Dechter, 2010, 2011; Otten et al., 2009). The most recent, most general approach used in Superlink-Online SNP’s parallel haplotyping component is based on machine learning methods, in particular linear regression (Otten and Dechter, 2012b). Similar methods have been successfully applied to propositional logic (SAT) solvers (Xu et al., 2008). For a parallel subproblem x, we model its complexity N(x) as log-linear in its subproblem features ϕ_i(x) through:

(1)

The set of features ϕ_i(x) used by DAOOPT includes:

• upper and lower bounds on the subproblem’s solution, derived from the probabilities of the Bayesian network by the mini-bucket heuristic and the search procedure;

• various structural parameters extracted from the underlying subproblem graph (induced width, search space depth, domain size statistics, etc.), as built from the pedigree instance.

In an offline step, we have compiled a substantial training set of example subproblems x_j, 1 ≤ j ≤ m, of varying sizes and from different pedigree instances, and recorded their feature values ϕ_i(x_j) and the respective solution complexity N(x_j). We apply linear regression with lasso regularization [to avoid overfitting and enhance numerical stability (Tibshirani, 1996)] on the training set feature values and log complexities, to minimize the regularized mean squared error:

(2)

This yields a set of weights λ_i for the general expression (1) above. The resulting regression model is used by the DAOOPT software in Superlink-Online SNP’s haplotyping component to predict the complexity of subproblem instances when deciding how to split the overall problem into parallel work units in a balanced way.

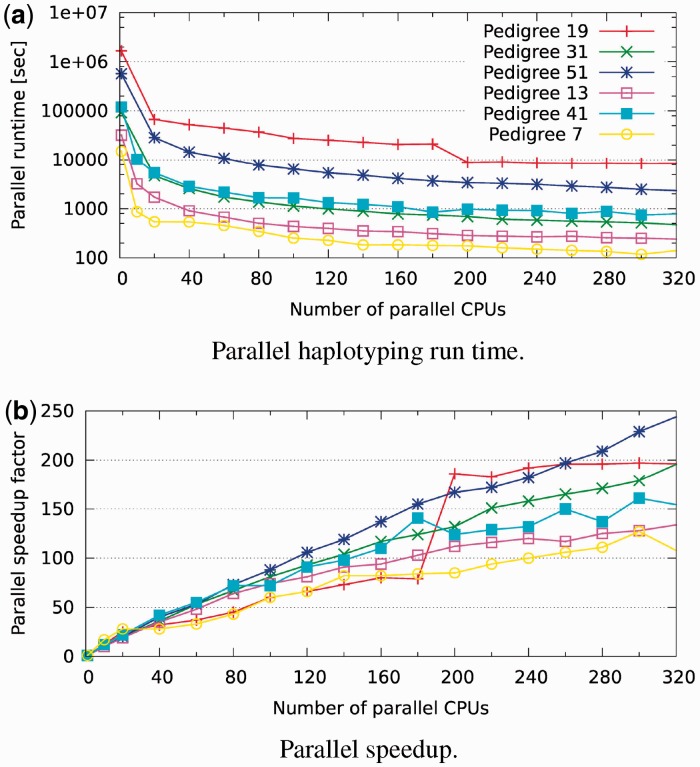
To evaluate the parallel performance of the haplotyping component, we conducted experiments on six complex haplotyping problems (Supplementary Material) using a dedicated cluster of 320 CPUs; these problems are based on pedigrees with 20–25 individuals and take many hours or even days to solve exactly using just a single processor. The results for varying degrees of parallelism are presented in Figure 5. We note that the most complex problems in particular provide very good parallel speedup (perfect linear speedup cannot be expected owing to overhead inherent to distributed processing)—the runtime of ‘pedigree19’, for instance, is reduced from nearly 1 week (158 h) to under 40 min, by a factor of almost 250; ‘pedigree51’ goes from >19 days (461 h) to 2 h and 20 min. As was to be expected, the simpler problems (taking just a few hours on a single CPU) are not as conducive to parallel speedup because the inherent parallel overhead has a relatively stronger impact, yet we still see good parallel performance.

Fig. 5.

Parallel haplotyping run time (log scale) on six hard pedigrees for varying number of CPUs and their corresponding parallel speedup

We note that the solution to the maximum-likelihood haplotyping problem is often not unique, namely there are typically several equally likely configurations, e.g. because of symmetries like untyped individuals without children. The current implementation of DAOOPT in Superlink-Online SNP returns only one of these equally likely solutions. The general problem of finding the m best solutions is an inherently harder task, yet of much practical interest. Besides finding all most likely ones it would also yield the set of second best, third best, etc. haplotype configurations for large enough values of m, at the expense of increased computational complexity. Recent improvements have been made to the sequential search algorithms that DAOOPT is based on to allow finding m best solutions in an efficient manner (Dechter et al., 2012), but more research and development effort is required to add this functionality to the distributed scheme.

Similarly, the issue of complexity prediction and load balancing is subject to ongoing work and we expect that refining the models for subproblem estimation will allow us to further improve on the results above.

4 DISCUSSION

We have described the system Superlink-Online SNP that provides geneticists a suite of genetic analysis utilities and is able to perform analyses that are infeasible elsewhere. The system provides tools for both exact and approximate analysis with a reliable accuracy measure. The system source code is freely available, and an online version is also available, enabling computations using tens of thousands of CPUs. In the online version, each user has a private password-protected account and unauthorized access is prevented to retain data privacy. Users can download their data and delete it from the system at any time. Users with higher privacy concerns can download the system source code and install it on their own clusters.

One line of future work we intend to pursue is better handling of LD (Schaid et al., 2002). The system currently reduces the amount of LD by randomly selecting a small subset of the input SNPs while preserving the relative SNPs density, which prevents two SNPs in very close proximity from both remaining in the analysis. It has been shown that LD rarely affects linkage analysis when SNP markers are separated by ≥0.1 cM (Evans and Cardon, 2004). The system also provides a manual filtering tool that can also help reduce the amount of LD. Nevertheless, in the future, we plan to utilize recently developed methods (e.g. Albers and Kappen, 2007; Bellenguez et al., 2009a; Cho and Dupuis, 2009; Kurbasic and Hssjer, 2008; Rinaldo et al., 2005; Webb et al., 2005; Zhang et al., 2009) to better handle this phenomenon.

The rapidly growing availability of high-throughput sequencing data presents new challenges, as well as new opportunities, for genetic linkage analysis (Wijsman, 2012). Although linkage analysis of sequencing data has already been successfully conducted (Smith et al., 2011), our initial experiments have shown that analysis of such data is more sensitive to genotyping errors, as well as to biological phenomena that violate the assumptions of genetic linkage analysis such as insertions, deletions and single-base mutations (data not shown). Our future plans include developing solutions to streamline the genetic linkage analysis of next generation sequencing data, and help geneticists exploit the potential of these promising new technologies.