Combined in vivo and in silico investigations of activation of glycolysis in contracting skeletal muscle

Abstract

The hypothesis was tested that the variation of in vivo glycolytic flux with contraction frequency in skeletal muscle can be qualitatively and quantitatively explained by calcium-calmodulin activation of phosphofructokinase (PFK-1). Ischemic rat tibialis anterior muscle was electrically stimulated at frequencies between 0 and 80 Hz to covary the ATP turnover rate and calcium concentration in the tissue. Estimates of in vivo glycolytic rates and cellular free energetic states were derived from dynamic changes in intramuscular pH and phosphocreatine content, respectively, determined by phosphorus magnetic resonance spectroscopy (³¹P-MRS). Computational modeling was applied to relate these empirical observations to understanding of the biochemistry of muscle glycolysis. Hereto, the kinetic model of PFK activity in a previously reported mathematical model of the glycolytic pathway (Vinnakota KC, Rusk J, Palmer L, Shankland E, Kushmerick MJ. J Physiol 588: 1961–1983, 2010) was adapted to contain a calcium-calmodulin binding sensitivity. The two main results were introduction of regulation of PFK-1 activity by binding of a calcium-calmodulin complex in combination with activation by increased concentrations of AMP and ADP was essential to qualitatively and quantitatively explain the experimental observations. Secondly, the model predicted that shutdown of glycolytic ATP production flux in muscle postexercise may lag behind deactivation of PFK-1 (timescales: 5–10 s vs. 100–200 ms, respectively) as a result of accumulation of glycolytic intermediates downstream of PFK during contractions.

glycolysis plays a central role in catabolism and anabolism for all cell types (20; 44). Identification of regulatory mechanisms has been important to many areas of biomedical research, ranging from basic understanding of the biochemistry of carbohydrate utilization to applications in biotechnology (48) and drug development for cancer therapies (39). In mammalian cells, skeletal muscle has been a key experimental model to study the regulation of glycolysis and glycogenolysis. It can increase the glycogenolytic ATP production flux by two orders of magnitude during rest to work transitions on a timescale of seconds (56). This exceptionally broad and dynamic operational range of glyco(genol)ytic flux puts a high duty cycle upon the control mechanism(s) of this pathway.

Several approaches have been used to elucidate the underlying regulatory mechanisms including physical isolation and in vitro kinetic characterization of individual enzymes from skeletal muscle providing a wealth of information on the individual components of this pathway (3). The application of noninvasive, nondestructive investigative techniques such as in vivo nuclear magnetic resonance spectroscopy (MRS) have since allowed studying the behavior of the intact pathway in muscle (8). For example, it has been demonstrated that glycolytic flux rapidly shuts down in the absence of muscle contraction (6, 12, 14, 15, 43). More recently, computational modeling approaches have been used to integrate the accumulated knowledge base at the molecular level including quantitative formulation of hypotheses on regulatory mechanisms with in vivo flux measurements to test this knowledge base against empirical data (3).

The precise biochemical mechanisms underlying the rapid shutdown of glycolysis in muscle upon termination of muscle contraction have remained poorly understood (3, 47). We have previously shown that reproducing this particular pathway characteristic solely on the basis of known in vitro enzymes kinetics is not possible (47). Specifically, silencing of glycolysis in noncontracting muscle requires rapid deactivation of the key crossover enzymes phosphofructokinase (PFK-1) and pyruvate kinase (PYK) in the pathway (47). The regulation at the level of PFK-1 was predicted to have a dominant role in glycolytic flux control, while in contrast the regulation of PYK was found to be more relevant to glycolytic metabolite concentration control particularly with respect to intermediate metabolites downstream of PFK-1. A mechanism that may explain the wanting additional regulation at the level of PFK-1 is calcium-calmodulin-mediated activation of this enzyme by binding of PFK-1 to, e.g., cytoskeleton and the contractile proteins (34, 36, 37). Whether or not this mechanism is qualitatively and quantitatively sufficient to reconcile the observed characteristics in vivo remains to be tested.

Here, this question was further investigated. Testing of the PFK-1 calcium activation hypothesis is, however, not straightforward for practical reasons. On the one hand, the 1) complexity of muscle cell structure (e.g., cytoskeletonal localization), and 2) ancillary processes (e.g., fast calcium release and uptake and calcium-calmodulin signaling) are difficult to include in an in vitro experimental system. On the other hand, in vivo experiments likewise suffer from practical limitations. These include the fact that 1) the pathway can only be studied as an integrated system, 2) few biochemical indicators are available to evaluate glycolytic output (for example intermediate metabolite concentrations are often unknown), 3) there is only limited control of individual variables [metabolite levels often covary with changes in flux (12, 14)], and 4) pathway flux may change with negligible variations in steady state metabolite concentrations.

To overcome these limitations, the present investigation of calcium regulation of PFK-1 activity in skeletal muscle via PFK-1-calmodulin interaction has employed an integrative approach of combining in vivo measurements of pathway behavior and the extensive database of known enzyme kinetics embedded in a computational model. The in vivo readouts were acquired in the rat using ³¹P-MRS of the ischemic tibialis anterior (TA) evoking contractions at different duty cycles, thereby inducing varying conditions of myocellular calcium concentration and glycolytic flux. The objective of the modeling studies was to reproduce both metabolite and pH dynamics for these different electrically induced contraction protocols and test whether pathway regulation proposed within the computational model was consistent with the measured physiologic behavior. It is shown that introduction of regulation of PFK-1 activity by binding of a calcium-calmodulin complex in combination with classic AMP and ADP activation was quantitatively necessary and sufficient for model predictions to be consistent with in vivo behavior.

METHODS

Study Design

The principal aim of this study was to investigate the regulation of glycolysis in muscle in vivo through the use of an integrated approach of experiments and computational modeling. The experimental work involved ³¹P-MRS of the exercising rat TA muscle. To prevent complications from oxidative ATP production, all experiments were performed under conditions of ischemia. Different metabolic workloads and levels of calcium were applied by varying the frequency of muscle excitation. From these data, measures for the metabolic status of the muscle (PCr concentration) and the glycolytic rate (deduced from pH dynamics) was determined. The aim of the modeling effort was to test if addition of calcium-calmodulin activation of PFK-1 allowed the model to reproduce both metabolic state of the muscle (PCr concentration) and glycolytic rate (pH dynamics). The recorded dynamics of the sugar phosphates were used as input signal of the model (for detailed description see Pathway supply flux). Therefore the model for glycogenolysis does not contain a kinetic description of glycogen phosphorylase (GP). The dynamics of GP activity, including the activation of GP by calcium (7), were included in the experimentally determined input flux.

Experimental Methods

Animals.

Adult male Wistar rats (385 ± 22 g, 15-wk-old, n = 28; Charles River Laboratories) were housed in groups at 20°C and 50% humidity on a 12-h light-dark cycle with ad libitum access to water and chow. The principles of laboratory animal care were followed, and all experimental procedures were approved by the Animal Ethics Committee of Maastricht University (Maastricht, The Netherlands). During preparatory surgical procedures and MRS experiments, animals were anesthetized using 0.8–1.2% isoflurane (Forene; Abbot, Wiesbaden, Germany) administered via a face mask with medical air and oxygen (0.2 and 0.1 l/min, respectively). Temgesic was used as analgesic [0.3 mg/ml Temgesic in saline solution (1:10), 0.10 mg/kg; Schering-Plough]. Body temperature was maintained at 37 ± 1°C using heat pads and monitored by a custom-built monitoring system. In the MR scanner, respiration was monitored using a pressure sensor registering thorax movement (Rapid Biomedical, Rimpar, Germany). Ischemia was applied by means of a silicone vessel loop (Identi Loops Supermaxi Blue; Dispo Medical), which was applied around the thigh to restrict blood flow in the leg.

Contractions were induced by using electrical stimuli applied via acute, subcutaneously implanted platinum electrodes positioned along the distal nerve trajectory of the n. peroneus communis. Excitation of this nerve induced contraction in the TA, extensor digitorum longus (EDL), peroneus longus, and brevis in the anterior compartment of the rat hindlimb (16, 17). Stimulation voltage ranged between 6 and 7 V, and pulse length was 1 ms. Contractile duty cycles were varied over a range of frequencies (5, 10, 40, and 80 Hz) and pulse train lengths summarized in Table 1. For each group, four to five successful measurements were obtained in different animals. All experiments were conducted under ischemic conditions. Successful occlusion of oxygen supply to the muscle was verified by the absence of any PCr and pH recovery in the 10 min after exercise.

Table 1.

Summary experimental groups

Group	Stimulation Frequency, Hz	Pulse Train Length, no. of pulses	Pulse Train Length, s	Duration of the Experiment, min
Group 1 (rest)	No stimulation			120 min
Group 2	1	5	5	20 min*
Group 3	5	10	2	20 min*
Group 4	10	10	1	20 min*
Group 5	40	10	0.25	20 min*
Group 6	40	20	0.5	20 min*
Group 7	80	10	0.125	20 min*

^*Protocol consisted out of 2-min rest, 8-min electrical stimulation, and 10-min rest.

³¹P-NMR acquisition parameters.

All MRS measurements were performed on a 6.3-T horizontal Bruker magnetic resonance spectrometer (Bruker, Ettlingen, Germany). ³¹P-MRS was performed by using a two-coil configuration. A circular ¹H surface coil (40 mm) was used to adjust the magnetic field homogeneity using the available proton signal from water, while a smaller elliptical surface coil (10/18 mm) was positioned over the TA to acquire phosphorus data. ³¹P-spectra were acquired applying an adiabatic excitation pulse with a flip angle of 90°. A fully relaxed spectrum (TR = 20 s, 32 averages) was measured at rest. A time series of spectra (TR = 5 s, 2 averages) before, during, and after electrical stimulation of ischemic TA. A time series consisted of a 2-min rest, 8-min stimulation, and 10 min after stimulation. An exception was the experiment without stimulation (group 1, Table 1), which had a duration of 120 min.

Coil sensitivity profile.

The sensitivity profile of the ³¹P coil was calculated from a two-dimensional (2D) chemical shift imaging (CSI) data set recorded in rest conditions with blood supply intact. 2D CSI acquisition parameters were as follows: field of view, 25 × 25 mm²; matrix size, 16 × 16 (reconstruction 32 × 32); TR = 5,000 ms; hamming weighted acquisition and postprocessing with 1,800 scans in total, and adiabatic excitation pulse with a flip angle of 90° (identical to the time series experiments). The intensity of the PCr peak was calculated for each voxel. The intensity of the PCr peak was integrated over the voxels of the muscle in which contractions were induced (TA, EDL, and peroneus longus + brevis), and the voxels in which no contractions were induced. These calculations indicated that 75% of the signal detected by the surface coil, originated from contracting muscle. The residual signal (25%) was received from the noncontracting muscle.

Data processing.

³¹P-MR spectra were fitted in the time domain by using nonlinear least squares algorithm in the jMRUI software package (53). The PCr peak was fitted to a Lorentzian line shape. The inorganic phosphate (P_i) and phosphor-monoester (PME) peaks and α- and γ-ATP peaks were fitted to Gaussian line shapes. The α- and γ-ATP peaks were fitted with equal peak areas. The β-ATP was not quantified because of concerns for the limited bandwidth of the excitation pulse. Absolute concentrations were calculated after correction for partial saturation with the assumption that the ATP concentration is 8.2 mM at rest (50, 54). Intracellular pH was calculated from the chemical shift difference between the P_i and PCr resonances (δ; measured in part per million), according to Eq. 1 (51).

$$\text{pH}=6.75+\log \left(\frac{\delta -3.27}{5.63-\delta }\right)$$ (1)

The ³¹P-coil received signal from both contracting muscle (75%) and noncontracting muscle (25%; see Coil sensitivity profile). The metabolite dynamics in the contracting muscle were derived from the measured dynamics according to the following calculations. The signal received by the ³¹P-MRS coil is described by Eq. 2.

$$X_{observed}(t)=X_{contraction}(t)*F_{contraction}+X_{noncontracting}(t)*F_{noncontracting}$$ (2)

where, X_observed, X_contraction, X_{noncontracting}, F_contraction, and F_{noncontracting} denote the measured metabolite concentration, the metabolite concentration in contracting muscle, metabolite concentration in the noncontracting muscle, the fraction of the signal originating from contracting muscle and the fraction of the signal originating from noncontracting muscle, respectively. F_contraction and F_{noncontracting} were set according to the values determined from the 2D-CSI data set: 0.75 and 0.25, respectively. X_{noncontracting}(t) was determined from the ischemia experiment without electrical muscle stimulation. According to this data set ATP_{noncontraction}(t) could be assumed constant during the first 30 min at 8.2 mM. PCr_{noncontracting}(t), Pi_{noncontracting}(t), and PME_{noncontracting}(t) during the first 30 min are well described by the equations: PCr_{noncontracting}(t) = PCr_rest − ATPase_rest·t, Pi_{noncontracting}(t) = Pi_rest + ATPase_rest·t and PME_{noncontracting}(t) = .092 + 0.000564·t, with PCr_rest, Pi_rest, and ATPase_rest set to 33.5 mM, 6.2 mM, and 0.01 mM/s, respectively. By addition of this information to Eq. 2, the equations for calculation of metabolite dynamics in the contracting muscle compartment become:

$$\begin{array}{c}PC{r}_{contracting}(t)=\frac{PC{r}_{observed}(t)-(33.5-0.01\cdot t)\cdot 0.25}{0.75}\\ P{i}_{contracting}(t)=\frac{P{i}_{observed}(t)-(6.2+0.01\cdot t)\cdot 0.25}{0.75}\\ AT{P}_{contracting}(t)=\frac{AT{P}_{observed}(t)-8.2\cdot 0.25}{0.75}\\ PM{E}_{contracting}(t)=\frac{PM{E}_{observed}(t)-(0.92+0.000564\cdot t)\cdot 0.25}{0.75}\end{array}$$ (3)

Selection of data included in computational analysis.

The ATP hydrolysis rate was modeled by mass action kinetics (Eq. 4). Because the ATP concentration is well buffered by creatine kinase at values close to 8.2 mM, effectively the ATP hydrolysis rate is assumed constant during exercise. The experimental data included in the numerical analyses were therefore limited to the part of the data set for which it was verified that this assumption was not violated by the onset of fatigue. The ATP hydrolysis flux during the experiment was calculated as the sum of the PCr breakdown rate and the glycolytic ATP production. Estimation of glycolytic ATP production rate was performed by application of a phenomenological model described by Conley et al. (9). From these calculations, it followed that the assumption of constant ATP hydrolysis rate was not violated for conditions of pH > 6.5. Therefore, model simulations were run until pH dropped below 6.5.

Computational Methods

Modeling glycolysis in skeletal muscle.

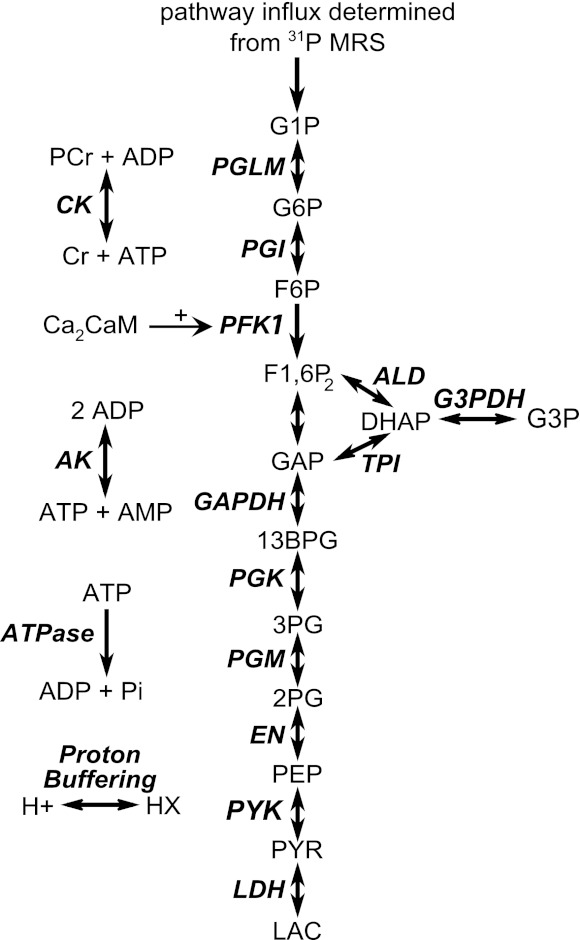
A previously developed detailed kinetic model of glycolysis in muscle was used as a basis of the computational analyses (55). A schematic overview of the model is shown in Fig. 1. The model includes flux descriptions of the glycolytic enzymes: GP, phosphoglucomutase (PGLM), phosphogluco-isomerase (PGI), phosphofructokinase (PFK-1), aldolase and triose phosphate isomerase (ALD and TPI), glycerol-3-phosphate dehydrogenase (G3PDH), glyceraldehyde-3-phosphate dehydrogenase (GAPDH), phosphoglycerate kinase (PGK), phosphoglyceromutase and enolase (PGM and EN), pyruvate kinase (PYK), and lactate dehydrogenase (LDH). In addition, the model contained detailed reaction kinetics of cellular ATP buffering processes: creatine kinase (CK) and adenylate kinase (AK). ATP hydrolysis was described by mass action kinetics (Eq. 4).

Fig. 1.

Schematic overview of the computational model. PGLM, phosphoglucomutase; PGI, phosphoglucoisomerase; PFK-1, phosphofructokinase; ALD, aldolase; TPI, triose phosphate isomerase; GAPDH, glyceraldehydes-3-phosphate dehydrogeanse; G3PDH, glycerol-3-phosphate dehydrogenase; PGK, phosphoglycerate kinase; PGM, phosphoglyceromutase; EN, enolase; PYK, pyruvate kinase; LDH, lactate dehydrogenase; CK, creatine kinase; AK, adenylate kinase; ATPase, ATP hydrolysis; G1P, glucose-1-phosphate; G6P, glucose-6-phosphate; F6P, fructose-6-phosphate; F1,6P₂, fructose-1,6-biphophate; DHAP, dihydroxyacetone-phosphate; G3P, glycerol-3-phosphate; GAP, glyceraldehydes-3-phosphate; 13BPG, 1,3-biphosphoglycerate; 3PG, 3-phosphoglycerate; 2PG, 2-phosphoglycerate; PEP, phosphoenolpyruvate; PYR, pyruvate; LAC, lactate; PCr, phosphocreatine; Cr, creatine; ADP, adenosine-diphospate; ATP, adenosine-triphosphate; Ca₂CaM, calcium-calmodulin complex; AMP, adenosine-monophosphate; Pi, inorganic phosphate; HX, protons bound to cellular proton buffer.

$$flu{x}_{ATP\_Hydr}=k_{ATP\_Hydr}[ATP]$$ (4)

During actual experimental conditions, large acidifications in cytosolic pH were observed (7.2–6.2). The effects of varying proton concentration on enzyme kinetics, pH dependency of enzyme V_max and equilibrium constants were included when known. Furthermore, proton buffering by metabolites and proteins and other cell structures was modeled by assuming a constant cellular buffer capacity (proteins) and dynamical buffer capacity that was calculated from metabolite concentrations. The stoichiometry of proton production and consumption was included for all modeled reactions to predict cellular proton accumulation. For further details on flux equations and kinetic parameter values we refer to the original work published by Vinnakota et al. (55). Ordinary differential equations (ODEs) were numerically solved using ODE15s, Matlab 7.5.0 (The Mathworks, Natick, MA).

Several changes to the Vinnakota model were made: first, the temperature for the model simulations was set to 35°C. Since the original framework by Vinnakota et al. used V_max parameters determined at 25°C, all V_max parameters were updated according to values determined at 37°C reported by Eagle and Scopes (18). Second, ATP synthesis flux by oxidative phosphorylation was removed because the current experiments were conducted under ischemic conditions. Third, the model for pathway supply of phosphorylated glucose was changed, and fourth, the kinetic model description of PFK-1 was substituted by a new rate equation. In the following sections, the changes for the model for pathway supply flux and rate equations of PFK will be described in detail.

Pathway supply flux.

The original model described by Vinnakota et al. (55) included GP to account for the pathway supply flux. However, model simulations revealed that the dynamic range of the GP model was insufficient to predict a realistic flux through this pathway (data not shown). This model behavior was probably due to lack of allosteric interactions of glucose-6-phosphate (G6P) in the flux descriptions and enzyme phosphorylation dynamics. At the moment, no better validated, detailed model of GP is available. Therefore, it was chosen to deduce pathway influx from our own experimental data. For conditions of constant ATP, it was assumed that the PME resonance represented the summed concentration of glucose-1-phosphate (G1P), G6P, and fructose-6-phosphate (F6P), which is in accordance with reports from other investigators (15, 56). The PME dynamics were well described by a linear function (data not shown). The derivative of this linear function was used to model the G1P input flux. The coefficients of the linear relation are provided in Table 2. It was assumed that all pathway influx was due to glycogen breakdown. The contribution of hexokinase was assumed negligible due to the complete occlusion of muscle blood flow blocking glucose supply to the muscles.

Table 2.

Linear fit to observed PME dynamics

Group	[PME] t = 0, mM	Slope, mM/s
Group 1 (rest)	0.9	0.00056
Group 2 (1 Hz)	1.5	0.010
Group 3 (5 Hz)	1.5	0.022
Group 4 (10 Hz)	1.5	0.023
Group 5 (40 Hz)	1.5	0.019
Group 6 (40 Hz)	1.5	0.019
Group 7 (80 Hz)	1.5	0.015

[PME], phosphor-monoester concentration.

Calcium-calmodulin mediated activation of PFK-1.

The PFK-1 model was substituted by the pseudorandom order, statistical inhibition model originally developed by Waser et al. (57) and adapted by Connett (10). In this section, the adaptations of this model are described. For the full set of equations governing this model, the reader is referred to in the appendix. Connett reported this model to be superior in terms of reproducing in vitro enzyme kinetics compared with the PFK-1 description used by Vinnakota et al. (55). It does not include regulation by citrate or fructose-2,6 biphosphate, both of which are strong allosteric modulators of PFK in vitro (38). The rationale for not including them in the kinetic model was that for mammals the dynamic range of these modulators in skeletal muscle is small, and therefore their contribution to the control of the enzyme in vivo is very limited (31, 41).

The model proposed by Connett featured an ADP- and AMP-dependent term to account for competitive binding of ADP and AMP to the ATP inhibition site. This term will hereafter be referred to as the “deinhibition” term. The definition of this term is:

$$deinhibition=1+\frac{AMP}{K_{AMP}}+\frac{ADP}{K_{ADP}}$$ (5)

where K_AMP and K_ADP are the AMP and ADP competitive binding constants, respectively, and AMP and ADP the AMP and ADP concentrations. Effectively, an increase of the deinhibition term as a result of elevated AMP and ADP levels relieves part of the ATP inhibition thereby activating PFK-1 flux. At physiological concentrations (∼8 mM), ATP inhibition results in a nearly full deactivation of the enzyme (>95%; Ref. 36). Therefore, reversing this inhibition will result in a significant increase of the enzymes catalytic activity.

In the present investigation, three different configurations of the PFK-1 model were evaluated (Fig. 2). The first configuration (model configuration i) represents conditions in which no calcium-calmodulin mediated activation of PFK-1 is present (Fig. 2A). This model includes the PFK-1 flux equation proposed by Connett (10). The parameter values of K_AMP and K_ADP were estimated from the PCr and pH time course data as described in Parameter estimation.

Fig. 2.

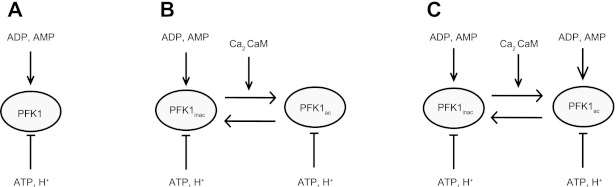
Schematic representation of the regulation of PFK-1 as modeled in each model configuration. Model configuration i (A) represented the hypothesis in which no regulation of PFK-1 by calcium-calmodulin signaling is present. Model configuration ii (B) represented the hypothesis in which binding of calcium-calmodulin complexes to PFK-1 partly reliefs ATP inhibition of the enzyme independent of the levels of ADP and AMP. Model configuration iii (C) represented the hypothesis in which binding of calcium-calmodulin complexes partly reliefs ATP inhibition by enhancing the competititve binding of AMP and ADP to the inhibitory ATP site.

The second configuration (configuration ii) included calcium-calmodulin activation of PFK-1 (Fig. 2B). Two forms of PFK-1 were defined: an inactive (PFK_inactive) and an active (PFK_active) form (36, 37). The inactive PFK-1 was described by the model proposed by Connett (10). Upon binding of two calcium-calmodulin complexes the enzymes switches from the inactive to the active isoform (36). Activation of the enzyme was suggested to occur via reversing the inhibitory effect of ATP (36). To account for this regulatory effect the deinhibition term of the active PFK-1 enzyme was modified to a constant (k_{deinhib_Act}; Eq. 6):

$$deinhibitio{n}_{activePFK}=k_{deinhib\_Act}$$ (6)

The value of k_{deinhib_Act} was estimated from the PCr and pH time course data as described in Parameter estimation. Effectively, the value of the deinhibition term of the active PFK enzyme was larger compared with the inactive PFK-1 enzyme. Consequently, switching from inactive to active form stimulates overall PFK-1 flux. The fractions of PFK-1 in active and inactive form were described by differential Eqs. 7 and 8. Switching of the enzyme from inactive to active form was stimulated by elevated cellular calcium-calmodulin concentrations, which is in accordance with observations by (7, 34, 36, 37). The values of k_on and k_off were estimated from the PCr and pH time course data as described in Parameter estimation.

$$\frac{dPF{K}_{active}}{dt}=k_{on}C{a}_{2}Ca{M}^2\cdot (1-PF{K}_{active})-k_{off}PF{K}_{active}$$ (7)

$$PF{K}_{inactive}=1-PF{K}_{active}$$ (8)

The deinhibition term of configuration ii (Eq. 6) was independent from cellular ADP and AMP levels. There are, however, indications that the flux through the activated PFK-1 enzyme is dependent on both cellular calcium levels and ADP and AMP levels (12). This particular regulatory scheme was represented by model configuration iii. To this end, the deinhibition term of the activated enzyme was modeled as a function of ADP and AMP concentrations, albeit with different competitive binding constants (K_AMP^act and K_ADP^act; Eq. 9).

$$deinhibitio{n}_{activePFK}=1+\frac{AMP}{K_{AMP}^{act}}+\frac{ADP}{K_{ADP}^{act}}$$ (9)

The values of K_AMP^act and K_ADP^actwere estimated from the PCr and pH time course data as described in Parameter estimation. Compared with the inactive enzyme, the values of the competitive binding constants K_AMP^act and K_ADP^act were lower. Consequently, the flux through the active PFK-1 enzyme is already increased at low AMP and ADP concentrations (compared to the inactive enzyme). The calcium-calmodulin fraction of PFK-1 in active and inactive form was modeled identical to model configuration ii: i.e., according to differential Eqs. 7 and 8.

For the full set of equations governing the PFK-1 model, the reader is referred to the appendix.

Calcium-calmodulin dynamics in muscle.

The differential equations of PFK-1 (de)activation are modeled as a function of Ca₂CaM (Eqs. 7 and 8). As a consequence, the PFK-1 (de)activation kinetics are determined by the particular reaction kinetics of calcium-calmodulin binding and unbinding, respectively. The latter were derived from a previously developed temperature dependent spatiotemporal model of skeletal muscle calcium handling (4, 26). The calcium handling model was extended by calcium-calmodulin reaction kinetics based on mass action kinetics. The values for the k_off and K_d were set to 100 s⁻¹ and 3.8 μM, and 5,000 s⁻¹ and 28.9 μM for the formation of Ca₂CaM and Ca₄CaM, respectively (2, 21, 29, 46). The spatially averaged calcium-calmodulin signal (Ca₂CaM) was calculated for 35°C and used as an input of the glycolysis model.

Parameter estimation.

The model contained several parameters for which an accurate value was either not available from any literature or were previously estimated in a computational study and likewise had no solid experimental basis (Table 3). These parameters were (re-)estimated from the newly recorded PCr and pH time-course data using a non linear least squares optimization algorithm (lsqnonlin, Matlab 7.5.0; The Mathworks, Natick, MA). The physiological meaning of each of the parameters included in the parameter estimation procedure is listed in Table 3. The algorithm adjusted parameter values during a series of model evaluations with the aim of minimizing the error (SSE) between model predictions and PCr and pH time-course data defined by Eq. 10. Because PCr and pH data are expressed in different units, a weighting parameter is required to balance the contribution of PCr and pH time-course data to the SSE. Instead of applying arbitrary defined weighting parameters, the accuracy of the measurement data (quantified by the SD of each data point) was used as weighting value. The confidence interval of the estimated parameter values was determined using Matlab routine nlparci, which exploited the Fisher information matrix to estimate the confidence intervals for each parameter.

Table 3.

Optimized parameter values

				Optimized Parameter Value withWidth Of 95% Confidence Interval Indicated Between Parentheses (%)
Parameter	Unit	Description	Initial Condition	Model conf. i	Model conf. ii	Model conf. iii
kATP Hydr (0 Hz)	s−1	ATPase rate constant 0 Hz	0.001a	0.0020 (±3.8%)	0.0020 (±5.1%)	0.0017 (±2.0%)
kATP_Hydr (5 Hz)	s−1	ATPase rate constant 5 Hz	0.01a	0.084 (±6.4%)	0.091 (±6.8%)	0.068 (±3.1%)
kATP_Hydr (10 Hz)	s−1	ATPase rate constant 10 Hz	0.01a	0.072 (±5.9%)	0.077 (±6.4%)	0.056 (±3.1%)
kATP_Hydr (40 Hz)	s−1	ATPase rate constant 40 Hz	0.01a	0.060 (±5.3%)	0.065 (±6.0%)	0.049 (±2.8%)
kATP_Hydr (80 Hz)	s−1	ATPase rate constant 80 Hz	0.01a	0.047 (±9.8%)	0.050 (±10.2%)	0.041 (±3.9%)
BuffCapFixed	M	Fixed buffer cellular proton buffer capacity	0.0142b	0.068 (±8.6%)	0.073 (±10.8%)	0.050 (±5.5%)
VmaxPFK	mM/s	Vmax PFK	0.93b	8.76 (±26.0%)	10.43 (±43.8%)	10.25 (±11.9%)
KAMP	mM	PFK deinhibition constant AMP	0.002c	0.0017 (±29.1%)	0.014 (±5.2%)	0.046 (±23.3%)
KADP	mM	PFK deinhibition constant ADP	0.030c	0.31 (±49.3%)	0.16 (26.6±%)	0.24 (±7.2%)
kdeinhib_Act	unitless	PFK deinhibition constant activated PFK	1c	—	8.72 * 106 (±2.45 * 105%)	—
KAMPact	mM	PFK deinhibition constant AMP activated PFK	0.002c	—	—	2.23 * 10−5 (±6.0%)
KADPact	mM	PFK deinhibition constant ADP activated PFK	0.030c	—	—	0.020 (±28.3%)
kon	μM−2/s	PFK, calcium-calmodulin binding constant	1 * 104–1 * 109	—	1.26 * 106 (±2.00 * 103%)	6.08 * 105 (±19.3%)
koff	s−1	PFK, calcium-calmodulin binding constant	1 * 101–1 * 104	—	4.75 * 103 (±23.3%)	106 (±13.3%)
kATP_Hydr (1 Hz)	s−1	ATPase rate constant 5 Hz	0.005a,d	0.036 (5.0%)	0.038 (15.6%)	0.032 (5.0%)
kATP_Hydr (40 Hz, 20 pulses)	s−1	ATPase rate constant 40 Hz 20 pulses	0.02a,d	0.050 (20.0%)	0.042 (35.3%)	0.072 (11.6%)

PFK, phosphofructokinase; conf., configuration.

^aEstimated from initial PCr breakdown rate;

^bvalues used as initial condition in Ref. 55;

^cvalues obtained from Ref. 10;

^destimated for validation experiments (Fig. 5).

The entire data set was divided into two groups: i.e., 1) data for parameterization, and 2) data for verification. The parameterization data [at 0, 5, 10, 40 (1 pulse train per 5 s, 10 pulses per pulse train), and 80 Hz] was used to estimate model parameter values. These parameters, initial conditions and the optimal values are given in Table 3. As indicated in Table 3, the initial parameter values were calculated from the MRS data or taken from other studies. An initial guess for the values of the PFK-1, calcium-calmodulin binding constant, i.e., k_on and k_off was however, not available. Therefore, the initial values for these parameters were randomly taken from uniform distributions with ranges as indicated in Table 3 using a multistart optimization approach (500 runs).

Model predictions were next tested against independent data (i.e, data not used in the parameter estimation procedure): 5 pulses per 5 s (1 Hz) and 1 pulse train per 5 s, 20 pulses per pulse train (40 Hz). For these simulations all parameters were left unchanged, except for the ATP hydrolysis rate constant k_{ATP_Hydr}. The resulting estimated values of these rate constants are provided in Table 3.

Quantification of model fit.

The goodness of fit of the different model configurations to the experimental data was quantified by the sum of squared errors (SSE). The SSE was summed over all data used for parameter estimation. Data points were weighted by the SD of the experimental data (n = 4–5; Eq. 10).

$$SSE={\displaystyle \sum _{j=1}^M{\displaystyle \sum _{i=1}^N{\left\{\frac{mean\left[PC{r}_{observed}(i)\right]-PC{r}_{predicted}(i)}{SD\left[PC{r}_{observd}(i)\right]}\right\}}^2+{\displaystyle \sum _{i=1}^N{\left\{\frac{mean\left[p{H}_{observed}(i)\right]-p{H}_{predicted}(i)}{SD\left[p{H}_{observd}(i)\right]}\right\}}^2}}}$$ (10)

In this equation PCr_observed(i) represents the mean PCr concentration ([PCr]; across-animal) at time point i; PCr_predicted(i) represents the predicted [PCr] at time point i; pH_observed(i) represents the mean pH (across-animal) at time point i; pH_predicted(i) represents the predicted pH at time point i; SD[PCr_observed(i)] represents the across-animal SD of the [PCr] at time point i; SD[pH_observed(i)] represents the across-animal SD of the pH at time point i; j denotes a specific experimental groups (e.g., 0, 5, 10, 40, and 80 Hz).

Akaike information criterion.

The Akaike information criterion (AIC; Ref. 1) was calculated for each model configuration to investigate if any improvement in SSE was merely the results of additional degrees of freedom of the model. AIC was calculated according to Eq. 11:

$$AIC=n*\ln (SSE/n)+2*K$$ (11)

In this equation, n denotes the number of datapoints (422) and K represents the number of estimated parameters (9, 12, and 13, for configurations i, ii, and iii, respectively). The AIC provides a means to select the preferred model (lowest AIC) taking into account the reduction of SSE while penalizing the additional degrees of freedom (K).

RESULTS

³¹P-MRS: Characterization of Pathway Dynamics

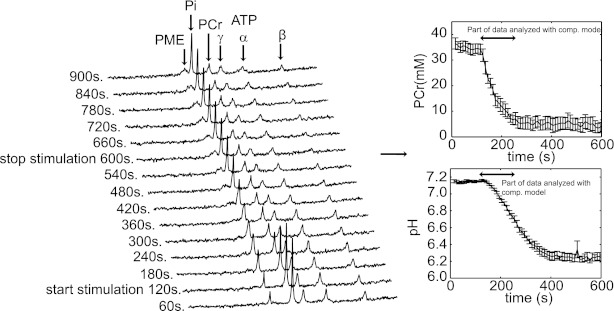
The dynamics of cellular metabolites: ATP, PCr, P_i, and PME as well as intracellular pH were monitored by ³¹P-MRS in ischemic rat TA muscle, under varying muscle stimulation frequencies (0–80 Hz). Figure 3A shows a stack plot of the spectra recorded during the 10-Hz stimulation protocol. These spectra were obtained by averaging 12 free-induction decays and processed with 5-Hz line broadening. In response to muscle contraction and corresponding elevated cellular ATP demand flux, the cellular ATP buffer PCr is consumed to balance energy demand and supply. PCr depletion coincides with the production of P_i, a product of ATP hydrolysis. In addition, during stimulation an increasing PME resonance was observed which was in the absence of any ATP depletion, attributed to the accumulation of sugar-phosphates (G1P, G6P, and F6P; Refs. 15, 56). Figure 3, B and C, shows an example (10 Hz) of the PCr and pH dynamics used for model testing (data expressed as mean ± SE). The part of the data used for model testing is indicated in Fig. 3. Any PCr and/or pH recovery was not observed during the period after stimulation. This observation validated the successful occlusion of blood circulation and obstruction of O₂ delivery to the muscle cells.

Fig. 3.

Characterization of in vivo pathway dynamics. Typical result of the experimental data obtained to characterize in vivo pathway behavior. A: stack plot of spectra obtained at 10-Hz stimulation. These spectra were obtained by averaging 12 free-induction decays and processed with 5-Hz line broadening. PME, P_i, phosphocreatine, PCr, and ATP resonances are indicated. Pooled PCr (B) and pH (C) dynamics at 10-Hz stimulation (n = 5). Error bars indicate SE. The part of the data analyzed by the computational model is indicated by a black arrow.

Model Simulations vs. Experimental Data

Model simulations according to the three different model configurations were compared with the experimental data (Fig. 4). Figure 4, A–E, shows the PCr dynamics for all three model configurations; Fig. 4, F–J, shows the pH dynamics for all three model configurations. The goodness of fit was used to test the hypothesis represented by each model configuration. Model configuration i (red lines) represented conditions lacking any calcium activation of PFK, whereas configurations ii (green lines) and iii (blue lines) both include calcium activation of PFK, albeit according to a different kinetic mechanism. Both model configurations i and ii failed in reproducing the experimental data. In contrast, model configuration iii could successfully reproduce both the energetic state of the muscle (PCr) as well as the glycolytic flux (pH dynamics) simultaneously. Compared with the model configurations i and ii, the sum of squared errors was reduced more than eightfold (386.7 and 354.6 vs. 44.8, respectively). The calculated AIC for model configurations i, ii, and iii were −8.1, −49.4, and −920.5 respectively. The large reduction in AIC for model configuration iii compared with configurations i and ii indicates that the improvement in the model fit (reduction in SSE) was much larger than could be expected from the additional number of estimated parameters. Based on these results, it was concluded that model configurations i and ii could not explain the in vivo sampled pathway dynamics. In contrast, these results provided evidence that calcium-calmodulin-mediated activation of PFK-1 in combination with activation of the enzyme by increased concentrations of AMP and ADP (model configuration iii) can explain the recorded dynamics of glycolytic flux in skeletal muscle in vivo.

Fig. 4.

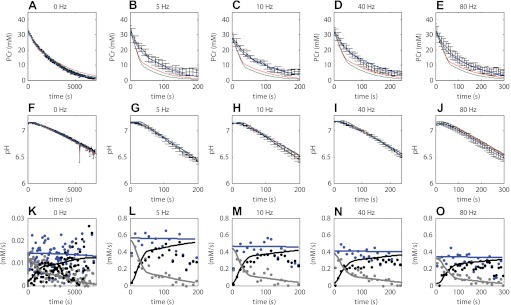
Quantitative hypotheses testing; experimental data vs. model simulations. Experimental data are indicated in black. Error bars indicate SE (n = 4–5). Simulation results according to model configuration i (without calcium activation of PFK-1, red lines) and model configuration ii and iii (with calcium activation of PFK-1, green and blue, respectively) are shown. Optimized model parameter values listed in Table 3 were obtained by fitting model stimulations to these data. A–E: PCr. F–J: pH. K–O: predictions according to model configuration iii (solid lines) of ATP supply flux by PCr hydrolysis (grey lines) and glycolysis (black lines) and ATP demand flux (blue lines), compared with values derived from the experimental data by using the phenomenological model (dots) described by Conley et al. (9). Calculations with the phenomenological model were performed using the estimated value of the static proton buffer capacity as listed in Table 3. As a result of the fast (de)activation kinetics of PFK-1 (see Fig. 7) the net glycolytic ATP synthesis flux was also pulsatile. For clarity of presentation, the glycolytic flux (black lines) indicated represents the net flux averaged over epochs of 5 s.

Figure 4, K–O, shows the predicted ATP supply flux by PCr hydrolysis (grey lines) and glycolysis (black lines) and ATP demand flux (blue lines), compared with values derived from the experimental data by using the phenomenological model described by Conley et al. (9). For clarity of presentation, these predictions are only showed for the model configuration iii. These results demonstrate that the fluxes predicted by the mechanistic model and the phenomenological model are consistent with one another. In retrospect, the predictions of the model configuration iii were also consistent with the calculations used to identify the part of the data at which the model assumption of constant ATP hydrolyses rates were not violated. The model predictions show that for conditions of pH >6.5 the sum of PCr breakdown rate (PCr dynamics) and glycolytic ATP production (pH dynamics) remain constant while being consistent with the experimental data.

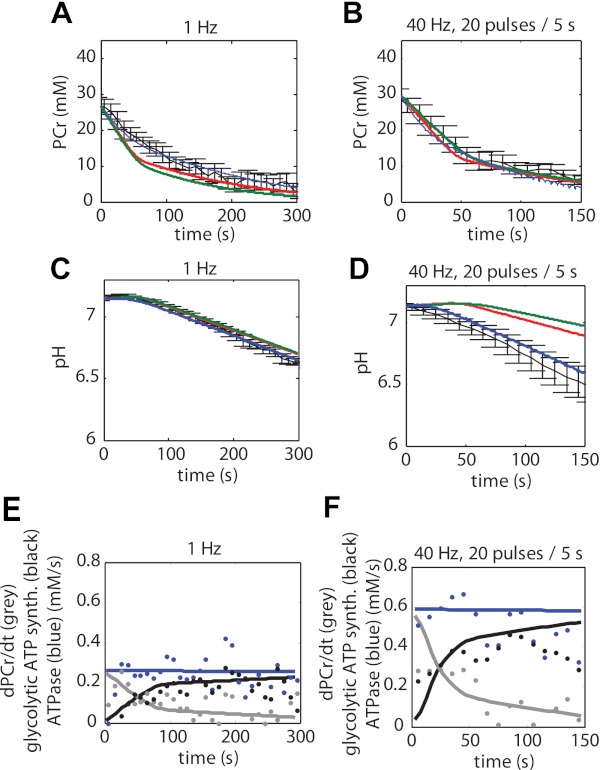
Model verification: model testing against independent data.

The veracity of the model was increased by using the algorithm on independent data sets. Experimental data of groups with a different number of excitation pulses per 5 s (compared with the data used for parameter estimation) was used: i.e., 1-Hz continuous stimulation (5 pulses/5 s) and 40 Hz (1 pulse train per 5 s, 20 pulses per pulse train). Experimental data vs. model predictions are shown in Fig. 5. These results show that the model can describe the behavior of the pathway for conditions of varying number of muscle excitation pulses. Model simulations are shown for the different configurations. The results show that only model configuration iii (blue lines) can reproduce the data. These results therefore act as validation of model configuration iii and they falsify model configurations i and ii. Figure 5, E and F, shows the predicted ATP supply flux by PCr hydrolysis (grey lines) and, glycolysis (black lines) and ATP demand flux (blue lines), compared with values derived from the experimental data by using the phenomenological model described by Conley et al. (9). For clarity of presentation, these predictions are only showed for the model configuration iii.

Fig. 5.

Model verification: comparison of model simulations and independent data for other stimulation frequencies than used for parameterization. Model simulations according to configurations i, ii, and iii are indicated in red, green and blue, respectively. Experimental data are indicated in black and correspond to muscle stimulation protocols of 1 Hz continues stimulation (A and C) and 40 Hz (1 pulse train per 5 s, 20 pulses per pulse train; B and D). Error bars indicate SE (n = 4–5). E and F: predictions according to model configuration iii (solid lines) of ATP supply flux by PCr hydrolysis (grey lines) and glycolysis (black lines) and ATP demand flux (blue lines), compared with values derived from the experimental data by using the phenomenological model (dots) described by Conley et al. (9). Calculations with the phenomenological model were performed using the estimated value of the static proton buffer capacity as listed in Table 3. As a result of the fast (de)activation kinetics of PFK-1 (see Fig. 7) the net glycolytic ATP synthesis flux was also pulsatile. For clarity of presentation, the glycolytic flux (black lines) indicated represents the net flux averaged over epochs of 5 s.

Model Predictions: Deactivation of Glycolysis Postexercise

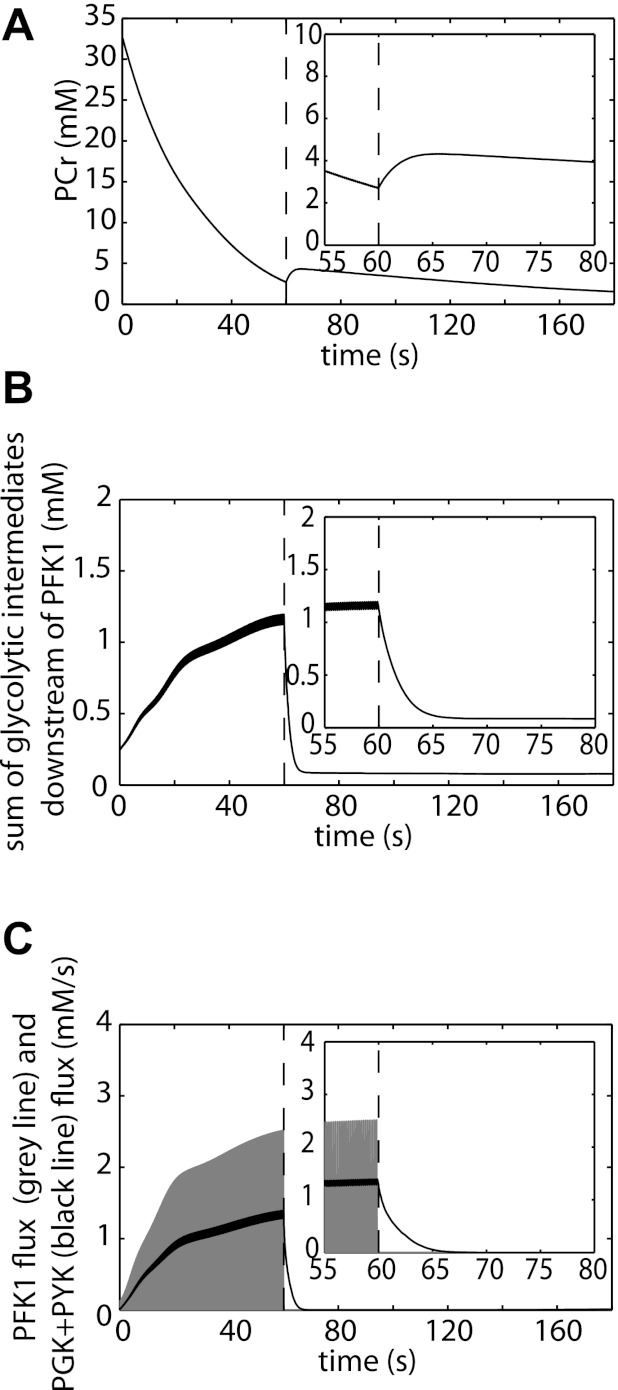
It has been well documented that glycolysis is rapidly silenced after termination of muscle contraction (6, 12, 14, 15, 43). We tested if adding calcium regulation of PFK to the model could indeed explain this pathway characteristic. Figure 6 shows model predictions of a rest-exercise (60-s, 10-Hz continuous muscle stimulation)-recovery protocol. The ATP synthesis by the pathway postexercise is reflected in the PCr dynamics. Figure 6A, inset, shows a small PCr resynthesis and thus glycolytic ATP production, postexercise. The time constant of the PCr resynthesis is between 5 and 10 s, and the ATP produced by the pathway during this period is ∼1 mM. These predictions are in excellent accordance with the time constant and magnitude of the PCr recovery due to glycolytic ATP production reported by Forbes et al. (19) and Crowther et al. (14). This result showed that the model can reproduce transients observed in other independent data sets, providing addition model verification. Results of simulations were explored to determine the origin of this small glycolytic ATP production in the first few seconds of recovery. It was concluded that these dynamics were caused by accumulation of pathway intermediates downstream of PFK-1 (Fig. 6B). Recovery of these intermediates to baseline levels occurred in 5–10 s, thereby yielding ∼1 mM ATP. Figure 6C shows PFK-1 flux, which closely tracked the rapid pulsatile Ca²⁺ release and reuptake during exercise. As a result, PFK-1 flux was quickly deactivated postexercise. In addition, the sum of the fluxes through the ATP producing steps in the pathway (PGK + PYK) is shown. These simulation results provided further evidence that, although PFK-1 flux is quickly silenced (100–200 ms), ATP production by glycolysis lags behind by 5–10 s.

Fig. 6.

Model predictions of the silencing of glycolysis in noncontracting muscle. Simulations of exercise (5-Hz continuous muscle excitation, 60 s)-recovery protocol. The dotted line indicates the end of exercise (time = 60 s). At the onset of recovery a small PCr resynthesis is observed (A). The PCr dynamics reflects the glycolytic ATP production at the beginning of recovery. B: model simulations of the summed concentration of glycolytic intermediates downstream of PFK-1 (F1,6P₂ + DHAP + G3P + GAP + 13BPG + 3PG + 2PG + PEP). C: PFK-1 flux (grey) and the PGK + PYK flux (black). PGK and PYK are the ATP generating steps of the pathway. These predictions show that although PFK flux is quickly deactivated postexercise, ATP production flux (PGK + PYK flux) is deactivated at a slower timescale.

Model Predictions: PFK Activation Dynamics

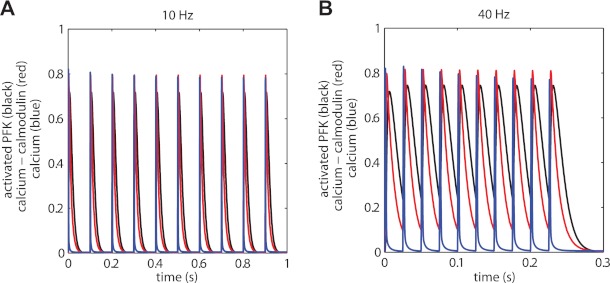
The time constant of activation and deactivation of calcium-calmodulin binding to PFK-1 have to this date remained unknown. This process was included in the model and values of kinetic k_on and k_off parameters were inferred from the in vivo experimental data. Simulations with the parameterized model were performed to investigate the (de)activation kinetics of PFK-1 for two stimulation frequencies, 10 and 40 Hz (Fig. 7, A and B). In addition, kinetics of calcium-calmodulin (red lines) and calcium (blue lines) are shown that were used as input of the model and drive the (de)activation of PFK-1 are shown. For illustrative purposes, the concentrations of these two molecules were scaled to the same order of magnitude as the fraction activated PFK. For calcium-calmodulin, 1 unit corresponds to 0.040 μM and for calcium 1 unit corresponds to 30 μM.

Fig. 7.

Calcium, calcium-calmodulin, and PFK-1 (de)activation kinetics. Predictions of (de)activation kinetics of PFK-1 (black), calcium-calmodulin kinetics (red) and calcium kinetics (bue) for 10 Hz (A) and 40 Hz (B). For illustrative purposes the concentrations of calcium-calmodulin and calcium were scaled to the same order of magnitude as the fraction activated PFK-1. For calcium-calmodulin 1 unit corresponds to 0.040 μM and for calcium 1 unit corresponds to 30 μM.

DISCUSSION

The principal result of this investigation was that incorporation of calcium-calmodulin mediated modulation of PFK-1 activity combined with activation of the enzyme by increased levels of AMP and ADP into a kinetic model of glycolysis in skeletal muscle significantly improved prediction of in vivo glycolytic flux in ischemic skeletal muscle. This main result, its implications, as well as several methodological considerations will be discussed.

Methodological Considerations: Computational Modeling

The modeling framework developed by Vinnakota et al. (55) was selected as basis for this investigation. A unique property of this specific model of glycolysis in muscle is that it includes a detailed description of proton buffering by metabolites and pH dependency of the different reactions. Modeling these aspects of the pathway in detail was essential because pH dynamics were used as reporter of glycolytic flux. Moreover, during the experiments large changes in pH were observed (7.2–6.2), which strongly influences glycolytic flux (see e.g., Refs. 22, 52).

In this study, the explanatory power of incorporation of calcium regulation of glycolytic flux at the level of PFK-1 was investigated in detail. It is, however, well known that calcium stimulates GP flux via enzyme phosphorylation (7). This process was not explicitly modeled, but instead the dynamics of GP activity were implicitly taken into account by using the recorded dynamics of the sugar phosphates as input signal of the model. This methodology allowed simplifying the analyses while still taking the calcium changes of GP activity into account. For the modeling of the calcium-calmodulin dynamics, a similar strategy was applied. These dynamics were sampled from a previously developed model of calcium handling in fast twitch skeletal muscle. Fast twitch is also the dominant (>95%) fiber type of rat TA muscle (35). This calcium handling model was shown to have excellent performance in reproducing calcium-dye dynamical data for excitation frequencies ranging from 1 to 80 Hz (25, 26) and was therefore considered a good representation of this aspect of muscle physiology.

In the model, the effect of, e.g., fructose-2,6-biphosphate or citrate on PFK-1 flux was not taken into account. The rationale for not including these interactions in the kinetic model was that for mammals the dynamic range of these modulators in skeletal muscle is small ,and therefore, their contribution to the control of the enzyme in vivo is expected to be rather limited (31, 41). However, there is also some evidence indicating that fructose-2,6-biphosphate concentration can change under some specific experimental conditions (45). It can therefore not be ruled out that during ischemia dynamics of this metabolite or others [e.g., citrate (38), glucose-1,6-biphosphate (31), or lactate (11)] exert some control on enzyme flux. Nevertheless, the simulation results indicated that it was not necessary to include these interactions in the model to explain the experimental data recorded in this study.

The proton buffer capacity (BuffCapFixed) of the muscle cells was previously estimated by Vinnakota and et al. (55) at 0.016 M. In this study, this parameter value was reestimated. It was verified that this choice did not affect the main outcome of the study: i.e., simulations showed that if the value of BuffCapFixed was not optimized but fixed at 0.016 M, model configuration iii could still reproduce the experimental data.

The simulation results shown for model configuration i and ii represent the best model fit to the data. These model configurations could not reproduce the PCr and pH dynamics simultaneously. Specifically, PCr dropped to fast and glycolytic flux increased too little. One could propose that this problem could be solved by increasing the V_max of PFK-1. This possibility was investigated by manually increasing the V_max of PFK-1. This parameter adaptation resulted in significantly worse fits for PCr and pH time course data recorded in ischemic muscle at rest (0-Hz stimulation): to whit, the predicted fall in pH became too fast and the decline in PCr too slow. Moreover, additional simulations indicated this problem could not be solved by just changing other estimated model parameters. Thus, even if V_max of PFK-1 was set to a higher activity the fit of model configuration iii was still superior and did not vitiate our conclusions.

The fits presented in Fig. 4 were obtained by minimizing the error (SSE) between model predictions and experimental data, according to the cost function (Eq. 10). Apparently, for configuration i and ii the error was minimal when the model reproduced the pH dynamics but failed to describe the PCr time-course data. It is important to realize this is the outcome of a mathematical optimization procedure. The observation that these (falsified) model configurations only reproduced pH data and failed to predict PCr data provided therefore no further physiological insights other than the conclusion that model configuration i and ii could not explain the experimental data. Indeed, the verification tests (Fig. 5) demonstrated that when no parameters were optimized except the ATPase rate constant (k_{ATP_Hydr}) model configurations i and ii indeed failed in reproducing both the PCr kinetics (Fig. 5A) and pH kinetics (Fig. 5D).

The confidence intervals for the estimated parameters were calculated using Matlab routine nlparci and were listed in Table 3. These results indicate that for model configuration i and iii all parameters could be estimated with relative high accuracy. In contrast, for model configuration ii, the confidence interval of parameters k_{deinhib_Act} and k_off was very large (see Table 3). This is probably a result of a strong correlation between these parameters. Because model configuration ii was already falsified by the results shown in Figs. 4 and 5, this observation was not analyzed in more detail.

Methodological Considerations: In Vivo ³¹P-MRS Measurements in Ischemic Rat Muscle

Electrical stimulation along the distal nerve trajectory of the n. peroneus communis-induced contractions in the TA, EDL, peroneus longus, and brevis, which was previously validated by functional MRI recordings (16, 17). Analysis of the sensitivity profile of the ³¹P coil by CSI indicated that 25% of the recorded signal originated from nonactivated muscle. This problem is not unique for this specific study. For example, it is well known that MRS recordings during voluntary exercise in humans often represent the lumped dynamics of both activated and non-activated motor units (13, 27, 28). Nevertheless, to improve the quality of the analysis this partial volume problem was taken into account and corrected for by a data postprocessing step described in methods. The percentage of signal originating from the noncontracting muscle is an influential parameter in these calculations. It was therefore verified that outcome of the study was not sensitive to the specific value of this parameter. Specifically, all simulations (parameter optimizations and model predictions) were performed assuming the signal originating from noncontracting muscle to be 20 or 30%. The results of these simulations (data not shown) indicated that reported conclusions were indeed not sensitive to the specific value of this parameter.

Calcium Modulation of PFK Activity

Past failure of model predictions lacking any regulation by calcium previously illustrated additional regulation must be present in vivo (47). Numerical analysis indicated PFK-1 as most likely site for the additional control (47). In addition, based on evidence provided by experimental studies (5, 36, 37), it was hypothesized that calcium-calmodulin activation of PFK-1 has a dominant role in controlling the response of pathway dynamics for varying muscle stimulation frequencies. This specific mechanism was therefore tested in the computational analysis. The effects of calcium-calmodulin on PFK-1 activity were reported to occur in a biphasic manner (37): at physiological Ca²⁺ concentrations PFK-1 is activated, however, if the Ca²⁺ concentration in the cells rises to pathological levels, PFK-1 is deactivated again. In the model, only the activation of PFK-1 was included. The rationale for this choice was that the analysis was restricted to the part of the data in which ATPase rate remained constant (pH > 6.5). For these conditions, it was not expected Ca²⁺ concentrations rise to pathological conditions.

The kinetic model of calcium-calmodulin mediated PFK-1 (de)activation was constructed using available information in the literature. Activation of PFK-1 is thought to occur via binding of two calcium-calmodulin complexes to a PFK-dimer (36). This binding reduces the inhibition of the enzyme by ATP (36). At physiological concentrations (∼8 mM) ATP inhibition results in a nearly full deactivation of the enzyme (>95%; Ref. 36). Therefore, reversing this inhibition will result in a significant increase of the enzymes catalytic activity. By competitive binding to the inhibition site, AMP and ADP are able to reverse the ATP inhibition of the inactive form of PFK-1 (10). It remains unknown whether for the activated form of the enzyme deinhibition is likewise mediated by competitive binding of ADP and AMP, albeit with a lower binding constant, or alternatively, if it is independent of ADP and AMP levels. Irrespectively, both scenarios were evaluated using the computational model (model configurations ii and iii, respectively). A detailed analysis showed that only a model containing deinhibition mediated by competitive binding of ADP and AMP could reproduce the experimental data. A possible concern could be that comparison of the three models was biased because each model had a different number of degrees of freedom; in general, models with a greater number of free parameters tend to fit data better. This concern was quantitatively addressed using the Akaike test. A large reduction in the value of AIC indicated that improvement of the fit of model configuration iii was larger than could be expected from the few additional degrees of freedom, suggesting a biological component responsible. Although kinetic data for validation of this prediction are unavailable, it is consistent with results reported by Crowther et al. (12), that both elevated calcium levels and increased ADP and AMP levels were required to increase flux downstream of glycogen phoshorylase (12). Further confidence in the validity of the computational model was provided by verification against data not used for parameter estimation (see Fig. 5). Finally, a corollary of the particular kinetic model for calcium control of PFK-1 that was developed and used here is that the kinetics of PFK-1 activation and deactivation were almost exclusively (but see Eq. 9) determined by the reaction kinetics of calcium-calmodulin interaction. Empirical studies have shown that the latter are extremely rapid (K_d 100 s⁻¹ or faster; see methods). As a result, PFK-1 (de)activation in the model was equally rapid. No data were available in the literature to verify that this model corollary is accurate, and it remains to be tested.

Silencing of Glycolysis in Noncontracting Muscle

It has been well documented that glycolysis is quickly silenced after termination of muscle contraction (9, 12, 14, 15, 43). In the present investigation, these observations were reproduced by the absence of PCr resynthesis in the period after stimulation. Two independent studies reported a deactivation of the pathway in the order of 10 - 20 s (14, 19). This timescale is slow compared with the rapid deactivation of PFK-1 (100–200 ms; see Fig. 6). However, simulations revealed that after intense muscle contractions the deactivation of the pathway is delayed as a result of accumulation of intermediates downstream of PFK-1. In addition, simulations indicated that glycolytic ATP production during the first seconds of recovery is dependent on the intensity of the preceding exercise (data not shown) and may explain the experimental observations that a complete absence of glycolytic flux at the onset of recovery occurs (6, 43). These findings may have important implications for the analyses of PCr recovery kinetics. PCr recovery kinetics are believed to predominantly reflect oxidative ATP production rate, and this rate of PCr recovery is frequently used as a measure of in vivo oxidative capacity and/or mitochondrial function (42). Two experimental studies already suggested that the first 10 s of recovery may be contaminated by glycolytic ATP production. The current simulation study provided additional support for this contention. These results therefore imply that to obtain PCr kinetics that truly reflect the oxidative ATP synthesis it is advisable to exclude the first 10 s of recovery from the data analyses.

Parallel Activation of ATP Consumption and Glycolytic ATP Production

The results of this study indicate that to meet energetic demands parallel activation of glycolytic ATP supply flux and muscle contraction by the same signaling event, i.e., calcium release in the myoplasm, is necessary. The effect of varying calcium stimulation frequency on parallel activation of these pathways has only been addressed in relatively few studies. Conley et al. (9) used ³¹P-MRS to determine the effect of varying muscle excitation at low frequencies (0.5–3 Hz) and concluded that at these low stimulation frequencies glycolytic flux scales linearly with contraction frequency. A similar conclusion was inferred from the model simulations. PFK-1 (de)activation kinetics remained pulsatile for muscle excitation frequencies <10 Hz. For this range of stimulation frequencies, PFK-1 activation was linearly related to muscle excitation. These simulations yield results with much broader implications for glycolytic flux than previously suggested in part because reproducing these characteristics also reported by Crowther et al. also permits model predictions for much higher frequencies. Remarkably, at these frequencies, the fusing of individual PFK-1 activation pulses was qualitatively similar to force dynamics of fast twitch muscle. These predictions also suggest that for these stimulation frequencies (>10 Hz) activation of PFK-1 remains closely linked to muscle ATP demand flux. We speculate that the regulation of glycolysis in skeletal muscle is optimized to facilitate this parallel activation throughout the wide dynamical range of muscle excitation frequencies.

Future Outlook

Recently, Vinnakota et al. (55) used the previous version of this computational model of glycolysis in skeletal muscle to analyze metabolite and pH dynamics in resting mouse EDL and soleus muscle. Although their model simulations reproduced these dynamics fairly well, the simulations failed to describe recorded dynamics during muscle excitation. A possible explanation for this model limitation was the lack of feed forward regulation downstream of glycogen phosphorylase, activated during mechanical work. This study has found that adding regulation by calcium mediated activation of PFK-1 improves the consistency of model predictions and experimental data over a wide operational range of muscle excitation frequencies (0–80 Hz). We therefore concluded that the proposed model does provide an improved basis for modeling energy metabolism in skeletal muscle. In this context, relevant questions or model limitations open for future study will be discussed below.

The predictions of the current model were tested for conditions of ischemia. It will be interesting to investigate if these predictions are also accurate for conditions of normoxia. This requires adding a description of ATP production by oxidative phosphorylation to the computational model and sampling the behavior of both mitochondrial and glycolytic pathway experimentally under normoxic conditions. In the present investigation, the experimental readout of the PME resonance allowed to bypass the need for a flux equation of GP. For future studies, it may become relevant to add this flux description. Hereto, an improved model of GP including allosteric regulation by G6P and the effects of enzyme phosphorylation on kinetic parameters is probably required. The present analysis was based on the experimental data in which muscle fatigue had no detectable effect on cellular ATP hydrolysis rate. Acquiring an experimental readout and modeling the effects of muscle fatigue on ATP hydrolysis rate will be key steps towards computational analyses of the remaining of the data. In addition, in future studies it may become necessary to include the effect of other metabolites and signaling molecules [e.g., fructose-2,6-BP and glucose-1,6-BP (31), or lactate (11)] on PFK-1. At the moment, it is still assumed that the effects of these molecules on PFK-1 activity in vivo are negligible. Measuring the dynamics of these metabolites during exercise protocols and extending the PFK-1 rate equation to incorporate the effect of these interactions on PFK-1 activity will provide new opportunities to investigate a possible regulatory role of these molecules.

With respect to extending the research on this topic, it may also be very interesting to investigate the role of calcium-calmodulin signaling on the flux control of glycolysis in tissues other than muscle. Based on the current results, it is predicted that calcium-calmodulin signaling has a very dominant flux control in skeletal muscle, but there is also evidence indicating this signaling mechanism activates glycolytic flux in nervous tissue (30, 33) and also various types of cancerous tissues (23, 24, 40, 49). In this view, it will be of particular interest to study if calcium-calmodulin related alterations in glycolytic flux observed for these cell types will also arise from model predictions.

In Summary

An integrative experimental and computational modeling approach was applied to test the hypothesis that calcium-calmodulin-mediated activation of PFK-1 in skeletal muscle is an important signal in flux control underlying in vivo pathway behavior. Model simulations revealed that incorporation of these mechanisms into a detailed model of skeletal muscle glycolysis was required for model predictions to be consistent with experimental data, thereby providing quantitative support for the hypothesis. Model predictions indicated that the (de)activation kinetics of PFK-1 in response to different stimulation frequencies is very similar to force dynamics in fast twitch muscle. However, in spite of these very fast PFK-1 deactivation kinetics overall shut down of glycolytic ATP production in noncontracting muscle postexercise may be delayed by 5–10 s as a result of the accumulation of glycolytic intermediates downstream of PFK-1.

GRANTS

This research was performed within the framework of the Center for Translational Molecular Medicine (www.ctmm.nl) Project PREDICCt Grant 01C-104, supported by The Netherlands Heart Foundation, Dutch Diabetes Research Foundation, and Dutch Kidney Foundation. It was funded in part by the National Institutes of Health through a subcontract to Grants HL-072011 and DK-095210. This work was carried out within the research programme of the Netherlands Consortium for Systems Biology, which is part of The Netherlands Genomics Initiative/Netherlands Organization for Scientific Research.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.P.S., W.G., R.W.W., J.J.P., J.A.J., and N.A.v.R. conception and design of research; J.P.S., W.G., B.W., and J.J.P. performed experiments; J.P.S., W.G., B.W., and J.J.P. analyzed data; J.P.S., W.G., B.W., R.W.W., P.A.H., K.N., J.J.P., J.A.J., and N.A.v.R. interpreted results of experiments; J.P.S. and W.G. prepared figures; J.P.S. and W.G. drafted manuscript; J.P.S., W.G., R.W.W., P.A.H., K.N., J.J.P., J.A.J., and N.A.v.R. edited and revised manuscript; J.P.S., W.G., B.W., R.W.W., P.A.H., K.N., J.J.P., J.A.J., and N.A.v.R. approved final version of manuscript.

APPENDIX

Model Configuration i

The PFK rate equation of model configuration i [obtained from Connett (10); Eq. A1].

$$\begin{array}{c}\frac{V}{V_{\max }}=\frac{kNUM}{E+E_A+E_{AB}+E_{BA}}\\ NUM=Q_1\cdot \left(1+\frac{\overline{Q}}{c_1{c}_2}+Q_6\right)+Q_2\cdot \left(1+\frac{\overline{Q}}{c_1{c}_2}+Q_5\right)\cdot \left(1+\frac{\overline{Q}}{c_1{c}_2}\right)\\ E=\left(1+\frac{\overline{Q}}{c_1{c}_2}+Q_5\right)\cdot \left(1+\frac{\overline{Q}}{c_1{c}_2}+Q_6\right)\cdot (1+Q_7)\\ E_A=Q_1\cdot \left(1+\frac{\overline{Q}}{c_1{c}_2}+Q_6\right)\cdot Q_3\cdot \left(1+\frac{\overline{Q}}{c_1}\right)\\ E_B=Q_2\cdot \left(1+\frac{\overline{Q}}{c_1{c}_2}+Q_5\right)\cdot Q_4\cdot \left(1+\frac{\overline{Q}}{c_2}\right)\\ E_{BA}+E_{AB}=NUM\left(1+\frac{Q}{c_1{c}_2}\right)\\ Q_A=\frac{[F6P]}{K_{m1}^{F6P}}\\ Q_B=\frac{[MgATP]}{K_{m1}^{MgATP}}\\ Q_1=Q_A\left(1+\frac{Q_7}{c_1}\right)\\ Q_2=Q_B\left(1+\frac{Q_7}{c_2}\right)\\ Q_3=\left(1+\frac{\overline{Q}}{c_1}\right)\cdot \left(\frac{K_{m2}^{MgATP}}{[MgATP]}\right)\\ Q_4=\left(1+\frac{\overline{Q}}{c_2}\right)\cdot \left(\frac{K_{m2}^{F6P}}{[F6P]}\right)\\ Q_5=\left(\frac{K_i^{F6P}}{[F6P]}\right)\cdot (1+\overline{Q})\cdot Q_3\cdot Q_A\\ Q_6=\left(\frac{Q_i^{MgATP}}{[MgATP]}\right)\cdot (1+\overline{Q})\cdot Q_4\cdot Q_B\\ Q_7=\frac{[H^{+}]}{K_a}\left[1+{\left(\frac{[ATPH]}{Q_i^{ATPH}}\right)}^4\right]\\ \overline{Q}=Q_7\frac{{\left(1+\frac{Q_A}{c_1}\right)}^3\cdot {\left(1+\frac{Q_B}{c_2}\right)}^3}{{(1+Q_A)}^3\cdot {(1+Q_B)}^3}\\ Q_i^{MgATP}=K_i^{MgATP}\cdot deinhibition\\ Q_i^{ATPH}=K_i^{ATPH}\cdot deinhibition\\ deinhibition=1+\frac{[ADP]}{K_{ADP}}+\frac{[AMP]}{K_{AMP}}\end{array}$$ (A1)

All model parameter values are provided in Table A1.

Table A1.

parameter values PFK-1 model

Parameter	Value
Km1F6P	68.49 μM*
Km2F6P	58.70 μM*
Km1MgATP	26.54 μM*
Km2MgATP	37.81 μM*
KiF6P	4.33 μM*
KiMgATP	124.60 μM*
KiATPH	0.649 μM*
Ka	0.0812 μM*
k	0.990*
c1	19.09*
c2	2.63*
KADP	Estimated (Table 3)
KAMP	Estimated (Table 3)

F6P, fructose-6-phosphate.

^*Value obtained from Ref. 10.

Model Configuration ii:

Model configuration ii contained two PFK-1 forms, an inactive modeled according to Eq. 11 and an active form for which the deinhibition term was described by Eq. A2.

$$deinhibition=k_{deinhib\_Act}$$ (A2)

Activation and deactivation of PFK-1 by binding of calcium-calmodulin was modeled by differential equations Eqs. A3 and A4:

$$\frac{{dPFK}_{actibe}}{dt}=k_{on}C{a}_{2}Ca{M}^2\cdot (1-PF{K}_{active})-k_{off}PF{K}_{active}$$ (A3)

$$PF{K}_{inactive}=1-PF{K}_{active}$$ (A4)

Parameter values of model configuration ii are listed in Tables 3 and A1.

Model Configuration iii

Model configuration iii contained two PFK-1 forms, an inactive modeled according to Eq. 11 and an active form for which the deinhibition term was described by Eq. A5.

$$deinhibition=1+\frac{AMP}{K_{AMP}^{act}}+\frac{ADP}{K_{ADP}^{act}}$$ (A5)

Activation and deactivation of PFK-1 by binding of calcium-calmodulin was modeled by differential Eqs. A3 and A4. Parameter values of model configuration iii are listed in Tables 3 and A1.