Estimation of a non-parametric variable importance measure of a continuous exposure

Abstract

We define a new measure of variable importance of an exposure on a continuous outcome, accounting for potential confounders. The exposure features a reference level x₀ with positive mass and a continuum of other levels. For the purpose of estimating it, we fully develop the semi-parametric estimation methodology called targeted minimum loss estimation methodology (TMLE) [23, 22]. We cover the whole spectrum of its theoretical study (convergence of the iterative procedure which is at the core of the TMLE methodology; consistency and asymptotic normality of the estimator), practical implementation, simulation study and application to a genomic example that originally motivated this article. In the latter, the exposure X and response Y are, respectively, the DNA copy number and expression level of a given gene in a cancer cell. Here, the reference level is x₀ = 2, that is the expected DNA copy number in a normal cell. The confounder is a measure of the methylation of the gene. The fact that there is no clear biological indication that X and Y can be interpreted as an exposure and a response, respectively, is not problematic.

1. Introduction

Consider the following statistical problem: One observes the data structure O = (W, X, Y) on an experimental unit of interest, where W ∈ 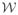stands for a vector of baseline covariates, and X ∈ ℝ and Y ∈ ℝ respectively quantify an exposure and a response; the exposure features a reference level x₀ with positive mass (there is a positive probability that X = x₀) and a continuum of other levels (a first source of difficulty); one wishes to investigate the relationship between X on Y, accounting for W (a second source of difficulty) and making few assumptions on the true data-generating distribution (a third source of difficulty). Taking W into account is desirable when one knows (or cannot rule out the possibility) that it contains confounding factors, i.e., common factors upon which the exposure X and the response Y may simultaneously depend.

We illustrate our presentation with an example where the experimental unit is a set of cancer cells, the relevant baseline covariate W, the exposure X and response Y are, respectively, is a measure of DNA methylation, the DNA copy number and the expression level of a given gene. Here, the reference level is x₀ = 2, that is, the expected copy number in a normal cell. The fact that there is no clear biological indication that X and Y can be interpreted as an exposure and a response, respectively, is not problematic. Associations between DNA copy numbers and expression levels in genes have already been considered in the literature (see e.g., [11, 26, 1, 17, 10]). In contrast to these earlier contributions, we do exploit the fact that X features both a reference level and a continuum of other levels, instead of discretizing it or considering it as a purely continuous exposure.

We focus on the case that there is very little prior knowledge on the true data-generating distribution P₀ of O, although we know/assume that (i) O takes its values in the bounded set 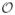(we will denote ||O|| = max{|W|, |X|, |Y|}), (ii) P₀(X ≠ x₀) > 0, and finally (iii) P₀(X ≠ x₀|W) > 0 P₀-almost surely. Accordingly, we see P₀ as a specific element of the non-parametric set of all possible data-generating distributions of O satisfying the latter constraints. We define the parameter of interest as Ψ (P₀), for the non-parametric variable importance measure Ψ: → ℝ characterized by

$$\begin{array}{l}\mathrm{\Psi }(P)=\underset{\beta \in \mathbb{R}}{argmin}{E}_P\left\{{(Y-E_P(Y\mid X=x_0,W)-\beta (X-x_0))}^2\right\}\\ =\underset{\beta \in \mathbb{R}}{argmin}{E}_P\left\{{(E_P(Y\mid X,W)-E_P(Y\mid X=x_0,W)-\beta (X-x_0))}^2\right\}\end{array}$$ (1)

for all P ∈ . Thus, Ψ (P)(X − x₀) is the best linear approximation of the form β (X − x₀) to (Y − E_P (Y|X = x₀, W)), hence also to (E_P(Y|X, W) − E_P (Y|X = x₀, W)). Parameter Ψ quantifies the influence of X on Y on a linear scale, using the reference level x₀ as a pivot and accounting for W. Note that this expression conveys the notion that the role of X and Y are not symmetric. As its name suggests, Ψ belongs to the family of variable importance measures, which was introduced in [21]. However, its case is not covered by the latter article because X is continuous. We will see how Ψ naturally relates to an excess risk, a prototypical variable importance measure of a binary exposure, when X takes only two distinct values.

The methodology presented in this article straightforwardly extends to situations where one would prefer to replace the expression β(X − x₀) in (1) by βf (X, W) for any f such that f(x₀, W) = 0 and E_P {f (X, W)²} > 0 for all P ∈ . We emphasize that in contrast to [15, 14, 28, 21, 20], we do not assume a semi-parametric model (which would here be written as Y = β (X − x₀) + η (W) + U with unspecified η and U such that E_P (U|X, W) = 0). This fact bears important implications. The parameter of interest, Ψ (P₀), is universally defined no matter what properties the unknown true data-generating distribution P₀ enjoys, or does not enjoy. This justifies the expression “non-parametric variable importance measure of a continuous exposure” in the title.

An obvious substitution estimator of Ψ (P₀) is

$${\widehat{\psi }}_n=\underset{\beta \in \mathbb{R}}{argmin}{E}_{P_n}\left\{{\left({\widehat{\theta }}_n(X,W)-{\widehat{\theta }}_n(x_0,W)-\beta (X-x_0)\right)}^2\right\},$$

an expression derived from (1) by substituting the empirical measure P_n for P₀ and the Nadaraya-Watson estimator θ̂_n(X, W) of E_P0 (Y|X, W) for it. Under regularity conditions of order k on the true conditional expectation, the optimal bandwith h_n for θ̂_n satisfies h_n = cn^−1/(2k+d) where d = 2 is the dimension of (X, W). Now it is possible to characterize a P₀ ∈ such that $E_{P_0}\{{\widehat{\psi }}_n-\mathrm{\Psi }(P_0)\}=c^{\prime }{h}_n^k+o(h_n)$. In particular, ψ̂_n cannot achieve $\sqrt{n}$-consistency under that P₀. We see that ψ̂_n suffers from the fact that the bias-variance trade-off, which is at the core of the construction of θ̂_n, is optimized for the sake of estimating the infinite-dimensional parameter E_P0 (Y|X, W) whereas we are eventually interested in estimating the one-dimensional parameter Ψ (P₀).

Here we fully develop a version of the semi-parametric estimation methodology called targeted minimum loss estimation (TMLE) [23, 22] tailored to the inference of Ψ (P₀). This involves iteratively updating an initial estimator such as ψ̂_n in order to produce another substitution estimator. Because the latter is targeted at the estimation of Ψ (P₀), it achieves $\sqrt{n}$-consistency under mild assumptions. Specifically, Corollary 1 on asymptotic normality only requires that the product of the convergence rate of $E_{P_n^{k_n}}(Y\mid X,W)$ by the minimum of the convergence rates of $E_{P_n^{k_n}}(X\mid W)$ and $P_n^{k_n}(X=0\mid W)$ be faster than $\sqrt{n}$. In particular, this condition may hold even in situations where none of the three above estimators achieves $\sqrt{n}$-consistency.

We cover the whole spectrum of the TMLE theoretical study, practical implementation, simulation study, and application to the aforementioned genomic example.

In Section 2, we study the fundamental properties of parameter Ψ. In Section 3 we provide an overview of the TMLE methodology tailored for the purpose of estimating Ψ (P₀). In Section 4, we state and comment on important theoretical properties enjoyed by the TMLE (convergence of the iterative updating procedure at the core of its definition; its consistency and asymptotic normality). The specifics of the TMLE procedure are presented in Section 5 (this section may be skipped on first reading). The properties considered in Section 4 are illustrated by a simulation study inspired by the problem of assessing the importance of DNA copy number variations on expression level in genes, accounting for their methylation (the real data application we are ultimately interested in), as described in Section 6. All proofs are postponed to the appendix.

We assume from now on, without loss of generality, that x₀ = 0. Following [25], for any measure λ and measurable function f, λf = ∫ fdλ. We set $L_0^2(P)=\{s\in L^2(P):Ps=0\}$. Moreover, the following notation are used throughout the article: for all P ∈ , θ(P)(X, W) = E_P (Y|X, W), μ(P)(W) = E_P (X|W), g(P)(0|W) = P(X = 0|W), and σ²(P) = E_P {X²}. In particular, Ψ (P) can also be written as

$$\mathrm{\Psi }(P)=\underset{\beta \in \mathbb{R}}{argmin}{E}_P\left\{{(\theta (P)(X,W)-\theta (P)(0,W)-\beta X)}^2\right\}.$$

2. The non-parametric variable importance parameter

It is of paramount importance to study the parameter of interest in order to better estimate it. Parameter Ψ actually enjoys the following properties (see Section A.2 for definitions and van der Vaart [25, Chapter 25, ] for an introduction to the theory of semiparametric models).

Proposition 1

For all P ∈ ,

$$\mathrm{\Psi }(P)=\frac{E_P\{X(\theta (P)(X,W)-\theta (P)(0,W))\}}{E_P\{X^2\}}.$$ (2)

Parameter Ψ is pathwise differentiable at every P ∈ with respect to the maximal tangent set $L_0^2(P)$. Its efficient influence curve at P is $D^{★}(P)=D_1^{★}(P)+D_2^{★}(P)$, where the two components $D_1^{★}(P)=D_1^{★}({\sigma }^2(P),\theta (P),\mathrm{\Psi }(P))$ and $D_2^{★}(P)=D_2^{★}({\sigma }^2(P),\theta (P),\mu (P),g(P))$ are $L_0^2(P)$-orthogonal and characterized by

$$\begin{array}{l}{D}_1^{★}({\sigma }^2,\theta ,\psi )(O)=\frac{1}{{\sigma }^2}(X(\theta (X,W)-\theta (0,W)-X\psi )),\\ D_2^{★}({\sigma }^2,\theta ,\mu ,g)(O)=\frac{1}{{\sigma }^2}(Y-\theta (X,W))\left(X-\frac{\mu (W)\mathbf{1}\{X=0\}}{g(0\mid W)}\right).\end{array}$$

Furthermore, the efficient influence curve is double-robust: for any (P, P′) ∈ 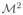, if either (μ(P′) = μ(P) and g(P′) = g(P)) or θ (P′)(0, ·) = (P)(0, ·) holds, then PD^★(P′) = 0 implies Ψ (P′) = Ψ (P).

The proof of Proposition 1 is relegated to Section A.2.

We emphasize again that we do not assume a semi-parametric model Y = βX + η(W)+U (with unspecified η and U such that E_P (U|X, W) = 0). Setting R(P, β)(X, W) = θ (P)(X, W) − θ (P)(0, W) − βX for all (P, β) ∈ × ℝ, the latter semi-parametric model holds for P ∈ if there exists a unique β(P) ∈ ℝ such that R(P, β(P)) = 0. Note that β is always solution to the equation βE_P {X²} = E_P {X (θ (P)(X, W) − θ (P)(0, W) − R(P, β)(X, W))}. In particular, if the semi-parametric model holds for a certain P ∈ , then β(P) = Ψ (P) by (2). On the contrary, if the semi-parametric model does not hold for P, then it is not clear what β(P) could even mean whereas Ψ (P) is still a well-defined parameter worth estimating. We discuss in Section 4.2 what happens if one estimates β(P) when assuming wrongly that the semi-parametric holds. The discussion allows to identify the awkward non-parametric extension of parameter β(P) that one then estimates.

Equality (2) also teaches us that

$$\mathrm{\Psi }(P)=\mathcal{F}(P)-\frac{E_P\{\mu (P)(W)\theta (P)(0,W)\}}{{\sigma }^2(P)}$$ (3)

for the functional : → ℝ characterized by

$$\begin{array}{l}\mathcal{F}(P)=\underset{\beta \in \mathbb{R}}{argmin}{E}_P\{{(Y-\beta X)}^2\}\\ =\underset{\beta \in \mathbb{R}}{argmin}{E}_P\{{(E_P(Y\mid X)-\beta X)}^2\}\equiv \frac{E_P\{XY\}}{{\sigma }^2(P)}\end{array}$$ (4)

(all P ∈ ). We see that (P) X is the best linear approximation of the form βX to Y, hence also to E_P (Y|X). In view of (1), overlooks the role played by W. The second term in the right-hand side of (3) is a correction term added to (P) in order to take W into account. We do not claim that Ψ (P) is superior to (P): they just do not quantify the same features of P. In the real data application of Section 6.7, we compare the estimators of Ψ (P₀) and (P₀) to illustrate that they target two different unknown quantities, and to check across genes whether accounting for W has an impact or not.

Whereas the roles of X and Y are symmetric in the numerator of (P), they are obviously not in that of the correction term. Less importantly, (2) also makes clear that there is a connection between Ψ and an excess risk. Indeed, consider P ∈ such that P(X ∈ {0, x₁}) = 1 for x₁ ≠ 0. Then Ψ (P) satisfies

$$\mathrm{\Psi }(P)=\frac{E_P\{(\theta (P)(x_1,W)-\theta (P)(0,W))h(P)(W)\}}{{\sigma }^2(P)}$$

for h(P)(W) = P(X = x₁|W), i.e., Ψ (P) appears as a weighted excess risk (the prototypical excess risk would be here E_P {θ (P)(x₁, W) − θ (P)(0, W)}).

Since Ψ is pathwise differentiable, the theory of semi-parametric estimation is applicable, providing a notion of asymptotically efficient estimation. Remarkably, the asymptotic variance of a regular estimator of Ψ (P₀) is lower-bounded by the variance Var_P0D^★ (P₀)(O) under P₀ of the efficient influence curve at P₀ (a consequence of the convolution theorem). The TMLE procedure takes advantage of the properties of Ψ described in Proposition 1 in order to build a consistent and possibly asymptotically efficient substitution estimator of Ψ (P₀). In view of (3), this is a challenging statistical problem because, whereas estimating (P₀) is straightforward (the ratio of the empirical means of XY and X₂ is an efficient estimator of (P₀)), estimating the correction term in (3) is more delicate, notably because this necessarily requires estimating the infinite-dimensional features θ (P₀)(0, ·) and μ(P₀).

3. Overview of the TMLE procedure tailored to the estimation of the non-parametric variable importance measure

We observe n independent copies O⁽ⁱ⁾ = (W⁽ⁱ⁾, X⁽ⁱ⁾, Y ⁽ⁱ⁾) (i = 1, …, n) of the observed data structure O ~ P₀ ∈ . The empirical measure is denoted by P_n. 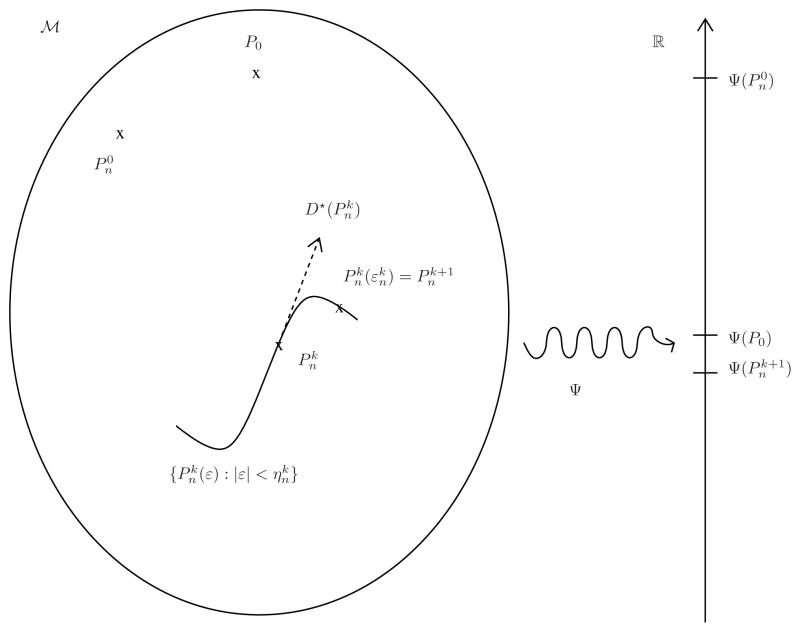The TMLE procedure iteratively updates an initial substitution estimator ${\psi }_n^0=\mathrm{\Psi }(P_n^0)$ of Ψ (P₀) (based on an initial estimator $P_n^0$ of the data-generating distribution P₀), building a sequence ${\{{\psi }_n^k=\mathrm{\Psi }(P_n^k)\}}_{k\ge 0}$ (with $P_n^k$ the kth update of $P_n^0$) which converges to the targeted minimum loss estimator (TMLE) ${\psi }_n^{\ast }$ as k increases. This iterative scheme is visually illustrated in Figure 1, and we invite the reader to consult its caption now.

Fig 1.

Illustration of the TMLE procedure (with its general one-step updating procedure). We intentionally represent the initial estimator $P_n^0$ closer to P₀ than its kth and (k +1)th updates $P_n^k$ and $P_n^{k+1}$, heuristically because $P_n^0$ is as close to P₀ as one can possibly get (given P_n and the specifics of the super-learning procedure) when targeting P₀ itself. However, this obviously does not necessarily imply that $\mathrm{\Psi }(P_n^0)$ performs well when targeting Ψ (P₀) (instead of P₀), which is why we also intentionally represent $\mathrm{\Psi }(P_n^{k+1})$ closer to Ψ (P₀) than $\mathrm{\Psi }(P_n^0)$. Indeed, $P_n^{k+1}$ is obtained by fluctuating its predecessor $P_n^k$ in the direction of Ψ ”, i.e., taking into account the fact that we are ultimately interested in estimating Ψ (P₀). More specifically, the fluctuation { $P_n^k(\epsilon ):\mid \epsilon \mid <{\eta }_n^k$} of $P_n^k$ is a one-dimensional parametric model (hence its curvy shape in the large model ) such that (i) $P_n^k(0)=P_n^k$, and (b) its score at ε = 0 equals the efficient influence curve $D^{★}(P_n^k)$ at $P_n^k$ (hence the dotted arrow). An optimal stretch ${\epsilon }_n^k$ is determined (e.g. by maximizing the likelihood on the fluctuation), yielding the update $P_n^{k+1}=P_n^k({\epsilon }_n^k)$.

It is not necessary to estimate the whole distribution P₀ in order to perform the estimation of Ψ (P₀). Only some features of P₀ must be estimated. One of the purposes of Section 3 is to identify the list of these features. To do so, it proves convenient (from notational and conceptual points of view) to rely on a sequence of estimators ${\{P_n^k\}}_{k\ge 0}$ of the whole distribution P₀, even though we are eventually only interested for each k ≥ 0 in the determined list of features of $P_n^k$.

We determine what initializing the TMLE procedure boils down to in Section 3.1. A general one-step targeted updating procedure is described in Section 3.2. How to conduct specifically these initialization and update (as well as two alternative tailored two-step updating procedures) will be addressed in Section 5.

3.1. Initial estimator

In this subsection, we describe what it takes to construct an initial substitution estimator of Ψ (P₀). Of course, how one derives the substitution estimator Ψ (P) from the description of (certain features of) P is relevant even if P is not literally an initial estimator of P₀.

By (2), building an initial substitution estimator $\mathrm{\Psi }(P_n^0)$ of Ψ (P₀) requires the estimation of θ (P₀), of σ² (P₀), and of the marginal distribution of (W, X) under P₀. Given $P_n^0$, initial estimator of P₀ with known $\theta (P_n^0),{\sigma }^2(P_n^0)>0$ and marginal distribution of (W, X) under $P_n^0,\mathrm{\Psi }(P_n^0)$ can indeed be obtained (or, more precisely, evaluated accurately) by the law of large numbers, as discussed below. We emphasize that such an initial estimator may very well be biased. In other words, one would need strong assumptions on the true data-generating distribution P₀ (which we are not willing to make; typically, assuming that P₀ belongs to a given regular parametric model) and adapting the construction of $P_n^0$ based on those assumptions (typically, relying on maximum likelihood estimation) in order to obtain the consistency of $\mathrm{\Psi }(P_n^0)$.

For B a large integer (say B = 10⁵), evaluating accurately (rather than computing exactly) the initial substitution estimator $\mathrm{\Psi }(P_n^0)$ of Ψ (P₀) boils down to simulating B independent copies (W̃ ^(b), X̃^(b)) of (W, X) under $P_n^0$, then using the approximation

$$\begin{array}{l}{\psi }_n^0=\mathrm{\Psi }(P_n^0)\\ =\frac{{\sum }_{b=1}^B{\stackrel{\sim }{X}}^{(b)}(\theta (P_n^0)({\stackrel{\sim }{X}}^{(b)},{\stackrel{\sim }{W}}^{(b)})-\theta (P_n^0)(0,{\stackrel{\sim }{W}}^{(b)}))}{B{\sigma }^2(P_n^0)}+O(B^{-1/2}).\end{array}$$ (5)

Knowing the marginal distribution of (W, X) under $P_n^0$ amounts to knowing (i) the marginal distribution of W under $P_n^0$, (ii) the conditional distribution of Z ≡ 1{X = 0} given W under $P_n^0$, and (iii) the conditional distribution of X given (W, X ≠ 0) under $P_n^0$. Firstly, we advocate for estimating initially the marginal distribution of W under P₀ by its empirical version, or put in terms of likelihood, to build $P_n^0$ in such a way that $P_n^0(W)=n^{-1}{\sum }_{i=1}^n\mathbf{1}\{W^{(i)}=W\}$. Secondly, the conditional distribution of Z given W under $P_n^0$ is the Bernoulli law with parameter $1-g(P_n^0)(0\mid W)$, so it is necessary that $g(P_n^0)$ be known too (and such that, $P_n^0$-almost surely, $g(P_n^0)(0\mid W)\in (0,1)$. Thirdly, the conditional distribution of X given (W, X ≠ 0) under $P_n^0$ can be any (finite variance) distribution, whose conditional mean can be deduced from $\mu (P_n^0)$:

$$E_{P_n^0}(X\mid X\ne 0,W)=\frac{\mu (P_n^0)(W)}{1-g(P_n^0)(0\mid W)},$$ (6)

and whose conditional second order moment $E_{P_n^0}(X^2\mid X\ne 0,W)$ satisfies

$$E_{P_n^0}\{(1-g(P_n^0)(0\mid W))E_{P_n^0}(X^2\mid X\ne 0,W)\}={\sigma }^2(P_n^0).$$ (7)

In particular, it is also necessary that $\mu (P_n^0)$ be known too.

In summary, the only features of $P_n^0$ we really care for in order to evaluate accurately (rather than compute exactly) ${\psi }_n^0=\mathrm{\Psi }(P_n^0)$ are $\theta (P_n^0),\mu (P_n^0),g(P_n^0),{\sigma }^2(P_n^0)$, and the marginal distribution of W under $P_n^0$, which respectively estimate θ (P₀), μ(P₀), g(P₀), σ² (P₀), and the marginal distribution of W under P₀. We could for instance rely on a working model where the conditional distribution of X given (W, X ≠ 0) is chosen as the Gaussian distribution with conditional mean as in (6) and any conditional second order moment (which is nothing but a measurable function of W) such that (7) holds. We emphasize that we do use here expressions from the semantical field of choice, and not from that of assumption; a working model is just a tool we use in the construction of the initial estimator, and we do not necessarily assume that it is well-specified. Although such a Gaussian working model would be a perfectly correct choice, we advocate for using another one for computational convenience, as presented in Section 5.1.

3.2. A general one-step updating procedure of the initial estimator

The next step consists in iteratively updating ${\psi }_n^0=\mathrm{\Psi }(P_n^0)$. Assuming that one has already built (k − 1) updates $P_n^1,\dots ,P_n^{k-1}$ of $P_n^0$, resulting in (k − 1) updated substitution estimators ${\psi }_n^1=\mathrm{\Psi }(P_n^1),\dots ,{\psi }_n^{k-1}=\mathrm{\Psi }(P_n^{k-1})$, it is formally sufficient to describe how the kth update $P_n^k$ is derived from its predecessor $P_n^{k-1}$ in order to fully determine the iterative procedure. Note that the value of ${\psi }_n^1=\mathrm{\Psi }(P_n^1),\dots ,{\psi }_n^{k-1}=\mathrm{\Psi }(P_n^{k-1})$ are derived as ${\psi }_n^0=\mathrm{\Psi }(P_n^0)$, by following (5) in Section 3.1 with $P_n^1,\dots ,P_n^{k-1}$ substituted for $P_n^0$.

We present here a general one-step updating procedure (two alternative tailored two-step updating procedures are also presented in Section 5.2). We invite again the reader to refer to Figure 1 for its visual illustration.

Set ρ ∈ (0, 1) a constant close to 1 (in Section 6, we use ρ = 0.999) and consider the path { $P_n^{k-1}(\epsilon ):\mid \epsilon \mid \le \rho {\left|\right|D^{★}(P_n^{k-1})\left|\right|}_{\infty }^{-1}$} characterized by

$$\frac{{dP}_n^{k-1}(\epsilon )}{{dP}_n^{k-1}}(O)=(1+\epsilon D^{★}(P_n^{k-1})(O)),$$ (8)

where $D^{★}(P_n^{k-1})$ is the current estimator of the efficient influence curve at P₀ obtained as the efficient influence curve at $P_n^{k-1}$ (see Proposition 1). The path is a one-dimensional parametric model that fluctuates $P_n^{k-1}$ (i.e., $P_n^{k-1}(0)=P_n^{k-1}$) in the direction of $D^{★}(P_n^{k-1})$ (i.e., the score of the path at ε = 0 equals $D^{★}(P_n^{k-1})$). Here, we choose minus the log-likelihood function as a loss function (i.e., we choose L: × → ℝ characterized by L(P)(O) = −log P(O)). Consequently, the optimal update of $P_n^{k-1},P_n^{k-1}({\epsilon }_n^{k-1})$, corresponds to the maximum likelihood estimator (MLE)

$$\begin{array}{l}{\epsilon }_n^{k-1}=\underset{\mid \epsilon \mid \le \rho {\left|\right|D^{★}(P_n^{k-1})\left|\right|}_{\infty }^{-1}}{argmax}\sum _{i=1}^{n}log{P}_n^{k-1}(\epsilon )(O^{(i)})\\ =\underset{\mid \epsilon \mid \le \rho {\left|\right|D^{★}(P_n^{k-1})\left|\right|}_{\infty }^{-1}}{argmax}\sum _{i=1}^{n}log\left(1+\epsilon D^{★}(P_n^{k-1})(O^{(i)})\right).\end{array}$$

The MLE ${\epsilon }_n^{k-1}$ is uniquely defined (and possibly equal to $\pm \rho {\left|\right|D^{★}(P_n^{k-1})\left|\right|}_{\infty }^{-1}$, hence the introduction of the constant ρ in the definition of the path) provided for instance that

$$\underset{i\le n}{max}\mid D^{★}(P_n^{k-1})(O^{(i)})\mid >0$$

(this statement is to be understood conditionally on P_n, i.e. it is a statement about the sample). Under mild assumptions on P₀, ${\epsilon }_n^{k-1}$ targets ${\epsilon }_0^{k-1}$ such that $P_n^{k-1}({\epsilon }_0^{k-1})$ is the Kullback-Leibler projection of P₀ onto the path { $P_n^{k-1}(\epsilon ):\mid \epsilon \mid \le \rho {\left|\right|D^{★}(P_n^{k-1})\left|\right|}_{\infty }^{-1}$}. We now set $P_n^k=P_n^{k-1}({\epsilon }_n^{k-1})$, thus concluding the description of the iterative updating step of the TMLE procedure. Finally, the TMLE ${\psi }_n^{\ast }$ is defined as ${\psi }_n^{\ast }={lim}_{k\to \infty }{\psi }_n^k$, assuming that the limit exists, or more generally as ${\psi }_n^{k_n}$ for a conveniently chosen sequence {k_n}_n≥0 (see Sections 4.1 and 4.2 regarding this issue).

This is a very general way of dealing with the updating step of the TMLE methodology. The key is that it is possible to determine how the fundamental features of $P_n^k(\epsilon )$ (i.e., the components of $P_n^k(\epsilon )$ involved in the definition of $D^{★}(P_n^k(\epsilon ))$ and in the definition of Ψ) behave (exactly) as functions of ε relative to their counterparts at ε = 0 (i.e., with respect to (wrt) $P_n^k$), as shown in the next Lemma (its proof is relegated to Section A.2).

Lemma 1

Set $s\in L_0^2(P)$ with ||s||_∞ < ∞ and consider the path $\{P_{\epsilon }:\mid \epsilon \mid <{\left|\right|s\left|\right|}_{\infty }^{-1}\}\subset \mathcal{M}$ characterized by

$$\frac{d{P}_{\epsilon }}{dP}(O)=(1+\epsilon s(O)).$$ (9)

The path has score function s. For all $\mid \epsilon \mid <{\left|\right|s\left|\right|}_{\infty }^{-1}$ and all measurable functions f of W,

$$\theta (P_{\epsilon })(X,W)=\frac{\theta (P)(X,W)+\epsilon E_P(Ys(O)\mid X,W)}{1+\epsilon E_P(s(O)\mid X,W)},$$ (10)

$$\mu (P_{\epsilon })(W)=\frac{\mu (P)(W)+\epsilon E_P(Xs(O)\mid W)}{1+\epsilon E_P(s(O)\mid W)},$$ (11)

$$g(P_{\epsilon })(0\mid W)=\frac{g(P)(0\mid W)+\epsilon E_P(\mathbf{1}\{X=0\}s(O)\mid W)}{1+\epsilon E_P(s(O)\mid W)},$$ (12)

$${\sigma }^2(P_{\epsilon })={\sigma }^2(P)+\epsilon E_P\{X^{2}s(O)\},$$ (13)

$$E_{P_{\epsilon }}\{f(W)\}=E_P\{f(W)(1+\epsilon E_P(s(O)\mid W))\}.$$ (14)

Regarding the computation of $\mathrm{\Psi }(P_n^k)$, it is also required to know how to sample independent copies of (W, X) under $P_n^k(\epsilon )$, see Section 3.1. Finally, we emphasize that by (14), the marginal distribution of W under $P_n^k$ typically deviates from its counterpart under $P_n^0$ (i.e., from its empirical counterpart).

TMLE and one-step estimation methodologies

By being based on an iterative scheme, the TMLE methodology naturally evokes the one-step estimation methodology introduced by Le Cam [8] (see [25, Sections 5.7 and 25.8] for a recent account). The latter estimation methodology draws its inspiration from the method of Newton-Raphson in numerical analysis, and basically consists in updating an initial estimator by relying on a linear approximation to the original estimating equation.

Yet, some differences between the TMLE and one-step estimation methodologies are particularly striking. Most importantly, because the TMLE methodology only involves substitution estimators, how one updates (in the parameter space ℝ) the initial estimator ${\psi }_n^0=\mathrm{\Psi }(P_n^0)$ of Ψ (P₀) into ${\psi }_n^1=\mathrm{\Psi }(P_n^1)$ is the consequence of how one updates (in model ) the initial estimator $P_n^0$ of P₀ into $P_n^1$. In contrast, the one-step estimator is naturally presented as an update (in the parameter space ℝ) of the initial estimator, for the sake of solving a linear approximation (in Ψ (P)) to the estimating equation P_nD^★ (P) = 0. The TMLE methodology does not involve such a linear approximation; it nevertheless guarantees by construction $P_n{D}^{★}(P_n^k)\approx 0$ for large k (see Section 4.1 on that issue). Furthermore, on a more technical note, the asymptotic study of the TMLE ${\psi }_n^{\ast }$ does not require that the initial estimator ${\psi }_n^0=\mathrm{\Psi }(P_n^0)$ be $\sqrt{n}$-consistent (i.e., that $\sqrt{n}({\psi }_n^0-\mathrm{\Psi }(P_0))$ be uniformly tight), whereas that of the one-step estimator typically does.

However, there certainly exist interesting relationships between the TMLE and one-step estimation methodologies too. Such relationships are not obvious, and we would like to investigate them in future work.

4. Convergence and asymptotics

In this section, we state and comment on important theoretical properties enjoyed by the TMLE. In Section 4.1, we study the convergence of the iterative updating procedure which is at the core of the TMLE procedure. In Section 4.2, we derive the consistency and asymptotic normality of the TMLE. By building on the statement of consistency, we also argue that it is more interesting to estimate our non-parametric variable importance measure Ψ (P₀) than its semi-parametric counterpart.

4.1. On the convergence of the updating procedure

Studying the convergence of the updating procedure has several aspects to it. We focus on the general one-step procedure of Section 3.2. All proofs are relegated to Section A.4.

On one hand, the following result (very similar to Result 1 in [23]) holds:

Lemma 2

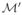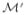Assume (i) that all the paths we consider are included in ⊂ such that sup_P∈ ||D^★ (P)||_∞ = M < ∞, and (ii) that their fluctuation parameters ε are restricted to [−ρ, ρ] for ρ = (2M)⁻¹. If ${lim}_{k\to \infty }{\epsilon }_n^k=0$ then ${lim}_{n\to \infty }{P}_n{D}^{★}(P_n^k)=0$.

Condition (i) is weak, and we refer to Lemma 4 for a set of conditions which guarantee that it holds. Lemma 2 is of primary importance. It teaches us that if the TMLE procedure “converges” (in the sense that ${lim}_{k\to \infty }{\epsilon }_n^k=0$) then its “limit” is a solution of the efficient influence curve equation (in the sense that for any arbitrary small deviation from 0, it is possible to guarantee $P_n{D}^{★}(P_n^k)\approx 0$ by choosing k large enough). This is the key to the proofs of consistency and asymptotic linearity, see Section 4.2. Actually, the condition ${lim}_{k\to \infty }{\epsilon }_n^k=0$ can be replaced by a more explicit condition on the class of the considered data-generating distributions, as shown in the next lemma.

Lemma 3

Under the assumptions of Lemma 2, suppose additionally that the sample satisfies (iii) ${inf}_{k\ge 0}{P}_n{D}^{★}{(P_n^k)}^2>0$, and (iv) that the log-likelihood of the data is uniformly bounded on ${\mathcal{M}}^{\prime }:{sup}_{P\in {\mathcal{M}}^{\prime }}{\sum }_{i=1}^{n}logP(O^{(i)})<\infty$. Then it holds that ${lim}_{k\to \infty }{\epsilon }_n^k=0$ and ${lim}_{n\to \infty }{P}_n{D}^{★}(P_n^k)=0$.

On the other hand, it is possible to obtain another result pertaining to the “convergence” of the updating procedure directly put in terms of the convergence of the sequences ${\{P_n^k\}}_{k\ge 0}$ and ${\{{\psi }_n^k\}}_{k\ge 0}$, provided that ${\{{\epsilon }_n^k\}}_{k\ge 0}$ goes to 0 quickly enough. Specifically,

Lemma 4

Suppose that $P_n^0(|\left|O\right||\le C)=1$ for some finite C > 0. Then we have $P_n^k(|\left|O\right||\le C)=P_n^k(\mid \theta (P_n^k)(X,W)\mid \le C)=P_n^k(\mid \mu (P_n^k)(W)\mid \le C)=1$ for all k ≥ 0. Suppose moreover that for all k ≥ 0, $g(P_n^k)(0\mid W)\ge c>0$ and ${\sigma }^2(P_n^k)\ge c$ are bounded away from 0. Then condition (i) of Lemma 2 holds. Assume now that ${\sum }_{k\ge 0}\mid {\epsilon }_n^k\mid <\infty$. Then the sequence ${\{P_n^k\}}_{k\ge 0}$ converges in total variation (hence in law) to a data-generating distribution $P_n^{\ast }$. Simultaneously, the sequence ${\{{\psi }_n^k\}}_{k\ge 0}$ converges to $\mathrm{\Psi }(P_n^{\ast })$.

It is necessary to bound $g(P_n^k)$ and ${\sigma }^2(P_n^k)$ away from 0 because conditions (i) and (ii) of Lemma 2 only imply that $g(P_n^k)(0\mid W)\ge g(P_n^0)(0\mid W){((1-\rho )/(1+\rho ))}^k$ and ${\sigma }^2(P_n^k)\ge {\sigma }^2(P_n^0){(1-\rho )}^k$. Now, it makes perfect sense from a computational point of view to resort to lower-thresholding in order to ensure that $g(P_n^k)(0\mid W)$ and ${\sigma }^2(P_n^k)$ cannot be smaller than a fixed constant. Assuming that the series ${\sum }_{k\ge 0}\mid {\epsilon }_n^k\mid$ converges ensures that ${\{P_n^k\}}_{k\ge 0}$ converges in total variation rather than weakly only. Interestingly, we do draw advantage from this stronger type of convergence in order to derive the second part of the lemma. In conclusion, note that Newton-Raphson-type algorithms converge at a k⁻²-rate, which suggests that the condition ${\sum }_{k\ge 0}\mid {\epsilon }_n^k\mid <\infty$ is not too demanding.

4.2. Consistency and asymptotic normality

We now investigate the statistical properties of the TMLE ${\psi }_n^{\ast }$. We actually consider a slightly modified version of the TMLE, henceforth denoted by ${\stackrel{\sim }{\psi }}_n^{\ast }$, in order to circumvent the issue of the convergence of the sequence ${\{{\psi }_n^k\}}_{k\ge 0}$ as k goes to infinity. The modified version is perfectly fine from a practical point of view. All proofs are relegated to Section A.5.

Consistency

Under mild assumptions, the TMLE is consistent. Specifically:

Proposition 2 (consistency)

We assume (i) that there exist finite values C > c > 0 such that ${\left|\right|\theta (P_n^{k_n})\left|\right|}_{\infty }\le C,g(P_n^{k_n})(0\mid W)\ge c$ and ${\sigma }^2(P_n^{k_n})\ge c$ for all n ≥ 1, (ii) that $\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n})$ and ${\sigma }^2(P_n^{k_n})$ respectively converge to θ₀ such that ||θ₀||_∞ ≤ C, μ₀, g₀ and ${\sigma }_0^2\ge c$ in such a way that $P_0{(\theta (P_n^{k_n})-{\theta }_0)}^2=o_P(1),P_0{(\theta (P_n^{k_n})(0,·))}^2=o_P(1),P_0{(\mu (P_n^{k_n})-{\mu }_0)}^2=o_P(1),P_0{(g(P_n^{k_n})(0\mid ·)-g_0(0\mid ·))}^2=o_P(1)$ and ${\sigma }^2(P_n^{k_n})={\sigma }_0^2+o_P(1)$, and (iii) that $D_1^{★}(P_n^{k_n})$ and $D_2^{★}(P_n^{k_n})$ belong to a P₀-Donsker class with P₀-probability tending to 1. In addition, we suppose that all assumptions of Lemma 3 are met, and that the (possibly random) integer k_n ≥ 0 is chosen so that $P_n{D}^{★}(P_n^{k_n})=o_P(1/\sqrt{n})$.

Define ${\stackrel{\sim }{\psi }}_n^{\ast }={\psi }_n^{k_n}=\mathrm{\Psi }(P_n^{k_n})$. If the limits satisfy either θ (0, ·) = θ (P₀)(0, ·) or (μ₀ = μ(P₀) and g₀ = g(P₀)) then ${\stackrel{\sim }{\psi }}_n^{\ast }$ consistently estimates Ψ (P₀).

It is remarkable that the consistency of the TMLE ${\stackrel{\sim }{\psi }}_n^{\ast }=\mathrm{\Psi }(P_n^{k_n})$ is granted essentially when the estimators $\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),{\sigma }^2(P_n^{k_n})$ converge and that one only of the limits θ₀ (0, ·) of $\theta (P_n^{k_n})(0,·)$ and (μ₀, g₀) of ( $\mu (P_n^{k_n}),g(P_n^{k_n})$) coincides with the corresponding truth θ (P₀)(0, ·) or (μ (P₀), g(P₀)). This property is mostly inherited from the double-robustness of the efficient influence curve D^★ of parameter Ψ (i.e., PD^★ (P′) = 0 implies Ψ (P′) = Ψ (P)) and from the fact that the TMLE solves the efficient influence curve equation (i.e., $P_n{D}^{★}(P_n^{k_n})\approx 0$.

Merit of the non-parametric variable importance measure over its semi-parametric counterpart

Again, we do not assume a semi-parametric model Y = βX + η (W) + U (with unspecified η and U such that E_P (U |X, W) = 0). However, if P ∈ is such that θ (P)(X, W) = β(P)X + θ (P)(0, W) (i.e., if the semi-parametric model holds under P) then Ψ (P) = β(P). Denote 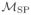⊂ the set of all such data-generating distributions. It is known (see for instance [28]) that β: → ℝ is a pathwise differentiable parameter (wrt the corresponding maximal tangent space), and that its efficient influence curve at P ∈ is given by

$$D_{\text{SP}}^{★}(P)(O)=\frac{Y-\beta (P)X-\theta (P)(0,W)}{v^2(P)(X,W)}\left(X-\frac{E_P(X/v^2(P)(X,W)|W)}{E_P(1/v^2(P)(X,W)|W)}\right),$$

with v²(P)(X, W) = E_P ((Y − θ (P)(X, W)) ²|X, W) is the conditional variance of Y given (X, W) under P. Note that the second factor in the right-hand side expression reduces to (X − μ (P)(W)) whenever v²(P)(X, W) only depends on W.

For the purpose of emphasizing the merit of the non-parametric variable importance measure over its semi-parametric counterpart, say that one estimates β(P₀) assuming (temporarily) that P₀ ∈ (hence Ψ (P₀) = β(P₀)). Say that one builds $P_{n,\text{SP}}^{\ast }\in {\mathcal{M}}_{\text{SP}}$ such that (i) $v^2(P_{n,\text{SP}}^{\ast })(X,W)$ does not depend on (X, W), and (ii) $P_n{D}_{\text{SP}}^{★}(P_{n,\text{SP}}^{\ast })=0$. Assume that $\beta (P_{n,\text{SP}}^{\ast }),v^2(P_{n,\text{SP}}^{\ast }),\mu (P_{n,\text{SP}}^{\ast })$ and $\theta (P_{n,\text{SP}}^{\ast })$ respectively converge to β₁, $v_1^2>0$, μ₁ and θ₁ (such that θ₁(X, W) = β₁X + θ₁(0, W)), and finally that one solves in the limit the efficient influence curve equation:

$$E_{P_0}\{(Y-{\beta }_{1}X-{\theta }_1(0,W))(X-{\mu }_1(W))\}=0$$ (15)

(this is typically derived from (ii) above; see the proof of Proposition 2 for a typical derivation). Then (by double-robustness of $D_{\text{SP}}^{★}$), the estimator $\beta (P_{n,\text{SP}}^{\ast })$ of β(P₀) is consistent (i.e., β₁ = β(P₀)) if either θ₁ = θ (P₀) (that is obvious) or μ₁ = μ (P₀). For example, suppose that μ₁ = μ (P₀). In particular, one can deduce from equalities E_P0 {X (X − μ(P₀)(W))} = E_P0 {(X − μ(P₀)(W))²} and (15) that

$${\beta }_1=\frac{E_{P_0}\{(\theta (P_0)(X,W)-{\theta }_1(0,W))(X-\mu (P_0)(W))\}}{E_{P_0}\{{(X-\mu (P_0)(W))}^2\}}$$

(provided that X does not coincide with μ (P₀)(W) under P₀). Equivalently, β₁ = b(P₀) for the functional b: 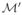= \{P ∈ : X = μ(P)(W)} → ℝ such that, for every P ∈ ,

$$b(P)=\underset{\beta \in \mathbb{R}}{argmin}{E}_P\left\{{[\theta (P)(X,W)-{\theta }_1(0,W)-\beta (X-\mu (P)(W))]}^2\right\}.$$

Note that one can interpret parameter b as a non-parametric extension of the semi-parametric parameter β (non-parametric, because its definition does not involve a semi-parametric model anymore). Now, we want to emphasize that b arguably defines a sensible target if θ₁(0, ·) = θ (P)(0, ·) (in addition to μ₁ = μ (P₀)), but not otherwise! This illustrates the danger of relying on a semi-parametric model when it is not absolutely certain that it holds, thus underlying the merit of targeting the non-parametric variable importance measure rather than its semi-parametric counterpart.

Asymptotic normality

In addition to being consistent under mild assumptions, the TMLE is also asymptotically linear, and thus satisfies a central limit theorem. We start with a partial result:

Proposition 3

Suppose that the assumptions of Proposition 2 are met. If ${\sigma }^2(P_n^{k_n})={\sigma }_0^2+O_P(1/\sqrt{n})$ then it holds that

$${\stackrel{\sim }{\psi }}_n^{\ast }-\mathrm{\Psi }(P_0)=(P_n-P_0)D^{★}({\sigma }^2(P_0),{\theta }_0,{\mu }_0,g_0,\mathrm{\Psi }(P_0))+P_0{D}^{★}({\sigma }^2(P_0),\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))(1+o_P(1))+o_P(1/\sqrt{n}).$$ (16)

Expansion (16) sheds some light on the first order properties of the TMLE ${\stackrel{\sim }{\psi }}_n^{\ast }$. It notably makes clear that the convergence of ${\stackrel{\sim }{\psi }}_n^{\ast }$ is affected by how fast the estimators $\theta (P_n^{k_n}),\mu (P_n^{k_n})$ and $g(P_n^{k_n})$ converge to their limits (see second term). If the rates of convergence are collectively so slow that they only guarantee $P_0{D}^{★}({\sigma }^2(P_0),\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))=O_P(1/n^r)$ for some r ∈ [0, 1/2[, then expansion (16) becomes

$${\stackrel{\sim }{\psi }}_n^{\ast }-\mathrm{\Psi }(P_0)=P_0{D}^{★}({\sigma }^2(P_0),\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))+o_P(1/n^r)$$

and asymptotic linearity fails to hold. On the contrary, we easily deduce from Proposition 3 what happens when θ₀(0, ·) = θ (P₀)(0, ·), μ₀ = μ (P₀), g₀ = g(P₀), with fast rates of convergence:

Corollary 1 (asymptotic normality)

Suppose that the assumptions of Proposition 3 are met. If in addition it holds that θ₀(0, ·) = θ (P₀)(0, ·), μ₀ = μ (P₀), g₀ = g(P₀) and

$$P_0{(\theta (P_n^{k_n})(0,·)-{\theta }_0(0,·))}^2\times (P_0{(\mu (P_n^{k_n})-{\mu }_0)}^2+P_0{(g(P_n^{k_n})(0\mid ·)-g_0(0\mid ·))}^2)=o_P(1/n)$$

then

$${\stackrel{\sim }{\psi }}_n^{\ast }-\mathrm{\Psi }(P_0)=(P_n-P_0)D^{★}({\sigma }^2(P_0),{\theta }_0,{\mu }_0,g_0,\mathrm{\Psi }(P_0))+o_P(1/\sqrt{n})$$

i.e., the TMLE ${\stackrel{\sim }{\psi }}_n^{\ast }$ is asymptotically linear with an influence function equal to D^★ (σ²(P₀), θ₀, μ₀, g₀, Ψ (P₀)).

Thus, $\sqrt{n}({\stackrel{\sim }{\psi }}_n^{\ast }-\mathrm{\Psi }(P_0))$ is asymptotically distributed from a centered Gaussian law with variance P₀D^★ (σ² (P₀), θ₀, μ₀, g₀, Ψ (P₀))². In particular, if θ₀ = θ(P₀) then the TMLE ${\stackrel{\sim }{\psi }}_n^{\ast }$ is efficient.

Corollary 1 covers a simple case in the sense that, by being $o_P(1/\sqrt{n})$, the second right-hand side term in (16) does not significantly contribute to the linear asymptotic expansion. In other words, the influence curve actually is D^★ (σ²(P₀), θ₀, μ₀, g₀, Ψ (P₀)). Depending on how $\theta (P_n^0),\mu (P_n^0)$ and $g(P_n^0)$ are obtained (we recommend relying on super-learning, cf. Section 5.3), the contribution to the linear asymptotic expansion may be significant (but determining this contribution would be a very difficult task to address on a case by case basis when relying on super-learning).

5. Specifics of the TMLE procedure tailored to the estimation of the non-parametric variable importance measure

In this section, we present practical details on how we conduct the initialization and updating steps of the TMLE procedure as described in Section 3. We introduce in Section 5.1 a working model for the conditional distribution of X given (W, X ≠ 0) which proves very efficient in computational terms. In Section 5.2, we introduce two alternative two-step updating procedures which can be substituted for the general one-step updating procedure presented in Section 3.2. Finally, we describe carefully what are all the features of interest of P₀ that must be considered for the purpose of targeting the parameter of ultimate interest, Ψ (P₀), via the construction of the TMLE.

5.1. Working model for the conditional distribution of X given (W,X ≠ 0)

The working model for the conditional distribution of X given (W, X ≠ 0) under $P_n^0$ that we build relies on two ideas:

• we link the conditional second order moment $E_{P_n^0}(X^2\mid X\ne 0,W)$ to the conditional mean $E_{P_n^0}(X\mid X\ne 0,W)$ (both under $P_n^0$) through the equality

  $$E_{P_n^0}(X^2\mid X\ne 0,W)={\varphi }_{n,\lambda }(E_{P_n^0}(X\mid X\ne 0,W))$$ (17)

  where ϕ_{n, λ} (t) = λt²+(1 − λ)(t(m_n+M_n)− m_nM_n) (with m_n = min_i≤n X⁽ⁱ⁾, M_n = max_i≤n X⁽ⁱ⁾), and λ ∈ [0, 1] is a tuning parameter;

• under $P_n^0$ and conditionally on (W, X ≠ 0), X takes its values in the set {X⁽ⁱ⁾: i ≤ n}\{0} of the observed X’s different from 0.

As the conditional distribution of X given (W, X ≠ 0) under $P_n^0$ is subject to two constraints, X cannot take fewer than three different values in general. Elegantly, it is possible (under a natural assumption on $P_n^0$) to fine-tune λ and to select three values in {X⁽ⁱ⁾: i ≤ n}\{0} in such a way that X only takes the latter values:

Lemma 5

Assume that $P_n^0$ guarantees that ${\sigma }^2(P_n^0)>0,P_n^0(X\ne 0)>0,g(P_n^0)(0\mid W)\in (0,1)P_n^0$-almost surely, and X ∈ [m_n + c, M_n − c] for some c > 0 when X ≠ 0. It is possible to construct $P_n^{00}\in \mathcal{M}$ in such a way that (i) W has the same marginal distribution under $P_n^{00}$ and $P_n^0,\mu (P_n^{00})=\mu (P_n^0),g(P_n^{00})=g(P_n^0),{\sigma }^2(P_n^{00})={\sigma }^2(P_n^0)$ and (ii) for all W ∈ , there exist three different values x⁽¹⁾, x⁽²⁾, x⁽³⁾ ∈ {X⁽ⁱ⁾: i ≤ n}\{0} and three non-negative weights p₁, p₂, p₃ summing up to 1 such that, conditionally on (W, X ≠ 0) under $P_n^{00}$, X = x^(k) with conditional probability p_k.

Hence, we choose to directly construct a $P_n^0$ satisfying the constraints of $P_n^{00}$ in Lemma 5. Note that, by (8), because the conditional distribution of X given (W, X ≠ 0) under $P_n^0$ has its support included in {X⁽ⁱ⁾: i ≤ n}\{0}, then so do the conditional distributions of X given (W, X ≠ 0) under $P_n^k$ (all k ≥ 1) obtained by following the general one-step updating procedure of Section 3.2. Similarly, because we initially estimate the marginal distribution of W under P₀ by its empirical counterpart, then the marginal distributions of W under $P_n^0$ and $P_n^k$ (all k ≥ 1) have their supports included in {W_i: i ≤ n}.

We discuss in Section 5.4 why it is computationally more interesting to consider such a working model (instead of a Gaussian working model for instance). We emphasize that assuming X ∈ [m_n + c, M_n − c] when X ≠ 0 (for a possibly tiny c > 0) is hardly a constraint, and that the latter must be accounted for while estimating μ(P₀), g(P₀), and σ² (P₀). The proof of the lemma is relegated to Section A.2.

5.2. Two tailored alternative two-step updating procedures

We present in Section 3.2 a general one-step updating procedure. Alternatively, it is also possible to decompose each update into a first update of the conditional distribution of Y given (W, X), followed by a second update of the marginal distribution of (W, X).

First update: fluctuating the conditional distribution of Y given (W, X)

We actually propose two different fluctuations for that purpose: a Gaussian fluctuation on one hand and a logistic fluctuation on the other hand, depending on what one knows or wants to impose.

Gaussian fluctuation

We use minus the log-likelihood function as a loss function, as we did for the general one-step updating procedure. First fluctuate only the conditional distribution of Y given (W, X), by introducing the path { $P_{n,1}^{k-1}(\epsilon ):\epsilon \in \mathbb{R}$} such that (i) (W, X) has the same distribution under $P_{n,1}^{k-1}(\epsilon )$ as under $P_n^{k-1}$, and (ii) under $P_{n,1}^{k-1}(\epsilon )$ and given (W, X), Y is distributed from the Gaussian law with conditional mean $\theta (P_n^{k-1})(X,W)+\epsilon H(P_n^{k-1})(X,W)$ and conditional variance 1, where the so-called clever covariate (an expression taken from [22]) H(P) is characterized for any P ∈ by

$$H(P)(X,W)=\frac{1}{{\sigma }^2(P)}\left(X-\frac{\mu (P)(W)\mathbf{1}\{X=0\}}{g(P)(0\mid W)}\right).$$

This definition guarantees that the path fluctuates $P_n^{k-1}$ (i.e., $P_{n,1}^{k-1}(0)=P_n^{k-1}$, provided that Y is conditionally Gaussian given (W, X) under $P_n^0$) in the direction of $D_2^{★}(P_n^{k-1})$ (i.e., the score of the path at ε = 0 equals $D_2^{★}(P_n^{k-1})$). Introducing the MLE

$$\begin{array}{l}{\epsilon }_{n,1}^{k-1}=\underset{\epsilon \in R}{argmax}\sum _{i=1}^{n}log{P}_{n,1}^{k-1}(\epsilon )(O^{(i)})\\ =\frac{{\sum }_{i=1}^n(Y^{(i)}-\theta (P_n^{k-1})(X^{(i)},W^{(i)}))H(P_n^{k-1})(X^{(i)},W^{(i)})}{{\sum }_{i=1}^{n}H(P_n^{k-1}){(X^{(i)},W^{(i)})}^2},\end{array}$$

the first intermediate update bends $P_n^{k-1}$ into $P_{n,2}^{k-1}=P_{n,1}^{k-1}({\epsilon }_{n,1}^{k-1})$.

Logistic fluctuation

There is yet another interesting option in the case that Y ∈ [a, b] is bounded (or in the case that one wishes to impose Y ∈ [a, b], typically then with a = min_i≤n Y⁽ⁱ⁾ and b = max_i≤n Y⁽ⁱ⁾, which allows to incorporate this known fact (or wish) into the procedure. Assume that θ (P₀) takes its values in (a, b) and also that $\theta (P_n^{k-1})$ is constrained in such a way that $\theta (P_n^{k-1})(X,W)\in (a,b)$. Introduce for clarity the function on the real line characterized by F_a,b(t) = (t − a)/(b − a). Here, we choose the loss function characterized by −L_a,b(P)(O) = F_a,b(Y) log F_a,b∘ θ(P)(X, W) + (1 − F_a,b(Y)) log(1 − F_a,b ∘ θ (P)(X, W)), with the convention L_a,b(P)(O) = + ∞ if θ (P)(X, W) ∈ {a, b}. Note that the loss L_a,b(P) depends on the conditional distribution of Y given (W, X) under P only through its conditional mean θ (P). This straightforwardly implies that in order to describe a fluctuation { $P_{n,1}^{k-1}(\epsilon ):\epsilon \in \mathbb{R}$} of $P_n^{k-1}$, it is only necessary to detail the form of the marginal distribution of (W, X) under $P_{n,1}^{k-1}(\epsilon )$ and how $\theta (P_{n,1}^{k-1}(\epsilon ))$ depends on $\theta (P_n^{k-1})$ and ε. Specifically, we first fluctuate only the conditional distribution of Y given (W, X), by making $P_{n,1}^{k-1}(\epsilon )$ be such that (i) (W, X) has the same distribution under $P_{n,1}^{k-1}(\epsilon )$ as under $P_n^{k-1}$, and (ii)

$$\theta (P_{n,1}^{k-1}(\epsilon ))(X,W)=F_{a,b}^{-1}\left(\text{expit}(\text{logit}{F}_{a,b}\circ \theta (P_n^{k-1})(X,W)+\epsilon H(P_n^{k-1})(X,W))\right).$$

Now, introduce the L_a,b-minimum loss estimator

$${\epsilon }_{n,1}^{k-1}=\underset{\epsilon \in \mathbb{R}}{argmin}\sum _{i=1}^n{L}_{a,b}(P_{n,1}^{k-1}(\epsilon ))(O^{(i)}),$$

which finally yields the first intermediate update $P_{n,2}^{k-1}=P_{n,1}^{k-1}({\epsilon }_{n,1}^{k-1})$. The following lemma (whose proof is relegated to Section A.2) justifies our interest in the loss function L_a,b and fluctuation { $P_{n,1}^{k-1}(\epsilon ):\epsilon \in \mathbb{R}$}:

Lemma 6

Assume that the conditions stated above are met. Then L_a,b is a valid loss function for the purpose of estimating θ (P₀) in the sense that

$$\theta (P_0)=\underset{P\in \mathcal{M}}{argmin}{P}_0{L}_{a,b}(P).$$

Moreover, it holds that

$$\frac{\partial }{\partial \epsilon }{L}_{a,b}(P_{n,1}^{k-1}(\epsilon )){\mid }_{\epsilon =0}(O)=-D_2^{★}(P_n^{k-1})(O).$$

The second inequality is the counterpart of the fact that, when using the Gaussian fluctuation, the score of the path at ε = 0 equals $D_2^{★}(P_n^{k-1})$.

Second update: fluctuating the marginal distribution of (W, X)

Next, we preserve the conditional distribution of Y given (W, X) and only fluctuate the marginal distribution of (W, X), by introducing the path { $P_{n,2}^{k-1}(\epsilon ):\mid \epsilon \mid \le \rho {\left|\right|D_1^{★}(P_{n,2}^{k-1})\left|\right|}_{\infty }^{-1}$} such that (i) Y has the same conditional distribution given (W, X) under $P_{n,2}^{k-1}(\epsilon )$ as under $P_{n,2}^{k-1}$, and (ii) the marginal distribution of (W, X) under $P_{n,2}^{k-1}(\epsilon )$ is characterized by

$$\frac{{dP}_{n,2}^{k-1}(\epsilon )}{{dP}_{n,2}^{k-1}}(X,W)=(1+\epsilon D_1^{★}(P_{n,2}^{k-1})(X,W)).$$ (18)

This second path fluctuates $P_{n,2}^{k-1}$ (i.e., $P_{n,2}^{k-1}(0)=P_{n,2}^{k-1}$) in the direction of $D_1^{★}(P_{n,2}^{k-1})$ (i.e., the score of the path at ε = 0 equals $D_1^{★}(P_{n,2}^{k-1})$). Consider again minus the log-likelihood as loss function, and introduce the MLE

$${\epsilon }_{n,2}^{k-1}=\underset{\mid \epsilon \mid \le \rho {\left|\right|D_1^{★}(P_{n,2}^{k-1})\left|\right|}_{\infty }^{-1}}{argmax}\sum _{i=1}^{n}log{P}_{n,2}^{k-1}(\epsilon )(O^{(i)}):$$

the second update bends $P_{n,2}^{k-1}$ into $P_n^k=P_{n,2}^{k-1}({\epsilon }_{n,2}^{k-1})$, concluding the description of how we can alternatively build $P_n^k$ based on $P_n^{k-1}$.

Note that, by (18), because the conditional distribution of X given (W, X ≠ = 0) under $P_n^0$ has its support included in {X⁽ⁱ⁾: i ≤ n}\{0} (a consequence of our choice of working model, see Section 5.1), then so do the conditional distributions of X given (W, X ≠ 0) under $P_n^k$ (all k ≥ 1) obtained by following either one of the tailored two-step updating procedure. Furthermore, it still holds that the marginal distributions of W under $P_n^0$ and $P_n^k$ (all k ≥ 1) have their supports included in {W_i: i ≤ n} (because we initially estimate the marginal distribution of W under P₀ by its empirical counterpart).

5.3. Super-learning of the features of interest

It still remains to specify how we wish to carry out the initial estimation and updating of the features of interest θ (P₀), μ(P₀), g(P₀), and σ² (P₀). As for σ²(P₀) = E_P0{X²}, we simply estimate it by its empirical counterpart i.e., construct $P_n^0$ in such a way that ${\sigma }^2(P_n^0)=n^{-1}{\sum }_{i=1}^n{(X^{(i)})}^2$. The three other features θ (P₀), μ(P₀) and g(P₀) are estimated by super-learning, and $P_n^0$ constructed in such a way that $\theta (P_n^0),\mu (P_n^0)$ and $g(P_n^0)$ equal their corresponding estimators. Super-learning is a cross-validation based aggregation method that builds a predictor as a convex combination of base predictors [24, 22] (we briefly describe in Section 6.5 the specifics of the super-learning procedure that we implement for our application to simulated and real data). The weights of the convex combination are chosen so as to minimize the prediction error, which is expressed in terms of the non-negative least squares (NNLS) loss function [7] and estimated by V -fold cross-validation. Heuristically the obtained predictor is by construction at least as good as the best of the base predictors (this statement has a rigorous form implying oracle inequalities, see [24, 22]).

Lemma 1 teaches us what additional features of $P_n^{k-1}$ must be known in order to derive the kth update $P_n^k$ from its predecessor $P_n^{k-1}$, starting from k = 1.

Specifically, if we rely on the general one-step updating procedure of Section 3.2 then we need to know:

• $E_{P_n^{k-1}}(Y{D}^{★}(P_n^{k-1})(O)\mid X,W)$ and $E_{P_n^{k-1}}(D^{★}(P_n^{k-1})(O)\mid X,W)$ for the update of $\theta (P_n^{k-1})$ (see (10));

• $E_{P_n^{k-1}}(D^{★}(P_n^{k-1})(O)\mid W)$ for the updates of $\mu (P_n^{k-1}),g(P_n^{k-1})$, and the marginal distribution of W under $P_n^{k-1}$ (see the right-hand side denominators in (11), (12), (14));

• $E_{P_n^{k-1}}(X{D}^{★}(P_n^{k-1})(O)\mid W)$ for the update of μ (P^k−1) (see the right-hand side numerator in (11));

• $E_{P_n^{k-1}}(\mathbf{1}\{X=0\}{D}^{★}(P_n^{k-1})(O)\mid W)$ for the update of $g(P_n^{k-1})$ (see the right-hand side numerator in (12));

• $E_{P_n^{k-1}}\{X^2{D}^{★}(P_n^{k-1})(O)\}$ for the update of ${\sigma }^2(P_n^{k-1})$ (see (13)).

It is noteworthy that if either one of the two-step updating procedures of Section 5.2 is used then the first two conditional expectations do not need to be known, because updating $\theta (P_n^{k-1})$ relies on the clever covariate $H(P_n^{k-1})$, which is entirely characterized by the current estimators $\mu (P_n^{k-1}),g(P_n^{k-1})$ and ${\sigma }^2(P_n^{k-1})$ of the features μ (P₀), g(P₀), and σ² (P₀), respectively. In the sequel of this sub-section, we focus on the general one-step updating procedure of Section 3.2. How to proceed when relying on either of the two-step updating procedures of Section 5.2 can be easily deduced from that case.

Once $\theta (P_n^0),\mu (P_n^0),g(P_n^0)$, and ${\sigma }^2(P_n^0)$ are determined (see the first paragraph of this sub-section) hence $D^{★}(P_n^0)$ is known, we therefore also estimate by super-learning the conditional expectations under P₀ of $Y{D}^{★}(P_n^0)(O)$ and $D^{★}(P_n^0)(O)$ given (X, W) and those under P₀ of $D^{★}(P_n^0)(O),X{D}^{★}(P_n^0)(O)$ and $\mathbf{1}\{X=0\}{D}^{★}(P_n^0)(O)$ given W; we simply estimate $E_{P_0}\{X^2{D}^{★}(P_n^0)(O)\}$ by its empirical counterpart. Then we constrain $P_n^0$ in such a way that the conditional expectations of the same quantities under $P_n^0$, and the expectation $E_{P_n^0}\{X^2{D}^{★}(P_n^0)(O)\}$ equal their corresponding estimators. This completes the construction of $P_n^0$, and suffices for characterizing the features $\theta (P_n^1),\mu (P_n^1),g(P_n^1)$ and ${\sigma }^2(P_n^1)$ of the first update $P_n^1$.

Now, if one wished to follow exactly the conceptual road consisting in relying on Lemma 1 in order to derive the second update $P_n^2$ from its predecessor $P_n^1$, one would have to describe how each conditional (and unconditional) expectation of the above list behaves, as a function of ε, on the path { $P_n^1(\epsilon ):\mid \epsilon \mid \le \rho {\left|\right|D^{★}(P_n^1)\left|\right|}_{\infty }^{-1}$}. This would in turn enlarge the above list of the features of interest of P₀ that one would have to consider in the initial construction of $P_n^0$. Note that the length of the list would increase quadratically in the number of updates. Instead, once $D^{★}(P_n^{k-1})$ is known, we estimate by super-learning the conditional expectations under P₀ of $Y{D}^{★}(P_n^{k-1})(O)$ and $D^{★}(P_n^{k-1})(O)$ given (X, W), and the conditional expectations under P₀ of $D^{★}(P_n^{k-1})(O),X{D}^{★}(P_n^{k-1})(O)$, and $\mathbf{1}\{X=0\}{D}^{★}(P_n^{k-1})(O)$ given W; as for $E_{P_0}\{X^2{D}^{★}(P_n^{k-1})(O)\}$, we simply estimate it by its empirical counterpart. Then we proceed as if the conditional expectations of the same quantities under $P_n^{k-1}$ were equal to their corresponding estimators. By doing so, the length of the list of the features of interest of P₀ is fixed, no matter how many steps of the updating procedure are carried out. Arguably, following this alternative road has little if no effect relative to following exactly the conceptual road consisting in relying on Lemma 1, because only second (or more) order expressions in ε are involved.

5.4. Merit of the working model for the conditional distribution of X given (W, X ≠ 0)

We explain here why (a) initially estimating the marginal distribution of W under P₀ by its empirical counterpart and (b) relying on the working model for the conditional distribution of X given (W, X ≠ 0) that we described in Section 5.1 is computationally very interesting. The key is that, under $P_n^0$ and its successive updates $P_n^k$ (all k ≥ 1), the distributions of (W, X) have their supports included in {(W⁽ⁱ⁾, X^(j)): i ≤ j ≤ n} (we say they are “parsimonious”).

Indeed, Lemma 1 and a simple induction yield that, for each k ≥ 1, a single call to $\theta (P_n^k),\mu (P_n^k)$ or $g(P_n^k)$ involves a number of (nested) calls to the “past” features of interest $\theta (P_n^{k^{\prime }}),\mu (P_n^{k^{\prime }})$ and $g(P_n^{k^{\prime }})$ (0 ≤ k′ < k) which is O(k). Furthermore, the evaluation of $\mathrm{\Psi }(P_n^k)$ (following (5) with $P_n^k$ substituted for $P_n^0$) requires in turn B calls (assuming for simplicity that the functions are not vectorized) to $\theta (P_n^k)$ (in order to evaluate the numerator of the right-hand side term of (5)), $\mu (P_n^k)$ and $g(P_n^k)$ (in order to simulate {(W̃ ^(b), X̃^(b)): b ≤ B}). Overall, at least O(Bk) calls to the set of all features of interest are performed at the kth updating step of the TMLE procedure. In practice (even if functions are vectorized) this leads to a large memory footprint and prohibitive running time of the algorithm, as each of these calls consists in the prediction of the corresponding feature, as described in Section 5.3.

By taking advantage of the “parsimony” of the distributions of (W, X) under the successive $P_n^k(k\ge 0)$, we manage to alleviate dramatically the time and memory requirements of our implementation. Indeed, the “parsimony” implies that, at the kth step of the TMLE procedure (k ≥ 0), it is only required to compute and store O(n²) quantities (including, but not limited to, $\theta (P_n^k)(X^{(i)},W^{(j)}),\mu (P_n^k)(W^{(j)})$ and $g(P_n^k)(W^{(j)})$ for all 1 ≤ i, j ≤ n) — see Section 5.3). In particular, the evaluation of $\mathrm{\Psi }(P_n^k)$ now requires retrieving O(B) values from a handful of vectors instead of performing O(Bk) memory and time-consuming (nested) function calls.

6. Application

We first present the genomic problem that motivated this study, in Section 6.1, and earlier contributions on the same topic, in Section 6.2. Two real datasets are described in Section 6.3. They play a central role in this article. We both (a) draw inspiration from one dataset and (b) use it in order to set up our simulation study, as presented in Section 6.4. We also apply the TMLE methodology directly to the other dataset. The specifics of the TMLE procedures that we undertake both on simulated and real data are given in Section 6.5, and their results are summarized in Section 6.6, for the simulation study, and in Section 6.7, for the real data application.

6.1. Association between DNA copy number and gene expression in cancers

The activity of a gene in a cell is directly related to its expression level (Y), that is, the number of messenger RNA (mRNA) fragments corresponding to this gene. Cancer cells are characterized by changes in their gene expression patterns. Such alterations have been shown to be caused directly or indirectly by genetic events, such as changes in the number of DNA copies (X), and epigenetic events, such as DNA methylation (W). Some changes in DNA copy number have been reported to be positively associated with gene expression levels [11]. Conversely, DNA methylation is a chemical transformation of cytosines (one of the four types of DNA nucleotides) which is thought to lead to gene expression silencing [5]. Therefore, DNA methylation levels are generally negatively associated with gene expression levels.

We propose to apply the methodology developed in the previous sections to the search for genes for which there exists an association between DNA copy number variation and gene expression level, accounting for DNA methylation.

6.2. Related works

In the context of cancer studies, various methods have been proposed in order to find associations between DNA copy number and gene expression at the level of genes. Because we cannot cite all of them, we try here to cite one relevant publication for each broad type of method. Most of them can be classified into two groups, depending on whether DNA copy number is viewed as a continuous or a discrete variable. When DNA copy number is viewed as a continuous variable, associations between X and Y are generally quantified using a correlation coefficient [11]. When it is viewed as a discrete variable, associations are typically quantified using a test of differential expression between DNA copy number states [26]. A common limitation to this two types of methods is that they are generally good at identifying genes that were already known, but less so at finding novel candidates. This is not surprising: for correlation-based methods, high correlation between X and Y requires both X and Y to vary substantially, in which case it is likely that these (marginal) variations have already been reported. For methods based on differential expression between copy number states, the latter often correspond to biological or clinical groups which are already known and for which differential expression analyses have already been carried out.

In the present paper, we acknowledge the fact that while DNA copy number is observed as a quantitative variable, the copy neutral state (two copies of DNA) generally has positive mass, in the sense that for a given gene, a positive proportion of samples have two copies of DNA.

Another major difference between our method and the ones cited above is that we explicitly incorporate DNA methylation into the analysis. Several papers where DNA copy number, gene expression and DNA methylation are combined have been published recently, but they typically analyze one dimension of (W, X, Y) at a time, and then use an ad hoc rule to merge or intersect the results [1, 17]. The CNAmet method [10] relies on two scores: a score of differential expression between copy number levels on the one hand, and between DNA methylation levels on the other hand. Then both scores are summed. In the method proposed here, the three dimensions are studied jointly.

6.3. Datasets

We exploit glioblastoma multiforme (GBM, the most common type of primary adult brain cancers) and ovarian cancers (OvCa, a cancerous growth arising from the ovary) data from The Cancer Genome Atlas (TCGA) project [2], a collaborative initiative to better understand several types of cancers using existing large-scale whole-genome technologies. TCGA has recently completed a comprehensive genomic characterization of these types of tumor, including DNA copy number (X), gene expression (Y), and DNA methylation (W) microarray experiments [18, 19].

Probe-level normalized GBM and OvCa data can be downloaded from the TCGA repository at http://tcga-data.nci.nih.gov/tcga/. In order to study associations between X, Y and W at the level of genes, these probe-level measurements first need to be aggregated into gene-level summaries. We choose to define X, Y and W as follows for a given gene:

• DNA methylation W is the proportion of “methylated” signal at a CpG locus in the gene’s promoter region;

• DNA copy number X is a locally smoothed total copy number relative to a set of reference samples;

• expression Y is the “unified” gene expression level across three microarray platforms, as defined by [27].

After this pre-processing step, each gene is represented by a 3 × n matrix, where 3 is the number of data types and n is the number of samples. Figure 2(a) represents DNA methylation, DNA copy number, and gene expression data for one particular gene, EGFR, which is known to be altered in GBM. For this gene, the association between copy number and expression is non-linear, and high methylation levels are associated with low expression levels.

Fig 2.

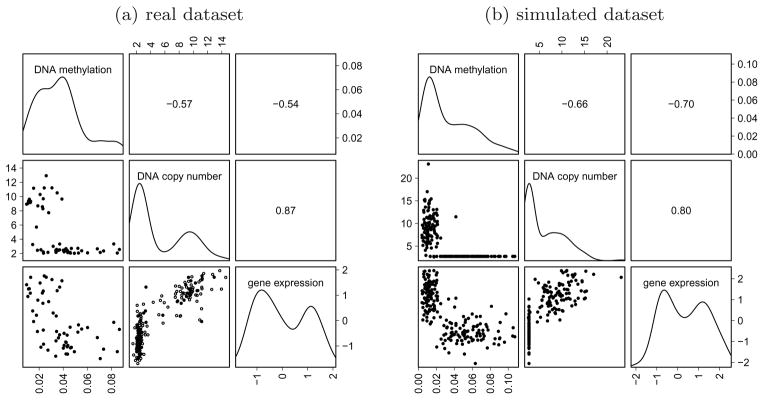
Illustrating DNA methylation, DNA copy number, and gene expression data. In both graphics, we represent kernel density estimates (diagonal panels), pairwise plots (lower panels), and report the pairwise Pearson correlation coefficients (upper panels). (a). Real dataset corresponding to the EGFR gene in 187 GBM tumor samples. For 130 among the 187 samples, only DNA copy number and gene expression data were available (circles in lower middle plot). (b). Simulated dataset consisting of n = 200 independent copies of the synthetic observed data structure described in Section 6.6. Note that the constant $O_2^X$ is added to each value of X so that graphics corresponding to real and simulated data can be more easily compared.

6.4. Simulation scheme

Because association patterns between copy number, expression and methylation are generally non-linear, setting up a realistic simulation model is a difficult task. We design here a simulation strategy based on perturbations of real observed data structures. It mimics situations such as the one observed in the Figure 2(a) for the EGFR gene in GBM. This strategy implements the following constraints:

• there are generally up to three copy number classes: normal regions, and regions of copy number gains and losses;

• in normal regions, expression is negatively correlated with methylation;

• in regions of copy number alteration, copy number and expression are positively correlated.

Our simulation scheme relies on three real observed data structures $O_1=(O_1^W,O_1^X,O_1^Y),O_2=(O_2^W,O_2^X,O_2^Y),O_3=(O_3^W,O_3^X,O_3^Y)$ corresponding to three samples from different copy number classes: loss (class 1), normal (class 2), and gain (class 3). We simulate a synthetic observed data structure O = (W, X, Y) ~ P^s as follows. Given a vector p = (p₁, p₂, p₃) of proportions such that p₁ + p₂ + p₃ = 1, we first draw a class assignment U from the multinomial distribution with parameter (1, p) (in other words, U = u with probability p_u). Conditionally on U, a measure W of DNA methylation is drawn randomly as a perturbation of the DNA methylation in the corresponding real observed data structure O_U: given a vector ω = (ω₁, ω₂, ω₃) of positive numbers,

$$W=\text{expit}(\text{logit}(O_U^W)+{\omega }_{U}Z),$$

where Z is a standard normal random variable independent of U. Finally, a couple (X, Y) of DNA copy number and expression level is drawn conditionally on (U, W) as a perturbation of the couple ( $O_U^X,O_U^Y$) in the corresponding real observed data structure O_U (with an additional centering applied to X so that the pivot value be equal to 0): Given σ² > 0, two variance-covariance 2 × 2-matrices Σ₁ and Σ₃ and a non-increasing mapping λ₀: [0, 1] → [0, 1],

• if U = 2, then $(X,Y)=(0,O_2^Y+{\lambda }_0(W)+{\sigma }_2{Z}^{\prime })$, where Z′ is a standard normal random variable independent of (U, W);

• if U ≠ 2, then (X, Y) is drawn conditionally on (U, W) from the bivariate Gaussian distribution with mean ( $O_U^X-O_2^X,O_U^Y$) and variance-covariance matrix Σ_U.

In particular, the reference/pivot value x₀ = 0. Note that λ₀ is chosen non-increasing in order to account for the negative association between DNA expression and methylation. Furthermore, the synthetic observed data structure O drawn from P^s is not bounded.

We easily derive closed-form expressions for the features of interest θ (P^s), μ(P^s), g(P^s), and σ²(P^s), which we report in the Appendix (see Lemma 7). Relying on Lemma 7 makes it possible to evaluate the value of Ψ (P^s), by following the procedure described in Section 3.1 (see details in Section 6.6).

Finally we provide in Figure 2(b), for the sake of illustration, a visual summary of a simulation run with n = 200 independent copies of the synthetic observed data structure O drawn from P^s and based on real observed data structure from two GBM samples for the EGFR gene which are described in Table 1. The parameters for this simulation were chosen as follows: p = (0, 1/2, 1/2), ω = (0, 3, 3), λ₀: w ↦ −w, σ² = 1, ${\mathrm{\sum }}_3=\left(\begin{array}{cc}9.96& 1\\ 1& 0.43\end{array}\right)$.

Table 1.

Real methylation, copy number and expression data used as a baseline for simulating the dataset according to the simulation scheme presented in Section 6.6. A visual of the simulated dataset is provided in Figure 2(b)

sample name	methylation $O_i^W$	copy number $O_i^X$	expression $O_i^Y$
TCGA-02-0001 (i = 2)	0.05	2.72	−0.46
TCGA-02-0003 (i = 3)	0.01	9.36	1.25

6.5. Library of algorithms for super-learning

We have explained in Section 5.3 that we rely on super-learning [24, 22] in order to estimate some relevant infinite-dimensional features of P₀, including (but not limited to) θ (P₀), μ (P₀) and g(P₀). This algorithmic challenge is easily overcome, thanks to the remarkable R-package SuperLearner [12] and the possibility to rely on the library of R-packages [13] built by the statistical community. As for the base predictors, they involve (by alphabetical order):

• Generalized additive models: we use the gam R-package [4], with its default values.

• Generalized linear models: we use the glm R-function with identity link (for learning θ (P₀) and μ (P₀)) and logit link (for learning g(P₀)), and with linear combinations of (1, X, W) or (1, X, W, XW) (for learning θ (P₀)) and linear combinations of (1, W) or (1, W, W²) (for learning μ (P₀) and g(P₀)).

• Piecewise linear splines: we use polymars R-function from the polspline R-package [6], with its default values.

• Random forests: we use the randomForest R-package [9], with its default values.

• Support vector machines: we use the svm R-function from the e1071 R-package [3], with its default values.

Note that none of the statistical models associated to the above estimation procedures contains P^s (see Lemma 7).

6.6. Simulation study

We conduct twice a simulation study where B′ = 10³ datasets of n = 200 independent observed data structures are (independently) generated under P^s (i.e., under the simulation scheme described in Section 6.4). In each simulation study and for every simulated dataset, we perform the TMLE methodology for the purpose of estimating the target parameter Ψ (P^s). From one simulation study to the other, we only change the setup of the super-learning procedure, by modifying the library of algorithms involved in the super-learning of the features of interest:

• the first time, we proceed exactly as described in Section 6.5 (we say that the full-SL is undertaken);

• the second time, we decide to include only algorithms based on generalized linear models (we say that the light-SL is undertaken).

We do not use any index to refer to the super-learning setup (full-SL or light-SL) for the sake of alleviating notations.

In each simulation study (i.e., for each setup of the super-learning procedure full-SL and light-SL) and for each b ≤ B′, we record the values ${\psi }_{n,b}^k=\mathrm{\Psi }(P_{n,b}^k)$ of the initial substitution estimator (k = 0) and subsequent updated substitution estimators (k = 1, 2, 3) targeting Ψ (P^s), as derived on the bth simulated dataset (whose empirical measure is denoted by P_n,b). The targeted update steps rely on the Gaussian fluctuations presented in Section 5.2 (the results are very similar when one applies either the general one-step updating procedure of Section 3.2 or the second tailored alternative two-step updating procedure of Section 5.2). We do not record the next updates because the ad hoc stopping criterion that we devise systematically indicates that this is not necessary (heuristically, the criterion elaborates on the gains in likelihood and the variations in the resulting estimates).

The value of Ψ (P^s) is evaluated by simulations, following (5) in Section 3.1 with P^s substituted for $P_n^0$ (we rely on B = 10⁵ simulated observed data structures, whose empirical measure is denoted by P_B; the features θ (P^s) and σ² (P^s) are explicitly known, see Lemma 7). In order to get a sense of how accurate our evaluation of Ψ (P^s) is, we also use the same large simulated dataset to evaluate Var_PsD^★ (P^s)(O) (as the empirical variance Var _PB D^★ (P^s)(O); again, D^★ (P^s) is known explicitly by Lemma 7). Denoting by ψ_B(P^s) and v_B(P^s) the latter evaluations, we interpret the intervals $[{\psi }_B(P^s)\pm {\xi }_{1-\alpha /2}\sqrt{v_B(P^s)/n}]$ and $[{\psi }_B(P^s)\pm {\xi }_{1-\alpha /2}\sqrt{v_B(P^s)/B}]$ as (1 − α)-accuracy intervals for the evaluation of Ψ (P^s) based on n = 200 and B = 10⁵ independent observed data structures. The gray intervals in Figure 3 represent these accuracy intervals for α = 5%, n = 200 (light gray) and B = 10⁵ (dark gray). Note that (by the convolution theorem) the length of $[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/n}]$ is the optimal length of a 95%-confidence interval based on an efficient (regular) estimator of Ψ (P^s) relying on n observations (assuming that the asymptotic regime is reached). The numerical values are reported in Table 2.

Fig 3.

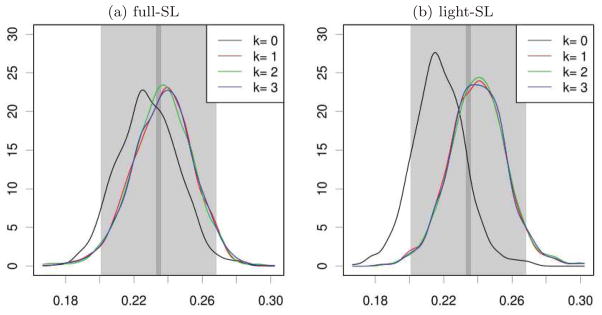
Empirical distribution of { ${\mathrm{\Psi }}_{n,b}^k:b\le B^{\prime }$} based on n = 200 independent observed data structures for k = 0 (initial estimator) and k iterations of the updating procedure (k = 1, 2, 3), as obtained from B′ = 10³ independent replications of the simulation study (using a Gaussian kernel density estimator). (a). The super-learning procedure involves all algorithms described in Section 6.5. (b). The super-learning procedure only involves algorithms based on generalized linear models. In both graphics, gray rectangles represent 95%-accuracy intervals $[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/n}]$ and $[{\psi }_B(P^{(s)})\pm {\xi }_{0.975}\sqrt{v_B(P^s)/B}]$ for the true parameter Ψ (P^s) based on 200 observed data structures (light gray) and B = 10⁵ observed data structures (dark p gray). The length of $[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/n}]$ is the optimal length of a 95%-confidence interval based on an efficient (regular) estimator of Ψ (P^s) relying on n observations (assuming that the asymptotic regime is reached).

Table 2.

Values of ψ_B(P^s) and v_B(P^s), estimators of Ψ (P^s) and Var_P^sD^★ (P^s)(O), and 95%-accuracy intervals $[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/n}],[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/B}]$ (n = 200, B = 10⁵)

ψB(Ps)	vB(Ps)	$[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/N}]$
		N = 200	N = 105
0.2345	0.05980232	[0.2006; 0.2684]	[0.2329; 0.2360]

The results of this joint simulation study are summarized by Figure 3 (which shows kernel density estimates of the empirical distributions of { ${\psi }_{n,b}^k:b\le B^{\prime }$} for 0 ≤ k ≤ 3) and Table 3. They illustrate some of the fundamental characteristics of the TMLE estimator and related confidence intervals: convergence of the iterative updating procedure, robustness, asymptotic normality, and coverage.

Table 3.

Testing the asymptotic normality of ${\psi }_n^k$ and the validity of the coverage provided by $[{\psi }_n^k\pm {\xi }_{1-\alpha /2}{s}_n^k/\sqrt{n}]$, with ${(s_n^k)}^2={\text{Var}}_{P_n}{D}^{★}(P_n^k)(O)$ for k = 0, 1, 2, 3, (a) for the full-SL procedure and (b) for the light-SL procedure. We report the gains in relative error and mean square error (first and second rows), the test statistics and corresponding p-values of Lilliefors tests of normality (third and fourth rows), the test statistics of the KS test of normality with null mean and variance equal to ψ_B(P^s) and v_B(P^s) (fifth rows; the corresponding p-values are all smaller than 10⁻⁴), and finally the empirical coverages $c_n^k=\frac{1}{B^{\prime }}{\sum }_{b=1}^{B^{\prime }}\mathbf{1}\{{\psi }_B(P^s)\in [{\psi }_{n,b}^k\pm {\xi }_{1-\alpha /2}{s}_{n,b}^k/\sqrt{n}]\}$ as well as their optimistic counterparts $c_n^{k+}=\frac{1}{B^{\prime }}{\sum }_{b=1}^{B^{\prime }}\mathbf{1}\{[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^{(s)})/B}]\cap [{\psi }_{n,b}^k\pm {\xi }_{1-\alpha /2}{s}_{n,b}^k/\sqrt{n}]\ne \varnothing \}$ (sixth and seventh rows)

(a) full-SL
iteration of the TMLE procedure	k = 0	k = 1	k = 2	k = 3
gain in relative error	0	0.0469	0.0625	0.0335
gain in relative mean square error	0	0.0365	0.0369	0.0035
Lilliefors test statistic	0.0183	0.0269	0.0298	0.0282
Lilliefors test p-value	0.5718	0.0861	0.0365	0.0582
KS test statistic	0.1566	0.0782	0.0743	0.0786
empirical coverage	–	0.896	0.905	0.898
empirical coverage (optimistic)	–	0.914	0.920	0.916
(b) light-SL
iteration of the TMLE procedure	k = 0	k = 1	k = 2	k = 3
gain in relative error	0	0.2871	0.2837	0.2866
gain in mean square error	0	0.2352	0.2293	0.2305
Lilliefors test statistic	0.0253	0.0224	0.0218	0.0295
Lilliefors test p-value	0.1251	0.2620	0.2999	0.0400
KS test statistic	0.4227	0.1327	0.1451	0.1377
empirical coverage	–	0.936	0.938	0.929
empirical coverage (optimistic)	–	0.945	0.948	0.941

Convergence of the iterative updating procedure, and robustness

A substantial bias in the initial estimation is revealed by the location of the mode of { ${\psi }_{n,b}^0:b\le B^{\prime }$} in Figure 3, both for the full-SL and light-SL procedures. We see that the full-SL initial estimator is less biased than its light-SL counterpart. As one can judge visually or by the first rows of Tables 3(a) and 3(b), this initial bias is diminished (if not perfectly corrected) at the first updating step of the TMLE procedure, illustrating the robustness of the targeted estimator. The empirical distributions of { ${\psi }_{n,b}^k:b\le B^{\prime }$} for k = 1, 2, 3 are not (visually) markedly different, an empirical indication that the TMLE procedure converges quickly.

Asymptotic normality

In order to check the asymptotic normality of the TMLE estimator (e.g. under the conditions of Corollary 1), we first perform Lilliefors tests of normality based on the empirical distributions of { ${\psi }_{n,b}^k:b\le B^{\prime }$} for k = 0, 1, 2, 3 (i.e., we perform Kolmogorov-Smirnov tests of normality without specification of the means and variances under the null). We report the values of the test statistics and corresponding p-values in the third and fourth rows of Tables 3(a) and 3(b). If we take into account the multiplicity of tests, there is no clear indication that the limit distributions are not Gaussian.

Second, we test the fit of the empirical distributions of { ${\psi }_{n,b}^k:b\le B^{\prime }$} to a Gaussian distribution with mean and variance given by the estimates ψ_B(P^s) and v_B(P^s) (which are independent of { ${\psi }_{n,b}^k:b\le B^{\prime }$}). We report in the fifth rows of Tables 3(a) and 3(b) the obtained values of the KS test statistics. If all p-values are smaller than 10⁻⁴, one notices that the test statistics are strikingly smaller for k ≥ 1 than for k = 0. Performing Anderson-Darling tests of normality with only the null mean or the null variance specified (i.e., KS tests of normality with specified null mean, equal to ψ_B(P^s), and unspecified null variance or specified null variance, equal to v_B(P^s), and unspecified null mean) teaches us that it is mainly the little remaining bias and not the choice of the variance under the null that makes the KS tests have so small p-values [values not shown].

Coverage

The theoretical convergence in distribution of the TMLE estimator to a Gaussian limit (e.g. under the conditions of Corollary 1) promotes the use of intervals [ ${\psi }_{n,b}^k\pm {\xi }_{1-\alpha /2}{s}_{n,b}^k/\sqrt{n}$] as (1 − α)-confidence intervals for Ψ (P^s) (k = 1, 2, 3), with ${(s_{n,b}^k)}^2={\text{Var}}_{P_{n,b}}{D}^{★}(P_{n,b}^k)(O)$. Interestingly, the theoretical result of Corollary 1 does not guarantee that it is safe to estimate the limit variance by ${(s_{n,b}^k)}^2$ (additional assumptions on the construction and convergence of $\theta (P_n^{k_n}),\mu (P_n^{k_n})$ and $g(P_n^{k_n})$ would be required to get such a result). We nonetheless check whether the latter intervals provide the desired coverage or not. For this purpose, we compute and report in the sixth and seventh rows of Tables 3(a) and 3(b) the empirical coverages $c_n^k=\frac{1}{B^{\prime }}{\sum }_{b=1}^{B^{\prime }}\mathbf{1}\{{\psi }_B(P^s)\in [{\psi }_{n,b}^k\pm {\xi }_{1-\alpha /2}{s}_{n,b}^k/\sqrt{n}]\}$ and their optimistic counterpart $c_n^{k+}=\frac{1}{B^{\prime }}{\sum }_{b=1}^{B^{\prime }}\mathbf{1}\{[{\psi }_B(P^s)\pm {\xi }_{0.975}\sqrt{v_B(P^s)/B}]\cap [{\psi }_{n,b}^k\pm {\xi }_{1-\alpha /2}{s}_{n,b}^k/\sqrt{n}]\ne \varnothing \}$ (the latter incorporates the remaining uncertainty of the true value of Ψ (P^s)). We conclude that the provided coverage is good for the light-SL procedure (with excellent optimistic coverage), but disappointing for the full-SL procedure (even for the optimistic coverage). The results may have been better if one had relied on the bootstrap in order to estimate the asymptotic variance of the TMLE. We will investigate this issue in future work.

6.7. Real data application

For the real data application, we focus the set 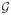of all 130 genes on chromosome 18 in the OvCa dataset. This choice is notably motivated by the associated sample size, approximately equal to 500 (thus much larger than the sample size associated to the GBM dataset). We estimate the non-parametric variable importance measure of X on Y accounting for W for each gene g separately (i.e., $\mathrm{\Psi }(P_0^g)$ where $P_0^g\in \mathcal{M}$ is the true distribution of O = (W, X, Y) for gene g), following exactly one of the statistical methodologies developed in the simulation study. Specifically, the targeted update step relies on the Gaussian fluctuations presented in Section 5.2, and the super-learning involves the library of algorithms that we report in Section 6.5. In particular, we estimate for each gene g the asymptotic variance of the TMLE ${\psi }_n^{g,\ast }$ of $\psi (P_0^g)$ with the empirical variance ${(s_n^{g,\ast })}^2$ of the efficient influence curve at $P_n^{g,\ast }$. In a future work solely devoted to this real data application, we will use the bootstrap in order to derive a more robust estimator of the asymptotic variance (again, Corollary 1 requires some conditions on $P_0^g$ and $P_n^{g,\ast }$in order to guarantee that ${(s_n^{g,\ast })}^2$ is a consistent estimator). We will also “extend” W, by adding to the DNA methylation of the gene of interest the DNA methylations, DNA copy numbers and gene expressions of its neighboring genes.

We only briefly summarize the results of the real data application. For this purpose, we report in Figure 4 the values of the test statistics $\sqrt{n}({\psi }_n^{g,3}-{\psi }_{\text{ref}}^g)/s_n^{g,3}(g\in \mathcal{G})$ derived from the TMLE after three updates, using two different reference values ${\psi }_{\text{ref}}^g\in \{0,\mathcal{F}(P_n^g)\}$. Here,

Fig 4.

Real data application to the 130 genes of chromosome 18 in the OvCa dataset (ovarian cancers). We represent the test statistics $\sqrt{n}({\psi }_n^{g,3}-{\psi }_{\mathit{ref}}^g)/s_n^{g,3}$ for ${\psi }_{\mathit{ref}}^g=0$ (left graphic) and ${\psi }_{\mathit{ref}}^g=\mathcal{F}(P_n^g)$ (right graphic) along the position of gene g on the genome. We report the names of the genes such that $\sqrt{n}\mid {\psi }_n^{g,3}\mid /s_n^{g,3}>45$ (left graphic) and $\sqrt{n}\mid {\psi }_n^{g,3}-\mathcal{F}(P_n^g)\mid /s_n^{g,3}>6$ (right graphic), the cut-offs being arbitrarily chosen.

$$\mathcal{F}(P_n^g)=\sum _{i=1}^n{X}^{(i)}{Y}^{(i)}/\sum _{i=1}^n{(X^{(i)})}^2$$

is the least square (substitution, asymptotically efficient) estimator of parameter $\mathcal{F}(P_0^g)$, see (4), a parameter which overlooks the role potentially played by W while quantifying the influence of X on Y. We know that is also path-wise differentiable at all P ∈ , with an efficient influence curve Δ ^★ (P) at P characterized by Δ ^★ (P)(O) = (XY − (P)X²)/σ²(P). We acknowledge that the variance of ( ${\psi }_n^{g,3}-\mathcal{F}(P_n^g)$) would be best approximated by the empirical variance of $D^{★}(P_n^{g,3})-{\mathrm{\Delta }}^{★}(P_n)$ rather than ${(s_n^{g,3})}^2$.

The reference value ${\psi }_{\text{ref}}^g=0$ is a natural null value to rely on from a testing perspective. Using ${\psi }_{\text{ref}}^g=\mathcal{F}(P_n^g)$ as another null value is relevant because that allows us to identify those genes for which the (possibly intricate) role played by W in quantifying the influence of X on Y is especially important and results in a stark deviation of $\mathrm{\Psi }(P_0^g)$ from $\mathcal{F}(P_0^g)$.

Looking at the left graphic in Figure 4 teaches us that a majority of the $\mathrm{\Psi }(P_0^g)(g\in \mathcal{G})$ are likely positive. Eight genes stand up (by having a test statistic $\sqrt{n}{\psi }_n^{g,3}/s_n^{g,3}>45$): two genes at 18p11.32 (USP14 and THOC1), a cluster of five genes at 18q11.2 (SNRPD1, RBBP8, RIOK3, NPC1, SS18), and gene MBP at 18q23. This suggests that the region 18q11.2 (especially 19–24 Mb) is of particular relevance in this set of ovarian cancers. Seven out of the latter eight genes (specifically: all of them but gene NPC1) also stand up in the right graphic of Figure 4: six out of the latter seven genes standing up in both graphics (specifically: all of them but gene MBP) exhibit a significantly small test statistic (by having $\sqrt{n}({\psi }_n^{g,3}-\mathcal{F}(P_n^g))/s_n^{g,3}<-6$), as does the additional gene SERPINB2, while gene MBP exhibits a significantly large test statistic (by having $\sqrt{n}({\psi }_n^{g,3}-\mathcal{F}(P_n^g))/s_n^{g,3}>6$), as do eight additional genes (MBD1, TXNL1, LMAN1, WDR7, NARS, ZNF236, ATP9B, TXNL4A). All genes standing up in the right graphic of Figure 4 are located at 18q2 (41–76 Mb).

Appendix A: Appendix

A.1. Miscellanea

Recall that P^s denotes the data-generating distribution of the synthetic observed data structure O = (W, X, Y) described in Section 6.6. We easily derive the following closed-form expressions for the features of interest θ (P^s), μ (P^s), g(P^s), and σ²(P^s).

Lemma 7

Let ϕ denote the density of the standard normal distribution. The following equalities hold:

$$\begin{array}{l}\theta (P^s)(X,W)=(O_2^Y+{\lambda }_0(W))P^s(U=2\mid X,W)+\sum _{u=1,3}\left(O_u^Y+\frac{{\mathrm{\sum }}_u(1,2)}{{\mathrm{\sum }}_u(1,1)}(X-(O_u^X-O_2^X))\right)\times P^s(U=u\mid X,W),\\ \mu (P^s)(W)=\sum _{u=1}^3(O_u^X-O_2^X)P^s(U=u\mid W),\\ g(P^s)(0\mid W)=P^s(U=2\mid W),\\ {\sigma }^2(P^s)=\sum _{u=1,3}{p}_u({\mathrm{\sum }}_u(1,1)+{(O_u^X-O_2^X)}^2),\end{array}$$

where, for each u = 1, 2, 3,

$$\begin{array}{l}{P}^s(U=2\mid X,W)\propto \frac{p_2}{{\omega }_2}\varphi \left(\frac{\text{logit}(W)-\text{logit}(O_2^W)}{{\omega }_2}\right)\mathbf{1}\{X=0\},\\ P^s(U=u\mid X,W)\propto \frac{p_u}{{\omega }_u}\varphi \left(\frac{\text{logit}(W)-\text{logit}(O_u^W)}{{\omega }_u}\right)\varphi \left(\frac{X-(O_u^X-O_2^X)}{\sqrt{{\mathrm{\sum }}_u(1,1)}}\right),\\ P^s(U=u\mid W)\propto \frac{p_u}{{\omega }_u}\varphi \left(\frac{\text{logit}(W)-\text{logit}(O_u^W)}{{\omega }_u}\right).\end{array}$$

A.2. Proofs of Lemmas 1, 6 and Proposition 1

Proof of Lemma 1

Consider (10). For any non-negative measurable function f of (X, W), it holds that

$$\begin{array}{l}{E}_{P_{\epsilon }}\{Yf(X,W)\}=E_P\{Yf(X,W)(1+\epsilon s(O))\}\\ =E_P\{\theta (P)(X,W)f(X,W)\}+\epsilon E_P\{Yf(X,W)s(O)\}\\ =E_P\{(\theta (P)(X,W)+\epsilon E_P(Ys(O)\mid X,W))f(X,W)\}\\ =E_{P_{\epsilon }}\{h(X,W)f(X,W)\}\end{array}$$

for h(X, W) equal to the right-hand side expression of (10), since (9) implies

$$\frac{d{P}_{\epsilon }}{dP}(X,W)=(1+\epsilon E_P(s(O)\mid X,W)).$$

The function f being arbitrarily chosen, the latter equalities yield (10). The remaining relationships are easily proven in the same spirit.

Proof of Lemma 6

Note that

$$P_0{L}_{a,b}(P)=E_{P_0}\{\text{KL}(F_{a,b}\circ \theta (P_0)(X,W),F_{a,b}\circ \theta (P)(X,W))\}+c(P_0),$$

where KL(p, q) is the Kullback-Leibler divergence between the Bernoulli distributions of parameters p, q ∈ (0, 1) and c(P₀) is a constant depending on P₀ only. Since KL(p, q) ≥ 0 with equality iff p = q, we obtain that θ (P₀) minimizes P ↦ P₀L_a,b(P) and also that another minimizer must satisfy θ (P)(X, W) = θ (P₀)(X, W) P₀-almost surely. The second equality is easily obtained by differentiating.

Recall that Ψ is pathwise differentiable at every P ∈ with respect to the maximal tangent space $L_0^2(P)$ with an efficient influence curve at P equal to $D^{★}(P)\in L_0^2(P)$ if, for all $s\in L_0^2(P)$ with ||s||_∞ < ∞ and $\{P_{\epsilon }:\mid \epsilon \mid <{\left|\right|s\left|\right|}_{\infty }^{-1}\}\subset \mathcal{M}$ characterized by (9), the mapping ε ↦ Ψ (P_ε) is differentiable at ε = 0 with a derivative satisfying

$${\frac{\partial }{\partial \epsilon }\mathrm{\Psi }(P_{\epsilon })|}_{\epsilon =0}=E_P\{D^{★}(P)(O)s(O)\}.$$

We refer to van der Vaart [25, Chapter 25] for an introduction to the theory of semiparametric models.

Proof of Proposition 1

By expanding the squared sum in (1), we obtain that

$$\mathrm{\Psi }(P)=\underset{\beta \in \mathbb{R}}{argmin}\{-2\beta E_P\{X(\theta (P)(X,W)-\theta (P)(0,W))\}+{\beta }^2{E}_P\{X^2\}\},$$

which straightforwardly yields (2). It is easily seen that $P{D}_1^{★}(P)D_2^{★}(P)=0$, or in other words that the two components are orthogonal in $L_0^2(P)$.

Regarding the pathwise differentiability, it is sufficient to consider paths of the form (9) for arbitrarily chosen $s\in L_0^2(P)$ with ||s||_∞ < ∞. Set such a s and $\mid \epsilon \mid <{\left|\right|s\left|\right|}_{\infty }^{-1}$. Using the telescopic equality a₁/b₁ − a₀/b₀ = (a₁ − a₀)/b₁ − (a₀/b₀)(b₁ − b₀)/b₁ yields

$${\epsilon }^{-1}(\mathrm{\Psi }(P_{\epsilon })-\mathrm{\Psi }(P))=\frac{T_{\epsilon }^1}{{\sigma }^2(P_{\epsilon })}-\mathrm{\Psi }(P)\frac{T_{\epsilon }^2}{{\sigma }^2(P_{\epsilon })},$$ (19)

with

$$\begin{array}{l}{T}_{\epsilon }^1={\epsilon }^{-1}\left(E_{P_{\epsilon }}\{X(\theta (P_{\epsilon })(X,W)-\theta (P_{\epsilon })(0,W))\}-E_P\{X(\theta (P)(X,W)-\theta (P)(0,W))\}\right),\\ T_{\epsilon }^2={\epsilon }^{-1}({\sigma }^2(P_{\epsilon })-{\sigma }^2(P))=E_P\{s(O)X^2\}\end{array}$$ (20)

by (13). Now, the same telescopic equality also yields that

$$T_{\epsilon }^1=E_P\{X(\theta (P_{\epsilon })(X,W)-\theta (P_{\epsilon })(0,W))s(O)\}+E_P\{X({\epsilon }^{-1}(\theta (P_{\epsilon })(X,W)-\theta (P)(X,W))-{\epsilon }^{-1}(\theta (P_{\epsilon })(0,W)-\theta (P)(0,W)))\}.$$

By (10) and the dominated convergence theorem (indeed, { ${\left|\right|\theta (P_{\epsilon })\left|\right|}_{\infty }:\mid \epsilon \mid <{\left|\right|s\left|\right|}_{\infty }^{-1}$} is bounded),

$$T_{\epsilon }^1=E_P\{X(\theta (P)(X,W)-\theta (P)(0,W))s(O)\}+o(\epsilon )+E_P\{X({\epsilon }^{-1}(\theta (P_{\epsilon })(X,W)-\theta (P)(X,W))-{\epsilon }^{-1}(\theta (P_{\epsilon })(0,W)-\theta (P)(0,W)))\}.$$

Furthermore, (10) also yields that

$${\epsilon }^{-1}(\theta (P_{\epsilon })(X,W)-\theta (P)(X,W))=E_P((Y-\theta (P)(X,W))s(O)\mid X,W)+o(\epsilon ).$$

Consequently, applying the dominated convergence theorem finally yields (by using the above telescopic equality and (10), one easily checks the boundedness of { ${sup}_{O\in \mathcal{O}}{\epsilon }^{-1}\mid \theta (P_{\epsilon })(X,W)-\theta (P)(X,W):\mid \epsilon \mid <{\left|\right|s\left|\right|}_{\infty }^{-1}$})

$$T_{\epsilon }^1=E_P\{X(\theta (P)(X,W)-\theta (P)(0,W))s(O)\}+E_P\{E_P(X(Y-\theta (P)(X,W))s(O)\mid X,W)-X{E}_P((Y-\theta (P)(X,W))s(O)\mid X=0,W)\}+o(\epsilon ),$$ (21)

where we emphasize that

$$E_P((Y-\theta (P)(X,W))s(O)\mid X=0,W)=E_P\left(\frac{\mathbf{1}\{X=0\}}{g(P)(0\mid W)}(Y-\theta (P)(X,W))s(O)|W\right).$$

Combining (19), (20), (21) and (13) teaches us that, for all $s\in L_0^2(P)$ with ||s||_∞ < ∞,

$${\epsilon }^{-1}(\mathrm{\Psi }(P_{\epsilon })-\mathrm{\Psi }(P))=E_P\{D^{★}(P)(O)s(O)\}+o(\epsilon ),$$

where D^★ (P) is defined in the statement of the proposition. In particular, Ψ is pathwise differentiable at P wrt the described collection of paths, and D^★ (P) is a gradient of Ψ at P. Since the related tangent space is $L_0^2(P)$ itself, it is necessarily the efficient influence curve.

It remains to prove that D^★ (P) is double-robust. For this purpose, note that

$$\begin{array}{l}{\sigma }^2(P^{\prime })P{D}^{★}(P^{\prime })-{\sigma }^2(P)(\mathrm{\Psi }(P)-\mathrm{\Psi }(P^{\prime }))\\ =E_P\{X(\theta (P^{\prime })(X,W)-\theta (P^{\prime })(0,W))-X(\theta (P)(X,W)-\theta (P)(0,W))\}\\ +E_P\left\{\left(X-\frac{\mu (P^{\prime })(W)\mathbf{1}\{X=0\}}{g(P^{\prime })(0\mid W)}\right)E_P(Y-\theta (P^{\prime })(X,W)\mid X,W)\right\}\\ =E_P\{X(\theta (P^{\prime })(X,W)-\theta (P^{\prime })(0,W))-X(\theta (P)(X,W)-\theta (P)(0,W))\}\\ +E_P\left\{\left(X-\frac{\mu (P^{\prime })(W)\mathbf{1}\{X=0\}}{g(P^{\prime })(0\mid W)}\right)(\theta (P)(X,W)-\theta (P^{\prime })(X,W))\right\}\\ =E_P\left\{X(\theta (P)(0,W)-\theta (P^{\prime })(0,W))-\mu (P^{\prime })(W)\frac{g(P)(0\mid W)}{g(P^{\prime })(0\mid W)}(\theta (P)(0,W)-\theta (P^{\prime })(0,W))\right\}\\ =E_P\left\{(\theta (P)(0,W)-\theta (P^{\prime })(0,W))\left(\mu (P)(W)-\mu (P^{\prime })(W)\frac{g(P)(0\mid W)}{g(P^{\prime })(0\mid W)}\right)\right\}.\end{array}$$

Now, the right-hand side expression vanishes as soon as either θ (P′)(0, ·) = θ (P)(0,) or (μ(P′) = μ (P) and g(P′) = g(P)). The conclusion readily follows.

A.3. Proof of Lemma 5

Proof of Lemma 5

Assume for the time being that, for all W ∈ , there exists λ_n such that (17) holds with λ_n substituted for λ. Then, for all W ∈ , the point with coordinates ( $E_{P_n^0}(X\mid X\ne 0,W),{\varphi }_{n,{\lambda }_n}(E_{P_n^0}(X\mid X\ne 0,W))$) lies in the convex envelope of the set {(X⁽ⁱ⁾, X⁽ⁱ⁾²): i ≤ n}\{(0, 0)}. Equivalently, there exist for all W ∈ three non-negative weights p₁, p₂, p₃ summing up to 1 and three different values x⁽¹⁾, x⁽²⁾, x⁽³⁾ ∈ {X⁽ⁱ⁾: i ≤ n}\{0} such that

$$E_{P_n^0}(X\mid X\ne 0,W)=\sum _{k=1}^3{p}_k{x}^{(k)},E_{P_n^0}(X^2\mid X\ne 0,W)=\sum _{k=1}^3{p}_k{x}^{(k)2},$$

the right-hand side expressions being, respectively, the mean and second order moment of the distribution ${\sum }_{k=1}^3{p}_k\text{Dirac}(x^{(k)})$. Thus, there exists $P_n^{00}\in \mathcal{M}$ such that (i) and (ii) hold.

Set W ∈ . Combining (6), (7) and (17) yields that if there exists λ_n such that (17) holds with λ_n substituted for λ, then it must be equal to ${\ell }_n=(T_n^1-{\sigma }^2(P_n^0))/(T_n^1-T_n^2)$, where $T_n^1=(m_n+M_n)E_{P_n^0}\{\mu (P_n^0)(W)\}-m_n{M}_n{E}_{P_n^0}\{1-g(P_n^0)(0\mid W)\}$ and $T_n^2=E_{P_n^0}\{\mu (P_n^0){(W)}^2/(1-g(P_n^0)(0\mid W))\}$. In order to conclude, it is therefore sufficient to check that ℓ_n ∈ [0, 1].

By Jensen’s inequality, it holds that $E_{P_n^0}(X^2\mid X\ne 0,W)\ge E_{P_n^0}{(X\mid X\ne 0,W)}^2$, which yields in turn with (6) and (7) that ${\sigma }^2(P_n^0)\ge T_n^2$. Finally, using again (6) and (7), ${\sigma }^2(P_n^0)-T_n^1$ equals

$$\begin{array}{l}{E}_{P_n^0}\{(1-g(P_n^0)(0\mid W))(E_{P_n^0}(X^2\mid X\ne 0,W)-(m_n+M_n)E_{P_n^0}(X\mid X\ne 0,W)+m_n{M}_n)\}\\ =E_{P_n^0}\{(1-g(P_n^0)(0\mid W))E_{P_n^0}((X-m_n)(X-M_n)\mid X\ne 0,W)\}\le -c^2{P}_n^0(X\ne 0),\end{array}$$

hence $T_n^2\le {\sigma }^2(P_n^0)<T_n^1$. Thus, ℓ_n ∈ [0, 1], which completes the proof.

A.4. Proofs of Lemmas 2, 3 and 4

Proof of Lemma 2

It is sufficient to verify that, under the stated assumptions,

$$\underset{(\epsilon ,k)\to (0,\infty )}{limsup}\left|P_n\frac{D^{★}(P_n^k)}{1+\epsilon D^{★}(P_n^k)}-P_n{D}^{★}(P_n^k)\right|=0.$$

Now, the absolute value above is straightforwardly upper-bounded by

$$\epsilon M^2{P}_n{\mid 1+\epsilon D^{★}(P_n^k)\mid }^{-1}=\epsilon M^2{P}_n{(1+\epsilon D^{★}(P_n^k))}^{-1}\le \epsilon M^2/(1-\rho M)=2\epsilon M^2.$$

This trivially entails the wished convergence, hence the result.

Introduce, for all k ≥ 0 and |ε| ≤ ρ, $\mid \epsilon \mid \le \rho ,{\ell }_n^k(\epsilon )=n^{-1}{\sum }_{i=1}^{n}log{P}_n^k(\epsilon )(O^{(i)})$ and

$$A_n^k(\epsilon )=-P_n\frac{D^{★}{(P_n^k)}^2}{{(1+\epsilon D^{★}(P_n^k))}^2}.$$

Obviously, the normalized log-likelihood ${\ell }_n^k(\epsilon )$ under $P_n^k(\epsilon )$ is twice differentiable wrt ε, with first derivative at ε = 0 equal to $P_n{D}^{★}(P_n^k)$ and second derivative at ε equal to $A_n^k(\epsilon )$.

Proof of Lemma 3, first part

We first show that ${lim}_{k\to \infty }{P}_n{D}^{★}(P_n^k)=0$ under the stated assumptions, by contradiction. Suppose that $P_n{D}^{★}(P_n^k)$ does not converge to 0 as k → ∞: there exist η > 0 and an increasing function ϕ: ℕ → ℕ such that, for all k ≥ 0,

$$\mid P_n{D}^{★}(P_n^{\varphi (k)})\mid \ge \eta >0.$$ (22)

We show that necessarily lim_k→∞ ε_ϕ(k) = 0, hence ${lim}_{k\to \infty }{P}_n{D}^{★}(P_n^{\varphi (k)})=0$ by Lemma 2, contradicting (22).

Set k ≥ 0. For any ${\epsilon }_n^{\prime \varphi (k)}\in [0,{\epsilon }_n^{\varphi (k)}]$, a Taylor expansion of ${\ell }_n^{\varphi (k)}(\epsilon )$ yields the existence of ${\epsilon }^{\prime }\in [0,{\epsilon }_n^{\prime \varphi (k)}]$ such that

$$\begin{array}{l}{\ell }_n^{\varphi (k)}({\epsilon }_n^{\varphi (k)})-{\ell }_n^{\varphi (k)}(0)\ge {\ell }_n^{\varphi (k)}({\epsilon }_n^{\prime \varphi (k)})-{\ell }_n^{\varphi (k)}(0)\\ ={\epsilon }_n^{\prime \varphi (k)}{P}_n{D}^{★}(P_n^{\varphi (k)})+\frac{{({\epsilon }_n^{\prime \varphi (k)})}^2}{2}{A}_n^{\varphi (k)}({\epsilon }^{\prime }).\end{array}$$ (23)

By assumption (iii) and since

$$-4M^2\le \underset{k^{\prime }\ge 0}{inf}\underset{\mid \epsilon \mid \le \rho }{inf}{A}_n^{k^{\prime }}(\epsilon )\le \underset{k^{\prime }\ge 0}{sup}\underset{\mid \epsilon \mid \le \rho }{sup}{A}_n^{k^{\prime }}(\epsilon )\le -\frac{4}{9}\underset{k^{\prime }\ge 0}{inf}{P}_n{D}^{★}{(P_n^{k^{\prime }})}^2,$$ (24)

there exists a constant κ > 0 (depending on P_n) such that the right-hand side term of (24) is upper-bounded by −κ, hence $A_n^{k^{\prime }}(\epsilon )\le -\kappa$ simultaneously for all k′ ≥ 0 and |ε| ≤ ρ.

The function $\epsilon \mapsto \frac{\partial }{\partial \epsilon }{\ell }_n^{\varphi (k)}(\epsilon )$ being decreasing and equal to $P_n{D}^{★}(P_n^{\varphi (k)})\ne 0$ at ε = 0, it necessarily holds that ${\epsilon }_n^{\varphi (k)}{P}_n{D}^{★}(P_n^{\varphi (k)})>0$ (i.e., ${\epsilon }_n^{\varphi (k)}$ and $P_n{D}^{★}(P_n^{\varphi (k)})$ share the same sign), hence ${\epsilon }_n^{\prime \varphi (k)}{P}_n{D}^{★}(P_n^{\varphi (k)})>0$ too. Furthermore, combining (23) and the left-hand side of (24) yields

$$\begin{array}{l}{\ell }_n^{\varphi (k)}({\epsilon }_n^{\varphi (k)})-{\ell }_n^{\varphi (k)}(0)\ge {\epsilon }_n^{\prime \varphi (k)}{P}_n{D}^{★}(P_n^{\varphi (k)})-2M^2{({\epsilon }_n^{\prime \varphi (k)})}^2\\ \ge \mid {\epsilon }_n^{\prime \varphi (k)}\mid \eta -2M^2{({\epsilon }_n^{\prime \varphi (k)})}^2.\end{array}$$ (25)

The conclusion is now at hand. Assume that the sequence ${\{{\epsilon }_n^{\varphi (k)}\}}_{k\ge 0}$ does not converge to 0: there exist c > 0 and another increasing function ψ: ℕ → ℕ such that, for all k ≥ 0, $\mid {\epsilon }_n^{\psi \circ \varphi (k)}\mid \ge c>0$. Note that c can be chosen small enough to guarantee in addition that cη − 2M²c² > 0. Impose now $\mid {\epsilon }_n^{\prime \psi \circ \varphi (k)}\mid =c$ for all k ≥ 0 (this uniquely defines ${\epsilon }_n^{\prime \psi \circ \varphi (k)}\in [0,{\epsilon }_n^{\psi \circ \varphi (k)}]$). According to (25), for all k ≥ 0,

$${\ell }_n^{\psi \circ \varphi (k)}({\epsilon }_n^{\psi \circ \varphi (k)})-{\ell }_n^{\psi \circ \varphi (k)}(0)\ge c\eta -2M^2{c}^2>0.$$

Using (a) ${\ell }_n^{k^{\prime }}({\epsilon }_n^{k^{\prime }})-{\ell }_n^{k^{\prime }}(0)\ge 0$ for all k′ ≥ 0 and (b) ${\ell }_n^{k^{\prime }}(0)={\ell }_n^{k^{\prime }-1}({\epsilon }_n^{k^{\prime }-1})$ for every k′ ≥ 1, one obtains that for all k ≥ 0,

$${\ell }_n^{\psi \circ \varphi (k)}({\epsilon }_n^{\psi \circ \varphi (k)})-{\ell }_n^0(0)\ge k(c\eta -2M^2{c}^2).$$

This contradicts assumption (iv). So the sequence ${\{{\epsilon }_n^{\varphi (k)}\}}_{k\ge 0}$ must converge to 0, Lemma 2 applies, and (22) is contradicted.

Proof of Lemma 3, second part

For all k ≥ 0, another Taylor expansion of ${\ell }_n^k(\epsilon )$ yields the existence of ${\epsilon }_n^{\prime k}\in [0,{\epsilon }_n^k]$ such that

$$0\le {\ell }_n^k({\epsilon }_n^k)-{\ell }_n^k(0)={\epsilon }_n^k{P}_n{D}^{★}(P_n^k)+\frac{{({\epsilon }_n^k)}^2}{2}{A}_n^k({\epsilon }_n^{\prime k}).$$

We derive from these inequalities that

$$0\le {({\epsilon }_n^k)}^2\kappa \le {({\epsilon }_n^k)}^2\mid A_n^k({\epsilon }_n^{\prime k})\mid \le 2{\epsilon }_n^k{P}_n{D}^{★}(P_n^k)\le \rho \mid P_n{D}^{★}(P_n^k)\mid ,$$

where the right-hand side converges to 0 as k → ∞ by virtue of the first part of the lemma. This completes the proof.

Proof of Lemma 4

We first show that the sequence ${\{P_n^k\}}_{k\ge 0}$ converges in total variation. For this purpose, note that $P_n^k$ is dominated by $P_n^0$, with a density $f_n^k$ characterized by $f_n^k(O)={\prod }_{k^{\prime }=0}^{k-1}(1+{\epsilon }_n^{k^{\prime }}{D}^{★}(P_n^{k^{\prime }})(O))$. Since (a) the functions $D^{★}(P_n^{k^{\prime }})$ are uniformly bounded by a common constant M, and (b) the series ${\sum }_{k\ge 0}\mid {\epsilon }_n^k\mid$ converges, the sequence of densities $\text{(wrt}{P}_n^0){\{f_n^k\}}_{k\ge 0}$ converges wrt the ||·||_∞-norm to a limit density ( $\text{wrt}{P}_n^0$) that we denote $f_n^{\ast }$. Density $f_n^{\ast }$ gives rise to a data-generating distribution $P_n^{\ast }$, the limit of $P_n^k$ in total variation (hence its weak limit too).

Now, it holds that

$${\psi }_n^k=\mathrm{\Psi }(P_n^k)=(E_{P_n^k}\{XY\}-E_{P_n^k}\{X\theta (P_n^k)(0,W)\})/E_{P_n^k}\{X^2\}.$$

The observed data structure O being bounded, the functions O = (W, X, Y) ↦ XY and O = (W, X, Y) ↦ X² are continuous and bounded, hence $E_{P_n^k}\{XY\}$ and $E_{P_n^k}\{X^2\}$ respectively converge to $E_{P_n^{\ast }}\{XY\}$ and $E_{P_n^{\ast }}\{X^2\}\ge c$ by weak convergence. Furthermore, the convergence of $f_n^k$ to $f_n^{\ast }$ wrt the ||·||_∞-norm trivially entails the pointwise convergence of $\theta (P_n^k)$ to $\theta (P_n^{\ast })$, then the wished convergence of $E_{P_n^k}\{X\theta (P_n^k)(0,W)\}$ to $E_{P_n^{\ast }}\{X\theta (P_n^{\ast })(0,W)\}$ by the dominated convergence theorem. This completes the proof.

A.5. Proof of Propositions 2 and 3 and of Corollary 1

Denote $D^{★}({\sigma }^2,\theta ,\mu ,g,\psi )=D_1^{★}({\sigma }^2,\theta ,\psi )+D_2^{★}({\sigma }^2,\theta ,\mu ,g)$. Let D₁ (σ², θ) be characterized by D₁ (σ², θ) (O) = (X(θ(X, W) − θ (0, W)))/σ², and denote D₁ (P) = D₁ (σ² (P), θ(P)). We use the notation a ≲ b for “a smaller than b up to a multiplicative constant”. We start with a useful lemma.

Lemma 8

Suppose that the assumptions of Proposition 2 are met. There exists ψ₀ ∈ ℝ such that ${\stackrel{\sim }{\psi }}_n^{\ast }={\psi }_0+o_P(1)$ (i.e., the TMLE converges in probability). Moreover, it holds that

$$P_0{(D_1^{★}({\sigma }^2(P_n^{k_n}),\theta (P_n^{k_n}),{\stackrel{\sim }{\psi }}_n^{\ast })-D_1^{★}({\sigma }_0^2,{\theta }_0,{\psi }_0))}^2=o_P(1),$$ (26)

$$P_0{(D_2^{★}(P_n^{k_n})-D_2^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0))}^2=o_P(1),\mathit{hence}$$ (27)

$$P_0{(D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0))}^2=o_P(1)$$ (28)

Proof

Recall that ||O|| is bounded under P₀ and that ${\sigma }^2(P_n^{k_n}),{\sigma }_0^2\ge c$. Using repeatedly the telescopic equality a₁/b₁ − a₀/b₀ = (a₁ − a₀)/b₁ − (a₀/b₀)(b₁ − b₀)/b₁ and inequality (a + b)² ≤ 2(a² + b²) yields that, under P₀, $(D_1(P_n^{k_n})-D_1({\sigma }_0^2,{\theta }_0)){(O)}^2\lesssim (\theta (P_n^{k_n})-{\theta }_0){(O)}^2+(\theta (P_n^{k_n})(0,·)-{\theta }_0(0,·)){(O)}^2$, and therefore that

$$P_0{(D_1(P_n^{k_n})-D_1({\sigma }_0^2,{\theta }_0))}^2=o_P(1).$$ (29)

Similarly, the same tricks as above and the facts that (a) both random variables $\mid (Y-\theta (P_n^{k_n})(X,W))/{\sigma }^2(P_n^{k_n})\mid$ and $\mid (Y-\theta (P_0)(X,W))/{\sigma }_0^2\mid$ are upper-bounded under P₀, and (b) $g(P_n^{k_n})(0\mid W)$, g₀(0|W) ≥ c imply that, under P₀, $(D_2^{★}(P_n^{k_n})-D_2^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0)){(O)}^2\lesssim (\mu (P_n^{k_n})-{\mu }_0){(O)}^2+(g(P_n^{k_n})(0\mid ·)-g_0(0\mid ·)){(O)}^2$, hence (27).

Now, rewrite $P_n{D}^{★}(P_n^{k_n})=o_P(1)$ as

$$\begin{array}{l}{\stackrel{\sim }{\psi }}_n^{\ast }\frac{E_{P_n}\{X^2\}}{{\sigma }^2(P_n^{k_n})}=(P_n-P_0)(D_1(P_n^{k_n})+D_2^{★}(P_n^{k_n}))\\ +P_0(D_1(P_n^{k_n})+D_2^{★}(P_n^{k_n})-D_1({\sigma }_0^2,{\theta }_0)-D_2^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0))\\ +P_0(D_1({\sigma }_0^2,{\theta }_0)+D_2^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0))+o_P(1)\end{array}$$ (30)

and consider the two first right-hand side terms. Since we have $D_1({\sigma }^2,\theta )(O)=D_1^{★}({\sigma }^2,\theta ,\psi )(O)+X^2\psi /{\sigma }^2$ and the class {O ↦ X²ψ/σ²: (ψ, σ²) ∈ ℝ × [c, ∞]} is P₀-Donsker, it holds that both $D_1(P_n^{k_n})$ and $D_2^{★}(P_n^{k_n})$ belong to a P₀-Donsker class with P₀-probability tending to 1, hence so does $D_1(P_n^{k_n})+D_2^{★}(P_n^{k_n})$. Therefore, by (29), (27) and Lemma 19.24 in [25], the first term is $O_P(1/\sqrt{n})=o_P(1)$. Combining (29) and (27) with the Cauchy-Schwarz inequality yields in turn that the second term is o_P (1). Finally, the law of large numbers and the fact that ${\sigma }_0^2\ge c$ entail that $E_{P_n}\{X^2\}/{\sigma }^2(P_n^{k_n})={\sigma }^2(P_0)/{\sigma }_0^2\times (1+o_P(1))$. Consequently, we deduce from (30) that there exists ψ₀ ∈ ℝ such that ψ_n = ψ₀ + o_P (1).

Because $D_1^{★}({\sigma }^2,\theta ,\psi )(O)=D_1({\sigma }^2,\theta )(O)-X^2\psi /{\sigma }^2$, (26) easily follows from (29) and the convergence in probability of ψ_n and ${\sigma }^2(P_n^{k_n})$ to ψ₀ and ${\sigma }_0^2$. Finally (26) and (27) imply (28), thus concluding the proof.

Proof of Proposition 2

We first rewrite $P_n{D}^{★}(P_n^{k_n})=o_P(1/\sqrt{n})$ as

$$P_0{D}^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0)=-(P_n-P_0)D^{★}(P_n^{k_n})-P_0(D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0))+o_P(1/\sqrt{n}).$$ (31)

Since $D_1^{★}(P_n^{k_n})$ and $D_2^{★}(P_n^{k_n})$ belong to a P₀-Donsker class with P₀-probability tending to 1, so does $D^{★}(P_n^{k_n})$. Therefore, (28) of Lemma 8 and Lemma 19.24 in [25] yield that the first right-hand term in (31) is $O_P(1/\sqrt{n})=o_P(1)$. Moreover, (28) of Lemma 8 and the Cauchy-Schwarz inequality imply that the second right-hand side term is o_P (1). Consequently, the deterministic quantity $P_0{D}^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0)$ is equal to 0, and the conditions on (θ₀, μ₀, g₀) ensure that necessarily ψ₀ = Ψ (P₀) i.e., that the TMLE ${\stackrel{\sim }{\psi }}_n^{\ast }$ is consistent.

Proof of Proposition 3

We resume the previous proof where we left it. The fundamental relationship of this proof, derived from $P_0{D}^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0)=0$ and $P_n{D}^{★}(P_n^{k_n})=o_P(1/\sqrt{n})$, is

$$\begin{array}{l}-P_0(D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast })-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0))\\ =(P_n-P_0)D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast })\\ +(P_n-P_0)(D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast }))\\ +P_0(D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast }))+o_P(1/\sqrt{n}),\end{array}$$ (32)

where the left-hand side term obviously equals $({\stackrel{\sim }{\psi }}_n^{\ast }-{\psi }_0){\sigma }^2(P_0)/{\sigma }_0^2$. Consider now the first right-hand term in (32). Since (a) { $D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,\psi ):\psi \in \mathbb{R}$} is a P₀-Donsker class and (b) $P_0{(D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast })-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0))}^2={({\stackrel{\sim }{\psi }}_n^{\ast }-{\psi }_0)}^2{E}_{P_0}\{X^4\}/{\sigma }_0^4=o_P(1)$, it holds that $(P_n-P_0)D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast })=(P_n-P_0)D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\psi }_0)+o_P(1/\sqrt{n})$ by Lemma 19.24 in [25]. Regarding the second right-hand side term in (32), note (a) that

$$(D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast }))(O)=(D_1(P_n^{k_n})+D_2^{★}(P_n^{k_n}))(O)+((1/{\sigma }_0^2-1/{\sigma }^2(P_n^{k_n}))X^2{\stackrel{\sim }{\psi }}_n^{\ast })-(D_1({\sigma }_0^2,{\theta }_0)+D_2^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0))(O),$$

(b) that we have already shown that the first random function between parentheses belongs to a P₀-Donsker class with P₀-probability tending to 1, (c) that second random function between parentheses belongs to the P₀-Donsker class { $O\mapsto (1/{\sigma }_0^2-1/{\sigma }^2)X^2\psi :(\psi ,{\sigma }^2)\in \mathbb{R}\times [c,\infty ]$}, and (d) that the last function of the decomposition is deterministic. Therefore, $D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast })$ belongs to a P₀-Donsker class with P₀-probability tending to 1. Now, by applying repeatedly the inequality (a + b)² ≤ 2(a² + b²) we deduce that

$$\begin{array}{l}{P}_0{(D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast }))}^2\\ \lesssim P_0{(D_1(P_n^{k_n})-D_1({\sigma }_0^2,{\theta }_0))}^2\\ +P_0{(D_2^{\ast }(P_n^{k_n})-D_2^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0))}^2\\ +{({\stackrel{\sim }{\psi }}_n^{\ast })}^2{E}_{P_0}\{({(1/{\sigma }_0^2-1/{\sigma }^2(P_n^{k_n}))}^2{X}^4\}.\end{array}$$

But ||O|| is bounded under P₀ and ${\sigma }^2(P_n^{k_n}),{\sigma }_0^2\ge c$, so that $E_{P_0}\{({(1/{\sigma }_0^2-1/{\sigma }^2(P_n^{k_n}))}^2{X}^4\}\lesssim {({\sigma }^2(P_n^{k_n})-{\sigma }_0^2)}^2=o_P(1)$. This fact combined with (29), (27) and ${\stackrel{\sim }{\psi }}_n^{\ast }=O_P(1)$ yield that $P_0{(D^{★}(P_n^{k_n})-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast }))}^2=o_P(1)$. Consequently, Lemma 19.24 in [25] implies that the second right-hand side term in (32) is $o_P(1/\sqrt{n})$. We now turn to the last right-hand side term in (32). It is easily seen that

$$\begin{array}{l}{D}^{★}(P_n^{k_n})(O)-D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,{\stackrel{\sim }{\psi }}_n^{\ast })(O)\\ =D^{★}({\sigma }^2(P_n^{k_n}),\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))(O)\\ -D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,\mathrm{\Psi }(P_0))(O)\\ -(1/{\sigma }^2(P_n^{k_n})-1/{\sigma }^2(P_0))X^2({\stackrel{\sim }{\psi }}_n^{\ast }-\mathrm{\Psi }(P_0)),\end{array}$$

where $(1/{\sigma }^2(P_n^{k_n})-1/{\sigma }^2(P_0))({\stackrel{\sim }{\psi }}_n^{\ast }-\mathrm{\Psi }(P_0))=O_P(1/\sqrt{n})\times o_P(1)=o_P(1/\sqrt{n})$. Using that $P_0{D}^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,\mathrm{\Psi }(P_0))=0$, the previous display yields that the third right-hand side term in (32) equals

$$P_0{D}^{★}({\sigma }^2(P_n^{k_n}),\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))+o_P(1/\sqrt{n})=P_0{D}^{★}({\sigma }_0^2,\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))(1+o_P(1))+o_P(1/\sqrt{n}).$$

In summary, we just showed that

$$({\stackrel{\sim }{\psi }}_n^{\ast }-\mathrm{\Psi }(P_0)){\sigma }^2(P_0)/{\sigma }_0^2=(P_n-P_0)D^{★}({\sigma }_0^2,{\theta }_0,{\mu }_0,g_0,\mathrm{\Psi }(P_0))+P_0{D}^{★}({\sigma }_0^2,\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))(1+o_P(1))+o_P(1/\sqrt{n}),$$

hence the stated relationship.

Proof of Corollary 1

This result relies on the decomposition:

$$\begin{array}{l}{P}_0{D}^{★}({\sigma }^2(P_0),\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))\\ =P_0(D^{★}({\sigma }^2(P_0),\theta (P_n^{k_n}),\mu (P_n^{k_n}),g(P_n^{k_n}),\mathrm{\Psi }(P_0))\\ -D^{★}({\sigma }^2(P_0),\theta (P_n^{k_n}),{\mu }_0,g_0,\mathrm{\Psi }(P_0)))\\ +P_0(D^{★}({\sigma }^2(P_0),\theta (P_n^{k_n}),{\mu }_0,g_0,\mathrm{\Psi }(P_0))-D^{★}({\sigma }^2(P_0),{\theta }_0,{\mu }_0,g_0,\mathrm{\Psi }(P_0))),\end{array}$$

where we use that P₀D^★ (σ² (P₀), θ₀, μ₀, g₀, Ψ (P₀)) = 0. Following the lines of the proof of Lemma 8 and using the Cauchy-Schwarz inequality yield that the first term of the left-hand side decomposition is upper-bounded (up to a multiplicative constant) by square-root of $P_0{(\theta (P_n^{k_n})(0,·)-\theta (P_0)(0,·))}^2\times (P_0{(\mu (P_n^{k_n})-{\mu }_0)}^2+P_0{(g(P_n^{k_n})(0\mid ·)-g_0(0\mid ·))}^2)$, while the second term equals zero. Thus the latter left-hand side expression is $o_P(1/\sqrt{n})$ by assumption, (32) yields the asymptotic linear expansion, and the central limit theorem completes the proof.