Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Jan 17;3:1081. doi: 10.1038/srep01081

Developing neuronal networks: Self-organized criticality predicts the future

Jiangbo Pu 1,2, Hui Gong 1,2, Xiangning Li 1,2, Qingming Luo 1,2,a
PMCID: PMC3547285  PMID: 23330063

Abstract

Self-organized criticality emerged in neural activity is one of the key concepts to describe the formation and the function of developing neuronal networks. The relationship between critical dynamics and neural development is both theoretically and experimentally appealing. However, whereas it is well-known that cortical networks exhibit a rich repertoire of activity patterns at different stages during in vitro maturation, dynamical activity patterns through the entire neural development still remains unclear. Here we show that a series of metastable network states emerged in the developing and “aging” process of hippocampal networks cultured from dissociated rat neurons. The unidirectional sequence of state transitions could be only observed in networks showing power-law scaling of distributed neuronal avalanches. Our data suggest that self-organized criticality may guide spontaneous activity into a sequential succession of homeostatically-regulated transient patterns during development, which may help to predict the tendency of neural development at early ages in the future.

The emergence of patterned activity spontaneously generated by transiently coupled neurons is a ubiquitous phenomenon in developing neuronal networks in vitro and in vivo1,2. Understanding these patterns is the key to reveal how brain works and what happens during neural development1,2,3. It is well known that a large diversity of spontaneous activity patterns was encountered in neuronal cultures and could be roughly classified corresponding to stages of maturation4,5,6,7,8. However, it remains unclear that how the network activity changes its pattern through developmental stages, especially, whether developmental dynamics changes abruptly or smoothly between successive developmental states.

Recently, evidence has been found suggesting that neural systems operating close to a critical dynamical state show advantages in information processing and pattern formation of developing neuronal networks8,9,10,11,12,13,14,15,16. Interestingly, even in the mature stage, developing neuronal networks were not always driven into the critical regime during development. Little is known about the role of criticality in shaping the dynamics in the entire development process and in the progressive refinement of neural activity patterns. In this study, we address these issues by analysing dynamical network states and neuronal avalanches in dissociated hippocampal networks cultured on multi-electrode arrays. Particularly, when we focus on the state transition of spontaneous activity in developing network, the question is: what is the difference between networks in the critical regime and those out of the critical regime?

Results

Mapping changes of network activity patterns in a complete in vitro developmental process

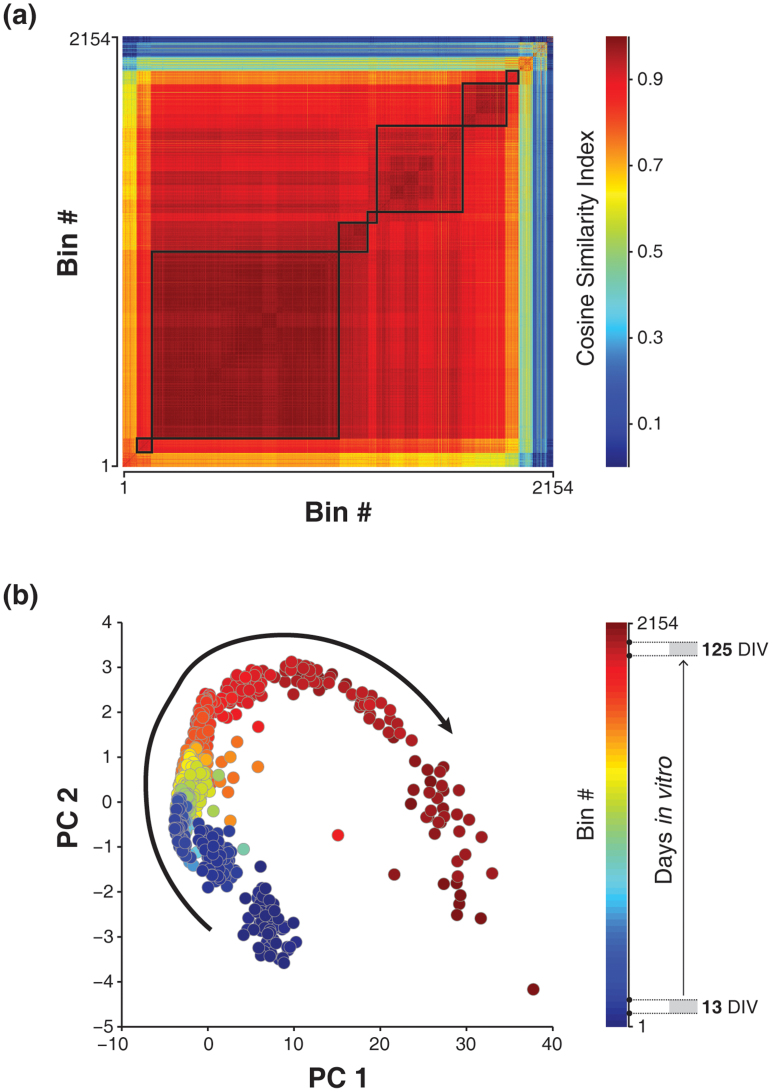
To examine developmental changes of spontaneous network activity, multi-electrode recordings were made from primary dissociated hippocampal cultures of E18 Wistar rat embryos (23 cultures from 20 plating batches, typical network and electrodes layout were shown in Supplementary Fig. 1). Spikes were detected using an adaptive amplitude threshold, and then were used to construct a neural activity vector (see Methods). To capture the global dynamics of network activity patterns (Typical firing patterns during development were shown in Supplementary Fig. 2), we first built a similarity matrix between vector pairs which respectively denoted a spatial neural activation pattern at the corresponding time point (Fig. 1a). Afterwards, we inspected the similarity matrix in a reduced dimensional space using principal component analysis (PCA, Fig. 1b). Network activity patterns were then mapped as dots in the PC (principal component) space where the distance between two dots were used for measuring the difference between the corresponding spatial patterns.

Figure 1. Unidirectional sequence of network state transitions during in vitro maturation.

Figure 1

Open in a new tab

(a), Similarity matrix of spatiotemporal firing patterns of a developing network. The colorbar indicates the range of similarity index. (b), Data in the PC coordinate shows a trail of clusters sequentially emerged through stages of development. The colorbar indicates the range of recorded life span. The arrow indicates the direction of sequential state transitions during development. DIV: days in vitro.

State transitions during development illustrated a homeostatically-regulated trajectory

After examining the entire development process in the PC space, we found a U-shape trajectory left by the sequential emergence of dot clusters which were referred to network states here (in 18 of 23 long-term recordings of hippocampal cultures, examples shown in Fig. 1b and in Supplementary Fig. 6a). Spatiotemporal activity patterns in the same recording session shared similar characteristics, but changed gradually in successive sessions.

From early to late stages, the trail of sequential network state transitions formed a unidirectional path, indicating that the predominant activity pattern in each stage changed progressively during development. By visualising and examining the developmental dynamics in long-term cultures, we found the trajectory was a common phenomenon which may reflect the network dynamics in the entire developing process.

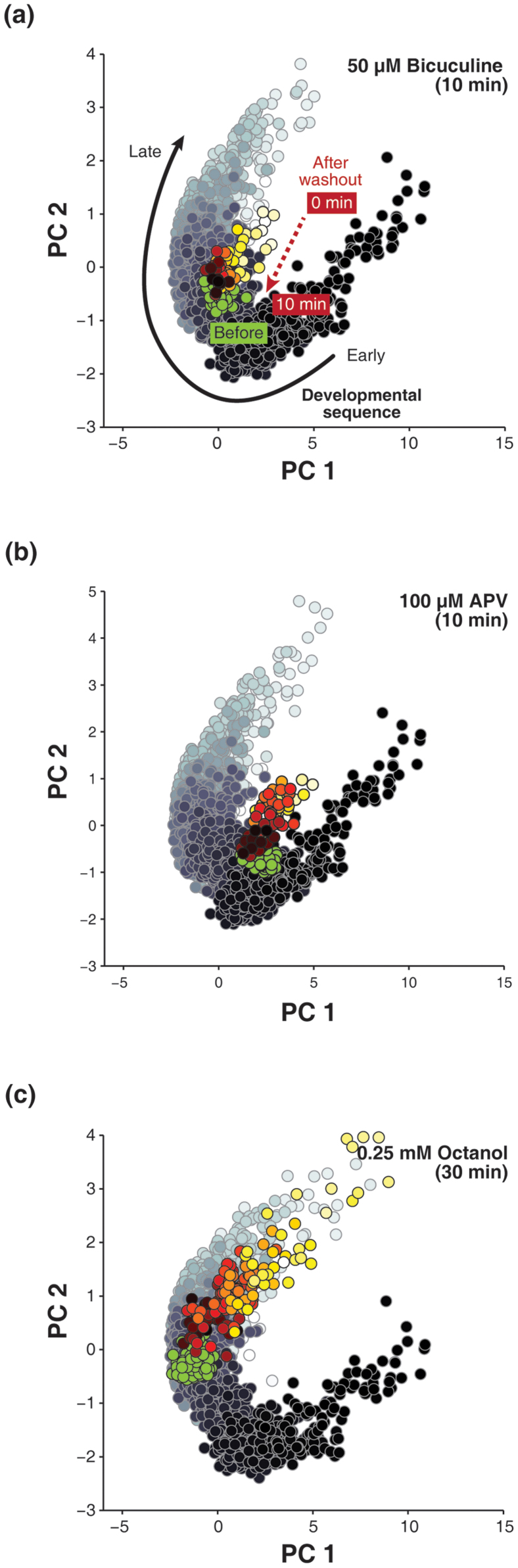
Previous studies have suggested that it is the excitation-inhibition balance that homeostatically maintains dynamical states and prevents external perturbations from driving the network towards pathological states17,18,19,20. To test whether the disturbance could alter the shape or direction of the trajectory, we added 50 μM bicuculline (BIC, a specific antagonist of GABA-A receptors) and 100 μM (2R)-amino-5-phosphonovaleric acid (APV, a specific antagonist of NMDA receptors) to the medium respectively (see Methods). In the presence of bicuculline, the network activity pattern changed to stereotypic rhythmic bursting. After washing out bicuculline by changing the entire medium three times, the network state did not immediately return to its original site in the PC space. Instead, it took approximately 10 minutes to recover from the overexcited state, leaving a markedly trail pointed towards the former trajectory (Fig. 2a). After the APV application which led to the inhibition of neural activity, the recovering network activity also left a similar trail (Fig. 2b). Such phenomenon was also observed after the application of 0.25 mM octanol (OCT, a putative blocker of electrical synapses, Fig. 2c). These observations suggest that network activity patterns in the development were homeostatically-regulated. After external perturbation was removed, the network could autonomously restore the global dynamics to a “preset” dynamical state corresponding to the “current” developmental stage (for more examples, please see Supplementary Fig. 10).

Figure 2. Disturbing the excitation-inhibition balance alters the developmental trajectory.

Figure 2

Open in a new tab

(a–c), The application of Bicuculline (50 μM), APV (100 μM) and Octanol (0.25 mM) breaks the excitation-inhibition balance and alters the trajectory. In the PC space, the inherent developmental sequence is shown by the grayscale trajectory (black to white) and the recovering track left by firing patterns after washing out drugs is indicated by colorized dots (light yellow to dark red). The green dots indicate the original firing patterns before the drug was applied. The black arrow and the red arrow indicates the direction of sequential state transitions during development, and the direction of changing firing patterns after the drug was washed out, respectively. Note firing patterns return to the approximately original position through the unidirectional recovering process, leaving a track pointed to the position where firing patterns before drug was applied (green dots). (Total recorded life span of the cultured network: 147 DIV, Experiment Day: APV: 33 DIV; BIC: 51 DIV, OCT: 101 DIV). Data are available online. DIV: days in vitro.

Networks activities were looking more similar in the middle stages

To investigate the changes of spatiotemporal activity patterns in the course of entire development process, we next examined the network states in different developmental stages. In the early and the late stages, the activity patterns were sparsely scattered in the PC space. In the first and the last few recordings, we could only distinguish individual “clusters” by responding recording dates. In contrast, clusters gradually became densely distributed in the middle stages when most neural ensembles were activated and acting correlatively (Supplementary Fig. 3a, 4, 5, 9), indicating enhanced pattern stability and greater activity synchronization over the network. By examining other cultures, we found this phenomenon of changing cluster distribution was common in the in vitro development. It is well known that the impact of topology on dynamics in complex networks is a fundamental but yet to be fully explored problem. Previous studies have suggest that maturation of functional connectivity leads into an intrinsic exploratory dynamics characterized by more stable and organized activity patterns9,11,21. While the tightness of the cluster may reflect the similarity of spatiotemporal activity patterns, crucial changes in network topology needs to be explored. We then estimated the global functional connectivity of in vitro neuronal networks (see Methods). In the first and the last few weeks, only seldom weak connections were identified in the network. The number of connections showed an age-dependent increase and the connectivity patterns became richer and more complex in the middle stage (the time range of middle stages varies from batch to batch, for example, 3–7 weeks in vitro as the example shown in Supplementary Fig. 3b). The above observation of network connectivity was in line with previous studies22. Next, we calculated betweenness centrality and assortativity of the functional network to quantitatively characterize statistical properties of its topology of individual stages. The results showed that hubs with high degrees and betweenness centrality emerged (Supplementary Fig. 3b, 5, 9, please note that hub nodes and “core” populations shares some common electrodes but not exactly identical) only in the middle stages. Consistent with previous extracellular recording studies, the assortativity coefficient in our hippocampal networks was less than zero22,23. The negative assortativity coefficient indicates that neural assembly which has many connections tends to connect to neural assembly that has a relatively small amount of connections. Interestingly, this coefficient increased and approached zero in middle stages (Supplementary Fig. 4), suggesting that the degree distribution turned to be more homogenous in the middle stages when the network was becoming more interconnected, even though the network showed disassortative mixing in the early and late stages. Considering the fact that more neural assemblies were engaged in the global firing activity during middle stages and that hub nodes were emerged in the same period, we suggest that these changes in network connectivity may help to diminish the diversity of spatiotemporal activity patterns.

The developmental trajectory was only showed in the self-organized network

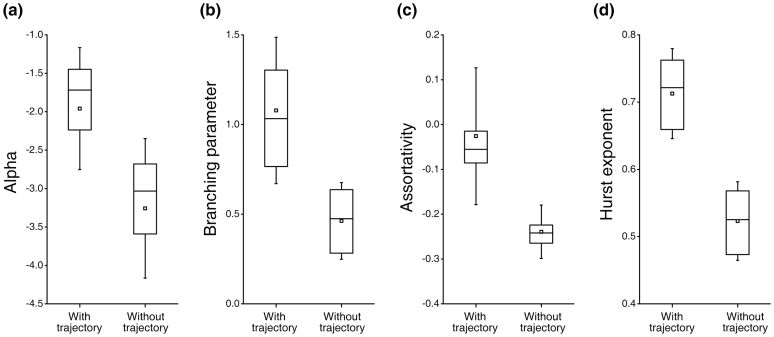
Recent studies have implicated self-organization as a fundamental process in the formation of spatiotemporal activity patterns12,13,24,25. The presence of self-organized criticality (SOC) in cultured networks has been characterized by power-law scaling of distributed neuronal “avalanche” activity8,10,16,26. To examine SOC in the course of entire development process, we tracked and analysed both avalanche events (“global”) and spike events (“individual units”) of all recordings (see Methods). In neuronal avalanche assay, the fitted slope value (α) found for the avalanche size distribution was −1.95 ± 0.79 (mean ± S.D., n = 1763 recordings), and the branching parameter which is a common metric describing avalanche propagation was close to unity: 1.07 ± 0.41 (mean ± S.D., Fig. 3), both suggesting emerging critical dynamics in the network. In addition, the Hurst exponent of the inter-spike intervals of individual spike trains was 0.71 ± 0.08 (mean ± S.D.), indicating strong long-range temporal correlations in the spontaneous activity of individual network units. These observations demonstrate the presence of SOC in networks which exhibited unidirectional sequential state transitions in the course of development (“with the trajectory”). However, we also noted that not all cultures exhibited such transitions. In those networks (6 of 23 cultures), we found irregular/abrupt transitions or reversible transitions of spontaneous activity patterns during development (Supplementary Fig. 6, 7, 8). The fitted slope value (α) was far from the universal power-law exponent value −1.5 (α = −3.25 ± 0.91, mean ± S.D., with the branching parameter: 0.46 ± 0.21, mean ± S.D., n = 231 recordings), suggesting that subcritical dynamics (randomness) existed in the developing process of these networks. Further, Hurst analysis showed that activity of individual neuronal ensembles in such networks exhibited very weak temporal correlation (Hurst exponent: 0.52 ± 0.07, mean ± S.D.). Taken together, the above data suggest that metastable state transitions may only occur in temporally evolving networks operating at or close to critical, which for the first time experimentally confirms the theoretical prediction of the close link between self-organized criticality and metastable transient dynamics in living neural networks27.

Figure 3. Network dynamics varies in cultures with/without developmental trajectory.

Figure 3

Open in a new tab

(a–d), Parameters of network dynamics between cultured networks with/without developmental trajectory: Data distribution of the fitted slope values in avalanche size distribution (a), the branching parameter of avalanche propagation (b), the assortativity coefficient of functional connectivity of networks (c), and the Hurst exponent of spiking activity of individual units (electrodes) of networks (d) with/without developmental trajectory are shown in box plots. In the box plot, 25th percentile, median, 75th percentile of data are represented by the box (the bottom, the band near the middle, and the top of the box, respectively), the mean value is represented by the square dot inside the box, and the standard deviation is represented by the whiskers of the box.

Discussion

Self-organized criticality in cultured neuronal networks is widely suggested in previous studies2,15,18,19,28. To demonstrate this, we recorded electrical activities from long-term cultured hippocampal networks and performed both neuronal avalanche assays and long-range correlation estimation on the data. There were two types of cultured networks in our study: the majority showed self-organized criticality, and the rest remained mostly in the subcritical regime. Our data confirms that not all neuronal networks stayed in the critical regime during development, which has been reported previously11,19. It was still unknown that how different activity propagating mode (critical or non-critical) could affect the developmental process. From the perspective of the entire development process, what is the influence of self-organized criticality on the developmental dynamics? On the ground of previous studies, our raw data contained all recordable network activities during the entire development of cultured network. We analysed the dynamical states which emerged successively in the developing networks. We observed a unique and unprecedented phenomenon that the majority of the neuronal networks showed progressively-changed activity patterns through developmental stages. Interestingly, we found the observed trajectory of metastable state transitions only showed in the networks in which population activity propagated in the critical mode. As a self-organized system, neural networks are believed to be able to optimise two critical aspects of neural computation: one aspect is in information transmission which is believed to be optimised while the system operates in the critical region16,17; the other aspect is in information storage which is optimised while metastable dynamics exists in the system6,7,27. The simultaneously existence of critical and metastable dynamics confirms the previously reported theoretical prediction which based on mathematical models27.

Further, we tried to find whether the homeostatic plasticity in developing networks could be reflected by the trajectory. In our study, homeostatic mechanisms closely related to AMPA-A and NMDA receptors and gap junctions were examined using commonly used chemical blockers. We found that disrupting the excitation-inhibition balance could alter the trajectory in shape and direction. After re-establishing the balance, the network returned to the original dynamical state, suggesting that homeostatic plasticity in developing networks may not only holds the activity level (firing rates) to a set point26, but more importantly, maintains nontrivial activity patterns and dynamical network states during development. The trajectory in our results showed that a progressively-changed activity pattern dominated the global mode in each stage, and that such firing patterns could be rebuilt even when it was disrupted.

In summary, we used long-term cultured hippocampal networks to demonstrate that large random developing networks showed sequential global dynamics during in vitro maturation, capturing metastable transitions in the entire developmental process. Our data suggest that a self-organized criticality mechanism with long range interactions hereby plays a potential role in the emergence of metastable activity states in an evolving network.

In temporally evolving networks, the coexistence of self-organized criticality and metastable state transition showed in our results provides an unprecedented experimental evidence for the hypothesis that critical networks should simultaneously exhibit criticality and metastability. Understanding the self-organized nature of developing networks may hold the key to elucidating the network-level mechanisms of brain development. Based on our result, it may be possible to predict how the network will evolve by examining the criticality in early stages. It will open a door to the investigation of age-related neuronal dysfunction, and ultimately to the forecasting of developmental dynamics of the brain.

Methods

Dissociated hippocampal cultures

As previously reported, hippocampi from E18-19 Wistar rat embryos were dissected and the hippocampal neurons were dissociated by enzymatic digestion with trypsin (10 min at 37°C) and mechanical dissociation29. Cells were then plated at a density of 2500 cells/mm2 onto multielectrode array dishes (Ayanda Biosystems SA, Lausane, Swiss) coated with poly-L-lysine. The culture medium in MEA dishes contained 1 ml Neurobasal medium with B27 (Invitrogen), 0.5 mM Glutamax (Invitrogen), and 10% equine serum (Hyclone). MEA dishes were kept in a 37°C, 5% CO2 water jacketed incubator, and half of the medium was changed every 2 days. All experimental procedures used in this study were approved by the Animal Ethics Committee of Huazhong University of Science and Technology.

Recording

Signals from 59 recording electrodes in the MEA dish were acquired simultaneously with a MEA1060 recording system (Multichannel Systems, Reutlingen, Germany). For each culture, after electrical activities became detectable by electrodes (~ after 1 week in vitro), extracellular signals were continuously sampled with a fixed schedule at 25 kHz for at least 1 hour every 2 days until no valid signal could be detected due to network deterioration (typical observation period last for 100–150 days in vitro). For each electrode, a threshold automatically set by 5× standard deviation of the noise was used to convert raw waveform data into a spike train.

Drugs

Bicuculline methiodide (Sigma), D(−)-2-amino-5-phosphonopentanoic acid (Sigma) and 1-Octanol (Sigma) were dissolved in culture medium. The volume of medium in the MEA chamber was maintained at 1 ml. Drugs were added directly to the MEA chamber, and the reaction was terminated by aspiration of the entire medium and replacement with fresh culture medium.

Data analysis

To capture slow changing dynamics of network firing patterns during the entire development process, raster plots of all valid recordings of a network during development were binned every 1–10 s. The binning was determined by the distribution of inter-spike interval (ISI) and inter-burst interval (IBI). Cultures with small ISIs and IBIs would be applied a smaller binning window. Detected spikes of individual electrodes were counted in each bin to construct a set of M-dimension activity vectors 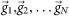Inline graphic (M: Total electrode number, N: Total bin number) which represents changing spatiotemporal pattern (i.e., active neural assembles and their activity levels) of network activity with time. 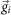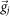We constructed the similarity matrix Si,j by calculating cosine similarity between Inline graphic and Inline graphic:

graphic file with name srep01081-m4.jpg

which has a value between 0 and 1. To visualize and identify possible network states emerged during development, we then applied PCA to the matrix. After PCA, the first two principal components (PC) spanned an orthogonal space where each pattern was mapped as a dot.

To follow the state transition, we used graph theory to analyze the functional topology of the network. To evaluate connection strength between nodes, mutual information between spike trains recorded by individual electrodes was computed by evaluating joint and single probabilities of two spike trains (X, Y):

graphic file with name srep01081-m5.jpg

where x, y denote a spike event and p(x,y) represents the joint probability (binning window = 1 ms). Then, the values are normalized between 0 and 1, which are used to measure the strength of the functional connectivity link between two assemblies22. Betweenness centrality of node i was computed by considering the number of shortest paths between the other two nodes that pass through i:

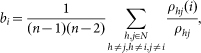graphic file with name srep01081-m6.jpg

where ρhj denotes the number of shortest paths between the other two node h and j, and ρhj(i) denotes the number of shortest paths between them but also passes through i28. Assortativity of a network was computed by the Pearson correlation coefficient of the degree distribution:

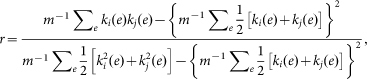graphic file with name srep01081-m7.jpg

Where ki(e) and kj(e) denotes the degrees of nodes at ends of link e, and m is the total number of links23. The network is assortative when r > 0 (correlated), disassortative when r < 0 (anti-correlated), and uncorrelated when r = 0.

The generation and propagation of network activity was examined by detecting and evaluating neuronal avalanches in the network. Self-organization criticality in network activity during development was identified by both properties of neuronal avalanches in the network and Hurst exponent of spiking activity of individual spike trains. Avalanches were detected by using the method presented in ref. 9,10,11 (with a 3-ms binning window), and the size of an avalanche is defined as the number of active electrodes inside the event. To validate criticality, we followed the maximum likelihood method with Kolmogorov-Simirnov test presented in ref 30. To evaluate propagation of avalanches, we defined the branching parameter as the average number of electrodes activated by prior electrodes in the propagation of neuronal avalanches. Both the scaling exponent (slope value: α) close to −1.5 and branching parameter close to 1 suggest self-organized critical dynamics in the network activity. To evaluate the presence of long-range correlation in the activity of individual units of the network, we first concatenated all detected spikes of each electrode during development into a spike train, and then applied the rescaled range method to estimate Hurst exponents on the inter-spike interval sequences31. A Hurst exponent value H close to 0.5 indicates a random walk, H > 0.5 indicates persistent behaviour, and H < 0.5 indicates anti-persistent behaviour.

Author Contributions

Q.L. and H.G. conceived the project, participated in its development and revised the manuscript. J.P. and X.L. prepared the neuronal cultures and performed the experiments. J.P. and H.G. analysed the data, and wrote the manuscript.

Supplementary Material

Supplementary Information

Supplementary Figures

srep01081-s1.doc (4.7MB, doc)

Acknowledgments

We thank members of Britton Chance Center for Biomedical Photonics for comments and advice, Wenjuan Chen for assistance with data analysis, Xiongfei Jiang, Geng Zhu and Xinxin Yan for their valuable discussions. This work is supported by the National Nature Science Foundation of China (81127002, 61121004, 30925013) and 985 project.

References

  1. Garcia N. V. D., Karayannis T. & Fishell G. Neuronal activity is required for the development of specific cortical interneuron subtypes. Nature 472, 351–U116 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Eckmann J. P. et al. The physics of living neural networks. Phys. Rep.-Rev. Sec. Phys. Lett. 449, 54–76 (2007). [Google Scholar]
  3. Johnson H. A., Goel A. & Buonomano D. V. Neural dynamics of in vitro cortical networks reflects experienced temporal patterns. Nat Neurosci 13, 917–919 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Destexhe A. & Contreras D. Neuronal computations with stochastic network states. Science 314, 85–90 (2006). [DOI] [PubMed] [Google Scholar]
  5. Spitzer N. C. Electrical activity in early neuronal development. Nature 444, 707–712 (2006). [DOI] [PubMed] [Google Scholar]
  6. Wagenaar D. A., Pine J. & Potter S. M. An extremely rich repertoire of bursting patterns during the development of cortical cultures. Bmc Neurosci 7 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Habets A. M., Van Dongen A. M., Van Huizen F. & Corner M. A. Spontaneous neuronal firing patterns in fetal rat cortical networks during development in vitro: a quantitative analysis. Experimental brain research. Experimentelle Hirnforschung. Experimentation cerebrale 69, 43–52 (1987). [DOI] [PubMed] [Google Scholar]
  8. Plenz D. & Thiagarajan T. C. The organizing principles of neuronal avalanches: cell assemblies in the cortex? Trends Neurosci 30, 101–110 (2007). [DOI] [PubMed] [Google Scholar]
  9. Stewart C. V. & Plenz D. Homeostasis of neuronal avalanches during postnatal cortex development in vitro. J Neurosci Meth 169, 405–416 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Beggs J. M. & Plenz D. Neuronal avalanches in neocortical circuits. J Neurosci 23, 11167–11177 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Pasquale V., Massobrio P., Bologna L. L., Chiappalone M. & Martinoia S. Self-organization and neuronal avalanches in networks of dissociated cortical neurons. Neuroscience 153, 1354–1369 (2008). [DOI] [PubMed] [Google Scholar]
  12. Bornholdt S. & Rohl T. Self-organized critical neural networks. Phys Rev E 67 (2003). [DOI] [PubMed] [Google Scholar]
  13. Chialvo D. R. Emergent complex neural dynamics. Nat. Phys. 6, 744–750 (2010). [Google Scholar]
  14. Gireesh E. D. & Plenz D. Neuronal avalanches organize as nested theta- and beta/gamma-oscillations during development of cortical layer 2/3. Proceedings of the National Academy of Sciences of the United States of America 105, 7576–7581 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kinouchi O. & Copelli M. Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2, 348–352 (2006). [Google Scholar]
  16. Yang H., Shew W. L., Roy R. & Plenz D. Maximal variability of phase synchrony in cortical networks with neuronal avalanches. J Neurosci 32, 1061–1072 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Sun Y. J. et al. Fine-tuning of pre-balanced excitation and inhibition during auditory cortical development. Nature 465, 927–931 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Shew W. L., Yang H., Yu S., Roy R. & Plenz D. Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J Neurosci 31, 55–63 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Marin-Burgin A., Mongiat L. A., Pardi M. B. & Schinder A. F. Unique processing during a period of high excitation/inhibition balance in adult-born neurons. Science 335, 1238–1242 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Turrigiano G. G. & Nelson S. B. Homeostatic plasticity in the developing nervous system. Nature reviews. Neuroscience 5, 97–107 (2004). [DOI] [PubMed] [Google Scholar]
  21. Chiappalone M., Bove M., Vato A., Tedesco M. & Martinoia S. Dissociated cortical networks show spontaneously correlated activity patterns during in vitro development. Brain Res 1093, 41–53 (2006). [DOI] [PubMed] [Google Scholar]
  22. Bettencourt L. M., Stephens G. J., Ham M. I. & Gross G. W. Functional structure of cortical neuronal networks grown in vitro. Phys Rev E 75, 021915 (2007). [DOI] [PubMed] [Google Scholar]
  23. Newman M. E. Assortative mixing in networks. Phys Rev Lett 89, 208701 (2002). [DOI] [PubMed] [Google Scholar]
  24. Beggs J. M. The criticality hypothesis: how local cortical networks might optimize information processing. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 366, 329–343 (2008). [DOI] [PubMed] [Google Scholar]
  25. Millman D., Mihalas S., Kirkwood A. & Niebur E. Self-organized criticality occurs in non-conservative neuronal networks during ‘up' states. Nat. Phys. 6, 801–805 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Levina A., Herrmann J. M. & Geisel T. Dynamical synapses causing self-organized criticality in neural networks. Nat. Phys. 3, 857–860 (2007). [Google Scholar]
  27. Haldeman C. & Beggs J. M. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys Rev Lett 94, - (2005). [DOI] [PubMed] [Google Scholar]
  28. Rubinov M. & Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069 (2010). [DOI] [PubMed] [Google Scholar]
  29. Chen W. J. A., Li X. N., Pu J. B. & Luo Q. M. Spatial-temporal dynamics of chaotic behavior in cultured hippocampal networks. Phys Rev E 81, - (2010). [DOI] [PubMed] [Google Scholar]
  30. Clauset A., Shalizi C. R. & Newman M. E. J. Power-Law Distributions in Empirical Data. Siam Review 51, 661–703 (2009). [Google Scholar]
  31. Hurst H. E. Long-term storage capacity of reservoirs. Trans. Amer. Soc. Civil Eng. 116, 770–808 (1951). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures

srep01081-s1.doc (4.7MB, doc)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES