The generation of oscillations in networks of electrically coupled cells

Abstract

In several biological systems, the electrical coupling of nonoscillating cells generates synchronized membrane potential oscillations. Because the isolated cell is nonoscillating and electrical coupling tends to equalize the membrane potentials of the coupled cells, the mechanism underlying these oscillations is unclear. Here we present a dynamic mechanism by which the electrical coupling of identical nonoscillating cells can generate synchronous membrane potential oscillations. We demonstrate this mechanism by constructing a biologically feasible model of electrically coupled cells, characterized by an excitable membrane and calcium dynamics. We show that strong electrical coupling in this network generates multiple oscillatory states with different spatio-temporal patterns and discuss their possible role in the cooperative computations performed by the system.

Many neuronal and non-neuronal systems exhibit synchronized oscillatory behavior in networks of electrically coupled cells. Experimental findings have revealed that in some of these systems electrical coupling is essential for the generation of oscillations and not only for their modulation. One example is the subthreshold oscillations observed in neurons of the inferior olive (IO). These neurons (when isolated) are nonoscillatory, and the synchronized subthreshold oscillations result from the abundant electrical coupling between the cells (1–3). Similarly, the oscillations observed in sympathetic preganglionic neurons (4) and the locus coeruleus (5) were attributed to the electrotonic coupling between the cells. Draguhn et al. (6) have shown that the high-frequency oscillations in hippocampal slices are independent of the chemical synapses, suppressed by gap junction blockers, and intensified by gap junction enhancers. The same phenomenon has been observed in non-neuronal biological systems. Oscillations occur in the electrically coupled network of β-pancreatic cells in the islets of Langerhans in the pancreas, whereas isolated cells are either quiescent or oscillate at frequencies that are much lower than those of the network oscillations (7, 8). Membrane potential and cytosolic calcium oscillations were observed in electrically coupled networks of aortic smooth muscle cells but not in the isolated cells (9). In addition, abnormal electrical coupling has been implicated in the generation of periodic electroencephalogram discharges in Creutzfeldt-Jakob disease (10).

The emergence of sustained oscillations in a network where identical nonoscillating cells are coupled seems to be paradoxical. If network oscillations are fully synchronized then there is no current flowing through the electrical coupling and the whole network behaves exactly as the single cell does [this is false when the cells are not identical and have a different resting potential (11, 12)]. Therefore, if the single cell does not oscillate the network will be quiescent. Hence, sustained oscillations in such a network must necessarily involve phase differences between the cells. However, phase differences will be suppressed by the electrical coupling that tends to equalize the membrane potentials of the coupled cells. Thus, one would expect that if single cells have a stable rest state it would be maintained in the presence of electrical coupling. This intuition is not always correct and it has been shown that moderate diffusive coupling (a generalized form of electrical coupling) of identical nonoscillating elements can destabilize the homogeneous rest state of the system and generate oscillations (13–17). However, the generality of these examples and their relevance to electrically coupled biological systems have been unclear, particularly because the membrane potential of electrically coupled networks often oscillate in phase, whereas in their examples the coupled elements cannot oscillate in phase. In this work we propose a general dynamic mechanism, which explains how electrical coupling of identical nonoscillatory cells may generate synchronized membrane potential oscillations. We demonstrate the implementation of this mechanism in a biologically feasible model of electrically coupled cells and study the spatio-temporal properties of the oscillations in large electrically coupled networks.

Mechanism for the Generation of Oscillations

Our mechanism is based on three assumptions: First, individual cells are described by their membrane potentials and additional “internal variables,” e.g., the amount of activation and inactivation of ionic channels or the concentrations of different ions and proteins. Second, these internal variables have a tendency to oscillate. Third, the interaction of the membrane potential with the internal variables provides a negative feedback that prevents the oscillations of these internal variables and stabilizes the cell. Thus, any factor that will suppress this negative feedback will expose the oscillatory nature of the internal variables. One such factor is the membrane conductance. If this conductance is sufficiently large the membrane potential is unable to respond to perturbations in the internal variables. The negative feedback is then disrupted and the internal variables will oscillate. The final element in our theory is that electrical coupling resembles an increase in membrane conductance. Therefore, when the electrical coupling is large the resting state of the coupled cells becomes unstable and the system will oscillate.

Model with Calcium Dynamics

We demonstrate the validity of the above mechanism by a biophysically feasible model of electrically coupled network consisting of identical cells that exhibit calcium dynamics. Oscillations in intracellular calcium concentration have been studied intensively in recent years. Goldbeter et al. (18) has proposed that calcium-induced calcium release mechanism in which release of calcium from internal stores is triggered by cytosolic calcium itself provides the necessary positive feedback loop for the oscillations in the calcium concentrations in the cytoplasm and in the internal stores. These oscillations are modeled by:

1

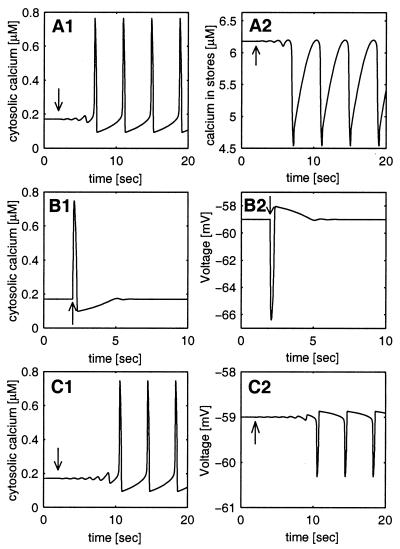
where X and Y denote the calcium concentrations in the cytoplasm and stores, respectively. J(X,Y) describes the interaction between the calcium concentrations; K⋅X is the efflux of calcium from the cell, and U is a constant calcium mediated electrical current. φ is a conversion factor from this current to change in calcium concentration. Details of the model are presented in the Appendix. Fig. 1A 1 and 2 describe the oscillations in the calcium concentration in the cytoplasm (Fig. 1A1) and the internal stores (Fig. 1A2). A small perturbation (arrow) drives the system away from the unstable fixed point and generates oscillations.

Figure 1.

Calcium and voltage oscillations in the modeled cell. (A) In a nonexcitable cell, the dynamics of calcium concentrations has an unstable fixed point. A small perturbation in the cytosolic calcium concentration (an increase by 10⁻³ μM), denoted by an arrow, drives the cell away from the fixed point into stable oscillations of both the cytosolic (A1) and the stores (A2) calcium concentrations. The constant calcium current U (see Eq. 1 and the Appendix) is taken to be U = −184 nAmp/cm². (B) In an excitable cell (see Eq. 2 and the Appendix), the membrane stabilizes the fixed point. A much larger perturbation (an increase of the cytosolic calcium concentration by 0.1 μM), denoted by an arrow, generates one spike in calcium concentration but the system converges back to the stable fixed point. An increase in the shunt conductance (an extra conductance of 2⋅10⁴ μS/cm²) destabilizes the fixed point such that even a small perturbation (same as in A), denoted by an arrow, leads to cytosolic calcium oscillations (C1) and consequently to membrane potential oscillations (C2). I_Ca at the fixed point is equal to U (−184 nAmp/cm²). The unstable fixed points in A and C are not realizable experimentally but serve to demonstrate the dynamical principle.

Figure 2.

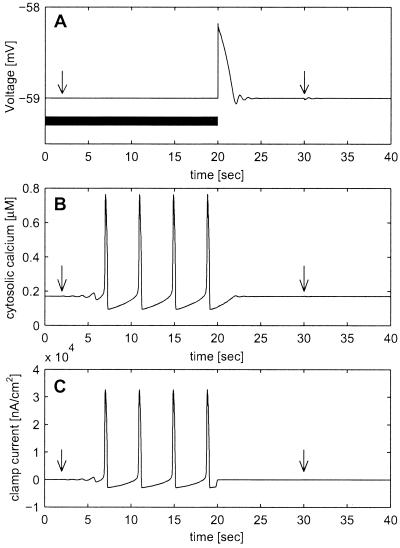
Calcium oscillations are generated by voltage clamping. A nonoscillating cell (parameters as in Fig. 1B) is voltage-clamped to its resting potential value for the first 20 sec (black bar in A). (A) The membrane potential. (B) The cytosolic calcium concentration. (C) The voltage clamp current. At time t = 2 (denoted by an arrow), a small perturbation of the cytosolic calcium concentration (same as in Fig. 1 A and C) drives the cell away from the unstable fixed point into stable oscillations of the cytosolic calcium concentration. These oscillations are reflected in the calcium-dependent potassium current, resulting in oscillations in the clamping current (C). Discontinuing the voltage clamp generates damped voltage oscillations (A) and prevents the calcium oscillations (B). Without the voltage clamping, the same cytosolic calcium perturbation (second arrow) has almost no effect on the cell dynamics. The unstable fixed point (at times t < 2) is not realizable experimentally but serves to demonstrate the dynamical principle.

A different behavior emerges if the calcium dynamics interacts with the membrane potential (V). This interaction is mediated via voltage-dependent calcium current, I_Ca(V), and a (cytosolic) calcium-dependent potassium current, I_{K_Ca}(X,V). Thus, the cell's dynamics is of the form:

2

The upper part of Eq. 2 describes the current balance equation in which an additional passive leak current, I_leak(V), was included. The equations for the calcium concentrations X,Y are as in Eq. 1, with the voltage-dependent calcium current I_Ca(V) substituting the constant calcium current U. Details of the model appear in the Appendix. The behavior of this system is described in Fig. 1B 1 and 2. In this case, even a large perturbation (arrow) does not induce oscillatory behavior either in the cytosolic calcium (Fig. 1B1) or the membrane potential (Fig. 1B2). The absence of the oscillations is due to the activation of I_{K_Ca} that hyperpolarizes the membrane potential, which in turn deactivates the calcium current and decreases the calcium influx into the cell.

The ability of the membrane potential to prevent the oscillations depends on the negative feedback that it exerts on the calcium oscillations. A detailed analysis of the effect of adding a shunt conductance (a passive conductance with a reversal potential that is equal to the resting potential value) with strength g_rest shows that for small values of g_rest the rest state is stable. Increasing g_rest beyond a critical value g_c destabilizes the rest state and gives rise to stable oscillations in a scenario known as normal Hopf bifurcation (19). This is illustrated in Fig. 1C1 for the cytosolic calcium and in Fig. 1C2 for the membrane potential. In this regime of g_rest, a small increase in the cytosolic calcium (arrow) increases I_{K_Ca}, as before, but the current that will flow through the extra large conductance will generate a smaller change in the membrane potential (compare Fig. 1 C2 to B2). Thus the resultant decrease in calcium influx will be small and insufficient to prevent the calcium oscillations. These oscillations will induce membrane potential oscillations via I_{K_Ca}. Thus, the addition of a large shunt conductance reduces the effect of the cytosolic calcium on the membrane potential, suppresses the efficacy of the negative feedback loop, and enables oscillations.

Our hypothesis about single cell properties yields a surprising experimental prediction. Because voltage clamp is in fact an addition of a large conductance with a reversal potential that is equal to the holding potential, we predict that voltage clamping the cell to its resting potential value will generate oscillations of the internal variables as shown in Fig. 2. When the cell is clamped to its resting potential value (thick line in Fig. 2A) a small perturbation to the cytosolic calcium concentration (first arrow) leads to cytosolic calcium oscillations (Fig. 2B) and consequently due to the calcium-dependent potassium current to oscillations in the current needed to maintain the membrane potential (Fig. 2C). When the clamp is terminated the calcium oscillations lead, as expected, to damped membrane potential oscillations (Fig. 2A). Under nonclamped conditions the same cytosolic calcium perturbation (second arrow) has almost no effect on either the calcium concentrations or the membrane potential.

The Effect of Electrical Coupling

Electrical coupling is modeled by adding a coupling current I_coupling to the current balance equation for each cell, thus the dynamics of the membrane potential of cell i is:

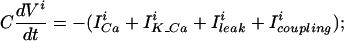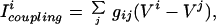3

where the sum is over all of the cells in the network and g_ij is the electrical coupling between the cells i and j.

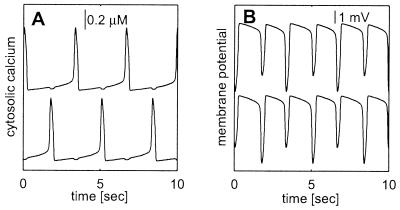
As was shown in the case of the reaction-diffusion equation (16), electrical coupling resembles an increase in the membrane conductance. This can be easily seen if we examine the effect of coupling on two identical nonoscillating cells both at their resting potential value. Perturbation of the membrane potential of one of the cells will generate a current flow from that cell to the other cell. Because the second cell is initially at the resting potential value, the current flow is proportional to the difference between the perturbed membrane potential and the resting membrane potential. Thus, shortly after the perturbation the cell behaves as if it was an isolated cell with an additional leak current whose reversal potential is equal to the resting potential value. Consequently, the addition of a sufficiently large electrical coupling between two cells of this type leads to oscillations as illustrated in Fig. 3, similar to the effect of increasing the membrane conductance in the isolated cell. Analysis of the effect of adding an electrical coupling with strength g between the two identical cells, which are described by Eqs. 2 and 3, shows that for small values of g the rest state is stable. Increasing g beyond a critical value (which equals to 0.5 g_c) destabilizes the rest state and gives rise to oscillations via a Hopf bifurcation. Fig. 3 shows that in contrast to the antiphase oscillations of the cytosolic calcium concentrations of the two cells (Fig. 3A) their membrane potentials oscillate in an almost in-phase fashion (Fig. 3B). In addition, the frequency of the calcium oscillations is half that of the membrane potential oscillations.

Figure 3.

Voltage and calcium oscillation in a network of two electrically coupled cells. Parameters of the cells are the same as in Fig. 1B, and coupling strength is 10⁴ μS/cm². (A) The time course of the cytosolic calcium concentration in the two cells. (B) Membrane potential of the two cells. Note that although the membrane potentials of both cells are very similar, the calcium oscillations of the two cells are out of phase and locked in a 1:2 manner to the membrane potential oscillations. A spike like in calcium concentration in one cell generates a strong hyperpolarization in that cell, and consequently a smaller hyperpolarization in the coupled cell.

The Limit of Strong Electrical Coupling

To understand the reasons for the behavior shown in Fig. 3 it is useful to consider the limit of strong electrical coupling, which means that the electrical coupling between the two identical cells is much stronger than the other conductances in the system. In this case, the electrical coupling forces the membrane potentials of the coupled cells to be close to each other at all times. The small difference in their value multiplied by a large coupling conductance g generates a significant current flowing through the gap junction between them. This current has to be compensated by a substantial difference in the other currents that flow into the cells, in our case the calcium current. Hence the calcium concentrations of the two cells oscillate out of phase. How do these concentrations oscillate out of phase in the presence of in-phase potentials? To understand the mechanism at work let us sum the equations describing the dynamics of the membrane potentials of the two cells corresponding to Eq. 3 with i = 1,2. Because I_coupling of the two cells is identical in magnitude but different in sign it cancels out when the two equations are summed, so that

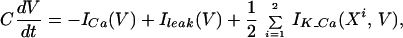4

where we have used the fact that V¹ ≈ V² = V. The dynamics of the calcium variables are given by:

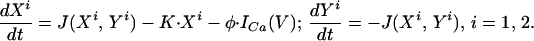5

The dynamic equations of the calcium variables of cell 1 (Eq. 5 with i = 1) are the same as that of cell 2 (Eq. 5 with i = 2), because the cells are identical and are forced by (nearly) the same potential oscillations. Nevertheless the trajectories of (X¹, Y¹) and (X², Y²) are not identical as is evident from Fig. 3A. This is possible because the locking of the calcium variables to the oscillating potential is not 1:1 but essentially 2:1, allowing for (X¹, Y¹) and (X², Y²) to be separated from each other by 180° of phase. Eq. 4 implies that in this case the frequency of the potential is double the frequency of the calcium variables.

Patterns of Oscillations in Electrically Coupled Networks

Our mechanism for the generation of oscillations is general and can be applied to networks with large numbers of cells and arbitrary architecture. For moderate coupling strength, the shape of the oscillations and the phase difference between the cells depends on the architecture of the coupling and their strengths. Here we concentrate on the cases of strong coupling, where general features can be extracted that are independent of the number of cells or the specific architecture.

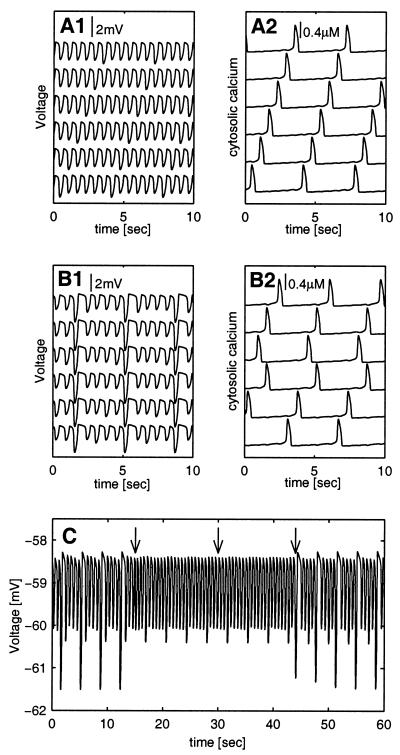
The equations that describe the dynamics of the network in the limit of strong coupling are similar to that of Eqs. 4 and 5 but with i running from 1 to N, N being the number of neurons in the network. The calcium variables of the different cells all obey the same dynamic equation and “see” (nearly) the same membrane potential. Therefore, the principle that calcium oscillates at lower frequency than the membrane potential and that the oscillations of the calcium concentrations are not all synchronized in phase applies in a general network. However, in a large network different realizations of out-of-phase calcium oscillations are possible and therefore the network possesses many stable states. The stable state in which the system will eventually settle is determined by the initial conditions. An example of this phenomenon is shown in Fig. 4 for a network of six coupled cells. Fig. 4A1 shows that the network settles in a state in which all six cells show in phase almost identical membrane potential oscillations. The calcium concentrations (Fig. 4A2), on the other hand, exhibit a different behavior. In each cell the frequency of the calcium oscillations is only one-sixth that of the voltage oscillations and they are out of phase with respect to each other. Hence, different cells “choose” different phases of locking to the membrane potential.

Figure 4.

Multiple stable states in a network of six strongly coupled cells. All cells in the network are coupled to all of the other cells. The parameters of the isolated cell are as in Fig. 1B. The six consecutive traces in each plot (from top to bottom) represent the activity in cells 1–6, respectively. (A) A stable state of the network, where the cytosolic calcium concentrations of all six cells are not in phase. The frequency of the membrane potential oscillations (A1) is six times that of the cytosolic calcium oscillations (A2). (B) Another stable state of this network, where the calcium concentrations of cells 2 and 4 are in phase, but are not in phase with the other cells (B2). This is reflected in the shape of the membrane potential oscillations (B1). Note that hyperpolarization resulted from the calcium spike of cells 2 and 4 is about twice as large as that of the other cells. (C) Transient stimuli can shift the network between stable states. The membrane potential of cell 1 is shown. Each arrow represents a transient increase in the cytosolic calcium concentration of the first cell (0.1 μM). Note that the same transient stimulus shifts the network from one stable state (same as in B) to another stable state (same as in A; first arrow), makes no sustained change in the network state (second arrow), or reverts to a stable state similar to A but now the calcium concentrations of cells 3 and 5 are in phase (third arrow). The coupling strengths between cells i and j were taken to be g_ij = (4 + 2⋅i + 2⋅j)⋅10³ μS/cm. For reasons of clarity the cells in the traces were ordered from top to bottom according to i = (2,6,5,3,4,1).

The same network can settle in another stable state (Fig. 4B), where the calcium oscillations of cells 2 and 4 (second and fourth traces in Fig. 4B2) are in phase but differ in phase from those of the other four cells. This structure is reflected in the nonharmonic shape of the membrane potential oscillations of all of the cells (Fig. 4B1). Thus the stable states of the network differ not only in the shape of the voltage oscillations but also in the grouping of the cells according to their in-phase calcium oscillations. We define a group of cells whose calcium oscillates in phase as a cluster.

One can induce transitions between the different stable states of the network by a transient cytosolic calcium perturbation to one of the cells. As demonstrated in Fig. 4C, the network is initially in the state shown in Fig. 4B. The same perturbation can either transform the network to the state described in Fig. 4A (first arrow), have only transient effect on the network (second arrow), revert to state in which the membrane potential oscillations are similar to the ones in Fig. 4B but now with the calcium concentrations of cells 3 and 5 in phase (third arrow), or transform the network to yet another state (not shown).

We have simulated large networks of up to 500 cells with the above calcium dynamics in the limit of strong coupling. We have found that typically the network forms 5–6 clusters whose sizes depend on the initial conditions. Fig. 5 shows an example of a strongly coupled network of 500 cells. The oscillations of the cytosolic calcium concentration (shown in Fig. 5B for 25 randomly chosen cells) show clear clustering into five clusters. The membrane potential shows different polarizations (Fig. 5A). Each of these peaks corresponds to a calcium spike that occurs in one of the clusters, and the size of this hyperpolarization corresponds to the size of the cluster. Thus the detailed shape of the common oscillating potential bears a signature of the clustering structure of the calcium variables.

Figure 5.

Oscillations in a large network of strongly coupled cells. Parameters of the isolated cells are as in Fig. 1B. The network consists of 500 cells and coupling is taken in the limit of very large coupling strength (i.e., identical membrane potentials as in Eqs. 4 and 5). (A) The voltage oscillations of a cell in the network. (B) Cytosolic calcium oscillations in 25 randomly chosen cells (for reasons of clarity the cells were ordered). Note that a hyperpolarization in the membrane potential follows an increase in the cytosolic calcium concentrations of some cells and the magnitude of the hyperpolarization depends on the number of cells in which there was simultaneous increase in the cytosolic calcium concentration. These hyperpolarizations result from the calcium-dependent potassium current.

Discussion

In this study we have demonstrated a possible solution to the seemingly paradoxical observation that electrical coupling of identical nonoscillating cells can generate synchronous membrane potential oscillations. The basic concept is that the interaction of the membrane potential with the internal variables suppresses the tendency of the latter to oscillate. Electrical coupling effectively acts as a shunt conductance and thus diminishes the suppression capacity of the potential, thereby giving rise to oscillations. We have realized our concept in a biologically feasible model in which calcium dynamics plays the role of internal variables.

Another model in which electrical coupling between identical nonoscillator cells generates oscillations has been previously proposed by Sherman and Rinzel (20). In that model, in addition to a stable rest state, stable oscillations of the membrane potentials exist in a restricted range of values of the electrical coupling. A continuum model of population dynamics with one diffusing species has been shown to undergo a Hopf bifurcation to oscillatory state (16). Both of these models predict the presence of antiphase oscillations in the coupled variables in a restricted range of coupling values. In contrast, the oscillations in the present model appear for arbitrary large electrical coupling. As we have explained above, this implies that the membrane potentials of the different cells may be nearly in phase. Moreover, the validity of this mechanism in a given network can be determined by investigating the dynamics of the single cells that comprise the network, in particular by testing whether the addition of a sufficiently large shunt conductance will generate oscillation in the isolated cell.

A model for the oscillations in the IO, which relies on heterogeneity in the cells' conductance, has been investigated by Manor et al. (11). In that model, although the isolated cells do not oscillate, when they are strongly coupled they behave similarly to an isolated cell with average properties. This average cell is oscillatory. Thus similar to our model, oscillations in this case are present even for arbitrarily strong coupling. However, in the model of Manor et al., the internal variables lock in a unique fashion to the oscillating potential and therefore they oscillate in phase. In contrast, our mechanism does not rely on heterogeneity and on the existence of an oscillatory average cell. Instead, the oscillations emerge from the different phases in which the calcium variables of different cells lock to the common potential (Eq. 5). Another consequence of our mechanism is the multiplicity of stable oscillatory states in networks with strong electrical coupling.

The spontaneous organization of large homogeneous networks into clusters of synchronized oscillators as shown in Fig. 5 is similar to the behavior of certain neuronal networks with global inhibition (21, 22). The analogy between our system and global inhibition is transparent in light of Eqs. 4 and 5. These equations indicate that in the presence of strong electrical coupling the membrane potential acts as a global inhibitor on the local internal variables (because its feedback effect on is negative). This global negative feedback suppresses synchronized oscillations but is unable to suppress out-of-phase oscillations.

It is important to emphasize that although we have assumed in our model that the cells are identical, it is robust to the introduction of a weak heterogeneity, because it will not destroy the oscillatory nature of the internal variables and the negative feedback that the different cells exert on each other via the membrane potential.

The fact that our network has several stable states of voltage behavior, each of which can be generated by many different time courses of the internal variables, endows the system with unique properties that have significant functional consequences. Calcium, for example, plays a crucial role in many neuronal processes such as synaptic transmission and plasticity (23). A network of cells that exhibit similar voltage behavior and different calcium distribution may induce spatially segregated changes in membrane and synaptic conductance. Thus the electrical coupling may give rise to a rich repertoire of oscillatory states, which endows the system with interesting capabilities for processing and representing different stimuli.

The analysis presented in this work can be applied also to single cells that contain localized regions of high densities of calcium channels in their dendrites (24). Each of these cells can be viewed as a network of excitable elements coupled electrically by the dendrites. According to our theory this coupling may give rise to oscillations in the membrane potential and calcium concentrations of the cell. Furthermore, if the coupling between the active zones is strong the cell will have multiple stable oscillating states. In each of these states the membrane potential across the cell will be nearly uniform. However, the active zones will group into clusters where the oscillatory calcium concentrations of zones belonging to different clusters differ in their phases. The role of dendritic coupling in the calcium dynamics of single cells has been recently studied.¶

Several biological systems including the IO, the locus coeruleus, the β-pancreatic cells, and the aortic smooth muscle cells exhibit oscillations, which depend in some way on electrical coupling. The proposed mechanism may be applicable to some of these systems. However, in general, the origin of the instability of the internal variables may not necessarily be related to calcium dynamics. Elsewhere we have realized the proposed dynamic mechanism in a network of two-compartment neurons. One compartment is an excitable soma whose parameters play the role of the internal variables and a passive dendrite whose membrane potential plays the role of V. The isolated soma of the neurons is oscillatory but its interaction with the dendrite dampens these oscillations, yielding nonoscillating cells. Electrical coupling via dendro-dendritic gap-junction in this model leads to sustained oscillations via the same mechanism described here.‖ This may provide an alternative model for the oscillations in the IO.

Regardless of the specific realization of the internal variables, our proposed mechanism emphasizes the role of electrical coupling in exposing the inherent instability. Traditionally, electrotonic coupling was regarded as a nonmodifiable communications path, which generates inflexible networks. However, in the seventies, Llinas et al. (25–27) suggested that the effective electrical coupling, and the synchrony between IO cells could be modulated by GABAergic synapses from the deep cerebellar nuclei. The present work suggests that by changing the effective strength of the electrical coupling the cerebellum also can initiate and terminate the sub threshold oscillations.

A growing number of studies in recent years have demonstrated that electrical coupling in the central nervous system is far more common than was previously considered. It has been described in cortical (28) and cerebellar inhibitory neurons (29) as well as in the hippocampus (6) and locus coeruleus (5). In all these studies it usually has been assumed that electrotonic coupling serves as a synchronizing device, or as a fast excitatory pathway. In this work we suggest that in addition, electrical coupling can serve as a generator of oscillatory activity. Although one would expect that oscillatory activity that is associated with electrotonic coupling will be rather homogeneous, we showed that it does not decrease the flexibility of the network. On the contrary it furnishes it with a wide range of dynamic features.

Abbreviation

IO

inferior olive

The Calcium Dynamics Cell Model

The calcium dynamics in Eqs. 1 and 2 is: J(X,Y) = −V₂ + (V₃ + K_s) ⋅ Y with

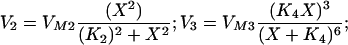K_s = 1 sec⁻¹; V_M2 = 50 μM/sec; K₂ = 0.2 μM; V_M3 = 600 sec⁻¹; K₄ = 0.69 μM. The parameters of J and K were taken from ref. 30 assuming that the inositol triphosphate concentration is constant and equal to 0.14 μM. The calcium efflux constant, K = 10 sec⁻¹ and φ = 9.221⋅10⁻³ μMcm²/(sec⋅nA) is the conversion factor from calcium current to change in cytosolic calcium concentration. For an appropriate regime of values of X and Y, the derivative of J(X,Y) with respect to X is positive, implying that X exhibits a positive feedback loop mediated by the calcium-induced calcium release. This positive feedback is terminated when the stores are depleted and the excess calcium is pumped out of the cell. The influx of calcium into the cell via voltage-dependent calcium current restores the necessary calcium for the next cycle. The currents in Eq. 2 are: I_leak = g_leak(V − V_leak); I_Ca = g_Cam_∞³h_∞(V − V_Ca); I_{K_Ca} = g_{K_Ca}σ(V − V_K) with

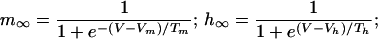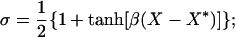with the parameters: V_leak = −55 mV; g_leak = 2,701 μS/cm²; V_m = −61 mV; T_m = 4.2 mV; V_h = −85.5 mV; T_h = 8.6 mV; V_Ca = 120 mV; g_Ca = 100 μS/cm²; β = 2.5 μM⁻¹; X^* = 0.4334 μM; V_K = −85 mV; g_{K_Ca} = 2,000 μS/cm², C = 1 μF/cm². The parameters of I_Ca were taken from in vitro measurements in the IO (11), assuming an instantaneous inactivation term.