Results Differ by Applying Distinctive Multiple Imputation Approaches on the Longitudinal Cardiovascular Health Study Data

Abstract

Objective

To examine sequential and simultaneous approaches to multiple imputation of missing data in a longitudinal dataset where losses due to death were common.

Method

Comparison of results from analyses and simulations of time to incident difficulty of activities of daily living (ADL) in the Cardiovascular Health Study when missing data were imputed simultaneously or sequentially.

Results

Results differed with imputation methods. The largest proportional differences in 12 risk factor parameter estimates were: heart failure by 106%, social support by 33%, and arthritis by 27%.

Conclusions

Decedents’ final characteristics were influential on future imputations of those with missing values.

Introduction

Missing data are a ubiquitous problem in longitudinal studies, especially those involving older adults. Study participants’ intercurrent health events and declines in functional status result in incomplete longitudinal data and death results in cessation of measurements (Hughs, et al., 1988; Masuda & Holmes, 1978; Murrel & Norris, 1984). Missing data can bias results, reduce power, and affect generalizability. Imputation of missing values in longitudinal datasets may be especially complicated since the missingness mechanism can vary over time (Rubin, 1976; Robins, et al., 1995; Youk, et al., 2004).

Over the past two decades, many new imputation methods for handling missing values have been developed; and corresponding statistical software has become available in many commercial computer languages, e.g., SAS procedures MI and MIANALYZE. In 2002, Twisk and de Vente published a comprehensive review of imputation methods as did Schafer and Graham (2002). Both papers reported a preference for the multiple imputation method. Following this, Harel et al. (2007) proposed a two-stage multiple imputation method to address incomplete data in the presence of mortality in aging studies. Two previous articles using the Cardiovascular Health Study (CHS) examined imputation methods for large datasets of older adults. Arnold and Kronmal (2003) used single and multiple imputation to replace missing values on approximately 150 variables collected at baseline where no death occurs yet and compared the modeling results obtained using the different approaches. Engels and Diehr (2003) evaluated 14 single imputation methods using the CHS longitudinal cohort of older adults. The present study extends these efforts by comparing two alternative multiple imputation methods (sequential and simultaneous)¹ for handling missing data using longitudinal data from the CHS.

The sequential approach imputes missing data for surviving participants temporally (year by year) removing participants after death. In contrast to the time ordering and exclusion of subjects after death in the sequential approach, the simultaneous approach like what Harel et al. (2007) used imputes all missing data together, including those post-death; then, before the analysis stage, all values imputed after a participant’s death are removed. In this study, we examined the risk factors for developing an ADL difficulty using discrete survival models with sequentially and simultaneously imputed CHS datasets. Our previous work has demonstrated the high prevalence of ADL difficulty and disability among CHS participants, and the importance of clinical, social, cognitive, and demographic factors in predicting decline in ADL status (Chaudhry et al., 2010). We compared the accuracy of imputed values between both imputation approaches using Engels and Diehr’s (2003) simulation study design. Our simulation constructed pseudo “missing” values by setting the first valid observation that follows a missing value to “missing”, and then imputed these using the sequential and simultaneous imputations. Thus, we were able to compare imputed values to values that were actually observed.

Methods

Data

CHS is a population-based longitudinal study, originally designed to identify risk factors for coronary heart disease and stroke in adults aged 65 years or older. In 1989, an original cohort of 5,201 participants was recruited, and in 1992-1993 a supplemental cohort of 687 African Americans was added to the study to enhance minority representation. All participants provided informed consent and the study protocol was approved by the institutional review boards at each of the participating centers. The CHS cohort has been described in detail in previously published reports (Fried, et al., 1991; Tell, et al., 1993).

In this study, we used the first 6 years of follow-up data (Visits 1 to 7) from each cohort, which included all of the annual clinic visits for the African American cohort and the first 6 follow-ups for the original cohort. Both imputation approaches were performed separately for the original and African American cohorts and the resulting data sets were combined for the analyses of health and functional outcomes.

After imputing the data, we used discrete survival models to study the risk factors associated with time to the first incident difficulty of ADL functioning for each imputation method respectively. The variables used in the regression analyses were:

Outcome variable

The outcome was time to the first report of any ADL difficulty: walking around the home, getting out of bed, eating, dressing, bathing or using the toilet, among participants free of difficulty at baseline.

Predictor variables

The predictors used in this study included: (1) congestive heart failure (CHF), coronary artery disease (CAD: angina or myocardial infarction), and stroke: these were ascertained based on self reports of hospitalizations and other acute events and medical records obtained and adjudicated by committee as previously described (Ives, et al., 1995); (2) social support (dichotomized): a series of 6 questions on participant’s perception on how well they are supported (e.g., “If I feel lonely, there are several people I can talk to.”). Each question was coded as: 1=definitely true, 2=probably true, 3=probably false, 4=definitely false, so higher scores indicate less support. We then dichotomized the total score for the 6 questions as: 1 if social support score was equal to 6 (maximal support), 0 if the score was between 6 and 24; (3) modified Mini Mental State Exam (3MS) (Folstein, et al., 1975; Teng & Chui, 1987) and Digital Symbol Substitution Test (DSST) (Lubben, 1988) scores were used to measure cognitive function. The 3MS is an expanded version of the Folstein Mini Mental State Exam, it incorporates four additional test items (date and place of birth, word fluency, similarities, and delayed recall of words), and expands the range of scores from 0-30 to 0-100 with higher score reflecting better functioning. The DSST explores attention and psychomotor speed. The final score is the number correctly completed in 90 seconds; thus higher scores reflect better performance; (4) diabetes: participants were considered diabetic if they reported a physician diagnosis of diabetes mellitus; had fasting serum glucose greater than 126 mg/dl; had a serum glucose of at least 200 mg/dL 2 hours following the oral glucose tolerance test; or reported use of diabetic medications; (5) arthritis: assessed using self-report of a physician-reported diagnosis; and (6) demographic covariates: education (less than high school vs. high school and above), race (non-white vs. white), sex, and age (in 5-year categories).

Types of Missing Data

In general, the mechanisms of missingness are distinguished into three types: missing at random (MAR), missing completely at random (MCAR), and missing not at random (MNAR) (Rubin, 1976, 1996).

Missing data are said to be MAR if the probability of missingness depends on the observed variables but not on missing characteristics. It implies that the observed data can be used to accurately predict the missing values for MAR data. The methods for handling missing values (e.g., maximum likelihood and multiple imputation) can therefore be used to avoid bias in parameter estimates and loss of statistical power that can occur when using a complete case analysis assuming MAR is true (Schafer & Graham, 2002; Hardy, et al., 2009).

MCAR is a special case of MAR when the probability of missingness does not depend on either observed or missing data. When missing data are MCAR, parameter estimates from complete case analyses will be unbiased.

Missing data are MNAR if the probability of missingness depends on the value of the outcome (Schafer & Graham, 2002). When missing data are MNAR, the mechanism of missing data must be modeled (Van Ness, et al., 2007).

We used Little’s test to examine whether data are MCAR. Little’s test is a Wald-type Chi-square statistic (χ²(1)), which tests the null hypothesis that missingness is MCAR versus the alternative hypothesis that missingness is not MCAR. Little’s test is carried out by dividing respondents into those with and without missing data and testing whether the key variables in these two groups differ significantly. An insignificant p-value of Little’s test is interpreted to mean that the missing data may be assumed to be MCAR (Little, 1988; Van Ness, et al., 2007). Regarding tests for MAR, Troxel’s index of sensitivity to non-ignorability (ISNI) was used to test whether missing values are randomly distributed (i.e., ignorable) across observations. ISNI uses a non-ignorability parameter (γ) that measures the extent to which the probability of a given observation being observed depends upon the given data, including values that are actually missing. When this parameter (γ) is equal to zero, then the missing values are interpreted to satisfy this MAR assumption. A second crucial parameter for calculating the ISNI is the model parameter whose sensitivity to non-ignorability is being assessed. The ISNI is simply the extent to which an estimate of this regression coefficient, for a given non-ignorability parameter (γ), depends on possible values for this parameter (γ) (Troxel, et al., 2004; Ma, et al., 2005; Van Ness, et al., 2007).

Imputation

Except for fixed demographic variables (e.g., gender and race), the values of variables recorded longitudinally (e.g., number of difficulties of ADL) may change over a 6 year period and are subject to right-censoring (e.g., death or drop-out). Two sets of variables were imputed separately. One set included psycho-social, cognitive, and functional variables: social support, 3MS, DSST, and number of difficulties of ADL with covariates of depressive symptoms, hearing impairment, vision impairment, self-reported health, and age; the other set included disease related variables of CHF, diabetes, CAD, arthritis, and stroke with covariates of weight, general health condition, and age. These two sets of variables were chosen based on the correlation analyses of baseline CHS variables by Arnold and Kronmal (2003). By imputing these correlated factors separately, we overcame computational limitation faced with large longitudinal datasets.

Sequential Multiple Imputation

In the sequential approach, we imputed the missing values of the 1^st annual follow-up using information from both the imputed baseline and the 1^st follow-up. We imputed the missing values of the 2^nd annual follow-up using information from the imputed baseline, the imputed 1^st follow-up, and the 2^nd follow-up. This imputation process was repeated until the 6^th annual follow-up. Participants who died between yearly follow-up interviews were not included in subsequent yearly imputations because imputing values for the deceased has been considered inappropriate (Greenland & Finkle, 1995; Little & Rubin, 2002). The sequential strategy retains the temporal-order of the longitudinal data and avoids retention of decedents in data imputations.

Simultaneous Multiple Imputation

In the simultaneous approach, we combined the observations of seven time waves into one data set, and then imputed all missing values of different follow-ups together for both non-decedents and decedents. To identify whether the missing value was the result of dying before the observation time, we added a death indicator variable for each participant at each follow-up in the simultaneous imputation. Simultaneous imputation is a method that is frequently used for cross-sectional data where the missingness is not due to death. When applying a simultaneous method to longitudinal data, missing observations after a participant’s death are first imputed with those before death, and then omitted before the analyses. For example, suppose that a subject was missing the ADL measure at year 3 and died before year 6, we used ADL measures from years 1, 2, 4, and 5 to impute the ADL missing at year 3 and post-death at years 6 and 7; then these post-death imputed ADL at years 6 and 7 were deleted prior to analysis. The simultaneous approach requires fewer imputations in a longitudinal data set, so would be easier to implement. We wanted to explore whether or not this simpler approach, that did not consider the sequential nature of the data and did not exclude participants who had died would provide similar results to the more complex sequential approach.

Multiple Imputation Technique

To implement the two multiple imputation approaches, we used SAS (version 9.1.3) PROC MI. Sex, race, and age were ascertained at baseline on everyone and CHF, CAD, and stroke were not imputed as the study has complete ascertainment of prevalent conditions at baseline, and of incident events throughout the CHS study. Because the missingness pattern of CHS data is not monotone, missing ordinal and continuous variables were both modeled from a multivariate normal distribution, thus, as continuous variables using the Markov Chain Monte Carlo (MCMC) method. Rounding if necessary was performed after imputation as done in Arnold and Kronmal (2003). Previous work has shown that the MCMC method is quite robust for modeling ordered categorical and indicator variables as from a multivariate normal distribution (Schafer & Graham, 2002). Since the original and African-American cohorts were collected at different times, we imputed the two cohorts separately.

Sensitivity Analysis on the Number of Imputed Datasets

There are no guidelines regarding the number of imputations required in a multiple imputation process. In practice, Horton and Lipsitz (2001) suggested that the appropriate number of imputations can be informally determined by carrying out replicate sets of m imputations and determining whether the parameter estimates are stable between sets. Thus, for testing the robustness of parameter estimates, we first generated 50 imputed datasets using the sequential and simultaneous multiple imputation, respectively. Subsequently, we applied SAS 9.1.3 PROC MIANALYZE to summarize replicate parameter estimates and obtained standard errors.

Cox’s Hazards Regression Analysis

A discrete survival model was used to analyze time to the development of a first incident ADL difficulty after baseline. The predictor variables of interest were CHF, social support, DSST, 3MS, diabetes, CAD, arthritis, and stroke. All of these were time-dependent measures. We also controlled for demographic factors of education, sex, race, and age.

Simulation Study

We followed Engels and Diehr’s (2003) simulation method to examine the performance of the two multiple imputation approaches. We calculated four summary measures from the two imputations according to Engels and Diehr (2003). The first measure is the root mean square deviation (RSMD) defined as:

$$\mathrm{RMSD}={(\Sigma {(y-\widehat{y})}^2∕n)}^{1∕2}$$

where y is the true value, $\widehat{y}$ is the imputed value, and n is the number of pseudo “missing” values. The second measure is the mean absolute deviation (MAD) defined as:

$$\mathrm{MAD}=\Sigma \mid y-\widehat{y}\mid ∕n$$

Both the RMSD and MAD are used to measure the accuracy of the imputed values compared to the true values. The third measure assesses standardized bias and is defined as:

$$\mathrm{SBIAS}=\left(\Sigma \right(y-\widehat{y})∕n)∕\mathrm{SE}\left(\widehat{y}\right)$$

and the last measure is the proportionate variance (PV) defined as:

$$\mathrm{PV}=\text{Var}\left(\widehat{y}\right)∕\text{Var}\left(y\right)$$

This assesses how well the imputed values preserve the variance of the true values. We used four longitudinal variables – ADL, 3MS, DSST, and social support – to compare the different imputation approaches as each variable had 200 or more missing values.

Results

The CHS cohort consisted of 5,888 participants, 4,404 had no difficulty in ADL at baseline. The amount of missing data ranged from 0 to 189 participants at baseline, and from 0 to 1301 at the 6^th annual follow-up. Deaths occurring during the intervening years accounted for at least 18, 25, 31, 33, 39, and 44 percent of the missing data (e.g., DSST) in the 1^st through the 6^th annual follow-up, respectively. Table 1 presents the number of observed and missing data points for the original and African American cohorts over time.

Table 1.

Amount of Observed and Missing Data for each of Annual Interviews

Covariate1		Baseline		1st follow-up		2nd follow-up		3rd follow-up		4th follow-up		5th follow-up		6th follow-up
	Total	5888		5773		5644		5480		5301		5099		4868
	Cohort	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA
		5201	687	5101	672	4988	656	4849	631	4694	607	4521	578	4316	552
	Death	0	0	100	15	113	16	139	25	155	24	173	29	205	26
ADL	Total	5878		5410		5127		4943		4499		4316		4269
	Cohort	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA
		5192	686	4856	554	4610	517	4396	547	3985	514	3835	481	3823	446
	Missing 2	9	1	245	118	378	139	453	84	709	93	686	97	493	106
Social	Total	5870		5470		4660		4391		3985		0		416
Support3	Cohort	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA
		5183	687	4896	574	4660	0	4391	0	3985	0	0	0	0	416
	Missing	18	0	205	98	328	0	458	0	709	0	0	0	0	136
DSST	Total	5699		5249		4899		4588		4133		3887		3567
	Cohort	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA
		5067	632	4737	512	4431	468	4142	446	3721	412	3499	388	3215	352
	Missing	134	55	364	160	557	188	707	185	973	195	1022	190	1101	200
3MS	Total	5768		5429		5107		4785		4393		4192		3839
	Cohort	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA
		5082	686	4865	564	4584	523	4285	500	3921	472	3751	441	3443	396
	Missing	119	1	136	108	404	133	564	131	773	135	770	137	873	156
Diabetes	Total	5882		5576		5585		5442		5271		5068		4850
	Cohort	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA
		5198	684	4906	670	4930	655	4812	630	4664	607	4490	578	4298	552
	Missing	3	3	195	2	58	1	37	1	30	0	31	0	18	0
Arthritis	Total	678		5377		5271		5365		5230		5045		4836
	Cohort	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA	Original	AA
		0	687	4706	671	4615	656	4734	631	4623	607	4467	578	4284	552
	Missing	0	0	395	1	373	0	115	0	71	0	54	0	32	0

¹CHF, CAD, and stroke had no missing values

²Missing counts the non-decedent missingness only.

³There is no imputation for non-observation. e.g., there is no imputed value for the social support variable in African American cohort from the 2nd to 5th follow up, as this was missing by design.

⁴DSST has the largest % of missing from non-decedents for each wave of interviews: 3%, 10%, 15%, 19%, 28%, 31%, and 36%.

Results of Missing Data Examination

Prior to imputing the missing data, we performed Little’s test and Troxel’s ISNI for examining the missing data pattern in each of 7 yearly interviews. The results are shown in Table 2. The ignorability assumption based on MAR was not rejected (all of the Troxel’s ISNI values were less than 0.5) while the assumption of MCAR was rejected (each year’s missingness pattern goodness of fit χ² statistics of Little’s tests was rejected at the 0.05 level).

Table 2.

Missing Data Tests for MCAR and MAR from Year 1 to Year 7

	Year 1	Year 2	Year 3	Year 4	Year 5	Year 6	Year 7
X2	8829	6067	9891	9334	11659	6856	8595
p(X2)	<.001	<.001	<.001	<.001	<.001	<.001	<.001
MCAR1	No	No	No	No	No	No	No
β	0.28	0.45	0.52	0.33	0.27	0.50	0.40
SE(β)	0.015	0.019	0.023	0.02	0.025	0.03	0.031
τ	0.19	0.3	0.39	0.35	0.46	0.66	0.72
ISNI	<.001	<.001	<.001	0.006	<.001	<.001	0.008
MAR2	Yes	Yes	Yes	Yes	Yes	Yes	Yes

¹MCAR: missing completely at random is rejected when p( Χ² ) < 0.05.

²MAR: missing at random is rejected when ISNI > 0.5.

Results of Sensitivity Analysis

We examined the parameter estimates of the survival models using 3 to 50 imputations. Although there was no apparent monotonic trend in parameter estimates over all of the different numbers of imputations for both multiple imputation approaches (results not shown), we found that the discrepancy of estimates for each parameter obtained between 10 and 20, 30, 40 or 50 imputed datasets was less than 10% (i.e., sd(β)/mean(β)<0.1). However, there were discrepancies of ≥ 10% for at least one parameter obtained between 3 and 10 imputed datasets. Thus, our parameter estimates were based on combined results from 10 imputations for each method.

Results of Cox’s Hazards Regression Analysis

There were an average of 244 more cases of incident ADL difficulty events in the simultaneous imputation dataset than the sequentially imputation datasets. To contrast the estimation results obtained from the survival models between the sequential and simultaneous imputations, we compared the % change in parameter estimates (i.e., ∣simultaneous estimate-sequential estimate∣/simultaneous estimate) and the minimum, median, and maximum correlation coefficients between ADL difficulty and the covariates for survivors over the 6-year period. We also compared the minimum, median, and maximum correlation coefficients between ADL difficulty and covariates for decedents at their last visit during the 6-year period. The results of these comparisons are presented in Table 3. The largest difference between simultaneous and sequential imputations was seen in the effect of CHF (106%; 0.159 vs. 0.327) on the first incident ADL difficulty, followed by education (102%; −0.045 vs. 0.001), social support (33%; −0.234 −0.311), and arthritis (27%; 0.677 vs. 0.494). The remaining differences were less than 20%.

Table 3.

The Percentage Change in Parameter Estimates of the Discrete Survival Regression on Time to Incident DL Difficulty from Sequential Imputation Model to Simultaneous Imputation Model

Covariate	Sequential Coefficient	Simultaneous Coefficient	% Change1	Correlation with ADL for Survivors2	Correlation with ADL at Last Visit for Decedents3
CHF	0.159	0.327	105.66	.09 (.08, .10)	.10 (.01, .21)
Social Support	−0.234	−0.311	32.91	−.03 (−.03, -.04)	−.12 (−.21, .04)
DSST	−0.434	−0.369	−14.98	−.10 (−.11, -.09)	−.15 (−.25, .01)
3MS	−0.411	−0.488	18.73	−.11 (−.12, -.07)	−.23 (−.29, -.07)
Diabetes	0.458	0.526	14.85	.07 (.03, .09)	.08 (−.07, .17)
CAD	0.209	0.218	4.31	.06 (.05, .06)	.08 (−.10, .13)
Arthritis	0.677	0.494	−27.03	.15 (.14, .17)	.17 (.11, .23)
Stroke	0.576	0.637	10.59	.11 (.08, .14)	.12 (.04, .17)
< High School	−0.045	0.001	102.22	.05 (.03, .08)	.10 (−.11, .19)
Non-white	0.179	0.191	6.70	.08 (.05, .10)	.04 (−.04, .08)
Female	0.421	0.346	−17.81	.06 (.05, .09)	−.03 (−.12, .22)
Age	0.276	0.275	−0.36	.10 (.08, .11)	.18 (.05, .21)

¹Percentage change is obtained from (the simultaneous estimate – the sequential estimate) / (the sequential estimate).

²The entry of correlation with the incident ADL difficulties for survivors is the median (min, max) of correlation coefficients for all 7 visits using non-imputed data.

³The entry of correlation with the incident ADL difficulties for decedents is the median (min, max) of correlation coefficients for the last visit prior to death during 6 years using non-imputed data.

For decedents, the median correlation between incident ADL difficulty and covariates at the last visit was greater than the median correlation between incident ADL difficulty and covariates for survivors over 6 annual follow-ups with respect to all covariates except race and sex. For example, a higher DSST score was correlated with fewer ADL difficulties. However, the correlations were stronger at the last visit among decedents. This stronger relationship would be carried forward in simultaneously imputed data because decedents remain in the imputation process. This correlation would induce the imputation of fewer ADL difficulties (better function) in the presence of high DSST. The difference in parameter estimates could be due to the greater correlation found for decedent’s final observed value. Among covariates with missing observations over follow-ups, DSST had the greatest amount of missing observations among survivors.

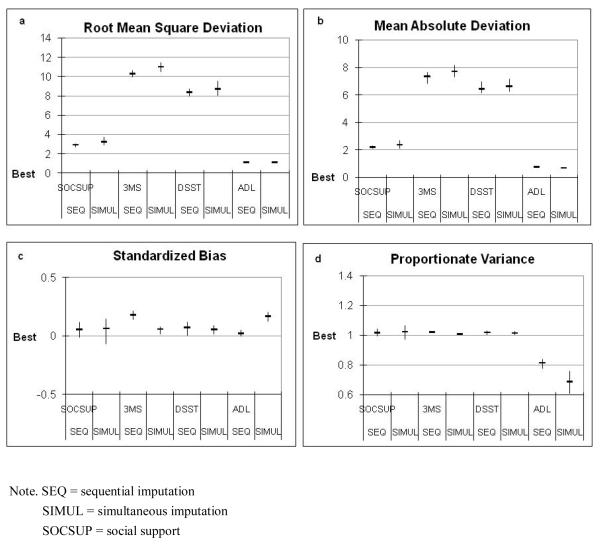
Results of Simulation Study

The average and range of RMSD, MAD, SBIAS, and PV measurements over ten replicates using two multiple imputations are displayed in Figures 1(a) – 1(d), respectively. A smaller positive number of the RMSD or MAD indicates a better accuracy of imputed values. Figure 1(a) shows that for all four variables the sequential method had the smaller average RMSD with a tighter range than the simultaneous method. Likewise, the sequential method had nearly equal or smaller average MAD with similar ranges compared to the simultaneous method. For Figure 1(c) a zero value indicates no bias of estimation. The sequential method had the smaller average and range of SBIAS for social support and ADL, but the greater average and range of SBIAS for 3MS and DSST than the simultaneous method. According to Engels and Diehr (2003), the PV measures each method’s effectiveness in preserving the variance of the true values. A PV of 1 implies that the variance of the imputed values was equal to the variance of the true values. Figure 1(d) shows that the sequential method had similar performance to the simultaneous approach in preserving the variance of the true values for social support, 3MS, and DSST while it underestimated the variance of true ADL values but was closer to one than the simultaneous approach and had a tighter range.

Figure 1.

Results of Simulation Study for Two Imputation Methods

Note. SEQ = sequential imputation SIMUL = simultaneous imputation

Discussion and conclusions

In the present study, we compared the regression results of a multivariable discrete survival model of time to the first incident ADL difficulty for which missing data were imputed, using sequential and simultaneous approaches respectively, in a longitudinal CHS cohort. We found important differences in several of the regression estimates obtained from two imputed datasets (e.g., 106% change in CHF, 102% change in education, and 33% change in social support; see Table 3). Researchers usually assume that missing values are non-informative. For decedents, the differences found between two multiple imputation methods suggest that cessations of observations due to death may differ from non-responses of those who remain alive. Although the simultaneous imputation allows interpolation of a missing value that Engels and Diehr (2003) found to be better than using only prior history, the advantage of ‘before and after data’ imputation approach did not hold for our study where decedents’ final observations may be unduly influential in the imputation process. The worsening health and increasing likelihood of ADL difficulty measured in the last year of life of decedents were used in the simultaneous imputation process for survivors and resulted in assigning more ADL difficulty. In the simulation study, unlike the other three tested variables (social support, 3MS, and DSST), ADL had meaningfully lower PV and higher positive standardized bias for the simultaneously imputed data. This reflects the fact that as deaths accumulate over time, the proportion of those with ADL difficulty prior to death increases and has more influence on the imputation of the survivor’s missing data.

In a recent paper on the CHS data, Kurland, Johnson, Egleston, and Diehr (2009) pointed out the limit of suitability of mixed models, which may implicitly impute data beyond death, in the analysis of longitudinal data with great imbalance due to death. Our results support their conclusion. However, because ADL status is highly associated with time to death and it makes time to incident ADL difficulty more sensitive to decedents remaining in imputation, the results of the present study may not be necessarily generalized to other outcomes that are less related to death. Yet, many if not most geriatric impairments and health conditions are likely to be related to death and still remain understudied (Murphy, et al., 2011). The present study provides evidence that the sequential method outperformed or was equivalent to the simultaneous method on most measures of accuracy and bias, and that natural declines observed prior to death may exert undue influence on imputed values for survivors in the simultaneous approach.

In summary, when decedents remain in the imputation process after their death, their final ADL status and other characteristics were influential on future imputations of those non-decedents with missing values. Our results demonstrate that the choice of imputation methods could lead to different conclusions about the risk factors of incident ADL difficulty. It may be that some combination of approaches (e.g., backward sequential imputation with full information maximum likelihood estimates of the covariance matrix) would improve analytic performance. Until such an approach is evaluated, our recommendation is to use the sequential approach for imputing missing data in longitudinal analyses when mortality is significant.