Steady-State Indicator of Intracranial Pressure Dynamic System using Geodesic Distance of ICP Pulse Waveform

Abstract

Normal functioning of the brain depends on the homeostasis (~ steady state) of its various physiological sub-systems, one of which is the intracranial pressure (ICP) dynamic system. ICP dynamic system of an injured brain is susceptible to various acute changes that should ideally be detected by ICP monitoring even for comatose patients. However, the status quo of ICP monitoring solely targets mean ICP. We aimed to demonstrate a novel approach to detect acute deviation from steady state of an ICP dynamic system in an absence of significant mean ICP changes. We hypothesized that steady state of ICP dynamic systems is reflected as ICP pulses of similar mean ICP levels resembling each other. A general framework was used to derive such a steady-state indicator that can accommodate different metrics of inter-pulse distance and different statistics of the distance histograms. In addition to conventional Euclidean distance and Pearson correlation, geodesic distance between pulses was introduced as a novel metric. These different ways of calculating steady-state indicators under the proposed framework were evaluated on three types of continuous ICP recordings: 1) those between two consecutive brain imaging studies that demonstrated acute ventricular enlargement for slit ventricle syndrome (SVS) patients undergoing a trial of shunt externalization and clamping (SVS+); 2) those between consecutive brain imaging studies from the SVS patients under the same trial but without ventricular enlargement (SVS−); 3) overnight recordings from patients with suspected normal pressure hydrocephalus (NPH). It was observed that only the standard deviation of geodesic distance correctly differentiated between SVS+ and SVS− and between SVS+ and NPH while avoiding discriminating between SVS− and NPH. It was also found that 45% SVS+ cases had a multimodal geodesic distance histogram while none of SVS− and 3.8% of NPH cases had such a multimodal histogram. Pulses with a large number of distant pulses for the five multimodal-histogram SVS+ cases fell in short time windows indicating that acute ventricular changes may have occurred in these confined time windows during which no significant changes of mean ICP were observed. In contrast, the pulses with a large number of distant pulses for the two multimodal-histogram NPH cases did not cluster temporally. In conclusion, the geodesic inter-pulse distance is a promising metric to quantify distance intrinsic to the underneath geometric structure of ICP signals and hence is an appropriate metric to derive a steady-state indicator of an ICP dynamic system.

1. Introduction

Disorders afflicting the brain can perturb homeostasis of cerebral perfusion, cerebral metabolism, and neuroelectrical activities. For a clinician caring for an afflicted patient in the acute period of traumatic brain injury (TBI), subarachnoid hemorrhage (SAH), and hydrocephalus, proper management ideally entails early detection of developing alterations from equilibrium. This is particularly challenging in comatose patients, in which there may be a paucity of clinical indicators and restricted availability to obtain imaging diagnostic tests. Using the terminology of systems engineering, in a normal healthy state various functional and anatomical sub-systems of the normal brain are in steady state. Early detection of deviation from steady state of these systems could theoretically facilitate recognition of pathological changes of the brain prior to crisis states. In the present work, we will focus on developing such a steady-state indicator for the intracranial pressure (ICP) dynamic system.

Our approach is motivated based on a first-order approximation of the ICP dynamic system using a pressure-volume (PV) curve. The concept of PV curve for the ICP dynamic system has been used widely to derive the brain compliance, which is the slope of a PV curve, and to interpret the phenomenon that ICP pulse waveform amplitude increases as mean ICP increases(Avezaat et al., 1979, 1980; Czosnyka et al., 2004). Conceptually, an ICP dynamic system in steady state can be represented using a single PV curve as illustrated in Fig. 1 (Panel A). The operating point of the system for any given mean ICP corresponds to different points along this single PV curve. When brain structural alternations occur, a different PV curve will be established and therefore the operating point of system at a same mean ICP level would reside on the new PV curves as illustrated in Panel B of Fig. 1. Following this reasoning, ICP pulses at a similar mean ICP level resemble each other when the ICP dynamic system is in a steady state because they correspond to the same operating point of the ICP dynamic system. However, if the intracranial pressure dynamics change, the ICP pulse morphology will differ from the steady-state form assessed at the same mean ICP, reflecting a different operating point on the new PV curve.

Figure 1.

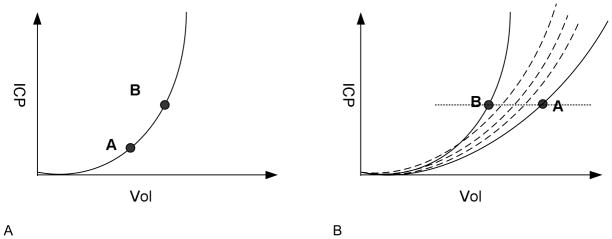
An illustration of the theoretical underpin of the proposed intracranial pressure (ICP) dynamic system steady state detection approach. Panel A displays a single pressure volume curve as a first-order approximation for an ICP dynamic system in a steady state. Points A and B on this curve have different mean ICP and hence different ICP pulse waveform amplitude and morphology. However, pulse amplitude and waveform morphology will be the same for a given mean ICP. In other words, individual pulses move along this curve as mean ICP oscillates in the form of B waves etc. Panel B shows an ICP dynamic system undergoing acute changes such that the system follows different pressure volume curves at different time points so that the pulses with same mean ICP will likely have different amplitude and waveform morphology because the system now jumps between different pressure volume curves. Therefore, a manifestation of the ICP dynamic system at steady state is that the ICP pulses at similar mean ICP resemble each other.

It follows from the above motivation that a steady-state indicator can be derived by characterizing diversity of the morphologies of ICP pulses at similar mean ICP levels. However, challenges always exist in analyzing ICP pulse waveform morphology for data recorded in a clinical environment because the inherent noise and artifacts can easily sabotage any effort to assess the pulse waveform morphology. Hence, our proposed strategy is to avoid assessing morphology of individual pulses on a beat-by-beat basis. Instead, we use a validated algorithm, termed Morphological Clustering and Analysis of Intracranial Pulse (MOCAIP)(Hu et al., 2009b), to extract artifact-free dominant pulses each of which is representative of a short recording interval of ICP. Such a strategy has been adopted by our group in many previous studies (Asgari et al., 2011a; Asgari et al., 2011c; Kasprowicz et al., 2010; Kim et al., 2011b). Once having extracted dominant ICP pulses, detecting morphological changes between waveforms is deceptively trivial, e.g., using the Euclidean distance between two pulses. We recognized, however, that this approach was insensitive to the low-dimensional geometric manifold where the time series of ICP pulses reside. Accordingly, we applied a novel distance metric, the geodesic distance, as a more powerful metric for measuring the inter-pulse distance. To our knowledge, the present work is the first in applying manifold learning(Roweis and Saul, 2000; Tenenbaum et al., 2000) concept in studying the ICP dynamic system.

2. Methods and Materials

2.1 Morphological Clustering and Analysis of Intracranial Pulse (MOCAIP)

The MOCAIP algorithm provides an automatic analysis of intracranial pulse morphology by designating the locations of three well-established sub-peaks in these pulses. This algorithm is able to cope with the practical issues such as handling noise and artifacts. MOCAIP starts by detecting individual pulses from a continuous raw signal using an algorithm developed in our previous work (Hu et al., 2009b). Consecutive sequences of these raw pulses are clustered to find the biggest cluster. The average pulse of this cluster is termed a dominant pulse. Then a library of validated reference pulses is used to recognize legitimate dominant pulses, and only these legitimate ones are further processed to detect candidates of sub-peaks. Finally, the distribution of the sub-peak positions in the same reference pulse library is leveraged to designate the candidate peaks to each of the three sub-peaks or a non-peak. In the present work, the MOCAIP algorithm is used on consecutive 30-second ICP segments to extract dominant pulse, determine whether the dominant pulse is legitimate, and then designate the sub-peaks of legitimate dominant pulses.

2.2 A general framework for deriving steady-state indicator

Figure 2 displays a general framework to calculate a steady-state indicator for a continuous ICP recording of certain duration. The key idea is that it is a necessary condition for ICP pulses at similar mean ICP level to resemble each other that the intracranial pressure dynamic system is at a steady state. Therefore, this framework is designed to accommodate different ways of characterizing the degree of similarity between two pulses given a matching mean ICP. It starts using the MOCAIP algorithm to form a series of dominant pulses for the given ICP recording. This pre-processing step is crucial in that it isolates the artifacts and noises in the ICP recording. Let us assume these pulses are denoted as x_i, i =1, 2,…, N. Then for each dominant pulse x_i, we find other pulses x_j which satisfy the following

Figure 2.

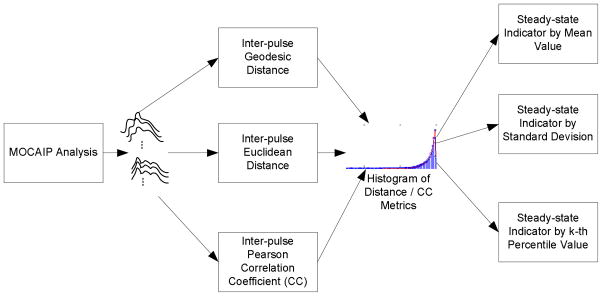
A general block diagram of an algorithm to derive steady-state indicator for the intracranial pressure dynamic system. This algorithm can accommodate different ways to characterize inter-pulse distance/similarity. In the present work, we evaluate geodesic distance, Euclidean distance, and Pearson correlation coefficient as three examples of such approaches. In addition, the proposed algorithm supports using different statistical metrics derivable from the distance histogram as steady-state indicator. The three metrics tested in the present work include mean, standard deviation, and 90^th percentile value.

$$\mid {\overline{x}}_i-{\overline{x}}_j\mid \le \mathrm{\Delta }\text{ICP},j\ne i$$

where x̄_i and x̄_j are the mean values of x_i and x_i, respectively.

We then calculate a similarity or distance measure between x_i and all x_j Repeating this calculation for all x_j, one obtains a long vector of similarity/distance metrics between pulses of matched ICP. The length of this vector is hence upper-bounded by N² In the present work, we will test the following three measures: 1) Euclidean Distance; 2) Pearson Correlation Coefficient; 3) Geodesic Distance. The first two metrics are trivial. The calculation of the geodesic distance will be described in next Section. It is noted that the pulses are required to have equal length for calculating the above three metrics. Given the variable heart rates, this is handled by first defining the end of the pulse to be at a point on the last descending edge of a pulse where its amplitude equals 1/e of the peak amplitude of the last peak. By this definition, the pulse length is smaller than that of the actual pulse length of each pulse. Then the final pulse for distance calculation is obtained by using the 95-percentile of this effective pulse length from all pulses in this ICP recording to extract a sub-segment from the original raw dominant pulse.

After obtaining distance metrics among all mean ICP matched pulses, a steady-state indicator can be calculated by different measures characterizing the distribution of these metrics. In particular, we will test the mean, the standard deviation, and 90^th percentile value as three different methods of deriving such an indicator. For Euclidean and geodesic distances, it is expected that the steady-state ICP will have a smaller mean and 90^th percentile values because ICP pulses resemble each other after matching the mean ICP. On the other hand, the metrics based on correlation coefficient will have a larger mean and 90^th percentile values. Irrespective of metrics used, the standard deviation of these metrics is expected to be smaller because a higher standard deviation will likely result from the analyzed ICP segment being a mixture of a steady state and a dynamical state.

2.3. Calculation of geodesic distance

In a strict mathematic term, geodesic distance is a generalization of length of a straight line connecting two points to that of a curve connecting the two points in a curved space. In the present work, each pulse x_i can be treated as a point in a high-dimensional Euclidean space. If assuming no geometric structures exist in the point cloud formed by pulses x_i, i =1, 2,… N, conventional Euclidean distance between two pulses can be used as distance metric. However, it has been well known since the publication of the two seminal papers(Roweis and Saul, 2000; Tenenbaum et al., 2000) that many seemingly high-dimensional data originating from the nature usually reside in a low-dimensional manifold. Revealing this low-dimensional manifold using nonlinear dimension reduction methods such as ISOMAP(Tenenbaum et al., 2000) and Local Linear Embedding (LLE)(Roweis and Saul, 2000) has been proven to be fruitful in visualizing the hidden geometrical structure of the data. There is no exception here for ICP pulses. As shown in Figure 3, we used LLE algorithm to project the original ICP dominant pulses from a subject onto a two dimensional space to reveal the geometric structure. Therefore, a more sensible measure of distance between two pulses should take into consideration of this geometric structure.

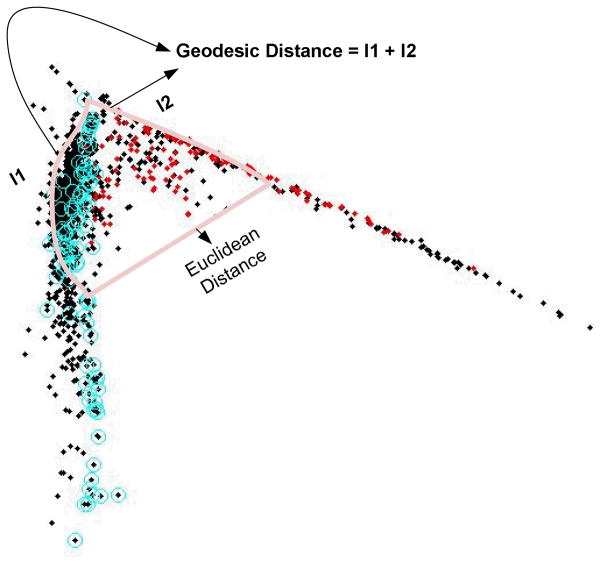
Figure 3.

A two dimensional projection of dominant ICP pulses using the local linear embedding (LLE) algorithm to illustrate the difference between Geodesic distance and Euclidean distance between two points on this two-dimensional trajectories. Each dot in this graph is a projection of the original pulse. It can be noted that the calculation of geodesic distance needs to follow the geometric structure of the data and hence may reflect the true distance between two pulses.

Geodesic distance is such a measure. As practiced in other related studies(Roweis and Saul, 2000; Tenenbaum et al., 2000; Cai et al., 2007; Zhu and Goldberg, 2009; Carter et al., 2011), we choose to approximate the calculation of geodesic distance by using a k-neighborhood graph. Assume a graph G (V, E) is used to describe x_i, i =1, 2,···, N where vertex V_i represents x_i and an edge is placed between V_i and V_j if x_i is among the k-nearest neighbors of x_i and we assign the Euclidean distance between x_i and x_j as the weight of this edge. This process is executed for all x_i to form the graph. After forming the graph, geodesic distance between any pairs of the pulses can be approximated by the total length of the shortest path along the graph linking the two vertices representing these two pulses. We used Dijkstra’s algorithm(Dijkstra, 1959; Cai et al., 2007) to find this shorted path. A graphic illustration of geodesic distance calculation is provided in Fig. 3.

2.4. Data source and data analysis protocol

A retrospective analysis of continuous ICP recordings from two patient populations was used to compare different methods of computing steady-state indicators as proposed in Section 2.2.

The first population consisted of a group of patients undergoing a diagnostic and therapeutic evaluation of symptomatic slit-ventricle syndrome (SVS). SVS patients typically have been shunted for many years, and have chronically very small (“slit”) ventricles with medically refractory headaches. Our protocol consisted of placing an intraparenchymal ICP monitor in the brain, and then externalizing the peritoneal end of the shunt so as to be able to completely shut off CSF flow(Bergsneider et al., 2008). In most patients, this resulted in acute hydrocephalus with expansion of the ventricles with or without marked changes in ICP. These patients either underwent an endoscopic third ventriculostomy or revision of the shunt. In other patients, the ventricles did not expand.

These SVS patients received multiple brain imaging assessments during these evaluations to assess ventricle size changes. This provided a controlled “laboratory” in which we could observe acute changes in the steady state due to acute ventricle volume changes over a period of hours. Based on the radiological reports of the consecutive imaging studies of these patients, we were able to establish which periods between two consecutive imaging studies were associated with observable ventricular changes. We assumed that the ICP recordings measured between these periods of ventricular change represented definitively change of the steady-state state. We use SVS+ to denote cases in this group. For those periods without evident acute ventricular changes or any brain structural changes, we assume that the ICP recordings in these periods were from a steady-state ICP dynamic system and denote them as SVS− cases.

In addition, we studied a cohort consisting of 56 elderly patients with suspected normal pressure hydrocephalus (NPH). Overnight continuous ICP monitoring was conducted as part of their NPH diagnosis evaluation prior to a 3-day lumbar drain trial in the hospital. Given the fact that NPH is a chronic condition that progresses over a period of months, we therefore assumed that the overnight ICP recordings of these patients were essentially acquired from a steady-state ICP dynamic system. Patients in both populations consented for the ICP monitoring and data analysis as approved by the UCLA Institute Review Board (IRB).

As proposed in Section 2.2, there are three distance/similarity metrics including geodesic distance, Euclidean distance, and Pearson correlation coefficient for comparing pulse shapes. In addition, three different steady-state indicators can be derived from the histogram formed by each of these distance/similarity metrics. Therefore, our data analysis experiment is set up to compare these nine different steady-state indicators among NPH, SVS+, and SVS− cases.

Mean ICP is a conventional measure used for routine diagnosis. We therefore also obtain the histograms of the mean ICP for the overnight recordings from NPH patients and those from the second patient population between consecutive brain imaging studies. In a similar fashion, we derive the mean, the standard deviation, and the 90^th percentile values from these histograms to compare the NPH, SVS+, and SVS− conditions.

A one-way analysis of variance was used first to see if each of the above 12 metrics was different among the three conditions. Then a t-test was used to compare each pair of the three case groups.

3. Results

Among the 32 pairs of consecutive brain imaging studies for the SVS patients, two cases were removed because of poor ICP pulse quality throughout the recording and four additional cases were excluded because the time interval between the two brain imaging studies was greater than 40 hours. The remaining 26 pairs were from 11 SVS patients. The mean age for these 11 patients (8 females) was 36 ± 16 years.

The number of cases with ventricular changes between two consecutive studies is 11. The mean duration of ICP recordings was 20.0 ± 6.8 hours for these positive cases and 20.6 ± 10.5 hours for the negative cases. The mean ICP was 7.1 ± 2.7 mmHg for the positive and 7.7 ± 2.3 mmHg for the negative cases. The mean standard deviation was 5.1 ± 2.8 mmHg for the positive and 6.7 ± 4.2 mmHg for the negative cases. There were 1929 ± 802 and 1915 ± 969 number of dominant pulses for the positive and the negative cases, retrospectively. The average time interval between two consecutive dominant pulses was 44.1 ± 33.5 seconds for the positive cases and 37.5 ± 4.5 seconds for the negative ones.

There were 20 female and 36 male patients in the NPH group. The average age for the NPH group was 72 ± 10 years. Mean duration of overnight ICP monitoring for the 56 NPH patients was 10.7 ± 2.4 hours. The mean ICP for these patients was 3.8 ± 3.8 mmHg. The mean standard deviation of these overnight ICP recordings was 2.9 ± 0.8 mmHg. The mean number of dominant pulses is 1122 ± 307 and the average time interval between two dominant pulses was 36.0 ± 12.6 seconds.

To obtain the results reported below, ΔICP has been chosen to be one mmHg to match mean ICP when deriving the steady-state indicators.

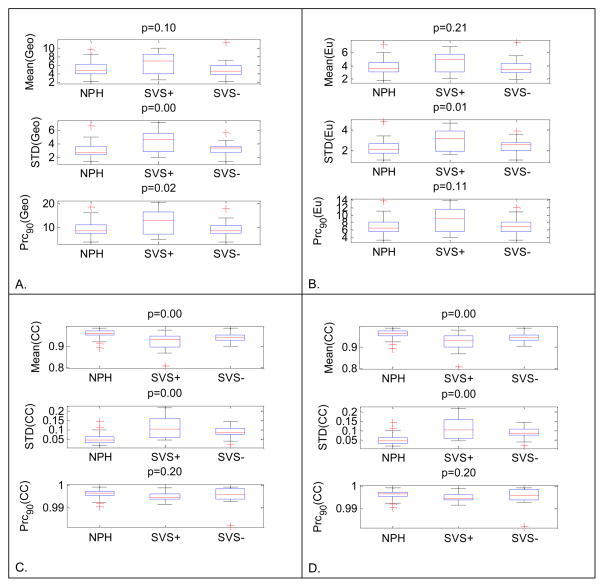
The results of twelve one-way analysis of variance experiments are shown in Fig. 4. We display the results of geodesic distance, Euclidean distance, Pearson correlation coefficient, and mean ICP in panels A through D, respectively. Each plot in each panel displays the result from using a particular statistical parameter of the distance histogram as a steady-state indicator. It can be seen that steady-state indicators based on the mean and standard deviation of the histograms of mean ICP, Pearson correlation coefficients, and geodesic distance achieved a significant p (p <0.05) for the ANOVA test while the steady-state indicators based on the standard deviation of geodesic and Euclidean distance also reached a significant p value.

Figure 4.

Twelve box-plots for one-way ANOVA group analysis of 12 different steady-state indicators in differentiating among NPH, SVS+, and SVS− groups. Geodesic distance, Euclidean distance, Pearson correlation coefficient, and mean ICP based results are displayed in panels A through D, respectively. In each panel, results from three different metrics are presented in a separate plot.

Since both SVS− and NPH cases represent a steady-state situation, the group analysis using ANOVA is not sufficient to 1) test if SVS+ cases can be separated from both SVS− and NPH cases; 2) if a steady-state indicator is different between SVS− and NPH cases. Therefore, we conducted three t-tests to compare these three groups in a pair-wise fashion. These results are reported in Table 1. We can observe that mean ICP steady-state indicators performed well in differentiating NPH from SVS+. Mean ICP was also different between SVS+ from SVS− groups (p = 0.041). However, mean and standard deviation of mean ICP histogram could also incorrectly differentiate between SVS− and NPH groups. Pearson correlation coefficient-based steady state indicators failed to differentiate between SVS+ and SVS−, incorrectly differentiated SVS− and NPH groups even though they could correctly differentiate between SVS+ and NPH. The Euclidean distance based approach did not incorrectly differentiate between SVS− and NPH groups but it also failed to differentiate between SVS− and SVS+ groups. The only steady-state indicator that could differentiate correctly between SVS+ and NPH/SVS− but also avoided discriminating between SVS− and NPH groups is based on the standard deviation of the geodesic distance(the second row in Table 1).

Table 1.

Table of p values from conducting t-tests comparing twelve different steady-state indicators for NPH vs SVS+, SVS + vs SVS −, and SVS vs NPH groups. It can seen that only the steady-state indicator based on the standard deviation of the Geodesic distance correctly differentiates between NPH and SVS +, SVS + and SVS - groups while avoids discriminating between SVS − and NPH.

Steady State Index		NPH vs SVS+ p	SVS+ vs SVS− p	SVS− vs NPH p
Geodesic Distance	Mean	0.014	0.086	0.515
	Standard Deviation	0.000	0.022	0.111
	90th Percentile	0.003	0.053	0.394
Euclidean Distance	Mean	0.036	0.127	0.493
	Standard Deviation	0.002	0.078	0.098
	90th Percentile	0.020	0.120	0.335
Pearson Correlation Coefficient	Mean	0.000	0.880	0.000
	Standard Deviation	0.000	0.844	0.000
	90th Percentile	0.000	0.907	0.000
Mean ICP	Mean	0.000	0.041	0.001
	Standard Deviation	0.000	0.081	0.000
	90th Percentile	0.032	0.442	0.094

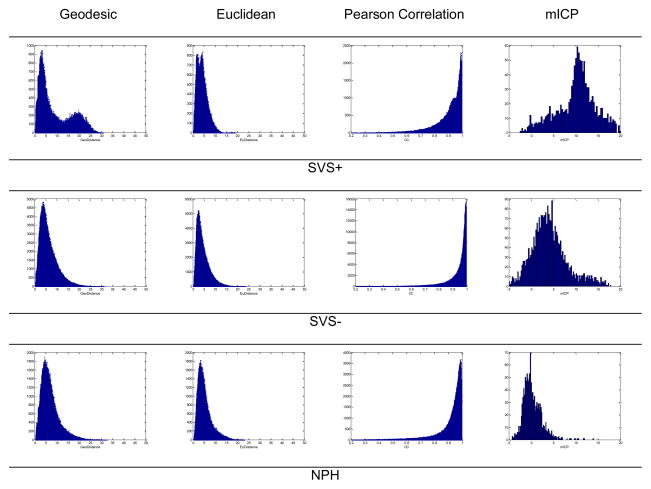
To assess the distributions of the four metrics including mean ICP, geodesic distance, Euclidean distance, and Pearson correlation coefficients, histograms of these metrics in one example case from each of the three case groups are presented in Fig. 5. It is clear by comparing these histograms that all three inter-pulse metrics of the SVS+ example have two peaks in their histograms while histograms of both NPH and SVS− groups have only one peak. However, the peaks in the histograms of the geodesic distance metric were better separated than those of the Euclidean and correlation coefficients. In contrast to this observation, histograms of mean ICP for all three cases had only one peak. It should be noted that this kind of multimodal histograms only existed for four additional SVS+ cases but it did not exist for any of the SVS− cases and only existed for 2 out of the 56 NPH patients.

Figure 5.

Histograms of the four metrics including inter-pulse geodesic distance, Euclidean distance, correlation coefficient, and mean ICP corresponding to one example from each of three groups SVS+, SVS−, and NPH, respectively. The appearance of multimodal histogram is a potentially strong marker of SVS+ group.

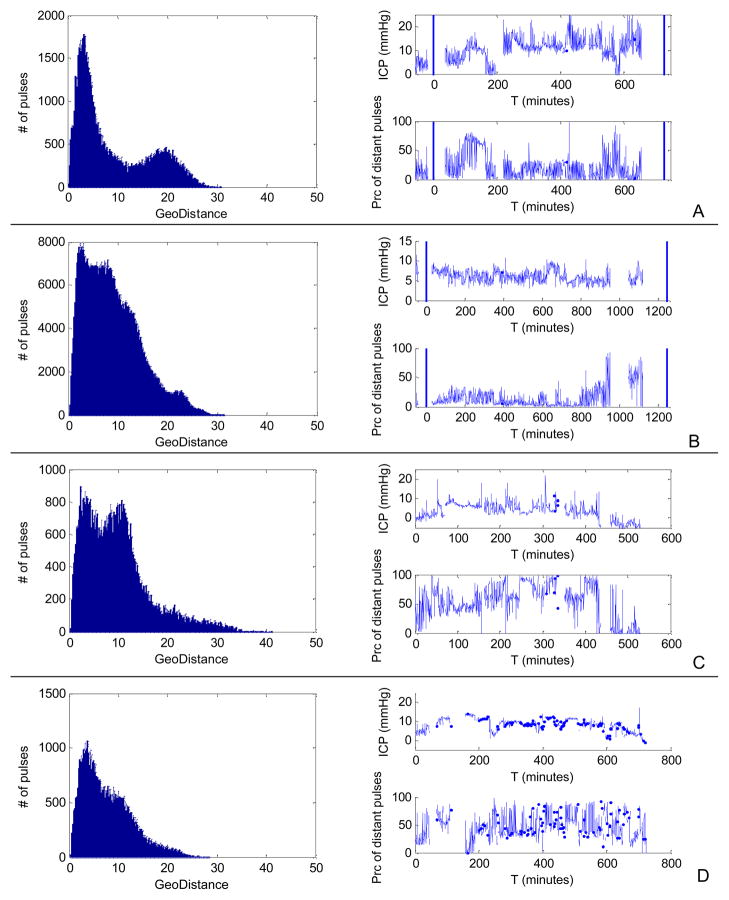
It was also found that the appearance of multimodal histogram of geodesic distance did not depend on the existence of abnormally high mean ICP as shown in Fig. 6 where we display histogram, mean ICP trend, and percentage of distant pulses (geodesic distance > 15 mmHg) for two SVS+ cases in panels A and B, and for two NPH cases (geodesic distance > 7 mmHg) in panels C and D, respectively. The two vertical lines in the time series plots indicate the time of brain imaging studies. We can observe that abnormally high mean ICP values were not present and that the periods of high percentage of distant pulses were confined in narrow temporal windows of approximately two hours long for the SVS+ cases but they are more scattered for the two NPH cases.

Figure 6.

Two SVS+ (A and B) and two NPH (C and D) cases with multimodal histograms of inter-pulse geodesic distance as examples to show that multimodal histogram of inter-pulse geodesic distance is not necessarily associated with abnormally high ICP. In addition to mean ICP trend, we also display the time series of the percentage of distant (geodesic distance > 15 mmHg for SVS+ and > 7 mmHg for NPH) pulses. For the two SVS+ cases, two vertical lines are used to show the timing of the two consecutive brain imaging studies. It is noted that there were localized periods when the ICP pulses had large number of distant pulses for the SVS+ cases. Such an observation is not held for the NPH cases. The two NPH cases shown here were also the only ones with multimodal histograms.

4. Discussion

A new approach is proposed in the present work to test the hypothesis that a consistent relationship between mean ICP and ICP pulse morphology is an indicator of an ICP dynamic system being at a steady state. We have shown that using standard deviation of the inter-pulse geodesic distances as a steady-state indicator was able to differentiate between SVS+ and NPH, SVS+ and SVS− and avoid discrimination between SVS− and NPH groups. Since it is a reasonable assumption that acute brain ventricular changes perturb the steady state of the ICP dynamic system that was present for the NPH and SVS− groups, our results hence demonstrate the effectiveness of the proposed approach to derive a steady-state indicator of an ICP dynamic system.

While a steady-state indicator based on conventional metrics including Euclidean distance and Pearson correlation coefficient was able to differentiate between NPH and SVS+ groups, this result alone is far from convincing to show that these two metrics can be used for detecting steady state of an ICP dynamic system. This is because both metrics failed to deliver a valid steady-state indicator capable of differentiating SVS+ and SVS−. Differentiating between SVS+ and SVS− groups, although more challenging, is also more clinically useful because continuous ICP monitoring can be leveraged using the proposed approach to detect deviation of the ICP dynamic system from a steady state, which can be used as a nonspecific harbinger for acute intracranial changes typically seen in brain injured patient under neurocritical care.

Although the comparison between SVS+ and SVS− groups helps demonstrate the superiority of using geodesic distance to measure inter-pulse distance as compared to Euclidean and Pearson correlation coefficient, one may argue that there was already a significant difference between mean ICP of these two groups (p = 0.041). This doubt can be cleared by two key observations. First, an even greater difference of mean ICP existed between SVS− and NPH groups, which are not unexpected given the fact that patients with suspected NPH and with slit ventricle syndrome are different in age, gender, the brain ventricular system, and plausibly the intracranial compliance state. However, in spite of such significant difference in mean ICP between these two groups, the steady-state indicator based on the geodesic distance still produced a valid result that treated the two groups as the same with regard to being a steady state. Second, the mean ICP trend for the SVS+ cases as shown in Fig. 6 did not show significant changes in terms of mean ICP, which would have failed to alert the clinicians that the ICP dynamic system of the patients was changing. To detect such changes, regularly scheduled brain scans had to be prescribed in the current standard of care.

The proposed approach of deriving a steady-state indicator of ICP dynamic system admits a general framework as proposed in Fig. 2. Within this framework, one novel element of our approach is the adoption of geodesic distance to quantify the similarity among ICP pulses. To the best of our knowledge, this is the first time that such a distance metric is used to analyze ICP pulses. It is likely that ICP pulse like many other naturally occurring signals is inherently low-dimensional. Exploiting the geometric structure in this low-dimensional space where ICP pulses reside is critical in developing metrics that can meaningfully quantify the distance between pulses. As has been done in many existing manifold learning algorithms, k-nearest neighbor (KNN) was used to construct a weighted graph to facilitate the approximation of geodesic distance using the shortest graph distance between vertices. Other approaches of constructing the graph remain to be studied in future work.

Standard deviation of the geodesic distance was found in the present work to be the best steady-state indicator. It should be noted that other metrics characterizing the distance histogram can be derived in future work. In particular, characterizing the multimodal distribution of inter-pulse distance as shown in Figs. 5 and 6 is a promising one. The existence of multiple peaks in the distribution of inter-pulse distance can be considered as a strong marker of a transient intracranial pressure dynamic system because each peak may represent a cluster of pulses from a steady-state period and the coexisting of these clusters may indicate that the system undergoes transition between different steady states. However, this statement should be considered speculative because two NPH cases also showed a multimodal distribution of inter-pulse geodesic distance. We could not ascertain the underlying causes of the existence of multimodal histograms for these two NPH patients given the retrospective nature of this study.

Although the present work has only studied the acute brain ventricular change, the same approach and data analysis experiment are applicable to investigating whether changes in the steady state of an ICP dynamic system can be detected when other forms of acute intracranial change occur. In neurocritical care of brain injury patients, such changes may include acute intracranial mass increase, massive edema, and acute hydrocephalus. If the proposed approach can be demonstrated to work in these conditions, the potential of extending ICP monitoring to brain injury patients susceptible to such acute changes is promising and significant as early detections and treatments of these conditions may result from continuously tracking a valid steady-state indicator of the ICP dynamic system.

Monitoring of mean ICP is useful for making patient management and therapeutic decisions by itself as conventionally practiced, however, recent studies across different groups have shown that more information with regard to brain compliance (Carrera et al., 2011; Kim et al., 2011a; Eide, 2006), cerebral blood flow (Hu et al., 2010a), prediction of acute mean ICP elevation (Hu et al., 2010b), cerebral vasculature status (Asgari et al., 2011b; Asgari et al., 2011c; Hu et al., 2009a), and autoregulation (Radolovich et al., 2011) can be further derived by analyzing the whole ICP pulse waveform using more advanced signal processing and pattern recognition techniques. The present work continues to add evidence supportive of such a potential in enhancing conventional ICP monitoring.

There are several limitations in the present work. The current approach of calculating a steady-state indicator cannot tell when the change starts to occur, which is a desirable feature for the monitoring purpose. In addition, the proposed approach in its current form will not be able to provide specific information regarding what types of acute intracranial changes are occurring. Obtaining such information is important to further provide decision support of managing those changes. This can potentially be obtained by combining other brain monitoring modalities and/or a more detailed ICP pulse waveform analysis, e.g., the elevation of the third sub-peak of an ICP pulse may indicate cerebral hypoperfusion(Hu et al., 2010a).

5. Conclusion

We have shown that a hallmark of an ICP dynamic system at a steady state is manifested as ICP pulses at similar mean ICP resembling each other. We have also demonstrated that geodesic distance is superior in measuring the inter-pulse distance to derive a steady-state indicator of the ICP dynamic system as compared to conventional metrics such as Euclidean distance and Pearson correlation coefficient. In addition, monitoring of the changes in the steady state of the ICP dynamic system can potentially provide more information than monitoring mean ICP alone. Further development of the approach to detect specific acute intracranial changes remains to be undertaken.