Measurement, Optimization, and Impact of Health Care Accessibility: A Methodological Review

Abstract

Despite spending more than any other nation on medical care per person, the United States ranks behind other industrialized nations in key health performance measures. A main cause is the deep disparities in access to care and health outcomes. Federal programs such as the designations of Medically Underserved Areas/Populations and Health Professional Shortage Areas are designed to boost the number of health professionals serving these areas and to help alleviate the access problem. Their effectiveness relies first and foremost on an accurate measure of accessibility so that resources can be allocated to truly needy areas. Various measures of accessibility need to be integrated into one framework for comparison and evaluation. Optimization methods can be used to improve the distribution and supply of health care providers to maximize service coverage, minimize travel needs of patients, limit the number of facilities, and maximize health or access equality. Inequality in health care access comes at a personal and societal price, evidenced in disparities in health outcomes, including late-stage cancer diagnosis. This review surveys recent literature on the three named issues with emphasis on methodological advancements and implications for public policy.

Despite spending more per capita on medical care than any other nation, the United States ranks behind other industrialized nations in key health performance measures (World Health Organization 2000). One major factor is the deep disparities in access to care and health outcomes. Maldistribution of the health care workforce leads to the “shortages amid surplus paradox” (Hart et al. 2002, 212). Disparities between races and between the haves and have-nots in health insurance lead to more than 100,000 excessive deaths each year (Physicians for Social Responsibility 2009). Enactment of the Patient Protection and Affordable Care Act will have enormous implications for the supply and distribution of health care providers and provide great opportunities for researchers, including geographers, on related issues.

The U.S. Department of Health and Human Services (DHHS) has implemented various programs including the designations of Medically Underserved Areas/Populations (MUA/P) and Health Professional Shortage Areas (HPSAs) for improving access to health care services for the underserved. The effectiveness of such programs relies on appropriate and accurate measures of accessibility so that resources can be allocated to the neediest areas. Recent advancements in this area have benefited from spatial analysis supported by geographic information systems (GIS) technologies. Many new methods have been developed to improve health care accessibility measures. These methods need to be integrated into one framework to reveal the connection among them and compare their advantages and weaknesses.

Most work uses optimization methods to site health care facilities to maximize service coverage, minimize travel needs of patients, limit the number of facilities, maximize health, or combine some of these goals. Equity in health and health care is widely accepted as an important goal of public policy. Among a diverse set of principles of equity, equal access to health care (for those in equal need) is considered the most appropriate principle for health care policymakers to pursue. Minimizing inequality in health care accessibility helps to identify the adjustments needed to close the gaps.

Inequality in health care access comes at a personal and societal price, evidenced in disparities in various health outcomes. Outcomes include differential rates in infant mortality and birth weight, vaccination, complications from preventive and common diseases, late-stage cancer diagnosis, and quality patient care and survival, among others. Cancer stage (based on tumor size and invasion) at the time of diagnosis plays a critical role in determining the prognosis of patients. This article uses the risk factors of late-stage cancer diagnosis as an example to examine the relationship between health access and outcomes.

This review surveys recent literature on these three closely linked issues with emphasis on methodological advancements. Due to limited space, only representative or the most recent literature is cited on an issue of discussion. The article attempts to synthesize related methods in existing work and identify room for improvements for future studies.

Health Care Accessibility Measures Synthesized

Accessibility refers to the relative ease by which services, here health care, can be reached from a given location. This article focuses on place accessibility, different from, although built on, the work on individual accessibility (Kwan 1998, 1999). Accessibility measures need to account for both spatial and nonspatial factors (Khan 1992). Spatial access emphasizes the importance of spatial separation between supply (i.e., health care providers) and demand (i.e., population) and how they are connected in space (Joseph and Phillips 1984) and thus is a classic issue for location analysis well suited for GIS to address. Nonspatial factors include many demographic and socioeconomic variables such as social class, income, age, sex, race, and so on, which also interact with spatial access (Meade and Earickson 2000, 389).

Spatial access is determined by where you are. A simple method measures spatial accessibility by the supply–demand match ratio in an area. For example, the DHHS (2008, 11236) uses a minimum population-to-physician ratio of 3,000:1 within a “rational service area” as a basic indicator for defining HPSAs. This neither reveals the detailed spatial variations within an area unit (e.g., a county or a subcounty area) nor accounts for interaction between population and physicians across areas, however.

Among others, the gravity-based accessibility model considers interaction between supply and demand located in different areas and has been applied in studying health care access (Joseph and Bantock 1982) and other areas, such as job access (Shen 1998). Accessibility at location i (A_i) is written as

$${\mathrm{A}}_i=\sum _{j=1}^n\left[S_j{d}_{\mathit{ij}}^{-\beta }∕\left(\sum _{k=1}^m{P}_k{d}_{\mathit{kj}}^{-\beta }\right)\right]$$ (1)

where P_k is population at location k, S_j is the capacity of the health care provider (e.g., number of doctors or hospital beds) at location j, d is the distance or travel time between them, β is the travel friction coefficient, and n and m are the total numbers of physician locations and population locations, respectively. It is essentially the ratio of supply (S) to demand (P), each of which is discounted by a distance factor. Although conceptually advanced, the model is not intuitive or transparent to public health professionals. Moreover, its distance friction parameter β requires additional data and work to define and might be region specific (Huff 2000).

Luo and Wang (2003) developed the two-step floating catchment area (2SFCA) method to measure spatial access. In the first step, define the catchment of physician location j as an area composed of all population locations (k) within a threshold travel time (d₀) from j and compute the physician-to-population ratio (R_j) within the catchment area as $R_j=S_j∕{\Sigma }_{k\in \{d_{\mathit{kj}}\le d_0\}}$ P_k. In the step, each population location i search all physician locations (j) within the threshold travel time (d₀) from i and sum up the ratios R_j at these locations:

$$A_i=\sum _{j\in \{d_{\mathit{ij}}\le d_0\}}{R}_j=\sum _{j\in \{d_{\mathit{ij}}\le d_0\}}\left(S_j∕\sum _{k\in \{d_{\mathit{kj}}\le d_0\}}{P}_k\right)$$ (2)

Again, the model in Equation 2 is basically a ratio between supply (S) and demand (P), which interact with each other only within a catchment area (e.g., thirtyminute driving time). The method is easy to implement in GIS.

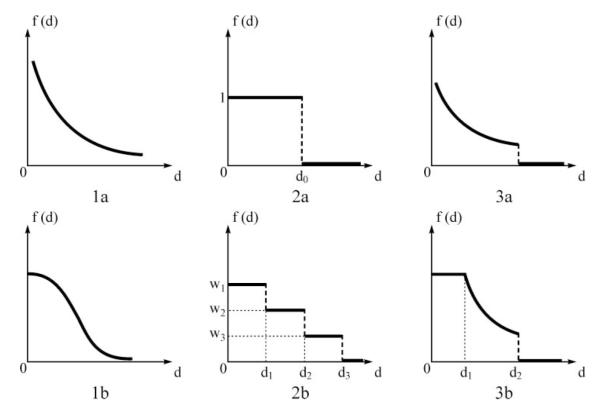
Since its inception, the 2SFCA method has been used in a number of studies measuring health care accessibility. Despite its relative popularity, the method’s major limitation is its dichotomous approach that defines a doctor inside a catchment as accessible and one outside the catchment as inaccessible. Several studies have attempted to improve it. A kernel density function (Guagliardo 2004) or a Gaussian function (Dai 2010) have been proposed to model the distance decay effect (i.e., a continuously gradual decay within a threshold distance and no effect beyond). The catchment radius might also vary by provider types or neighborhood types (Yang, Goerge, and Mullner 2006). Weights can be assigned to different travel time zones to account for the distance decay effects within each catchment area (Luo and Qi 2009). McGrail and Humphreys (2009) proposed a constant weight within ten minutes, a zero weight beyond sixty minutes, and a weight of gradual decay between. The aforementioned methods have different assumptions for conceptualizing distance decay in patient–physician interactions, as illustrated in Figure 1. By generalizing the distance decay effect as a term f(d), we can synthesize all measures of spatial accessibility in a model similar to the models in Equations 1 and 2:

$$A_i=\sum _{j=1}^n\left[S_{j}f\left(d_{\mathit{ij}}\right)∕\left(\sum _{k=1}^m{P}_{k}f\left({\mathit{dk}}_j\right)\right)\right]$$ (3)

where f(d) can be a continuous function (Cases 1a and 1b in Figure 1), a discrete variable (Cases 2a and 2b), or a hybrid of the two (Cases 3a and 3b).

Figure 1.

Conceptualizing distance decay in patient–physician interactions: (1a) gravity function, (1b) Gaussian function, (2a) binary discrete, (2b) multiple discrete, (3a) kernel density, and (3b) three-zone hybrid.

The main debate centers on what is (are) the reasonable catchment area size(s) of physician services and which is the best function to capture the distance decay behavior in physician visits. Any debate over the best function or the right size for catchment areas cannot be settled without analyzing real-world health care utilization behavior. This pursuit is related to a long-standing interest of geographers in activity space, defined as the local areas within which an individual moves or travels on a regular basis (Gesler and Albert 2000). For example, Sherman et al. (2005) used various GIS-based methods to define activity space for health care access by rural residents in North Carolina, and Arcury et al. (2005) demonstrated that geographic and spatial behavior factors (including location, availability of a driver’s license, and transportation modes) play important roles in rural health care utilization. Such studies are useful to help define appropriate catchment areas (likely to be different in rural and urban areas) when the distance decay is treated as a discrete variable. To model the wide spectrum of propensity for physician visits corresponding to trip lengths, more rigorous modeling is needed to derive the best fitting analytical functions and related parameters.

We now turn our attention to nonspatial access, which captures how access is influenced by who you are. Nonspatial factors include a wide selection of demographic and socioeconomic variables that affect health care access. These variables include demographics (e.g., seniors, children, women of childbearing ages), socioeconomic status (e.g., poverty, female-headed households, homeownership, and median income), housing conditions (e.g., crowdedness, basic amenities), and linguistic barriers and education. A major challenge is integrating these variables. Some suggest standardizing the variables and then combining them to produce a composite score (e.g., Field 2000), but many variables are correlated and thus contain duplicate information. Wang and Luo (2005) used factor analysis to consolidate these variables into fewer independent factors. The DHHS (2008, 11263–69) also proposed using factor analysis to help design the weights to aggregate the variables together in HPSA designations.

Nonspatial factors also interact with spatial access. For example, transit-dependent residents might be considered a nonspatial issue because of their age, medical condition, or lack of economic means, but they also tend to travel longer times to health care providers, thus affecting their spatial access (e.g., Lovett et al. 2002; Martin, Jordan, and Roderick 2008). Various population groups might also have different levels of health care needs and travel behavior (Morrill and Kelley, 1970). The Agency for Healthcare Research and Quality (2010, 177) identified seven priority populations (racial and ethnic minorities, low-income groups, women, children, older adults, residents of rural areas, and individuals with disabilities or special health care needs) for high health care needs. McGrail and Humphreys (2009, 420) used principal component analysis to consolidate seven sociodemographic variables into one summary score of health needs. This allows nonspatial factors to be used to adjust the definition of demand in spatial accessibility measures, providing one way of integrating spatial access and nonspatial factors in a unified accessibility measure.

The preceding review provides a glimpse of the diversity and complexity of issues on health care accessibility measures. Naturally, the methodology gets more advanced and complicated as more issues arise, but the increasing complexity also hinders its implementation and adoption. An equally important and tall task is to develop simplified and transparent proxy measures that require limited data but capture variation patterns of actual health care utilization across space and demographic groups consistent with otherwise more sophisticated methods.

Optimization Models in Health Care Accessibility

Several models in classic location–allocation problems (e.g., Church 1999) can benefit the study of planning for health care facilities (Table 1). The p median problem seeks to locate a given number of facilities among a set of candidate sites so that the total travel distance or time between demands and supply facilities is minimized. For example, Wang (2006, 203–11) used a case study in Cleveland to demonstrate its implementation in ArcGIS (Environment System Research Institute, Inc. 2012) to allocate health clinics to serve clients in the most efficient way (i.e., minimizing total distance or time). The location set covering problem (LSCP) minimizes the number of facilities needed to cover all demand within a critical distance or time. For example, Shavandi and Mahlooji (2008) employed a queuing theory in a fuzzy framework to solve an LSCP in allocating health care facilities at different levels in Iran. The maximum covering location problem (MCLP) maximizes the demand covered within a desired distance or time threshold by locating p facilities. For example, Pacheco and Casado (2005) used a hybrid heuristic algorithm to solve an MCLP in allocating health care resources in Burgos, Spain. The center model identifies a location arrangement for p facilities that minimizes the maximum distance to cover all clients. Additional constraints can be added to these models, and multiobjective models can also be constructed by combining the objectives of the models.

Table 1.

Optimization models of health care facilities

Model	Objective	Constraints	Health care application example
P median problem	Minimize total  distance/time	Locate p facilities; cover all demands (optional: demand  must be within a specified distance/time)	Wang (2006, 203–11)
Location set covering  problem (LSCP)	Minimize the number of  facilities	Cover all demands	Shavandi and Mahlooji (2008)
Maximum covering  location problem (MCLP)	Maximize coverage	Locate p facilities; cover demand if within a specified  distance/time (optional: demand not covered must be  within a second larger distance/time)	Pacheco and Casado (2005)
Center model	Minimizes the maximum  distance	Locate p facilities; cover all demands	N/A
Equity model	Minimize inequality in  accessibility	Adjust supplies in p facilities but maintain the same total  supply	Wang and Tang (2010)

The preceding models emphasize various objectives such as minimal travel, minimal resources, maximal coverage, or a combination of them (i.e., multiobjective) that focuses on either the supply or demand side of health care service delivery. Some recent work accounts for both sides, particularly their match ratios considered in spatial accessibility measures. For example, Perry and Gesler (2000) used a target ratio of health personnel versus population and a maximum travel distance as criteria to adjust health personnel distribution to improve overall access. Zhang, Berman, and Verter (2009) developed an optimal health care location model with a unique feature of accounting for distance decay in probability of using a health care facility. Gu, Wang, and McGregor (2010) used a biobjective model to identify optimal locations for health care facilities that maximize total coverage of population as well as their total accessibility. None of these studies has equity as an objective, however. Equity in health and health care can be defined as equal access to health care, equal utilization of health care services, or equal (equitable) health outcomes, among others (e.g., Culyer and Wagstaff 1993). Most agree that equal access is the most appropriate principle of equity from a public health policy perspective (Oliver and Mossialos 2004, 656). Some (e.g., Hemenway 1982) have argued that health maximization is the most justifiable objective. Quantifying the conversion from health care provision to outcome remains a challenge, however.

Wang and Tang (2010) developed an equity model with an objective of minimizing inequality in accessibility. Given an accessibility measure as defined in any of the Equations 1 through 3, it is known that the weighted mean of accessibility is equal to the ratio of total supply to total demand in a study area (Shen 1998), denoted by a constant a. The objective is to minimize the variance (i.e., least squares) of accessibility index A_i across all population locations by redistributing the total amount of supply S among health care facilities, written as:

$$\min =\sum _{i=1}^m{P}_i{(A_i-a)}^2$$ (4)

In this objective function, accessibility gaps (A_i – a)² are weighted by corresponding population P_i. One constraint is the total supply such as:

$$S_1+S_2+\dots +S_n=S$$ (5)

Additional constraints (e.g., threshold service population, as in Gu, Wang, and McGregor 2010) can be added.

This formulation fits a quadratic programming (QP), where the objective function is a quadratic function of variables S_i subject to linear constraints (here just one) on these variables (Nocedal and Wright 2006). There are various free and open-source programs to solve QP problems (Gould and Toint 2012). Note that the problem does not have a trivial solution such as distributing physicians proportionally to population in all areas because of complexity of interaction between health care supplies and demands across area units. In rare cases, the optimization yields equal accessibility across all population locations. Comparing the existing physician distribution to the “optimal” pattern that maximizes access equality, one could identify areas with severe shortage of services and adjustment needed toward maximal access equality.

Association of Health Care Access Inequality with Late-Stage Cancer Diagnosis

Inequality in health care access leads to disparities in various health outcomes, including differential rates in infant mortality and birth weight, vaccination, and complications from preventive and common diseases, among others. Cancer is a leading cause of death in the United States, second to heart disease (Centers for Disease Control and Prevention 2010). Cancer stage (based on tumor size and invasion) at the time of diagnosis plays a critical role in determining the patient’s prognosis. This section uses late-stage cancer diagnosis as an example to illustrate the impact of health care access inequality. There is an enormously rich body of literature on analyzing various risk factors of late-stage cancer (Wang, Luo, and McLaffferty 2010). In summary, the risk factors include (1) spatial access to both cancer screening facilities and primary care physicians and (2) nonspatial factors at both the individual and neighborhood levels (see Table 2). For example, poorer spatial access to mammography is associated with its lower utilization and consequently higher late-stage breast cancer rate (Menck and Mills 2001). Similar effects are found for spatial access to primary care physicians (Wang et al. 2008) and nonspatial factors (McLafferty and Wang 2009). The accessibility measures discussed previously will help to improve the definitions of the preceding risk factors. This section focuses on methodological issues of examining the association of these factors with late-stage cancer diagnosis.

Table 2.

Regression models for analyzing late-stage cancer risks

Variables	OLS	Poisson	Multilevel logit
Late-stage cancer rate	Y
Number of late-stage cancer cases		Y
Number of all cancer cases		Offset
Individual cancer cases  (1 = late-stage, 0 = otherwise)		Y
Individual cancer patient  sociodemographic attributes			X
Neighborhood demographic and  socioeconomic factors	X	X	X
Neighborhood urban–rural  classification	X	X	X
Spatial access to primary care	X	X	X
Spatial access to cancer screening	X	X	X

Note: Y indicates the dependent variable, and X indicates an independent variable in a model. OLS = ordinary least squares.

For data in large analysis units such as state and county, it is appropriate to use ordinary least squares (OLS) regression, where the dependent variable is late-stage cancer rate (i.e., ratio of number of late-stage cancer cases to total cancer cases) and independent variables are the aforementioned risk factors. For cancer data in small areas such as ZIP code area and census tract with a small number of cancer counts, late-stage cancer rate is sensitive to missing data and other data errors, has a high variance, and is less reliable, commonly known as the small population problem. Several spatial strategies have been proposed to mitigate the problem. Conceptually similar to moving averages that smooth observations over a longer time interval, spatial smoothing computes the average late-stage cancer rates around each area using a larger spatial window. Spatial smoothing methods include the floating catchment area method, kernel density estimation (Wang 2006, 36–38), empirical Bayes estimation (Clayton and Kaldor 1987), locally weighted average (Shi et al. 2007) and adaptive spatial filtering (Tiwari and Rushton 2004). Another geographic approach is regionalization, which groups small areas to form larger geographic areas with more reliable late-stage cancer rates. Some earlier methods emphasized either homogeneity of attributes within the new areas (e.g., Haining, Wises, and Blake 1994) or spatial proximity between the areas to be grouped (e.g., Lam and Liu 1996). Recent research aims to develop GIS-based automated methods that take into account both spatial contiguity and attribute homogeneity within the derived areas (e.g., Guo 2008; Mu and Wang 2008). When similar areas are merged, it mitigates the spatial autocorrelation problem commonly observed in data of geographic areas and simplifies subsequent regression analysis.

There are also regression methods that are suitable for analysis of small-area cancer data (see Table 2). One is Poisson regression (e.g., Wang et al. 2008), where the dependent variable is the number of late-stage cancer cases and the total number of cancer cases serves as an offset variable. A spatial Poisson regression model (Best, Ickstadt, and Wolpert 2000) is needed to account for spatial autocorrelation in the data. Another method is logit regression to model the risk of individual cancer cases being late stage, where the dependent variable is binary (0, 1). A multilevel logistic model is needed to examine the effects of both individual- and neighborhood-level risk factors (e.g., McLafferty and Wang 2009). Similarly, more advanced logit models are needed to control for spatial autocorrelation (Griffith 2004).

Summary

This article reviews recent methodological advancements in three issues related to inequality in health care accessibility: measurement, optimization, and impact. Various methods have been proposed to measure health care accessibility, accounting for both spatial and nonspatial factors. Various measures of spatial accessibility differ in ways of conceptualizing the distance decay effect as a continuous function, a discrete variable, or a hybrid of the two. The selection of an appropriate model needs to be based on analysis of real-world health care utilization behavior. Nonspatial factors include a wide selection of demographic and socioeconomic variables, which can be consolidated into a few independent factors by factor analysis. The increasing complexity of accessibility models hinders its implementation and adoption by public health professionals and calls for the development of simplified and transparent proxy measures.

The classic location–allocation problems have been widely used in planning for health care facilities. There is a lack of operation research on equity in health care access. An equity model explicitly formulates the objective function as minimizing inequality in accessibility across demand locations and can be solved by quadratic programming. Results from the model identify adjustments needed for maximizing access equality.

The final issue is assessing the impact of accessibility disparities on an important health indicator, late-stage cancer diagnosis. OLS regression can be used to examine risk factors in influencing the variation of late-stage cancer rate across large areas. Poisson and logit regressions are often used for analysis of cancer data in small areas. Some geographic strategies, such as spatial smoothing and regionalization methods, have also been proposed to mitigate the small population problem.