Abstract
This study investigated the effects of retention or promotion in first grade on growth trajectories in mathematics and reading achievement over the elementary school years (grades 1–5). From a large multiethnic sample (n = 784) of children who were below the median in literacy at school entrance, 363 children who were either promoted (n = 251) or retained (n = 112) in first grade could be successfully matched on 72 background variables. Achievement was measured annually using Woodcock-Johnson W scores; scores of retained children were shifted back one year to permit same-grade comparisons. Using longitudinal growth curve analysis, trajectories of math and reading scores for promoted and retained children were compared. Retained children received a one year boost in achievement; this boost fully dissipated by the end of elementary school. The pattern of subsequent retention in grades 2, 3 and 4 and placement in special education of the sample during the elementary school years is also described and their effects are explored. Policy implications for interventions for low achieving children are considered.
Studies on the effects of grade retention, having to repeat a grade, on academic and psychosocial adjustment have a long history, dating from the early 20th century (Owings & Magliaro, 1998). The nearly unanimous conclusion from reviews of this research (for meta-analytic reviews, see Allen, Chen, Willson, & Hughes, 2009; Holmes, 1989; Jimerson, 2001a; for narrative reviews, see Jimerson, 2001b; Shepard, Smith, & Marion, 1996; Sipple, Killeen, & Monk, 2004) is that students retained in a grade fare the same or worse in terms of academic achievement than they would if they had been promoted. However, the majority of studies included in these reviews are plagued by significant methodological limitations, with the key limitation being the lack of a comparison group of promoted peers equivalent prior to retention on achievement and other variables predictive of achievement (for discussions see Hong & Raudenbush, 2005; Lorence, 2006). Studies that do a better job of controlling for student characteristics associated with selection into the retention intervention are less likely to find that grade retention has a negative effect on achievement (Allen, et al., 2009). The interpretation of this result is complicated by the use of same-age versus same grade comparison standards and different post retention intervals in the evaluation of effects across studies (explained below).
A second limitation of current research is that grade retention is treated as a fixed, one time intervention. Typically, the achievement of students who are retained in a specific “target” grade is compared with a group of academically at-risk students who are promoted at that same grade at a given number of years post-retention (e.g., Jimerson, Carlson, Rotert, Egeland, & Sroufe, 1997; McCoy & Reynolds, 1999). In reality, low performing students who were promoted or retained in the target grade may be retained in a later grade or may be assigned to special education. These interventions potentially represent additional “treatment”, complicating the interpretation of observed post-retention differences.
The overall goal of the current study was to investigate the effects of retention versus promotion in first grade on the trajectories of achievement scores in math and reading through 5th grade in low achieving children. Grades 1 through 5 typically comprise the elementary school years in the state in which the study was conducted. Comparison of trajectories permits us to answer two key questions: (1) Does retention lead to an immediate “boost” in achievement following the retention year? (2) Is the rate of growth in achievement following the retention year maintained so that the any boost in achievement is retained or possibly enhanced over the elementary school period?
The present study also sought to address the two limitations of prior research identified above. To address the first limitation, propensity score matching was used to ensure that retained and promoted students had an equal probability of being retained in first grade based on an extensive set of baseline variables. Propensity score matching, a technique with advantages over previous matching methods when there are many measured variables (see Rosenbaum, 2010), was used to equate the promoted and retained groups. Described in more detail below, propensity scores are the estimated probabilities of being assigned to the treatment group, here grade retention. To address the second limitation, the natural history of low achieving students’ pattern of grade retention and placement into special education is tracked from first through fifth grade. This information was then used to probe the effect of subsequent retention in Grades 2–4 on the trajectories across the elementary school years of initially low achieving students.
Review of Recent Research on Effects of Retention on Achievement
Contributing to the difficulty in reaching conclusions regarding the effects of grade retention on achievement are methodological variations in studies that may be predictive of achievement effects. In a recent meta-analysis, Allen et al. (2009) sought to explain variability in empirical studies of the effect of grade retention on achievement. These authors used multi-level modeling to investigate characteristics of 207 effect sizes across 22 studies published between 1990 and 2007, examining methodological features at both the between study and within study levels. Special attention was given to the rigor with which studies controlled for possible pre-retention differences between retained and promoted students. For example, more rigorous studies used a combination of matching retained and promoted students prior to retention on achievement-related variables and statistical controls for pre-retention measures of the achievement outcome. Less rigorous studies employed a low achieving comparison group without controlling for pre-retention performance on the achievement outcome. Methodological rigor moderated effect sizes, such that effects of retention were more positive (or less negative) for studies with stronger statistical and methodological controls. Retention effects generally were more positive immediately following the retention intervention than they were three or more years post-intervention.
However, this worsening of outcomes with increased years post-retention was greater for studies using same-grade comparisons than for studies using same-age comparisons. Same-age comparisons compare retained and promoted students when they are the same age (i.e., the same calendar year). Comparisons are made with the original age cohort of students even though promoted students are one year ahead in school (in a different grade). Except in rare cases, retained children have no opportunity to catch up with the grade level placement of their original classmates. Same-grade comparisons compare retained students with promoted peers when they are in the same grade. Comparisons are made between retained and promoted students only after they have been exposed to the same grade level material, even though the retained students are one year older than the promoted students. To implement a same-grade comparison, one of two procedures is used, with the second procedure having two variants: (1) retained students are “shifted back” a year such that their performance in a given grade is assessed a year later than is the case for their cohort of promoted peers, (2a) retained students are directly compared with their new and younger grade mates, or (2b) retained students are compared with test norms for their current grade, so that grade norms serve as a proxy for same-grade comparisons. Studies which (1) shift retained students back a year or (2a) directly compare students with grade mates provide stronger same-grade comparisons than studies using grade normed-scores (Karweit, 1999; Lorence, 2006).
Allen et al. (2009) concluded from their meta-analysis that the question, “what is the effect of grade retention on achievement?” is too broad to guide educational policy, as effects differ systematically on the basis of the comparison used (age-or grade-based) and the number of years post-retention. Also, presenting a single overall effect size calculated from studies that vary widely in the adequacy of their controls for selection effects provides an inadequate basis for characterizing the effects of grade retention.
A new generation of studies using more rigorous controls for selection effects and employing growth curve modeling is providing a more nuanced understanding of the effects of grade retention (e.g., Hong & Raudenbush, 2005; Hughes, Chen, Thoemmes, & Kwok, 2010). For example, Wu et al. (2008a) investigated the effects of retention in first grade on short-term and longer term (3 years post retention, covering the period through fourth grade for non-retained and third grade for retained students) growth trajectories for reading and math. Propensity score matching was used to create pairs of promoted and retained students who had an equal probability of being retained based on a large and comprehensive set of variables assessed prior to any student being retained. They analyzed growth trajectories separately for Woodcock Johnson III (WJ) Broad Reading and Broad Math using either “W” scores or grade-normed scores. W scores are a Rasch-type measure of ability that allow comparison of the rate of growth in the underlying latent construct of math or reading of retained and promoted students for the same time interval. Using W scores to compare retained and promoted peers at the same time intervals constitutes a same-age comparison. The analyses using grade-normed scores as a proxy for same-grade comparisons compared retained and promoted students relative to well-established norms for their current grade placement, which was 1 year lower for retained compared to promoted students. Results differed based on the comparison used. For the same-age W score comparisons, grade retention decreased the growth rate in the short term, but had either no significant effect on the growth rate (math) or increased the growth rate (reading) over the longer term. For same-grade comparisons using grade-normed scores, grade retention increased the growth rates of both the WJ math and reading grade standard scores during the retention year, but led to a decreased rate of growth of both scores in the longer term. In other words, retained students obtained an initial boost in their achievement relative to their (younger) grade mates during the repeat year, but this benefit eroded as retained students encountered a novel and more challenging curriculum during the subsequent years.
Effects of Subsequent Retention and Special Education Placement
When students fail to master grade-level academic competencies by the end of the year, parents and educators are faced with several options. They may retain the student, with the hope that with another year of maturity and exposure to the curriculum the student will be “back on track” for success in future grades. They may promote the student to the next grade, with the hope that the student will overcome whatever barriers have limited his or her performance. Grade retention or promotion might be combined with a third option, placement in special education upon determination of a disability. These options are not limited to a single point in time. Children with academic deficiencies at the end of one school year who are nevertheless promoted to the next grade may be placed in special education or selected for grade retention at some subsequent grade. Similarly, children retained in grade may be selected for retention in a later grade or for placement in special education in the future. We sought to describe the extent to which these options are utilized with low achieving children. Research on the effects of grade retention on future academic achievement has largely ignored these subsequent “interventions.” This omission is potentially important. If two students in a target grade have an equal likelihood of being retained, but one is retained and the other is promoted, it is reasonable to expect that the promoted student may be at an increased probability of being retained or placed in special education during the course of the next few years, relative to the retained student. If this is the case, part of the “promoted” group is more accurately described as a “delayed intervention” group. Educators and parents are reluctant to retain students more than once during the elementary grades due to potential problems created for the student and classmates when a student is two or more years older than his or her classmates. Previously retained students who continue to struggle academically may be at greater risk for special education placement than are similar yet previously promoted peers.
Beebe-Frankenberger, Bocian, MacMillan, and Gresham (2004) investigated similarities and differences between four groups of children in three California school districts: (a) children retained in second grade, (b) children promoted following second grade but receiving special education services the next year, (c) children “at risk” for retention in 2nd grade based on standardized test scores but promoted, and (d) non-at risk promoted children. Retained children and children receiving special education services the next year did not differ on any of the measured variables, including IQ, academic competencies, or social and behavioral functioning. The authors concluded that the basis for selection into special education versus retention is not well understood. These authors also found that over 50% of the students receiving special education services at the end of second grade had already been retained once, prior to being eligible for special education services. They concluded that “retention may be both an intervention and a precursor to formal evaluation for special education services” (p. 211).
Study Purpose
The current study investigates the effects of retention in first grade on future achievement, extending previous research in several important ways:
With 6 potential waves of data, the children are followed from Grade 1 through Grade 5 providing a full description of the effects of retention in first grade on achievement through the elementary school years. No child in the sample exceeded two retentions in elementary school. This period represents one of the longer longitudinal assessments of the effects of grade retention.
Several researchers have argued that same grade comparisons are more consistent with the purpose of retention, which is to provide students the opportunity to be more successful in meeting the academic demands of future grades (e.g., Karweit, 1999; Lorence, 2006). These authors argue that it is unfair to expect retained students to demonstrate the same level of mastery of a skill when they have not been exposed to instruction in that skill at the higher grade. Wu et al. (2008a) were only able to compare achievement of retained and promoted children with grade- level norms. The present data permit the direct comparison of the achievement of the retained children to their promoted peers when in the same grade, but not in the same year. This is accomplished by using children’s achievement scores from the repeated first grade and subsequent Grades 2–5 (i.e., shifting back the retained students one year).
Most studies show trajectories for reading and math in the elementary grades are curvilinear (quadratic), with the rate of positive growth showing a decrease in grades 3–5 relative to grades 1–3 (Sonnenschein, Stapleton, & Benson, 2010; Li-Grining, Votrube-Drzal, Maldonado-Carreño, & Haas, 2010). Two additional measurement waves permit testing of quadratic trajectories of development over Grades 1 to 5. The use of longitudinal growth models provides direct answers to the two questions posed above in a single model: (1) Does retention lead to an immediate “boost” in achievement following the retention year? (2) Is the rate of growth in achievement following the retention year maintained so that the any boost in achievement is retained or possibly enhanced over the elementary school period? Separate comparisons of retained and promoted children at each grade level do not provide direct answers to the second question because they do not address the trajectories of achievement over the elementary school period.
The present data permit the description of the natural history of an ethnically diverse sample of low performing students as they pass through their elementary school years. Of central interest is the pattern of educational interventions including retention and placement in special education received by these students.
Finally, an exploratory investigation of the effects of (a) subsequent retention of children and (b) enrollment in special education classes in Grades 2, 3, or 4 on the students’ achievement trajectories over the elementary school years was conducted.
Method
Participants
Participants were taken from a larger sample of students participating in a longitudinal study focused on the effect of grade retention on achievement and psychosocial outcomes. Two cohorts of students entering first grade in three school districts in a Southwestern state were recruited: cohort 1 entered first grade in fall 2000; cohort 2 entered first grade in fall 2001. Two of the school districts were small city districts, and one was an urban district. The first small city school district was composed of students who were 40% White non-Hispanic, 61% economically disadvantaged, and 11% limited in English proficiency. The second small city school district was composed of students who were 69% White non-Hispanic, 24% economically disadvantaged, and 5.2% limited English proficient. The urban school district was composed of students who were 41% White non-Hispanic, 37% economically disadvantaged, and 11% limited English proficient. In each school district, written policies emphasized that failure to master grade level curriculum, as evidenced by grades and by standardized measures of achievement and literacy skills, should be the primary factor in a decision to retain a child. Consistent with this policy, of variables linked in prior research to grade retention, only teacher-rated achievement, performance on a standardized measure of reading, and a measure of parent involvement in education uniquely predicted retention in the larger longitudinal sample (Willson & Hughes, 2009).
In order to be eligible to participate in the longitudinal study, students had to score below the median on a state-approved measure of literacy, speak English or Spanish, not be receiving special education services other than speech and language services in first grade, and not have been previously retained in first grade. A total of 1,374 students met the eligibility requirements. Incentives (small prizes and a chance to win a larger prize) were provided for children to return a signed consent form, regardless of the parent’s decision regarding participation. This procedure greatly enhanced the probability that consent forms were returned even if the decision was not to participate. Of the 1,200 consent forms that were returned, 784 (65%) of the parents granted permission for their child to participate in the study. There were no significant differences in demographic, social, or academic variables between the students who obtained consent and those who did not. The sample of 784 students whose parents granted permission was 52.6% male. In terms of ethnicity, this sample was composed of 37% Hispanic (36% of these in bilingual classes), 34% White non-Hispanic, 23% African American, and 6% of other ethnicity. Their mean age at the beginning of the study was 6.57 years (SD = .39). Fifty-seven percent were eligible for free or reduced lunch and 13 percent lived in single parent homes. All research was approved by the school districts’ research advisory teams and the Institutional Review Boards of the authors’ universities.
Participants for the present study consisted of 363 children (31% retained in Grade 1, 54% male) who could be successfully matched with respect to their propensity to be retained in first grade (see following description of propensity matching procedure). The children were 34% Hispanic (38% in bilingual classes), 34% White non-Hispanic, 27% African American, and 4% of other ethnicity. Their mean age at the beginning of the study was 6.5 years (SD = 0.36). Sixty percent were eligible for free or reduced lunch and 15 percent lived in single parent homes. Data from participants with at least 1 observation on the outcome measures over the 6 observation periods were included in the analysis1.
Measures and Design
Baseline measures
At the first wave of data collection in the fall of 2000 and 2001, 72 baseline variables were collected for use in propensity score estimation (see Appendix A for list of variables). These 72 variables included measures of the child’s demographic family background, academic and cognitive performance, self-regulation, and social and emotional functioning as well as classroom and school characteristics. These data were obtained from school records; teacher-, parent-, and child reports; peer sociometric interviews, and child performance measures. These variables potentially relate to retention in grade, academic achievement, or both; they were used to create propensity scores, the predicted probability that the child would be retained in first grade. Propensity scores reduce bias in estimates of treatment effects to the extent that a rich set of baseline variables are utilized that represent potential confounders that are related to the outcome and treatment assignment. The propensity scores were used to create matched sets of children (see below).
Appendix.
List of 72 background variables used in propensity score matching.
| Variable name | Source |
|---|---|
| Cohort | |
| Child ethnicity | Archival |
| Child's gender | Archival |
| Child age at eligibility determination | Archival |
| Child's school district at Time 1 | Archival |
| Child language | Archival |
| Enrollment in pre-first grade | Archival |
| Economically disadvantaged status | Archival |
| Title 1 status | Archival |
| Migrant status | Archival |
| Limited English proficiency status | Archival |
| Bilingual class status | Archival |
| English as a second language status | Archival |
| Special education status | Archival |
| At risk status | Archival |
| Cognitive competence subscale (Harter) | Child |
| Peer acceptance subscale (Harter) | Child |
| Physical competence (Harter) | Child |
| Maternal acceptance (Harter) | Child |
| Sense of school belonging | Child |
| Peer nomination aggression | Classmates |
| Peer nomination prosocial | Classmates |
| Peer nomination hyperactive | Classmates |
| Peer nomination sad/withdrawn | Classmates |
| Peer nomination teacher support | Classmates |
| Peer social preference score | Classmates |
| Family language | Parent |
| Parent literacy status | Parent |
| Rent or own home | Parent |
| Highest level of education of in household | Parent |
| Parent educational aspirations for child | Parent |
| Number of adults living in the household | Parent |
| Number of children living in household | Parent |
| Child attended kindergarten | Parent |
| Parent satisfaction with home-school relationship | Parent |
| Parent sense of responsibility for child's education | Parent |
| Parent satisfaction with teacher | Parent |
| Parent self efficacy for helping child in school score | Parent |
| Parent positive perceptions about school | Parent |
| Home-school communication | Parent |
| Parent-teacher shared responsibilities | Parent |
| Parent school-based involvement | Parent |
| Parent rated ADHD behaviors | Parent |
| Parent rated prosocial behaviors | Parent |
| Parent rated conduct problems | Parent |
| Parent rated internalizing behaviors | Parent |
| Minutes per day child watches television | Parent |
| Number of shared family meals | Parent |
| Parent acculturation | Parent |
| Composite district literacy test score | Performance |
| UNIT full scale IQ | Performance |
| Woodcock-Johnson III broad reading W score | Performance |
| Woodcock-Johnson III broad math W score | Performance |
| Dweck puzzles task choice | Performance |
| Effortful (inhibitory) control | Performance |
| Property value of residence | Public records |
| Teacher educational aspirations for child | Teacher |
| Home-school alliance | Teacher |
| Parent involvement | Teacher |
| Teacher-initiated parent involvement | Teacher |
| Teacher rated ADHD behaviors | Teacher |
| Teacher rated prosocial behaviors | Teacher |
| Teacher rated conduct problems | Teacher |
| Teacher rated internalizing behaviors | Teacher |
| Child agreeableness | Teacher |
| Child conscientiousness | Teacher |
| Teacher-student Conflict | Teacher |
| Teacher-student support | Teacher |
| Parent reading with child | Teacher |
| Parent positive involvement with child | Teacher |
| Parent discipline | Teacher |
| Child's academic performance | Teacher |
Note. Full information on the variables may be obtained from the 3rd author.
Academic achievement scores
The primary outcome measures for the study were standardized measures of academic achievement. The WJ-III Tests of Achievement (Woodcock et al., 2001) is an individually administered measure of academic achievement for individuals ages 2 to adulthood. The WJ-III Broad Reading W Scores (Letter-Word Identification, Reading Fluency, Passage Comprehension subtests) and the WJ-III Broad Math W Scores (Calculations, Math Fluency, and Math Calculation Skills subtests) were used. The Reading and Math W scores are based on the Rasch measurement model, yielding an equal interval scale, which facilitates modeling growth in underlying latent achievement (Khoo, West, Wu, & Kwok, 2005; Willson & Hughes, 2006). Extensive research documents the reliability and construct validity of the WJ-III and its predecessors (Woodcock & Johnson, 1989; Woodcock, et al., 2001).
The Batería Woodcock-Muñoz: Pruebas de aprovechamiento – Revisada (Woodcock & Munoz-Sandoval, 1996) is the comparable Spanish version of the Woodcock-Johnson Tests of Achievement—Revised (WJ-R; Woodcock & Johnson, 1989), the precursor of the WJ-III. If children or their parents spoke any Spanish or were in bilingual classrooms, children were administered the Woodcock- Muñoz Language Test (Woodcock & Muñoz-Sandoval, 1993) by a Spanish-English bilingual examiner to determine the child’s language proficiency in English and Spanish. Based on the language in which the child exhibited greater proficiency, children were administered either the WJ-III or the Batería-R. The Woodcock Compuscore (Woodcock & Muñoz-Sandoval, 2001) program yields W scores for the Batería-R that are comparable to W scores on the WJ-R. The Broad Reading and Broad Mathematics W Scores were used in this study.
Achievement was assessed each year beginning in Grade 1 and continuing until the child completed elementary school (Grade 5). Assessors were undergraduate psychology students registered for a field experience course and graduate students in school psychology. All assessors received a minimum of 12 hours of instruction in administration of the Woodcock Johnson or Batería and demonstrated a high level of proficiency in administration of the tests in practice administrations prior to being allowed to conduct assessments for the study. Each test protocol was checked for errors by two members of the research staff. In a small number of cases, errors were found (typically a failure to obtain a basal or ceiling in test administration). If errors were found, assessors were required to correct the error, if possible. Achievement testing occurred primarily in the late Fall and Winter. Repeated attempts were made to assess missing children over the entire school year. In all cases at least 8 months separated yearly testing occasions.
Retention status
Students who were in the same grade for two consecutive years were classified as being retained in that grade the second year. Information on students’ grade placement was obtained from school records or, if missing, from parent or teacher report.
Special education status
Special education status was obtained each year from school rosters and teacher questionnaires. A student was classified as receiving special education services if a) school rosters received at the beginning of each school year indicated the student was receiving special education services or b) the teacher reported on the questionnaire administered in the spring of each year that the student was receiving special education services. The specific disability condition qualifying a student for special education services beyond first grade was typically not reported. Students receiving special education services other than speech and language services in first grade at the time of initial recruitment into the study were excluded from participation. In first grade, 29 students received special education services due to a speech or language impairment.
Propensity Score Estimation
Propensity scores, the predicted probability of being retained in first grade, were estimated for the full sample of 768 children for whom retention information was available. A total of 72 background variables (see Appendix for a complete list) collected at the initial testing were used, including child demographic variables, child, peer, teacher, and parent data covering the areas of academic aptitude (e.g., the Universal Nonverbal Intelligence Test), academic achievement (Woodcock Johnson III or the Spanish-language Batería-R Broad Math and Reading), personality (e.g., agreeableness; effortful control), behavioral and social adjustment, peer relations, and family adversity. Methods based on logistic regression (Rosenbaum, 2010; Rosenbaum & Rubin, 1983) were used to estimate propensity scores, , where p̂ is the estimated probability of being in the retained group, Xi is the ith predictor (baseline variable), bo is the intercept, and bi is the regression coefficient for the ith predictor, The term on the left side of the equation can be transformed to a probability of being retained conditional on the student’s level on the baseline variables. The logistic regression equation led to relatively good prediction of the decision to retain or promote each child, Nagelkerke pseudo R2 index of .552 (see Cohen, Cohen, West & Aiken, 2003, section 13.2).
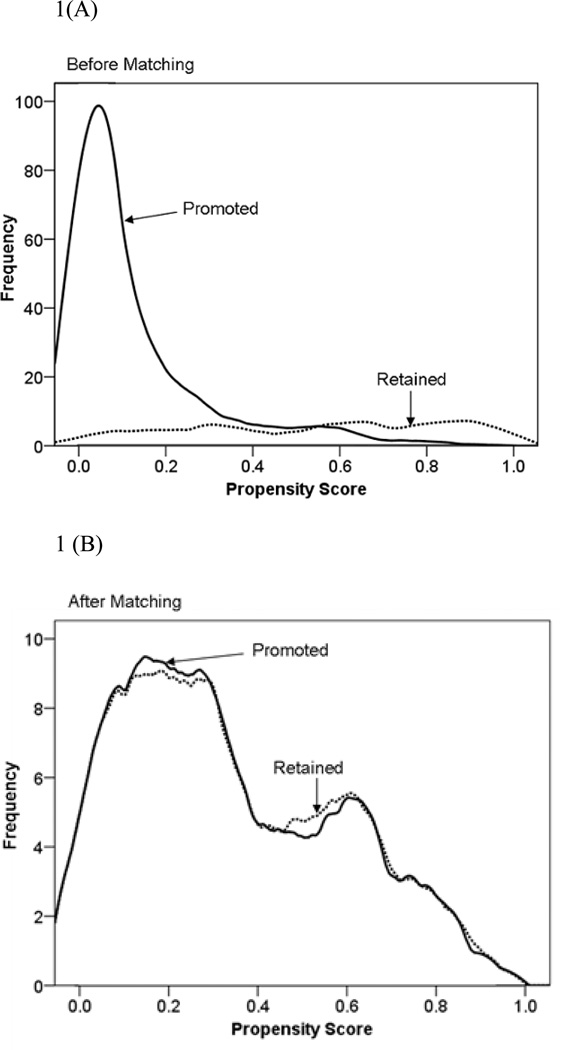
The propensity score (probability) can theoretically range from 0 to 1. The larger the propensity score, the higher the probability the child would be retained in the first grade. For the 768 cases who were below the median on reading at school entrance the propensity score ranged from .0003 to .989 with M = .215 and SD = .215. In this full sample of “at risk” children, the children who were subsequently promoted had substantially lower mean propensity scores (N = 603; M = .126, SD = .163) than those who were subsequently retained (N = 165; M = .540; SD = .292; t(766) = −23.816; Cohen’s d = −2.092). Figure 1(A) shows separate overlaid kernel density estimates of the distribution of propensity scores for promoted and retained children for the 768 cases. Kernel density estimates smooth the data, providing an estimate of the distributions for the retained and promoted children in the population (Cohen et al., 2003, pp. 105–108). The figure shows that the distribution of propensity scores for the promoted children was highly right skewed, whereas the distribution for the retained children was relatively uniform across the full range of propensity scores.
Figure 1.
Kernel density plots of the frequency distributions of the propensity score for promoted and retained children. Panel (A) depicts the distributions for the promoted (n = 603) and retained (n = 165) in the full sample. Panel (B) depicts the distributions for one target child and one matched child (randomly selected if there was more than one match) for each of the matched sets (n = 80 in each group). In all, there were n = 251 promoted children and n = 124 retained children after 1:many matching. The scale of the Y-axes differs between the two panels. Source: Wu, W., West, S. G., & Hughes, J. N. (2010). Effect of grade retention in first grade on psychosocial outcomes. Journal of Educational Psychology, 102, p. 142.
Matching Procedure
We used what Rosenbaum (2010) has termed a “variable 1:many matching procedure.” Ming and Rosenbaum (2001) showed that this is the optimal matching procedure when the goal is to simultaneously minimize bias and maximize sample size and statistical power. Over the range of propensity scores from .00 up to .50, there were more promoted children than retained children in the sample. For this range, we matched one retained child with up to 5 (i.e., 1, 2, 3, 4, or 5) promoted children. Over the range of propensity scores from .50 up to 1.00, there were more retained children than promoted children in the sample. For this range, each promoted child was matched with up to 5 retained children. Otherwise stated, a target child was selected from the smaller group (retained group for propensity score < .50; promoted group for propensity score ≥ .50) and was then matched with up to 5 children from the other, larger group. Matching more than 5 children to the target child does not lead to further increases in statistical power. To assure high-quality matching, caliper distance = .025 was imposed, representing the maximum distance in propensity scores allowed for a match to take place. That is, any pair of retained and promoted children who differed in their propensity scores by more than .025 could not be matched with each other.
SAS 8.0 PROC ASSIGN was used to implement the matching (Ming & Rosenbaum, 2001). PROC ASSIGN matches retained children with promoted children so that the sum of the distances between the propensity scores within each of the matched sets was minimized for the whole sample. A total of 80 matched sets were constructed using a total of 251 promoted and 124 retained children. For the 80 matched sets, the propensity score ranged from .003 to .934 with M = .31 and SD = .25. The empirical range covered virtually the entire theoretical range for the propensity scores (.00 to 1.00). Figure 1(B) presents overlayed kernel density plots for each target child and one randomly selected comparison child from the matched set to equalize sample sizes. The two groups were closely equated on their propensity scores following the optimal matching process, with the two distributions almost overlapping each other.
To further check whether the matching provides good balance between the retained and promoted groups, the retained and promoted groups were compared on all baseline measures used to calculate the propensity score and the baseline measures for all of the outcomes examined in the study, which includes 72 baseline measures in total. Given space limitations, balance for 20 most important baseline measures is reported. The propensity scores were divided into 5 strata (quintile groups): 0 – 19th percentile; 20 –39th percentile, 40th –59th percentile, 60th –79 percentile, and 80th –100th percentile. For the continuous variables, a 2 (retained vs. promoted) × 5 (quintile) Analysis of Variance (ANOVA) was conducted using the baseline measures (Table 1). For dichotomous variables, a parallel 2 (retained vs. promoted) × 5 (quintile) analysis was conducted using logistic regression (Table 2). If a baseline measure is well balanced between the retained and promoted groups, then neither the main effect of retention nor the retention × quintile interaction should be different from 0. Tables 1 and 2 show the matching procedure provided good balance on 18 of the 20 important baseline measures. On the full set of 72 baseline variables2, the number that were statistically significant (6) did not exceed the number expected (7.2) based on the nominal α = .05 level. The effect sizes were small, never exceeding Cohen’s d = 0.30 standard deviation difference.
Table 1.
Checks on the Success of Variable Many to One Matching. Continuous Variables: F-tests from Analyses of Variance
| Variable | Main effect of retention (F, df = 1,251) |
Retention × Quintile Strata (F, df = 4,251) |
|---|---|---|
| Behavioral Adjustment | ||
| Externalizing behaviors | ||
| Teacher-reported Hyperactivity | 0.05 | 0.07 |
| Teacher-reported Conduct Problems | 0.35 | 0.53 |
| Peer-reported Hyperactivity | 0.14 | 1.38 |
| Peer-reported Conduct Problems | 0.05 | 2.08 |
| Internalizing behaviors | ||
| Teacher-reported Emotional Problems | 0.55 | 1.86 |
| Peer-reported Sad/Withdrawn | 2.56 | 0.55 |
| Engagement | ||
| Teacher-reported Behavioral Engagement | 0.01 | 0.82 |
| Child-reported School Belonging | 1.47 | 0.18 |
| Child-reported Academic Self Efficacy | 0.01 | 0.05 |
| Social Acceptance | ||
| Peer-reported Liking | 1.30 | 0.29 |
| Other measures | ||
| Child Age | 0.08 | 0.64 |
| Child IQ | 0.01 | 1.07 |
| Parent Highest Level of Education | 0.85 | 0.93 |
| Parent Highest Level of Employment | 0.87 | 0.39 |
| Child Woodcock Johnson Math W score | 0.20 | 2.68* |
| Child Woodcock Johnson Reading W score | 1.05 | 1.34 |
Note.
p < .05. Tables 1 and 2 report the 40 tests for the 20 important variables, of which 3 were statistically significant across both tables. Two of the total number of tests would be expected to be significant by chance. Source: Wu, W., West, S. G., & Hughes, J. N. (2010). Effect of grade retention in first grade on psychosocial outcomes. Journal of Educational Psychology, 102, p.144.
Table 2.
Checks on the Success of Variable Many to One Matching. Binary Variables: Wald-tests from Logistic Regression.
| Logistic Regression | ||
|---|---|---|
| Baseline Measures | Main effect of retention (Wald χ2, df = 1) |
Retention × Quintile strata (Wald χ2, df = 1) |
| Child Ethnicity: White vs. Non-white | 5.40* | 7.25* |
| Child Gender | 1.20 | 0.52 |
| Child Bilingual Status (1: yes; 0: no) |
0.13 | 0.001 |
| Child Economic Disadvantage Status (1: yes; 0: no) |
0.03 | 0.16 |
Note. Tables 1 and 2 report the 40 tests for the 20 important variables, of which 3 were statistically significant across both tables. Two of the total number of tests would be expected to be significant by chance. Source: Wu, W., West, S. G., & Hughes, J. N. (2010). Effect of grade retention in first grade on psychosocial outcomes. Journal of Educational Psychology, 102, p. 144.
In summary, the checks showed that the propensity score matching procedure overall achieved reasonable balance. The goal of propensity score matching is bias reduction so that typically a portion of the sample is not matched. The number of usable participants was maximized by using variable 1:many matching. The chief reason for failing to locate a match was the excess number of promoted students with low propensity scores relative to retained students with similar low propensity scores.
Of the original 375 children who were successfully matched at the end of first grade, 12 children had no data on math and reading scores for Grades 1 (repeated), 2, 3, 4, or 5. These children were removed from the analysis. Of these 12 children (7 female, 5 male), 7 (58%) were Caucasian, 4 (33%) were Hispanic, and 1 (8%) was African American. The 12 children without any achievement data did not differ significantly on their propensity scores from the 363 children who had achievement data and were included in the main analyses, t(373) = 1.02, p = .31. Of these 363, 14 (4%) WJ scores were missing at Grade 1, 37 (10%) at Grade 2, 37 (10%) at Grade 3, 53 (15%) at Grade 4 and 69 (19%) at Grade 5.
Results
Specification of Multilevel Analysis
Three level multilevel analyses of the achievement data using SAS 9.2 PROC Mixed (SAS Institute, Inc., 2008) were conducted to answer the research questions. The standard multilevel analysis options of constant variance and zero covariance of residuals and Satterthwaite3 df in SAS 9.2 were employed. For each student, time was scored as the elapsed time in years and tenths of years of the exact year and month of each subsequent measurement session relative to the modal month of measurement in first grade4 (November, 2001 for cohort 1; November, 2002 for cohort 2). Time was coded as 0 for the first grade measurement and outcomes at this first measurement point are termed initial status.
Following the results of earlier research (Sonnenschein, et al., 2010; Li-Grining, et al., 2010), at Level 1 (repeated measures) we estimated both a linear and a quadratic effect of time. In cases in which a child was retained in grade 1, the W scores from the repeat year were taken as the measure of Ytip for grade 1. Each Ytip was shifted back one year so that the child’s performance in grades 2, 3, 4, and 5 was represented. In other words, time was scored relative to November of the second (repeat) year of grade 1 for retained students.
- Level 1:
(1)
Here subscript t indicates grade, subscript i indicates individual, and p represents matched set. Ytip is the outcome, T represents elapsed time in years and months from the first measurement point (November of first grade) to each subsequent measurement point (roughly 0, 1, 2, 3, 4 corresponding to Grades 1 to 5, with specific values depending on the exact time of testing), and etip is the level 1 error of prediction which is assumed to be normally distributed with a variance of σ2. In growth models involving quadratic effects, special care must be exercised in interpreting growth parameters. π0ip represents the intercept, the predicted value of Y for person i in matched set p at the first measurement (initial status). π1ip represents the linear rate of increase for person i in matched set p in the value of Y per year at the first measurement (initial linear slope). This initial rate of increase is modified by π2ip which represents the rate of acceleration for person i in matched set p. Reflecting the nonlinear relationship, during each subsequent year the linear rate of increase will change by an amount equal to the acceleration.
At Level 2, several potential forms of effects of retention were considered. Equation (2) below estimates an effect representing a shift in level of achievement in Grade 1 on initial status. This effect represents the difference between the retained children assessed in November of the repeat year and the matched group of subsequently promoted children assessed in their first (and only) year of first grade. Equation (3) captures a potential effect of retention on the initial linear slope in Grade 1. Equation (4) captures a potential effect of retention on the rate of acceleration (or deceleration).
- Level 2:
(2) (3) (4)
Here β00p, β10p, and β20p represent the intercepts for the equations predicting the intercept, the initial linear slope, and the quadratic parameter, respectively, for the children in the Level 1 equation. β01p, β11p, and β21p represent the effect of retention on the intercept, initial linear slope, and quadratic parameter, respectively, for the children in the Level 1 equation. r0ip, r1ip, and r2ip represent residuals (errors of prediction) in the three Level 2 equations. Random effects were estimated for the intercept, initial slope, and acceleration at level 2 to capture potential individual differences in each of the parameters.
Level 3 accounts for the dependency (clustering) in the matched sets.
- Level 3:
(5)
γ000, γ100, and γ200 represent the mean of the intercept, initial linear slope, and rate of acceleration, respectively, for the promoted group (promoted = 0; retained = 1). γ010, γ110, and γ210 represent the effects of retention in first grade on the intercept, initial linear slope, and rate of acceleration, respectively, for the promoted group. u00p, u10p, and u20p represent residuals. Random effects were estimated for the intercept at level 3 to capture potential mean differences among matched sets in these parameters. Unless there are multiple pretests over time, groups are typically equated only on the baseline level (intercept). In addition, the cluster size (2–6) for the matched sets is too small to permit proper estimation of random effects for the slope and acceleration.
Baseline Models of the Form of Growth at Level 1
Prior to conducting the analysis of the focal research questions, three preliminary baseline analyses were conducted to verify that the hypothesized quadratic model was necessary to represent the growth trajectories of the children. In Model 1 (intercept), the predictors at level 1 (T, T2) were deleted from equation (1) and the predictor at level 2 (RETENTION) was deleted from equations (2), (3), and (4). Model 1 represents no growth. Model 2 (linear) added the predictor T at level 1 representing linear growth. Model 3 (quadratic) added the predictor T2 at Level 1 representing an increment from quadratic growth. Tables 5A and 5B present the estimates of the fixed effect parameters and the random variance components for the WJ Math and WJ Reading scores, respectively. Tables 6A and 6B present measures of model fit. The AIC and BIC are information theoretic indices for which lower values indicate better model fit (West, Taylor & Wu, in press). Both indices can show increased values when unimportant parameters are included in the model with the nature of the penalty for too many parameters differing between the two indices. The deviance values permit Likelihood Ratio (LR) tests testing the decrease in deviance relative to the nested comparison model. The results showed that, of the baseline models considered, the quadratic model provided the best fit to the data for both WJ Math and Reading in terms of the AIC, BIC, and LR tests, supporting the use of the quadratic model at level 1.
Table 5.
| A. Baseline Models for WJ Math | |||
|---|---|---|---|
| Term | Model 1 | Model 2 | Model 3 |
| Fixed Effects | |||
| Intercept | 484.95* | 463.18* | 459.80* |
| Linear | -------- | 10.37* | 14.46* |
| Quadratic | -------- | -------- | −1.15* |
| Variance Components | |||
| Intercept (L2) | 0.18 | 4.99 | 26.75* |
| Linear (L2) | ------- | 1.77* | 14.45* |
| Quadratic (L2) | ------- | ------- | 0.31 |
| Intercept (L3) | 30.46* | 86.84* | 87.58* |
| Residual (L1) | 302.77* | 36.58* | 30.16* |
| Covariance Components | |||
| Intercept and Slope | ------- | −3.35* | −22.17* |
| Intercept and Quadratic | ------- | ------- | 3.44* |
| Slope and Quadratic | ------- | ------- | −2.06* |
| B. Baseline Models for WJ Reading | |||
|---|---|---|---|
| Term | Model 1 | Model 2 | Model 3 |
| Fixed Effects | |||
| Intercept | 470.89* | 437.64* | 427.76* |
| Linear | -------- | 15.87* | 31.43* |
| Quadratic | -------- | -------- | −3.54* |
| Variance Components | |||
| Intercept (L2) | 31.39* | 47.47* | 55.67* |
| Linear (L2) | ------- | 1.20 | 14.06* |
| Quadratic (L2) | ------- | ------- | 0 |
| Intercept (L3) | 70.54* | 201.08* | 205.87* |
| Residual (L1) | 765.25* | 146.90* | 107.70* |
| Covariance Components | |||
| Intercept and Slope | ------- | −5.28 | −16.34 |
| Intercept and Quadratic | ------- | ------- | 1.23 |
| Slope and Quadratic | ------- | ------- | −1.34* |
Note. No retention effects were estimated. Model 1 includes an intercept at level 2. Model 2 includes an intercept and linear trend at level 2. Model 3 includes an intercept, linear trend, and quadratic deceleration at level 2. All models estimate the corresponding random variance components at level 2. All models estimate a random variance component at level 3 to account for the matching.
p < .05. Time was coded as years and tenths of years elapsed since the initial measurement in first grade (November) which was coded as 0. Tests of fixed effects are two-tailed; tests of variance components are one-tailed since variances must be positive or zero. L1 = level 1, L2 = level 2, L3 = level 3. ------- indicates not estimated. The quadratic variance component at Level 2 was fixed to 0 by the program.
Table 6.
| A. Model Fit WJ Math | ||||
|---|---|---|---|---|
| AIC | BIC | Deviance | Difference in deviance (LR test) from Comparison Model |
|
| Model 1- Intercept | 13865.3 | 13874.9 | 13857.3 | -------- |
| Model 2- Linear | 11288.7 | 11305.5 | 11274.7 | 2582.6, χ2 (3), p < .001 vs. Model 1 |
| Model 3- Quadratic | 11092.9 | 11119.2 | 11070.9 | 203.8, χ2 (4), p < .001 vs. Model 2 |
| B. Model Fit WJ Reading | ||||
|---|---|---|---|---|
| AIC | BIC | Deviance | Difference in deviance (LR test) From Comparison Model |
|
| Model 1- Intercept | 15379.2 | 15388.8 | 15371.2 | -------- |
| Model 2- Linear | 13323.9 | 13340.6 | 13309.9 | 2061.3, χ2 (3), p < .001 vs. Model 1 |
| Model 3- Quadratic | 12835.8 | 12859.7 | 12815.8 | 494.1, χ2 (4), p < .001 vs. Model 2 |
Note. AIC Akaike information criterion. BIC Bayesian information criterion. LR Likehood ratio.
Models of the Intervention Effect
Now consider the central research question of the effect of retention in grade 1 on achievement during the elementary school years. We added each of the intervention effects in turn represented by Level 2 equations (2), (3), and (4) to the baseline quadratic model of growth (Model 3). Model 4, the no growth model, estimated a constant change in level due to retention over the 5-year period (equation 2). Model 5, the linear model, estimated an initial change in level, plus potential differences in the linear component of the trajectories due to retention (equations 2, 3). Model 6, the quadratic model, estimated an initial change in level, an initial difference in linear slopes, plus potential differences in the rates of quadratic deceleration of growth due to retention (equations 2, 3, 4). Tables 6A and 6B, rows 1 to 3, present the estimates of the fixed effect parameters and the random variance components for the WJ Math and WJ Reading scores, respectively. Tables 7A and 7B present measures of model fit, again in rows 1 to 3. Model 6, the quadratic intervention model provided the best fit to the data in terms of the AIC and BIC. The LR tests showed that Model 6, the quadratic intervention model was a significant improvement over the linear intervention model for both WJ Math and Reading, χ2(1) = 8.50, p < .05, χ2(1) = 10.70, p < .01, respectively5.
Table 7.
| A. Models Including Intervention Effects for WJ Math | ||||
|---|---|---|---|---|
| Term | Model 4 | Model 5 | Model 6 | Model 7 |
| Fixed Effects | ||||
| Intercept | 459.41* | 458.71* | 458.10* | 459.46* |
| Linear | 15.47* | 15.81* | 16.54* | 16.51* |
| Quadratic | −1.15* | −1.14* | −1.31* | −1.30* |
| Retention Grade 1 | 1.28 | 3.62* | 5.51* | 4.48* |
| Retention 1 × linear | -------- | −1.18* | −3.62* | −3.52* |
| Retention 1 × quadratic | -------- | -------- | 0.54* | 0.51* |
| Retention Grades 2–4 | -------- | -------- | -------- | −7.51* |
| Variance Components | ||||
| Intercept (L2) | 26.21* | 26.04* | 25.89* | 26.77* |
| Linear (L2) | 14.44* | 13.47* | 11.94* | 11.98* |
| Quadratic (L2) | .31 | 0.31 | 0.26* | 0.26* |
| Intercept (L3) | 86.21* | 85.96* | 85.63* | 78.24* |
| Residual (L1) | 30.16* | 29.71* | 29.66* | 29.64* |
| Covariance Components | ||||
| Intercept and Slope | −21.60* | −20.52* | −19.70* | −19.33* |
| Intercept and Quadratic | 3.36* | 3.2* | 3.07* | 2.91* |
| Slope and Quadratic | −2.06* | −1.99* | −1.70* | −1.70* |
| B. Models Including Intervention Effects for WJ Reading | ||||
|---|---|---|---|---|
| Term | Model 4 | Model 5 | Model 6 | Model 8 |
| Fixed Effects | ||||
| Intercept | 426.65* | 424.06* | 423.22* | 424.88* |
| Linear | 31.42* | 32.45* | 33.81* | 33.79* |
| Quadratic | −3.54 | −3.54* | −3.82* | −3.82* |
| Retention Grade 1 | 3.53 | 11.59* | 14.52* | 13.11* |
| Retention 1 × linear | -------- | −3.36* | −8.02* | −8.03* |
| Retention 1 × quadratic | -------- | -------- | 1.00* | 1.00* |
| Retention Grades 2–4 | -------- | -------- | -------- | −8.78* |
| Variance Components | ||||
| Intercept (L2) | 60.04* | 74.79* | 82.55* | 48.43* |
| Linear (L2) | 14.04* | 13.41* | 14.00* | 14.03* |
| Quadratic (L2) | 0 | 0 | 0 | 0 |
| Intercept (L3) | 198.54* | 197.62* | 198.33* | 191.04* |
| Residual (L1) | 99.45* | 94.81* | 93.85* | 93.83* |
| Covariance Components | ||||
| Intercept and Slope | −15.33 | −17.57 | −23.97* | −23.70* |
| Intercept and Quadratic | 1.10 | 0.94 | 2.22 | 2.21 |
| Slope and Quadratic | −1.34* | −1.26* | −1.32* | −1.33* |
Note. Model 4 estimates the effect of retention in grade 1 on the intercept. Model 5 estimates the effect of retention in grade 1 on the intercept and linear slope. Model 6 estimates the effect of retention on the intercept, linear slope, and quadratic acceleration. Model 7 estimates the effect of retention at grade 1 on the intercept, linear slope, and quadratic acceleration, plus the effect of retention in grades 2–4 on the level. All models estimate the corresponding random variance and covariance components for the intercept, slope, and quadratic acceleration at level 2. These components are conditional on the specific grade retention effects included in the model. All models estimate a random intercept variance component for the intercept at level 3 to account for the matching.
p < .05. Time was coded as years and tenths of years elapsed since the initial measurement in first grade (November) which was coded as 0. Tests of fixed effects are two-tailed; tests of variance components are one-tailed since variances must be positive or zero. L1 = level 1, L2 = level 2, L3 = level 3.
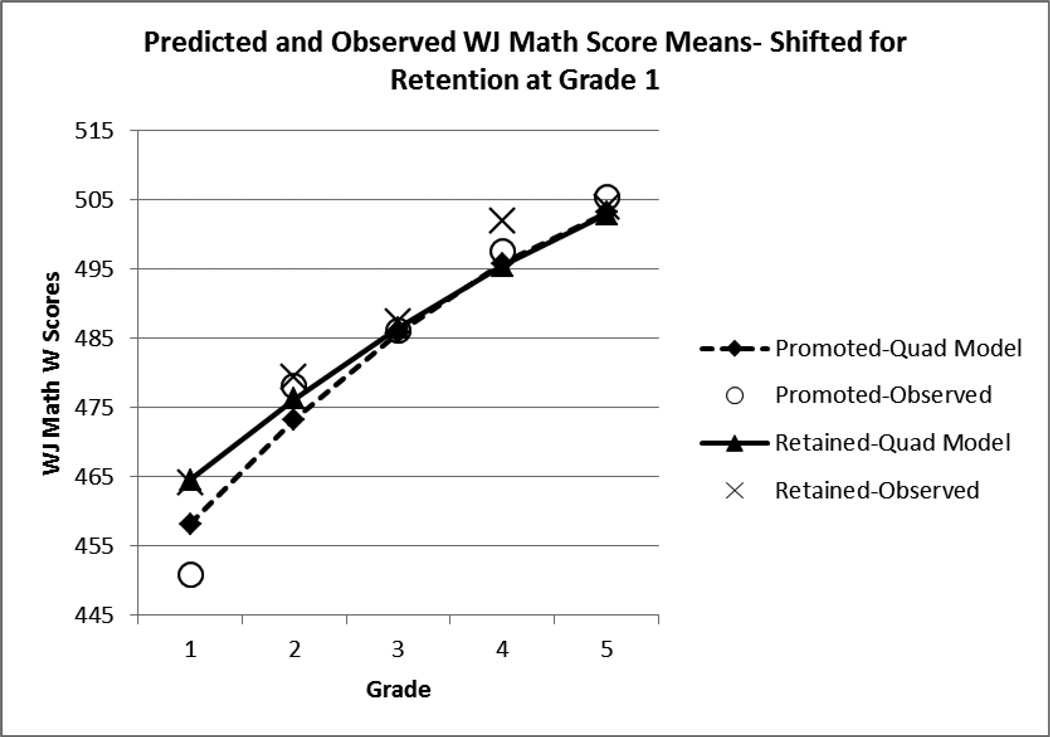
For the WJ Broad Math scores, the results showed a significant initial linear slope in the trajectory of the WJ Math scores for the promoted group, γ̂100= 16.54, t(75.6) = 27.66, p < .001, which was modified by a significant negative quadratic effect, γ̂200= −1.31, t(86.2) = −11.47, p < .001. This pattern indicated that the rate of yearly gain decreased slightly in each subsequent year. Of key importance were the three effects involving retention in first grade. The effect of retention on the initial level of the Math scores in Grade 1 was significant, γ̂010 = 5.51, t (580) = 4.05, p < .001, modified by a significant difference in the initial linear slope in the two groups, γ̂110 = −3.62, t(757) = −4.21, p < .001, and a significant difference in the quadratic acceleration of the two groups, γ̂210 = 0.54, t(633) = 2.97, p = .003. To put in perspective the estimate for the effect of retention on the initial level of math, γ̂010 = 5.51, consider that the average annual increase in Math W scores between ages 6 and 7 for the WJ-III normative sample is 13.97 (1.16 W points per month). To put in perspective the difference in initial slope estimates, γ̂110 = −3.62, consider that the average annual increase in Math W scores between ages 7 and 11 is 9.85 (0.82 W points per month, McGrew & Woodcock, 2001). As depicted in Figure 2, the students who were retained in Grade 1 showed an increase in WJ Broad Math scores during their repeat Grade 1 year, relative to comparable students during their initial year in Grade 1. However, over subsequent Grades 2 to 5 the net result is that this initial advantage dissipates. We tested this difference between the retained and promoted groups at Grade 2, the first year following retention by re-centering Time at Grade 2. The mean difference in WJ Math between the two groups was estimated to be 2.43, t(312) = 2.20, p = .03 indicating an immediate effect of retention when new material was encountered. We then tested this difference at Grade 5 by re-centering Time at Grade 5. The difference between the two groups was estimated to be −0.36, which is not significantly different from 0, t(447) = −.30, p = .77.
Figure 2.
Estimated quadratic growth curves of WJ Math W scores for children retained or promoted in first grade. Observed means for the promoted and retained groups are also depicted. Grade 1 scores for retained children are scores from their repeated first grade year.
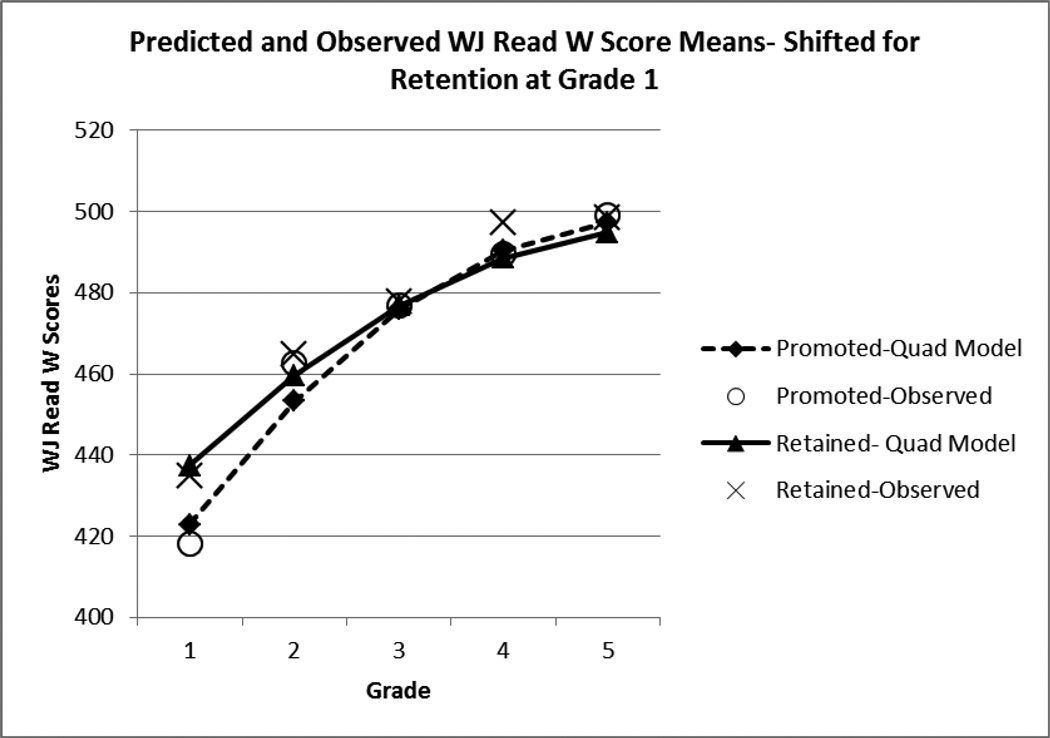
Similar results were obtained for the WJ Broad Reading scores. The results showed a significant initial linear slope in WJ Reading scores for the promoted group, γ̂100 = 33.81, t(710) = 38.38, p < .001, which was modified by a significant quadratic effect, γ̂200= −3.82, t(890) =−23.36, p < .001, again indicating that the rate of yearly gain decreased in each subsequent year. Of key importance were the three Level 2 effects involving retention. The initial effect of retention on Reading scores in Grade 1 was significant, γ̂010 = 14.52, t(643) = 6.42, p < .001, modified by a significant difference in the initial linear slope in the two groups, γ̂110 = −8.03, t(1118) = −5.58, p < .001, and a significant difference in the quadratic acceleration of the two groups, γ̂210 = 1.00, t(724) = 3.40, p < .001. To put in perspective the estimate for the effect of retention on the initial level of reading, γ̂010 = 14.52, consider that the average annual increase in Reading W scores between ages 6 and 7 for the WJ-III normative sample is 18.25 (1.52 W points per month). To put in perspective the difference in initial slope estimates, γ̂110 = −8.03, consider that the average annual increase in Reading W scores between ages 7 and 11 is 12.45 (1.04 W points per month, McGrew & Woodcock, 2001). As depicted in Figure 3, the students who were retained in Grade 1 show an increase in WJ Broad Reading scores during their repeat year, relative to comparable students during their only year in first grade. However, over subsequent Grades 2 to 5 the net result is that this initial advantage dissipates. We tested this difference between the retained and promoted groups at Grade 2, the first year following retention by re-centering Time at Grade 2. The mean difference in WJ Reading between the two groups was estimated to be 7.49, t(441), p < .001, indicating an immediate effect of retention when new material was encountered. We then tested this difference at Grade 5 by re-centering Time at Grade 5. The difference between the two groups was estimated to be −1.44, which is not significantly different from 0, t(379) = −0.75, p = .45.
Figure 3.
Estimated quadratic growth curves of WJ Reading W scores for children retained or promoted in first grade. Observed means for the promoted and retained groups are also depicted. Grade 1 scores for retained children are scores from their repeated first grade year.
In sum, these results show an initial increase in both Math and Reading scores during the repeat year which dissipates over time. Note that retained children are on average 1 year older than continuously promoted children at the completion of 5th grade.
Natural History of Retention and Special Education Placement in Elementary School
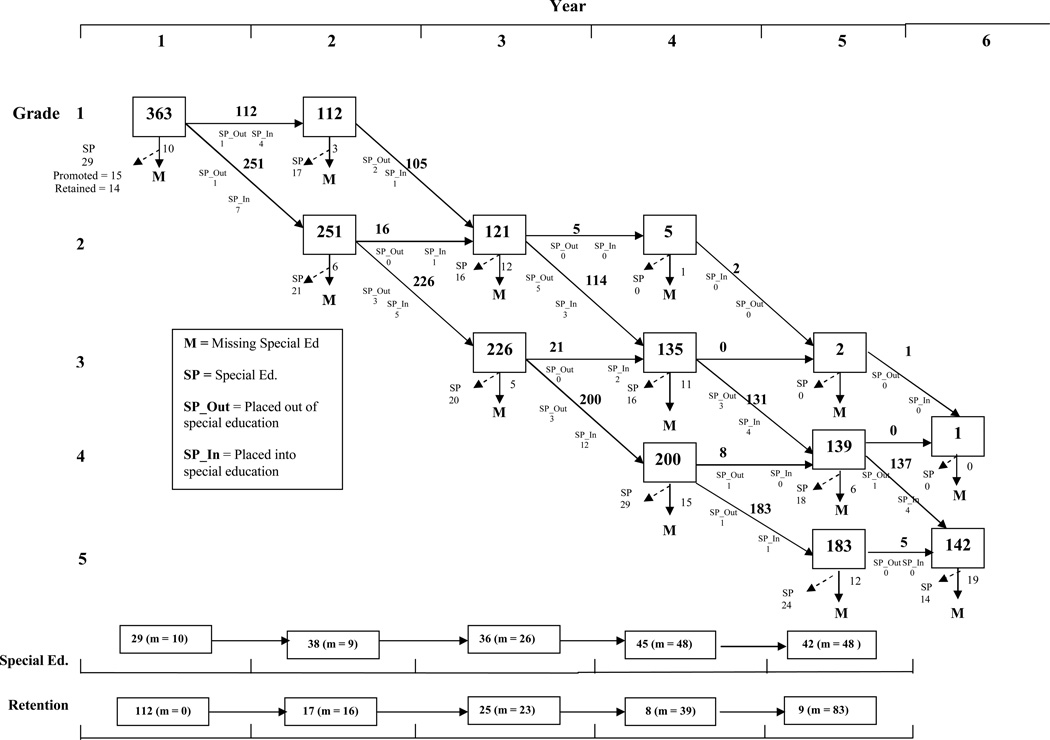
Figure 4 presents a flow chart illustrating the natural history of the students in this study. Focusing on the transitions from each year, the figure shows that approximately 4 to 9% of the students initially promoted in first grade were retained in each subsequent year (46 of 251 children promoted in first grade were subsequently retained), whereas only 4 of 112 children retained in first grade were subsequently retained a second time. The data also show that 28 of the 251 children promoted in first grade subsequently received placements into special education (with only 9 placing out of special education), whereas 8 of 112 children retained in first grade received placements in special education (with 10 placing out of special education). Tables 3 and 4 portray the demographics of students who were retained or promoted in each grade.
Figure 4.
Grade Retention and Special Education Assignment by Year. The flow chart depicts the pattern of retentions across the elementary school years. It also depicts the transitions into an out of special education each year. Missing cases are also indicated.
Table 3.
Number of Students Retained or Promoted at each Grade by Gender, Ethnicity, and Language
| Retained | Promoted | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Grade1 | Grade2 | Grade3 | Grade4 | Grade5 | Grade1 | Grade2 | Grade3 | Grade4 | Grade5 | |
| Gender | ||||||||||
| Male | 64 | 9 | 12 | 5 | 5 | 133 | 180 | 175 | 173 | 150 |
| Female | 48 | 8 | 13 | 3 | 4 | 118 | 150 | 140 | 143 | 121 |
| Ethnicity | ||||||||||
| Caucasian | 33 | 5 | 4 | 5 | 2 | 90 | 111 | 109 | 103 | 96 |
| Hispanic | 37 | 7 | 8 | 1 | 4 | 88 | 115 | 113 | 113 | 90 |
| African American | 37 | 5 | 12 | 1 | 3 | 62 | 90 | 82 | 90 | 78 |
| Asian | 3 | 0 | 1 | 1 | 0 | 8 | 9 | 7 | 6 | 5 |
| Other | 2 | 0 | 0 | 0 | 0 | 3 | 5 | 4 | 4 | 2 |
| Language | ||||||||||
| English | 101 | 7 | 20 | 7 | 7 | 217 | 273 | 274 | 255 | 239 |
| Spanish | 10 | 2 | 5 | 0 | 2 | 34 | 35 | 32 | 30 | 19 |
Note. Table includes only those students for whom retention status was known.
Table 4.
Number of Students Assigned or Not Assigned to Special Education at Each Grade by Gender and Ethnicity
| Special Education | Not in Special Education | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Grade1 | Grade2 | Grade3 | Grade4 | Grade5 | Grade1 | Grade2 | Grade3 | Grade4 | Grade5 | |
| Gender | ||||||||||
| Male | 19 | 25 | 24 | 29 | 26 | 170 | 164 | 157 | 144 | 147 |
| Female | 10 | 13 | 12 | 16 | 16 | 154 | 152 | 144 | 126 | 123 |
| Ethnicity | ||||||||||
| Caucasian | 12 | 17 | 15 | 16 | 15 | 110 | 102 | 97 | 89 | 91 |
| Hispanic | 6 | 7 | 5 | 9 | 6 | 114 | 115 | 112 | 104 | 105 |
| African American | 10 | 14 | 16 | 19 | 20 | 85 | 85 | 79 | 69 | 71 |
| Asian | 1 | 0 | 0 | 1 | 1 | 10 | 9 | 9 | 7 | 4 |
| Other | 0 | 0 | 0 | 0 | 0 | 5 | 5 | 4 | 1 | 2 |
| Language | ||||||||||
| English | 29 | 34 | 36 | 39 | 41 | 283 | 254 | 260 | 220 | 232 |
| Spanish | 0 | 0 | 0 | 1 | 1 | 39 | 38 | 37 | 32 | 29 |
Note. Table includes only those students for whom special education assignment was known.
Based on the natural history, two broad questions can be addressed. First, were children retained in first grade less likely than their promoted peers to be retained in subsequent grades? Children retained at the end of first grade were subsequently retained in a later grades at a lower rate (3.6%) than children promoted at the end of first grade (18.3%), χ2(1) = 10.45, φ correlation = .17, p < .001. The decision to retain a child in a grade was less likely if the child has been previously retained, with only approximately 3% of the children in the entire sample being doubly retained. Second, were children retained in first grade less likely to ever be placed in special education than children promoted at the end of first grade? The rate at which children retained at the end of first grade (7.1%) did not differ from the rate at which children promoted at the end of first grade (11.2%) were placed in special education, χ2(1) =.04, φ correlation = .01, p = .84.
How Does Retention in Later Grades Affect Math and Reading Achievement Scores?
The effect of retention in later grades on Math and Reading scores was examined by modifying the Level 2, Equation (2) to include a second dummy variable for retention in Grades 2, 3, or 4, in addition to the dummy variable for retention in Grade 1.
- Level 2:
(5)
Only the effects of retention in Grades 1 to 4 were examined so that the performance of all children could be assessed following retention during at least one year in which they encountered new material rather than repeating material from the previous year.
Does retention in Grades 2, 3, or 4 lead to a shift in the level of the growth trajectories at the point of retention? We addressed this question in two ways. First, only W scores for students retained in first grade were shifted back one grade, exactly as was done in the main analysis above. This analysis permits a grade-based comparison for the students retained in first grade, but not for students retained in later grades. This comparison parallels those commonly made in previous research on grade retention. Otherwise stated, the retention effects in Grades 2 through 4 do not reflect later adjustments for grade level of classmates for students who are retained beyond first grade (i.e., these later retained students are not shifted back for retentions beyond first grade). For WJ Broad Math, retention in Grades 2, 3, or 4 was associated with a drop in level of −7.51, t(359) = −5.20, p < .001. For WJ Broad Reading, retention in Grades 2, 3, or 4 was associated with a drop in level of −8.78, t(344) = −3.71, p < .001. To put the magnitude of these differences in perspective, consider that at ages 8, 9, and 10 the average annual increase in Broad Math scores in the standardization sample was 14.45, 9.17, and 8.7 W points, respectively. For Broad Reading the average annual increase at ages 8, 9, and 10 was 19.49, 14.32, and 11.2 W points, respectively (McGrew & Woodcock, 2001). Although the groups that are retained versus promoted in first grade were matched on propensity scores based on variables measured during the initial year of the study prior to any retention, effects of later retention were not adjusted for any time-varying measures that occur after first grade (e.g., child’s subsequent achievement, behavioral adjustment). Rosenbaum (1984) notes that controlling for covariates measured after treatment (here, retention in grade 1) can seriously confound the interpretation of the results of later treatment effects.
In the second set of analyses, performance was evaluated relative to the retained student’s current grade mates, regardless of when the student was retained. When children were subsequently retained in Grades 2, 3, or 4, the score on the Woodcock-Johnson was used from the second year the child was in the grade in which retention occurred. In other words, the data were shifted back one year at each retention point to allow comparison with the then current grade mates of the retained and promoted students, permitting a grade-based comparison. When the data were also shifted back at the later retention points, the effect of retention in Grades 2, 3, and 4 no longer showed a significant drop when the performance of promoted students was compared with that of the retained students the second time they took the grade. For WJ Broad Math, retention in Grades 2, 3, or 4 led to a non-significant change of −2.74, t(360) = −1.87, p = .06; For WJ Broad Reading, retention in Grades 2, 3, or 4 led to a non-significant change of −2.69, t(353) = −1.11, p = .27. Presumably, no improvement in achievement was shown for retention in Grades 2–4 because the additional learning opportunity for the retained students is confounded with the selection of the poorer performing students for retention.
Discussion
In the present research, the effects of retention in first grade and in subsequent grades were examined, comparing the math and reading achievement of retained children to their closely matched promoted peers when they were in the same grade as the retained child. The potential use of a second intervention option, placement into special education, in lieu of further retentions was also examined. Finally, the natural history of at-risk students was described, mapping students’ retention status and special education status from Grades 1 through 5, including the entrance and exit into special education status at each grade.
Effects of Retention in First grade
For both math and reading achievement scores, there is an initial advantage in achievement for students’ repeated first grade scores compared to their promoted peers’ first grade scores. However, this effect dissipates over time, such that by Grade 5 the retained students have somewhat lower math and negligibly lower reading scores than their promoted peers at 5th grade. By shifting back students retained in first grade by one year, retained students are compared with their promoted peers at the same grade but not at the same age. Retained students are, on average, 1 year older than their propensity-matched peers. The yearly rate of increase in achievement decreases each year (negative acceleration) as the child ages regardless of the child’s retention status. The boost provided by the repeat year slowly dissipates over the elementary school years because of the reduced rate of gain of the retained students relative to the promoted students. To the best of our knowledge, this study is the first to provide a direct test of the impact of retention in first grade on children’s achievement throughout the elementary grades, relative to same-grade peers, employing state of the art controls for selection effects, and considering the possible effects of later retentions. These results suggest that had the students who were retained in first grade been promoted instead, they would have performed as well by the end of fifth grade on a well-validated, nationally standardized measure of reading and math achievement as they did. These results challenge the conclusion drawn from often-cited meta-analytic studies that grade retention negatively impacts students’ achievement (Holmes, 1989; Jimerson, 2001a). However, results of the current study offer little evidence that grade retention has longer-term beneficial effects on students’ achievement.
Natural History of Grade Retention
The descriptive data on two interventions, grade retention and special education placement, for a sample of 363 students who were at equal risk for retention during their first year in first grade over the course of their elementary school career were revealing. Prior studies on the impact of grade retention have rarely provided such information. The most striking finding is that early grade retention protects students from later grade retention. First graders who were promoted following their first year in first grade despite having an equivalent probability of being retained in first grade, were more than 5 times as likely to be retained in Grades 2–4 than were their peers who were retained in first grade. Within the initial sample of students at equivalent risk of being retained in first grade, some children are retained in first, some children are retained in subsequent grades, and some children are never retained. Research on the effects of retention has rarely examined differences between these three groups of students. Although educators believe that retention in kindergarten or first grade is less harmful to students than is retention in higher grades (Tomchin & Impara, 1992), the present results indicate that in terms of same-age comparisons, which have the most straightforward interpretation, retention leads to similar magnitude of drops in achievement relative to similar children who were promoted, across the elementary school period of Grades 1–5. This finding is consistent with results of a recent meta-analytic study that reported no difference in effect of retention as a function of the grade retained (Allen et al., 2009).
Students retained in Grades 1–4 and students consistently promoted were equally likely to receive special education services. Whereas grade retention may decrease the risk of subsequent retention in grade, it apparently does not change the risk of enrollment in special education by Grade 5.
Effects of Retention in Subsequent Grades
Subsequent retentions in Grades 2, 3, or 4 were associated with a drop of 7.51 points in Math and 8.78 in Reading relative to peers matched at entrance to first grade who were promoted in those grades. When retained children were compared to their same-grade promoted peers (i.e., scores shifted back for each subsequent retention), there were no significant drops in math or reading scores.
Strengths, Limitations, and Future Research
Strengths and Limitations
The present study has many strengths, the first of which is the use of propensity scores to match at risk students who were retained in first grade with at risk students who were promoted in first grade on a wide array of variables. The use of propensity score matching reduces biases between the promoted students and retained students, as it effectively controls for pre-existing differences on the 72 measured variables. Rubin (2007) has argued that the use of propensity scores based on an extensive set of covariates and careful checking of the balance that is achieved between treatment and control groups yields a design that mimics the randomized experiment as closely as possible with respect to the observed covariates. Shadish, Clark, and Steiner (2008) showed in an experiment in which participants were randomized to an experiment or a parallel observational study in which participants chose their treatment condition that the estimates of the treatment effect in the randomized and non-randomized arms did not differ when a rich set of baseline variables was used in the analysis of the observational study. In the present study, our examination of the effects of grade retention on achievement makes the assumption that the 72 measured baseline variables fully account for differences between the retained and promotion groups at baseline. To the extent that additional unmeasured baseline variables can be identified that are related to both retention status and achievement outcomes over and above the present 72 measured baseline variables, the results may be biased.
In this study, 6 waves of data were used, permitting the testing of the hypothesized nonlinear (quadratic) trajectory of the Math and Reading scores. The analyses detected the quadratic curve of scores for retained and promoted students, highlighting the eventual diminishing “boost” of retention observed in first grade on math and reading scores. The use of 6 waves of data also permitted the examination of the effects of both the initial retention in first grade, and the effects of subsequent retentions. Shifting students for the initial retention and the subsequent retentions allowed for a more direct comparison of retained students with their grade-based promoted peers.
Aside from examining the effects of grade retention, subsequent placement into special education was also explored. These two types of interventions are not mutually exclusive, as can be seen in Table 4. In the present study, a natural history of the students’ grade retention or promotion and placement into special education has been provided. The pattern of grade retention and special education entrance and exit were displayed. This provides descriptive information as to the number of children who receive each type of intervention.
An important limitation of this study is the fact that while the propensity score matching does provide good control for differences between the retained and promoted children on 72 baseline variables measured at the beginning of the study, differences in some of these variables that may have occurred after the first wave of data collection were not statistically controlled. Thus, there may be effects of changes in measured covariates such as behavioral conduct or teacher-student relations on students’ Math or Reading scores after the first wave of data collection that are not accounted for in the present study. Developing appropriate statistical controls for covariates measured after an intervention has taken place is extremely challenging (Rosenbaum, 1984; Singer & Willett, 2002).
An additional potential limitation is our data on special education status. Our goal is this study was only to examine whether special education might be used as a second form of intervention with our target population of low achieving students, not to study the effects of special education programs. These data came from three sources; school district records, teacher questionnaires, and parents report. If information from at least one of these sources was known, it was included in the analyses. In rare cases, reporting sources had discrepant information. In these cases, priority was given to school district report, teacher report, and parent report, in that order. Furthermore, school district records, the primary source of information on special education status, did not specify the disability condition under which children were enrolled in special education placement. Our results do not necessarily generalize to higher achieving students who are retained in grade or to children enrolled in special education in first grade for other than speech and language services.
Another limitation is that due to attrition, there were missing data on both the outcomes and predictors. Data were collected from 100% of the sample year 1 of the study and 80% of the sample year 6. Procedures adapted from Ribisl et al. (1996) were used to maximize the proportion of students in the sample that were retained across the up to 6 years of data collection. Given that missing data inevitably occurs, full information maximum likelihood (FIML) estimation was used to handle missing data. FIML provides proper adjustment for all variables included in the analysis (Enders, 2010; Schafer & Graham, 2002). FIML does not adjust for the unique effects of other, unmeasured variables over and above the measured variables. Nor does it always provide proper adjustment if the participant’s (missing) level on the variable is a source of missingness. Nonetheless, FIML has been shown to substantially reduce biases that may be due to missing data and is currently viewed as one state of the art method for its treatment.
Future Research
Retention has been treated as a dichotomous event (retained or promoted in a given grade). Yet the flow chart showing the natural history of retained and promoted students suggests that such a dichotomy is an oversimplification. Children at equal risk of retention in first grade form three primary groups: Retained in first (32.3%), promoted in first but retained in Grades 2–5 (delayed retention, 16.2%), and continuously promoted (51.5%). Future research is needed to determine the psychosocial and academic consequences of these 3 histories. For example, do children retained in first grade differ in achievement or psychosocial adjustment in middle school, relative to their propensity matched, “delayed retention” peers?
Policy Implications
The initial improvement retained students make, relative to their younger grade mates, is likely a powerful motivator for educators. Teachers of the retained students observe their success in the repeat year classroom but may not have the opportunity to observe these students’ performance 2 to 5 years later. If teachers were made aware that the immediate boost retained children experience dissipates over the following 3–4 years, they might be less likely to recommend this intervention. In essence, by the end of elementary school, children retained and children promoted in first grade do not differ in their levels of achievement in math or reading, but with an additional cost of one year of additional schooling for the retained children.
The critical role of early literacy to normal school progression is widely acknowledged (National Institute for Literacy, 2007, as cited in Landry, Anthony, Swank, & Monseque-Bailey, 2009; Snow, Burns, & Griffin, 1998). Consistent with this view, in previous research, the strongest predictor by far of being retained in first grade was low performance in 1st grade on the WJ Broad Reading test (Willson & Hughes, 2009). Neither a measure of general cognitive ability nor measures of social, emotional, or behavioral characteristics or demographic variables (e.g., SES, race and ethnicity) substantially improved prediction over academic achievement and age. Therefore, effective early reading interventions would be expected to decrease the number of children who are retained in first grade. Other types of interventions (e.g., disciplinary interventions) may be needed for other populations of children with behavioral or other deficits.
For children who are retained, the repeat year should involve intensive remediation efforts. Most retained students are exposed to the same material and instructional resources as used in the previous year (Peterson & Hughes, 2011; Stone & Engel, 2007). However, retained students who are provided supplemental, individualized resources and supports during the repeat year increase more in achievement (Karweit, 1999; Holmes, 1989; Stone & Engel, 2007). Such intensive interventions may begin to prepare retained students to meet the academic challenges beyond the repeat year, when they encounter novel material. However, it is likely that low achieving retained students may need additional interventions in later grades if they are to continue to maintain their improvement in achievement.
Conclusions
These results extend previous research on retention effects. Using a more direct test of the effects of retention on students’ performance relative to their grade-mates, these results extend and refine those of Wu et al. (2008a). Retention in first grade results in an initial increase in scores on a nationally standardized measure of reading and math achievement that dissipates beyond the repeat year and is lost by the time students are in 5th grade. It is important to note that these results may have differed had achievement been measured with a curriculum-aligned measure, such as the state accountability test. Indeed, when students in a longitudinal sample were in the 3rd grade, students retained in first grade were somewhat more likely to pass the state accountability math test than were their propensity score-matched, promoted peers (Hughes, Chen, Thoemmes, & Kwok, 2010). The ability to teach to the test may lead to improvement in the specific areas assessed on the state accountability test, but not to more general improvement in math and reading achievement. Thus, the answer to the question, “What is the effect of retention on achievement?” likely differs based on how achievement is assessed.
The current study analyzed growth trajectories of scores on a psychometrically strong measure of reading and math ability. The use of a strong measure of achievement and propensity matching to control for child differences associated with selection into the retention intervention, and the analysis of growth trajectories based on six annual waves of data provides some of the clearest evidence to date that grade retention fails in its goal of “recalibrating” students who are struggling academically by giving them another year to “catch up” with their peers. Four years after the repeat year, students retained in first grade were no closer to their 5th grade peers in achievement than they would have been if they had been promoted.
Table 8.
| A. Model Fit WJ Math | ||||
|---|---|---|---|---|
| AIC | BIC | Deviance | Difference in deviance (LR test) from comparison model |
|
| Model 4- Retention Grade 1-Level |
11093.6 | 11122.3 | 11069.6 | 1.3, χ2 (1), ns vs. Model 3 |
| Model 5- Retention Grade 1--Linear |
11073.7 | 11104.8 | 11047.7 | 21.9, χ2 (1), p < .001 vs. Model 4 |
| Model 6- Retention Grade 1-Quadratic |
11067.2 | 11100.7 | 11039.2 | 8.5, χ2 (1), p < .01 vs. Model 5 |
| Model 7- Retention Grades 1 plus 2 – 4 |
11043.7 | 11079.6 | 11013.7 | 25.5, χ2 (1), p < .001 vs. Model 6 |
| B. Model Fit WJ Reading | ||||
|---|---|---|---|---|
| AIC | BIC | Deviance | Difference in deviance (LR test) from comparison model |
|
| Model 4- Retention Grade 1-Level |
12834.5 | 12860.9 | 12812.5 | 3.3, χ2 (1), ns vs. Model 3 |
| Model 5- Retention Grade 1--Linear |
12769.9 | 12798.7 | 12745.9 | 66.6, χ2 (1), p < .001 vs. Model 4 |
| Model 6- Retention Grade 1-Quadratic |
12761.2 | 12792.3 | 12735.2 | 10.7, χ2 (1), p < .01 vs. Model 5 |
| Model 7- Retention Grades 1 plus 2 – 4 |
12749.7 | 12783.3 | 12721.7 | 13.5, χ2 (1), p < .001 vs. Model 6 |
Acknowledgments
This research was supported by NICHHD grant # HD39367 to Jan N. Hughes.
Footnotes
Six observation periods captures the full elementary school period for all promoted and singly retained children. Doubly retained children (n = 4) had missing data in grade 5.
The many to one matching procedure led to overall good balance on 72 baseline variables. A series of 2 (retention) × 5 (quantile strata) ANOVAs for continuous variables and logistic regressions for dichotomous variables identified 6 significant effects at p < .05, whereas 7.2 would be expected by chance. The maximum effect size on the baseline measures (η2 = .047) was less than moderate in magnitude according to Cohen’s (1988) guidelines. Significant baseline main effects or interactions involving retention were found on math raw achievement, ethnicity (white vs. nonwhite), parent rated internalizing problems, percentage of white students in class, and family adversity among the 75 baseline measures. Sensitivity analyses conducted using (a) the five unique significant measures from the full set of 72 baseline measures as covariates in the level-2 model to adjust for baseline differences. The effects of retention after partialling out these sets of covariates did not differ materially from those without the covariates added.
We also explored the Kenward-Roger correction for standard errors in small samples (Littell, Milliken, Stroup, & Wolfinger, 2006). Obtained t-values changed by a maximum of 0.02 and no conclusion of any analysis was affected.
These exact time analyses reported below are potentially more precise than grade level analyses (Mehta & West, 2000). All analyses were also conducted using grade level as the time interval. No conclusion of any analysis was changed by the alteration of the time metric; the estimates were only modestly different than those reported below.
A variety of other nonlinear models within the polynomial and exponential families could also be considered. Given five fixed measurement points (the fixed time design is approximated here given the small variation in the measurement times), the highest order trajectory that can be tested in the polynomial family is a quartic model. We estimated a quartic model with random effects, but it failed to converge for either WJ Math or Reading. Given that that we hypothesized a quadratic trajectory and it produced a very good fit to the means at each grade level (see Figure 2), we did not pursue other models.
Contributor Information
Stephanie E. Moser, Department of Psychology, Arizona State University
Stephen G. West, Department of Psychology, Arizona State University
Jan N. Hughes, Department of Educational Psychology, Texas A & M University
References
- Allen C, Chen Q, Willson V, Hughes JN. Quality of design moderates effects of grade retention on achievement: A meta-analytic, multi-level analysis. Educational Evaluation and Policy Analysis. 2009;31:480–499. doi: 10.3102/0162373709352239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beebe-Frankenberger M, Bocian KM, MacMillan DL, Gresham FM. Sorting second-grade students: Differentiating those retained from those promoted. Journal of Educational Psychology. 2004;96:204–215. [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. 2nd Ed. Hillsdale, NJ: Erlbaum; 1988. [Google Scholar]
- Cohen P, Cohen J, West SG, Aiken LS. Applied multiple regression/correlation analysis for the behavioral sciences. 3rd Ed. Hillsdale: Erlbaum; 2003. [Google Scholar]
- Enders CK. Applied missing data analysis. New York: Guilford; 2010. [Google Scholar]
- Holmes CT. Grade-level retention effects: A meta-analysis of research studies. In: Shepard LA, Smith ML, editors. Flunking grades: Research and policies on retention. London: The Falmer Press; 1989. pp. 16–33. [Google Scholar]
- Hong G, Raudenbush SW. Effects of kindergarten retention policy on children's cognitive growth in reading and mathematics. Educational Evaluation and Policy Analysis. 2005;27(3):205–224. [Google Scholar]
- Hughes JN, Chen Q, Thoemmes F, Kwok O. An investigation of the relationship between retention in first grade and performance on high stakes test in 3rd grade. Educational Evaluation and Policy Analysis. 2010;32:166–182. doi: 10.3102/0162373710367682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimerson SR. Meta-analysis of grade retention research: Implications for practice in the 21st century. School Psychology Review. 2001a;30:420–437. [Google Scholar]
- Jimerson SR. A synthesis of grade retention research: Looking backward and moving forward. The California School Psychologist. 2001b;6:47–59. [Google Scholar]
- Jimerson S, Carlson E, Rotert M, Egeland B, Sroufe LA. A prospective, longitudinal study of the correlates and consequences of early grade retention. Journal of School Psychology. 1997;35:3–25. [Google Scholar]
- Karweit N. Grade Retention: Prevalence, Timing, and Effects. Baltimore: Johns Hopkins University, Center for Research on Students Placed at Risk; 1999. [Google Scholar]
- Khoo S-T, West SG, Wu W, Kwok O-M. Longitudinal methods. In: Eid M, Diener E, editors. Handbook of psychological measurement: A multimethod perspective. Washington, DC: American Psychological Association books; 2005. [Google Scholar]
- Landry SH, Anthony JL, Swank PR, Monseque-Bailey P. Effectiveness of comprehensive professional development for teachers of at-risk preschoolers. Journal of Educational Psychology. 2009;101:448–465. [Google Scholar]
- Li-Grining CP, Votruba-Drzal E, Maldonado-Carreño C, Haas K. Children's early approaches to learning and academic trajectories through fifth grade. Developmental Psychology. 2010;46:1062–1077. doi: 10.1037/a0020066. [DOI] [PubMed] [Google Scholar]
- Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberber O. SAS for Mixed Models. 2nd ed. Cary, NC: SAS Publishing; 2006. [Google Scholar]
- Lorence J. Retention and academic achievement research revisited from a United States perspective. International Education Journal. 2006;7:731–777. [Google Scholar]
- McCoy AR, Reynolds AJ. Grade retention and school performance: An extended investigation. Journal of School Psychology. 1999;37:273–298. [Google Scholar]
- McGrew KS, Woodcock RW. Technical manual: Woodcock-Johnson III. Itasca, IL: Riverside Publishing; 2001. [Google Scholar]
- Ming K, Rosenbaum PA. A note on optimal matching with variable controls using the assignment algorithm. Journal of Computational and Graphical Statistics. 2001;10:455–463. [Google Scholar]
- Mehta P, West SG. Putting the individual back in individual growth curves. Psychological Methods. 2000;5:23–43. doi: 10.1037/1082-989x.5.1.23. [DOI] [PubMed] [Google Scholar]
- Owings WA, Magliaro S. Grade retention: A history of failure. Educational Leadership. 1998;56:86–88. [Google Scholar]
- Peterson L, Hughes JN. Differences between retained and promoted children in educational services received prior to and after retention year. Psychology in the Schools. 2011;48:156–165. doi: 10.1002/pits.20534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribisl KM, Walton MA, Mowbray CT, Luke DA, Davidson WS, II, Bootsmiller BJ. Minimizing participant attrition in panel studies through the use of effective retention and tracking strategies: Review and recommendations. Evaluation and Program Planning. 1996;19:1–25. [Google Scholar]
- Rosenbaum PR. The consequences of adjustment for a concomitant variable that has been affected by treatment. Journal of the Royal Statistical Society, Series A. 1984;147:656–666. [Google Scholar]
- Rosenbaum PR. Design of observational studies. New York: Springer; 2010. [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70:41–55. [Google Scholar]
- Rubin DB. The design versus the analysis of observational studies for causal effects: Parallels with the design of randomized trials. Statistics in Medicine. 2007;26:20–36. doi: 10.1002/sim.2739. [DOI] [PubMed] [Google Scholar]
- SAS Institute Inc. Base SAS 9.2 procedures guide. Cary, NC: SAS Institute Inc.; 2008. [Google Scholar]
- Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychological Methods. 2002;7:147–177. [PubMed] [Google Scholar]
- Shadish WH, Clark MH, Steiner PM. Can nonrandomized experiments yield accurate answers? A randomized experiment comparing random and nonrandom assignments. Journal of the American Statistical Association. 2008;103:1334–1344. [Google Scholar]
- Shepard LA, Smith ML, Marion SF. Failed evidence on grade retention [Review of the book, On the success of failure: A reassessment of the effects of retention in the primary grades] Psychology in the Schools. 1996;33:251–261. [Google Scholar]
- Singer JD, Willett JB. Applied longitudinal data analysis: Modeling change and event occurrence. New York: Oxford; 2003. [Google Scholar]
- Sipple JW, Killeen K, Monk DH. Adoption and adaptation: School district responses to state imposed learning and graduation requirements. Educational Evaluation and Policy Analysis. 2004;26:143–168. [Google Scholar]
- Snow CE, Burns MS, Griffin P, editors. Preventing reading difficulties in young children. Washington, DC: National Academy Press; 1998. [Google Scholar]
- Sonnenschein S, Stapleton LM, Benson A. The relation between the type and amount of instruction and growth in children’s reading competencies. American Educational Research Journal. 2010;47:358–389. [Google Scholar]
- Stone S, Engel M. Same old, same old? Students' experiences of grade retention under Chicago's ending social promotion policy. American Journal of Education. 2007;113:605–634. [Google Scholar]
- Tomchin EM, Impara JC. Unraveling teachers’ beliefs about grade retention. American Educational Research Journal. 1992;29:199–123. [Google Scholar]
- West SG, Taylor AB, Wu W. Model Fit and Model Selection in Structural Equation Modeling. In: Hoyle RH, editor. Handbook of Structural Equation Modeling. New York: Guilford; (in press). [Google Scholar]
- Willson VL, Hughes JN. Retention of Hispanic/Latino students in first grade: Child, parent, teacher, school, and peer predictors. Journal of School Psychology. 2006;44:31–49. doi: 10.1016/j.jsp.2005.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willson VL, Hughes JN. Who is retained in first grade? A psychosocial perspective. The Elementary School Journal. 2009;109:251–266. doi: 10.1086/592306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock RW, Johnson MB. Woodcock-Johnson Psycho-educational Battery-Revised. Allen, TX: DLM Teaching Resources; 1989. [Google Scholar]
- Woodcock RW, Munoz-Sandoval AF. Woodcock-Munoz Language Survey. Riverside, CA: Riverside Publishing; 1993. [Google Scholar]
- Woodcock RW, Muñoz-Sandoval AF. Batería Woodcock-Muñoz: Pruebas de aprovechamiento – Revisada. Itasca, IL: Riverside Publishing; 1996. [Google Scholar]
- Woodcock RW, Munoz-Sandoval AF. Woodcock-Munoz Language Survey Normative Update. Itasca, IL: Riverside Publishing; 2001. WMLS Normative Update Scoring and Reporting Program [Computer software] [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson III Tests of Achievement. Riverside, CA: Riverside Publishing; 2001. [Google Scholar]
- Wu W, West SG, Hughes JN. Effect of retention in first grade on children’s achievement trajectories over four years: A piecewise growth analysis using propensity score matching. Journal of Educational Psychology. 2008a;100:727–740. doi: 10.1037/a0013098. [DOI] [PMC free article] [PubMed] [Google Scholar]