Smoothed functional principal component analysis for testing association of the entire allelic spectrum of genetic variation

Abstract

Fast and cheaper next-generation sequencing technologies will generate unprecedentedly massive and highly dimensional genetic variation data that allow nearly complete evaluation of genetic variation including both common and rare variants. There are two types of association tests: variant-by-variant test and group test. The variant-by-variant test is designed to test the association of common variants, while the group test is suitable to collectively test the association of multiple rare variants. We propose here a smoothed functional principal component analysis (SFPCA) statistic as a general approach for testing association of the entire allelic spectrum of genetic variation (both common and rare variants), which utilizes the merits of both variant-by-variant analysis and group tests. By intensive simulations, we demonstrate that the SFPCA statistic has the correct type 1 error rates and much higher power than the existing methods to detect association of (1) common variants, (2) rare variants, (3) both common and rare variants and (4) variants with opposite directions of effects. To further evaluate its performance, the SFPCA statistic is applied to ANGPTL4 sequence and six continuous phenotypes data from the Dallas Heart Study as an example for testing association of rare variants and a GWAS of schizophrenia data as an example for testing association of common variants. The results show that the SFPCA statistic has much smaller P-values than many existing statistics in both real data analysis examples.

INTRODUCTION

Resequencing of genomes will generate unprecedentedly high-dimensional genetic variation data that allow nearly complete evaluation of the genetic variation including several million common (>5% population frequency), low frequency (<1% and <5% population frequency) and rare variants (<1% population frequency) in the typical human genomes.^{1, 2} Despite their promise, next-generation sequencing (NGS) technologies suffer from three remarkable limitations: high error rates, enrichment of rare variants and large proportion of missing values.^{3, 4} Since an individual rare variant would have a relatively small impact on the common disease and the rare variants have very low frequencies in the populations, the power of the traditional analytical tools that are mainly designed for the purpose of detecting common variants, for testing association of rare variants will be limited. Developing new analytical tools for the analysis of the massive sequencing data poses a novel and great challenge to statistical analysis.⁵

Genetic studies of complex diseases are undergoing a paradigm shift from the single market analysis to the joint analysis of multiple variants in a genomic region that can be genes or other functional units.⁶ Large simulations have shown that combining information across multiple variants in a genomic region of analysis will greatly enhance power to detect association of rare variants.² In the past several years, various versions of collapsing methods in which all rare variants are collapsed and treated as a single variable for analysis have been developed.^{2, 3, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17} Although in some cases group tests have a higher power than the individual tests, they also suffer limitations. First, group tests ignore difference in the effects of SNPs at different genomic locations on phenotype. Second, group tests do not leverage linkage disequilibrium (LD) in the data. And third, since sequence errors are cumulative when rare variants are grouped, group tests are sensitive to the genotyping errors and missing data. To utilize the advantages of both single variant analysis and group tests and address the limitations inherent by single variant analysis and group tests, we view the genome as a continuum and variants in the genome as a realization of a stochastic process which can be modeled as a random function and proposed to use functional principal component analysis (FPCA) for testing the association of rare variants with disease.¹⁸ FPCA can greatly enhance the power to detect association of variants. However, when the genetic variant functions in FPCA rapidly change within the genomic region, the basis expansion in the FPCA cannot approximate the genetic variation data well, which will decrease the power of FPCA. To overcome this limitation, we propose to develop the smoothed FPCA (SFPCA) for testing the association of rare variants that combines a measure of goodness-of-fit with a roughness penalty to retain the advantages of basis expansion, but circumvent its limitation.

Group tests often make implicit homogeneity assumptions where all putatively functional variants within the same genomic region are assumed to have the same direction of effects. However, in practice, the variants with opposite directions of effects will be simultaneously presented in the same genomic region.⁵ Group tests have difficulties in dealing with heterogeneity due to size and effect signs. The second purpose of this paper is to show that the SFPCA will take the sign and size heterogeneity of the variants into account and be less sensitive to the presence of variants with opposite directions of effect.

There is increasing consensus that complex diseases are caused by common and rare variants. Many statistics can be used to test for association of either common variants or rare variants, but very few can be used to test association of both common and rare variants. Third purpose of this report is to demonstrate that the SFPCA can be used to test the association of the entire allelic spectrum of genetic variation.

To accomplish these goals, we will use large-scale simulations to calculate the type 1 error rates and evaluate the power of 12 alternative statistical methods: the SFPCA discretization, SFPCA Fourier expansion, FPCA discretization, FPCA Fourier expansion, collapsing method, combined multivariate and collapsing (CMC) method,⁸ generalized T²,^{2, 19} multivariate principal component analysis (MPCA), the weighted sum statistic (WSS)⁹ and the variable threshold (VT) method¹⁰ under various scenarios. To further evaluate its performance, the SFPCA is applied to the ANGPTL4 sequence and six continuous phenotypes data from the Dallas Heart Study²⁰ and a GWAS of schizophrenia data.

MATERIALS AND METHODS

Smoothed FPCA

We first review the definition of genetic variant profiles.¹⁸ Let t be the position of a genetic variant within a genomic region and T be the length of the genomic region being considered. For convenience, we rescale the region [0,T] to [0,1]. Because the density of genetic variants is high, we can view t as a continuous variable in the interval [0,1]. Assume that n_A cases and n_G controls are sampled and sequenced. We define the genotype of the ith case as

where M is an allele at the genomic position t. Similarly, we can define a genetic variant function X_i(t), 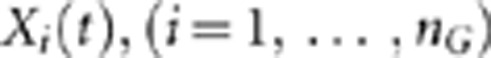for the ith control.

Now, we review the concept of functional principal component for association studies.¹⁸ To capture variation of genetic variant function, we define a linear combination of functional values:

where β(t) is a weight function and X(t) is a centered genetic variant function defined in equation (3). The functional principal components can be obtained by choosing weight function β(t) to maximize the variance of f:¹⁸

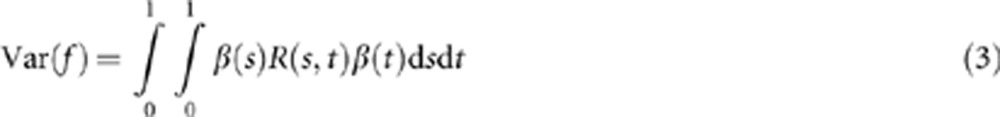where R(s,t) is the covariance function of the genetic variant function X(t).

The observed genetic variant profiles are typically not smooth, which leads to substantial variability in the estimated functional principal component curves. To improve the smoothness of the estimated functional principal component curves, we impose the roughness penalty on the functional principal component weight functions. We often penalize the roughness of the functional principal component curve using its integrated squared second derivative. The balance between the goodness-of-fit and the roughness of the function is controlled by a smoothing parameter μ.

The smoothed functional principal components can be obtained by solving the following integral equations (see Appendix):

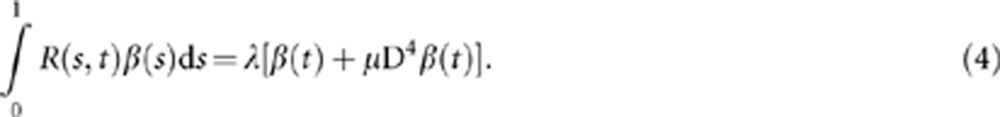Note that when μ=0, the SFPCA is reduced to an unsmoothed FPCA.

Computations for the smoothed principal component function and the principal component score

The eigenfunction is an integral function and difficult to solve in closed form. A general strategy for solving the eigenfunction problem in (4) is to convert the continuous eigen-analysis problem to an appropriate discrete eigen-analysis task.²¹ In this paper, we use basis function expansion methods to achieve this conversion (see Supplementary File 1).

Let {φ_j(t)} be the series of Fourier functions. For each j, define ω_2j−1=ω_2j=2πj. We expand each genetic variant profile X_i(t) as a linear combination of the basis function φ_j:

Define the vector-valued function X(t)=[X₁(t),…X_N(t)]^T and the vector-valued function φ(t)=[φ₁(t),…φ_T(t)]^T. The joint expansion of all N genetic variant profiles can be expressed as

where C is a coefficient matrix C=(C_ij)_{N × T}.

In matrix form, we can express the variance-covariance function of the genetic variant profiles as

Similarly, the eigenfunction β(t) can be expanded as

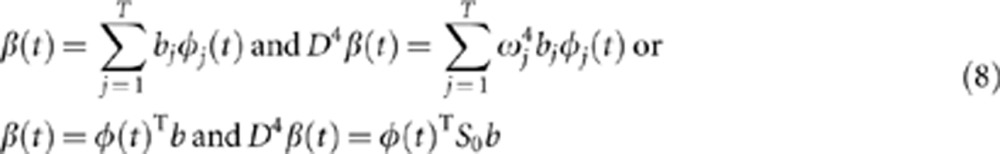where b=[b₁,…,b_T]^T and S₀=diag (ω₁⁴,…,ω_T⁴). Let S=diag ((1+μω₁⁴)^−1/2,…,(1+μω_T⁴)^−1/2). Then, we have

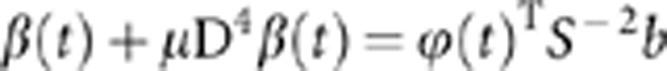Substituting expansions (7) and (8) of variance-covariance R(s,t) and eigenfunction β(t) into the functional eigen equation (4), we obtain

which can be rewritten as

where u=S⁻¹b. Thus, b=Su and β(t)=φ(t)^Tb is a solution to eigen equation (4).

Note that <u_j, u_j>=1 and <u_j, u_k>=0 for k<j. Therefore, we obtain a set of orthonormal eigenfunctions as shown in equation (11):

where an inner product of two functions is defined as 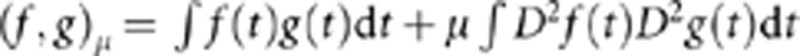, where .

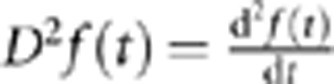Test statistic

We use the pooled genetic variant profiles X_i(t) of cases and Y_i(t) of controls to estimate the set of orthonormal principal component function 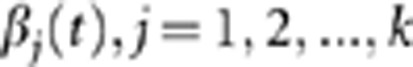(eigenfunctions) using the basis expansion methods. By the K-L decomposition, the smoothed functional principal component score can be obtained by

We denote vectors of averages of functional principal component scores in cases and controls by 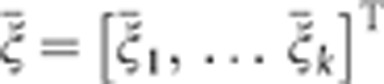and 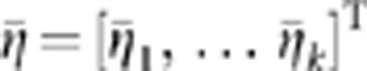, where 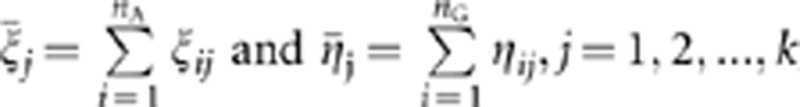, and define the pooled covariance matrix 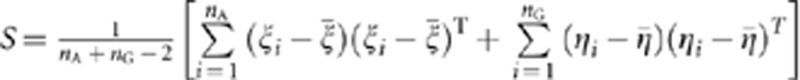, where 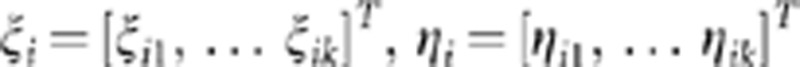. Let 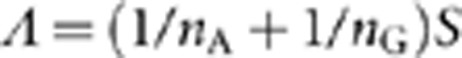. Then, the statistic is defined as .

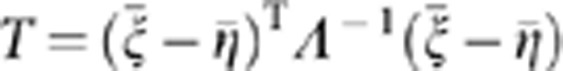Under the null hypothesis of no association of the genomic region with a disease, the statistic T is asymptotically distributed as a central 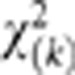distribution.

RESULTS

Null distribution of test statistics

When the sample size is large, the distribution of the SFPCA test statistic for testing the association of the genomic region with a trait of interest is distributed under the null hypothesis of no association as a central 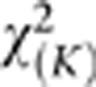distribution, where K is the number of functional principal components used in the test. To examine the validity of this statement, we performed a series of simulation studies.

We used the MS software²² to generate a population of 2 000 000 chromosomes, each with 60 common SNPs (MAF≥0.05) and 180 rare SNPs (MAF≤0.05) in a genomic region on the basis of a coalescent model that mimics the LD pattern and the population history. The frequencies of minor alleles in the genomic region vary from 10⁻⁵ to 0.43. A number of individuals, ranging from 1000 to 5000, each consisting of two chromosomes, were sampled from the population and equally assigned to cases and controls. A total of 10 000 data sets were generated and the proposed test statistics were performed for each data set. For each test, we selected the number of functional principal components that account for 90% of the total variations.

Table 1 summarized the type 1 error rates of the SFPCA test statistics for testing the association of rare variants within a genomic region. It showed that the estimated type 1 error rates of the test statistic were not appreciably different from the nominal levels α=0.05, α=0.01 and α=0.001. We also performed simulation studies to examine the validity of the null distribution of the test statistics in testing the association of a set of both common and rare variants within a genomic region. All 240 common and rare variants were used to calculate the type 1 error rates. Table 2 summarized the type 1 error rates of the SFPCA statistic for testing the association of all 240 variants in the genomic region with the disease. It showed that the estimated type 1 error rates of the SFPCA statistic were also not appreciably different from the nominal levels α=0.05, α=0.01 and α=0.001.

Table 1. Type 1 error rates of the smoothed FPCA statistic for testing the association of the rare variants in a genomic region with a disease.

Sample size	α=0.05	α=0.01	α=0.001
1000	0.0473	0.0100	0.0008
2000	0.0489	0.0095	0.0009
3000	0.0487	0.0099	0.0009
4000	0.0492	0.0106	0.0010
5000	0.0490	0.0100	0.0009

Table 2. Type 1 error rates of the smoothed FPCA statistic for testing the association of both common and rare variants in a genomic region with a disease.

Sample size	α=0.05	α=0.01	α=0.001
1000	0.0493	0.0111	0.0010
2000	0.0518	0.0107	0.0010
3000	0.0523	0.0105	0.0011
4000	0.0475	0.0098	0.0010
5000	0.0500	0.0107	0.0009

Power evaluation

To evaluate the performance of the FPCA-based statistics for testing the association of a set of rare variants with disease, we used the same data set as that for type 1 error rate calculation to estimate their power to detect a true association. We considered four disease models: additive, dominant, recessive and multiplicative.

An individual's disease status was determined based on the individual's genotype and the penetrance for each locus. Let A_i be a rare risk allele at the ith locus. Let 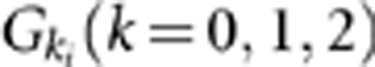be the genotypes a_ia_i, A_ia_i and A_iA_i, respectively, and f_ki be the penetrance of genotypes 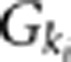at the ith locus. The relative risk (RR) at the ith locus is defined as R_1i=f_1i/f_0i and R_2i=f_2i/f_0i, where f_0i is the baseline penetrance of the wild-type genotype at the ith variant site. We assume that for the additive disease model, R_2i=2R_1i−1; for the dominant disease model, R_2i=R_1i; for the recessive disease model, R_1i=1; and for the multiplicative disease model, R_2i=R_1i². The genotype RR was assumed to be inversely proportional to the MAF where the population attributable risk (PAR) of each group was assumed to be 0.005.⁷ We assumed equal RR across all variant sites and the independence of the variants influencing disease susceptibility. Each individual was assigned to the group of cases or controls depending on their disease status. The process for sampling individuals from the population of 2000 000 haplotypes was repeated until the desired samples were reached for each disease model.

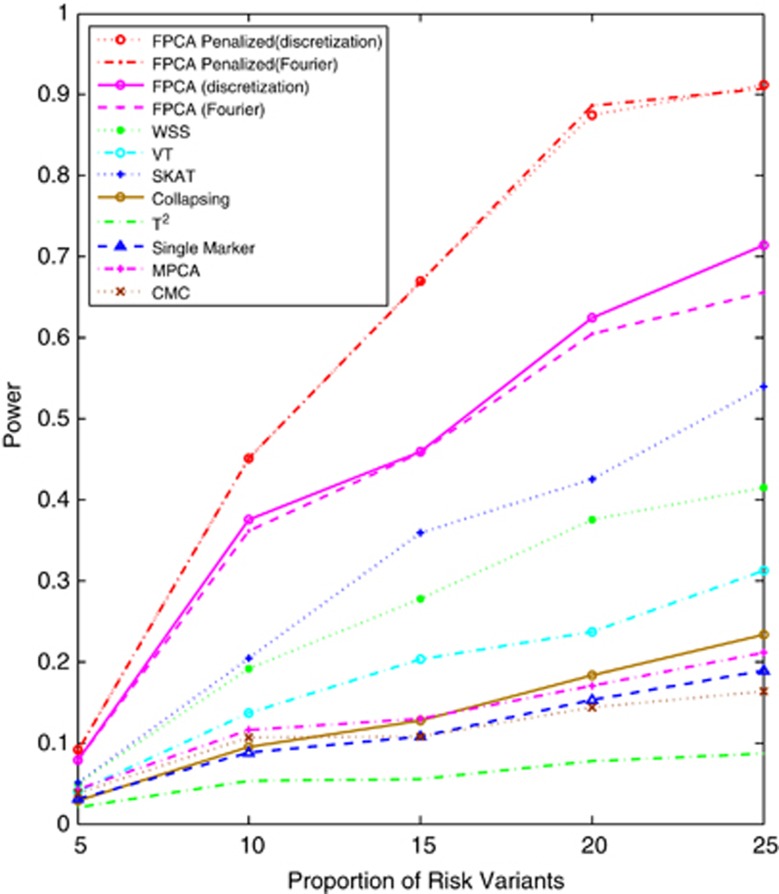
Figure 1 and Supplementary Figures 1–3 plot the power curves of 12 statistics: SFPCA discretization, SFPCA Fourier expansion, FPCA discretization, FPCA Fourier expansion, sequence kernel association test (SKAT),²³ WSS, VT, MPC-based statistic, Collapsing method and Generalized T² statistic, Single marker χ² test where permutation was used to adjust for multiple testing and the CMC method (variants with frequencies ≤0.005 were collapsed) as a function of the proportion of risk increasing variants for testing the association of 180 rare variants with disease under additive, dominant, multiplicative and recessive disease models, respectively, assuming a baseline penetrance of 0.01, and that 2000 cases and 2000 controls were sampled for additive, dominant and multiplicative models, and 3000 cases and 3000 controls for the recessive models. The SFPCA-based statistics had the highest power, followed by the classical FPCA-based statistics, SKAT, WSS and VT under four disease models. The single marker test, generalized T² and CMC methods under all disease models had the lowest power to detect association of rare variants. When the PAR is assumed a constant, the number of risk increasing variants determines the marginal PAR of each variant in the group. From these figures, we can see that the power of all 12 statistics is an increasing function of the proportion of risk variants.

Figure 1.

Power of 12 statistics: the SFPCA (discretization approach) statistic, SFPCA (Fourier expansion approach) statistic, FPCA (discretization approach)-based statistics, FPCA (Fourier expansion approach)-based statistic, SKAT, multivariate PC-based statistic, WSS, VT, collapsing method, generalized T² statistic, single marker χ² test and CMC method (the variants with frequencies ≤0.005 were collapsed) as a function of the proportion of risk increasing variants for testing the association of 180 rare variants at significance level α=0.05 with the disease under the additive disease model, assuming baseline penetrance of 0.01 and 2000 cases and 2000 controls.

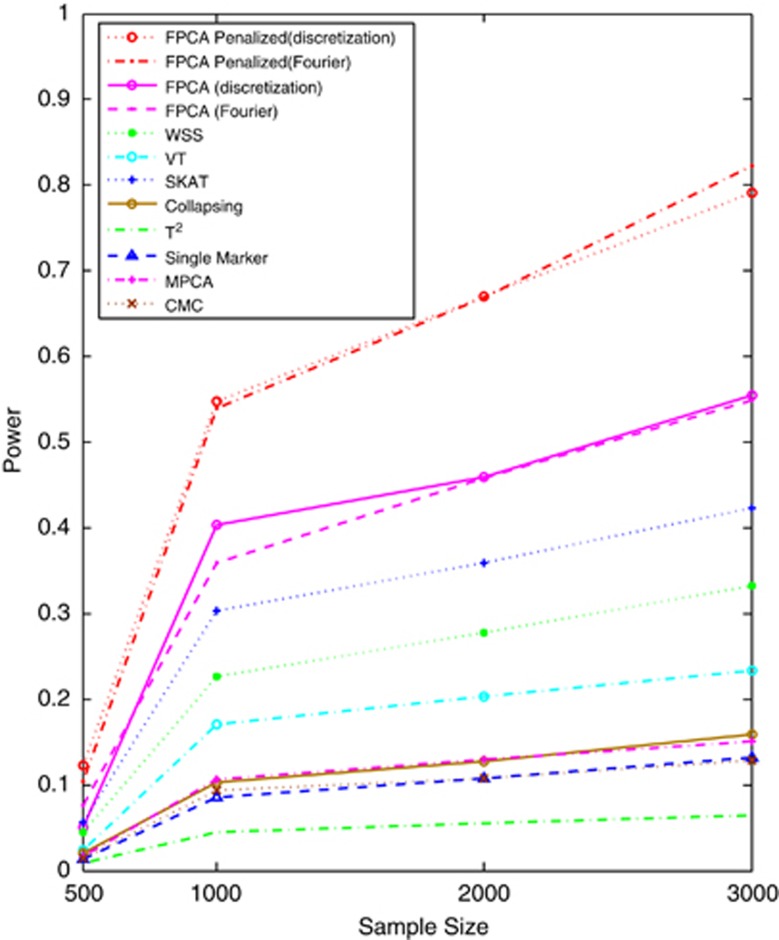
Next, we evaluate the impact of the sample sizes on the power. We assume that 15% of rare variants were risk increasing variants. Figure 2 and Supplementary Figures S5 and S6 showed the power of the above 12 statistics as a function of sample sizes under additive, dominant, multiplicative and recessive models, respectively. Similarly to Figure 1 and Supplementary Figures S1–S3, we observed that the SFPCA-based statistics had the highest power in all settings. Differences in the power between the SFPCA-based statistics and eight other non-FPCA statistics increased as the sample sizes increased. We also observed that most of the time the difference in power between the FPCA by expansion and FPCA by the discretization method is small.

Figure 2.

Power of 12 statistics: the SFPCA (discretization approach) statistic, SFPCA (Fourier expansion approach) statistic, FPCA (discretization approach)-based statistics, FPCA (Fourier expansion approach)-based statistic, SKAT, multivariate PC-based statistic, WSS, VT, collapsing method, generalized T² statistic, single marker χ² test and CMC method (the variants with frequencies ≤0.005 were collapsed) as a function of sample sizes for testing the association of 180 rare variants, 15% of which were risk increasing variants, with the disease under the additive disease model at significance level α=0.05, assuming baseline penetrance of 0.01.

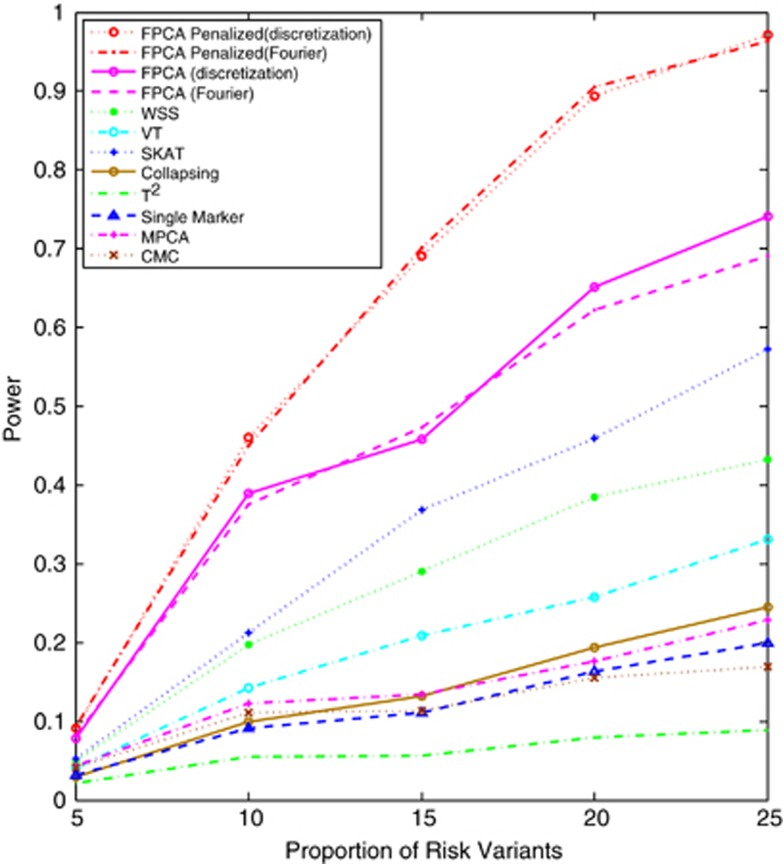
Next, we investigate the power of statistics for testing association of both common and rare variants. Figure 3 plotted the power of 12 statistics for testing association of all 240 common and rare variants as a function of proportion of risk variants under the additive model, assuming that 2000 cases and 2000 controls were sampled and Supplementary Figure S7 showed the power of 12 statistics for testing association of all 240 common and rare variants as a function of sample sizes under the additive model, assuming 15% of risk variants. The power pattern of 12 statistics under other diseases models was similar to that of the tests under additive models (data not shown). From these figures, we observed that the SFPCA substantially outperform the non-SFPCA and other statistics. As sample sizes increased the difference in power between the SFPCA and other tests rapidly increased.

Figure 3.

Power of 12 statistics: the SFPCA (discretization approach) statistic, SFPCA (Fourier expansion approach) statistic, FPCA (discretization approach)-based statistics, FPCA (Fourier expansion approach)-based statistic, SKAT, multivariate PC-based statistic, WSS, VT, collapsing method, generalized statistic, single marker test and CMC method (the variants with frequencies 0.005 were collapsed) as a function of the proportion of risk increasing variants for testing the association of 240 common and rare variants at significance level with the disease under the additive disease model, assuming baseline penetrance of 0.01 and 2000 cases and 2000 controls.

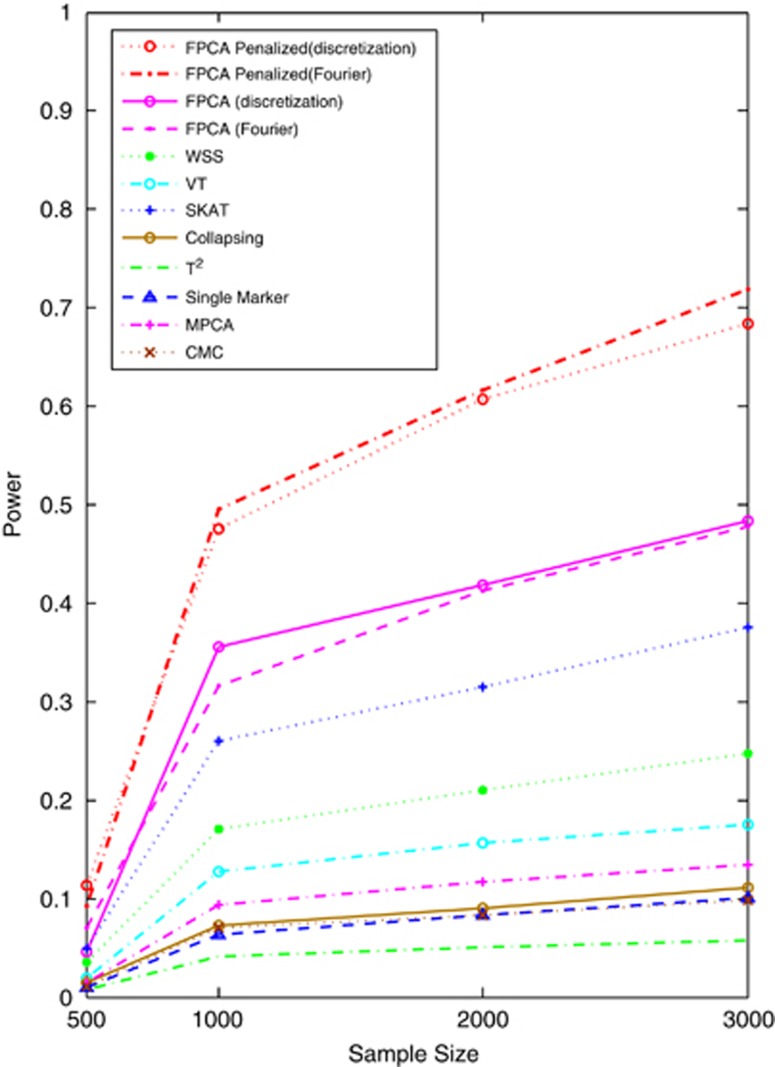
To examine the impact of the direction of association of risk alleles with disease on the power of the tests, we randomly select 7.5% of variants as risk variants and 7.5% of variants as protective variants. We plotted Figure 4 to show the power curves of the 12 statistics for testing association of 180 rare variants as a function of sample size under additive model and Supplementary Figure S8 to show the power curves of the 12 statistics for testing association of all 240 common and rare variants as a function of sample sizes under additive model. The patterns of power curves of the 12 statistics under the dominant, multiplicative and recessive models were similar to Figure 4 and Supplementary Figure S8 (data not shown). These results clearly demonstrated that the power of the SFPCA was the highest, followed by the classical FPCA, SKAT, WSS and VT. We also observed that the generalized T², single marker test, collapsing method and CMC almost had no power to detect association of either rare variants or both common and rare variants in the presence of both risk and protective variants. It is interesting to note that the FPCA-based statistics do not assume that all variants within the genomic region being tested have the same direction of effect and do not require a testing stage to predict direction of effect. The results showed that the SFPCA and FPCA statistics can effectively deal with the simultaneous presence of both risk and protective variants without additional computation.

Figure 4.

Power of 12 statistics: the SFPCA (discretization approach) statistic, SFPCA (Fourier expansion approach) statistic, FPCA (discretization approach)-based statistics, FPCA (Fourier expansion approach)-based statistic, SKAT, multivariate PC-based statistic, WSS, VT, collapsing method, generalized statistic, single marker test and CMC method (the variants with frequencies 0.005 were collapsed) for testing the association of 180 rare variants as a function of the sample sizes under the additive model at significance level α=0.05, assuming that 7.5% of rare variants were risk increasing variants and 7.5% of rare variants were protective variants, and baseline penetrance of 0.01.

Application to real data examples

To further evaluate their performance for testing association of rare variants, the SFPCA tests were first applied to the ANGPTL3, 4, 5 and 6 sequence and phenotype data from the Dallas Heart Study.²¹ The total numbers of rare variants with a minor allele frequency <0.05 in the ANGPTL3, 4, 5 and 6 genes which were identified from 3553 individuals were 49, 83, 91 and 66, respectively. Since the SFPCA method requires that each individual should have at least two rare variants in the genomic region being tested, we excluded 98 individuals with only one rare variant. The total number of rare variants with a minor allele frequency <0.03 in ANGPTL 4 was 71. To examine the phenotypic effects of the rare variants in the ANGPTL 3, 4, 5 and 6 genes, two groups of individuals with the lowest and highest quartiles of the five traits related to lipid metabolism were selected. The individuals with plasma triglyceride (Trig) levels less than or equal to the 25th percentile were classified as the lowest quartiles of the Trig and the individuals with plasma Trig greater than or equal to the 75th percentile were grouped as the highest quartiles of the Trig. We can similarly classify the individuals as the lowest and highest quartiles of high density lipoprotein cholesterol (HDL), total cholesterol, very low density lipoprotein cholesterol (VLDL) and body mass index (BMI). P-values from the SFPCA methods, the classical FPCA methods, SKAT, WSS, VT, MPCA-based statistic, the generalized T² statistic, single marker χ² test where permutation was used to adjust for multiple testing, collapsing and CMC methods for testing association of 71 rare variants (MAF≤0.03) in ANGPTL4 with the five traits, were summarized in Table 3. For the CMC method, variants with an allele frequency <0.005 were collapsed. The results in Table 3 clearly demonstrated that the SFPCA methods had the smallest P-values. We observed that P-values (1.01 × 10⁻⁵ and 4.47 × 10⁻⁵) by the SFPCA-based statistics for testing association of the rare variants in ANGPTL4 with triglyceride were much smaller than the P-value (0.016) in their original studies.²¹ Particularly, we observed that only the FPCA-based statistic and SKAT identified an association of the rare variants in ANGPTL4 with HDL and the P-values by the smoothed FPCA methods were even much smaller than the P-values by the SKAT and FPCA methods. This demonstrated that the smoothing techniques can largely increase the power to detect association of rare variants in some cases due to the improved accuracy to fit the data by the smoothed functional principal component curves. P-values from the 12 statistics for testing association of rare variants in the ANGPTL 3, 5 and 6 genes with the five traits are summarized in Supplementary Tables 1–3, respectively. We observed the same pattern as that in Table 3.

Table 3. P-values of 12 statistics for testing the association of rare variants in ANGPTL4 with five traits in the Dallas Heart Study.

	Phenotype
Statistical method	BMI	Cholesterol	Triglyceride	VLDL	HDL
Smoothed FPCA (discretization)	0.002	0.1121	4.47E-05	0.1743	2.88E-05
Smoothed FPCA (Fourier)	0.0011	0.1267	1.01E-05	0.2076	5.49E-04
FPCA (discretization)	0.0043	0.5928	0.0077	0.1950	0.0271
FPCA (Fourier)	0.0033	0.1229	0.0062	0.1540	0.0205
SKAT	0.0096	0.2586	0.0024	0.3189	0.0092
T2	0.1876	0.4343	0.0573	0.0730	0.2392
Collapsing	0.4363	0.3853	0.7954	0.6561	0.1065
χ2 (permutation)	0.0518	0.4787	0.0740	0.0887	0.3853
CMC	0.0056	0.8383	0.1718	0.2302	0.6425
WSS	0.0088	0.4959	0.1641	0.2390	0.1000
VT	0.0726	0.7659	0.4163	0.4697	0.1482
MPCA	0.0103	0.2129	0.0098	0.2030	0.1096

To illustrate that the SFPCA methods can be applied to common variants, they were applied to a GWAS of schizophrenia data that were downloaded from dbGaP to test the association of common variants within a genomic region. The samples were of the European origin and included 1135 individuals with schizophrenia and 1362 controls with 727 479 typed SNPs. The total number of genes being tested is 13 804. The threshold for declaring genome-wide significance after the Bonferroni correction is 3.6 × 10⁻⁶. The number of genes significantly associated with schizophrenia by 14 statistics: the SFPCA, FPCA, SKAT, Collapsing, CMC, WSS, VT, single marker χ² test T² test, MPCA test, FPCA, linear combination test (LCT), quadratic test (QT), de-correlation test (DT)²⁴ is listed in Table 4. We also listed the top 10 significantly associated genes that were identified by the SFPCA (Fourier Expansion) in Table 5. Since in many cases the frequency of individuals with at least one minor alleles present is close to one, the collapsing test statistic cannot be calculated and hence its P-values were not listed in Table 5. The results clearly showed that the number of significantly associated genes identified by the SFPCA is much larger than that identified by the unsmoothed FPCA and other statistics, and the P-values by the SFPCA were much smaller than the P-values by the unsmoothed FPCA and other statistics. Therefore, the smoothing techniques provide a large improvement over the FPCA methods without smoothing. Among genes in Table 5, PDLIM5 was reported to be associated with schizophrenia and bipolar disorder,²⁵ CERKL was associated with narcolepsy,²⁶ HAAO was associated with Parkinson's disease²⁷ and MTA3 was associated with cancer.²⁸

Table 4. Number of genes significantly associated with schizophrenia by 13 statistics.

	Collapse	CMC	T2	χ2	WSS	VT	LCT	QT	DT	MPCA	SKAT	FPCA	SFPCA
Number of genes	0	5	5	2	2	6	3	5	2	0	9	8	56

Table 5. P-values of the top 10 significantly associated genes identified by SFPCA.

Gene	SFPCA	FPCA	SKAT	CMC	T2	χ2	WSS	VT	LCT	QT	DT	MPCA
LRSAM1	1.7E−19	3.0E−06	5.7E−4	2.1E−03	2.1E−03	2.3E−04	2.3E−01	3.0E−02	6.9E−02	8.6E−02	8.1E−02	4.2E−03
RUNDC3B	3.1E−18	2.4E−08	8.8E−8	5.6E−07	5.6E−07	9.0E−07	2.6E−01	2.5E−01	6.7E−01	8.2E−01	2.0E−01	8.3E−01
DTL	2.9E−12	5.8E−04	3.2E−6	3.5E−04	3.5E−04	8.1E−07	4.3E−01	5.1E−01	1.6E−01	1.8E−01	1.1E−01	7.7E−01
MRPS17	4.2E−12	3.4E−05	1.9E−4	2.1E−03	2.1E−03	3.7E−03	5.0E−02	1.3E−01	6.3E−01	4.0E−01	6.9E−01	4.1E−02
PDLIM5	1.6E−11	1.1E−06	2.5E−5	5.5E−05	5.5E−05	5.6E−05	5.8E−05	1.7E−03	5.8E−01	7.2E−01	9.5E−01	3.3E−05
CECR1	1.7E−11	4.3E−05	6.3E−6	5.3E−05	5.3E−05	3.6E−03	7.0E−02	1.0E−02	2.0E−01	5.1E−01	3.7E−01	2.6E−02
CERKL	2.2E−11	8.3E−07	4.4E−6	5.2E−05	5.2E−05	1.4E−03	3.1E−01	3.2E−01	9.1E−01	4.6E−01	3.3E−01	2.6E−01
EVI5	3.3E−11	6.8E−09	3.8E−3	5.2E−02	5.2E−02	2.0E−05	1.3E−04	5.0E−05	4.9E−02	9.6E−02	4.7E−02	6.3E−06
HAAO	5.7E−11	5.4E−01	5.2E−1	3.0E−08	3.0E−08	4.6E−04	5.0E−02	4.2E−01	4.6E−01	2.9E−01	5.7E−01	6.0E−01
MTA3	7.2E−11	6.3E−01	9.4E−7	6.7E−07	6.7E−07	4.6E−04	5.8E−01	3.0E−02	7.3E−01	8.6E−01	8.2E−01	9.4E−01

DISCUSSION

We have demonstrated here that the SFPCA statistics can be used to test association of both common and rare variants and have broad applicability to NGS data. The SFPCA statistics have several remarkable advantages over many previously proposed group tests.

The first advantage of the SFPCA is utilization of merits of both single variant analysis and group tests. The smoothed functional principal component scores take information across all variants in the genomic region into account and hence include all single variant variation. The SFPCA statistic is to globally compare differences in the average of functional principal component scores between cases and controls. In other words, it tests accumulation of differences in all variant variation in the genomic region between cases and controls. Therefore, the SFPCA overcomes limitations inherent by single variant analysis and group tests and effectively employ the merits of both single variant tests and group tests.

The second advantage is that the SFPCA methods can efficiently use information of both risk and protective variants and allow for sign and size heterogeneity of genetic variants. In general, the risk and protective variants will be present in different locations in the genomic region. Information of risk and protective variants usually will be reflected in different eigenfunctions and hence will be included in different functional principal component scores. The SFPCA test statistic is to summarize the square of the differences in the smoothed functional principal component scores between cases and controls. Therefore, the opposite effects of risk and protective variants on the phenotype will not compromise each other in the SFPCA statistics. The FPCA statistics automatically take the opposite effects of the risk and protective variants on the phenotype into account and do not require additional computations. By simulations we showed that the SFPCA test statistics had substantially higher power than the existing approach in the presence of both risk and protective variants in the genomic region being investigated.

The third advantage is that the SFPCA statistics can be used to test the association of either rare or common variants or both rare and common variants. Empirical and theoretical studies support potential roles for both rare and common variants in complex diseases. There is an increasing need to develop statistics that can be used to test association of rare variants or common variants or both rare and common variants. From large-scale simulations and real data analysis, we showed that the SFPCA statistics had the correct type 1 error rate and high power in all scenarios. The fourth advantage is that the smoothing techniques can largely increase the accuracy of fitting the data by FPCA and hence greatly improve the power to detect association of variants. The FPCA is often enhanced by the use of penalty techniques. The observed genetic variation records are not smooth. Consequently, we often observe that the principal component curves show substantial fluctuations. To reduce the variability of principal component curves, we need to either smooth or regularize the estimated principal component curves. The smoothing method removes the roughness in the raw principal component curves and hence improves the accuracy of the estimated functional principal component scores, which will lead to improved type 1 error rates and power.

The fifth advantage is that random genetic variant function in the SFPCA is flexible. The variable x_i(t) at the single variant site can take integer values to code alleles or genotypes, or real numbers to represent the number of reads of the sequences, the probability of SNP call, and the probability of the variant being functional or weights at the variant site.

NGS techniques generalize extremely high dimensional genomic data. Transition of analysis from low dimensional data to extremely high dimensional data demands changes in statistical methods from multivariate data analysis to functional data analysis. Functional data analysis coupled with smoothing techniques will provide a powerful tool for NGS data analysis. However, the results in this report are considered preliminary. The number of eigenfunctions in the expansion of genetic variant function and penalty parameters will influence the performance of the smoother FPCA for association studies. How to simultaneously identify the associated genomic regions and causal variants within them and the optimal selection of these parameters in genome-wide association studies are still open questions in practice. We are facing great challenges in developing efficient and powerful analytic platforms for association analysis of NGS data.

WEB RESOURCES

The URL for the 1000 Genomes Project data is as follows: http://www.1000genomes.org/. A program for implementing the smoothed FPCA can be downloaded from our website http://www.sph.uth.tmc.edu/hgc/faculty/xio ng/index.htm.

Appendix

We define an extended inner product as

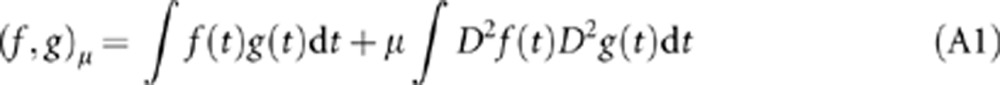where 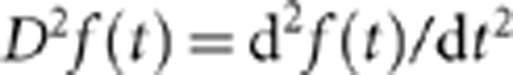. Similarly to equation (3), the penalized sample variance is defined as

where .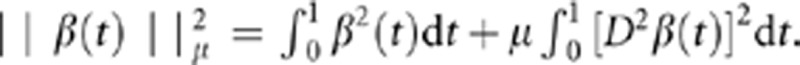

To find the functional principal component, we seek to maximize F in equation (A2) which is equivalent to solving the following optimization problem:

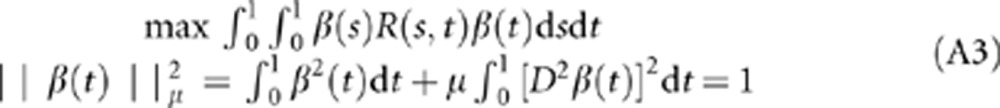Using the Lagrange multiplier, we reformulate the constrained optimization problem (A3) into the following non-constrained optimization problem:

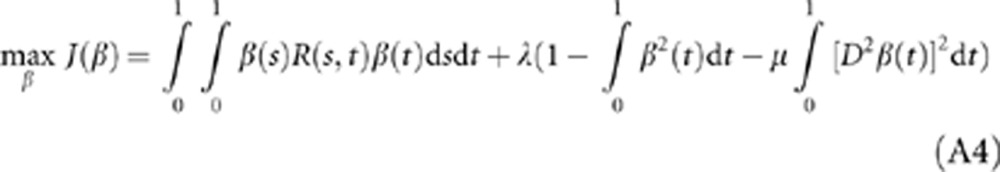where λ is a parameter. Its first variation is given by

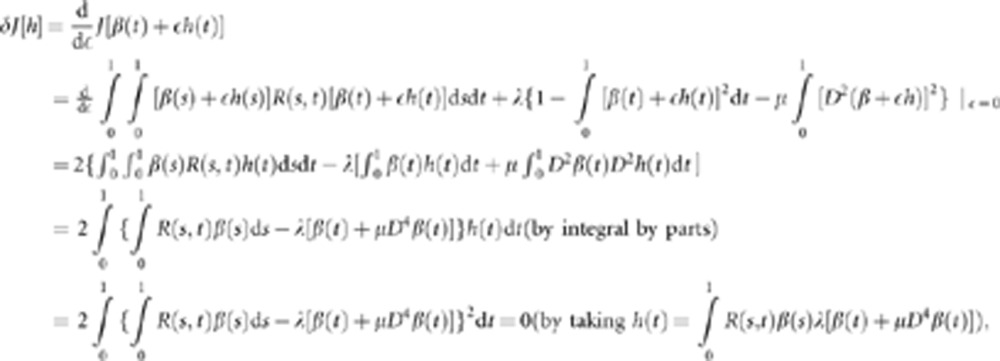which implies the following integral function: .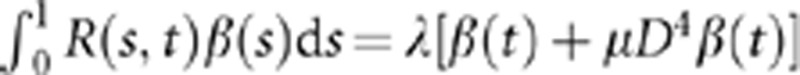

The authors declare no conflict of interest.