Using identity by descent estimation with dense genotype data to detect positive selection

Abstract

Identification of genomic loci and segments that are identical by descent (IBD) allows inference on problems such as relatedness detection, IBD disease mapping, heritability estimation and detection of recent or ongoing positive selection. Here, employing a novel statistical method, we use IBD to find signals of selection in the Maasai from Kinyawa, Kenya (MKK). In doing so, we demonstrate the advantage of statistical tools that can probabilistically estimate IBD sharing without having to thin genotype data because of linkage disequilibrium (LD), and that allow for both inbreeding and more than one allele to be shared IBD. We use our novel method, GIBDLD, to estimate IBD sharing between all pairs of individuals at all genotyped SNPs in the MKK, and, by looking for genomic regions showing excess IBD sharing in unrelated pairs, find loci that are known to have undergone recent selection (eg, the LCT gene and the HLA region) as well as many novel loci. Intriguingly, those loci that show the highest amount of excess IBD, with the exception of HLA, also show a substantial number of unrelated pairs sharing all four of their alleles IBD. In contrast to other IBD detection methods, GIBDLD provides accurate probabilistic estimates at each locus for all nine possible IBD sharing states between a pair of individuals, thus allowing for consanguinity, while also modeling LD, thus removing the need to thin SNPs. These characteristics will prove valuable for those doing genetic studies, and estimating IBD, in the wide variety of human populations.

Introduction

The ability to discover recent positive selection in the human genome is one compelling reason to estimate identity by descent (IBD) in a cohort of largely unrelated individuals. In particular, IBD can be used to find selection on standing variation, a situation where many methods used for detecting selection may not perform well.¹ Additionally, other genetic questions can be well addressed by estimating IBD within a set of individuals. These include, detection of unknown or mistaken relationships,^{2, 3, 4, 5, 6} estimation of heritability and genomic partitioning of genetic variance,^{7, 8} and mapping by the identification of shared segments.^{9, 10, 11, 12, 13} IBD, however, is not directly observed but must be inferred from the available data. Traditionally, the combination of a pedigree with genotype data enabled the efficient computation of IBD using either ‘peeling'¹⁴ or hidden Markov models (HMMs).^{15, 16, 17} More recently, however, the large amounts of information made available from high density SNP genotyping arrays has enabled estimation of IBD even for very distantly related pairs of individuals (ie, >10 generations) in the absence of pedigree information. This additional data, however, also presents the difficulty of accommodating the linkage disequilibrium (LD) present between SNPs. Though HMMs enable efficient computation of IBD probabilities given multipoint genotype data, they, unfortunately, require the absence of LD. One approach to take LD into account is to eliminate SNPs that are in LD with each other leaving a reduced set for which the standard HMM should hold.⁹ Even though this typically eliminates much of the available genotype data, the rationale is that IBD regions are typically sufficiently large that enough SNPs remain in these segments to easily identify them. Although it is true that, conditional on distant relatives sharing a segment IBD, the expected value of the segment is fairly large (5 cM for relatives separated by 20 meioses (ie, 10 generations)), the exponential shape of the size distribution means that ∼63% of IBD segments are smaller than the mean and 39% are <1/2 the mean size. Thinning the SNPs is likely to reduce the power to identify these small IBD regions and increase uncertainty in IBD estimates for larger regions. Although some problems, such as detecting close relatives is likely to be robust to finding only large IBD regions, other population-based questions, such as detecting selection, will likely require much higher resolution.

An alternative strategy to thinning is to allow for LD within the method. One approach is to infer IBD based on the presence of matching haplotypes in a pair of individuals.^{5, 10} Although very fast, these methods do not, by themselves, result in a posterior probability of IBD at each locus. Another approach is to create a model, typically based on a HMM, that allows for LD.^{11, 12, 18, 19, 20, 21} Model-based methods have the advantage of being able to quantify the level of certainty in an IBD estimate, but will generally be more computationally intensive and slower than matching haplotypes. We propose a novel method, GIBDLD, a modified HMM that extends our previous work²⁰ to allow use when pedigree data are not known. It is computationally fast; allows the use of all SNPs, even in the presence of high LD; estimates the posterior probability of each of nine possible IBD states for a pair of individuals at all SNPs given all of their genotype data; detects shared segments; and works equally well whether the cohort is outbred or has substantial cryptic relatedness or consanguinity. We apply GIBDLD to the Maasai in Kinyawa, Kenya (MKK) from the HapMap 3 data set²² and find several regions that are likely to have experienced recent positive selection as well as both confirm previously known close relatives²³ and detect numerous new, more distant ones.

Materials and methods

Here, we restrict ourselves to a brief description of GIBDLD and, because our previous method on which it is based required a pedigree, an explanation of the extensions implemented for when pedigree data are unavailable.

Statistical model

In our HMM, the hidden Markov states are the nine condensed identity states²⁴ (see Supplementary Figure S1 for the condensed identity states) that are formed by all possible groupings of four alleles into IBD and non-IBD sets, where the maternal and paternal origin of the alleles in an individual are ignored. Thus, inbreeding is accounted for because the two alleles in an individual are allowed to be IBD. The model we use for the emission probabilities (ie, the conditional probabilities of the observed genotypes) are functions of the allele frequencies and allows for both missing genotypes and genotyping error. In the standard HMM, these emission probabilities are conditionally independent given the underlying Markov state, but in the presence of LD, the probability of observing a genotype at a given locus also depends on the genotypes at other loci. We allow for this in our model by computing what is essentially a person-specific allele probability given the genotypes at L previous loci. We set L=20 and approximate this allele probability using a linear model where the genotypes at the L previous loci are predictors and the outcome is the probability of the possible genotypes at the current locus. Specifically,

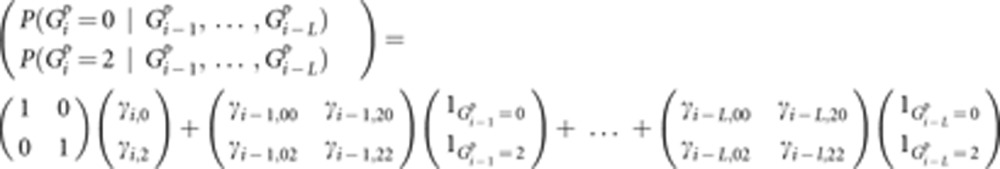Here, 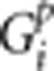is the genotype of person p at locus i, 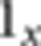is the indicator function equaling 1 when x is true and 0 when x is false, 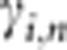are the LD parameters associated with locus i and the genotypes are coded as 0, 1, or 2, with 1 being the genotype of a heterozygote. Details are given in reference 20. The LD parameters of this linear model are estimated from a training sample of individuals in whom the LD is representative of the LD pattern in the group of people who are being analyzed for IBD. To prevent possible overfitting, we use ridge regression to estimate these coefficients.

In practice, we find that setting the training sample to the same group as the one in whom IBD is being estimated gives accurate results. Finally, we estimate the unconditional probabilities of the identity states and the parameters governing the transition probabilities between states using maximum likelihood. Given this model, we use the standard forward–backward algorithm²⁵ to compute the posterior probabilities of the condensed identity states at each SNP for the pair of individuals.

We summarize the amount of IBD sharing at a locus using the estimated proportion of alleles shared IBD , where 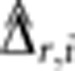is the posterior probability of condensed identity state r at locus i. Note that this definition of 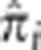has expected value equal to the kinship coefficient of the pair (ie, the probability that a randomly drawn allele from the first person is IBD with a randomly drawn allele from the second person). We also define the genome-wide empirical kinship coefficient 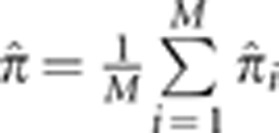, where M is the number of markers in the genome.

Simulations

Because a valuable characteristic of GIBDLD is that it retains its accuracy in both outbred populations and populations where all individuals are potentially related, we generated data for closely and distantly related individuals using both an outbred pedigree structure and the 13 generation pedigree from the South Dakota Hutterites.²⁶ Both the outbred pedigrees and the inbred pedigree were constructed so that the pairs considered by the method were a pair consisting of a person with himself, full siblings, an avuncular pair, first cousins, and second cousins. We note that because of the complex, inbred nature of the pedigree, the inbred pairs have kinship coefficients approximately, but not exactly, equal to the corresponding kinship coefficients for outbred pairs.

To generate genotype data with a realistic LD structure, we used the CEPH (Utah residents with ancestry from northern and western Europe) (CEU) haplotypes from the HapMap project.²⁷ We created a population of phased chromosomes from the CEU HapMap data by removing haplotypes that were from non-founder individuals, resulting in 234 phased haplotypes, and only using markers that were also present on the 500-k Affymetrix gene chip. We only used SNPs from chromosome 8 that had minor allele frequency >0.05, resulting in 11 643 total SNPs with inter-marker genetic map distances as provided by the HapMap project. For each pedigree, we simulated genotypes by assigning each founder of the pedigree a pair of randomly selected phased chromosomes from the population, where the chromosomes were drawn without replacement. The chromosomes were then allowed to segregate through the pedigree until all individuals had genotype data. Because GIBDLD requires both a study sample consisting of pairs in whom IBD will be estimated, and a training sample from whom LD is determined, each replicate in our simulations in the outbred pedigrees consisted of a study sample with 33 pairs of each relationship type, taken from 33 four-generation pedigrees, resulting in a total of 198 individuals. The training sample was set equal to the 198 individuals in the study sample. For the inbred pedigree, a replicate consisted of a study sample with one pair of each relationship type and a training sample comprising the study sample plus 192 random individuals from the last two generations of the pedigree (200 total individuals were in the training sample). When running GIBDLD on a replicate all phase information was ignored. To examine robustness to genotyping error and missing data, each replicate had two genotype data sets with the first being the simulated genotypes at all markers and the second where each genotype was assigned an incorrect value with a 1% probability and a missing value with a 2% probability. All simulation studies consisted of 1000 replicates.

Subjects

The MKK data sample contains 184 individuals, many of whom are specified as being siblings or parent–offspring pairs.²² We used the quality controlled genotype data available from the HapMap website and removed SNPs that had minor allele frequency less 0.05 or >20% missing data leaving a total of 1255 766 SNPs.

Computation time

Computation time varies depending on the number of SNPs in the data set and can be divided into two computational tasks: (1) estimating the LD parameters and (2) estimating the IBD probabilities of each marker for a pair of individuals. In our MKK analyses, using all the SNPs, step 1 took 2355 s and step 2 took ∼180 s for a single pair. Analyses of additional pairs repeats only step 2 for each pair and can be easily done in parallel. These times were obtained using a single core of a 2.66-GHz Intel Xeon E5430 processor on a Red Hat Linux platform.

Results

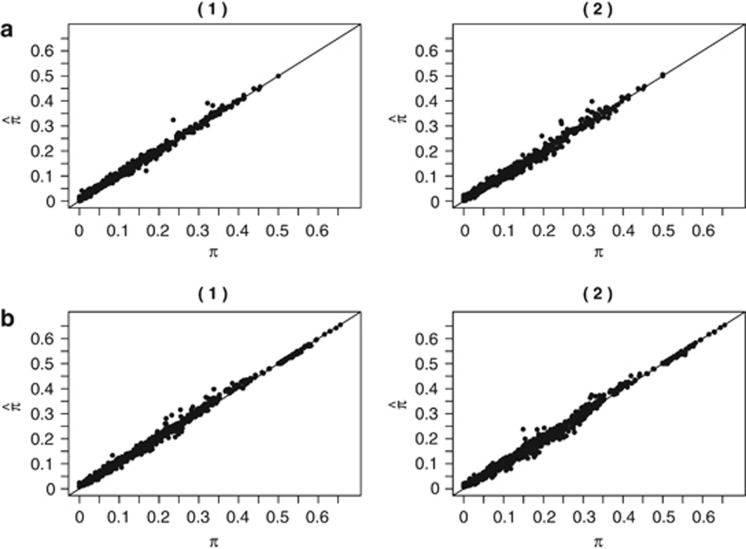
One application of obtaining conditional probabilities of the IBD states given the data is to obtain the empiric kinship coefficients of a pair or unknown relatedness. We first sought to check the accuracy of GIBDLD's estimate of IBD sharing by estimating 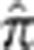for each pair of individuals in the simulated data set that used the CEU data and comparing this to the true average proportion of alleles shared IBD. Figure 1 shows these estimated values compared with the true values for all outbred and inbred pairs for all simulations. Accuracy is very high with a correlation in outbred pairs of 0.9990 when there is neither missing genotype data nor genotyping error, and 0.9982 in the simulations where there is. In the inbred pairs, the correlations were 0.9985 and 0.9977, when there is no error or missing data and when there is, respectively.

Figure 1.

Estimated vs true IBD sharing. Estimated IBD sharing, averaged over all SNPs as a function of the true IBD sharing, averaged over all SNPs, for (a) outbred pairs and (b) inbred pairs where the genotype data (1) have neither missing data nor error and (2) have 5% missing data and 2% error.

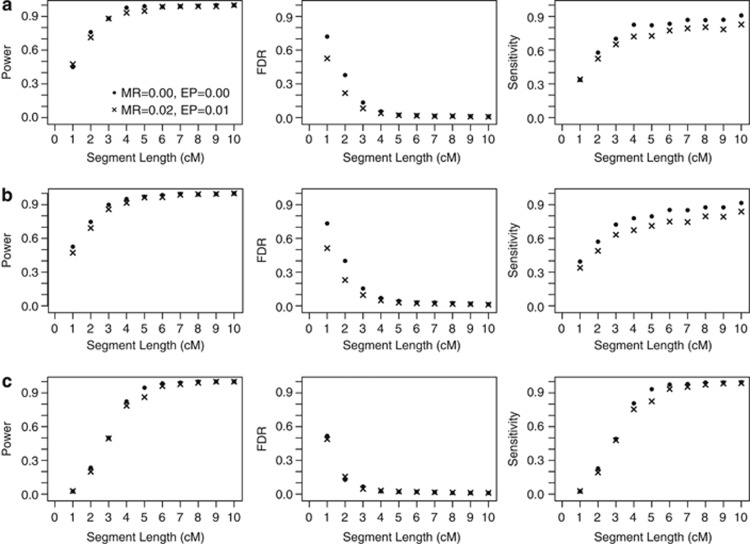
Another application of obtaining locus-specific estimates of IBD is to use these to define segments that are potentially shared IBD. In the same simulated CEU data set, we defined a detected segment as a set of at least two consecutive SNPs each with a probability >50% of sharing at least one allele IBD and checked the accuracy of these detected segments (Figure 2). For IBD segments that are 2 cM or larger, the power (ie, the fraction of true IBD segments that have at least one detected segment in it) and sensitivity (ie, the fraction of SNPs within an IBD segment that exceeded the IBD detection threshold) range from 0.7 to 1.0 and 0.5 to 0.9, respectively. False discover rates (ie, the fraction of SNPs within a detected segment that are not IBD) range from 0.4 to 0.01. Note that a more conservative threshold could also be used with a resulting decrease in false discover rates at the cost of lower power and sensitivity. In general, we find that GIBDLD is robust to missing genotypes and genotyping error when detecting shared IBD segments and consistently gives highly accurate estimates of IBD sharing.

Figure 2.

Power, FDR, and sensitivity of segment detection. Segments are placed into the nearest integer length (in cM) bin (eg, 0.5–1.5 cM length segments are placed into the 1-cM bin). The 10-cM bin contains all segments longer than 9.5 cM. Displayed are (a) outbred pairs, (b) inbred pairs, and (c) autozygous segments in the inbred pairs. MR is the missing data rate and EP is the probability of a genotyping error.

It was previously discovered that there are numerous relative pairs in the MKK, only some of which were documented in the HapMap phase 3 data release.^{23, 28} The presence of these undocumented relative pairs, many of which are distant (ie, first cousins or greater) suggests that consanguineous matings may also be present or that pairs of individuals may have more than a single recent common ancestor. We applied GIBDLD in the MKK population to identify and characterize related pairs and then search for additional IBD in the nominally unrelated pairs.

Although we seek to distinguish related from unrelated pairs, doing so in the MKK is problematic because of a generally elevated level of background relatedness in the population. To demonstrate this, we repeated the simulations for outbred pairs described above, using the Yoruba in Ibadan, Nigeria (YRI) haplotypes. Instead of using a single chromosome, we sampled entire autosomes, using 206 016 SNPs with minor allele frequency>0.05, and sampled unrelated rather than related pairs. Autosomes were sampled without replacement and recombination in the unrelated panel was simulated by gene dropping through 1, 2, or 3 generations. A training sample of 200 individuals was used to estimate the LD parameters. Previous work has found relatively little cryptic relatedness in the YRI.²³ From a simulated sample of 1000 unrelated pairs, the mean genome-wide value of 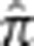was 0.0035 with a maximum of 0.0083 (Supplementary Figure S2). In contrast, the MKK mean genome-wide value of 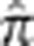across all pairs is 0.0086 (Supplementary Figure S3). Based on the YRI simulations, we set a threshold of 0.01 for 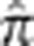in the MKK above which we define a pair as ‘related' and below which we define a pair as ‘unrelated,' although ‘very distantly related' is likely to be a more accurate characterization. The related MKK pairs were then binned into relationship types depending on their genome-wide empirical kinship coefficient 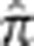(Table 1) where the bin boundaries were based, in part, on the location of gaps in the distribution of 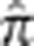(Supplementary Figure S3). Note that there were no pairs that had 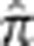in the ranges 0.28–0.5 and 0.16–0.22. The 84 first-degree relatives we find agree with previous results,²³ while we detect 73 second-degree relatives to Pemberton et al's 80. Seven of Pemberton et al's 80 second-degree relatives we inferred to be third-degree relatives. In addition, we found 137 new third-degree and 1655 fourth- and fifth-degree pairs. All pairs in each relationship category are given in the Supplementary Data. In addition, the Supplementary Table S1 contains maximal subsets of individuals such that all pairs in the subset have 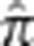less than a specified threshold. These subsets were constructed following a strategy similar to that previously used for the HGDP-CEPH panel.²⁹ It is worth noting that even though the vast majority of MKK pairs are unrelated, there are only 36 individuals who are not detectably related to at least one other individual. Furthermore, even in the pairs categorized as unrelated, a number of pairs show evidence of possibly distant relatedness. For instance, there are 22 unrelated pairs that have IBD segments at least 30 cM long, and 21 pairs that have at least 16 segments of length 2 cM or larger (Supplementary Tables S2 and S3). We detect only low levels of consanguinity, however, with a maximum empirical inbreeding coefficient of 0.0228. We find 10 individuals with autozygous segments of at least 10 cM and 19 with at least three autozygous segments of length 2 cM or longer (Supplementary Tables S4 and S5).

Table 1. Relationship and genome-wide empirical kinship coefficient categories.

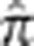	Relationship	Number of pairs
≥0.5	Monozygotic twin	1a
0.22–0.28	First-degree relative (PO, FS)	68 (PO), 16 (FS)
0.10–0.16	Second-degree relative (HS, AV, GG)	73
0.05–0.10	Third-degree relative (1C, GAV)	144
0.01–0.05	Fourth- and fifth-degree relative (1.5C, 2C)	1655
0–0.01	Unrelated pairs	14 728

Abbreviations: PO, parent–offspring; FS, full sibling; HS, half sibling; AV, avuncular; GG, grandparent–grandchild; 1C, first cousin; GAV, grand-avuncular; 1.5C, first cousin once removed; 2C, second cousin.

^aLikely a duplicate sample.²³

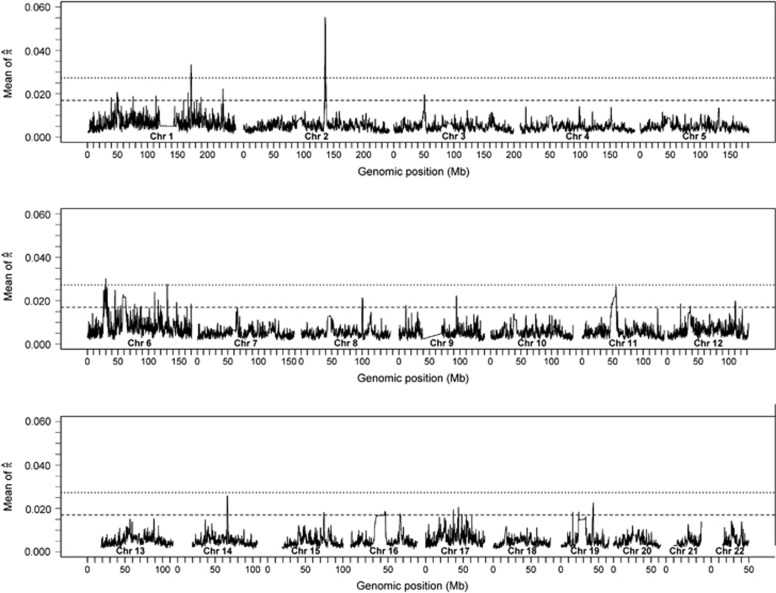
A particularly compelling application of estimating IBD in a population is the potential for detecting recent or ongoing positive selection, particularly when it acts on standing variation – a form of selection that is especially challenging to detect.¹ We searched for regions in the genome that may have been under selection in the MKK population by identifying loci that have anomalously high IBD sharing. To find these loci, we computed 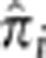at every SNP i for every unrelated pair of individuals. At each SNP, we then computed the mean of 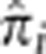across all the unrelated pairs. Figure 3 shows these values at all SNPs across the genome with horizontal lines showing the arbitrary thresholds below which 99.9 and 99% of all SNPs are located. The mean of 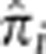across all unrelated pairs and all SNPs is 0.005. At our most stringent threshold, four regions show excess IBD sharing: chromosome 1 (171.76–174.26 Mb), chromosome 2 (135.05–136.55 Mb), and two regions on chromosome 6 (29.77–30.17 Mb and 130.61–130.81 Mb). At the 99% threshold, we detect 50 regions showing evidence for excess IBD sharing (Supplementary Table S6).

Figure 3.

Mean 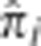over the genome. The mean value of 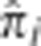at all SNPs i in the genome, averaged over all unrelated pairs in the MKK. The upper (dotted) line is the threshold below which 99.9% of all SNPs are located and the lower (dashed) line the threshold below which 99% of all SNPs are located.

We considered the possibility that high levels of LD in a region may not be fully modeled by GIBDLD, resulting in artificially inflated estimates of IBD. To evaluate this possibility, we divided the genome into 0.1 cM bins and computed the mean 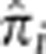for all bins where the average r² across pairs of SNPs was >0.2. We saw no evidence of systematically inflated 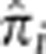in these regions (Supplementary Figure S4).

Of the previously mentioned four regions exceeding our most stringent threshold, the chromosome 2 region showed the largest excess of IBD sharing in the genome with a mean 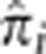of 0.055. This 1.5 Mb region contains 27 genes including LCT, the gene encoding lactase. This region has been implicated as the genetic basis for lactase persistence in several African populations, including some from Kenya, and has evidence of having undergone recent, strong positive selection.³⁰ The first region on chromosome 6 (29.77–30.17 Mb) is coincident with the HLA class I region, a portion of the genome well known as being under strong selective pressure due to its importance in immune system function.³¹ The second highest peak on chromosome 6 (130.61–130.81 Mb) contains only two known genes, KIAA1913 and SAMD3. This region has previously been implicated as possibly having been under selection in the YRI, with a signal peak lying between these two genes,^{32, 33} though we are unaware of any studies finding such evidence in other populations.

Of the four highest peaks in our genome scan, the one on chromosome 1 (171.76–174.26 Mb) was the second most extreme, behind only the signal on chromosome 2. Unlike the three other regions, the published literature contains less support for selection having acted here. In the study by Tang et al,³⁴ a gene in this region, G protein-coupled receptor 52 (GPR52), was listed as showing evidence of having undergone selection, but only in Europeans using the Perlegen data set. This signal was not replicated in the European HapMap data. The region we detect is fairly broad (2.5 Mb) and contains 22 genes. Although this may be an independent replication of the GPR52 signal, the fact that we are looking in a substantially different population and that IBD is expected to have little power to detect selection that has taken a haplotype to near fixation,¹ while the method of Tang et al³⁴ is designed to find regions that are at fixation due to selection, we feel it is possible that we are detecting an independent and novel signal.

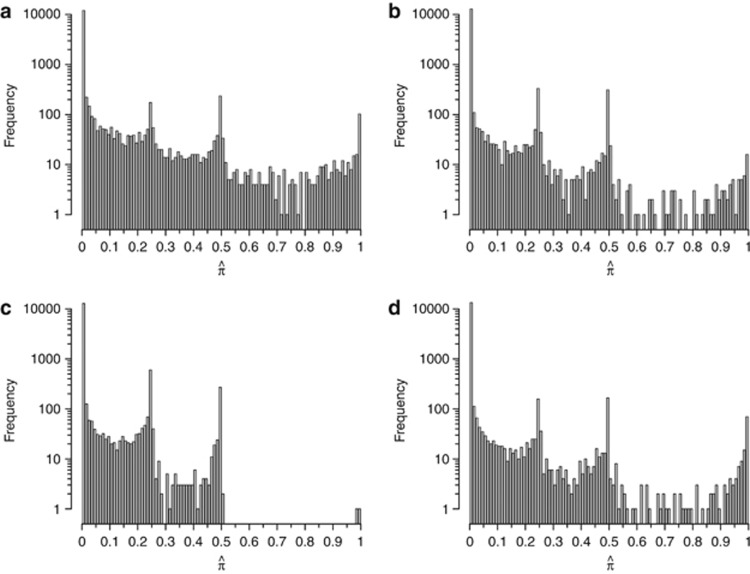
In Figure 4, we plot the distributions of 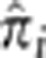across pairs for the top four loci. It is worth noting that in each case ∼12 000 pairs had 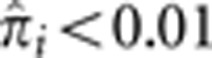. The resultant elevated sharing, then, is due to nearly 2000 pairs having significant amounts of IBD sharing and not caused by relatively few, possibly related, pairs. Also evident are peaks in the distributions of 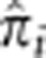at 0.25 and 0.50, corresponding to high probabilities for these pairs to have IBD sharing of one and two alleles, respectively. Interestingly, there are also a substantial number of pairs with 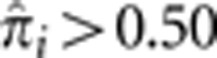. This amount of IBD sharing is only possible when there is a non-zero probability that all four alleles in the pair are shared IBD (IBD=4) with 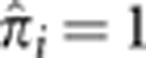being certainty of this state. Figure 4 shows that, at these loci, many unrelated pairs show a significant probability of IBD=4. The exception to this is the HLA locus (Figure 4c). Even though there are similar numbers of pairs with IBD=1 or 2 compared with the other three loci, there are only two pairs with 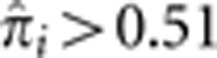. This is consistent with the view that HLA is under balancing selection with homozygosity being detrimental. In fact, we find that the number of pairs with 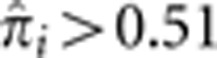is smaller at the HLA locus than any of the other 20 loci with mean 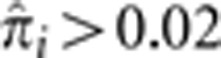(Supplementary Figure S5).

Figure 4.

Distributions of . The distributions of 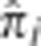for all unrelated pairs at the peak SNP in the regions on (a) chromosome 2 (135.05–136.55 Mb), (b) chromosome 1 (171.76–174.26 Mb), (c) chromosome 6 (29.77–30.17 Mb), and (d) chromosome 6 (130.61–130.81 Mb). Note that the vertical axis is on the log scale.

We also looked for regions of the genome that show evidence of increased autozygosity in the entire panel of 183 subjects. Aside from relatively higher levels at three of the top four loci (ie, not HLA), we did not find loci with clearly elevated levels of autozygosity. We note that the sample size for this analysis (n=183) is substantially smaller than the pairwise IBD analysis (n=14 728 pairs). Even though the pairs are not independent, added variability due to a smaller sample size may make it more difficult to identify regions with anomalous levels of autozygosity.

Of the top 50 regions showing excess IBD, 44% are in regions where other studies have also detected evidence for selection while 56% appear to be novel (Supplementary Table S6). Notable among these 50 regions are five distinct peaks in different HLA regions, comprising both class I and class II genes. On chromosome 11, there is a peak that was close to, but did not exceed, our most stringent threshold of 99.9%. This region was among the top signals reported by Albrechtsen et al¹ for several HapMap populations, including the MKK. This region is of interest with respect to selection because of the clusters of olfactory receptors it contains.

Discussion

Our analysis to detect excess IBD uses the same population and data as Albrechtsen et al,¹ who also search for genome regions with excess IBD, yet our results are not identical. In fact, the elevated regions of IBD they detect in the MKK (on chromosomes 6 and 11) are also found in our analysis, but we also find many additional signals. The primary reason for this difference, we suspect, is that they pruned away many SNPs to eliminate LD, while our method models LD directly, allowing us to use all SNPs in our analysis. Following data cleaning and pruning, their data set consisted of about 200 000 SNPs, whereas we used 1 255 766 SNPs. This additional SNP data can provide substantial information for detecting IBD. Furthermore, we note that the method used by Albrechtsen et al allows for IBD states only up to two, whereas GIBDLD estimates probabilities for all nine condensed identity states, including IBD=4. At loci where there are many pairs that have substantial probability of sharing all four alleles IBD, methods that allow IBD sharing only up to either two or one allele will give negatively biased estimates of 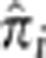. Nevertheless, we believe it is primarily the extra information available from using all SNPs, as well as the increased resolution they provide, that allowed us to detect excess IBD in numerous additional regions.

Recently, another study³⁵ evaluated IBD sharing in the HapMap populations. In the MKK, they find a peak of IBD sharing on chromosome 2, likely overlapping the LCT gene region, and another more marginal peak on chromosome 8. The method used by the authors finds regions, of length at least 3 cM, shared IBD in pairs of individuals. By restricting IBD detection to segments of at least this size, they have high confidence that these regions are truly IBD. In contrast, our IBD estimates are not based on identification of shared segments. Instead, our IBD estimate at a locus is a weighted sum of IBD sharing across all pairs where the weights are the probabilities of sharing. For the problem of estimating average sharing across many pairs, restricting the sum to only high confidence IBD will tend to result in negatively biased estimates. GIBDLD, on the other hand, shows little evidence of bias in our simulations and it is for this reason, we suspect, it finds more peaks of IBD sharing.

Although several regions have anomalously high IBD sharing, we do not have a formal test to assess statistical significance. In principle, simulations could be done to obtain an empirical distribution on 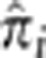, but doing so would necessarily depend on a variety of demographic assumptions, such as population size, structure within the population and method of ascertainment of the study sample. In addition, it may also be the case that some genomic characteristics of specific regions (eg, inversions) would result in apparently inflated IBD estimates. In general, such genomic characteristic would have to allow for enough diversity that there could be significant evidence in favor of IBD – simply making all haplotypes identical reduces IBD estimates to zero – but at the same time inhibit the creation of new variation (ie, through recombination or mutation) for a long enough period of time that similarity should not be considered IBD. This is a question deserving of further study. For these reasons, we choose here to take an empiric approach and identify outlier IBD regions. Such regions, though consistent with and possibly indicative of selection, should not, in isolation, be considered conclusive evidence of selection. Nevertheless, the fact that regions such as HLA and LCT, where there has been abundant evidence in favor of natural selection, have elevated IBD suggests that the approach taken here is a useful one at helping to identify targets of natural selection.

Substantial amounts of unmodeled LD could also artificially inflate estimates of IBD. In our analysis, however, we allowed up to 20 SNPs up to 0.1 cM away from the target SNP (ie, the SNP where IBD is being estimated) to be included in the LD model. Our experience suggests that this allows us to adequately capture LD between the target SNP and other SNPs in the region. Looking across the genome in regions of high LD, we see no evidence of inflation of IBD estimates. There are some regions of the genome, however, where pairwise LD may remain substantial outside the region included in our model. Indeed, it has been pointed out that some regions showing extended LD may be mistakenly interpreted as signals of selection.³⁶ Of the four regions we highlight, the LCT and HLA regions have long range LD. In general, though, we expect long range pairwise LD will not introduce substantial bias in our estimates of IBD. This is because even when the target SNP is in LD with a distant SNP, it is also in LD with nearby SNPs that are included in our model. The distant SNP will also be in LD with the nearby SNPs, resulting in most or all of its predictive information on the target SNP being captured in the model.

Identification of genomic regions undergoing selection is one of the several applications of IBD estimation that have the potential to greatly enhance our insight into genetics. In our analysis, we are able to both replicate previous signals of selection detected using other methods as well as find novel regions. Much of this, however, was accomplished because we were able to use the full spectrum of genotype data available. We believe that using all the genetic information available – as opposed to thinning and thus eliminating much of the data – to determine IBD sharing at loci will also facilitate greater insight into other genetic questions. However, tools that are able to use all the information, and to provide probabilistic measures of IBD, are needed. Furthermore, as interest increases in genetic studies in a diversity of human populations, methods that are effective for a wide range of relatedness levels, including the possibility of inbreeding, will be critical. In the loci that show the highest excess IBD sharing in the MKK, for instance, there are substantial numbers of pairs that show evidence of sharing more than two alleles IBD or have near certainty of sharing all four alleles IBD, even though the pairs are effectively unrelated based on a genome-wide measure. Although a method that does not allow for inbreeding may detect a high probability of IBD for these pairs, it would be unable to detect this level of sharing. This is a particular concern for studies in populations that are of limited size, genetically isolated or, like the MKK, are largely outbred but have significant cryptic relatedness. Our software, GIBDLD, accommodates these needs, providing a beneficial tool for those wishing to estimate IBD.

GIBDLD is part of the IBDLD software package http://sourceforge.net/projects/ibdld/.

The authors declare no conflict of interest.