Optimal Drug Cocktail Design: Methods for Targeting Molecular Ensembles and Insights From Theoretical Model Systems

Abstract

Drug resistance is a significant obstacle in the effective treatment of diseases with rapidly mutating targets, such as AIDS, malaria, and certain forms of cancer. Such targets are remarkably efficient at exploring the space of functional mutants and at evolving to evade drug binding while still maintaining their biological role. To overcome this challenge, drug regimens must be active against potential target variants. Such a goal may be accomplished by one drug molecule that recognizes multiple variants, or by a drug “cocktail” — a small collection of drug molecules that collectively binds all desired variants. Ideally, one wants the smallest cocktail possible due to the potential for increased toxicity with each additional drug. Therefore, the task of designing a regimen for multiple target variants can be framed as an optimization problem — find the smallest collection of molecules that together “covers” the relevant target variants. In this work, we formulate and apply this optimization framework to theoretical model target ensembles. These results are analyzed to develop an understanding of how the physical properties of a target ensemble relate to the properties of the optimal cocktail. We focus on electrostatic variation within target ensembles, as it is one important mechanism by which drug resistance is achieved. Using integer programming, we systematically designed optimal cocktails to cover model target ensembles. We found that certain drug molecules covered much larger regions of target space than others, a phenomenon explained by theory grounded in continuum electrostatics. Molecules within optimal cocktails were often dissimilar, such that each drug was responsible for binding variants with a certain electrostatic property in common. On average, the number of molecules in the optimal cocktails correlated with the number of variants, the differences in the variants’ electrostatic properties at the binding interface, and the level of binding affinity desired. We also treated cases in which a subset of target variants was to be avoided, modeling the common challenge of closely related host molecules that may be implicated in drug toxicity. Such decoys generally increased the size of the required cocktail and more often resulted in infeasible optimizations. Taken together, this work provides practical optimization methods for design of drug cocktails and a theoretical, physics-based framework through which useful insights can be achieved.

1 Introduction

Drug resistance is a major hurdle in the fight against numerous diseases. The ability of targets to evolve and generate mutant forms that escape drug interaction can lead to loss of drug potency over time. For example, patients with advanced chronic myelogenous leukemia (CML) treated with potent drugs such as imatinib (Gleevec)¹ often relapse due to drug-resistant mutations in the kinase domain of the BCR-ABL target protein.² Drug resistance is especially problematic for communicable diseases; in HIV treatment, newly infected, treatment-naive patients can already harbor drug-resistant strains of the virus, indicating that these variants survive and can be successfully transmitted.^3–5

Understanding the molecular basis for drug resistance in these systems can help in the development of “second generation” inhibitors with improved resistance profiles. To that end, structural analyses of the mutant forms of BCR-ABL and the HIV target proteins (such as the reverse transcriptase and the protease) have been extensively reviewed (references^{6 and7} and reviews cited therein). Recent efforts to consider binding to multiple variants of HIV-1 protease have yielded promising drug candidates such as darunavir (TMC114, Prezista)^8–10 that show different, generally flatter, resistance profiles and induce fewer drug-resistant mutations. Rational design strategies that account for structural resistance mechanisms have also been valuable in CML treatment; nilotinib (AMN107)^11–13 and dasanitib (SPRYCEL)¹⁴ are promising candidates that bind to multiple imatinib-resistant target variants.

Nevertheless, although efforts to design drugs that recognize multiple target variants have met with some success, there are still substantial hurdles with the “one-molecule” approach. For example, in spite of its promising resistance profile toward existing BCR-ABL mutants, dasatinib was found to generate additional resistance mutations.^{15, 16} Interestingly, these mutations do not confer resistance to imatinib, suggesting that a cocktail of these two drugs could be a potent solution,^{16, 17} collectively “covering” — or binding to mutants within — a larger region of target functional mutational space than either drug alone. In the case of HIV treatment, darunavir shows promise as a next-generation inhibitor, but there are still forms of the protease toward which it is less effective.^{18, 19} To help prevent resistance associated with the one-molecule approach, many retroviral treatments involve a cocktail of drug molecules that may either bind to the same or to different viral targets. Highly Active Anti-Retroviral Therapy, or HAART,^{20, 21} is a regimen of multiple reverse transcriptase inhibitors and, more recently, protease inhibitors as well, and has been highly effective in treating HIV patients.²² However, such cocktails are still not 100% effective; patients undergoing HAART still often succumb to drug resistance, and sometimes attempts at salvage therapy through altered regimens are not adequate.⁵ A systematic approach toward rational cocktail design in the future may allow for the development of more potent regimens.

In order to design a drug cocktail toward multiple target variants, it is helpful to understand the physical determinants of drug binding toward the ensemble; one seeks molecules that bind to many variants of the target (often referred to as drugs with “broad binding specificity” or “robust binding”). Many of these determinants will be system-specific, but there may also be general physical and structural principles that can be incorporated into the rational design of molecules that comprise cocktails. Common trends from studies on natural or designed molecules suggest the existence of such general, qualitative principles. Among the noted physical characteristics of natural molecules capable of binding to multiple partners are conformational flexibility and a predominance of hydrophobic interactions; such characteristics are generally elucidated through specific examples.^23–32 In one analysis, small, lipophilic molecules were found to bind with high affinity to more partners than their larger or more polar counterparts.³³ Other beneficial features may include the presence of asymmetric functional groups and conformational flexibility that is limited to the especially variable portions of the binding interface.³⁴ Some structural principles may be especially applicable to rapidly-mutating targets; in the case of HIV, the ability to fit within the “substrate envelope” (that is, the active site volume occupied by the natural substrates of HIV-1 protease) has been hypothesized to allow maintenance of binding to functional mutants.^{9, 35}

In addition to having useful principles for designing individual molecules within the cocktail, one must understand the role each drug plays, relative to the others. As a trivial example, it would be redundant to have multiple molecules with identical resistance profiles within the cocktail; a more desirable scenario would be to have mutually dissimilar binding and resistance profiles amongst the drugs. With an appropriate framework, it may be possible to discover principles for grouping target variants such that one drug from a small cocktail can be developed to bind to all members of a group and each group is covered by at least one drug.

In this work, we extract general, physics-based principles that can be useful in the design of molecular cocktails targeting ensembles. We approach cocktail design as an optimization problem and analyze it from a theoretical perspective using model molecules. In an abstract sense, the design problem can be framed as follows: the target has a viable variational space that is evolutionarily accessible (that is, a set of related sequences that are all functional beyond some threshold). The goal is to design drugs that cover the largest region of this space possible. Ideally, this would be accomplished with a single broadly-binding molecule, but in the likely event that one molecule cannot bind to all the variants with adequate affinity, a drug cocktail would be necessary. Because of the increased toxicity associated with a greater number of drug molecules as well as the potential for cross interaction, it is desirable to use the smallest cocktail possible to effectively cover all ensemble members. To that end, we have developed methods to design optimally small cocktails toward an arbitrary set of target variants. Our methods are based on integer programming and can be generally applied to arbitrary target ensembles to design cocktails of practical interest. The first method uses pre-computed binding free energies between potential drug molecules and target variants and solves the standard set cover problem³⁶ to determine the optimally small cocktail. The second method does not require pre-designed molecules; it simultaneously designs them from a combinatorial fragment library as it minimizes the size of the resulting cocktail. This method explicitly takes all target variants into account during the molecular design process, and is a novel integration and extension of the set cover formulation and existing formulations for combinatorial molecular and library design.^37–41

Although we have used the word “drug” throughout this work, the set-cover-based methods can be generally applied to design cocktails of lead compounds as well, and the combinatorial fragment-based methods we describe may be especially well-suited for lead compound cocktail design. We refer to the designed molecules as “drugs” throughout to represent the more clinically important intended use.

Our goal was to use these methods to design cocktails toward target ensembles and to uncover general trends that relate the physical properties of the target ensemble to the nature of the designed cocktails. To systematically model various physical attributes of target ensembles, optimization techniques were applied to ensembles of theoretical model molecules; these molecules captured relevant physical characteristics of actual biological molecules in that they could vary in charge distribution, shape, and size, but they were not limited by the constraints of chemistry, such that these properties could be systematically and exhaustively tested. In this work, we limited our studies to target variants that differ in their electrostatic properties, thus keeping the shapes and sizes of the variants the same. While drug resistance is often mediated by such changes in charge distribution (including the HIV-1 protease mutations Asp30 → Asn and Asn88 → Asp, which confer resistance to nelfinavir^{42, 43}), we recognize that resistance is often achieved by other means as well, such as changes in target shape and flexibility. It should be noted that the cocktail design methods discussed here are generally applicable to drug cocktails and target ensembles that vary arbitrarily in their properties (i.e., charge, shape, size, etc.), and these other attributes are the focus of ongoing and future work.

Our study revealed that model drugs with certain charge distributions were able to cover much larger regions of target space with high affinity than other drugs could cover, and an analysis using continuum electrostatics explained this result and could predict such broadly-binding charge distributions for systems in general. Specifically, such charge distributions tended to lie along certain vector directions in a multidimensional space that represented the drug’s charge distribution, and could thus indicate, for a given system, whether broadly-binding molecules tended to have an overall monopole, a strong dipole, etc. Moreover, it was found that molecules selected for optimal cocktails were often mutually dissimilar, in that each drug molecule covered target variants that shared a particular electrostatic property, such as being positively charged at the interface or having a shared type of asymmetric charge distribution. Such properties may serve to rationally group variants in future drug design applications. By designing optimal cocktails toward thousands of ensembles with variants randomly selected from model functional spaces, several general trends relating target ensembles to their optimal cocktails were elucidated. We also considered cases in which there were potential targets that all drug molecules in the cocktail must avoid. Such off-target binding is a major issue in many drug applications, such as kinase inhibitors for cancer treatment,^{44, 45} where the ATP-binding domains of different kinases tend to be similar.

Taken together, this work casts cocktail design as an optimization problem and introduces useful methods for developing such optimal cocktails. Also, through applying these methods to model molecules within a theoretical framework, we have highlighted specific physics-based principles that can be useful in future cocktail design applications.

2 Methods

Cocktail Design as an Optimization Problem

A successful cocktail can conquer drug resistance by collectively recognizing all the evolutionarily accessible functional target mutants. The most practical and, likely, least toxic cocktail is one that contains the fewest number of drug molecules yet covers all relevant mutants. Stated in terms of a formal optimization, the aim is to minimize the number of drug molecules selected for the cocktail subject to the constraint that all relevant target variants are covered by at least one selected drug. This optimization statement can be represented and solved by integer programming formulations.³⁶ In this section, we present multiple such formulations that can be applied to cocktail design problems, with some being more suited to different variants of the problem at hand.

Integer-Programming-Based Formulations for Cocktail Design

The first set of formulations presented are applicable when a large number of potential drug molecules already exists, either virtually or experimentally, and their binding affinities to target variants have been computationally or experimentally pre-determined. In this case, the goal is to select the smallest number of drugs from this existing set that covers all target variants. This is an example of the set cover problem in computer science.³⁶

Let X represent the set of potential target variants to be covered, and Y the set of drug molecules considered for the cocktail. The goal is to choose the smallest number of molecules in Y such that each molecule in X is covered by at least one chosen drug. To quantify the term covered, we define an affinity threshold t_i for each target i in X. A drug that binds to target variant i with binding free energy less than t_i effectively covers it.

Let E be the matrix of binding free energies — experimentally or computationally determined — between every drug–target pair. E has dimensions m × n, where m is the number of target variants in X and n is the number of drugs in Y. We turn this matrix of binding free energies into a binary matrix A, such that

$$A_{i,j}=1\text{iff}{E}_{i,j}\le t_i,A_{i,j}=0\text{otherwise}.$$ (1)

A is an m × n matrix whose nonzero entries represent the drug–target pairs for which coverage is achieved. Each drug j in Y is associated with a binary variable y_j, where y_j = 1 if drug j is selected for the cocktail, and 0 if not. The integer programming (IP) formulation for the optimization problem is shown in Table 1, IP 1.1. In words, this formulation minimizes the number of drugs chosen for the cocktail subject to the constraint that the coverage of each target variant is at least 1. IP 1.1 is the standard formulation of the set cover problem, which is NP-hard,³⁶ and the worst-case runtime of current algorithms scales exponentially in the number of drugs. In practice, for our systems of interest, we have achieved globally optimal solutions very quickly.

Sometimes the set of potential drug molecules cannot feasibly cover all variants, or other practical requirements might limit the number of drug molecules allowed in a cocktail. In such a case, one may wish instead to make a cocktail of fixed size d that covers the maximal number of target variants possible. The relevant formulation is shown in Table 1, IP 1.2, and uses additional binary variables v_i such that v_i = 1 if variant i is covered by any drug selected for the cocktail, 0 if not. We have found this formulation useful in understanding the factors influencing how cocktails of a fixed size can maximally cover regions of target space.

In either formulation, there may be more than one optimum; for IP 1.1, there may be multiple cocktails of the same optimally small size that cover all target variants, while in IP 1.2, there may be multiple ways to cover the same maximal number of variants with d drugs. To differentiate between the multiple optima, one may wish to run a subsequent integer program that constrains the solution to search within the space of optimal answers from the first optimization and minimizes a secondary objective function. As an example, IP’s 1.3 and 1.4 in Table 1 minimize the sum of the binding free energies of each drug toward the covered variants, while constraining the search to the optimal space found in the earlier optimization. Here, the pre-computed E_i,j values are explicitly used, and a set of binary variables z_i,j is used to account for which variants are covered by a particular drug in order to properly compute the objective function. If one is optimizing a very large problem, such that explicitly using z_i,j variables would be computationally intractable, one can capture the mean, maximum, or minimum binding free energy of each drug toward its covered variants in a vector p⃗(of length n = number of drugs) and minimize p⃗_T y⃗ = Σ_j p_jy_j within the optimal space found by either IP 1.1 or IP 1.2. Such a formulation does not add any additional variables but loses much of the specific energetic information.

Table 1.

Formulations for optimal cocktail design that select the optimal drug set from a pre-existing set of potential drug molecules. Drug–target binding affinities have been pre-computed, and A is a binary matrix that represents whether each drug covers each target. The decision variables are the binary variables y_j, which are set to 1 if drug j is to be included in the cocktail. IP 1.1 is the formulation of a standard set cover problem (i.e., minimize the number of drugs in the cocktail given the constraint that each target is covered by at least one drug). In IP 1.2, the vector v⃗ is composed of binary variables v_i that indicate whether a target variant i is covered by the optimal cocktail when the number of drugs is fixed at d; here the integer program maximizes the number of targets covered for the fixed number of drugs. IP 1.3 and 1.4 can be run after IP 1.1 and 1.2 respectively to discriminate between multiple optima based on energy. In these formulations, E is the original binding free energy matrix enumerating all target–drug binding energies. In words, constraints (1) and (2) in IP 1.3 choose exactly one drug to count toward the objective function for each target, and this drug must cover the target (though there may also be other selected drugs that additionally cover the target as well, by chance). Constraints (3) and (4) ensure that the total number of unique drug molecules used is set to the optimal value (constraint (3) turns on any drug that is used toward at least one target). The statements in IP 1.4 are similar, except they constrain the total number of drugs to a user-input value d and constrain the total coverage to the optimal value while minimizing the combined binding free energy, given d drugs.

IP 1.1	IP 1.2
minimize Σj yj subject to	maximize Σi vi subject to
Ay⃗ ≥ b⃗,	Ay⃗ ≥ v⃗,
b⃗ is a length-m vector of all ones.	Σj yj = d
IP 1.3 (run after IP 1.1)	IP 1.4 (run after IP 1.2)
minimize Σi Σj Ei,jzi,j subject to	minimize Σi Σj Ei,jzi,j subject to
(1) ∀i, Σj Ai,jzi,j = 1,	∀i, ΣjAi,jzi,j = vi,
(2) ∀i, Σj zi,j = 1,	∀i, Σj zi,j = vi,
(3) $\forall j,y_j\ge \frac{1}{I}{\sum }_i{z}_{i,j}$,	$\forall j,y_j\ge \frac{1}{I}{\sum }_i{z}_{i,j}$,
(4) Σj yj = opt1.1,	Σj yj = d,
where opt1.1 is the optimal number of drugs found in IP 1.1 and I is the number of target variants in the ensemble.	Σi vi = opt1.2,
	where opt1.2 is the optimal number of target variants found in IP 1.2 and I is the number of target variants in the ensemble.

This set of IP’s can have great practical use; often in molecular design or experimental screens, one will have a ranked list of many thousands of potential drug molecules for a given target. When running parallel molecular designs to multiple target variants, such integer programs can quickly process all results and identify optimal cocktails to tightly bind ensembles. One advantage of this method is that the cocktail design is independent of the methods or metrics used to assign energies, whether experimental or computational. One disadvantage of the method is that it requires that all drug molecules be pre-enumerated and all drug–target energies be pre-computed or measured.

To address this potential disadvantage, we developed a second set of formulations, each of which rationally designs the molecular cocktail members simultaneously as it designs the optimal cocktail. In essence, this second set of formulations could apply to an arbitrary design problem toward ensembles. The approach taken here is based on combinatorial schemes that begin with a molecular scaffold (or protein backbone, if the therapeutic cocktail consists of proteins or peptides) that contains sites for variable functional group placement. As is done commonly,^{46, 47} we allow for rotamerization of each of the possible functional groups, such that it can exist in discrete possible conformations, and we also allow for multiple conformations of the molecular scaffold. With B positions and H total conformations of all groups at each position, the total number of possible designable molecules is H^B per scaffold conformation. Such a design framework is very useful when a combinatorial synthetic scheme can be used to design the cocktail members.

In such combinatorial formulations, the total binding free energy of a molecule toward a target is often taken as a linear sum of self and pair energy terms,

$$\mathrm{\Delta }{G}_{\text{bind}}=\mathrm{\Delta }{G}_{\text{bind}}(\text{scaffold})+\sum _b\mathrm{\Delta }{G}_{\text{bind}}(h_b)+\sum _{b1}\sum _{b2>b1}\mathrm{\Delta }{G}_{\text{bind}}(h_{b1},h_{b2}),$$ (2)

where each ΔG_bind term is taken as a difference between the free energies in the bound and unbound states, and h_b represents the group (and conformation) selected at position b on the scaffold. Such pairwise additive energy functions are commonly used in combinatorial protein design applications.⁴⁸ For each scaffold conformation, the only pre-computations required for this case are the self and pair binding free energy contributions of all functional group conformations toward each target variant and the self energies of the scaffold conformation. Such pre-computation scales polynomially as the number of functional groups positions, rather than exponentially, as the precomputation of all drug–target binding energies would. The initial cocktail design formulation of this kind is shown in Table 2, IP 2.1. IP 2.1 is both slow and memory intensive in practice, as the number of variables scales exponentially with the number of functional group positions allowed. To deal with this issue, the variables in IP 2.2 (Table 3) scale polynomially with all design specifications. IP 2.2 takes an additional parameter, D, which is an upper bound guess to the number of drugs in the cocktail.

Table 3.

Alternate formulation to IP 2.1 whose variables do not scale with the combinatorial number of potential molecules. The formulation shown assumes one possible molecular scaffold (that can exist in multiple conformations), but extensions are possible to consider multiple scaffold molecules as well. The user inputs D, a number of “drug placeholders”, which should be an upper bound estimate on the number of required drugs. Note that the analog of IP 1.2 is easily attainable through minimal perturbation of this formulation, but analogs of IP 1.3 and 1.4 are not natural extensions.

IP 2.2
Definitions:
I total target variants, Ai scaffold conformations per variant i,
Ba functional group positions per scaffold conformation a,
Ga,b functional groups per position b,
Cb,a total confs. of all functional groups at position b on scaffold conf. a,
D drugs allowed
Variables:
si,a,d = 1 if scaffold conformation a for variant i is used to make drug d
ub,g,d = 1 if functional group g at position b is used for drug d
fi,a,b,c,d = 1 if conf. c at position b for scaffold a is used for variant i, in drug d
pi,a,b1,b2,c1,c2,d = 1 if both fi,a,b1,c1,d and f i,a,b2,c2,d = 1 on drug d
qi,d = 1 if drug d covers variant i
ki = 1 if variant i is covered
yd = 1 if drug d is included in the cocktail
Parameters:
Emax upper bound constant for the binding energy
es i,a energy of scaffold a for variant i
ei,a,b1,b2,c1,c2: self and pair energies (pre-computed)
m i,a,b,g,c = 1 if conformation c at position b is of func. group g (on scaffold a for variant i)
ti: threshold affinities for each variant i
Minimize Σd yd	Minimize number of drugs used
subject to
∀i, d, qi,d ≤ yd	Only used drugs cover variants
∀d > 1 yd ≤ yd−1	Use placeholders in order
Σi ki ≥ I	All variants are covered
∀i, ki ≤ Σd q i,d	i covered if any drug covers it
∀i, d, Σa si,a = yd	One scaffold conf. per variant
∀d, b Σg ub,g,d = yd	One func. group per position
∀i, a, b, d, Σc fi,a,b,c,d = si,a,d	One conf. per position
∀i, d, Emax(1 − qi,d) ≥ −ti +Σa si,a,desi,a+ Σa,b,c fi,a,b,c,dei,a,b,b,c,c + Σa,b,c1 Σa,b2>b1,c2 pi,a,b1,b2,c1,c2,dei,a,b1,b2,c1,c2	Does drug d cover i?
∀i, a, b 1, b2 > b1, c1, c2, d pi,a,b1,b2,c 1,c2,d ≤ fi,a,b1,c 1,d	Turns on correct pair variable
∀i, a, b 1, b2 > b1, c1, c2, d pi,a,b1,b2,c 1,c2,d ≤ fi,a,b2,c 2,d	Turns on correct pair variable
∀i, a, b 1, b2 > b1, c1, c2, d pi,a,b1,b2,c 1,c2,d ≥ fi,a,b1,c 1,d + fi,a,b2,c2,d − 1	Turns on correct pair variable
i, b, g, d, Σa Σc m i,a,b,g,cfi,a,b,c,d = ub,g,d	Ties confs. to func. groups

Analogously to IP 1.2, one can minimally perturb IP 2.1 or 2.2 to maximize coverage given a fixed number of drugs. Additionally, one can run a second IP related to IP 2.1 after either IP 2.1 or 2.2 to differentiate between multiple optimal cocktails by minimizing the sum of the binding free energies between each drug and its covered variant(s), analogously to IP 1.3. A simple variant of IP 2.2 to differentiate between multiple optimal cocktails in this way may not be as straightforward, and such extensions are future work. While we do not explicitly state these additional formulations, we have used them in our results, and they require minor alterations to the ones shown in Tables 2 and 3.

Table 2.

IP formulation through which the molecules within a cocktail are designed simultaneously as the cocktail is designed. Each molecule is built from a scaffold and potential functional groups at positions on the scaffold, for a combinatorial number of total possible molecules. In addition, scaffolds and functional groups can exist in discrete conformations, and, with some extension, multiple unique scaffolds can be considered. Individual conformations of functional groups are chosen to ensure the binding energy of each molecule toward its covered target variants is less than the desired threshold. Note that targets may be double-covered by chance, but this formulation ensures at least one designed drug will cover each target. The m parameters are the link between conformations at a position and a molecule’s identity. Two molecules are the same if they have all the same functional groups at their respective positions, no matter their conformations, and so the m variables ensure this connection. Note that analogs of IP 1.2, 1.3, and 1.4 are attainable through minimal perturbation of this formulation.

IP 2.1
Definitions:
I total target variants, Ai scaffold conformations per variant i,
Ba functional group positions per scaffold conformation a,
Cb,a total conformations of all functional groups per position b on scaffold conformation a
Variables:
si,a = 1 if scaffold conf. a for variant i used
fi,a,b,c = 1 if conf. c at position b for scaffold conf. a is used for variant i
pi,a,b1,b2,c1,c2 = 1 if both fi,a,b1,c1 and fi,a,b2,c2 = 1
qi,j = 1 if variant i is covered by unique molecule j†
yj = 1 if unique molecule j is made.
Parameters:
esi,a energy of scaffold conf. a for variant i
ei,a,b1,b2,c1,c2 self and pair energies (pre-computed)
mi,a,j,b,c = 1 if conf. c is at position b for molecule j (on scaffold conf. a for variant i)
ti: threshold affinities for each variant i
Minimize Σj yj	Minimize number of drugs
subject to
∀i, Σa si,a = 1	One scaffold conf. per variant
∀i, a, b, Σc fi,a,b,c = si,a	One conf. per position
∀i, ti ≥ Σa si,aesi,a + Σa,b,c fi,a,b,cei,a,b,b,c,c+ Σa,b,c1 Σa,b2>b 1,c 2 pi,a,b1,b2,c1,c 2ei,a,b1,b2,c 1,c2	Enforces affinity constraint
∀i, a, b1, b2 > b1, c1, c2, pi,a,b1,b2,c1,c2 ≤ fi,a,b1,c1	Turns on correct pair variable
∀i, a, b1, b2 > b1, c1, c2, pi,a,b1,b2,c1,c2 ≤ fi,a,b2,c2	Turns on correct pair variable
∀i, a, b1, b2 > b1, c1, c2, pi,a,b1,b2,c1,c2 ≥ fi,a,b1,c1 + fi,a,b 2,c2 − 1	Turns on correct pair variable
∀i, j, a, qi,j ≥ Σb,c mi,a,j,b,c fi,a,b,c − (Ba − 1)	Converts to a unique molecule
∀j, $\forall j,y_j\ge \frac{1}{I}{\sum }_i{q}_{i,j}$	Counts a used drug molecule

^†The q_i,j variables can be eliminated if the problem size is very large, at the expense of the IP not providing direct information about which drugs cover which target variants.

In practice, all these formulations guarantee globally optimal solutions, assuming termination. Currently, the formulations in IP 2.x are substantially more time-intensive than those in IP 1.x, but we believe that they are a novel method to explicitly design toward multiple targets and a current priority is to shorten the solution time of these formulations for practical problems. One speedup is to pre-process the functional group space by running dead-end elimination^{49, 50} with an energy cutoff that guarantees that functional groups within the optimal cocktail are retained. Implementing this pre-processing step has dramatically increased performance in several cases, but further improvements will be important in increasing the global applicability of the IP 2.x methods.

Model System Framework and Binding Free Energy Calculations

Theoretical model systems were chosen as a first application of the cocktail design methods in order to elucidate general design principles through variation of target ensemble characteristics. Theoretical model molecules allow for the systematic and exhaustive variation of characteristics such as charge, size, and shape and for the generation of large amounts of data for statistical analyses. Model molecules were built up from spheres that were bonded into rods, as shown in Fig. 1. The molecules used to generate results in Sections 3.1–3.3 (Fig. 1a) were composed of spheres with radius of 2.0Å. The bond lengths between atoms joined into rods was 1.5 Å, and the rods were offset 4.0Å from each other. In the bound complex, the drug and target spheres at the binding interface were 3.7 Å apart along the binding axis. The molecules used in the statistical analyses (Sections 3.4–3.5, Fig. 1b) were built from spheres of radius 1.8 Å with bond lengths of 1.5Å; rods were offset by 3.6Å, and the drug and target interfacial spheres were 3.6Å apart along the binding axis. The shapes of the model molecules could be varied by moving each of these rods along their respective axes in discrete steps. Moreover, certain spheres within the molecules could be charged to arbitrary values, thus creating varied charge distributions. In this work, we used target ensembles consisting of model molecules that were the same size and shape, and differed only in their charge distribution. Our drug molecules were also identically-shaped, and they formed identically-shaped complexes with each target; this allowed us to focus our study on mutants with altered electrostatic characteristics. However, all the IP formulations used here are fully general and are not limited to constant-shape, purely electrostatic changes between target ensemble and drug cocktail members.

Figure 1.

Representations of model molecules used in this study. Model drug molecules are shown in blue, bound to model targets, in red. Numbered spheres are ones that were allowed to bear charge in creating the target ensembles and drug libraries. (a) Model molecules used for the studies in Sections 3.1–3.3. The yellow dashed line indicates the axis of a rod, as described in the text. (b) Model molecules used for the studies in Sections 3.4–3.5. The target and drug shapes are also shown individually for clarity. In certain designs, target spheres labeled with “*” or “+” were constrained to lie within narrow charge ranges (see text).

In order to design the optimal cocktail using the IP 1.x methods, binding free energies were pre-computed between each target–drug pair (in a fixed orientation), and were computed as

$$\mathrm{\Delta }{G}_{\text{bind}}=\mathrm{\Delta }{G}_{\text{bind},\text{vdW}}+\mathrm{\Delta }{G}_{\text{bind},\text{SASA}}+\mathrm{\Delta }{G}_{\text{bind},\text{elec}}.$$ (3)

ΔG_bind,vdW is the van der Waals (vdW) energy for which a standard Lennard-Jones potential was used. For all spheres, the Lennard-Jones well-depth was set to −0.1200 kcal/mol, with R_min/2 (one-half the optimal sphere–sphere distance) set to 2.0 Å for molecules used in Sections 3.1–3.3 and 1.8 Å for those used in Sections 3.4–3.5. ΔG_bind,SASA accounts for the change in solvent entropy and solvent–solute van der Waals interaction upon binding and is proportional to the change in solvent-accessible-surface area (SASA) upon binding. SASA energies of the bound and unbound states were found using the formula (5 cal/Ų) × (SASA) + 860 cal,⁵¹ and a 1.4-Å probe radius was used to calculate the SASA. Van der Waals and SASA energies were computed for the bound and unbound states of each complex shape using the CHARMM molecular mechanics software package.⁵²

ΔG_bind,elec was computed using a continuum electrostatics framework,^53–56 according to the equation

$$\mathrm{\Delta }{G}_{\text{bind},\text{elec}}={\overrightarrow{q_d}}^{T}D\overrightarrow{q_d}+{\overrightarrow{q_t}}^{T}T\overrightarrow{q_t}+{\overrightarrow{q_t}}^{T}C\overrightarrow{q_d}.$$ (4)

The first two terms represent the unfavorable energetic cost of each binding partner (d drug, t target) being desolvated by the other upon binding, while the third term represents the solvent screened interaction between the charges on the two binding partners. $\overrightarrow{q_d}$ is a vector whose elements are the charge values on each of the spheres on a drug molecule; in the model system corresponding to Fig. 1a, $\overrightarrow{q_d}$ has length 4. Analogously, $\overrightarrow{q_t}$ has length 2, as there were only two spheres that bore charge on each target variant in this system. D and T are the drug and target desolvation matrices, respectively; the i, j^th element of the D or T matrix is one-half the electrostatic potential difference upon binding at the i^th charge value due to a total charge of +1.0e on the j^th charge value in the drug or target molecule, respectively (the factor of one-half exists for the off-diagonal elements to avoid double-counting, and the diagonal elements are halved because the free energy of a point charge interacting with its own reaction field potential is 0.5qφ, where q is the charge value and φ is the reaction field potential generated⁵⁴). The C matrix is defined analogously, except the two charged values are on different partners. All three matrices depend only on the shapes of the binding partners and the complex and the locations of the charges, and were therefore constant for all drug–target interactions computed. Matrix elements were computed by solving the linearized Poisson equation (zero ionic strength); separate runs were done in which each atom center that was allowed to vary in charge was charged to +1.0e in both the bound and unbound states, and the potential difference was calculated. These potential differences were then assembled appropriately to generate the matrices.⁵⁶ Potentials were computed using a locally-modified version of the DELPHI package.^57–59 A two-stage focusing procedure was used, such that the molecules first occupied 23% and then 92% of the entire grid’s volume. A 129x129x129 grid was used, corresponding to approximately 6.5 grids/Å at the higher focusing for the system shown in Fig. 1a and 7.0 grids/Å for the system in Fig. 1b. Three translations of the grids were averaged. The solvation radius of each atom was set to its van der Waals radius. Trial calculations using non-zero ionic strength (145 mM) and the linearized Poisson–Boltzmann equation did not alter the major ideas here for biologically relevant charge magnitudes.

To cast the problem as one for which the IP 2.x formulations were appropriate, we decomposed the above energy function (Eq. 3) into constant, self, and pair energy components for every charge value at each sphere center. This breakdown was done for every target variant. The constant “scaffold” piece toward each target was the sum of van der Waals, SASA, and target desolvation pieces, which are all independent of the charges on each potential drug molecule. The self term for a given charge value q_i on a sphere i was the sum of its individual desolvation penalty and its interaction with the target charges,

$$\mathrm{\Delta }{G}_{\text{bind}}(q_i)=q_i{D}_{i,i}{q}_i+{\overrightarrow{q_t}}^T\overrightarrow{C_i}{q}_i$$ (5)

where C⃗_i is the i^th column of C. Finally, the pair term between q_i on sphere i and q_j on sphere j is

$$\mathrm{\Delta }{G}_{\text{bind}}(q_i,q_j)=q_i{D}_{i,j}{q}_j+q_j{D}_{j,i}{q}_i$$ (6)

(or 2q_iD_i,jq_j, as D is symmetric).

The final binding energies (i.e., summing over all terms in Eq. 3) and the self- and pair-energy contributions used for the IP 2.x formulations were calculated with MATLAB.⁶⁰ In addition, data anlysis was done using MATLAB.

3 Results

3.1 Proof of Principle: Covering Six Discrete Model Target Variants

We began with a simple model ensemble of six target variants and a combinatorial design scheme capable of producing 625 unique model drug molecules. The target variants all had the same shape (shown in red in Fig. 1a), as did the potential drug molecules (shown in blue in Fig. 1a). The potential drug molecules were made of four atom-sized spheres, each of which could bear a charge value between −1e and +1e in increments of 0.5e, for a total of 625 possible molecules. The six target variants differed in charge at two sphere centers at the binding interface, indicated in Fig. 1a. Each variant’s charge distribution was randomly chosen from a two-dimensional continuous charge space bounded by −1e and +1e on each of the two spheres. All other target spheres were uncharged. Integral charge distributions were not enforced in these model systems, as the model molecules could represent smaller regions of larger species.

IP 1.1, IP 2.1, and IP 2.2 were each applied to the randomly-generated six-target ensemble, and each was followed by a second IP that minimized the objective function shown in IP 1.3 within the optimal space of the first IP run. Cplex 9.0⁶¹ in the GAMS software package⁶² was used to solve all integer programs. All three procedures produced identical drug cocktails for a given target ensemble. A sample result is shown in Figure 2a. Here, with an affinity threshold of −3.3 kcal/mol for every target variant (chosen to ensure feasibility), two drugs were needed for the optimal cocktail, one that covered four variants, the other two. Note that the optimal cocktail naturally grouped the variants based on the similarity of their charge distributions, and in this case, the value on target sphere 1 shown in the figure was important in determining the clusters; drug 1 covered the variants that were negatively charged at that sphere (Fig. 2a, blue rounded rectangle), while drug 2 covered the two variants that were positively charged at that sphere (Fig. 2a, green rounded rectangle). The optimal drug charge distributions reflected the electrostatic nature of the variants they covered (also shown in Fig. 2a); drug 1 had positive and negative charges at spheres 2 and 4, respectively, such that it could favorably interact with target variants in “quadrant 2” of the target charge space (upper left of figure). Drug 2 had only sphere 2 charged, and to a negative value, to reflect the fact that the variants it covered were positively charged on one varying sphere and fairly neutral at the other.

Figure 2.

Optimal cocktails designed toward six model target variants that differ in charge values at two spheres. Each variant is represented by an ‘x’ in 2-D charge space that represents the charge values at its two spheres. Variants that are covered by the same drug are grouped within the same rectangle. Each rectangle corresponds to a drug molecule in the cocktail that covers the drugs within it. The affinity threshold used was −3.3 kcal/mol. The charge distribution of the drug molecule(s) in each cocktail is listed below the plots. The order of the charge values for both the drug molecules and the variants corresponds to the numbering in the schematic above the plots. The quadrant-numbering convention used throughout this work is indicated with Roman numerals.(a) Optimal cocktail that covers all target variants. (b) Optimal coverage achievable from only one drug.

IP 1.2 (and appropriate variants of IP 2.x) was also applied to design a cocktail of fixed size D with maximal coverage. Again, these runs were followed by a second IP to refine the optimal cocktail. When D was set to 2, we obtained the same answer shown in Fig. 2a, as expected. However, when D was set to 1, we found that one drug molecule alone was capable of covering five out of the six variants (Fig. 2b). Interestingly, the optimal drug was completely hydrophobic — with all spheres assigned a charge of zero — and covered all variants except the one with the highest-magnitude charges. This finding is in line with the anecdotal hypothesis that hydrophobic molecules are more broadly-binding, an idea that will be explored further below. Nevertheless, the fact that this molecule was not chosen in the optimal two-drug cocktail to cover all variants shows the potential importance of considering the simultaneous relationships between drugs in cocktail design. If one were to use a sequential, greedy approach, first choosing the drug that covers the most variants with optimal energy sum, then choosing the one covering the most remaining ones, etc., the cocktail would include the completely hydrophobic drug, making it suboptimal according to our secondary objective function. That is, one could cover all drugs to at least threshold affinity, but higher overall affinities are achievable and would be missed; in this case, the sum of affinities in the optimal cocktail shown in Fig. 2a was −22.1 kcal/mol, while a two-drug cocktail constrained to have the completely hydrophobic ligand present could optimally achieve a secondary objective function of −21.9 kcal/mol.

Here conformations were invariant and the only differences between molecules, be they targets or drugs, was electrostatic. Targets were effectively clustered by their electrostatic properties, and a single ligand capable of binding all members of a cluster resulted from the design algorithm.

Designing a cocktail toward specific target variants can ensure that the current set of mutants is covered effectively, but targets continually evolve, and ideally, a drug cocktail could be designed in anticipation of potential future mutants in addition to existing ones. In the next section, instead of targeting specific charge distributions, we assumed that the potential mutant space of the target can lie anywhere within a fixed region of charge space. For these and all remaining results presented here, the IP 1.x formulations have been used, as they were faster in practice for our work on model systems. However, below, we also discuss the potential utility of the IP 2.x formulations for other applications.

3.2 “Tiling the Mutation Space” of Targets

To model the potential mutation space of the model target, the charge value on each of the two interfacial spheres on the target could lie anywhere between −1e and +1e, creating a continuous, two-dimensional mutation space. In order to carry out the cocktail design, we discretized this space by placing “dummy” target variants on a regular lattice within it; the lattice spacing used here was 0.2e in both dimensions, yielding 121 variants in the dummy ensemble.

Using IP 1.1 followed by IP 1.3, an optimal cocktail was designed from the 625 potential drug molecules described above. Four drugs were needed to cover the space; their charge distributions and the regions of target space they covered are shown schematically in Fig. 3a. As demonstrated in the figure, the regions are localized into “tiles”, each of which covers one of the four quadrants of charge space. Interestingly, the regions overlap; the IP formulation guarantees that each target variant be covered by at least one drug, and the overlapping regions correspond to variants that can bind to more than one drug with a binding free energy of less than −3.3 kcal/mol. These variants generally have at least one of the two spheres charged to a near-neutral or neutral value. The regions closer to the corners — corresponding to variants that have two high-magnitude charges — were not covered redundantly.

Figure 3.

Optimal cocktails to cover a model mutation space of a target. The space is discretized with target variants whose charge distributions at each sphere are sampled at 0.2e intervals within the space (black x’s). Each variant’s location on the x-axis corresponds to its charge value at sphere 1, while its location on the y-axis is its charge value at sphere 2. (a) Optimal cocktail to cover the entire space. Four drugs were needed, and their charge distributions are indicated. Charges are listed in order (1– 4) according to the schematic shown in Fig. 2. (b) Optimal coverage achieved with one drug. The drug with all spheres uncharged was chosen as optimal. (c–d) optimal coverages achieved with two and three drugs, with their charges indicated.

The optimal drugs in this cocktail were mutually different in their electrostatic properties and reflected the target variants they covered. Each one presented a unique electrostatic face at the interface (drug spheres 2 and 4) – one positively charged, one negatively charged, and two with opposing alternations of positively and negatively charged spheres. These two drugs (1 and 4) are related by a rotation, suggesting that a molecule that was free to present multiple faces to its potential target could cover many more variants. Below we allow for such rotational freedom of the drug molecules, using it as a model for conformational flexibility and multiple-mode binding in order to probe how such properties can affect a drug molecule’s target coverage.

Interestingly, not all drugs covered the same number of target variants — the tiles were not all equal in size. The two tiles covering quadrants 1 and 3 (upper right and lower left quadrants in figure) were qualitatively different from those covering quadrants 2 and 4. This suggests that the overall charge distribution of a drug molecule can impact its broad binding specificity. It should be noted that the charge distributions in quadrants 1 and 3 consist of two like charges, whereas 2 and 4 consist of two opposite charges. Below, we further explore how a drug’s electrostatic properties can predictably affect how many variants it can potentially cover, or the size of its corresponding tile.

Figure 3b–d shows the optimal coverages achieved using one, two, and three drug molecules. Like the simple six-variant case, the completely hydrophobic drug had the greatest overall coverage, and was chosen for the optimal one-drug cocktail (Fig. 3b). The two-drug cocktail covered regions of space that had high-magnitude monopoles, leaving the other regions uncovered (Fig. 3c). This suggests that in this system, better binding free energies can be obtained toward such variants, thereby making them the optimal ones to cover first. Finally, these results again demonstrate that taking a greedy approach to design the cocktail would not yield an optimal set of drugs to cover the entire space, as the completely hydrophobic drug was absent from the optimal cocktail. In fact, a greedy algorithm that serially chose the drug that covered the most uncovered targets yielded a five-drug cocktail to cover the entire space, instead of the optimal size of four drugs (data not shown); additionally, the optimal size of a cocktail constrained to contain the completely hydrophobic drug was five drugs when using IP 1.1 (data not shown).

Does a completely hydrophobic drug always cover the largest region of potential target space? Fig. 4 provides an answer to this question within the model framework. Here, the potential target mutant space was extended to include charges with magnitudes up to 1.6e. Now, the drug molecule that covered the largest region in this space was not completely hydrophobic, and bore an overall monopole (green tile in Figure 4). This suggests that theoretically, there can be charged molecules that exhibit very broad binding profiles. However, individual partial atomic charges in biological molecules rarely exceed magnitudes of +1e; usually, such charge magnitudes are found on metal ions and other species that are not highly predominant within proteins. Therefore, while these charged molecules could exhibit broad binding, they are near the edges of biological charge space, such that there are fewer partners with which they can bind. This result suggests that hydrophobic molecules might be more broadly-binding not because their charge distribution is inherently more favorable for binding, but because they lie in the center of potential target space and not near an edge.

Figure 4.

Comparison of the coverages of two drugs when the mutation space is extended to include target variants with charge magnitudes up to 1.6e on either sphere. Now there are charged drugs, such as drug 2 (green) that cover more target variants than the completely hydrophobic drug (blue). Charges are listed in the order according to the schematic shown in Fig. 2.

The trends exhibited through cocktail design on these model systems can be generalized using theory grounded in continuum electrostatics. The theory quantitatively establishes a relationship between a drug molecule’s charge distribution and the size, location, and shape of its corresponding tile in target charge space, and is described in Section 3.3.

We also considered the effect of conformational flexibility on broad molecular recognition. Conformational flexibility was modeled by allowing model drug molecules to bind in any of their four shape-invariant conformations. As the model drug molecules could represent small regions of a molecular binding interface, this captured the effect of a flexible drug molecule’s ability to present different faces of a functional group or side chain toward target variants. It could also represent the ability of a small molecule to bind in multiple modes to target variants, another potential mechanism for increased broad-binding ability.

The binding free energies of the 625 drug molecules were pre-computed against each of the 121 target variants, although now, an overall free energy was computed by summing over the Boltzmann-weighted binding free energies, $e^{-\frac{\mathrm{\Delta }{G}_{\text{bind},i}}{kT}}$, of each of the four shape-invariant binding orientations i. This resulted in a partition function Q, and the expression ΔG = −kT lnQ was used to compute the overall binding free energy. The zero of energy was taken to be the unbound state, and T was set to 298.15 K. In computing the partition function, we did not remove duplicate bound states resulting from orientational symmetry, as biological molecules would likely have isotopic variation and more realistic geometries that would break perfect symmetry.

IP 1.1 and IP 1.3 were applied to design the optimal cocktail using a threshold of −3.3 kcal/mol, and the optimal tiling is shown in Fig. 5a. Recall that when drugs were bound in a fixed orientation to the target variants, four drugs were needed to cover the space. Now, only one drug was needed. Moreover, this drug molecule lacked a plane of symmetry, such that each shape-invariant orientation could present a unique face toward the target, allowing it to obtain maximal coverage. Interestingly, none of the orientations presents a completely hydrophobic face to the target, but all orientations present at least one sphere at the interface that is uncharged, with the other capable of being either positively or negatively charged. Fig. 5b shows the tiles corresponding to each individual orientation of the drug molecule. Interestingly, the target variants in the corners of charge space and the completely hydrophobic variant were not covered by any single orientation. The entropic contribution due to multiple orientations having similar energies was responsible for their ultimate coverage.

Figure 5.

(a) Optimal “cocktail” to cover the space of model mutant target variants when drug molecules were allowed to bind in any of their four shape-invariant conformations. Such orientational freedom was used as a model for conformational flexibility of a portion of a drug molecule, and also for multi-mode binding. The cocktail contains only one drug, whose charge distribution is indicated. Charges are listed in the order corresponding to the schematic shown in Fig. 2. (b) The tiles corresponding to each of the four individual orientations of the drug in (a). Note that some target variants are not covered by any individual orientation, but the entropic contribution due to multiple orientations allows for overall coverage.

This result demonstrated that one drug molecule can cover multiple — even all — “quadrants” of target space when it can orient itself in multiple ways at the interface. Whether or not this is accomplished via conformational flexibility or multiple binding modes, this suggests that in practice, an asymmetrically-charged, conformationally flexible drug molecule can be a potent cocktail member, especially if the asymmetric group can easily reorient itself relative to a target upon binding. The importance of conformational flexibility and multi-mode binding is demonstrated by the potency of TMC125-R165335 (Etravirine) against wild-type and multiple drug-resistant HIV-1 reverse transcriptase variants; the molecule’s ability to reorient and conform itself to accomodate the varying shapes and chemical environments of the mutants likely plays a large role in its broad recognition spectrum.⁶³ In such biological examples, both the shape and electrostatic characteristics of the binding pockets will likely change from variant to variant, but the general principle found here will likely hold — the ability to conform such that complementary interfaces can be generated toward each variant can result in the coverage of mutants with different physico-chemical properties.

3.3 A Continuum Electrostatic Framework Can Provide a Quantitative Relationship Between a Drug Molecule’s Charge Distribution and its Target Coverage

The case of constant-shape, fixed-orientation binders can be productively explored in a continuum electrostatic framework that allows for quantitative predictions of the relationship between a molecule’s charge distribution and the broadness of its binding profile. This framework can provide a useful starting point in analyzing drug–target coverage in more complicated, biologically realistic systems.

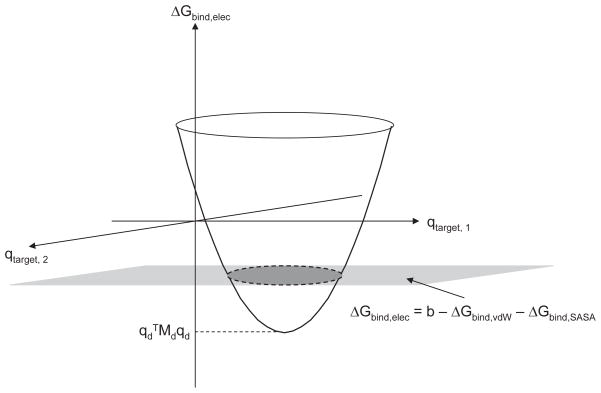
To quantify the extent to which a drug molecule is able to bind with high affinity to multiple target variants, we define the coverage, C_b, of a drug as the number of variants within the target ensemble to which it binds with a free energy of less than or equal to b kcal/mol:

$$C_b=(\text{number}\text{of}\text{target}\text{variants}i\text{s}.\text{t}.\mathrm{\Delta }{G}_{\text{bind},i}\le b)$$

Consider a drug molecule presented with an ensemble of identically-shaped target variants; rigid binding in a fixed orientation is assumed. In such a case, the only varying energetic term between the drug–target pairs, according to Eq. 3, is ΔG_bind,elec. In the continuum electrostatics framework, the electrostatic binding free energy is obtained via Eq. 4. Within the target ensemble, there will be one variant to which the drug molecule will bind most tightly. In a theoretical ensemble containing target variants of all possible charge distributions, the optimal variant is found by minimizing ΔG_bind,elec (Eq. 4) for a given ligand charge distribution $\overrightarrow{q_d}$ by setting the derivative with respect to $\overrightarrow{q_t}$ equal to zero (a minimum exists because T is positive semi-definite, as electrostatic desolvation is always a penalty):

$${\overrightarrow{q}}_{t,\text{opt}}=-\frac{1}{2}{T}^{-1}C\overrightarrow{q_d}.$$ (7)

q⃗_t,opt is the target charge distribution that will maximize affinity to a drug with charges $\overrightarrow{q_d}$. Substituting q⃗_t,opt into Eq. 4 yields the optimal electrostatic binding free energy for the drug, which we will show is related to its coverage:

$$\mathrm{\Delta }{G}_{\text{opt},\text{elec}}={\overrightarrow{q_d}}^T(D-\frac{1}{4}{C}^T{T}^{-1}C)\overrightarrow{q_d}={\overrightarrow{q_d}}^T{M}_d\overrightarrow{q_d},$$ (8)

where $M_d=D-\frac{1}{4}{C}^T{T}^{-1}C$. Given a ligand with charge distribution $\overrightarrow{q_d}$, if ${\overrightarrow{q_d}}^T{M}_d\overrightarrow{q_d}+\mathrm{\Delta }{G}_{\text{bind},\text{vdW}}+\mathrm{\Delta }{G}_{\text{bind},\text{SASA}}>b$, the ligand will have a coverage value C_b of zero — it cannot bind to any target variants in the space tighter than b kcals/mol because its optimal binding free energy to any variant is higher than b kcal/mol. Conversely, if ${\overrightarrow{q_d}}^T{M}_d\overrightarrow{q_d}+\mathrm{\Delta }{G}_{\text{bind},\text{vdW}}+\mathrm{\Delta }{G}_{\text{bind},\text{SASA}}\ge b$, then the ligand will have nonzero coverage if the appropriate variants are within the ensemble. Assuming the target ensemble contains every variant from a continuous charge space, the larger the value of $(b-({\overrightarrow{q_d}}^T{M}_d\overrightarrow{q_d}+\mathrm{\Delta }{G}_{\text{bind},\text{vdW}}+\mathrm{\Delta }{G}_{\text{bind},\text{SASA}})$, the greater the drug molecule’s coverage toward the target ensemble.

This idea is shown pictorially in Fig. 6. Here, the target has two charge-bearing spheres, and for a given drug with charge distribution $\overrightarrow{q_d}$, the free energy of binding plotted against all possible target charge distributions traces out a paraboloid (ΔG_elec is quadratic in either $\overrightarrow{q_d}$ or $\overrightarrow{q_t}$, and both the D and T matrices are positive semi-definite). The minimum value of this paraboloid is given by ${\overrightarrow{q_d}}^T{M}_d\overrightarrow{q_d}$. Imposing an overall binding affinity threshold to variants of b kcal/mol for the ligand amounts to placing a horizontal plane at ΔG_elec = b − ΔG_bind,vdW − ΔG_bind,SASA. Only the target variants contained within the ellipse at the intersection of the paraboloid and plane will be covered by the drug. Assuming an infinite set of variants, the drug’s coverage is proportional to the area of this ellipse. These ellipses gave rise to the tiles observed in Fig. 3, which are approximately elliptical, and would be exactly so in the limit of infinitely fine sampling within the space.

Figure 6.

Schematic representation of a drug molecule’s coverage in the continuum electrostatic framework. The coverage for a hypothetical drug with charge distribution $\overrightarrow{q_d}$ is shown. The paraboloid traces out the ΔG_bind,elec of this drug toward identically-shaped target variants as a function of target charge distribution. If a threshold is set for all variants at ΔG_bind = b, then only those variants contained within the shaded ellipse will be covered by the drug. For a different $\overrightarrow{q_d}$, this paraboloid would be translated both horizontally and vertically; therefore different drugs cover different regions and sizes of target charge space. ${\overrightarrow{q_d}}^T{M}_d\overrightarrow{q_d}$ determines the minimum value of the paraboloid for a drug with charge distribution $\overrightarrow{q_d}$, and so it therefore relates charge distribution to coverage.

Generally, in systems with an n-dimensional target charge space, the tile is an n-dimensional hyperellipsoid. The shape of the tile — i.e., on which directions its axes lie and their respective lengths — is determined by the eigendecomposition of the T matrix, because T determines the quadratic dependence of the binding energy on target charge. Eigenvectors of T that correspond to large eigenvalues will be directions in target charge space along which the tile is “short” because the binding energy changes rapidly along these directions.

Because the shape and orientation of a tile is determined by the T matrix, these features are independent of a drug’s charge distribution. However, the size of the tile crucially depends on the drug’s charge values. When $\overrightarrow{q_d}$ changes, the minimum value of the binding free energy paraboloid is translated in energy space according to the M_d matrix. In effect, the size of the tiles as a function of ligand charge distribution is determined by the eigenvectors and eigenvalues of the M_d matrix.

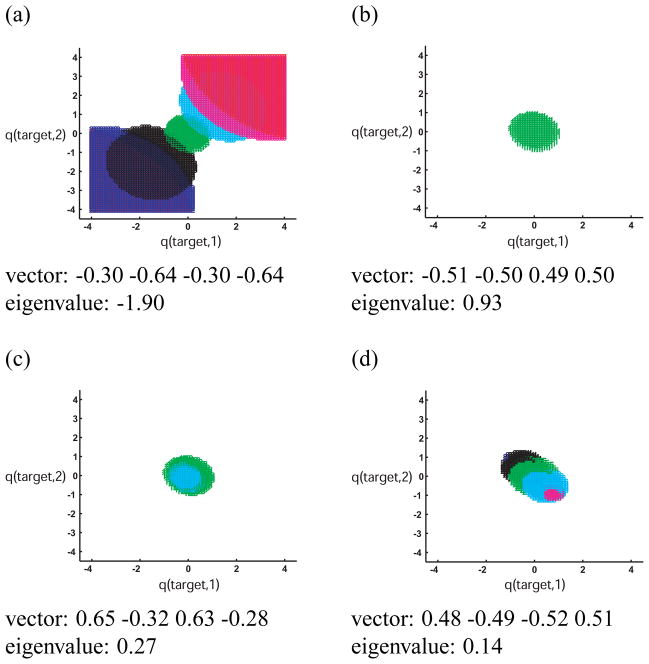
Using this framework, one can explore why the sizes of the tiles corresponding to cocktail drugs in Section 3.2 (Fig. 3a) were not always the same. Figure 7 is a plot of the tiles of selected drugs whose charge distributions lie along each of the four eigendirections of the M_d matrix for the system. Drugs were sampled at integral multiples of the eigenvectors, from −3 to 3. Notice that along the direction corresponding to the negative eigenvalue, the tiles become larger and larger as the drug molecule’s charge magnitudes increase (using an affinity cutoff of −3.3 kcal/mol), and the regions of target space they cover correspond to variants with high-magnitude monopoles. The optimal binding free energy decreases as charge magnitudes increase along this direction, and therefore the coverage increases. As a result, drugs that are highly charged along this eigenvector have extremely high coverages. On the other hand, the tiles along a direction corresponding to a positive eigenvalue (Fig. 7d) become smaller, eventually disappearing. These drugs have little to no coverage. In fact, for the sampled drugs whose charge distributions lie along eigenvector 2, only the completely uncharged drug covers any target variants at all (Fig. 7b).

Figure 7.

Coverages of model drug molecules whose charge distributions are sampled along the eigenvectors of the M_d matrix for this system. Each of the four eigenvectors and corresponding eigenvalues are indicated in a–d. Charges in each eigenvector are listed in order (1 −4) according to the schematic shown in Fig. 2. Red, blue, black, green, cyan, magenta, and red tiles correspond to drug molecules sampled at −3, −2, −1, 0, 1, 2, and 3 times the eigenvector, respectively. If a color is absent from a plot, then the corresponding drug covered no target variants within the space (the affinity cutoff used was −3.3 kcal/mol). Note that drugs sampled along the eigenvector with negative eigenvalue (shown in (a)) covered many variants, and the tiles became bigger as the drugs’ charge magnitudes increased. The opposite was true for eigenvectors with positive eigenvalues.

In this system, drugs and target variants with high monopole charge distributions (quadrants 1 and 3) are “easy” to bind with high affinity, while those with alternating charges are not. In fact, target variants in this system with one highly-positively charged and one highly-negatively charged sphere cannot be covered at all with binding free energy less than −3.3 kcal/mol (the analogous matrix M_t can be derived for targets, such that $M_t=(T=\frac{1}{4}C{D}^{-1}{C}^T)$, allowing one to analyze how coverable a target charge distribution $\overrightarrow{q_t}$ is). This idea may be biologically relevant, in that particular target residues might preferentially evolve toward such hard-to-bind charge distributions, especially if the residues are not crucial for binding the natural substrates or ligands. This may also be why, when only two drugs were used to cover model target mutation space (Fig. 3c), drugs that covered quadrants 1 and 3 were preferentially chosen.

The M_d matrix can be computed for any drug–target shape pair, and can link coverage with drug charge distribution, allowing for rational design of broadly-binding drug molecules. One important future goal is to more fully understand the physical aspects of a system that affect the eigenvalues and eigenvectors of the M_d matrix. It has been shown that when two molecules have perfect shape complementary without cavities in both binding partners and infinite degrees of freedom to represent charge distributions, then the optimal binding free energy to a ligand is always favorable.⁶⁴ In such a case, all the eigenvalues of the M_d matrix are negative, and increasing the magnitudes on a drug molecule’s charges will always increase coverage. The completely hydrophobic molecule will cover the fewest molecules (assuming an unbounded, continuous target charge space). However, when the shape complementarity between drug and target is poor, such that charged or polar binding partners cannot sufficiently interact well enough to overcome their desolvation penalties upon binding, it is possible for all eigenvalues of the M matrix to be positive. In such cases, the completely hydrophobic drug necessarily covers more target variants than any other molecule. Future studies on biological complexes will further develop our understanding of the physical determinants of M_d or M_t matrix characteristics.

Taken together, the continuum electrostatic framework can explain the shapes, sizes, and orientations of the tiles observed in cocktail designs toward model ensembles. Assuming constant ligand, target, and complex shapes, it can also be used to predict drug charge distributions that can confer broad-binding for systems of biological interest.

3.4 The Number of Drugs in an Optimal Cocktail Depends On Multiple Target Ensemble Properties

A target that can mutate to generate ensembles that are difficult to cover would be especially drug resistant. Analyzing the potential coverability of a target’s viable mutation space can therefore help in predicting both the future resistance capabilities of a target and the prospects for effective cocktail therapy. To that end, our goal here was to determine general properties of target ensembles that affect the difficulty with which an ensemble can be covered; here, difficulty is quantified by the number of drugs required for the optimal cocktail, or, in extreme cases, whether or not a design is even feasible given the design specifications. In the previous sections, we limited the target to vary along two degrees of freedom so that the results would be easily visualizable and so an exhaustive target space could be covered with relatively few drug molecules. Here, we considered a second, larger set of model molecules, shown in Fig. 1b. Again, the system contained a target that varied only in charge, although it could now vary at any of twelve spheres, indicated in Fig. 1b. In addition, the drug molecules had eight spheres, each of which could be charged.

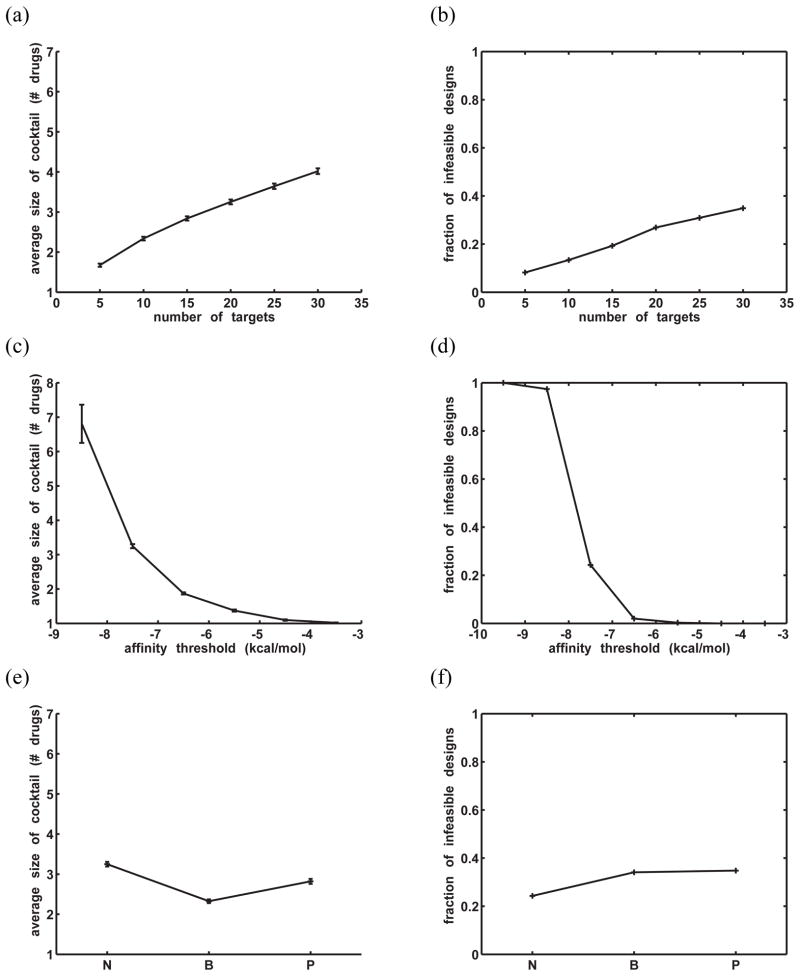
One basic target ensemble property is the number of molecules (potential or actual) contained within it. To study the effect of target ensemble size on the optimal drug cocktail size, target ensembles were generated with 5, 10, 15, 20, 25, and 30 members. For each ensemble size, 1000 such ensembles were generated and optimally covered using IP 1.1. Rigid binding in a fixed orientation was assumed in this system and in all remaining systems discussed here. Target variants were randomly sampled from the continuous 12-dimensional charge space, with the charge magnitude on each sphere limited to 0.5e. A total of 50,625 drug molecules were considered for each cocktail, resulting from combinatorially sampling from −0.5e to +0.5e in 0.25e increments on the 4 highly buried spheres (2, 4, 6, and 8 in Fig. 1b) and in 0.5e increments on the four partially-buried spheres (1, 3, 5, and 7). The affinity threshold for all target variants was −7.5 kcal/mol, chosen such that most of the designs were feasible. Fig. 8a shows that for the successful designs, the average number of drugs needed for the optimal cocktail increased roughly linearly with the number of variants, from only 1.7 drugs to 4.0 drugs over the range of target ensemble sizes tested (the barely-visible error bars in the figure represent ±2× standard error). Presumably, having many ensemble members increases the chance that very dissimilar variants exist within an ensemble. Moreover, as the number of variants increased, the fraction of infeasible designs — in which at least one ensemble member could not be bound by any drug with sufficient affinity —also increased (Fig. 8b). Overall, these results support the idea that evolutionarily constrained drug targets — ones whose variation will lead to smaller ensembles than targets without such constraints — would be better suited for cocktail design.

Figure 8.

General trends in cocktail design toward model ensembles as a function of target ensemble properties. (a) Average number of drugs needed in the optimal cocktail vs. the number of variants within the ensemble. Error bars indicate ±2 × (standard error). The barely visible error bars correspond to magnitudes of approximately < 0.1 drug. (b) Fraction of infeasible designs (out of 1000 attempts) vs. the number of variants in the ensemble. A design was infeasible if any ensemble member could not be bound by any potential drug better than the threshold affinity (−7.5 kcal/mol). (c) Average cocktail size vs. the target variant affinity threshold. 20 targets were used in all designs. Error bars indicate ±2 × (standard error). No feasible designs were sampled at a threshold of −9.5 kcal/mol. (d) Fraction of infeasible designs (out of 1000) vs. the affinity threshold. (e)/(f): Average size of optimal cocktail/fraction of infeasible designs (out of 1000) for ensembles with different constraints on their members’ charge distributions. “N” indicates no charge constraint (other than the maximum magnitude at any charged sphere being 0.5e). “B” indicates that the four highly buried, interfacial spheres (1–4 in Fig. 1b) must bear charges between −0.1e and −0.4e. “P” indicates that four partially buried interfacial spheres (5–8 in Fig. 1b) are constrained to charges between −0.1e and −0.4e. In all cases, 20 targets were in each ensemble and the affinity threshold was −7.5 kcal/mol.

Another ensemble property is the affinity threshold with which one must bind the ensemble members. Assuming the target recognizes a natural molecule for its function, one must ensure that the drug–target affinity is sufficient to compete off the natural binding partner(s), allowing for biologically safe dosing levels. To study the effect of the affinity constraint on cocktail design difficulty, affinity thresholds toward ensembles were varied from −3.5 kcal/mol to −9.5 kcal/mol, and cocktails were designed toward 1000 randomly-generated target ensembles at each threshold using IP 1.1. Here, all ensembles contained 20 variants each. For simplicity, we assumed that all variants in an ensemble were to be bound by a drug with identical affinities, although the method can accommodate individual thresholds for each target variant; generally, target variants do not all have the same affinity toward their substrates or ligands, as drug-resistant mutants often lose natural activity or affinity, although compensatory mutations commonly can recover natural potency or fitness.⁶⁵ Figures 8c and d show that as the energy cutoff was lowered, or made more stringent, the average size of the cocktail increased dramatically, as did the fraction of infeasible designs. There was a very drastic transition between an affinity threshold of −7.5 kcal/mol and −8.5 kcal/mol. In fact, with an affinity threshold of −9.5 kcal/mol, no feasible designs were sampled at all. These results suggest that the best threshold for a given system may likely reflect a balance between the need to bind tightly enough to ensure efficacy and the ability to feasibly achieve broad coverage of all relevant target variants. One could argue that in our model system framework, this balance may occur at approximately −6.5 kcal/mol, assuming that such an affinity is sufficient to outcompete natural binding partners here, as designs are generally feasible and cocktail sizes remain relatively small at this threshold value.

Finally, the effect of variation in charge distribution between ensemble members on optimal cocktail size was considered. Three scenarios were considered. In the first scenario, target variants could be charged to any distribution within the twelve-dimensional space. In the second scenario, four interfacial spheres that were completely buried upon binding (indicated by ‘*’ in Fig. 1b) were constrained to have a charge value within the narrow range of −0.10e and −0.40e. This scenario served as a model for targets that were constrained at the binding interface in order to carry out their function. In the third scenario, four partially buried spheres (indicated by ‘+’ in Fig. 1b) were constrained to have a charge value lying between −0.10e and −0.40e, serving as a model for targets that may be more constrained by a catalytic function than by binding substrate tightly. For each scenario, 1000 optimal cocktail designs were carried out (using IP 1.1., a −7.5 kcal/mol threshold, and 20 target variants). Data from previous runs was re-used for the first scenario.

Ensembles that were constrained at a highly buried portion of the interface required approximately 0.5 fewer drugs on average to cover than those that were constrained at a more peripheral location (‘B’ vs. ‘P’ in Fig. 8e). This result suggests that the variation in charge distribution at highly-buried interfacial regions is more important in determining the size of the optimal cocktail. Because binding affinity is most sensitive to the magnitudes of charges that are highly desolvated upon binding,⁶⁶ large variation in these magnitudes leads to very different binding free energies between any single drug and the ensemble members, presumably resulting in multiple drugs for adequate coverage. Taken together, the results here indicate that ensembles that are electrostatically constrained at the most highly buried interfacial regions upon drug binding could be more attractive candidates for cocktail design. Interestingly, while the constrained systems required fewer drugs on average for coverage than the unconstrained system for feasible designs, they both had slightly higher fractions of infeasible designs (Fig. 8f). There did not appear to be a robust, repeatable difference in the fraction of infeasible designs of either constrained system (data from repeated sets of 1000 trials not shown).

3.5 The Effect of Decoys: Designing Against Related Molecules

An important aspect of drug development is the avoidance of off-target binding. For example, HIV-1 protease inhibitors are commonly tested for their specificity toward HIV-1 protease over other human aspartyl proteases, such as pepsin and cathepsin D (see references^{67, 68} for examples). Avoiding such off-target binding is especially difficult in kinase inhibitor therapy, as the active sites of functionally different kinases can be very similar.^{44, 45} Often in molecular design applications where binding specificity is crucial, a negative design strategy is taken,^69–71 in which undesired binding interactions (decoys) are explicitly modeled and the energies of the undesired states is maximized relative to the desired states.

To explore how the incorporation of a single decoy affects the difficulty of cocktail design toward our model ensembles, optimal cocktails were designed toward randomly-generated target ensembles containing 20 molecules each, 19 of which were considered targets and the randomly-selected remaining one was made a decoy. The affinity threshold for desired target variants was fixed at −7.5 kcal/mol. A separate threshold was chosen for the decoy, such that any drugs that bound the decoy with free energy lower (tighter) than this threshold were pre-eliminated from the potential cocktail.

Fig. 9a shows that for feasible designs, the average cocktail size increased as the minimum binding free energy for the decoy was increased, from approximately 3.5 drugs when the decoy threshold equaled the target threshold to nearly 5 drugs when decoys were required to be bound at least 3 kcal/mol (approximately 1000-fold at 298 K) worse than any target (1000 designs were attempted at each decoy affinity threshold). Moreover, an average of 3.15 drugs was needed to cover 19 targets without any decoy (data not shown); this value was less than all average cocktail sizes when a decoy was introduced. Also, the fraction of infeasible target ensembles increased substantially as the decoy threshold was raised, even though the fraction that were infeasible due to a hard-to-bind target variant remained relatively constant at approximately 25 percent (Fig. 9b). In other words, when the binding energy difference between drug–target and drug–decoy interactions was required to be very high, there was no combination of drugs that could cover all target variants while avoiding the decoy, even though all targets could be feasibly covered by at least one drug. As a whole, these results suggest that incorporating negative design into cocktail development may greatly increase the difficulty of such designs, though such designs can still be possible.

Figure 9.

General trends in cocktail design toward model ensembles when one of the twenty ensemble members is a decoy. (a) The average size of the cocktail is plotted against the allowed lower-bound free energy of binding toward the decoy. The required threshold affinity toward targets is −7.5 kcal/mol. 1000 designs were attempted, and the error bars indicate ±2 × (standard error). (b) Fraction of infeasible designs (out of 1000) as a function of the decoy lower-bound free energy threshold. Each infeasible design is grouped into one of two categories; “target infeasibility” means that at least one target variant within the ensemble cannot feasibly be bound with appropriate affinity by any potential cocktail member. “Decoy infeasibility” means that all targets in the ensemble can be feasibly covered, but there is no way to cover all targets while still avoiding the decoy.

4 Discussion

This work explores optimal cocktail design through applying integer-programming-based design methods to theoretical model systems. Here the methods were applied to simple lattice-model systems of constant shape that varied in their electrostatic properties, and the results are to be interpreted in that context. We stress, however, that the optimization framework is generally applicable to ensembles that are not limited to electrostatic-only variation.

Using systematically-generated ensembles, it was found that the cocktail design strategy automatically grouped target variants by their electrostatic similarity, with each group covered by a single drug. Theory grounded in continuum electrostatics explains this behavior and predicts how the coverage of a drug may depend on its electrostatic properties; the theory also relates a target’s charge distribution to its maximal achievable affinity to a drug. Statistical sampling of model ensembles was used to demonstrate that, on average, cocktail design should be easier toward a target that is evolutionarily constrained to generate relatively few variants. Design should also be easier toward a target when the target is dissimilar from other natural molecules, such that there are no decoys to avoid. The hurdles presented by decoys are likely to be overestimated in this study because of the imposed shape constancy; variation in shape, charge distribution, and flexibility would provide more handles by which to distinguish decoys from targets. Nevertheless, the overall design complexities introduced by decoys are likely to be real.

The results in this work highlight some general principles for designing potent cocktail members. First, molecules that are fairly hydrophobic will often cover more target variants because they lie far from the “edges” of target mutational space. Moreover, conformationally flexible molecules with asymmetric charge distributions can make good cocktail members because their flexibility allows them to adapt to target variation. Also, effective cocktails should contain dissimilar molecules, with the dissimilarities addressing the physical differences between the target variants. For example, the HIV-1 protease inhibitor nelfinavir loses significant potency against the Asp30 → Asn protease variant;⁴² this mutation is a signature of nelfinavir treatment, and is thought to result in the loss of electrostatic interactions between the m-phenol group on nelfinavir and Asp30.^{72, 73} Other protease inhibitors, on the other hand, do not show a significant loss of affinity toward this mutant, likely due in part to their differing electrostatic properties. Nevetheless, certain other inhibitors, such as atazanavir, have their own physically-based “signature mutations” that do not affect nelfinavir and the remaining inhibitors.^{74, 75} Such examples suggest that mutual differences in physical properties between inhibitors may allow for broad collective coverage.

There may be more subtle connections between the properties of target ensemble members and the properties of the resulting cocktail. For example, theoretical continuum electrostatic analyses showed that for identically-shaped target variants and drug molecules, the M and T matrices quantitatively predicted which drug and target variants could bind to the most partners with desired affinity. Eigenvectors of these matrices with large, positive eigenvalues corresponded to directions in drug charge space with poor coverage (M_d), or directions in target charge space that were difficult to cover (T or M_t), either because the drug coverage tiles were very short along these directions, or because the sizes of these tiles decreased or disappeared along these directions. In the model systems considered in Section 3.1–3.3, the hard-to-bind charge distributions corresponded to charges of equal magnitude and opposite sign on the two receptor charge basis points. If members of such a target ensemble differ greatly in their charge distributions along these particular eigenvectors, they might be especially difficult to cover. Indeed, preliminary analyses indicated that ensembles with high variation and magnitude along eigendirections of the M_t matrix with positive eigenalues generally required more drugs in their optimal cocktails (data not shown).

One future goal is to further understand the connection between a physical system and the properties of the M matrices. As noted earlier, eigenvectors of the M matrices with negative eigenvalues correspond to directions in drug and target charge space in which optimal binding affinity becomes increasingly tighter as charge magnitudes are increased. These drugs and targets could theoretically bind to many more partners with high affinity. Shape complementarity, the number and location of charge points, and the balance between desolvation and potential interactions appear to play large roles in determining the properties of the M matices, but further work is required to more fully understand the connection and to apply such analyses to biological systems. Moreover, there have been numerous system-specific studies linking electrostatic properties of ligands or targets with tight binding. These studies include other applications of charge optimization,^{76, 77} identifying electrostatic “hot spots” that are important for recognition and bound state stabilization,^{78, 79} and fitting electrostatic and other physics-based characteristics to experimental binding data to create predictive models,^79–85 among many others. Integrating our general framework for predicting target coverage with such system-specific informatic or other physics-based approaches could prove to be a powerful tool in designing promiscuous drugs and drug cocktails for a given target.

The focus of our analysis was electrostatic variation between members of a target ensemble. To allow for controlled study, the framework resulting in the M matrices and the quantitative relationship between drug electrostatic properties and target coverage assumes two highly-constraining characteristics: first, the shapes of the possible drugs, the target variants, and all possible complexes do not vary; second, targets variants are at regular intervals in a hypothetical charge space, such that the size of a tile associated with a drug is directly proportional to its target coverage. In actual biological systems, these assumptions are not generally true; most target mutations result in changes in structural shape or flexibility in addition to changes in electrostatics, such as the HIV-1 protease mutations Val82 → Ala, Ile84 → Val, and Leu90 → Met, which confer resistance to nearly all current clinically-approved inhibitors.¹⁹ In such systems, several factors in addition to electrostatics will govern drug coverage of targets, including molecular packing and solvent entropy differences. Therefore, to loosen this first assumption, we have incorporated shape variation into our model target ensembles, and our analysis of the effect of shape variation on cocktail design is ongoing. There is currently no analytical framework for analyzing systems that vary in both shape and charge using continuum electrostatics, and the two properties are highly coupled, although recent work has shown that the framework can be qualitatively powerful even when molecular shapes vary.⁸⁶ We hope that useful insights can be achieved and that general principles for grouping targets based on their similarity in both shape and charge — and other physical characteristics — can be extracted. Moreover, we hope to analyze the effect of the second assumption above by applying our method to a highly varying target, such as HIV-1 protease.

In this work, we have demonstrated that simultaneous design or choosing of cocktail members, rather than a serial, “greedy” approach can result in smaller, more optimal cocktails. Currently, cocktails arise somewhat retroactively, after the serial process of individual drug development over long periods of time. Perhaps the future of disease treatment will involve a pre-analysis of the potential mutation space of all potential targets associated with a particular disease, a selection of a target or targets based on ease of cocktail design, prediction and pre-clustering of potential target variants based on their physical properties, and simultaneous design of multiple molecules that cover the evolutionarily accessible space of the target(s). Of course, such a procedure would require a level of efficient, robust drug design procedures and target mutation analysis that is currently unavailable, but such a problem framing can be useful for steering the future of drug design. One current application of our approach is in vaccine design, where one is interested in maximizing coverage of highly variable epitopes. Integer-programming/set-cover-based methods could produce optimally small or diverse cocktails and provide a complementary approach to those based in genetic algorithms,^{87, 88} and “greedy” approaches.^{89, 90}

We stress that the IP 1.x methods presented in this work can be used with either theoretical or experimental binding affinity measurements and so they are not limited by the accuracy of one particular method for acquiring binding affinity. Moreover, the integer-programming formulations presented here can be easily altered to suit problem-specific needs. For example, drug and target variant concentrations can be explicitly accounted for in the IP 1.x formulations, and dose values can be used to determine coverage rather than affinity thresholds; each drug can be “multiplexed” into various dosings, with each dose being a separate decision variable that can cover its own particular subset of target variants; constraints can be added that ensure that no more than one concentration of each drug is selected and that limit the maximal dose of drug combinations. In designing against decoys, one might need to consider the additive effects of two drugs that individually do not bind the decoy, but when dosed together, can. Such constraints disallowing pairs or other combinations of drugs can be incorporated into the IP formulation. Other options, such as explicitly considering individual target variant conformations and requiring that only one of them should be bound, or considering the additive effects of multiple drugs that cover a target when dosed together, can also be added. Pharmacokinetic or bioavailability scores or other non-energetic evaluations of drug molecules can also be incorporated into weights that can be minimized or maximized in secondary objective functions. Finally, one could account for either experimental or model uncertainty in binding affinity values by choosing conservative thresholds that account for such uncertainty, if possible.

Qualitatively, IP 1.1 and IP 1.2 took on the order of 1 second on a 2 GHz processor to reach optimality for the systems discussed in Sections 3.1 and 3.2, and on the order of 10 seconds to optimize for the systems in Section 3.4. IP’s 1.3/1.4 took approximately 1 second to optimize the secondary objective function for the system in Sections 3.1, and approximately 15 seconds to do so for the much larger system of 121 targets in Section 3.2. The IP 2.x formulations are currently significantly slower. Nevertheless, they represent a novel method for optimally designing toward a target ensemble. Using a combinatorial scheme, they can design a molecule capable of binding with desired affinity to multiple partners, or, if one molecule cannot do so, they create the optimally small cocktail that will. In their current naive implementations, they are too time-intensive for many practical applications, taking anywhere from several seconds (IP 2.2) to several tens of minutes or hours (IP 2.1 and secondary objective function optimization) to optimize the system shown in Section 3.1. A current priority is to refine the formulation and implementation to improve performance.

Drug design toward an evolving target is a challenging prospect that requires consideration of more than just one drug binding tightly to the existing target molecule. In this work, we have cast such designs as an optimization problem and have developed methods for solving it. The physical insights and framing we have achieved here, coupled with the ongoing methodology development, can lead to rational, physics-based strategies for optimal cocktail design in the future.