Acoustic and perceptual effects of changes in body layer stiffness in symmetric and asymmetric vocal fold models

Abstract

At present, it is not well understood how changes in vocal fold biomechanics correspond to changes in voice quality. Understanding such cross-domain links from physiology to acoustics to perception in the “speech chain” is of both theoretical and clinical importance. This study investigates links between changes in body layer stiffness, which is regulated primarily by the thyroarytenoid muscle, and the consequent changes in acoustics and voice quality under left-right symmetric and asymmetric stiffness conditions. Voice samples were generated using three series of two-layer physical vocal fold models, which differed only in body stiffness. Differences in perceived voice quality in each series were then measured in a “sort and rate” listening experiment. The results showed that increasing body stiffness better maintained vocal fold adductory position, thereby exciting more high-order harmonics, differences that listeners readily perceived. Changes to the degree of left-right stiffness mismatch and the resulting left-right vibratory asymmetry did not produce perceptually significant differences in quality unless the stiffness mismatch was large enough to cause a change in vibratory mode. This suggests that a vibration pattern with left-right asymmetry does not necessarily result in a salient deviation in voice quality, and thus may not always be of clinical significance.

INTRODUCTION

An ultimate goal of voice production research is to understand how changes in biomechanical properties of the vocal folds, due to either intentional laryngeal adjustments or pathological variations, affect the acoustics and perception of the produced sound. Although there have been significant research efforts toward understanding how changes in biomechanical properties produce different vibratory patterns and acoustics (voice production) and how listeners perceive the produced voice (voice perception), such research efforts often focus separately on either production or perception. There has been little cross-domain, cause-effect investigation that attempts to directly link individual biomechanical properties of the vocal folds to perceived vocal quality. Understanding such cross-domain links between production and perception is essential to determine which physiological laryngeal properties are most relevant for generating perceptually important (and thus clinically and linguistically meaningful) changes in quality. Clinically, such information could suggest the mechanical or behavioral adjustments needed to restore or improve voice, providing surgeons and speech-language pathologists with greater insight to choose the appropriate treatment options.

In this paper, we present a step toward this cross-domain cause-effect understanding by investigating the acoustic and perceptual consequences of the activation of the thyroarytenoid (TA) muscle. In humans, the TA muscle (along with the cricothyroid, which is not studied here) is considered the main regulator of vocal fold body stiffness. Although TA contraction is also known to deform vocal fold shape, causing the vocal folds to bulge toward the glottal midline (Choi et al., 1993; Herbst et al., 2011), this study focused only on its body-stiffening effect. Body layer stiffness plays an important role in control of voice production. In the body-cover theory of phonation, Hirano (1974) argued that different body-cover stiffness conditions could produce different vibration patterns and voice types. Increasing body stiffness has been shown to restrict vocal fold motion in the body layer (Story and Titze, 1995; Zhang, 2009) and to lead to increased vertical phase difference in medial-lateral motion between the upper and lower margins of the medial surface (Fex and Elmqvist, 1973; Hirano, 1974; Story and Titze, 1995; Lowell and Story, 2006; Zhang, 2009, 2010a). Lowell and Story (2006) also showed that a large body-cover stiffness ratio led to increased speed of vocal fold closure. Although these studies provided valuable insights into the process of voice production, they mainly focused on the effects of varying body stiffness on the resulting vibration patterns. In contrast, the acoustic and perceptual effects of changes in body stiffness have not been well studied.

A related question of clinical importance is the acoustic and perceptual relevance of left-right asymmetries in vocal fold vibration, often observed in pathological conditions such as unilateral recurrent laryngeal nerve (RLN) paresis, in which reduced TA muscle activation on one side presumably leads to corresponding asymmetry in body stiffness. Clinicians often evaluate left-right vibrational asymmetry using videostroboscopy, and its presence is often considered an indication for further clinical intervention (e.g., Kimura et al., 2010a; Kimura et al., 2010b). However, no systematic studies of the perceptual relevance of such vibratory asymmetry have appeared, and it remains unclear whether or how much left-right vibratory asymmetry produces noticeable differences in voice quality, although Bonilha et al. (2008) found most normal speakers exhibit mild left-right and anterior-posterior asymmetries.

In this study, the acoustic and perceptual consequences of changing body stiffness were investigated using a two-layer self-oscillating physical model of the vocal folds. Compared with in vivo or ex vivo physiological vocal fold models, physical models can be precisely controlled, and experiments are easy to replicate exactly. In this study, the use of physical models allowed us to vary body stiffness independently while keeping other model parameters constant, thus isolating its effects. Similar models were used in our recent study (Zhang, 2011), which showed that increasing body stiffness better maintained vocal fold adductory position and facilitated the excitation of high-order harmonics. However, no systematic acoustic and perceptual analyses were performed in that study to investigate the relationships among body stiffness, acoustics, and their perceptual consequences. Therefore the objective of this study was to further investigate the cause-effect relationship between changing body stiffness and resulting changes in the acoustics and perceived voice quality for both symmetric and asymmetric stiffness conditions.

METHOD

Physical model experiments

The experimental setup was the same as that used in previous studies (Zhang et al., 2006; Mendelsohn and Zhang, 2011), where it is described in detail. Briefly, the setup consisted of an expansion chamber (50.8 cm long, with a 23.5 × 25.4 cm rectangular cross section) simulating the lungs, a 11-cm straight circular PVC tube (inner diameter of 2.54 cm) simulating the tracheal tube, a silicon self-oscillating model of the vocal folds (described further in the following text), and a 17-cm long vocal tract tube with a 2.54 × 2.54 cm rectangular cross section. The expansion chamber was connected upstream to a pressurized airflow supply through a 15.2 -m-long rubber hose. The left and right vocal fold models were mounted on two supporting plates and were slightly compressed medially toward each other so that the glottis at rest was completely closed.

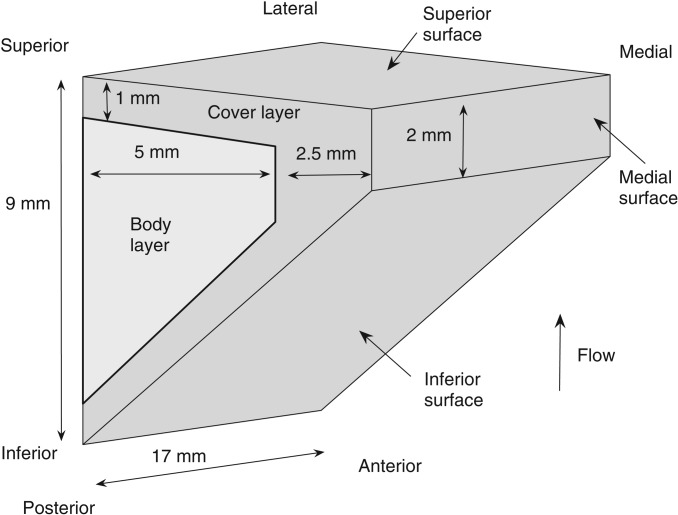
For simplicity, the two-layer physical model of this study had a uniform cross-sectional geometry along the anterior-posterior direction. The cross-sectional geometry was defined as in Zhang (2009) and is shown in Fig. 1. The vocal fold models were made by mixing a two-component liquid polymer solution (Ecoflex 0030, Smooth On, Easton, PA) with a silicone thinner solution with different composition ratios resulting in different model stiffnesses. The Young's modulus E of each composition was measured using an indentation method (Chhetri et al., 2011) with a cylindrical indenter with a 1 mm diameter and an indentation depth of 1 mm on a cubic sample with dimensions 25.4 × 25.4 × 25.4 mm.

Figure 1.

A sketch of the physical vocal fold model used in this study.

In this study, three sets of vocal folds were constructed and studied in separate experiments (Table TABLE I.). The first series included left-right symmetric conditions, i.e., the left and right vocal folds had identical geometry and material properties, and the body stiffness was varied symmetrically while other vocal fold properties (geometry and cover material properties) remained constant. The other two series represented left-right asymmetric conditions with varying left-right mismatches in body stiffness. These were created by varying the body stiffness of the left vocal fold while the right vocal fold remained unchanged. In series II, the right vocal fold had a very stiff body layer while in series III the body layer on the right was very soft (Table TABLE I.).

TABLE I.

Geometry and stiffness conditions of the physical models used in the experiments. The subscripts b and c denote the body and cover layer, respectively.

Series	I	II	III
Number of conditions	9	9	8
Eb,left (kPa)	3.25–73.16	3.25–73.16	3.25–36.14
Ec,left (kPa)	3.25	3.25	3.25
Eb,right (kPa)	Eb,right = Eb,left	73.16	3.25
Ec,right (kPa)	3.25	3.25	3.25

For each physical model configuration, a flow-ramp experimental procedure was used. The flow rate was increased in discrete increments from zero to a value above onset of vibration (or to around 2000 ml/s if no vibration was observed). At each step, after a delay of 1–2 s after the flow rate change, the mean subglottal pressure (measured at 2 cm from the entrance of the glottis), mean flow rate, acoustic pressure inside the tracheal tube (2 cm from the entrance of the glottis), and outside acoustic pressure (about 20 cm downstream of the vocal tract exit and about 30° off axis) were measured for 1 s at a sampling rate of 50 kHz. Phonation threshold pressure was then extracted for each physical model configuration as the mean subglottal pressure at which a sudden increase in the acoustic pressure was observed as the flow rate was increased from zero. Outside acoustic signals that were recorded when mean subglottal pressure equaled 1.1 times the corresponding phonation threshold pressure were used in the acoustic analyses and perceptual testing. For a given mean subglottal pressure P_s, a flow rate Q, and air density ρ, the mean glottal opening area was estimated as

$$A=\frac{Q}{\sqrt{2P_s/\rho }}.$$ (1)

Acoustic measures

Because pitch and loudness changes are so salient that they may mask other differences in quality (Kreiman and Sidtis, 2011), prior to acoustic analysis and perceptual testing, audio samples in each stimulus series were normalized for amplitude and re-synthesized using praat's pitch-synchronous overlap-and-add (PSOLA) algorithm (Boersma and Weenink, 2009; Moulines and Charpentier, 1990), so that F₀ for each token equaled the mean F₀ for that series (about 185 Hz). This process produces a signal with a different fundamental frequency but the same spectrum as the original, so that other vocal qualities remain the same (e.g., Esposito, 2010; Gold et al., 2011). Esposito (2010) found that only F₀ changes of more than 40 Hz produced spectral changes but that such changes were no greater than 1 dB. The acoustic attributes of these F₀-altered voice stimuli were then assessed using analysis-by-synthesis, as previously described (Kreiman et al., 2010). Briefly, acoustic recordings were downsampled to 10 kHz and inverse filtered using the method described by Javkin et al. (1987). The resulting source waveforms were then imported into the UCLA voice synthesizer. Spectral displays of each source were generated, and four features were defined: The source spectral slopes from H1 to H2 (H1-H2), from H2 to H4 (H2-H4), from H4 to the harmonic nearest 2 kHz in frequency (H4-2k), and from the harmonic nearest 2 kHz to the harmonic nearest 5 kHz (2 k-5 k). Because the amplitudes of individual harmonics within these frequency ranges have little perceptual importance, amplitudes of individual harmonics were adjusted so that the source spectrum within each of these ranges decreased in a straight line (Fig. 2; see Kreiman et al., 2010, for more details of the analysis-by-synthesis approach). Formant frequencies and bandwidths were adjusted to approximate the response of the vocal tract model, after which the noise-to-harmonics ratio (NHR) and the slopes of the four spectral slope features were adjusted interactively until the quality of the synthetic voice token matched that of the original voice sample in the opinions of the second and fourth authors. Once a match had been achieved, the current values of each spectral feature and of the NHR were recorded.

Figure 2.

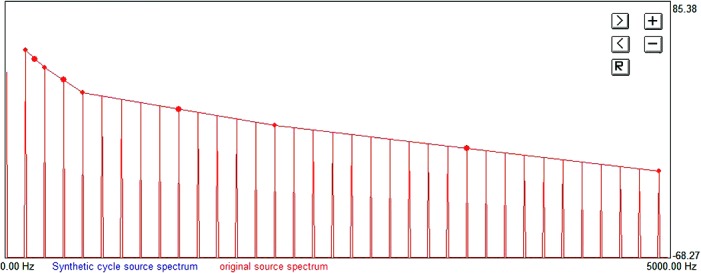
(Color online) The four-feature source spectral model with amplitudes of individual harmonics adjusted so that slope decreased smoothly within each frequency range. More details of the analysis-by-synthesis approach can be found in Kreiman et al. (2010).

Finally, spectra of the original voice samples were calculated using Welch's method (Matlab, 1998) with a Hanning window, and the number of harmonics (NumHarm) below 8 kHz that were visible above the noise baseline was counted independently by the first and second authors. Disagreements were resolved by discussion. Although this measure is conceptually related to the cepstral peak prominence (CPP; Hillenbrand et al., 1994), it was chosen in preference to the CPP because recent evidence (Awan et al., 2012) indicates that changes in the mode of phonation affect CPP values in ways that have not been well studied.

Perceptual testing procedure

Seventeen listeners (7 male) participated in an experiment designed to evaluate the perceptual impact of changes in the vocal fold models. None spoke a language that uses phonation variations contrastively, and all reported normal hearing. Three were expert in the assessment of voice quality.

Stimuli were presented in a visual sort-and-rate task implemented in PowerPoint (Granqvist, 2003; Esposito, 2010). Three PowerPoint slides were created, one for each series of stimuli, in which each audio sample in that series was represented as a sound icon (Fig. 3; nine stimuli for series I and II, and eight for series III). Icons were displayed in the slide in a random order above a straight line the endpoints of which were unlabeled.

Figure 3.

(Color online) The visual sort-and-rate task as implemented in PowerPoint. Listeners played each stimulus by clicking on an icon, then placed it on the line by clicking and dragging.

Listeners were tested individually in a double-walled sound booth. Stimuli were presented at a comfortable listening level over Etymotic ER-1 insert earphones (Etymotic Research, Elk Grove Village, IL). Listeners completed one trial for each series of stimuli in random order. In each trial, they clicked the icons to play the stimuli and then placed each icon on the line (by clicking and dragging) so that stimuli were arranged along the perceived dimension of variation, such that the distance between stimuli on the line reflected their perceptual distances (similar in quality = close together). No instructions were provided about the nature of this dimension. Listeners were simply asked to put the stimuli in order according to whatever organizing percept they chose. They were free to play the stimuli as often as they liked, in any order, until they were satisfied with their sort for that stimulus series, after which testing advanced to a new slide. This procedure can be considered a variant of direct magnitude estimation but without the problem of drift in scale values due to memory limitations. This task also avoids verbal labels, such as rough or breathy, associated with poor listener reliability (Kreiman et al., 2007). Although no time limits were enforced, the complete test generally lasted less than 1 h.

Listeners' ratings were measured with a digital caliper as the distance from the left end of the line to the leading edge of each stimulus icon, to the nearest 0.1 mm. Twelve percent of ratings were independently re-measured to assess reliability of this procedure; the mean absolute difference between the first and second ratings was 0.14 mm (s.d. = 0.12 mm). Because listeners differed in how much of the line they used in a trial, responses for each stimulus series for each listener were normalized to a range of 0%–100%.

Data analysis

For each listener and trial, we calculated the absolute distance between the measured placement of each pair of stimuli on the normalized scale and then assembled these distances into dissimilarity matrices (one lower-half matrix per listener per stimulus series). Individual differences non-metric multidimensional scaling (MDS) was then applied to determine what perceptual dimension(s) listeners shared when making their judgments (systat software, version 12.02.00; Systat Software, San Jose, CA). Solutions were calculated in one and two dimensions for each stimulus series. Based on values of R² and stress (which measures the fit between the model and the input data; e.g., Schiffman et al., 1981; Table TABLE II.), one-dimensional solutions were selected for all three group analyses.

TABLE II.

R² and stress values for the MDS analyses and the identified major acoustic correlates.

Stimulus series	Listener subgroup	R2	Stress	Major acoustic correlates
I	Complete	0.57	0.24	NumHarm
	Smaller	0.65	0.25	1. H1-H2; 2. NHR
	Larger	0.66	0.25	NumHarm
II	Complete	0.78	0.26	NHR/NumHarm
III	Complete	0.63	0.22	–
	Smaller	0.70	0.19	1. NHR; 2. H1-H2
	Larger	0.71	0.19	1. 2 k–5 k; 2. H4–2 k

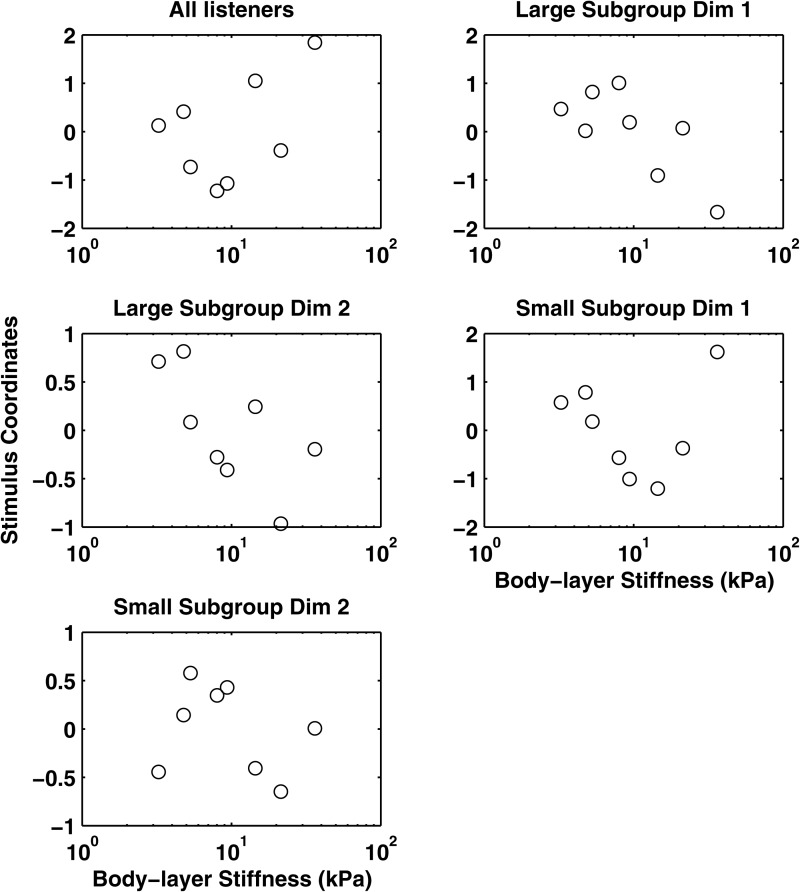
Examination of subject weights in the MDS solutions suggested that subgroups of listeners with different perceptual strategies existed for series I (symmetrical folds) and III (asymmetrical, right fold soft) but not for series II (right fold stiff). Correlations among the unscaled ratings provided by individual listeners in these conditions pointed to two subgroups of listeners (n = 4 and n = 13 for both series). The two smaller groups overlapped by two listeners; each group included both expert and naive listeners. As a result, additional MDS analyses were run separately on data from each listener subgroup. Based on R² and stress (Table TABLE II.), a one-dimensional solution was selected for the larger listener group for series I. Two-dimensional solutions were selected for both of the smaller listener subgroups and for the larger group for series III.

RESULTS

Symmetric conditions (series I)

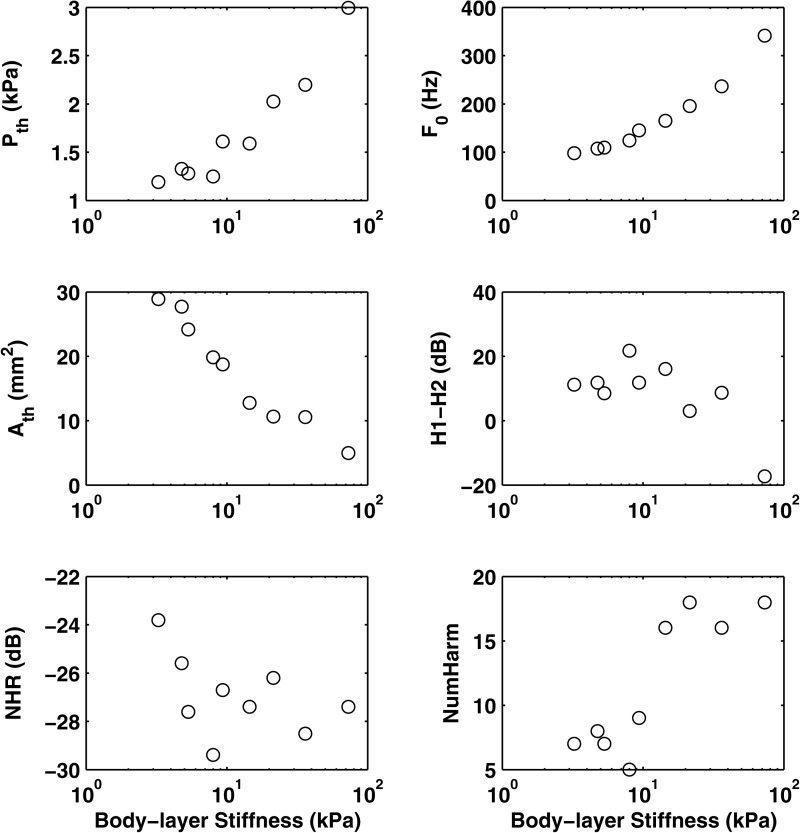
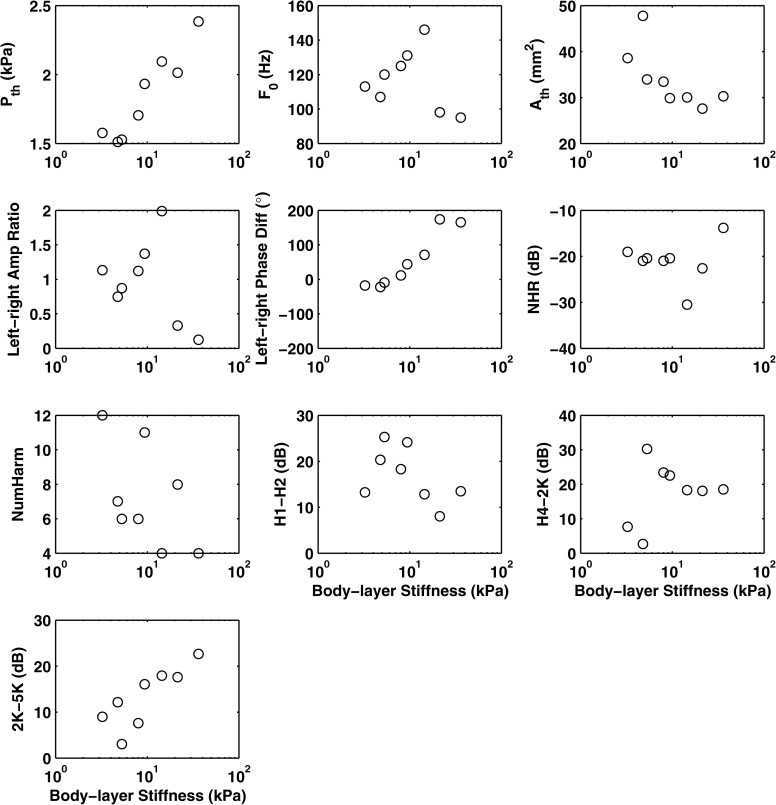
Figure 4 shows the different physical variables and acoustic measures, and Fig. 5 shows stimulus coordinates from the group MDS solution as a function of symmetrical changes in the body stiffness of the physical models for series I. The three physical variables (phonation threshold pressure, mean glottal opening at phonation onset, and phonation onset frequency) all showed a monotonic relation with body stiffness. Both phonation threshold pressure (P_th) and onset frequency (F₀) increased with increasing body stiffness, while the mean glottal opening area at phonation onset (A_th) decreased.

Figure 4.

Selected physical variables and acoustic measures as a function of the body stiffness of the symmetric physical models (series I). P_th = phonation threshold pressure; A_th = mean glottal opening area at phonation onset; F₀ = phonation onset frequency.

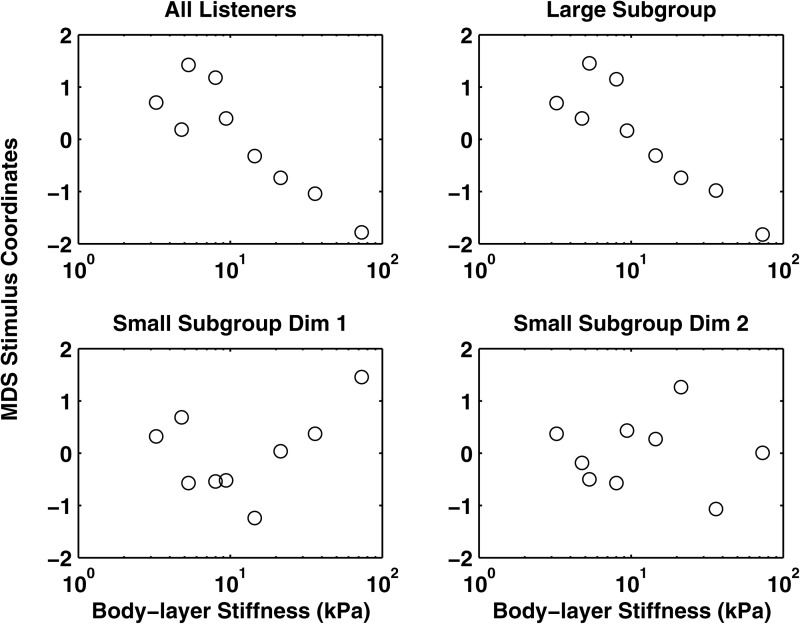
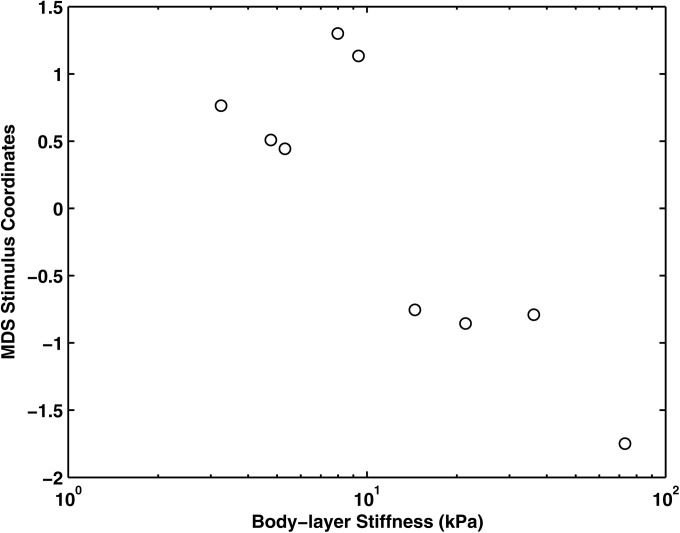
Figure 5.

MDS stimulus coordinates as a function of the body stiffness of the symmetric physical models in series I.

Multiple linear regression was applied to assess the cause-effect relationship between changes in vocal fold stiffness and changes in acoustic measures and stimulus coordinates in the perceptual spaces. (Bonferroni corrections have been applied in all analyses to adjust p values for multiple comparisons.) Acoustically, the body stiffness was significantly correlated with H1–H2, NHR, and NumHarm [F(3,5) = 26.87, p < 0.01; R² = 0.94], with standard coefficients of −0.72, −0.37, and 0.35, respectively. This indicates that varying the body stiffness had a strong effect on the harmonic structure of the spectrum. Specifically, increasing body stiffness reduced H1–H2 and increased the number of higher-frequency harmonics, both suggesting a flatter spectral slope. Increasing body stiffness also led to lower NHR, indicating reduced noise production. Perceptual ratings were best explained by NumHarm [F(1,7) = 36.81, p < 0.01; R² = 0.84], although ratings were also significantly correlated with H1–H2 (r = −0.72). The perceptual ratings also showed a nearly monotonic relation with body stiffness (r = −0.86, p < 0.01), and were well correlated with all physical variables (r = 0.80 – 0.92).

Thus for the symmetric condition, across all listeners there was a straightforward relationship among body stiffness, acoustics, and perception. Variations in body stiffness resulted in significant increases in NumHarm and decreases in spectral slopes at low frequencies, which were easily perceptible to the listeners.

Further analysis showed that not all listeners applied the same perceptual strategy when sorting these complex stimuli, as discussed in the preceding text (Table TABLE II.). Further, previous experience with voice quality analysis did not predict group membership. MDS analyses of data from the larger subgroup of listeners (n = 13) were consistent with results found for the complete group, showing a single dimension that was significantly and negatively correlated with Young's modulus [Fig. 5; R² = 0.76; F(1,7) = 21.04, p < 0.01] and NumHarm [R² = 0.84; F(1,7) = 36.37, p < 0.01]. Parallel analyses of data from the smaller subgroup of listeners revealed two perceptual dimensions: One that was best explained by H1–H2 [F(1,7) = 8.69, p < 0.02; r = −0.74] and one best explained by the NHR [F(1,7) = 12.95, p < 0.01, r = 0.81].

Asymmetric conditions with a stiff-body reference vocal fold (series II)

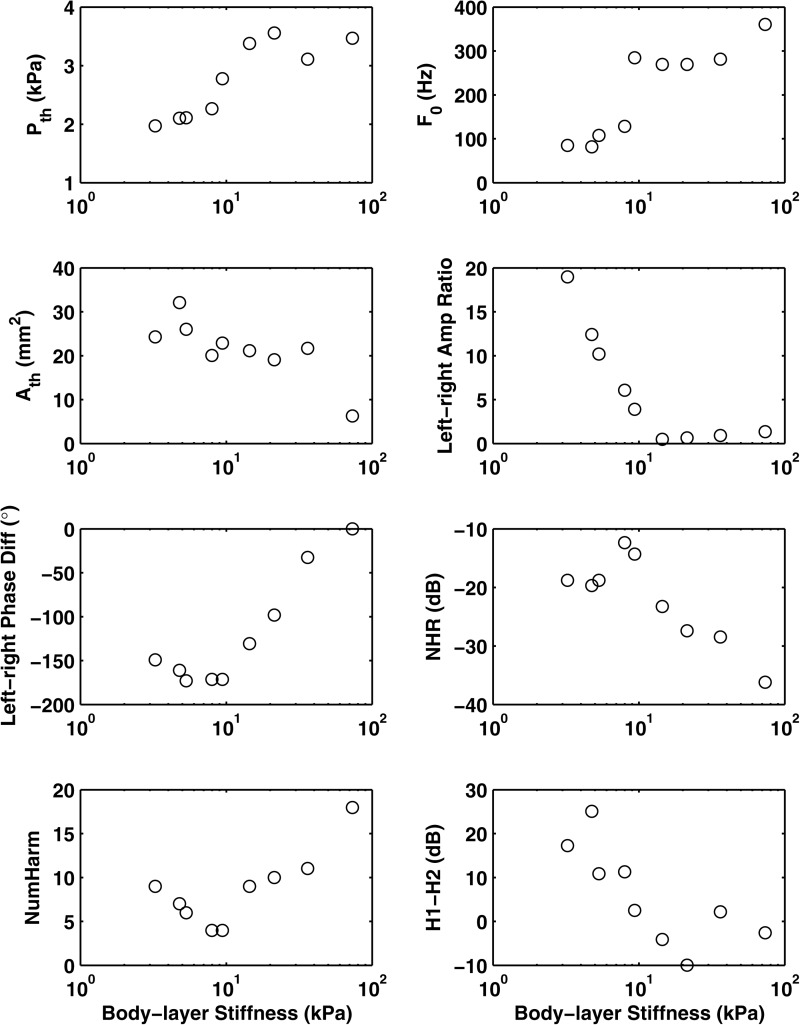
In this series, stiffness of the right vocal fold model was held constant at Young's modulus = 73.2 kPa. This stiff fold was paired with models of the left fold the body stiffness of which varied between 3.25 and 73.16 kPa. Figure 6 shows the different physical variables and acoustic measures, and Fig. 7 shows the group perceptual ratings, all as functions of the body stiffness of the left vocal fold model. Two regimes of distinct vibratory pattern were observed as the body stiffness of the left vocal fold model was varied. For small values of body stiffness (E_b,left < 10 kPa or large left-right stiffness mismatch), only the soft left vocal fold was strongly excited, whereas the stiff fold barely vibrated. Phonation frequency was determined by the stiffness of the soft fold alone and followed close to that of the soft fold in a symmetric condition (see Zhang and Luu, 2012, for more details of the vibration pattern). The left-right amplitude ratio in this regime was thus very large, and there was a phase difference of about 180° between the vibration of the two folds (Fig. 6). As the body stiffness of the left fold approached that of the right (reference) vocal fold (reduced left-right stiffness mismatch), a new regime occurred in which both folds were equally excited with comparable vibratory amplitudes and the stiff fold leading in phase. Phonation frequency in this regime was determined by stiffness of both folds. More details of the vibratory pattern within these two regimes can be found in Zhang and Luu (2012).

Figure 6.

Selected physical variables and acoustic measures as a function of the body stiffness of the asymmetric physical models in series II. P_th = phonation threshold pressure; A_th = mean glottal opening area at phonation onset; F₀ = phonation onset frequency. Note that a phase difference of 180° is the same as −180°.

Figure 7.

MDS stimulus coordinates as a function of body stiffness of the asymmetric physical models in series II.

In Fig. 6, the existence of two regimes can be observed in the clustering in phonation onset frequency, left-right amplitude ratio, and left-right phase difference. Acoustically, similar data clustering can be easily observed in values of NHR and NumHarm. The first regime, which was characterized by the soft fold vibrating alone, shows high NHR and H1–H2 values compared to regime 2, when the two (stiff) folds were vibrating together, which shows decreased NHR and H1-H2 (equivalent to less noise and a flatter spectral rolloff in the low frequencies). The transition between regimes occurred at a body stiffness of about 10 kPa. Multiple regression analysis showed that body stiffness was strongly correlated with NumHarm [F(1,7) = 28.59, p < 0.01; R² = 0.80]. Note that in contrast to series I, for which NHR and NumHarm were not significantly correlated, in this series, the NHR was well correlated with NumHarm (r = −0.96) so that a strong correlation also existed between the body stiffness and NHR (r = −0.88).

Clustering was also observed in the perceptual ratings, as shown in Fig. 7. A one-way ANOVA (dependent variable = coordinates in the perceptual space; independent variable = body stiffness) showed that voice stimuli with Young's modulus <10 kPa differed perceptually from stimuli with Young's modulus > 10 kPa [F(8,144) = 23.83, p < 0.01, R² = 0.57]. Tukey's post hoc comparisons showed that every stimulus in one cluster differed significantly from every stimulus in the other cluster in perceptual score, but no significant differences were observed between stimuli within the same cluster (p < 0.01). Multiple regression analysis showed that the perceptual ratings were most strongly (and positively) correlated with NHR [F(1,7) = 109.65, p < 0.01; R² = 0.94]. Due to the strong negative correlation between NumHarm and NHR in this series, a similar strong but negative correlation also existed between the perceptual ratings and NumHarm (R² = 0.81). No subgroups of listeners were apparent for this series of stimuli.

In summary, although left-right stiffness mismatches produced left-right asymmetric vibratory patterns, such vibrational asymmetry was of minimal perceptual importance unless the stiffness mismatch was large enough to induce a qualitative change in vibration pattern. Such regime changes were also accompanied by significant, perceptually salient changes in the NHR and NumHarm.

Asymmetric conditions with a soft-body reference vocal fold (series III)

In this series, a vocal fold model (right fold) with a soft body layer (3.25 kPa) was paired with vocal fold models of varying body stiffness (between 3.25 and 36.14 kPa). Figure 8 shows the different physical variables and acoustic measures, and Fig. 9 shows the perceptual ratings, all as functions of the body stiffness of the left vocal fold models. Similar to series II, two regimes with distinct vibratory patterns were observed as the body stiffness of the left vocal fold model was varied. For small values of body stiffness of the left vocal fold (E_b,left < 15 kPa or small left-right stiffness mismatch), both folds were excited with comparable vibrational amplitude with the stiff fold leading in phase. As the body stiffness of the left fold was increased above a threshold (E_b,left > 15 kPa or large left-right stiffness mismatch), the vibration pattern changed to one that was again dominated by the soft reference vocal fold (the right vocal fold in this case), which was accompanied by a significant decrease in phonation onset frequency. The soft fold dominated in the sense that only the soft fold was strongly excited (Fig. 8), and phonation frequency was determined primarily by the properties of the soft fold (Zhang and Luu, 2012). The other fold was entrained to vibrate at the same frequency but with a much smaller amplitude.

Figure 8.

Selected physical variables and acoustic measures as a function of body stiffness in the asymmetric physical models in series III. P_th = phonation threshold pressure; A_th = mean glottal opening area at phonation onset; F₀ = phonation onset frequency.

Figure 9.

MDS coordinates for stimuli in series III as a function of asymmetric body stiffness in the physical models.

Multiple regression showed that the acoustic measure best correlated with the body stiffness of the left fold was spectral slope from 2 kHz to 5 kHz [F(1,6) = 11.31, p < 0.01; r = 0.81], which increased with increasing stiffness. MDS analysis of the group perceptual data resulted in a one-dimensional solution (R² = 0.63) that was not significantly associated with any acoustic measures [F(1,6) = 4.09, p > 0.05]. However, further analysis of the perceptual ratings showed two subgroups of listeners who paid attention to different aspects of the stimuli. Separate MDS analyses for the two listener subgroups showed two-dimensional solutions for each subgroup as noted in Table TABLE II.. For the smaller subgroup, the first dimension corresponded to NHR [F(1,6) = 9.35, p = 0.02; r = 0.78], and the second dimension corresponded to H1–H2 [F(1,6) = 39.74, p < 0.01; r = 0.93]. For the larger subgroup, the first dimension corresponded to 2 k–5 k [F(1,6) = 18.76, p < 0.01; r = 0.87] and to Young's modulus (r = −0.81), and the second dimension corresponded to H4–2 k [F(1,6) = 4.65, p = 0.05; r = 0.81].

In summary, although changes in the body stiffness in this series also led to two regimes of distinct vibratory pattern, stimulus clusters like those found for series II did not appear in the perceptual spaces (Fig. 9), suggesting that the perceptual effect of the change in phonatory regime that occurred with the soft reference vocal fold model in this stimulus series was small relative to that observed for cases with a stiffer reference fold in series II. This may have occurred in part because the major consequence of the regime change in this series was a jump in F₀ for which all stimuli were normalized prior to perceptual testing. The remaining major acoustic effect of the observed regime change was a change in the spectral slope at high frequencies, which was found to be perceptually important, at least for a subgroup of listeners. Listeners also noticed changes in acoustic measures characterizing the low-frequency portion of the spectra (H1–H2 and H4–2 k).

DISCUSSION AND CONCLUSIONS

Hirano (1974) proposed a simplified body-cover description of vocal fold structure and argued that variations in the stiffness properties of the body and cover layers can lead to different vibratory modes. The present study further showed that when vocal folds are symmetrically stiff, as in series I, the major acoustic effect of varying body stiffness was the extent to which the folds excited high-order harmonics in the produced sound spectrum as demonstrated by the strong correlations between body stiffness and the number of harmonics above the noise baseline in the spectrum for that series. Because listeners are perceptually sensitive to changes in the harmonic structure and slopes of harmonic spectra (Kreiman and Gerratt, 2012), the number of harmonics became the single most important acoustic measure that linked physiology (body stiffness) to perception in the symmetric conditions in series I. Although contraction of the cricothyroid muscle also plays a role, the TA muscle is the primary regulator of body layer stiffness (Hirano, 1974). Thus the results of this study suggest that the TA muscle likely plays an important role in regulating voice quality.

Harmonic structure (represented by the number of prominent harmonics in the spectrum) also apparently linked physiology and perception in the first series of asymmetric conditions (series II). This was expected because the vibratory patterns observed across models in series II covered a range similar to that in series I, from one involving a soft-body model only (for small body stiffnesses in Figs. 46) and transitioning to a vibration pattern involving two stiff-body models (for large body stiffnesses in Figs. 46). The only major difference between series I and II was the existence of two distinct regimes and the abrupt transition between them. The acoustic changes (primarily changes in harmonic structure) that occurred when vocal fold vibration transitioned from one regime to the other in series II were so large that listeners uniformly based their perceptual judgments on this qualitative change with no measurable attention to smaller changes in quality that may have occurred within subgroups of stimuli. On the other hand, vibration in series III involved only soft-body models: The two folds either both had a soft-body or one fold was much stiffer than the other but only the softer model vibrated. Consequently, in series III, changes in the harmonic structure were much smaller and much less salient perceptually. The reduced perceptual prominence of changes in harmonic structure also increased the salience of other aspects of the voice quality in series III, which may explain the multiple perceptual dimensions that emerged from the perceptual ratings. These results indicate that we cannot assume any acoustic event is perceptually salient, even one as “dramatic” as a change in vibratory regime.

Although the presence of asymmetries in vibration is often considered undesirable and sometimes as an indication for further clinical intervention, our study showed that asymmetry in vibrational amplitude and phase was perceptually insignificant unless the vibratory pattern changed from one regime to the other (as in series II), and sometimes not even then (as in series III). Clinically, this suggests that a vibration pattern with left-right asymmetry may not necessarily cause a salient change in voice quality. However, measures of such asymmetry may provide information regarding the underlying stiffness mismatch and thus may still be important in the diagnosis of a weakened fold in unilateral vocal fold paresis and paralysis (Zhang and Luu, 2012).

Finally, it is worth pointing out that the results of this study were obtained based on one specific vocal fold geometry and one particular physical model of the vocal folds. Further studies using a wider range of stimuli and physiologically more realistic models of phonation are necessary to confirm and extend the findings of this study before conclusions about clinical applicability can be firmly drawn. For example, the geometry of the physical models in this study was different from that of realistic human vocal folds. Changes in vocal fold geometry could have significant influence on vocal fold vibration (Zhang, 2010b) and thus could affect the validity of the observations of this study. Further, contraction of the TA muscle also causes changes in vocal fold properties other than the body stiffness, the effects of which should be included in future investigations (e.g., medial compression may enhance the role of the TA muscle in regulating glottal closure and voice quality). The acoustic and perceptual effects of changes in cover layer stiffness, which were not investigated in this study, will also be a topic of future studies.