Droplet microfluidics driven by gradients of confinement

Abstract

The miniaturization of droplet manipulation methods has led to drops being proposed as microreactors in many applications of biology and chemistry. In parallel, microfluidic methods have been applied to generate monodisperse emulsions for applications in the pharmaceuticals, cosmetics, and food industries. To date, microfluidic droplet production has been dominated by a few designs that use hydrodynamic forces, resulting from the flowing fluids, to break drops at a junction. Here we present a platform for droplet generation and manipulation that does not depend on the fluid flows. Instead, we use devices that incorporate height variations to subject the immiscible interfaces to gradients of confinement. The resulting curvature imbalance along the interface causes the detachment of monodisperse droplets, without the need for a flow of the external phase. Once detached, the drops are self-propelled due to the gradient of surface energy. We show that the size of the drops is determined by the device geometry; it is insensitive to the physical fluid properties and depends very weakly on the flow rate of the dispersed phase. This allows us to propose a geometric theoretical model that predicts the dependence of droplet size on the geometric parameters, which is in agreement with experimental measurements. The approach presented here can be applied in a wide range of standard applications, while simplifying the device operations. We demonstrate examples for single-droplet operations and high-throughput generation of emulsions, all of which are performed in simple and inexpensive devices.

The production of droplets in microchannels is generally performed in one of three dominant geometries: T-junctions (1), flow-focusing devices (2), and coflow devices (3). Since the initial introduction of these devices, many studies have focused on understanding their underlying physics (see refs. 4–6 for recent reviews), as well as on extending their range of operation, for instance by parallelizing the injection nozzles to increase the total throughput (7, 8) or to generate drops with variable contents (9, 10). In parallel to such mechanical studies, a large body of recent work has dealt with applications of droplet methods to biological or chemical analysis, where each droplet is considered as a mobile microreactor (see, e.g., refs. 11–13 for reviews).

All three methods allow the production of a well-calibrated train of droplets by continuously injecting the droplet and carrier fluids through a well-designed microfluidic geometry. At the junction where the fluids meet, drops detach due to the hydrodynamic forces that are determined by a coupling of the flow rates with the geometric parameters and fluid properties. This fixes the size, volume fraction, transport velocity, and production frequency of the droplets (4–6). It is not possible to vary one of these parameters without affecting the others, except by using active external forcing (14–17).

This contrasts with nonmicrofluidic methods to produce drops, such as micropipetting or ink-jet printing. In these methods, only the dispersed phase is injected and the drop detachment is due to a local loss of equilibrium between the force due to surface tension and a body force: weight or inertia, respectively. The simplicity of the physical mechanisms of these methods yields a high degree of flexibility and stability, which explains their widespread use from the production of a single drop on demand to highly parallel automated platforms. However, these techniques cannot be applied at microfluidic scales, because body forces become negligible as the drop size decreases. Instead, the flow behavior in microchannels is usually dominated by surface tension and viscous effects.

In this context, gradients of surface energy were recently shown to resemble gradients of gravitational potential energy (18). These surface energy gradients, which were produced by local variations in drop confinement, could apply sufficient forces to guide or trap drops using microfabricated grooves, which were called “rails” and “anchors” for guides and traps, respectively (19). We now address the question of whether gradients of confinement alone are sufficient to generate microfluidic droplets, to mimic the behavior of a pipette at microfluidic scales.

Producing Drops of Controlled Size

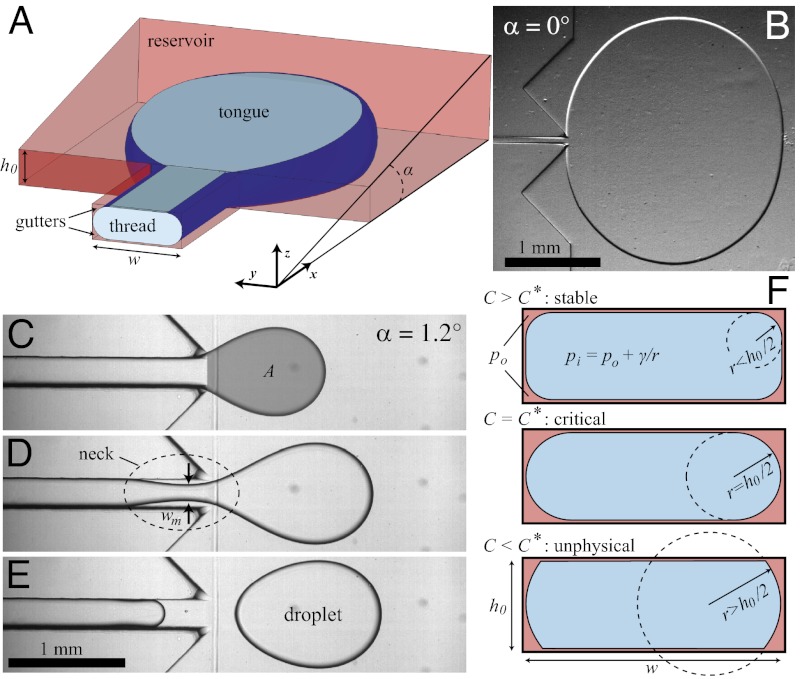
We address this question using the device sketched in Fig. 1A, which provides a constant confinement gradient in a microfluidic chamber. It consists of an inlet channel of rectangular cross-section that leads to a wide reservoir whose top and bottom walls can be inclined at an angle α (see SI Materials and Methods and Fig. S1 for microfabrication details). The device is initially filled with the liquid that will form the continuous phase and its surface is treated to provide good wetting for this liquid. The second fluid is then injected into the reservoir through the inlet channel. If the top and bottom walls of the reservoir are parallel, there is no gradient of confinement and a circular tongue grows indefinitely into the reservoir and does not break off (Fig. 1B).

Fig. 1.

Device geometry and mechanism for drop formation through a confinement gradient. (A) Three-dimensional sketch of a device during operation. The dispersed phase is pushed through the inlet channel (width w and height 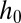) into a wide reservoir containing a stationary continuous phase. The top wall of the reservoir is inclined at an angle α. Fluid from the continuous phase remains in the corners of the inlet channel, forming gutters connected to the reservoir. (B) For a flat reservoir (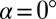), the circular tongue grows indefinitely without detaching. (C–E) Even a small slope () leads to a modification of the tongue shape and to a drop detaching. (C) A tongue of water in oil has a projected surface area A. (D) A neck appears in the inlet channel and its width 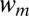decreases in time. (E) The thread ruptures, when 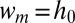, releasing a self-propelled droplet. (F) Cross-sectional shape of the confined thread in the inlet channel for different imposed 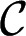. If , the interface flattens against all four walls and the gutter radius of curvature . For , 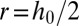: The inner fluid is tangent to the side walls. When 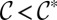, the shape of the interface is unphysical. The curvature in this case must adjust in the out-of-plane direction.

This is not the case when the ceiling is inclined with respect to the floor, even for a small inclination angle 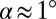, as illustrated in Fig. 1 C–E. In this case, the thread expands into an elongated tongue upon entering into the reservoir. The tongue’s equivalent radius 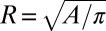, where A is the projected surface area, grows until it reaches a critical value 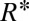. At this point the thread locally forms a neck (Fig. 1D) that shrinks before suddenly pinching off, thus liberating a droplet of radius 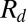. The drop then spontaneously moves away from the nozzle (Fig. 1E). This scenario is generic to all of the sloped nozzles that we have investigated, spanning angles in the range 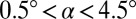, widths from 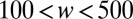μm, operated at flow rates 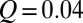–40 μL/min. A phase diagram of the drop pinch-off is illustrated by Movie S1.

Physical Mechanism for Droplet Breakup

The physical mechanism behind the droplet breakup originates from the Laplace pressure jump, which locally relates the mean curvature 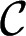of an interface to the difference between the inner and outer pressure fields, and 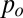, through the interfacial tension γ: 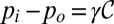. In the quasi-static case, i.e., when pressure variations due to flow can be neglected, the pressures 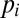and 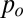are constant in each of the phases. This fixes the curvature that must be adopted by the thread in the inlet channel, particularly in the gutters that separate the dispersed phase from the channel walls in the corners of the rectangle (20, 21). The Laplace equation therefore implies that the curvature of the thread in the gutters must adapt to match the mean curvature of the tongue in the reservoir. However, its ability to adjust is limited by the confinement because increasing the radius of curvature r of the gutters beyond 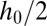leads to the unphysical situation of a kinked interface at the channel wall, as shown by Fig 1F. This fixes a minimum 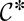for the curvature in the inlet channel: .

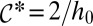In the reservoir, the curvature decreases as the tongue grows. When the floor and ceiling are parallel, the quasi-static shape of the tongue is a circular pancake of radius R and curvature 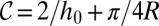(22). Although 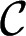decreases as R increases, it never becomes smaller than , meaning that the critical state for the thread is never reached. This contrasts with the case of a sloped reservoir for which the depth of the tongue also increases as it grows, leading to a further decrease in mean curvature. In this case the tongue adopts the shape of a 2D pendant drop, to equilibrate the in-plane and transverse curvatures in the reservoir (see Materials and Methods for model derivation), and 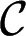drops below 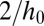when the tongue reaches the critical size

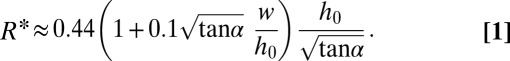When 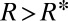, the curvature of the thread in the inlet channel cannot decrease to the value imposed by the tongue. The Laplace law then implies a lower pressure of the continuous phase in the gutters than in the reservoir. This drives a reverse flow into the gutters and leads to the necking of the thread upstream of the nozzle. Finally, the thread ruptures when it locally thins to a cylinder of diameter 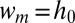, due to the Rayleigh–Plateau instability (23).

This breakup mechanism also explains the droplet formation at a step change in the microchannel depth, known as step emulsification (24–27). As in those cases of a sudden step, the size of the drop that is formed decreases linearly with the channel height, which allows micrometer-scale droplets to be reached by using equivalently thin channels (24, 26). In contrast, however, the value of the slope here provides an additional control parameter to tune the drop size. It is also responsible for the spontaneous transport of the drops away from the nozzle toward regions of greater depth. In our experiments, we have observed that this reduces the interactions between successive drops and leads to improved control of the droplet size (27).

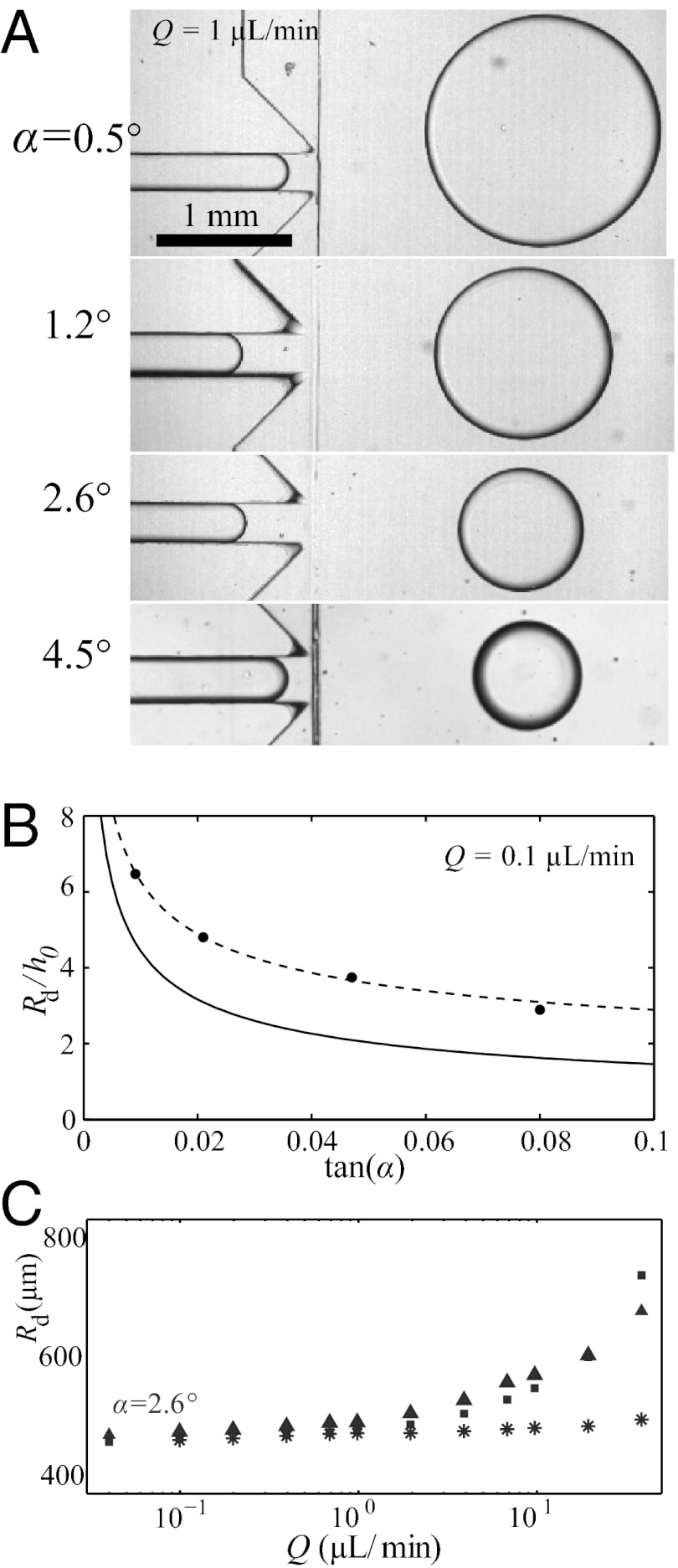
The analysis leading to Eq. 1 predicts that the drop size should decrease for increasing α. This is verified in Fig. 2A, which shows drops being produced with four different slopes. Eq. 1, however, underestimates 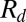(Fig. 2B, solid line), because it predicts only the critical value 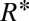at which the necking is initiated. In particular, it fails to consider the volume of liquid from the neck that is absorbed by the droplet. Given that this additional volume is proportional to w, Eq. 1 can be modified through an empirical correction with a single fitting prefactor, which yields

This expression for the radius shows excellent agreement with the measurements of 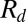in our devices, as shown by the dashed line in Fig. 2B.

Fig. 2.

Characterization of the droplet size for one inlet geometry (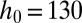 μm, 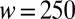μm). (A) Images of oil drops in water for four different slopes, 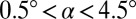. (B) Measured radii 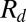(circles) compared with the predictions of Eq. 1 (solid line) and Eq. 2 (dashed line). (C) Variation of drop radius 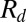with the flow rate Q shows a weak dependence; a 1,000-fold increase in Q at most doubles the drop size. The different symbols correspond to different fluid pairs: Oil in water ( 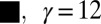mN/m), water in oil ( 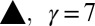mN/m), and air in water ( 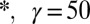mN/m). The drop size is independent of the fluid properties at low Q.

Eqs. 1 and 2 highlight the peculiarity of this method of droplet production, because they predict that neither γ nor other fluid properties have any influence on the drop size. This is tested by varying the fluid pairs, as shown in Fig. 2C, where the sizes of water drops in oil, oil drops in water, and air bubbles in water are plotted for different flow rates (see also Fig. S2 for different slopes). The drop and bubble sizes are indeed indistinguishable from each other at the low flow rates, for which the quasi-static approximation holds.

These experiments also reveal that Q has only a small influence on 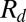: a 1,000-fold increase in flow rate barely doubles the value of 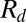for the liquid drops and increases the gas bubble radius only by about 25%. Hence, although the flow in the inlet channel leads to a viscous pressure drop, it only weakly perturbs the quasi-static curvature argument presented above. Moreover, the radii of the first few drops are within 5% of the long-time average and the steady-state polydispersity index of the produced emulsions is as small as 0.1%, an order of magnitude better than other microfluidic systems (3) (histogram in Fig. S3). Such stability in droplet size can be intuitively understood by recalling that the drop size is determined by the geometry, which is invariant throughout the experiment. This contrasts with methods where the drop size depends on the local velocities of the inner and outer fluids, which go through large fluctuations initially and until the flows have reached a statistical steady state. The insensitivity of the drop production to the flow rate implies that the method can be applied in different regimes. Below we explore the extreme cases, corresponding first to the production of a single drop on demand and then to the high-throughput production of emulsions.

Reactions on Demand in Single Droplets

The first application of this method is to generate individual droplets on demand to perform controlled chemical reactions. The aim here may be to test an unknown sample vs. a range of substrates or concentrations, to verify the sample contents. For this, independent parallel channels can lead to a single test region where two rails are etched in the sloped surface to guide the drops toward an anchor where they meet and react together.

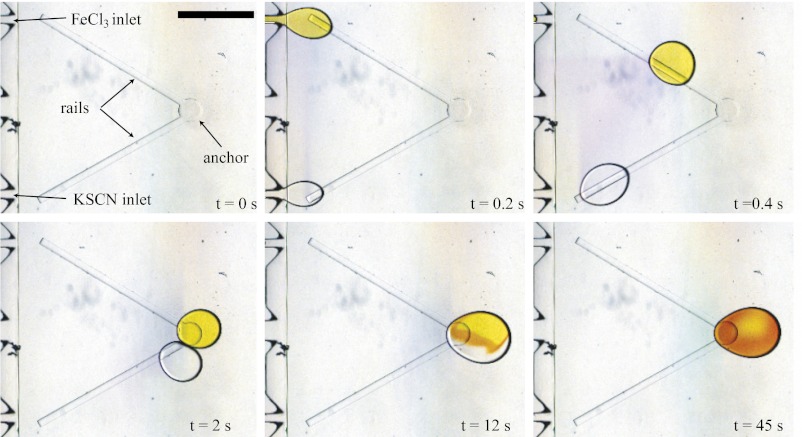
Here we demonstrate the proof of principle with a single reaction, where two aqueous drops containing different reagents are formed from two independent inlets (Fig. 3). The drops are produced by a programmable syringe pump that injects 170 nL into each nozzle and stops; the rest of the experiment takes place without any imposed flow. Each droplet detaches and is propelled by the confinement gradient while being guided toward the central anchor site by an oblique rail. Although the two drops have different surface tensions due to the interactions between the chemicals and the surfactant, they are equally guided by the rails and only the speed at which they travel differs. The faster drop is trapped in the anchor and waits until the slower one arrives, at which point the conjugate action of the slope and rails presses the two drops together and leads to coalescence, initiating the chemical reaction.

Fig. 3.

Initiating a chemical reaction with individual droplets: At t = 0 s, two inlet channels bring aqueous solutions of (dyed with yellow food coloring) and KSCN. A programmable syringe pump injects the two solutions at 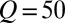μL/min during 0.2 s. A single droplet detaches from each nozzle and travels into the reservoir, where an oblique rail guides it toward the central anchor. The fast drop waits for the slower one. The two collide at 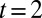s and remain pressed together. Coalescence occurs 10 s later, initiating the chemical reaction, which produces 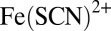complex (red). The coalesced drop remains at the anchor and the reaction is monitored in time. 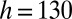Nozzle dimensions: μm, μm. . (Scale bar, 1 mm.)

Here, the anchor is designed to be sufficiently strong to hold the merged droplet in place, thus allowing long-term observation of the reaction product. Although the operation of this device is slow compared with the state of the art in microchannels, the throughput can be improved by optimizing the geometry, for instance by using smaller droplets and larger slopes, or by relying on active merging techniques (5).

Nevertheless, the current example provides similar functionality and performance to those of digital microfluidic devices: a reaction is triggered on demand in a few seconds and by using submicroliter sample volumes. In contrast with those devices, however, the operations here are hard wired, therefore not requiring any programming. Furthermore, the current device is made of polymer with no active elements, making it inexpensive and easy to replicate using molding methods. As such, it is well suited for diagnostics or other applications that require a robust, disposable, drop-on-demand platform and for which digital microfluidics are prohibitively complex.

High-Throughput Emulsification

The throughput of drop production can be increased by parallelizing the nozzles. This is first demonstrated in Fig. 4A (Movie S2 and Fig. S4), where an emulsion of drops with different dyes is produced by mixing the three primary colors two-by-two upstream of the production nozzles. Even though the dyes interact with the surfactants to change the surface tension across the nozzles, the drop size is monodisperse. Moreover, the device can be operated at a wide range of flow rates (here Q was varied from 1 to 100 μL/min) by simply changing the inlet flow rates. Because only the dispersed phase must be pumped, the throughput can be changed instantaneously and without affecting the drop size, unlike in previously reported devices where the flow rates must be reequilibrated (7, 10). Finally, note that the design and fabrication of the injection channels is simplified compared with other parallel schemes (7, 8, 10), because only channels and inlets of the dispersed phase need to be considered.

Fig. 4.

High-throughput production of controlled emulsions: (A) An emulsion with variable contents is produced by combining the three primary colors. Although the food coloring interacts with the surfactant and modifies the surface tension, the drop sizes are independent of their content. (B–E) Massive parallelization in an inflatable device. (B) A set of 256 parallel nozzles of identical dimensions (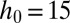 μm, 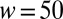μm) connect the dispersed phase channel to the central region. (C) The continuous phase in the reservoir is pressurized using a pressure controller that leads to a roof deformation, as illustrated in this cross-section. (D) Droplets detach from each of the nozzles and form a monodisperse array that remains on the chip. Here, the reservoir overpressure is 100 mbar, and the flow rate is set at 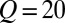μL/min such that the nozzles produce 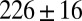pL droplets at a frequency of 1.5 kHz. (E) The reservoir pressure controls inflation and as a result the drop size: inlet pressures of 25, 50, 100, and 200 mbar lead to drop radii of 41, 39, 37.5, and 36.5 μm, respectively, with a size dispersion under 3%.

Finally, massive parallelization can be achieved to reach high-throughput emulsification or to efficiently divide a sample into a multitude of droplets that are held on chip. This is demonstrated in the device in Fig. 4 B–D, which contains 256 parallel nozzles that lead to a wide central region. The device is initially filled with the continuous phase, to which an overpressure is applied. This inflates the reservoir and creates a slope at each of the nozzles. At this stage, the dispersed phase is injected with a syringe pump and divides into equal-sized droplets upon exiting the nozzles. The size of the drops in this case is controlled by the applied overpressure (Fig. 4E). In the example shown in Fig. 4D, an initial 5-μL sample is dispersed into an array of 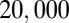droplets, each measuring pL, at a frequency of 1,470 drops/s. The drops can then be kept on the chip or extracted through an exit in the center of the device, as shown in Movie S3, in which case a slight external flow is needed, as in the case of Fig. 4A.

The drop production in the above examples is determined locally at the exit of each nozzle. This is because the outer fluid is stationary, meaning that the pressure field is constant throughout the reservoir into which the droplets flow. Furthermore, the flattened “Hele-Shaw” geometry of the reservoir screens the effects of each drop on its neighbors. These features allow the device to be scaled up to a larger number of nozzles, without any fundamental limit, although practical limits on flow rates or device size may become important.

Discussion

We have presented microfluidic devices to produce drops by using the gradient of confinement due to nonparallel top and bottom walls. In these experiments, the size of the drops is determined principally by the geometry of the device, as described by Eqs. 1 and 2. It is independent of the drop contents, even when those contents modify the value of the surface tension or the viscosity; this is visible in Fig. 4A, where drops of different colors have different surface tensions but the same size. However, the velocity at which the droplets flow away from the nozzles depends on the fluid properties, which sets a limit on the throughput that is achievable from each nozzle.

The weak sensitivity of the drop size on the production rate allows each nozzle to operate at a wide range of flow rates, from producing a single drop to several drops per second. This aspect facilitates the parallelization, because fluctuations in flow rates between the different nozzles do not affect the emulsion monodispersity. Indeed, the nozzles in Movie S3 start producing droplets at different moments and do so at different rates. Nevertheless, all of the drops have the same size, starting from the very first drops that are produced near the top of the image (Fig. S5).

All of these aspects distinguish the current technique from the standard microfluidic methods for producing drops, because they decouple the drop size from the production rate and from the physical forces acting on the interface. In practice, they imply that a monodisperse emulsion is obtained without any losses from the initial sample. This is particularly important for cases when the emulsion is kept on chip for further analysis (28, 29), because the complete initial sample can be analyzed.

Finally, the ability to produce drops in a quiescent outer fluid paves the way for hand-operated emulsification chips. In such a protocol, the chip is initially filled with the outer fluid, using a hand-held pipette. Then the dispersed phase can be injected by hand, also using a pipette. The fluid then spontaneously breaks up into monodisperse drops as it passes the nozzles. The manual production of thousands of monodisperse nanoliter-scale drops is shown in Movie S4, where the parallel device of Fig. 4B is operated by a hand-help pipette and filmed in real time. This greatly reduces the complexity of droplet microfluidics, which should allow its greater adoption by biologists and chemists.

Materials and Methods

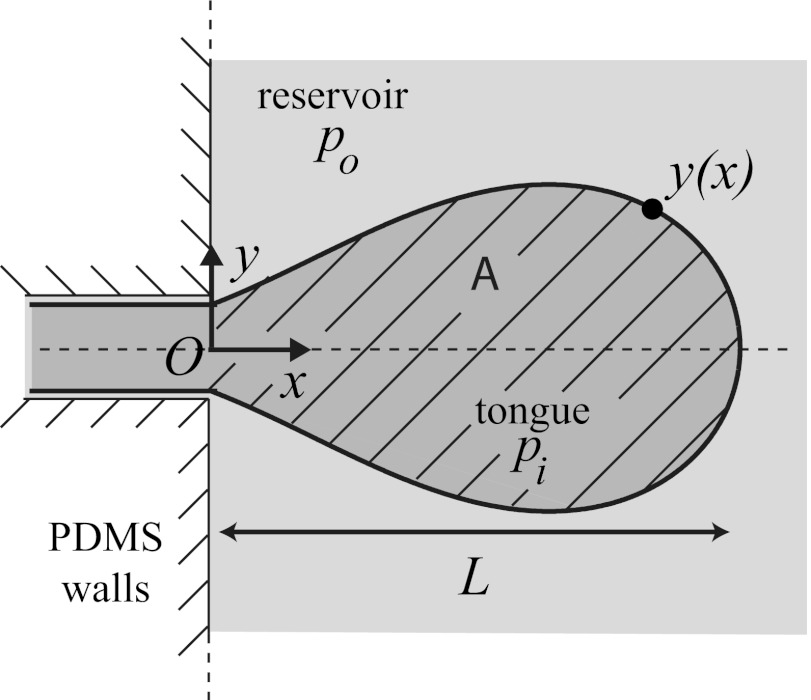
Shape, Mean Curvature, and Critical Size of the Water Tongue.

To relate the curvature criteria for droplet breakup (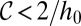) to a critical size 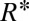of the tongue, a detailed description of the tongue geometry is required. To this end, we define a function 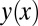that describes the shape of the tongue in the horizontal 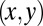plane of the reservoir, of origin O at the injection nozzle as sketched in Fig. 5. The function must verify two geometric constraints: a continuity condition at the nozzle tip 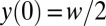and tangent continuity at the apex of the tongue 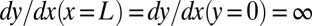, where L is the length of the tongue. However, tangent continuity is not required at the nozzle tip (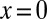) because of the sharp angle of the channel side walls.

Fig. 5.

Sketch of the coordinate system used to describe the tongue shape.

Recalling the Laplace equation, the interface verifies

with 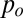the pressure of the continuous phase in the reservoir, the pressure of the dispersed phase in the tongue, and 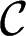the mean curvature of the free surface. In a quasi-static situation for which flow-induced pressure variations are negligible, the pressures 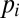and 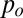are constants. Hence, the Laplace equation implies that the mean curvature 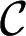is constant everywhere on the interface.

The mean curvature has two local contributions: the curvature 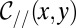of the projected shape in the 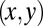plane and the vertical transverse curvature 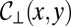. For a nonwetting tongue, the latter is constrained by the top and bottom walls of the reservoir, of local height 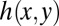, with a correction that depends on the local in-plane curvature 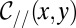to verify the condition of constant mean curvature (22). Under these conditions,

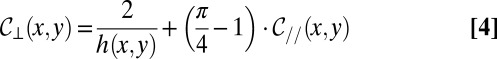and consequently, the mean curvature is given by

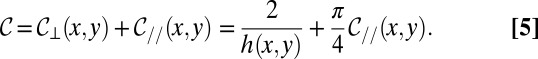Constant curvature then implies that

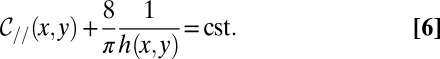In the case of a reservoir of constant height 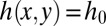, the in-plane curvature is then also constant. Therefore, the tongue adopts a circular shape at equilibrium, which is in agreement with experimental observations as shown in Fig. 1B. Its mean curvature is given by

In the case of a reservoir with walls wedged at an angle α, the height of the channel increases linearly with x from 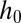at the nozzle tip: 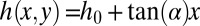. Assuming small height variations over the length of the tongue (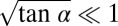), Eq. 6 expands and simplifies to

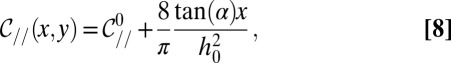with 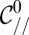the curvature at the nozzle. This shape equation is identical to the one describing the shape of a 2D pendant drop for which the curvature increases linearly away from the needle tip due to gravity. This analogy points out the existence of a characteristic length 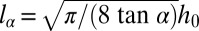, equivalent to the classical capillary length 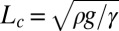for pendant drops.

However, whereas is a function of the fluid properties (density ρ and interfacial tension γ), the length scale 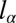depends entirely on the geometry of the sloped reservoir (initial height 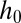and angle α), independently of the fluids. Consequently, the tongue shape does not depend on the fluid properties, not even on interfacial tension, which is at the root of the shape definition mechanism.

As a result, the droplet shape is described by a unique equation

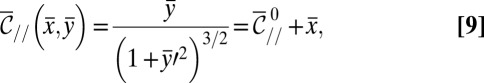once all lengths are made nondimensional by the characteristic length 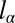: 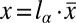, , 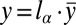and . The two geometric boundary conditions become

Eq. 9 is a second-order differential equation in 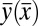with two boundary conditions and a shape parameter 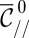, the in-plane curvature at the nozzle. Consequently, for any value of 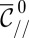, there is at most one solution for the tongue shape. Or equivalently, given a value of the tongue nondimensional surface area 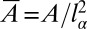, there are also a unique 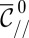and shape that verify Eq. 9. Using MatLab, we can then generate the family of shapes the tongue takes as it grows from a nozzle as illustrated by Fig. 6A.

Fig. 6.

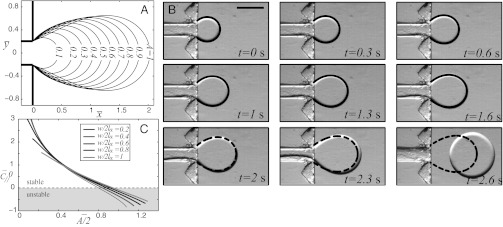
(A) Universal tongue shapes for various surface areas 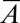, attached to a nozzle of nondimensional width 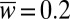. (B) Image sequence of the production of a water droplet in a reservoir of FC40 + PEG-PFPE from a nozzle whose dimensions are 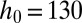μm, 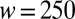μm, and 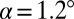. Lines are the predicted shapes for the water tongue growing in the reservoir: Solid line, the shapes have a mean curvature 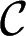that verifies the stability criterion 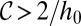; dashed line, the shapes violate this criterion. (Scale bar, 500 μm.) (C) 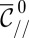vs. 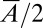for five different nozzle widths 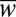ranging from 0.2 to 1.

These shapes can be compared with experimental observations. Fig. 6B displays nine successive images of a tongue growing at a flow rate 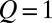μL/min into a sloped reservoir, along with predicted shapes. A single fitting step at 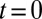is used to produce the series of theoretical shapes: The surface area A is extracted from the experimental image at 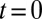and the corresponding theoretical shape is computed. The predicted time evolution of the tongue shape and surface area 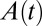is then obtained by assuming the tongue volume 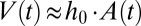increases linearly at the flow rate μL/min. Fig. 6B shows the eight predicted geometries corresponding to the experimental time steps of the image acquisition. Excellent agreement is observed until necking of the thread appears after 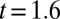s.

From Eq. 9, we also obtain numerically the relationship between and . Consequently, we can identify the critical tongue surface area 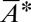for droplet breakup by applying the stability criterion .

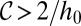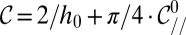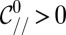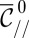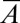At the nozzle, the mean curvature is given by , using Eq. 5. Hence, we can rewrite the criterion as in nondimensional terms. Fig. 6C features the plots of vs. for five different nozzle widths 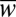. 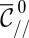always decreases below the stability threshold 0 as 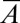increases.

Finally, we obtain that the stability threshold is reached for

which translates back to

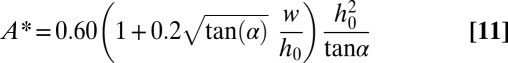in dimensional quantities.

In terms of equivalent radius 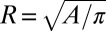, we find

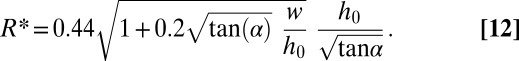For small angles α, this expression simplifies to

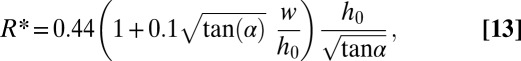by expanding the square root.

This prediction of the critical tongue size 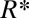is in good agreement with experimental observations as illustrated in Fig. 6B, where the theoretical shapes that violate the stability criterion of the thread in the nozzle are shown by a dashed line. The transition takes place between frames 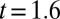s and 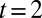s, which also corresponds to the appearance of a neck upstream in the nozzle.