Cleaved-coupled nanowire lasers

Abstract

The miniaturization of optoelectronic devices is essential for the continued success of photonic technologies. Nanowires have been identified as potential building blocks that mimic conventional photonic components such as interconnects, waveguides, and optical cavities at the nanoscale. Semiconductor nanowires with high optical gain offer promising solutions for lasers with small footprints and low power consumption. Although much effort has been directed toward controlling their size, shape, and composition, most nanowire lasers currently suffer from emitting at multiple frequencies simultaneously, arising from the longitudinal modes native to simple Fabry–Pérot cavities. Cleaved-coupled cavities, two Fabry–Pérot cavities that are axially coupled through an air gap, are a promising architecture to produce single-frequency emission. The miniaturization of this concept, however, imposes a restriction on the dimensions of the intercavity gaps because severe optical losses are incurred when the cross-sectional dimensions of cavities become comparable to the lasing wavelength. Here we theoretically investigate and experimentally demonstrate spectral manipulation of lasing modes by creating cleaved-coupled cavities in gallium nitride (GaN) nanowires. Lasing operation at a single UV wavelength at room temperature was achieved using nanoscale gaps to create the smallest cleaved-coupled cavities to date. Besides the reduced number of lasing modes, the cleaved-coupled nanowires also operate with a lower threshold gain than that of the individual component nanowires. Good agreement was found between the measured lasing spectra and the predicted spectral modes obtained by simulating optical coupling properties. This agreement between theory and experiment presents design principles to rationally control the lasing modes in cleaved-coupled nanowire lasers.

As miniaturized lasers see a rapid increase in applications for digitized communication and signal processing, the monochromaticity of the lasing output becomes an important figure of merit (1). Laser emission at multiple frequencies can lead to both temporal pulse broadening and false signaling because of group-velocity dispersion (2). These problems are avoided by controlling the laser to oscillate at a single frequency. Single-mode lasing is obtained when the spectral spacing between the modes, the free spectral range, is larger than the bandwidth of the optical gain (3–5). Although they are intriguing miniaturized lasers (6–11), individual semiconductor nanowires would need to be as short as a couple of microns to lase at a single optical frequency because of their relatively broad gain profile (>10 nm at room temperature) (12, 13). With the low reflectivity of the end facets (14), such short nanowires are inefficient resonators and may not have a lasing threshold that can be reached with the limited gain of the material (15, 16); with this in mind, coupling nanowire cavities is a promising route to produce single-mode operation. Previous reports of laterally coupled nanowires required micromanipulation to create a coupling structure. This form of evanescent wave coupling is highly sensitive to geometric parameters, such as internanowire distances, lengths of the coupled segments, and perimeters of the nanowire loops (17, 18). The reliance on micromanipulation, with its innate imprecision, limits the control over the coupling properties, introduces surface contamination that alters cavity modes, and restricts the miniaturization of the overall dimension of the devices. An alternative photonic architecture to increase the free spectral range is the radiative coupling of two Fabry–Pérot cavities axially through an air gap, known as the cleaved-coupled cavity (19–22). To achieve this geometry in nanowires, the two cavities can be defined by cutting a single nanowire, which ensures that the two cavities are axially aligned. This approach eliminates the need to position two separate nanowires next to each other with nanoscale precision, a feat that is required by the lateral coupling scheme. However, applying this axial coupling concept to nanowires introduces a new complication: the range of gap widths is limited because diffraction losses at the gap increase with the reduction of the cavity’s cross-sectional dimensions. In this work, we use design principles derived from finite-element method simulations and transfer matrix methods to experimentally demonstrate single-mode lasing in cleaved-coupled nanowires. The modeling and optical measurements show that a gap width smaller than λ/2 is paramount for effective optical coupling, which eliminates the applicability of the rule of λ/2 to cleaved-coupled nanowires (23). A gap at this scale provides the complementary benefits of single-mode lasing at a lower threshold gain than that of the individual component nanowires. Such nanoscale gaps can be defined precisely using readily available fabrication techniques. Because they require no positioning of the nanowires, cleaved-coupled cavities constructed out of single nanowires allow us to achieve reliable and reproducible control of the lasing modes.

Results and Discussion

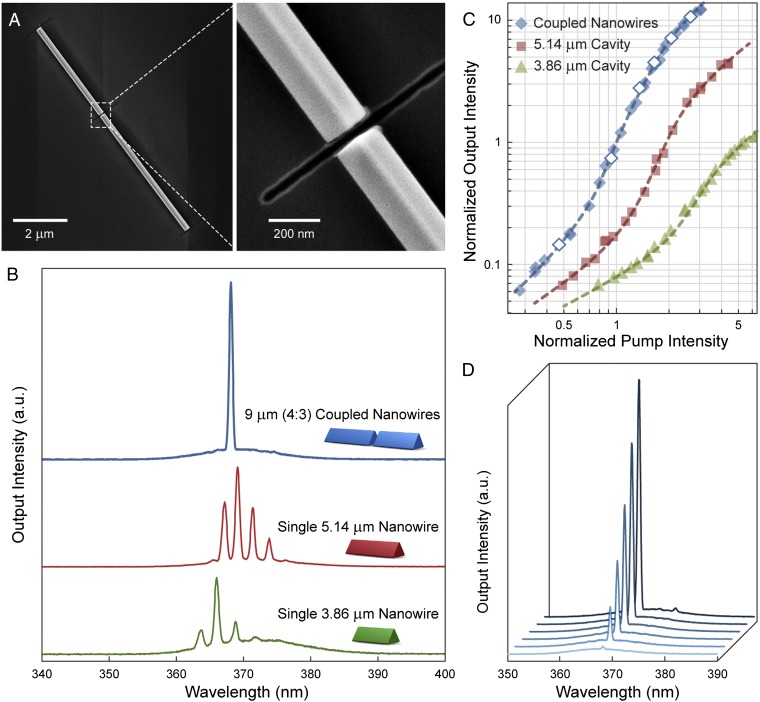
Cleaved-coupled nanowires were obtained by defining the optical cavities on single-crystalline gallium nitride (GaN) nanowires using focused ion beam milling (FIB; Fig. 1A and Methods). A metallic protection layer was used to prevent the degradation of the luminescent properties of the nanowires during the ion beam milling. Photoluminescence measurements showed negligible differences in the optical quality of the nanowires before and after fabrication. This fabrication technique provides precise control over two critical parameters for spectral manipulation of the lasing modes: cavity lengths and intercavity gap widths (as narrow as 30 nm). The smooth-end facets and gap facets obtained from FIB milling also contribute to the low diffraction loss of the cavities. Multiple Fabry–Pérot modes are observed in the lasing spectra of the individual nanowires with lengths of 3.86 μm and 5.14 μm (Fig. 1B and Methods). In contrast, when these two cavities are aligned axially with a 40-nm intercavity gap, single-frequency lasing is generated from the 9-μm (4:3) cleaved-coupled nanowire cavity (Fig. 1B). [The notation x μm (y:z) describes a cleaved-coupled cavity with a total length of x μm, and y:z is the ratio between the lengths of the two component nanowires.] In addition to the reduced number of lasing modes, the lasing transition occurs at a lower pump intensity in the cleaved-coupled nanowires (Fig. 1C). The relationship between the output intensity and the pump intensity was modeled and fitted using a rate equation analysis (SI Appendix). The reduction in the lasing threshold by the addition of active material is pronounced because the suboptimal reflectivity of the nanowires’ end facets makes them inherently inefficient resonators. These two advantages cannot be achieved simultaneously in single Fabry–Pérot nanowire cavities or using some previously reported nanowire coupling schemes (18) where a larger free-spectral range is accompanied by a higher threshold gain. The cleaved-coupled nanowires exhibit stable single-mode operation over a large range of pump intensities (Fig. 1D). At pump intensities far above the lasing threshold, a small satellite peak appears at a longer wavelength. Such mode-hopping is usually observed when the gain profile red-shifts under high excitation intensities (21), possibly due to band-gap renormalization (24, 25).

Fig. 1.

Single-frequency lasing in 9-μm (4:3) cleaved-coupled nanowires. (A) SEM images showing the axially coupled GaN nanowires on a Si substrate with 250-nm–thick thermal oxide. The two-component nanowires are ∼100 nm in radius and coupled via an intercavity gap ∼40 nm wide. (B) Single-wavelength lasing is observed from the coupled cavity (blue line), and each component nanowire lases at multiple wavelengths when they are separated. (C) Clear lasing transitions can be seen from the power-dependent measurements. The pump intensity and the output intensity are both normalized to the values at the threshold of the cleaved-coupled nanowires. The dashed lines were fitted using a rate equation analysis (SI Appendix, section S11). (D) Output spectra of the cleaved-coupled nanowires show clean single-wavelength lasing at different excitation intensities corresponding to the open diamonds in C.

In macroscopic cleaved-coupled cavity lasers, large intercavity gap widths can be used for effective coupling. At a certain wavelength, the transmittance T and the reflectance R at the intercavity gap vary periodically with the gap width as expected in a Fabry–Pérot cavity with infinite cross-sectional dimensions (SI Appendix). The coupling strength, quantified by the coupling constant T/R, repeats as the gap width is changed by multiples of λ/2, which is known as the rule of λ/2 (23). Therefore, traditional cleaved-coupled cavities, which are made of submillimeter-scale crystals, can be fabricated with micrometer-scale gaps (26, 27). This geometric tolerance cannot be applied to cleaved-coupled nanowire lasers with cross-sections comparable to the lasing wavelength because the finite cross-sections of the cavities induce severe diffraction losses at the intercavity gaps. Using finite-element methods (COMSOL 4.2 software), the optical properties of the gaps between nanowires were calculated from 3D, full-wave simulations (SI Appendix). At a fixed wavelength of 370 nm, the transmittance through the gap decreases monotonically with an increase in gap width (Fig. 2A); consequently, the periodic behavior of the coupling constant is highly damped, and significant optical loss is observed (Fig. 2B). Both the coupling constant and the optical loss are key factors for the effectiveness of a gap in coupling the nanowire cavities. When the gap width is much smaller than the operating wavelength (e.g., 20 nm), the coupling constant is so large that the physical gap becomes optically invisible. As the gap widens, the intensity of the field scattered by the gap to the outside of the nanowire waveguides increases in the simulated field maps (Fig. 2C), which corresponds to a dramatic increase in optical losses at wider gaps. When the gap width is further increased beyond 300 nm, the coupling constant approaches zero and the optical loss stabilizes at about 0.8, indicating that the two nanowire cavities are optically decoupled. To maintain effective coupling, the gap width between axially coupled nanowires needs to be ∼30–100 nm, where low optical loss and a moderate coupling constant can be obtained.

Fig. 2.

Optical properties of intercavity gaps depend upon geometric factors. (A and B) Numerically simulated optical properties of the gap between 100-nm radius GaN nanowires with triangular cross-sections on glass substrates at the wavelength of 370 nm. (C) Simulated electric field maps with gap widths of 20, 100, 150, and 200 nm. The TM00 guided mode was injected from the top edge of the images. The white dashed lines indicate the boundaries of the nanowires. Significant diffraction loss can be seen at gap widths larger than 100 nm.

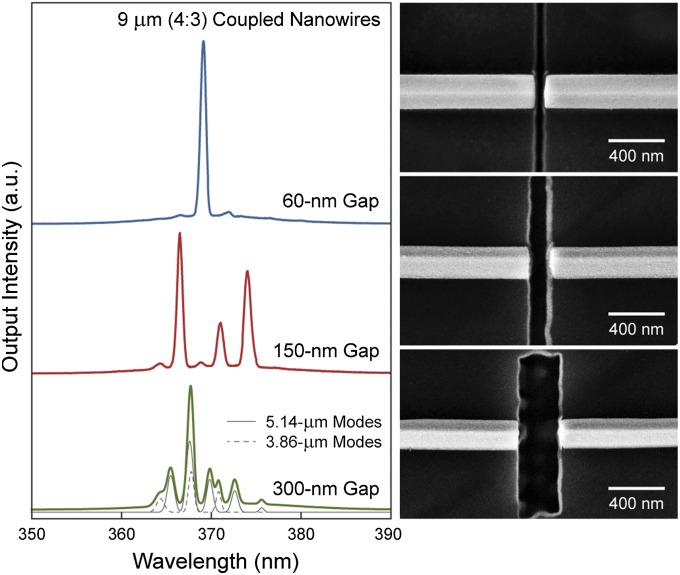
Experimental measurements on cleaved-coupled nanowires with varying gap widths confirm the predictions from simulations. Though 9-μm (4:3) coupled nanowires with a 60-nm gap can produce single-frequency lasing, multimode operation is observed when the gap width was increased to 150 nm (Fig. 3, Left, red line). Although the strength of the mode suppression is reduced, spectral modulation of the mode intensities is still observable with a 150-nm gap, which is in contrast to the well-defined lasing modes from traditional Fabry–Pérot cavities. Additional peaks corresponding to the Fabry–Pérot modes of the individual 3.86-μm and 5.14-μm cavities appear when the gap is expanded to ∼300 nm (Fig. 3, Left, green line). From the simulated results (Fig. 2), the transmittance through a 300-nm gap is much smaller than the reflectance, and the optical loss reaches saturation; therefore, the coupling between the nanowires becomes weak enough that each component nanowire behaves as an independent lasing cavity. These results further confirm the design principles obtained from the simulations. Although optical loss can be neglected in the design of macroscale cleaved-coupled cavity lasers, the importance of this phenomenon emerges during miniaturization of the cleaved-coupled cavity to dimensions comparable to the wavelength; it is the key parameter that dictates the design of nanoscale cleaved-coupled cavities. A more detailed discussion on the relevant theoretical analysis of the effect of gap widths on the threshold modulation can be found in SI Appendix.

Fig. 3.

Lasing spectra from 9-μm (4:3) coupled nanowires with different gap widths. Though single-mode operation is observed with the 60-nm gap, a less-effective threshold modulation with a 150-nm gap results in multiple lasing modes. For a very wide intercavity gap (300 nm), the lasing spectrum contains the modes of both component nanowires, which are indicated by the Gaussian peak fitting shown in the gray curves. (Right) Corresponding SEM images of the gaps.

The spectral modulation of modes observed in cleaved-coupled nanowire lasers can be predicted using transfer matrix methods. Although the Vernier effect provides an intuitive explanation for the mode modulation, it does not account for the phase of the coupled modes. Modes with wavelengths shared by the uncoupled component nanowires may not necessarily lase when the nanowires are coupled because of the phase delay of T relative to R at the gap (SI Appendix). A more rigorous analysis can be done using transfer matrix methods to predict the new modes and their respective threshold gain (SI Appendix) (28). This analytical model makes use of the optical properties obtained from the finite-element method simulations. The calculated eigenvalues for 9-μm (4:3) coupled nanowires with a 40-nm gap show significant modulation of the threshold gain among different lasing modes (Fig. 4, blue diamonds). Within the bandwidth of the GaN gain profile, only one mode with the lowest threshold gain is outstanding. In contrast, modes predicted for single nanowires have nearly equal threshold gain, and multiple modes are expected in their lasing output.

Fig. 4.

Lasing modes calculated based on transfer matrix methods. A smaller absolute value along the y axis indicates a lower lasing threshold. A spectrally modulated threshold can be seen for the cleaved-coupled nanowire with a 40-nm gap, whereas single cavities exhibit flat threshold profiles. The spectral range shaded in purple represents the nominal optical gain region in GaN.

Besides single-mode operation, the calculation also predicts the relationship between the lasing thresholds of the coupled nanowires and the component nanowires. For the modes of cleaved-coupled cavities, both component nanowires provide the optical gain; therefore, the modal gain required for cleaved-coupled nanowires to reach lasing transitions is expected to be lower than that for each individual nanowire (Fig. 4, red squares and green triangles). The calculated threshold gain agrees with the experimental results (Fig. 1C) and confirms the two benefits (i.e., lower threshold and fewer lasing modes) of the cleaved-coupled nanowire lasers. Moreover, with a 40-nm gap width, the threshold of the outstanding mode of the coupled cavities is slightly larger than the threshold of a 9-μm single nanowire (Fig. 4, gray circles). This small difference further highlights the importance of maintaining a narrow gap for minimizing diffraction losses such that single-wavelength operation in coupled nanowires does not sacrifice the optical efficiency of the laser resonator.

The analytical model for mode calculations allows rational design of cleaved-coupled nanowires for the selection of desirable modes. Integer or fractional ratios between the lengths of the component nanowires make a significant difference in the free spectral range of the coupled nanowires. Following the Vernier effect, coupled nanowires with integer ratios would produce the free spectral range of the shorter nanowire. The lasing spectra confirm that 9-μm (1:1) and 9-μm (2:1) coupled nanowires show a modulation in the threshold gain that follows the resonances in the shorter cavities (Fig. 5). In the cases where the depth of threshold modulation between neighboring modes is not large enough, satellite peaks appeared between neighboring favorable modes, which further reduce the mode spacing and increase the number of modes in the lasing spectra (SI Appendix). Alternatively, fractional ratios lead to a modulation in the threshold gain at low-frequency spectral periodicities by a beating effect (SI Appendix). Such mode modulation can result in one favorable mode that has a threshold gain lower than all other modes within the spectral window of the gain profile; therefore, a fractional ratio between the lengths of the component nanowires is critical for achieving single-frequency operation in cleaved-coupled nanowire lasers.

Fig. 5.

Measured lasing spectra and calculated modes of cleaved-coupled nanowires with integer ratios between the lengths of the component nanowires. Good agreement is found between the experimental lasing spectra (blue lines) and theoretical predictions (blue diamonds) for both (A) 9-μm (1:1) and (B) 9-μm (2:1) coupled nanowires. The free spectral ranges of these coupled nanowires coincide with those of the shorter component nanowires (red squares).

Our work offers a promising and practical route to improve the quality of lasing from semiconductor nanowires. Along with simple geometric designs and precise fabrication techniques, the agreement between the theoretical predictions and the experimental observations allows rational design of the cleaved-coupled cavities in nanowires. Though single-frequency lasing is demonstrated here in GaN nanowires, the principles for selecting modes using this architecture should not be restricted to a specific material, operating wavelength, or pumping scheme. The idea of axial coupling can also be extended to cleaved-coupled cavities containing more than two nanowires to achieve more complicated modulation of the lasing modes (29). Although the wavelength-scale cross-sectional dimensions of nanowires induce severe optical losses at intercavity gaps, our theoretical analysis predicts a range of gap widths that can produce single-mode operation and can be reliably achieved using available nanofabrication techniques. Though focused ion beam milling was used in this work, there should be no fundamental limitations with using other lithographical techniques with comparable spatial resolution to create the cleaved-coupled cavity structures in nanowires. The cleaved-coupled nanowire lasers demonstrated here are suitable for miniaturization, highly reproducible by using theoretically predicted design principles, and can be integrated into lithography-based semiconductor processing. The highly monochromatic light from cleaved-coupled nanowire lasers is anticipated to provide ultracompact photon sources for laser-based remote sensing, optical data storage, and long-distance optical communication.

Methods

Growth of GaN Nanowires and Fabrication of Cleaved-Coupled Nanowire Lasers.

GaN nanowires were synthesized using nickel-catalyzed chemical vapor transport on c-plane sapphire substrates in a hot-wall furnace (8). The furnace was held at 1,030–1,050 °C to facilitate the reaction between NH₃ gas and gallium metal (99.9995% metals basis; Sigma Aldrich). Using a micromanipulator, single GaN nanowires were transferred onto silicon substrates with a 250-nm–thick thermal oxide layer. A 100-nm metal protection layer was then deposited on the samples by sputtering tungsten for 30 s with the shutter closed (for the purpose of cleaning the sputtering target), followed by 5 min with the shutter opened at 200 W DC in a 9-mtorr Ar environment. Protected nanowires were milled using a focused ion beam (FEI Stata 235 Dual Beam FIB), which defined the dimensions of the coupled cavities with gaps as narrow as 30 nm. Nanowires were milled using a Ga beam current of 10 pA, and the milling times for individual 1-μm-long cuts varied between 1 and 2 s, subject to the focusing conditions. The dwell time and percentage overlap for every cut was 1 μs and 99%, respectively. For maximum positional accuracy of the milling line with respect to the nanowire, a single Ga ion image was recorded at a scan speed of 0.3 s before cuts were made. Following milling, the protection layer was removed with hydrogen peroxide (30% w/w; Sigma Aldrich) at 80 °C for 7–10 min and then washed with deionized water. The micromanipulator was then used to remove excess nanowire pieces, leaving behind the completed cleaved-coupled nanowires.

Measurements of Lasing Spectra.

Optical measurements were performed using the frequency-quadrupled 266-nm output from a Nd:YAG laser (Spectra Physics; 8-ns pulse width, 10-Hz repetition rate). Using an iris diaphragm and a focusing lens, a 200-µm Gaussian beam spot was obtained and used to excite individual devices uniformly. The output power of the excitation source was adjusted using a Q-switch and monitored with an external energy meter and a photodetector (Newport 818J-09). Emission from nanowires was collected with a dark-field microscope objective (Nikon 50×, N.A. 0.55, in a Nikon ME600 optical microscope) and routed via a bundled optical fiber to a UV-visible spectroscopy spectrometer (Princeton Instruments/Acton) equipped with a 1,200-groove/mm grating blazed at 300 nm and a liquid N₂-cooled charge-coupled device. The comparison of the lasing properties between coupled and single nanowires in Fig. 1 was made with the same device by using the micromanipulator to separate the coupled nanowires.