Functioning of a metabolic flux sensor in Escherichia coli

Abstract

Regulation of metabolic operation in response to extracellular cues is crucial for cells’ survival. Next to the canonical nutrient sensors, which measure the concentration of nutrients, recently intracellular “metabolic flux” was proposed as a novel impetus for metabolic regulation. According to this concept, cells would have molecular systems (“flux sensors”) in place that regulate metabolism as a function of the actually occurring metabolic fluxes. Although this resembles an appealing concept, we have not had any experimental evidence for the existence of flux sensors and also we have not known how these flux sensors would work in detail. Here, we show experimental evidence that supports the hypothesis that Escherichia coli is indeed able to measure its glycolytic flux and uses this signal for metabolic regulation. Combining experiment and theory, we show how this flux-sensing function could emerge from an aggregate of several molecular mechanisms: First, the system of reactions of lower glycolysis and the feedforward activation of fructose-1,6-bisphosphate on pyruvate kinase translate flux information into the concentration of the metabolite fructose-1,6-bisphosphate. The interaction of this “flux-signaling metabolite” with the transcription factor Cra then leads to flux-dependent regulation. By responding to glycolytic flux, rather than to the concentration of individual carbon sources, the cell may minimize sensing and regulatory expenses.

Regulation of metabolic operation is crucial for cells’ survival. The canonical view is that this regulation occurs in response to extracellular cues, where, for instance, nutrient-specific transmembrane or intracellular receptors sense the presence of a nutrient and transfer respective commands to the regulatory machinery (1–5).

Recently, however, a novel impetus for metabolic regulation was proposed: cells could regulate their metabolism as a function of the actually occurring intracellular metabolic fluxes (6, 7). According to this concept, changes in extracellular nutrient abundances would first—in a rather passive manner—result in changes in intracellular metabolic fluxes. In a second instance, the metabolic fluxes would be sensed by molecular systems (“flux sensors”), which in turn would transmit the sensed “flux signal” to the regulatory machinery that consequently would adjust metabolic operation (6). On the basis of a detailed mathematical model of Escherichia coli’s central metabolism and its regulation, Kotte et al. suggested that this organism would have such flux sensors in place that establish a correlation between a metabolic flux and the concentration of certain so-called flux-signaling metabolites, which in turn affect the activity of transcription factors and thus would allow for transcriptional regulation in a flux-dependent manner.

Using intracellular flux to regulate metabolism is an appealing concept as it would omit the need for nutrient-specific sensors for many different nutrients, and would allow the integration of multiple nutrient inputs directly at the level of metabolism. Although it was shown in a synthetic system that such a flux-sensing could indeed work (8), there is currently no experimental evidence that Escherichia coli has flux-sensing systems and uses them for flux-dependent regulation.

Here, we provide experimental evidence for the existence of a flux sensor and flux-dependent regulation in Escherichia coli’s central metabolism. Specifically, we show that indeed glycolytic flux could be sensed by the interaction of the transcription factor Cra with the flux-signaling metabolite fructose-1,6-bisphosphate (FBP) and that this sensing mechanism is independent of the glycolytic carbon source used (as shown with a number of exemplary substrates). Furthermore, we decipher the molecular components of the supposed flux-sensing systems and unravel how flux information may be imprinted into certain metabolite concentrations. This work expands our view on Escherichia coli’s metabolism and its regulation.

Results

FBP is an intermediate of glycolysis and acts as an inhibitor of the transcription factor Cra (9), which is a known regulator of glycolytic and gluconeogenic genes in Escherichia coli (10–12) (Fig. 1A). Recently, Kotte et al. (6) suggested on the basis of a comprehensive modeling study of Escherichia coli’s central carbon metabolism and its regulation that the FBP–Cra interaction could be part of a flux sensor, which senses the metabolic flux through glycolysis. Here, we aimed at seeking experimental evidence for this computationally derived hypothesis.

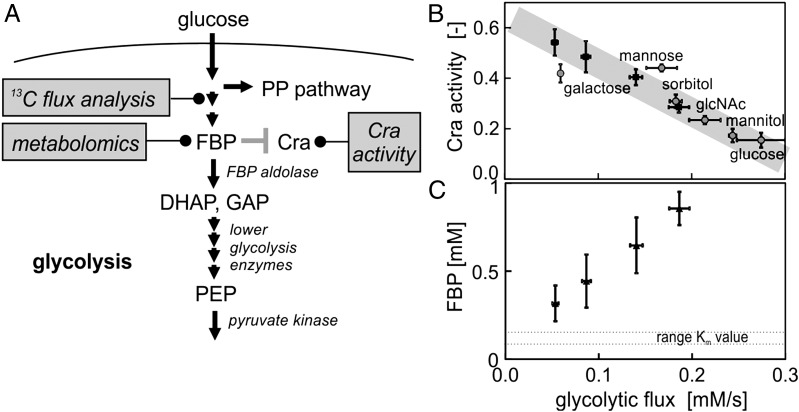
Fig. 1.

(A) Schematic illustration of the proposed flux sensor, its embedding in the glycolytic pathway, and the experimental methods used. (B) Cra activity as a function of glycolytic flux (at the FBP aldolase reaction) in glucose-limited chemostat cultures (black squares) and batch cultures (gray circles) with different carbon sources (glcNAc, N-acetylglucosamine). Cra activity is defined as the fraction of time that Cra spends bound to the promoter—in this case the pykF promoter, which is solely repressed by Cra (53). All substrates with the exception of galactose are substrates that are transported into the cell via the phosphotransferase system using phosphoenolpyruvate as cosubstrate. (C) FBP concentration as a function of glycolytic flux in glucose-limited chemostat cultures. All measurements were done in triplicate, and errors bars represent 1 SD.

In our quest to generate experimental evidence for the existence of this flux sensor, we first asked whether the transcription factor’s activity correlates with the glycolytic flux, which is an important requisite for the in vivo existence of a flux sensor. Indeed, when we experimentally perturbed the glycolytic flux through glucose-limited chemostat cultures (13) and used ¹³C-metabolic flux analysis (14, 15) to quantify the flux through glycolysis, we found that the Cra activity—inferred from GFP-based transcriptional reporter plasmids (16) (Materials and Methods)—correlates with the glycolytic flux (Fig. 1B). Next, we determined the FBP concentrations at the different glycolytic fluxes using a targeted metabolomics approach (17) and found a positive, linear correlation of this metabolite’s concentration with the glycolytic flux over a wide range of flux values (Fig. 1C), in agreement with what was observed earlier (18). Thus, our experimental findings are consistent with the notion that the activity of the transcription factor Cra is regulated via FBP in a flux-dependent manner, as predicted by Kotte et al. (6).

If Cra activity indeed is regulated in a glycolytic flux-dependent manner, then the flux sensor’s output (i.e., the Cra activity) should be independent of the type of glycolytic carbon source or the type of cultivation condition (i.e., substrate excess versus substrate limitation) used. To test this, we grew E. coli in batch cultures with various glycolytic carbon sources with different entry points into glycolysis, measured the respective glycolytic flux and Cra activity, and plotted these data together with the data obtained from the glucose-limited chemostat cultures. Here, we found that, for all tested conditions and substrates, the established glycolytic flux/Cra activity correlation holds (Fig. 1B). Note that, under all of the tested conditions, cells grow with different growth rates. Because the growth rate and the glycolytic flux correlate to some extent, we wanted to exclude that the correlation observed in Fig. 1B is a mere result of a growth rate effect and thus determined the Cra activity also on the gluconeogenic substrates acetate, pyruvate, and succinate. As the Cra activities measured for these additional substrates and those determined for the glycolytic substrates did not show a correlation with the growth rate, we could exclude that Cra acts as a reporter of growth rate. Taken together, the experimental evidence presented here, albeit fundamentally correlative in nature, strongly supports the hypothesis that the FBP–Cra pair is part of a flux-sensing system reporting the glycolytic flux.

Under the assumption that FBP indeed signals the magnitude of the glycolytic flux, we next wanted to elucidate the molecular system that translates flux information into the concentration of the flux-signaling metabolite FBP. We hypothesized that this “transfer function” would reside on the level of the kinetics of enzymes and their regulation. At first sight, it might be conceivable that the FBP-consuming fructose-1,6-bisphosphate aldolase (FBP aldolase) reaction establishes this transfer function. Establishing a linear transfer function between flux and FBP concentration would be possible if this enzyme were to follow an irreversible Michaelis–Menten kinetic and if the substrate concentration FBP would be much lower than the K_m for this substrate. However, neither is the aldolase reaction irreversible, nor are reported K_m values of the E. coli FBP aldolase (0.13–0.17 mM) (19–21) in the range of reported in vivo FBP concentrations (3–15 mM) (18, 22, 23).

Because the presumed flux-signaling metabolite FBP is consumed in a reaction with a reversible Michaelis–Menten kinetic, the FBP concentration is not only a function of the flux but also of the concentrations of the downstream products. Consequently, the cell could only use FBP to unequivocally infer the glycolytic flux, if it either also measures the reaction products glyceraldehyde 3-phosphate (GAP) and dihydroxyacetone phosphate (DHAP) as well or is able to somehow couple GAP and DHAP to the flux. Because DHAP- and GAP-binding transcription factors are not known in Escherichia coli, we focused on the second option and asked whether the product concentrations (GAP and DHAP) could be coupled to the flux in such a way that the FBP concentration would just depend on the flux.

The reactions in lower glycolysis following the FBP aldolase are all reversible reactions. Therefore, the concentration of a reversible reaction’s product can be replaced with another reversible Michaelis–Menten equation for the next reversible reaction and so forth until the next reaction is an irreversible one, which here is the case with the pyruvate kinase reaction. As the kinetics of irreversible reactions is only dependent on the substrate concentration, one can finally obtain an expression that makes the concentration of FBP only dependent on the metabolic flux through lower glycolysis.

If indeed the FBP concentration is coupled to lower glycolysis, then changing the abundances of enzymes of lower glycolysis should affect FBP concentration and thus Cra activity. To test this, we tuned pyruvate kinase I copy numbers below and above wild-type levels by expressing it in a pykF deletion strain from an isopropyl β-D-1-thiogalactopyranoside (IPTG)-inducible expression plasmid (24), and determined the activity of Cra and FBP levels. We found that Cra activity (Fig. 2B) and FBP concentration (Fig. S1) can indeed be influenced by changing the pyruvate kinase abundance demonstrating that reactions in lower glycolysis can have control over the FBP concentration.

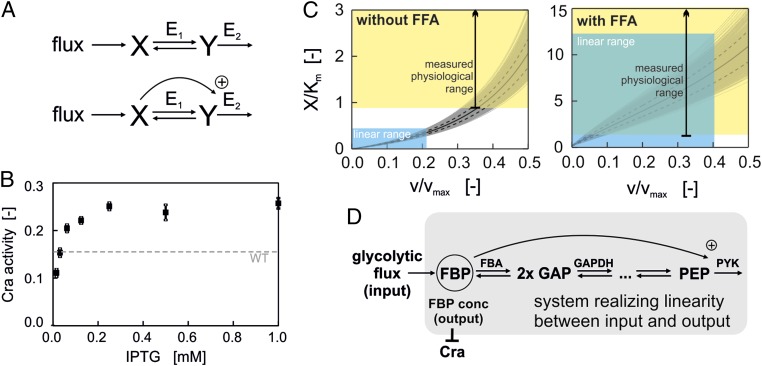
Fig. 2.

(A) (Upper) Structure of mathematical model without feedforward activation (FFA). E₁ is assumed to follow reversible Michaelis–Menten kinetics, and E₂ is assumed to follow irreversible Michaelis–Menten kinetics. (Lower) Structure of mathematical model with FFA of E₂ by X. E₁ is assumed to follow reversible Michaelis–Menten kinetics, and E₂ is assumed to follow MWC kinetics. (B) Cra activity as a function of IPTG concentration (used as a proxy for pyruvate kinase abundance) determined in glucose batch cultures of a pykF mutant strain bearing an IPTG-inducible PYK I expression plasmid (black squares). Dashed line, Cra activity in wild-type strain in glucose batch culture. (C) Simulation of model without (Left) or with (Right) FFA. Kinetic parameters: K_m = K_m.X.E1 = K_m.Y.E1 = K_m.Y.E2 = 0.2 mM; v_max = v_max.E1 = v_max.E2 = 1 mM/s; K_eq = 50; K_mA.X.E2 = 0.6 mM; L = 4·10⁶; n = 4. K_mA.X.E2, L, and n were used only for the model including FFA. The gray lines show the range of X when repeating the simulation 1,000 times while sampling the parameter values from a uniform distribution within 10% deviation of the original parameter values. The continuous black lines show the mean value of X across all simulations, and the dashed black lines show the corresponding SD. The blue areas are visual aids to highlight the approximate linear range of X. The yellow areas denote the range of physiological X/K_m ratios. The green shading indicates the area, where a linear relationship between X and v is possible at physiological X/K_m ranges. This is only the case for the system with the feedforward activation. (D) Structure of the flux sensing mechanism: Reversible reactions between FBP and PEP couple FBP to lower glycolysis, and the FFA of PYK by FBP is essential for establishing the linear correlation of FBP and glycolytic flux beyond the K_m value.

We next wanted to test whether the identified system (i) would be able to establish the observed linear correlation between flux (the system input) and FBP (the system output) over a wide range of glycolytic fluxes and (ii) whether this would also work for FBP concentrations above the K_m value of FBP aldolase, as was found experimentally (Fig. 1C). To test this, we developed a simple model, in which we lumped the reversible reactions between FBP and phosphoenolpyruvate (PEP) into one reversible Michaelis–Menten reaction. In the model, molecule X, resembling the flux-signaling metabolite FBP, is converted into one molecule of Y, resembling PEP, by an enzyme termed E₁. A second enzyme, termed E₂ and following irreversible Michaelis–Menten kinetics, converts Y to void, resembling the pyruvate kinase reaction (Fig. 2A, Upper). Note that, in contrast to the much more comprehensive model published previously (6), this simple model does not account for all possible transcriptional and posttranscriptional regulatory mechanisms. However, this simple model allows us to test hypotheses more directly by omitting potentially confounding variables. Further note that the simple model used here does not consider any fluxes to be drained off to biosynthesis or any flux to enter from the pentose phosphate pathway. As the biosynthetic fluxes are very low compared with the glycolytic flux and the back-flux from the pentose phosphate pathway scales with the glycolytic flux (25), we assume these omissions not to have an effect on our model predictions.

We solved the respective model equations (SI Text 1, Eq. S6) for X and found that linearity between X and the rate v (note, the rate v is equivalent the flux through the pathway) can be obtained if v << v_max: in this case, Eq. S6 simplifies to the following flux-dependent relationship between X and v:

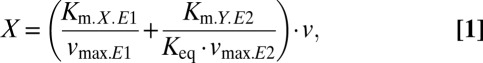with K_m.X.E1, K_m.Y.E1, and K_m.Y.E2 denoting the K_m values for X and Y of E₁ and for Y of E₂, respectively, K_eq describing the equilibrium constant of the reaction catalyzed by E₁, and v_max.E1 and v_max.E2, the maximal reaction rates of E₁ and E₂, respectively. With all values in the bracket of Eq. 1 being constants, this equation describes a linear relationship between the concentration of FBP (denoted as X) and the glycolytic flux v.

As noted above, in our experiments we found that the FBP concentration follows a linear trend with the glycolytic flux even at FBP concentrations that exceed the K_m value of the FBP aldolase (Fig. 1C). When considering in vivo relevant values for the kinetic parameters, the model shown in Eq. 1 cannot allow for a linear relationship at FBP concentrations that exceed the K_m value (i.e., X exceeding K_m.X.E1): First, the first term in Eq. 1 alone does not allow FBP to exceed the K_m value, because v/v_max.E1 is always <1 and thus the whole term is smaller than K_m.X.E1. Second, linearity could be reached if the second term is much larger than the first term, which would be possible if K_m.X.E1 << K_m.Y.E2 and K_eq << 1. However, the K_m values of the glycolytic enzymes are all very similar (in the submillimolar range) (26) and the K_eq values are around 1 or much larger than 1 (in the case of phosphoglycerate kinase) (26, 27). Thus, this model together with in vivo parameter values cannot explain the observed linearity between the glycolytic flux and FBP concentrations exceeding the FBP aldolase’s K_m values for FBP.

Thus, we asked whether the PEP-consuming enzyme pyruvate kinase I (PYK I)—the main pyruvate kinase in Escherichia coli—and in particular its allosteric activation by FBP (28, 29) could play a role in establishing the flux/FBP linearity beyond the FBP aldolase’s K_m value of FBP. This feedforward activation was found to ensure the structural robustness of glycolysis against perturbations (27, 30, 31). To test this hypothesis, we developed a variant of the model described above, which includes the allosteric activation of E₂ by X (Fig. 2A, Lower; see SI Text 2 for the model equation) using Monod–Wyman–Changeux (MWC) kinetics in accordance to previous studies on pyruvate kinase (30, 32, 33). With this model, we tested whether the additional feedforward activation affects the linearization of X beyond the K_m value.

We solved this augmented model numerically using kinetic parameters in the same range as the reported kinetic parameters of the enzymes of glycolysis (26) (refer to the caption of Fig. 2C for parameter values). Note that in all cases we assumed that the v_max values are constant and do not depend on v, which corresponds to constant enzyme concentrations across different glycolytic fluxes. We validated this assumption through targeted proteomics experiments, in which we determined the absolute concentrations of the proteins of lower glycolysis. Here, we found that these concentrations are remarkably constant across environmental conditions (Fig. S2). The results of our simulations demonstrate that, when including the feedforward activation, X shows a linear correlation with the flux v also at concentrations of X exceeding the K_m.X.E1 value (Fig. 2C, Right). In contrast, the numerical solution of the model lacking the feedforward activation only yielded a linear correlation of X and v below K_m.X.E1 (Fig. 2C, Left), in accordance to the analytical solution described above. Remarkably, the system with the feedforward activation can also establish the linearity at flux values closer to v_max (Fig. 2C, Right), which was not possible with the systems lacking the feedforward activation, making the system with the feedforward activation even more efficient in terms of enzyme costs.

Interestingly, several enzymes around the presumed flux-signaling metabolite FBP are repressed by Cra (12), raising the question how these enzyme levels could be constant across conditions (Fig. S2). Counterintuitively, it may precisely be this Cra repression that keeps these enzyme levels constant: It was recently shown that with increasing growth rate the concentration of constitutively expressed (=nonregulated) proteins decreases (34). The same study further showed that transcriptional repression is able to keep a protein’s concentration constant across different growth rates. Thus, the Cra-mediated transcriptional repression of enzymes around the flux-signaling metabolite FBP may in fact ensure constant protein concentrations and only thereby turn the proposed system into a faithful flux-sensing system that is independent from growth rate effects.

Overall, our results suggest one potential mechanism, by which cells could translate glycolytic flux into the concentration of FBP. This mechanism is not governed by a single reaction, but rather emerges as a property of the system constituted of the enzyme reactions of lower glycolysis with their specific kinetics and regulation (Fig. 2D): (i) the reversible glycolytic reactions from FBP aldolase down to enolase, (ii) the irreversible PEP-consuming reaction, and (iii) the feedforward activation of the pyruvate kinase by FBP, which is essential to allow a linear correlation between FBP and flux over a wide range of FBP concentrations and beyond the K_m value of FBP for FBP aldolase. We consider the aggregate of this system—together with the interaction of the flux-signaling metabolite FBP with the transcription factor Cra—a flux sensor system.

Discussion

In this work, we showed that glycolytic flux may be sensed by Escherichia coli and used as a control variable for transcriptional regulation. The flux-dependent transcriptional regulation output is not restricted to glucose but shows the same behavior with other glycolytic carbon sources. Our findings suggest that flux information is imprinted into the concentration of FBP via a system of enzymatic reactions in lower glycolysis including feedforward activation for linearization of the relationship of FBP and flux beyond the K_m value. Analogously, also in technical systems feedforward activations are used to linearize input–output relationship; e.g., feedforward loops are incorporated into power amplifiers of electrical circuits to sense the magnitude of an input and to respond accordingly (35). Furthermore, the flux information in the form of the FBP concentration is then being read out by the transcription factor Cra. The integrated function of the above-described mechanisms (the enzyme reactions and their kinetics and allosteric regulation, the FBP/Cra interaction) forms then the emerging function of a flux sensor.

If this is generally true, why would have Escherichia coli evolved a flux-sensing mechanism? Next to regulating metabolism in response to signals from nutrient-specific receptors, intracellular flux sensing represents an alternative way to get informed about environmental changes. As E. coli can grow on many different carbon sources with computational predictions mentioning numbers of up to 180 growth-sustaining carbon sources (36), relying on dedicated nutrient-specific receptors to sense the environment would require the simultaneous expression of a large number of receptors imposing a large burden on the cell. Instead, the intracellular flux-sensing concept moves the measurement into cellular metabolism, and with the sensor described here, even into core central metabolism. Considering that metabolic networks have a bow tie architecture (37), this means that measuring at the center of the bow tie (i.e., core metabolism) with flux sensors seems particularly attractive: in this way, the integration of signals from different receptors is not necessary as the metabolic flux emerging from simultaneous metabolizing of different present carbon sources already provides an integrated “signal.” Last, flux-sensing mechanisms can be integrated into regulatory control circuits: a nutrient flows into a cell and realizes a metabolic flux that is being measured and used for regulation of protein expression, which (in the case of enzymes) will in turn influence flux, overall resulting in robust control loops.

Although in this work we provide extensive evidence for the existence of a flux sensor in E. coli and its functioning, we stress that the flux-sensing function is an emergent property and as such cannot be proven in the strict sense. We hope that future studies by us and others can provide additional support for the hypothesis put forward in this work. Notably, there is indication that flux-sensing mechanisms might also be present in other organisms: recently, it was reported that the budding yeast Saccharomyces cerevisiae shows a similar relationship between the glycolytic flux and FBP (7, 38) and also its pyruvate kinase is feedforward activated by FBP (39). Thus, our findings are likely relevant also for other organisms.

Materials and Methods

Strains and Media.

The Escherichia coli K-12 strain BW25113 was used in all experiments. The pykF gene deletion was transferred to the wild-type strain by P1 phage transduction (40) from the corresponding deletion strain of the Keio collection (41) to yield the pykF mutant strain. The mutant was then cured from its kanamycin resistance as described previously (42) and transformed with an IPTG-inducible PYK I expression plasmid obtained from ref. 24. A GFP-based transcriptional reporter plasmid containing the pykF promoter was obtained from ref. 16, and a deregulated version of this reporter plasmid—in which the Cra binding site (CTTGAATGGTTTCAGC) was removed by introduction of a randomized sequence with the same length (TCAGGATATGTGGCGG)—was constructed by PCR following the protocols of the original study (16).

M9 minimal medium was used in the growth experiments and was prepared as follows: to 700 mL of purified and autoclaved water, 200 mL of 5× base salt solution [211 mM Na₂HPO₄, 110 mM KH₂PO₄, 42.8 mM NaCl, 56.7 mM (NH₄)₂SO₄, autoclaved], 10 mL of trace elements (0.63 mM ZnSO₄, 0.7 mM CuCl₂, 0.71 mM MnSO₄, 0.76 mM CoCl₂, autoclaved), 1 mL 0.1 M CaCl₂ solution (autoclaved), 1 mL of 1 M MgSO₄ solution (autoclaved), 2 mL of 500× thiamine solution (1.4 mM, filter sterilized), and 0.6 mL of 0.1 M FeCl₃ solution (filter sterilized) were added. The resulting solution was filled up to 1 L with water. Carbon sources were added from sterilized stock solutions (adjusted to pH 7) to a final concentration of 1 g/L for chemostat experiments and 5 g/L for batch experiments, and media were filtered (Steritop-GP; 500 mL; Millipore). All chemicals were purchased from Sigma-Aldrich unless stated otherwise.

Chemostat and Batch Cultivations.

Cultivation of glucose-limited chemostats was performed as described previously (13, 43). Briefly, eight parallel reactors with M9 glucose medium (1 g/L) were inoculated with an overnight M9 glucose culture to a starting OD₆₀₀ of 0.1 and then incubated for 4 h at 37 °C (in a water bath) with aeration. After 4 h, the feeding pump was started (feeding solution: M9 glucose medium with 1 g/L glucose).

Batch cultivation was performed in a 96-well format: deep-well plates (Kühner AG) containing M9 medium were inoculated 1:50 with LB precultures and incubated overnight at 37 °C with shaking. For experiments involving the IPTG-inducible PYK I expression plasmids, IPTG was added to the M9 overnight cultures to the same concentration as in the main culture. Subsequently, 96-well flat transparent plates (Nunc) containing M9 medium (fill volume, 200 µL) were inoculated 1:200 with the overnight cultures and sealed with parafilm to reduce evaporation. Dynamic measurements of OD₆₀₀ and fluorescence (excitation wavelength, 500 nm; emission wavelength, 530 nm) were performed at 37 °C with shaking using a plate reader (TECAN infinite M200, Tecan Group) at 10-min intervals.

Metabolomics.

From the chemostat cultures, 1 mL of cell suspension was withdrawn with a 5-mL syringe filled with 4 mL of −40 °C quenching solution [60% (vol/vol) methanol, 40% (vol/vol) deionized water, and 10 mM CuCl₂] and transferred to a 15-mL centrifugation tube. After a centrifugation step (5,000 × g, −20 °C, 4 min), the supernatant was discarded, and the cell pellet was frozen in liquid nitrogen. Afterward, samples were extracted three times by adding 500 μL of 78 °C hot extraction solution containing 60% (vol/vol) ethanol and 40% (vol/vol) deionized water and incubating at 78 °C for 1 min. Each extraction step was followed by centrifugation (14,000 × g, room temperature, 30 s), and the supernatant was collected in a 2-mL tube. Before the first extraction, 50 μL of fully ¹³C-labeled yeast cell extract was added to the sample as an internal standard to correct for matrix effects during the measurement. After the last extraction, samples were dried at 120 μbar (Christ RVC 2-33 CD centrifuge and Christ Alpha 2-4 CD freeze dryer) and stored at −80 °C. Before the measurement, dried samples were resuspended in 50 μL of water, of which 12.5 μL were transferred to 350-μL HPLC vials and sealed with rubber caps. Measurement, data acquisition, and data analysis was performed as described previously (17). Briefly, separation of compounds was achieved by ion-pairing ultrahigh performance liquid chromatography (UPLC) using a Waters Acquity UPLC with a Waters Acquity T3 end-capped reverse phase column (dimensions, 150 mm × 2.1 mm × 1.8 μm; Waters Corporation), followed by compound detection using a tandem mass spectrometer (Thermo TSQ Quantum Ultra triple quadrupole; Thermo Fisher Scientific). Data acquisition and peak integration were performed with in-house software. To determine the absolute concentration of metabolites, a 1:3 dilution series of a standard solution (containing more than 80 metabolites of the central carbon metabolism) with ¹³C internal standard was prepared and measured in parallel.

¹³C Flux Analysis.

Chemostat experiments were performed as described above using 1 g/L [1-¹³C]-labeled glucose (>99%; Cambridge Isotope Laboratories). After six volume changes, 1 mL was withdrawn from each reactor using a syringe with a sterile needle and transferred to a 2-mL tube. After a centrifugation step (14,000 × g, 4 °C, 2 min), supernatants were transferred to 2-mL tubes. Cell pellets and supernatants were stored at −20 °C. Sample preparation was performed as described previously (13, 44, 45). Briefly, cell pellets were hydrolyzed in 6 M HCl at 105 °C for 24 h in sealed 2-mL tubes and subsequently dried at 60 °C in a heating block under a stream of air. The dried hydrolysates were derivatized at 85 °C in 20 μL of dimethylformamide (Fluka) and 20 μL N-(tert-butyldimethylsilyl)-N-methyl-trifluoroacetamide with 1% (vol/vol) tert-butyldimethylchlorosilane (Fluka) for 60 min. Derivatized amino acids were analyzed on a 6890N gas chromatograph (Agilent Technologies) combined with a 5973 Inert SL mass spectrometer (Agilent Technologies). The GC-MS–derived mass isotope distributions of proteinogenic amino acids were then corrected for naturally occurring isotopes (46), and the flux ratio of glycolysis to pentose phosphate pathway (as serine derived through glycolysis) was calculated with FiatFlux software (15). To calculate the absolute glycolytic flux, glucose uptake rates were calculated converting OD₆₀₀ into cellular volume according to a recent publication (47) and then multiplied with the flux ratio obtained above, assuming no residual glucose as was found by others (13).

Batch experiments were performed as described previously (14, 44) using 5 g/L [1-¹³C]-labeled glucose and galactose (>99%; Cambridge Isotope Laboratories), as well as 5 g/L [1-¹³C]-labeled mannose, sorbitol (>99%; CortecNet), mannitol (>99%, Sigma), or N-acetylglucosamine (>99%; Omicron Biochemicals). Briefly, 500-mL shake flasks with 30 mL of M9 medium containing the respective labeled carbon source were inoculated to a starting OD₆₀₀ of 0.05 with WT overnight cultures with the same medium and incubated at 37 °C with shaking (300 min⁻¹). Aliquots of 1 mL were harvested at an OD₆₀₀ of 1 by centrifugation (14,000 × g, 4 °C, 2 min), and sample processing and analysis of cell pellets was performed as described above, yielding the flux ratio of glycolysis to pentose phosphate pathway. One-milliliter supernatant aliquots were harvested by centrifugation (14,000 × g, 2 min) during exponential growth and analyzed with a HPX-87H Aminex, ion-exclusion column (Bio-Rad) on a HPLC HP1100 system (Agilent Technologies) as described previously (48, 49), and used to calculate carbon uptake rates converting OD₆₀₀ into cellular volume as described above. Absolute glycolytic fluxes were calculated by multiplying the carbon uptake rate with the flux ratio of glycolysis to pentose phosphate pathway.

Determination of Cra Activity.

Cra activity is defined as the fraction of time Cra spends bound to the promoter and was calculated as 1 − pa_{pykF.regulated}/pa_{pykF.deregulated} based on previous studies (50). pa_{pykF.regulated} and pa_{pykF.deregulated} denote the promoter activity for the regulated pykF promoter (16) and the deregulated pykF promoter (in which the Cra binding site was removed as described above), respectively. Promoter activities for batch cultures were calculated as dGFP/dt/OD during exponential growth. For chemostat cultures, samples were withdrawn after five volume changes, and OD and GFP fluorescence (excitation, 500 nm; emission, 530 nm) were measured using a plate reader (TECAN Infinite M200; Tecan Group). Promoter activity was then calculated as D·GFP/OD, where D denotes the dilution rate. Correction for background fluorescence for batch and chemostat cultures was performed using a strain bearing a promoterless GFP reporter plasmid taken from ref. 19.

Targeted Mass-Spectrometric Analysis of Protein Abundances.

In the initial discovery phase (identification), whole-cell protein extracts were enzymatically digested using trypsin and aliquots of 1 μg analyzed on an Orbitrap LC-MS platform (Thermo Fisher Scientific) to identify and select proteotypic peptides for targeted MS assay development. In the scoring phase (quantification), proteins of interest were quantified from digested cell lysates (1 μg per analysis) across all samples using selected reaction monitoring and spiked in heavy labeled reference peptides on a Vantage LC-MS platform (Thermo Fisher Scientific) as previously described (51, 52). Condition-dependent intracellular volumes were taken from a recent publication (47).

Mathematical Modeling.

Mathematical modeling was performed with MATLAB (version 2010a; Mathworks). Model equations were solved numerically for X and Y with the function fsolve. The number of maximal iterations was set to 10,000. The function fsolve requires initial guesses for X and Y, which were generated randomly with the function randn. Parameter vectors were sampled 1,000 times from a uniform distribution within 10% deviation of the original parameter values.