Abstract
When you reach with your straw for the final drops of a milkshake, the liquid forms a train of plugs that flow slowly initially because of the high viscosity. They then suddenly rupture and are replaced with a rapid airflow with the characteristic slurping sound. Trains of liquid plugs also are observed in complex geometries, such as porous media during petroleum extraction, in microfluidic two-phase flows, or in flows in the pulmonary airway tree under pathological conditions. The dynamics of rupture events in these geometries play the dominant role in the spatial distribution of the flow and in determining how much of the medium remains occluded. Here we show that the flow of a train of plugs in a straight channel is always unstable to breaking through a cascade of ruptures. Collective effects considerably modify the rupture dynamics of plug trains: Interactions among nearest neighbors take place through the wetting films and slow down the cascade, whereas global interactions, through the total resistance to flow of the train, accelerate the dynamics after each plug rupture. In a branching tree of microchannels, similar cascades occur along paths that connect the input to a particular output. This divides the initial tree into several independent subnetworks, which then evolve independently of one another. The spatiotemporal distribution of the cascades is random, owing to strong sensitivity to the plug divisions at the bifurcations.
Keywords: microfluidics, respiratory flow
The motion of liquid plugs through a connected network of channels may involve many degrees of freedom evolving via a similarly large number of interactions: each immiscible interface introduces a degree of freedom into the problem owing to its ability to deform and to move, whereas each connecting branch between different areas introduces an interaction path that allows the flow in one region to influence the behavior in other areas of the network. The resulting flow pattern determines, among other things, how water or oil is extracted from porous media (1–3), the imbibition of paper (4, 5), and the stability of flow in a microfluidic device (6, 7).
Liquid–gas two-phase flows also occur in the pulmonary airway tree, which is constantly coated with a thin liquid film. When the thickness of this film increases beyond some limit, plugs of liquid may form (8, 9) and therefore occlude the flow of air to the distal branches. Evidence of such behavior has been observed in pathologies ranging from asthma (10, 11) to cystic fibrosis (12). Furthermore, liquid plugs may be used as means to deliver medical treatment into the lung, e.g., in surfactant replacement therapy (13), and these plugs were observed to go through complex divisions, breaking and reforming before reaching their intended target (14).
The structure of the lung as a branching binary tree has motivated many studies on the motion of gas–liquid flows into bifurcating channels (15–20), with numerical work also taking into account the elasticity of the pulmonary walls, (e.g refs. 21 and 22). However, nearly all the model experiments and simulations have considered the simplest situations, either studying the motion of a single liquid plug or gas finger or concentrating on the flow through a single bifurcation, or both. This reduces the number of independent degrees of freedom and, by the same token, the range of behaviors those models can explore.
These studies therefore cannot account for complex interactions that involve many levels in the tree, which are observed in the real lung. Indeed, experiments on animal lungs have shown that multilevel interactions are primordial during the reinflation of a collapsed lung. Alencar et al. (23, 24) reported that reopening takes place through an avalanche of events in which distinct regions are reopened in nearly singular bursts. However, ex vivo observations of the spatial behavior during reinflation are prohibitively complex, therefore limiting the comparison between the experiments and the theoretical models to measurements at the root of the tree (25).
Here we study the flow and rupture of liquid plugs that initially occlude microfluidic channels, as they are submitted to an imposed pressure head. Our experiments are conducted in microfluidic systems consisting of a straight channel or a branching network of channels, formed in a polydimethylsiloxane (PDMS) substrate using conventional soft lithography techniques. We show that the dynamics of a train of plugs differ from those of a single occlusion because the plugs interact via both short- and long-range mechanisms. The physics underlying plug interactions are first deduced from the reopening of a single straight channel, by comparing experimental measurements with the results of a one-dimensional analytical model. Experiments in a branching tree are then performed, showing the existence of cascades of ruptures that occur along well-defined paths through purely hydrodynamic effects.
Collective Behavior of Plugs in a Straight Channel
Single-Plug Behavior.
When a single plug of length  is pushed at constant pressure in a channel of width w and height h, it rapidly reaches a velocity
is pushed at constant pressure in a channel of width w and height h, it rapidly reaches a velocity  that depends on its initial resistance to flow. In its wake, it leaves a liquid film that remains at rest on the channel wall. This implies a shortening of the plug, which ruptures when its length
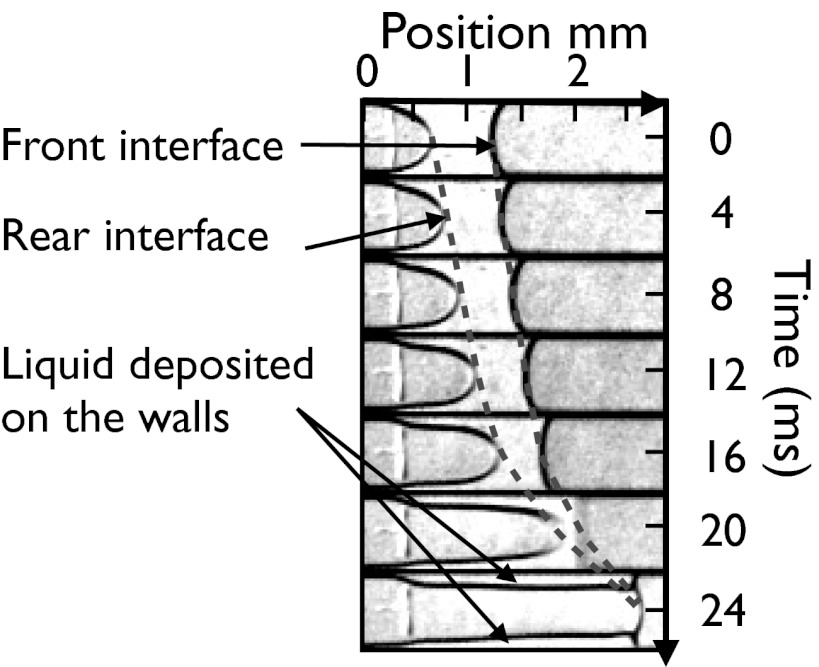
that depends on its initial resistance to flow. In its wake, it leaves a liquid film that remains at rest on the channel wall. This implies a shortening of the plug, which ruptures when its length  reaches zero. The airway then is opened in the sense that the flow of air becomes limited only by the viscous resistance of the gas. An example of such behavior is shown in Fig. 1, which displays snapshots of the experiment, taken at constant time intervals (see also Movie S1). The positions of the rear and front interfaces in each frame are located and interpolated to form two curves whose horizontal distance gives the length
reaches zero. The airway then is opened in the sense that the flow of air becomes limited only by the viscous resistance of the gas. An example of such behavior is shown in Fig. 1, which displays snapshots of the experiment, taken at constant time intervals (see also Movie S1). The positions of the rear and front interfaces in each frame are located and interpolated to form two curves whose horizontal distance gives the length 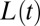 of the plug. The velocity
of the plug. The velocity 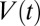 is given by the slope of the curve for the rear interface. In this experiment, the velocity of the plug varies from 3 cm/s when the pressure head is applied to 28 cm/s when the plug ruptures. This acceleration generates an increase of the thickness of the liquid film left behind the plug and a subsequent rapid decrease of its length, leading to rupture after 24 ms.
is given by the slope of the curve for the rear interface. In this experiment, the velocity of the plug varies from 3 cm/s when the pressure head is applied to 28 cm/s when the plug ruptures. This acceleration generates an increase of the thickness of the liquid film left behind the plug and a subsequent rapid decrease of its length, leading to rupture after 24 ms.
Fig. 1.
Spatiotemporal evolution of a single plug of initial length 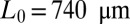 pushed at constant pressure head 2 kPa. The montage is produced by stacking snapshots of the channel taken every 4 ms on top of one another. The liquid appears bright and the air dark. The dashed lines show the positions of the front and rear interfaces as functions of time.
pushed at constant pressure head 2 kPa. The montage is produced by stacking snapshots of the channel taken every 4 ms on top of one another. The liquid appears bright and the air dark. The dashed lines show the positions of the front and rear interfaces as functions of time.
The dynamics of this plug can be understood by introducing an Ohm-like law for the pressure vs. velocity (18, 26), 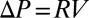 , where
, where 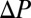 is the pressure head. The velocity V of the rear interface is a measure of the flow rate, and R is the resistance due to the presence of the liquid in the channel. This resistance is the sum of capillary contributions
is the pressure head. The velocity V of the rear interface is a measure of the flow rate, and R is the resistance due to the presence of the liquid in the channel. This resistance is the sum of capillary contributions 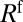 and
and 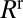 of the front (“f”’) and rear (“r”) interfaces, and a bulk viscous resistance
of the front (“f”’) and rear (“r”) interfaces, and a bulk viscous resistance 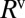 . Resistances
. Resistances 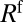 and
and 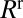 are a result of the deformation of the two interfaces from their rest shape in response to the large velocity gradients in the corners of the moving liquid bridge, and they depend nonlinearly on
are a result of the deformation of the two interfaces from their rest shape in response to the large velocity gradients in the corners of the moving liquid bridge, and they depend nonlinearly on 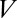 . At low capillary number
. At low capillary number 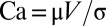 , where μ is the viscosity of the liquid and σ its surface tension, one gets
, where μ is the viscosity of the liquid and σ its surface tension, one gets 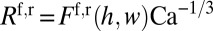 . The explicit expressions of
. The explicit expressions of 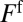 and
and 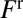 are obtained, respectively, from the Hoffman–Tanner law (27, 28) and the Bretherton law (29) adapted to rectangular channels (30). In turn, the bulk resistance of a long-enough plug can be estimated by modeling the flow inside it as a Poiseuille flow in a rectangular channel:
are obtained, respectively, from the Hoffman–Tanner law (27, 28) and the Bretherton law (29) adapted to rectangular channels (30). In turn, the bulk resistance of a long-enough plug can be estimated by modeling the flow inside it as a Poiseuille flow in a rectangular channel: 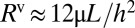 for large aspect ratio
for large aspect ratio 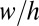 (31). The relation between pressure head and speed has been validated experimentally by Ody et al. (18).
(31). The relation between pressure head and speed has been validated experimentally by Ody et al. (18).
The model describing the plug dynamics is closed with an equation for 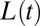 that accounts for the liquid left in the stationary films on the sidewalls. Bretherton’s law (29) provides a way to estimate this thickness for flow at small Ca in circular tubes. We rely for this on the empirical law proposed by Aussillous and Quéré (32) for circular tubes, as extended to channels of rectangular cross-section and larger Ca by de Lózar et al. (33), which we introduce in the mass balance equation for the liquid phase: Let
that accounts for the liquid left in the stationary films on the sidewalls. Bretherton’s law (29) provides a way to estimate this thickness for flow at small Ca in circular tubes. We rely for this on the empirical law proposed by Aussillous and Quéré (32) for circular tubes, as extended to channels of rectangular cross-section and larger Ca by de Lózar et al. (33), which we introduce in the mass balance equation for the liquid phase: Let 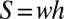 be the area of the channel cross-section and
be the area of the channel cross-section and 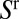 and
and 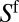 the areas of the lumens open to air behind the plug and ahead of it, respectively. During a time interval
the areas of the lumens open to air behind the plug and ahead of it, respectively. During a time interval 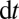 , the advancing plug absorbs a volume
, the advancing plug absorbs a volume 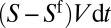 at its front interface, where V is the velocity. The volume left behind is
at its front interface, where V is the velocity. The volume left behind is 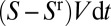 and the variation of the plug’s volume
and the variation of the plug’s volume 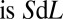 , so the balance reads
, so the balance reads 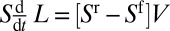 .
.
Whereas 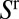 is a function of V as recalled above,
is a function of V as recalled above, 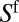 reflects the thickness of the film present ahead of the plug at the considered time. In particular,
reflects the thickness of the film present ahead of the plug at the considered time. In particular, 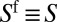 when the plug is moving along a dry channel. Details on the model, its derivation, and its numerical simulation are given in SI Text.
when the plug is moving along a dry channel. Details on the model, its derivation, and its numerical simulation are given in SI Text.
The dynamics of a single plug therefore may be understood with the model ingredients described above: When the pressure 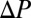 is applied, the plug starts moving at a velocity fixed by its initial length and physical parameters. The length then progressively decreases because of liquid deposition, thus lowering the viscous resistance
is applied, the plug starts moving at a velocity fixed by its initial length and physical parameters. The length then progressively decreases because of liquid deposition, thus lowering the viscous resistance 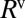 so that the plug accelerates. The interfacial resistance scales as
so that the plug accelerates. The interfacial resistance scales as 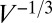 and therefore also decreases, contributing further to the velocity increase. Finally, when the length of the plug approaches zero, it ruptures. A similar behavior has been observed by Fujioka et al. (34) through direct numerical simulations of the flow field inside a moving plug.
and therefore also decreases, contributing further to the velocity increase. Finally, when the length of the plug approaches zero, it ruptures. A similar behavior has been observed by Fujioka et al. (34) through direct numerical simulations of the flow field inside a moving plug.
Multiple-Plug Behavior.
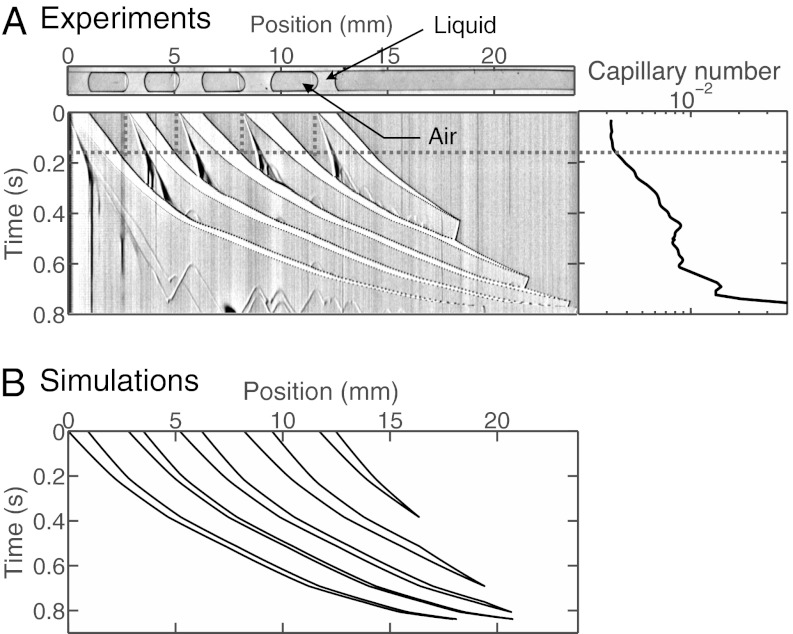
The evolution of a set of 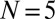 plugs, forced at constant pressure head 2 kPa, is depicted in the spatiotemporal graph of Fig. 2A (see also Movie S2). The plugs are initially distributed as shown in the top image and start advancing when the pressure head is applied at
plugs, forced at constant pressure head 2 kPa, is depicted in the spatiotemporal graph of Fig. 2A (see also Movie S2). The plugs are initially distributed as shown in the top image and start advancing when the pressure head is applied at 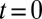 . Plugs are numbered from right to left, beginning with the most advanced one. The distance
. Plugs are numbered from right to left, beginning with the most advanced one. The distance 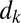 between the rear interface of plug k and the rear interface of plug
between the rear interface of plug k and the rear interface of plug 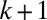 remains nearly constant because the air compressibility is negligible at these pressures. As a consequence, all plugs move at the same velocity
remains nearly constant because the air compressibility is negligible at these pressures. As a consequence, all plugs move at the same velocity 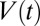 and the behavior of the plug train may be characterized by a single capillary number, which is plotted in Fig. 2A, Right. We observe that Ca stays constant up until
and the behavior of the plug train may be characterized by a single capillary number, which is plotted in Fig. 2A, Right. We observe that Ca stays constant up until 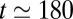 ms, then increases up to the time when plug 1 ruptures at
ms, then increases up to the time when plug 1 ruptures at 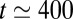 ms, then more irregularly until
ms, then more irregularly until 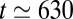 ms (rupture of plug 2), and finally diverges around
ms (rupture of plug 2), and finally diverges around 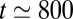 ms, when plugs 3–5 break nearly simultaneously.
ms, when plugs 3–5 break nearly simultaneously.
Fig. 2.
Dynamics of a set of equally spaced monodisperse plugs. The initial length of the plugs is 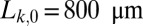 , and the distance separating two adjacent plugs is
, and the distance separating two adjacent plugs is 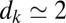 mm. The whole train is pushed at constant pressure head 2.0 kPa. (A) Image corresponding to the experiment. (Upper) Initial plug configuration; liquid (air) appears light (dark) gray. (Lower) Spatiotemporal diagram displaying the gray values along the center line of the channel as a function of time. Velocities and lengths of the plugs are obtained from the slopes of the boundaries and the distances between them, respectively. The gray dashed line indicates the moment when the plugs reach the initial position of their immediate predecessor. (Right) Capillary number of the plug train as a function of time. (B) Spatiotemporal diagram obtained numerically from the model for the same conditions as in A.
mm. The whole train is pushed at constant pressure head 2.0 kPa. (A) Image corresponding to the experiment. (Upper) Initial plug configuration; liquid (air) appears light (dark) gray. (Lower) Spatiotemporal diagram displaying the gray values along the center line of the channel as a function of time. Velocities and lengths of the plugs are obtained from the slopes of the boundaries and the distances between them, respectively. The gray dashed line indicates the moment when the plugs reach the initial position of their immediate predecessor. (Right) Capillary number of the plug train as a function of time. (B) Spatiotemporal diagram obtained numerically from the model for the same conditions as in A.
Examination of this cascade leads us to identify two plug interaction mechanisms: Long range effects arise from the superpositions of resistances within the plug train, whereas short range interactions take place between nearest neighbors via the wetting film. Indeed, plug k gains some fluid left behind by plug 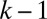 and leaves some fluid, which is taken up by plug
and leaves some fluid, which is taken up by plug 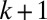 . Because the film thickness depends on the instantaneous capillary number (see SI Text for discussion), the balance between the liquid intake and deposition generates plug length variations when the two layers have different thicknesses. When the train of plugs is forced at a constant velocity—for example, by using a syringe pump—the thickness of the liquid films between the plugs remains constant, so the plugs (except plug 1) always lose as much liquid as they gain and thus keep their initial length. When the plugs are pushed at constant pressure, as in Fig. 2, their velocity changes, leading to variations in the film thickness. These variations couple back with the resistance to flow and velocities in two ways, as discussed below.
. Because the film thickness depends on the instantaneous capillary number (see SI Text for discussion), the balance between the liquid intake and deposition generates plug length variations when the two layers have different thicknesses. When the train of plugs is forced at a constant velocity—for example, by using a syringe pump—the thickness of the liquid films between the plugs remains constant, so the plugs (except plug 1) always lose as much liquid as they gain and thus keep their initial length. When the plugs are pushed at constant pressure, as in Fig. 2, their velocity changes, leading to variations in the film thickness. These variations couple back with the resistance to flow and velocities in two ways, as discussed below.
First, the resistance 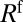 associated with the displacement of the front interface decreases as the thickness of the precursor film increases. This has been demonstrated experimentally (26) and justified theoretically (35) for a single plug in a prewetted channel. In our experiment, the thickness of the film left behind a plug may display large changes, as seen in Fig. 1, which generates resistance variations for the following plug. In a train of plugs, the capillary number of a plug affects the next one with a delay equal to the time required to cover the distance that separates them. So when plug k arrives at the position initially occupied by plug
associated with the displacement of the front interface decreases as the thickness of the precursor film increases. This has been demonstrated experimentally (26) and justified theoretically (35) for a single plug in a prewetted channel. In our experiment, the thickness of the film left behind a plug may display large changes, as seen in Fig. 1, which generates resistance variations for the following plug. In a train of plugs, the capillary number of a plug affects the next one with a delay equal to the time required to cover the distance that separates them. So when plug k arrives at the position initially occupied by plug 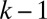 , it encounters a thicker film that decreases the resistance of its front interface and leads to an increase in velocity. This sudden acceleration is observed at
, it encounters a thicker film that decreases the resistance of its front interface and leads to an increase in velocity. This sudden acceleration is observed at 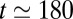 ms, as marked by the dotted horizontal line in Fig. 2A. The second way in which neighboring plugs interact is via the mass balance. Like the lubrication effect, this takes place with a delay because the plugs are traveling at finite speed. Liquid exchange tends to lengthen the cascade duration because the fluid taken up by a plug increases its length. The two short-range effects therefore are antagonistic.
ms, as marked by the dotted horizontal line in Fig. 2A. The second way in which neighboring plugs interact is via the mass balance. Like the lubrication effect, this takes place with a delay because the plugs are traveling at finite speed. Liquid exchange tends to lengthen the cascade duration because the fluid taken up by a plug increases its length. The two short-range effects therefore are antagonistic.
Using an analogy with electrical circuits, the train of plugs submitted to a constant pressure head 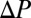 may be viewed as a series of resistors and the total resistance as the sum of the individual resistances. Therefore, rupture of plug k leads to long-range effects because it corresponds to a sudden drop to zero of the corresponding resistance. Consequently, the speed of the remaining plugs suddenly increases, further hastening the deposition of the wetting film and inducing new ruptures. This catastrophic speeding-up is at the origin of the cascade observed in our experiments. It is easier to observe when the initial distribution of plugs is irregular and their size polydisperse. An example is shown in Fig. S1, in which a train of 10 plugs is pushed at constant pressure head (see also Movie S3). The evolution of the train is dominated mainly by short-range interactions until
may be viewed as a series of resistors and the total resistance as the sum of the individual resistances. Therefore, rupture of plug k leads to long-range effects because it corresponds to a sudden drop to zero of the corresponding resistance. Consequently, the speed of the remaining plugs suddenly increases, further hastening the deposition of the wetting film and inducing new ruptures. This catastrophic speeding-up is at the origin of the cascade observed in our experiments. It is easier to observe when the initial distribution of plugs is irregular and their size polydisperse. An example is shown in Fig. S1, in which a train of 10 plugs is pushed at constant pressure head (see also Movie S3). The evolution of the train is dominated mainly by short-range interactions until 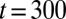 ms (dotted line), when three plugs break nearly simultaneously. The velocity of the remaining plugs then displays a large increase, and the subsequent ruptures take place within shorter and shorter time intervals, with all the remaining plugs broken between
ms (dotted line), when three plugs break nearly simultaneously. The velocity of the remaining plugs then displays a large increase, and the subsequent ruptures take place within shorter and shorter time intervals, with all the remaining plugs broken between 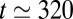 ms and
ms and 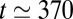 ms. The rapid variation of the velocity points to the finite-time singularity nature of the cascade.
ms. The rapid variation of the velocity points to the finite-time singularity nature of the cascade.
Model and Simulations.
Because at a given time all plugs move at the same speed, interactions between plugs may be treated by generalizing the equation for a single plug to a series of plugs: 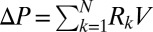 , where
, where 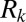 is the resistance ascribed to plug k. The lubricating role of the wetting film thickness is taken into account by expressing the front interface resistance
is the resistance ascribed to plug k. The lubricating role of the wetting film thickness is taken into account by expressing the front interface resistance 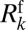 as a function of the cross-sectional area
as a function of the cross-sectional area 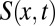 of the lumen open to air ahead of plug k. This area is given by
of the lumen open to air ahead of plug k. This area is given by 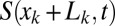 , which is determined by the history of the previous plugs
, which is determined by the history of the previous plugs 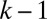 ,
, 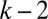 , … The surface in front of plug 1 is just
, … The surface in front of plug 1 is just 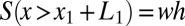 . The fluid distribution in the channel then may be computed as a function of time, once the conservation of liquid is expressed. For each plug, we get
. The fluid distribution in the channel then may be computed as a function of time, once the conservation of liquid is expressed. For each plug, we get 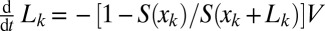 . The area
. The area 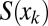 of the lumen behind plug k then serves as an input in the computation for plug
of the lumen behind plug k then serves as an input in the computation for plug 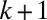 . Plug rupture takes place when
. Plug rupture takes place when 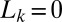 and is accounted for by setting
and is accounted for by setting 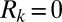 . The positions of the plugs may be obtained by integrating the velocity V, as discussed in SI Text.
. The positions of the plugs may be obtained by integrating the velocity V, as discussed in SI Text.
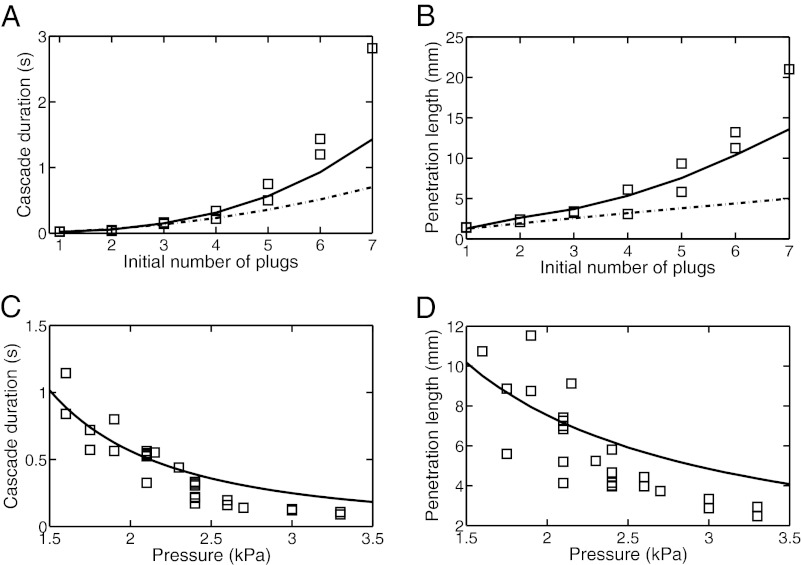
The results of the model are shown in the bottom panels of Fig. 2 (monodisperse) and in Fig. S1 (polydisperse). In both cases, the motion of the plugs and the order of plug ruptures are reproduced correctly. Quantitative predictions from the model were compared with results from experiments with trains made of one to seven plugs. Two quantities were measured: (i) the time 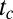 required for complete reopening of the airway (all plugs have ruptured), called “cascade duration,” and (ii) the penetration length
required for complete reopening of the airway (all plugs have ruptured), called “cascade duration,” and (ii) the penetration length 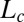 , which is the distance between the initial position of plug 1 and its position when it breaks, also indicating the necessary channel length for a cascade to be observed. Results are presented in Fig. 3, in which each square marks a single run. (The simulation derivation is supported by Figs. S2–S6 and the physical parameters are listed in Tables S1 and S2.)
, which is the distance between the initial position of plug 1 and its position when it breaks, also indicating the necessary channel length for a cascade to be observed. Results are presented in Fig. 3, in which each square marks a single run. (The simulation derivation is supported by Figs. S2–S6 and the physical parameters are listed in Tables S1 and S2.)
Fig. 3.
Evolution of the cascade duration (A and C) and the penetration length (B and D) as functions of the number of plugs (A and B) and applied pressure (C and D) for a set of monodisperse plugs of length 0.78 mm separated by 2.1 mm. In A and B, the pressure head is 2.0 kPa. Squares correspond to experiments, solid lines to the full model, and dash/dotted curves to predictions from the model without plug interactions.
The solid line corresponds to the predictions obtained with the full model, which takes into account all the processes described above. In contrast, the dash/dotted lines in Fig. 3 A and B show the predictions when short-range effects are neglected, i.e., when the resistances of all plugs are just summed as if each of them were alone in the channel: 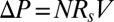 , with N the total number of plugs and
, with N the total number of plugs and 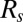 the resistance of an isolated plug. When the interactions are neglected, the cascade duration and the penetration length are grossly underestimated and the discrepancy increases with the number of plugs, stressing the role of liquid exchange between plugs. This shows that the interactions play a dominant role in the dynamics of the train, increasing the quantities of interest by a large factor. The experiments were repeated to measure the cascade duration and penetration length as functions of the imposed pressure head; the results are shown in Fig. 3 C and D. The model agrees quantitatively with the experiments at low pressures, but discrepancies appear above 2.5 kPa. This departure is attributed to the fact that the theoretical expressions used for interface resistances are valid only at low capillary numbers. Although individual resistances are not sufficiently well estimated during the fastest part of the cascade, the model still may serve as a good basis for predicting the cascade duration and penetration lengths in straight rectangular channels.
the resistance of an isolated plug. When the interactions are neglected, the cascade duration and the penetration length are grossly underestimated and the discrepancy increases with the number of plugs, stressing the role of liquid exchange between plugs. This shows that the interactions play a dominant role in the dynamics of the train, increasing the quantities of interest by a large factor. The experiments were repeated to measure the cascade duration and penetration length as functions of the imposed pressure head; the results are shown in Fig. 3 C and D. The model agrees quantitatively with the experiments at low pressures, but discrepancies appear above 2.5 kPa. This departure is attributed to the fact that the theoretical expressions used for interface resistances are valid only at low capillary numbers. Although individual resistances are not sufficiently well estimated during the fastest part of the cascade, the model still may serve as a good basis for predicting the cascade duration and penetration lengths in straight rectangular channels.
Cascade of Plug Ruptures in a Bifurcating Network
When considering an initially occluded tree structure, such as the pulmonary airway, the processes described above must be adapted to account for geometric effects: the division of plugs at bifurcations and the interactions across different regions in the network (19). This has been studied in a series of reopening experiments performed by replacing the straight channel with a six-generation tree network, as shown in Fig. 4. The widths of the channels in successive generations are chosen according to the diameter ratio in Weibel’s symmetric model of the human lung (36), i.e., 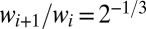 , where
, where 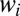 is the width of channels in generation i and
is the width of channels in generation i and 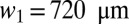 . The height of channels is
. The height of channels is 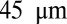 everywhere.
everywhere.
Fig. 4.
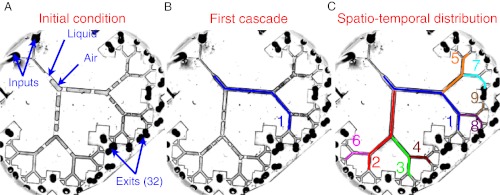
Initial distribution of plugs and spatial distribution of successive airway reopenings obtained by pushing an initial set of liquid plugs by 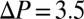 kPa in a six-generation network. A given path is “open” when all the plugs obstructing the airflow from the entrance to the exit have ruptured. (A) Initial plug distribution in the network. (B) The path taken by the first cascade. (C) Spatio temporal distribution of successive cascades. Paths are numbered according to the order in which they reopen.
kPa in a six-generation network. A given path is “open” when all the plugs obstructing the airflow from the entrance to the exit have ruptured. (A) Initial plug distribution in the network. (B) The path taken by the first cascade. (C) Spatio temporal distribution of successive cascades. Paths are numbered according to the order in which they reopen.
The same protocol as for the straight channels is used. The experiment begins by alternately injecting liquid and air into the root channel to form seven successive plugs that are distributed into the tree. Indeed, each plug splits into two daughters when it reaches a bifurcation in the branching tree, thus distributing the liquid into all regions of the network (19, 20). Although the sequence of pressures during the plug formation is computer controlled and kept unchanged for all runs, slight perturbations affect the plug divisions at each run. The initial distributions therefore differ slightly from one experiment to the next despite the network symmetry.
A typical experiment is shown in Fig. 4 (see also Movie S4). Once the initial plug distribution is installed (Fig. 4A), after waiting sufficient time to make sure the system is at rest, a high pressure head (3.5–5.5 kPa) is applied at the root, whereas the exits of the network are maintained at atmospheric pressure. The flow rate in each path is determined by the pressure difference, which is equilibrated by the sum of the resistances through each branch of the path. The small differences in initial distribution of plugs lead to variations in flow rates among paths, which then are amplified as the liquid plugs make their way in the network. Ultimately, one path reopens through a cascade of plug ruptures (Fig. 4B).
This first cascade is followed by several others, each opening a different path, as shown in Fig. 4C, in which the numbers indicate the order in which cascades occur. The spatial distribution of the cascades is irregular; they may take place either in adjacent paths (e.g., 3 and 4) or in well-separated paths (e.g., 4 and 5). Each cascade divides the network into independent subnetworks that evolve separately from the rest.
The pressure driving each subnetwork may be inferred by considering the airflow in the reopened path. Because the pressures 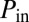 at the root and
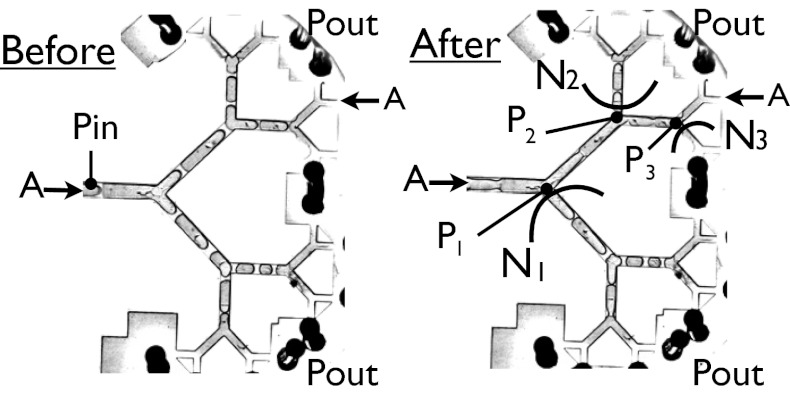
at the root and 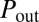 at the exit are fixed, the flow of air that takes place in the reopened path determines the intermediate values of the pressure along the path. A typical situation is shown in Fig. 5, in which the last five generations of the network are displayed before and just after reopening of path A. The whole subnetwork initially is driven at the common pressure
at the exit are fixed, the flow of air that takes place in the reopened path determines the intermediate values of the pressure along the path. A typical situation is shown in Fig. 5, in which the last five generations of the network are displayed before and just after reopening of path A. The whole subnetwork initially is driven at the common pressure 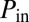 . However, once the cascade takes place along path A, the tree gets separated into three subnetworks, N1, N2, N3, driven at three intermediate values of the pressure,
. However, once the cascade takes place along path A, the tree gets separated into three subnetworks, N1, N2, N3, driven at three intermediate values of the pressure, 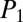 ,
, 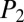 , and
, and 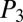 . The smaller the subnetwork, the lower the pressure head driving it. On the other hand, the smaller the subnetwork, the fewer plugs it contains, and hence the lower the resistance to flow. It therefore is not possible to predict the path that will be followed by the next cascade.
. The smaller the subnetwork, the lower the pressure head driving it. On the other hand, the smaller the subnetwork, the fewer plugs it contains, and hence the lower the resistance to flow. It therefore is not possible to predict the path that will be followed by the next cascade.
Fig. 5.
Snapshots taken before and after the reopening of path A, corresponding to the first cascade in the network. 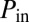 and
and 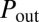 are the pressures at the entrance and exit of the tree.
are the pressures at the entrance and exit of the tree. 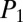 ,
, 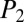 , and
, and 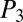 indicate the intermediate pressures at the first, second, and third nodes after reopening, with
indicate the intermediate pressures at the first, second, and third nodes after reopening, with 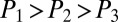 .
.
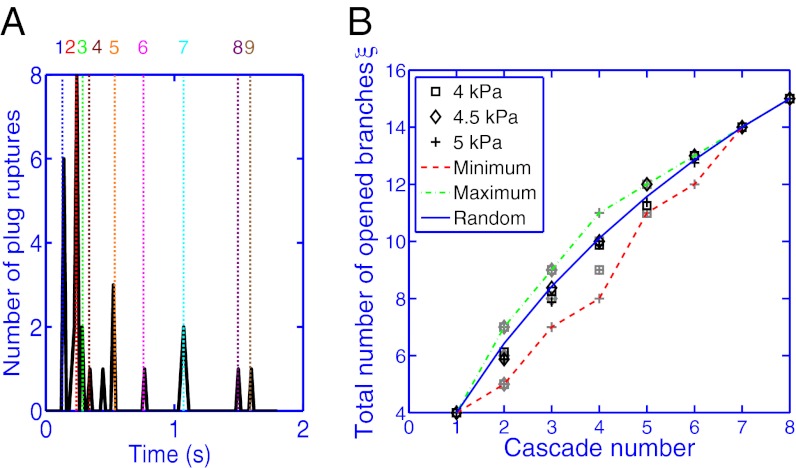
The readjustment of the driving pressure after each cascade leads to a delay of successive cascades in time. This is shown in Fig. 6A, which displays a histogram of individual plug ruptures plotted as a function of time. Ruptures are clustered in groups that correspond to each cascade, which we label using the same numbering scheme as in Fig. 4. The initial cascades develop when a large part of the network is still occluded and therefore involve many simultaneous plug ruptures. In contrast, later cascades involve fewer plugs and affect shorter paths of the tree. The time separating successive cascades, initially short, gradually increases in all experiments.
Fig. 6.
(A) Histogram of the number of plug ruptures as a function of time for the same experiment as in Fig. 4. The dotted line numbering corresponds to the cascades identified on the image. (B) Total number ξ of opened branches (in which air can flow freely) measured after each cascade. The black symbols show the variations of ξ obtained experimentally for the driving pressures shown in the legend by averaging results over eight experiments for each pressure. The gray symbols correspond to individual experiments. The curves connect maximum (dash/dotted green) and minimum (dashed red) values of ξ observed and the average predicted value for supposedly random openings.
The spatial distribution of reopenings is characterized by introducing a quantity 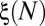 that measures the cumulated number of branches, between the root and generation 4, that are reopened by cascades 1 to N (Fig. 6B). The first cascade always corresponds to
that measures the cumulated number of branches, between the root and generation 4, that are reopened by cascades 1 to N (Fig. 6B). The first cascade always corresponds to  , because all four generations are initially occluded. However, the evolution of ξ between successive cascades depends on the size of the reopened subnetwork and thus on the spatial distribution of successive reopenings. The minimum and maximum possible evolutions of
, because all four generations are initially occluded. However, the evolution of ξ between successive cascades depends on the size of the reopened subnetwork and thus on the spatial distribution of successive reopenings. The minimum and maximum possible evolutions of 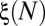 , shown in Fig. 6B, may be calculated by simulating different reopening scenarios in the network. Alternatively, the evolution of
, shown in Fig. 6B, may be calculated by simulating different reopening scenarios in the network. Alternatively, the evolution of 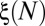 for a random distribution of reopenings is calculated numerically by performing a Monte Carlo simulation of the successive paths and taking the mean value of
for a random distribution of reopenings is calculated numerically by performing a Monte Carlo simulation of the successive paths and taking the mean value of 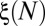 for a large number of realizations.
for a large number of realizations.
Measurements of ξ were performed for three different driving pressures, 4.0, 4.5, and 5.0 kPa, by repeating each experiment eight times. The average value of 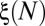 for the eight realizations is indistinguishable from the random prediction, as shown by the black symbols in Fig. 6B. The results for a particular experiment, however, may fall anywhere between the minimum and maximum values, as shown by the light-gray symbols. The value of ξ is statistically random over a set of runs.
for the eight realizations is indistinguishable from the random prediction, as shown by the black symbols in Fig. 6B. The results for a particular experiment, however, may fall anywhere between the minimum and maximum values, as shown by the light-gray symbols. The value of ξ is statistically random over a set of runs.
This large difference between particular runs is a result of the complexity of fluid redistribution when a plug divides at a bifurcation. Indeed, the exact timing of the cascade with respect to the plug passage through a bifurcation may lead to two different outcomes: If the plug passes a bifurcation before the cascade takes place, it separates into two daughter plugs, one in each of the daughter branches, only one of which will rupture during the cascade (Fig. S2). Conversely, if the plug bursts before the division, the occluded subnetwork does not acquire an extra plug. Therefore, the resistance in the occluded subnetwork, and the time necessary to reopen it, may display large fluctuations between individual runs. Indeed, the timing of the cascades and the distribution of the liquid were found to display extreme sensitivity to the initial conditions, making the prediction of the cascade path impossible. On average, Fig. 6 shows that the behavior is indistinguishable from a random distribution.
Discussion
The geometry of the bifurcating tree introduces several modifications to the physical picture developed for the cascades in straight channels. First, the plug divisions at the successive bifurcations add a strong random component to the dynamics in the network, as described above. This greatly limits the ability to predict the cascade timing or path. Second, the model proposed for the straight channels is insufficient to describe the cascades in the network because the plugs in a given path of the network do not flow at the same velocity in all generations. Instead, the velocity of the plugs decreases with the generation number, because the cross-section increases. This means that plugs closer to the root have higher capillary numbers than those close to the exits, so the value of the resistance 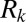 of each plug depends on the generation number in which the plug is flowing.
of each plug depends on the generation number in which the plug is flowing.
The network’s geometry also implies that the distance between plugs may vary in time, through two mechanisms: (i) Plugs that are in different generations get closer together as they advance into the network because those closer to the root of the network are traveling faster. (ii) The distances separating them may change if an air bubble, which separates two plugs, divides asymmetrically at a bifurcation. These mechanisms imply that the short-range interactions also become more complex in the network.
These modifications in plug distances and velocities imply that reopening the microfluidic network is more efficient when the plugs have not yet penetrated deep into the tree, particularly because the stabilizing short-range interactions play a smaller role in this case. Therefore, the strategy for reopening such a network should be to work at high driving pressures. When extrapolating this statement to the lung reopening, however, one should consider biological factors such as the effects of the shear stresses and pressure fluctuations on the epithelial cells, both during the motion of the plugs (37) and at the location of rupture (38). The magnitude of these efforts in vivo cannot be obtained from the current model.
Indeed, the relevance of our study to pulmonary airway reopening is limited in that we consider a highly idealized system. In contrast, the actual lung involves many supplementary mechanisms, such as surfactant (15, 39) or elastic interconnected airways (21, 40), in addition to being made up of rough tubes bifurcating asymmetrically. All these effects will complicate the behavior compared with what is observed here. For instance, surfactants will introduce several effects. They may retard the plug bursting compared with clean interfaces, as in the case of soap bubbles, but they also may enhance the liquid deposition on the walls (39), in addition to inducing deformations in the leading films that may increase the shear stress on the wall (37).
A more complete model must also include a description of airway deformation, which is particularly important because breathing takes place through the dilation of the diaphragm and rib cage, which induces a negative pressure that draws the air into the lung. Because a plug’s length and resistance are coupled with the cross-section of the tube containing it, an increase in tube diameter will reduce the resistance to flow, leading to faster cascades.
Nevertheless, our simple model has allowed us to identify some basic mechanisms that will remain important in real pulmonary flows. Indeed, the lung will still display the collective behavior that we have observed for a train of plugs, namely through local and global interactions, and the choice of a particular path in the network for each cascade. Only the quantitative details will be modified as more ingredients are added to the airway model but not the qualitative behavior.
Materials and Methods
Microfluidics and Observations.
The microfluidic devices are prepared using dry-film soft lithography techniques (41). The channels are etched in PDMS and bonded on a PDMS-covered glass slide. Perfluorodecalin is used as the working fluid because of its good wetting properties (contact angle 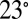 with PDMS) and its compatibility with PDMS (42). The pressure at the network inlet and driving the liquid is imposed using a Fluigent MFCS-8C controller, which is programmed to achieve specific pressure sequences. The observations are performed through a stereomicroscope using a fast camera (Photron Fastcam 1024) filming at 1,000 frames per second. The image sequences then are analyzed using MatLab and ImageJ.
with PDMS) and its compatibility with PDMS (42). The pressure at the network inlet and driving the liquid is imposed using a Fluigent MFCS-8C controller, which is programmed to achieve specific pressure sequences. The observations are performed through a stereomicroscope using a fast camera (Photron Fastcam 1024) filming at 1,000 frames per second. The image sequences then are analyzed using MatLab and ImageJ.
Experimental Protocol.
A train of liquid plugs is created inside the channels by alternately pushing liquid and air slowly through a Y-junction (18). The Y-junction then leads to the experimental region, which consists of either a straight channel (rectangular cross-section of width 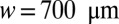 and height
and height 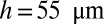 ) or a branching network. Once the plugs are created and placed, the pressure is set to zero for a few seconds to achieve a stationary initial condition, after which a constant pressure head
) or a branching network. Once the plugs are created and placed, the pressure is set to zero for a few seconds to achieve a stationary initial condition, after which a constant pressure head  is applied at the channel entrance of the channel. More details are given in SI Materials and Methods.
is applied at the channel entrance of the channel. More details are given in SI Materials and Methods.
Supplementary Material
Acknowledgments
The authors thank Tim Pedley for a careful reading of and comments on the manuscript. C.B. acknowledges early discussions of this work with Jihad Touma. This work was funded by the Agence Nationale de Recherche under the “Transport et Transfert via le Système Pulmonaire Humain” project (M.B.). The Fluigent corporation generously lent us the MFCS-8C pressure source.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1211706110/-/DCSupplemental.
References
- 1.Lenormand R, Zarcone C, Sarr A. Mechanisms of the displacement of one fluid by another in a network of capillary ducts. J Fluid Mech. 1983;135:337–353. [Google Scholar]
- 2.Dias MM, Payatakes AC. Network models for two-phase flow in porous media Part 1. Immiscible microdisplacement of non-wetting fluids. J Fluid Mech. 1986;164:305–336. [Google Scholar]
- 3.Stark J, Manga M. The motion of long bubbles in a network of tubes. Transp Porous Media. 2000;40:201–218. [Google Scholar]
- 4.Davis SH, Hocking LM. Spreading and imbibition of viscous liquid on a porous base. Phys Fluids. 1999;11:48–57. [Google Scholar]
- 5.Rost M, Laurson L, Dubé M, Alava M. Fluctuations in fluid invasion into disordered media. Phys Rev Lett. 2007;98(5):054502. doi: 10.1103/PhysRevLett.98.054502. [DOI] [PubMed] [Google Scholar]
- 6.Engl W, Roche M, Colin A, Panizza P, Ajdari A. Droplet traffic at a simple junction at low capillary numbers. Phys Rev Lett. 2005;95(20):208304. doi: 10.1103/PhysRevLett.95.208304. [DOI] [PubMed] [Google Scholar]
- 7.Champagne N, Vasseur R, Montourcy A, Bartolo D. Traffic jams and intermittent flows in microfluidic networks. Phys Rev Lett. 2010;105(4):044502. doi: 10.1103/PhysRevLett.105.044502. [DOI] [PubMed] [Google Scholar]
- 8.Duclaux V, Clanet C, Quéré D. The effects of gravity on the capillary instability in tubes. J Fluid Mech. 2006;556(1):217–226. [Google Scholar]
- 9.Heil M, Hazel AL, Smith JA. The mechanics of airway closure. Respir Physiol Neurobiol. 2008;163(1-3):214–221. doi: 10.1016/j.resp.2008.05.013. [DOI] [PubMed] [Google Scholar]
- 10.Wright SM, et al. Altered airway surfactant phospholipid composition and reduced lung function in asthma. J Appl Physiol. 2000;89(4):1283–1292. doi: 10.1152/jappl.2000.89.4.1283. [DOI] [PubMed] [Google Scholar]
- 11.Hohlfeld JM, et al. The role of surfactant in asthma. Respir Res. 2002;3(4):1–8. doi: 10.1186/rr176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Griese M, Birrer P, Demirsoy A. Pulmonary surfactant in cystic fibrosis. Eur Respir J. 1997;10(9):1983–1988. doi: 10.1183/09031936.97.10091983. [DOI] [PubMed] [Google Scholar]
- 13.Engle WA. American Academy of Pediatrics Committee on Fetus and Newborn Surfactant-replacement therapy for respiratory distress in the preterm and term neonate. Pediatrics. 2008;121(2):419–432. doi: 10.1542/peds.2007-3283. [DOI] [PubMed] [Google Scholar]
- 14.Cassidy KJ, et al. A rat lung model of instilled liquid transport in the pulmonary airways. J Appl Physiol. 2001;90(5):1955–1967. doi: 10.1152/jappl.2001.90.5.1955. [DOI] [PubMed] [Google Scholar]
- 15.Espinosa FF, Kamm RD. Bolus dispersal through the lungs in surfactant replacement therapy. J Appl Physiol. 1999;86(1):391–410. doi: 10.1152/jappl.1999.86.1.391. [DOI] [PubMed] [Google Scholar]
- 16.Cassidy KJ, Gavriely N, Grotberg JB. Liquid plug flow in straight and bifurcating tubes. J Biomech Eng. 2001;123(6):580–589. doi: 10.1115/1.1406949. [DOI] [PubMed] [Google Scholar]
- 17.Zheng Y, Anderson JC, Suresh V, Grotberg JB. Effect of gravity on liquid plug transport through an airway bifurcation model. J Biomech Eng. 2005;127(5):798–806. doi: 10.1115/1.1992529. [DOI] [PubMed] [Google Scholar]
- 18.Ody CP, Baroud CN, de Langre E. Transport of wetting liquid plugs in bifurcating microfluidic channels. J Colloid Interface Sci. 2007;308(1):231–238. doi: 10.1016/j.jcis.2006.12.018. [DOI] [PubMed] [Google Scholar]
- 19.Song Y, Manneville P, Baroud CN. Local interactions and the global organization of a two-phase flow in a branching tree. Phys Rev Lett. 2010;105(13):134501. doi: 10.1103/PhysRevLett.105.134501. [DOI] [PubMed] [Google Scholar]
- 20.Song Y, Baudoin M, Manneville P, Baroud CN. The air-liquid flow in a microfluidic airway tree. Med Eng Phys. 2011;33(7):849–856. doi: 10.1016/j.medengphy.2010.10.001. [DOI] [PubMed] [Google Scholar]
- 21.Howell PD, Waters SL, Grotberg JB. The propagation of a liquid bolus along a liquid-lined flexible tube. J Fluid Mech. 2000;406:309–335. [Google Scholar]
- 22.Grotberg JB, Jensen OE. Biofluid mechanics in flexible tubes. Annu Rev Fluid Mech. 2004;36:121–147. [Google Scholar]
- 23.Alencar AM, Buldyrev SV, Majumdar A, Stanley HE, Suki B. Avalanche dynamics of crackle sound in the lung. Phys Rev Lett. 2001;87(8):088101. doi: 10.1103/PhysRevLett.87.088101. [DOI] [PubMed] [Google Scholar]
- 24.Alencar AM, et al. Physiology: Dynamic instabilities in the inflating lung. Nature. 2002;417(6891):809–811. doi: 10.1038/417809b. [DOI] [PubMed] [Google Scholar]
- 25.Majumdar A, et al. Fluid transport in branched structures with temporary closures: A model for quasistatic lung inflation. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;67(3 Pt 1):031912. doi: 10.1103/PhysRevE.67.031912. [DOI] [PubMed] [Google Scholar]
- 26.Bico J, Quéré D. Falling slugs. J Colloid Interface Sci. 2001;243(1):262–264. [Google Scholar]
- 27.Hoffman RL. Study of advancing interface. A. Interface shape in liquid-gas systems. J Colloid Interface Sci. 1975;50(2):228–241. [Google Scholar]
- 28.Tanner LH. Spreading of silicone oil drops on horizontal surfaces. J. Phys. D. 1979;12:1473–1484. [Google Scholar]
- 29.Bretherton FP. The motion of long bubbles in tubes. J Fluid Mech. 1971;10:166–188. [Google Scholar]
- 30.Hazel AL, Heil M. The steady propagation of a semi-infinite bubble into a tube of elliptical or rectangular cross-section. J Fluid Mech. 2002;470:91–114. [Google Scholar]
- 31.White FM. Viscous Fluid Flow. 2nd Ed. New York: McGraw-Hill; 1991. [Google Scholar]
- 32.Aussillous P, Quéré D. Quick deposition of a fluid on the wall of a tube. Phys Fluids. 2000;12(10):2367–2371. [Google Scholar]
- 33.de Lózar A, Hazel AL, Juel A. Scaling properties of coating flows in rectangular channels. Phys Rev Lett. 2007;99(23):234501. doi: 10.1103/PhysRevLett.99.234501. [DOI] [PubMed] [Google Scholar]
- 34.Fujioka H, Takayama S, Grotberg JB. Unsteady propagation of a liquid plug in a liquid-lined straight tube. Phys Fluids. 2008;20(6):062104. doi: 10.1063/1.2938381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chebbi R. Deformation of advancing gas-liquid interfaces in capillary tubes. J Colloid Interface Sci. 2003;265(1):166–173. doi: 10.1016/s0021-9797(03)00415-6. [DOI] [PubMed] [Google Scholar]
- 36.Weibel ER. The Pathway for Oxygen. Structure and Function in the Mammalian Respiratory System. Cambridge, MA: Harvard Univ Press; 1984. [Google Scholar]
- 37.Fujioka H, Grotberg JB. The steady propagation of a surfactant-laden liquid plug in a two-dimensional channel. Phys Fluids. 2005;17(8):082102. [Google Scholar]
- 38.Huh D, et al. Acoustically detectable cellular-level lung injury induced by fluid mechanical stresses in microfluidic airway systems. Proc Natl Acad Sci USA. 2007;104(48):18886–18891. doi: 10.1073/pnas.0610868104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tavana H, et al. Dynamics of liquid plugs of buffer and surfactant solutions in a micro-engineered pulmonary airway model. Langmuir. 2010;26(5):3744–3752. doi: 10.1021/la903038a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Halpern D, Naire S, Jensen OE, Gaver DP. Unsteady bubble propagation in a flexible channel: Predictions of a viscous stick-slip instability. J Fluid Mech. 2005;528:53–86. [Google Scholar]
- 41.Stephan K, et al. Fast prototyping using a dry film photoresist: Microfabrication of soft-lithography masters for microfluidic structures. J Micromech Microeng. 2007;17(69–N):74. [Google Scholar]
- 42.Dangla R, Gallaire F, Baroud CN. Microchannel deformations due to solvent-induced pdms swelling. Lab Chip. 2010;10(21):2032–2045. doi: 10.1039/c003504a. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.