Hyperspectral remote sensing of foliar nitrogen content

Abstract

A strong positive correlation between vegetation canopy bidirectional reflectance factor (BRF) in the near infrared (NIR) spectral region and foliar mass-based nitrogen concentration (%N) has been reported in some temperate and boreal forests. This relationship, if true, would indicate an additional role for nitrogen in the climate system via its influence on surface albedo and may offer a simple approach for monitoring foliar nitrogen using satellite data. We report, however, that the previously reported correlation is an artifact—it is a consequence of variations in canopy structure, rather than of %N. The data underlying this relationship were collected at sites with varying proportions of foliar nitrogen-poor needleleaf and nitrogen-rich broadleaf species, whose canopy structure differs considerably. When the BRF data are corrected for canopy-structure effects, the residual reflectance variations are negatively related to %N at all wavelengths in the interval 423–855 nm. This suggests that the observed positive correlation between BRF and %N conveys no information about %N. We find that to infer leaf biochemical constituents, e.g., N content, from remotely sensed data, BRF spectra in the interval 710–790 nm provide critical information for correction of structural influences. Our analysis also suggests that surface characteristics of leaves impact remote sensing of its internal constituents. This further decreases the ability to remotely sense canopy foliar nitrogen. Finally, the analysis presented here is generic to the problem of remote sensing of leaf-tissue constituents and is therefore not a specific critique of articles espousing remote sensing of foliar %N.

The importance of nitrogen in terrestrial ecosystem carbon dynamics and related potential climatic feedbacks is well known (1 –4). The interaction between carbon and nitrogen at the leaf level is among one of the fundamental mechanisms controlling the dynamics of the terrestrial carbon cycle (5, 6). Leaf-level processes influence absorption and scattering of solar radiation by foliage. In addition, the architecture of individual plants, their spatial distribution, and reflectivity of the ground (or understory) beneath a vegetation canopy also determine the angular patterns of reflected radiation (7), or the bidirectional reflectance factor (BRF, dimensionless), which is measured by air- and satellite-borne sensors. The BRF describes surface reflective properties in the absence of atmosphere and is a standard product from a new generation of global imaging spectro-radiometers (8 –10). All of the above factors must be taken into account to link satellite data and leaf-level physiological processes.

A strong positive correlation between canopy BRF at the near infrared (NIR) wavelengths (800−850 nm) and canopy mass-based foliar nitrogen concentration (%N) (in grams per 100 g of dry foliage mass) has been reported in some temperate and boreal forests (11). These sites represent sufficiently dense canopies and include a range of forest types. A similar correlation was also reported to be valid between broadband canopy albedo (400–2500 nm) and %N, not surprisingly, because vegetation canopy reflectance at wavelengths greater than 800 nm is an order of magnitude larger than that in the shorter wavelength region of the solar spectrum, i.e., the photosynthetically active radiation (PAR) (400–700 nm) region, save for a few wavelength intervals of water absorption bands.

The significance of this result, if true, is threefold. First, it may indicate an additional and overlooked role for nitrogen in the climate system via its influence on surface albedo and thus biosphere–atmosphere interactions, as hypothesized in ref. 11. Second, it may offer a simple and effective approach for monitoring foliar nitrogen using broadband satellite data, as suggested in refs. 11 –13. Finally, it may serve as the basis for a new parameterization of surface albedo that would provide a natural link to ecosystem processes, as proposed in ref. 14.

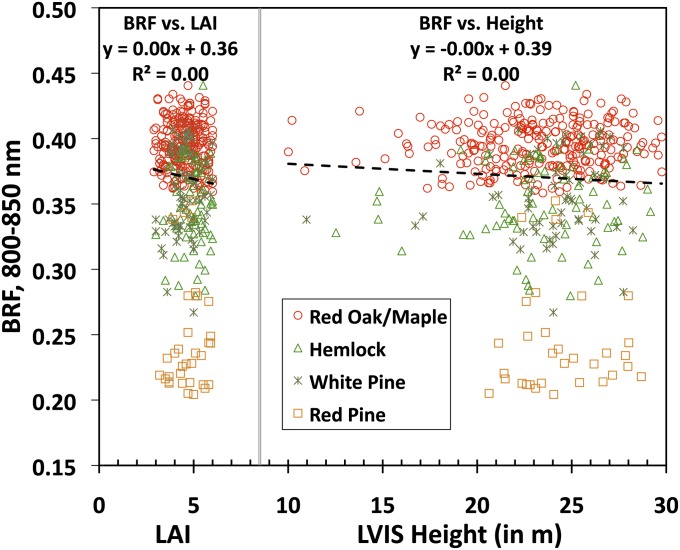
An examination of the reported relationship between NIR BRF and %N reveals in ref. 11 at least two incongruencies. First, this positive correlation is a counterintuitive example of radiative transfer processes—an increase in the foliar absorbing constituents should enhance absorption and accordingly decrease reflection. This physical argument suggests other factors, e.g., canopy structure (15), which not only suppress the absorption effect, but also become dominant determinants of the system’s behavior. In their analyses the authors of refs. 11 and 14 argued that vegetation canopy structure had no influence on the observed relationship on the basis of the absence of correlation between NIR BRF and proxies of canopy structure such as leaf area index (LAI) and canopy height (Fig. 1). However, this lack of correlation is well known in vegetation remote sensing literature as “reflectance saturation,” commonly observed in dense vegetation (16, 17); i.e., the surface reflectance reaches an asymptote and thus is insensitive to LAI and/or canopy height.

Fig. 1.

BRF in the near infrared (NIR) spectral band (800–850 nm) vs. leaf area index (LAI) and vs. LVIS canopy height ( Materials and Methods ) for the Harvard Forest. Values of LAI and LVIS height vary between 2.9 and 6 (mean = 4.6; SD = 0.76) and between 10 m and 30 m (mean = 23.5 m; SD = 3.3), respectively. Different species tend to occupy different locations along the vertical axis, suggesting a dependence of NIR BRF on 3D forest structure although it does not correlate with two important canopy structural characteristics—LAI and canopy height.

Fig. 1 demonstrates that the level of NIR reflectance at which saturation occurs depends on the species, which is indicative of 3D effects of vegetation structure because species differ in their structural attributes (e.g., Red Oak/Maple vs. Red Pine). That is, the same amount of leaf area can be distributed in many ways to form canopies of varying topology: e.g., as canopies of conical or ellipsoidal tree crowns. The BRF values can be different although the canopy LAI and height are same in all cases (18, 19). Moreover, the effects of 3D structure on radiative processes can affect the sensitivity of canopy NIR reflectance to leaf optical properties (20). Therefore, the hypothesis that canopy structure has no influence on the relationship between NIR BRF and %N simply because the data were limited to dense canopies requires further analysis.

Second, in their theoretical analyses (14, 21), the authors do not address the physics of how radiation interacts with foliage and traverses in the 3D vegetation canopy, which is the mechanism that generates the remotely measured signal and constitutes the basis for monitoring nitrogen from space. Light scattered by a leaf includes two components, specular and diffuse. The first component emanates from light reflected at the air–cuticle interface. This portion of reflected radiation is, in general, but not always, partly polarized and exhibits a weak spectral dependency (22). It does not interact with pigments inside the leaf, but depends on the properties of the leaf surface (22 –27), and therefore conveys no information about the constitution of the leaf tissue. Fresnel reflection is the principal cause of light polarization at the leaf surface (22, 23). The diffuse component, which results from radiation interactions within the leaf interior and any large particles on the leaf surface (hair, dust, and micro- to millimeter-scale wax structures), is not polarized. Its spectral behavior is mainly determined by the intrinsic optical properties of leaf constituents. The fraction of leaf surface reflected radiation can be greater than that of the diffuse field and it varies greatly between species (24, 27 –29). This can weaken the sensitivity of canopy reflectance to the amount of leaf constituents. For instance, in the spectral band about 650 nm, where chlorophyll absorption is strong, a polarized reflectance of 9% may account for 58% of the total radiation reflected by the leaf (28). In the NIR (800–850 nm) where pigments do not absorb anymore, variation between species in the radiation scattered from the leaf interior can be comparable to or smaller than that of the leaf surface reflected radiation (SI Text 3). Thus, scattering from a leaf contains radiation fields that convey information about leaf interior and leaf surface characteristics, both of which are further transformed by the multiple scattering process, which in turn is strongly affected by the 3D canopy structure. The problem of leaf surface and leaf interior physics and the 3D radiative transfer process needs to be untangled if one wishes to remotely sense the content of certain constituents inside the leaf.

These two incongruencies, namely influence of canopy structure and its transformation of signals generated by interaction of radiation with leaves, justify a reexamination of the previously reported positive relationship between canopy NIR reflectance and foliar %N (11). The problem investigated here, with the data used in ref. 11, is generic to the issue of remote sensing of leaf constituents and is therefore not a specific critique.

Results and Discussion

Canopy Structure Is the Dominant Factor That Positively Relates NIR BRF and Foliar %N.

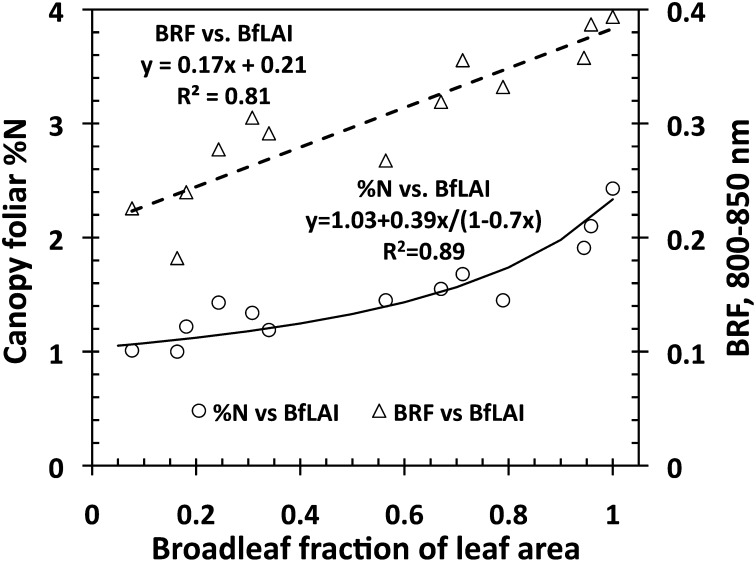
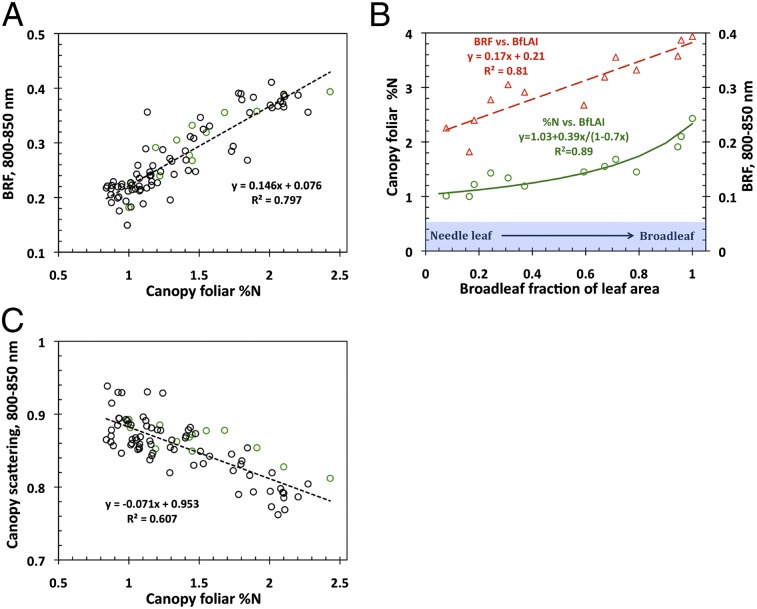
Fig. 2 shows that both canopy %N and NIR BRF are strongly and positively related to broadleaf fraction of leaf area (BfLAI, in m²/m²). The BfLAI characterizes variations in forest structure due to changing proportions of structurally different broad- and needleleaf species. We examine its role in this relationship.

Fig. 2.

Canopy foliar %N vs. BfLAI (vertical axis on the left side) and BRF in the near infrared (NIR) spectral band (800–850 nm) vs. BfLAI (vertical axis on the right side) relationships for the Bartlett Forest (Table 1). The former can accurately be approximated by equations (solid line) that relate %N, broadleaf fraction of the leaf dry mass (BfM), and BfLAI ( Materials and Methods and SI Text 1): RRMSE = 10%. Values of R ², slope, and intercept of the measured %N vs. approximated %N regression line are 0.89, 0.997, and 0.001, respectively (SI Text 1).

The nonlinear %N vs. BfLAI relationship follows from equations used to estimate canopy foliar %N from field data ( Materials and Methods ). The plots are characterized by a strong gradient in the proportion of needle- and broadleaf species. The contributions from leaves and needles to the canopy %N depend on the broadleaf fraction of the leaf dry mass (BfM, in g/g), which is an increasing function of the BfLAI ( Materials and Methods ). The difference in the leaf (%n _L = 2.17 g/100 g) and needle (%n _N = 1.24 g/100 g) nitrogen concentrations is responsible for a positive tendency in %N from pure (meaning 100%, hereafter) needle- to pure broadleaf plots. The differences in dry mass per leaf (m _L = 66.3 g/m²) and needle (m _N = 224.2 g/m²) area determine the convexity of the relationship. Thus, BfLAI is the structural variable that controls contributions from needles and leaves and consequently determines variations in canopy %N.

The NIR BRF vs. BfLAI relationship (Fig. 2) has the following interpretation. First, due to high dry matter content in a needle, absorption by needles could be stronger compared with that of leaves (30). Second, due to relatively strong needle scattering in the NIR spectral band (23, 31), the structure of a coniferous shoot gives rise to multiple photon–needle interactions within a shoot (32 –34). The shoot acts as a “photon trap,” within which photons travel until they are either absorbed or scattered out. Photons scattered out of one shoot can in turn be either trapped by another shoot or escape the canopy. Each within-shoot interaction increases the likelihood of photon absorption; thus, the shoots appear darker compared with needles (34 –36). Because this effect is not present in broadleaf canopies, NIR reflectance tends to be greater than its coniferous counterpart (32). In dense, mixed canopies, an increase in the fraction of broadleaf trees therefore tends to make the forest canopies appear brighter in the NIR spectral region. The topology of the upper surface of a canopy is another factor that causes an increase in the NIR BRF from pure needle- to pure broadleaf leaf forests. This effect is discussed later.

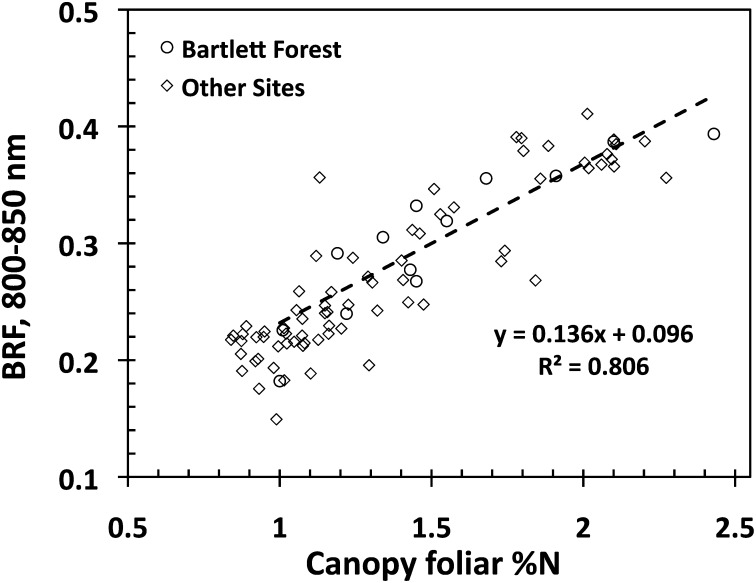
Finally, Fig. 3 shows the relationship between NIR BRF and %N, which follows from Fig. 2. Indeed, the lowest BRF values correspond to pure needle-leaf forests (Fig. 2) where only nitrogen-poor needles contribute to the mean canopy foliar nitrogen concentration. An increase in the fraction of broadleaf species enhances the contributions from nitrogen-rich flat leaves to %N, lowers the foliar dry matter content, and dampens the darkening effect of shoot structure. The former augments %N whereas the two latter factors make the canopy appear brighter, as discussed above. This suggests that canopy structure is the dominant factor that governs variations in NIR BRF and %N and consequently results in the spurious relationship between the canopy reflectance and foliar nitrogen. Therefore, NIR and/or SW broadband satellite data cannot be directly linked to leaf-level processes.

Fig. 3.

Relationship between canopy BRF in the NIR spectral band (800–850 nm) and canopy foliar %N. The regression line is for the Bartlett Forest plots shown in Fig. 2; for all sites y = 0.146x + 0.076, R ² = 0.797.

These empirical results are based on data from the Bartlett Forest. Our goal is to understand the physics behind empirical relationships, identify the role of canopy structure on the NIR BRF vs. %N relationship across all study areas, and if needed develop a method to account for canopy structural influence in remote sensing of leaf tissue constituents. We begin with an analysis of the radiative transfer process in a vegetation canopy and specification of variables that account for the cumulative effects of canopy structural properties at different scales on canopy reflectance.

Understanding the Multiple-Scattering Process Is Critical to Quantifying Canopy Structure.

The study sites represent closed-canopy forests with relatively high LAI values (11). Our analyses of NDVI values (defined in Table 1) and BRF spectra (SI Text 7) suggest that the impact of canopy background, be it bare ground or understory vegetation, on canopy reflectance is negligible. The canopy structure and optical properties of the leaves in the canopy are the dominant factors that determine the spectral BRF. As reported in ref. 11 and confirmed in Fig. 1, there is no relationship between NIR BRF and proxies of structure such as LAI and canopy height; i.e., the reflectances are saturated. Is the lack of correlation with proxies of structure evidence for a negligible role of structure in variations of NIR BRF and consequently a bigger role of leaf optics on canopy reflectance? As Figs. 1 and 2 suggest, structure can affect the magnitude of the saturated BRF. Here, we identify a structural variable that controls variations in BRF under saturation conditions.

Table 1.

Site description

Site	Lat, oN	Long, oW	Solar zenith angle at AVIRIS flight, °	Description	No. 20 × 20-m plots	Mean (SD) over plots
						NDVI*	%N
Austin Cary Memorial Forest † , FL	29.75	82.20	25.89	Planted and natural pine	4	0.72 (0.01)	0.90 (0.05)
Bartlett Experimental Forest ‡ , NH	44.05	71.28	33.16	Mixed northern hardwood	13	0.88 (0.03)	1.52 (0.42)
Duke Forest § , NC	35.97	79.09	33.19	Pine, pine–hardwood, upland hardwood, and bottomland hardwood	16	0.88 (0.04)	1.57 (0.40)
Harvard Forest ¶ , MA	42.54	72.17	35.11	Mixed temperate forest	19	0.89 (0.02)	1.77 (0.29)
Howland Forest ║ , ME	45.20	68.74	35.59	Boreal-northern hardwood transitional forest	18	0.87 (0.01)	1.02 (0.10)
Wind River Experimental Forest**, WA	45.82	121.95	25.22	Temperate evergreen	15	0.86 (0.03)	1.10 (0.22)

Lat, latitude; long, longitude.

*NDVI is defined here as the difference between AVIRIS plot BRFs in the nadir direction at 855 nm and 655 nm normalized by their sum.

^† http://sfrc.ufl.edu/handbook/acf.html.

^‡ www.fs.fed.us/ne/durham/4155/bartlett.htm.

^§ www.dukeforest.duke.edu/.

^¶ http://harvardforest.fas.harvard.edu/.

^║ http://howlandforest.org/.

**www.fs.fed.us/pnw/exforests/wind-river/index.shtml.

Solar radiation reflected by a vegetation canopy and measured by a satellite-borne sensor results from photons that enter the canopy, interact with the green foliage and nongreen woody material (branches, trunks, etc.), travel between interactions inside the vegetation canopy, and finally escape the canopy through gaps toward to the sensor. To simplify the problem at hand, we consider green foliage matter in the canopy only. For sufficiently dense vegetation where the impact of canopy background is negligible the photon–canopy interactions, or equivalently the radiative transfer process in vegetation canopies, depend on (i) how individual leaves scatter the radiation, i.e., leaf optics, and (ii) how the foliage is distributed in the canopy space, i.e., canopy structure. We use the leaf albedo, ω _λ, to characterize the scattering ability of the foliage in the canopy. This variable is the fraction of radiation incident on the leaf that is reflected or transmitted (SI Text 3). Scattering from a leaf responds differently at different wavelengths to changes in leaf properties such as pigment concentrations, chemical constituents, internal structure, and leaf surface properties. The leaf albedo spectrum therefore is the only optical variable that conveys information about leaf biochemical constituents, e.g., nitrogen content.

Leaf optical properties, however, cannot be directly measured from space because the radiation scattered from leaves and exiting the canopy in the direction of the sensor is strongly affected by the 3D canopy structure. The canopy structural organization acts as a labyrinth for photons. Photons enter the “labyrinth” and run into leaves. A fraction of these incoming photons disappears as a result of absorption, whereas the remainder are scattered from leaves, i.e., change the direction of their travel. The scattered photons in turn can either hit leaves again or escape the vegetation through gaps between the foliage. The photons wander between interactions throughout the labyrinth until they either are absorbed or exit the canopy.

We use the concept of recollision probability, p, to quantify the complexity of canopy structural organization. This is the probability that a photon scattered by material in the canopy will interact with matter in the canopy again (31, 35, 37, 38). If, for example, a vegetation canopy can be treated as a “big leaf” (i.e., no structure, LAI = 1), the recollision probability is zero because photons reflected from or transmitted through such a leaf will not encounter another leaf. If one cuts this big leaf into “small pieces” and uniformly distributes these pieces in the canopy space, i.e., a simple structure is introduced with the leaf area unaltered, the recollision probability changes its value from 0 to about 0.3 (35). The recollision probability depends on canopy geometrical properties at different scales such as the spatial distribution of trees on the ground, tree crown shape and size, and within-crown foliage arrangement (33 –35, 39 –42). The greater its value is, the higher the likelihood of photon absorption and consequently fewer photons exit the vegetation. For the same amount of foliage area, for example, the recollision probability for coniferous forests is larger compared with that for broadleaf species due to the difference in the small-scale structural organization, i.e., coniferous shoot vs. flat leaf, respectively (35). This makes the coniferous forests appear darker in the NIR region compared with their broadleaf counterparts (32), as discussed above and illustrated in Figs. 1 and 2.

The probability that a photon scattered by canopy elements will not recollide, i.e., exit the canopy through gaps between foliage elements inside the canopy, is 1 − p. Some of these photons will be registered by the sensor on a satellite viewing the canopy along the direction, Ω. Using Stenberg’s (43) definition of a gap—a point on the leaf surface within the canopy that is visible from outside the canopy along the direction Ω—a “directional gap density,” ρ(Ω), can be defined (SI Text 2). The quantity ρ(Ω)LAI quantifies the fraction of leaf area inside the canopy that is visible from outside the canopy along a given direction. The directional gap density therefore depends on the leaf area inside the canopy and how these leaves are distributed within the canopy space; i.e., it is a function of the canopy structure.

It should be noted that a fraction of photons incident on the canopy can pass through the vegetation without experiencing a collision and thus do not participate in the radiative transfer process discussed above. A fraction of intercepted photons, i ₀, termed the canopy interceptance, initiates the process of photon–canopy interactions. This variable depends on canopy structure and can vary with the solar direction. However, it is close to unity in the case of dense vegetation canopies. The wavelength-dependent leaf albedo, ω _λ, along with three spectrally invariant (wavelength-independent) quantities—canopy interceptance, recollision probability, and directional gap density—determines the angular patterns of reflected and diffusely transmitted radiation fields (SI Text 2).

The three spectrally invariant parameters can be combined into one variable, a directional area scattering factor (DASF),

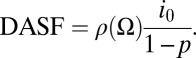This variable is the canopy BRF if the foliage does not absorb radiation (SI Text 2). In this case, photons travel between interactions until they exit the canopy. The factor i ₀/(1 − p) is the mean number of interactions before a photon exits the canopy (31, 37, 38). Multiply scattered photons thus densely fill the 3D canopy space and consequently sample a significant portion of foliage area. The mean number of interactions therefore provides an estimate of the total area of leaves (SI Text 2). Thus, DASF ∼ ρ(Ω)LAI. It is an estimate of the ratio between the leaf area that forms the canopy boundary as seen along a given direction and the total (one-sided) leaf area. Thus, the DASF actually characterizes the texture of the canopy’s “upper boundary.” In nonabsorbing canopies, the exitant radiation field is determined entirely by the structural construction of the vegetation canopy.

In reality, foliage absorbs solar radiation. Absorption exhibits a strong spectral dependency. This causes a deviation between the measured BRF and DASF. At weakly absorbing wavelengths, however, the effect of multiple scattering is strong. For example, in the NIR (800–850 nm) spectral band where foliage absorbs little radiation, a photon can undergo up to 10 interactions before it either is absorbed or exits the canopy (figure 3a in ref. 31). Consequently, incoming photons in this spectral region permeate the vegetation canopy, from the top to the bottom, and the more interactions the photons undergo, the more densely scattered photons fill the 3D canopy space. Thus, the upper and lower sides of the leaves are illuminated by multiply scattered photons. This is similar to the radiative transfer in a nonabsorbing canopy. However, the number of photons scattered by leaves is reduced due to absorption. Scattered photons can be treated as radiation sources on foliage surfaces. The magnitude of these sources depends on the leaf albedo. In weakly absorbing wavelengths, the exitant radiation field becomes dependent on both canopy structure and leaf albedo.

The recollision probability and DASF can be retrieved from spectral BRF if leaf albedo at two or more weakly absorbing wavelengths is known (SI Text 2), but such information is not available when interpreting satellite data. Therefore, our next step is to show that whereas leaf albedo is required to obtain two structural variables, ρ(Ω)i ₀ and 1 − p, their ratio, which defines the DASF, can be estimated from the BRF spectrum in the 710- to 790-nm interval without prior knowledge or ancillary information regarding leaf scattering properties. To understand this, we begin with an analysis of how radiation interacts with individual leaves.

Spectral BRF in the Interval Between 710 and 790 nm Is Required to Derive DASF and Remove the Effect of Canopy Structure.

Radiation scattered by a green leaf includes information from two dissimilar sources—the surface and the interior of the leaf (SI Text 3). In the PAR, the amount of radiation exiting from the leaf interior is mainly governed by the photosynthetically active pigments and decreases with their increasing concentrations. In the NIR, where such pigments do not absorb and there is no significant absorption by water, the main factors determining scattering from the leaf interior are its anatomical structure and the amount of dry matter. The latter exhibits a weak but significant absorption (44). The leaf cuticle acts as a “barrier” for photons to enter the mesophyll and be absorbed, thus tending to increase the leaf albedo. The fraction of radiation incident on leaf surface that does not penetrate the leaf is determined by leaf surface properties. This fraction of reflected radiation is largely wavelength independent and varies with the direction of incident radiation (22, 23, 25, 28).

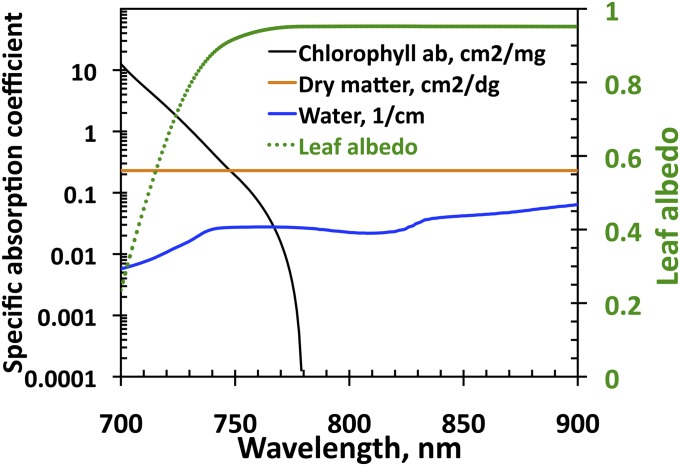
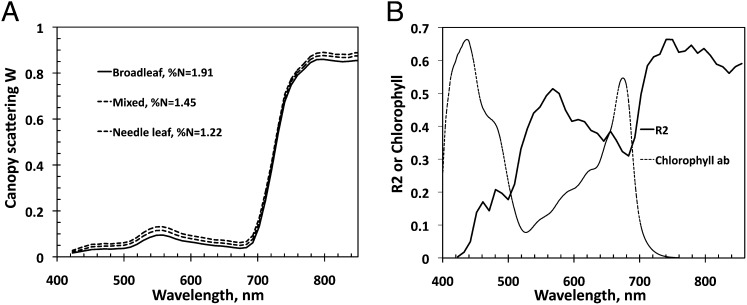
In the interval between 710 nm and 800 nm, the spectral behavior of the radiation scattered from the leaf interior is mainly determined by the absorption spectra of chlorophyll and dry matter (Fig. 4). The chlorophyll absorption spectrum declines rapidly with wavelength and vanishes at about 770 nm. This generates a sharp jump in the spectrum of leaf albedo from its minimum to a plateau around 800 nm. The magnitude of this plateau is controlled by the amount of dry matter and mesophyll structure. The dry matter exhibits little absorption and its spectrum is flat in this spectral range. In this spectral interval, leaf scattering is strong enough to trigger the multiple-scattering process that has significant impact on canopy reflectance.

Fig. 4.

Absorption spectra of chlorophyll ab (in cm²/mg), dry matter (in cm²/dg), and water (in cm⁻¹) (vertical axis on the left side) and spectrum of leaf albedo (vertical axis on the right side) from the PROSPECT-5 model (45). In these units values of typical concentrations of these absorbing pigments are on the order of 0.05. Impact of water absorption can be neglected.

Empirical (33, 46) and theoretical (39) analyses show that the spectral distribution of radiation reflected from the leaf interior in the interval between 710 nm and 790 nm is related to a known intrinsic leaf scattering spectrum and the wavelength-independent within-leaf recollision probability. This is similar to how the canopy reflectance is related to the recollision probability and leaf albedo (SI Text 4). This intrinsic leaf reference spectrum is mainly determined by the absorption spectra of chlorophyll and dry matter (Fig. 4), whereas the within-leaf recollision probability is a function of their concentrations and mesophyll structure. Technically, it means that the BRF in the 710- to 790-nm spectral interval can be expressed in terms of either actual leaf albedo and spectral invariants—the recollision probability and directional gap density—or the known reference spectrum and the spectral invariants transformed to new values, which become dependent on canopy structure, leaf surface properties, mesophyll structure, and amount of chlorophyll and dry matter (SI Text 5). It was found (33), however, that the ratio, ρ(Ω)/(1 − p), is independent of the leaf spectrum used to express the BRF (SI Text 5). This property underlies a simple algorithm for retrieving the DASF from the BRF spectrum in the 710- to 790-nm spectral interval, which does not rely on information about leaf scattering properties. It was used to generate DASF values from National Aeronautics and Space Administration (NASA)’s Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) data across all study areas. Technical details are given in SI Text 5 and Fig. S1A. Note that this technique results in the sensitivity of the DASF to leaf surface properties (SI Text 5).

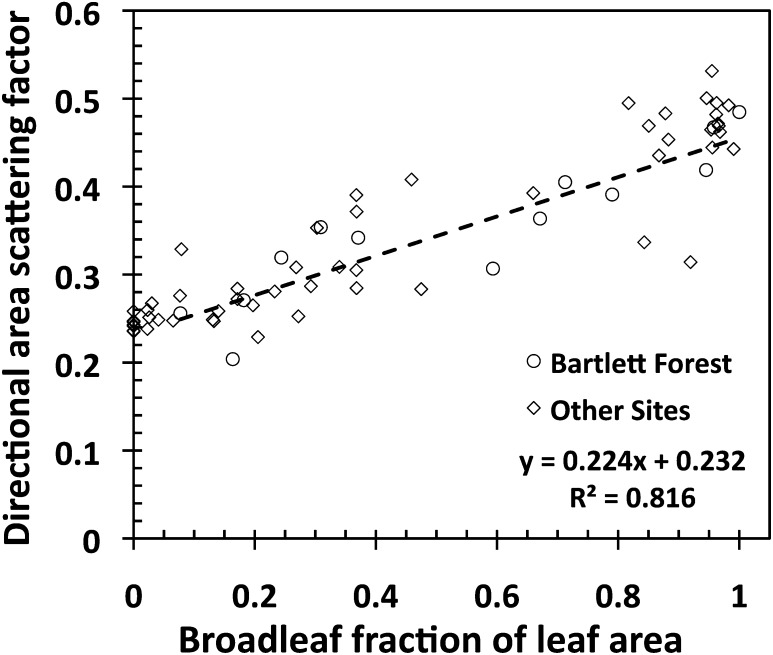
Fig. 5 shows a strong positive correlation between the DASF in the zenith direction and BfLAI. In this example, the nadir-viewing AVIRIS sensor can see about 25% of the foliage area of conifer forests. This is due to dense packing of needles in shoots. In a broadleaf forest, the flat leaves allow the sensor to see up to 50% of its leaf area. These differences can be attributed also to the topology of the upper surface of the canopy (33). According to common assumptions, broadleaf trees have spherical- to ellipsoidal-shaped crowns whereas the needle species are ellipsoidal to conical in shape. In broadleaf forests, the crowns form a fairly smooth or continuous canopy upper surface. This feature lowers the likelihood of photons escaping the canopy through gaps in oblique (i.e., off-zenith) directions. Gaps, as seen upward from leaf surfaces, are more likely to be concentrated around the vertical direction. In needle-leaf forests, the upper canopy exhibits high heterogeneity because of pointed tree crowns (47). This increases the probability of seeing a gap from foliage surfaces in off-zenith directions and distributes the gaps over a wider range of directions, thus lowering the gaps in any particular direction. Thus, the compositional mix of needle- and broadleaf species in a canopy determines a positive tendency in the near-zenith DASF from pure needle- to pure broadleaf forests. A detailed analysis of its sensitivity to conical- and ellipsoidal-shaped trees can be found in ref. 33, figure 8.

Fig. 5.

Correlation between the directional area scattering factor (DASF) in the zenith direction and broadleaf fraction of leaf area. The regression line is for the Bartlett Forest for which BfLAI values were obtained from in situ species fractions of the canopy leaf dry mass. Values of the BfLAI for other sites were obtained by converting %BN data (SI Text 1). The regression line for all plots is y = 0.231x + 0.239, R ² = 0.835.

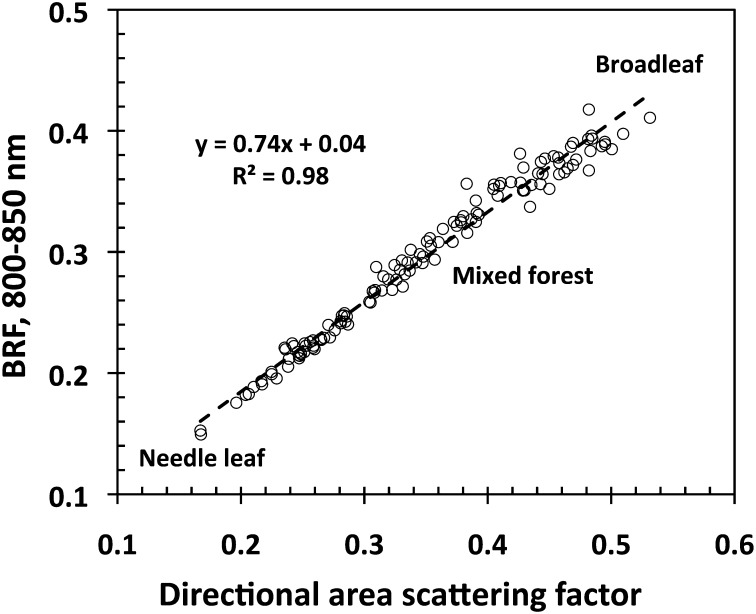
Fig. 6 shows that BRF in the NIR spectral band (800–850 nm) is almost proportional to the DASF, a parameter that describes reflectance of nonabsorbing canopies. As discussed earlier, this is the effect of multiple scattering at weakly absorbing wavelengths, which makes the canopy radiative regime very similar to that of the nonabsorbing canopy. Note that the canopy radiative regimes differ significantly between strongly absorbing, e.g., PAR region, and weakly absorbing wavelengths. This can result in weak or no correlation between BRF and DASF at absorbing wavelengths. The deviation of canopy BRF from its nonabsorbing counterpart DASF must, however, be due to leaf absorption. Recall that only photons that enter the leaf interior can be absorbed, and the fraction of those photons is determined by leaf surface properties. Therefore, the difference between wavelength-independent DASF and BRF spectra is a function of leaf interior and leaf surface properties. Thus, the DASF provides critical information to remove the effect of canopy structure on the relationship between hyperspectral canopy reflectance and leaf properties. Fig. 6 also demonstrates that the canopy structure is the dominant factor responsible for variation in NIR BRF under the saturation conditions. This extends the empirical result from data collected at the Bartlett site, which documents the importance of canopy structure, to all study areas. Consequently, without knowledge of canopy structure, NIR and/or SW broadband satellite data cannot be directly linked to leaf-level processes and therefore used to monitor foliar nitrogen from space.

Fig. 6.

Relationship between canopy BRF in NIR spectral band (800–850 nm) and directional area scattering factor (DASF) in the zenith direction for 129 plots across our study area. The DASF is a key structural parameter responsible for variation in NIR BRF.

Spectral Reflectance Corrected for Forest Structure Effect Is Negatively Related to %N.

We use the BRF to DASF ratio to suppress the sensitivity of BRF to canopy structure. This ratio is an estimate of a well-defined physical quantity called the canopy scattering coefficient, W _λ (SI Text 6), i.e., the fraction of intercepted radiation that has been reflected from, or diffusively transmitted through, the vegetation (35, 39, 48). The canopy scattering coefficient is a function of leaf interior and surface properties.

As Fig. 7A illustrates, the scattering coefficient mimics the shape and magnitude of typical leaf albedo spectra documented in the literature (49). It decreases with increasing canopy foliar %N. Unlike BRF that exhibits either positive (Fig. 3) or no relation (SI Text 6 and Fig. S2) with nitrogen in the PAR and NIR regions, the scattering coefficient is negatively correlated with foliar %N at all wavelengths in the interval between 423 and 855 nm; i.e., the higher the foliar nitrogen concentration is, the more the foliage absorbs. This is illustrated in Fig. 7B , which shows the R ² coefficient of W _λ vs. %N negative correlation as a function of wavelength. Notably, the R ² mirrors the chlorophyll absorption spectrum. This can be interpreted as follows. When leaf absorption is high, the diffuse component of the leaf albedo decreases, and consequently the surface scattering dominates (SI Text 3 and Eq. S3.2). Conversely, when leaf absorption is low, the surface contribution is reduced compared with the diffuse component. In Fig. 7B we see that the principal foliage pigments absorb in the same region, in the vicinity of 445 nm (50). This results in a negligible contribution from the diffuse component of the leaf albedo, thus making the leaf albedo, and consequently W _λ, more sensitive to foliage surface properties rather than its interior (SI Text 3). The opposite is seen where absorption spectra of the principal pigments, except chlorophyll, decline rapidly and vanish before the green spectral region (555 nm). An increase in chlorophyll absorption near the red spectral region (645 nm), followed by a sharp decrease beyond, is accompanied by the respective increase and decrease of the contribution of surface reflected radiation to the leaf albedo and consequently its sensitivity to the leaf interior. This behavior is consistent with observed patterns of leaf scattering; that is, the contribution of the leaf surface reflected radiation to the leaf albedo is small when its diffuse component is large, as in the NIR region, and is large when the diffuse component is small, as in the pigment-absorbing blue and red spectral bands (23, 26, 28). This result suggests that leaf surface properties have an impact on canopy BRF.

Fig. 7.

(A) Canopy scattering coefficient W _λ as a function of wavelength for three plots at the Bartlett Forest representing broadleaf (%N = 1.91), mixed (%N = 1.45), and needle leaf (%N = 1.22) forests. (B) Spectral variation in the R ² coefficient of W _λ vs. %N negative correlation (solid line) and absorption coefficient of chlorophyll (dotted line). The absorption spectrum at 1 nm spectral resolution from the PROSPECT-5 model (45) is normalized to match the maximum R ² value.

Conclusions

The previously reported positive correlation between forest canopy reflectance and foliar %N (11) is a counterintuitive example of the physics of radiative transfer in a medium—an increase in the amount of absorbing foliar constituents enhances absorption and correspondingly decreases canopy reflectance. This physical argument suggests that other factors, i.e., canopy structure, which suppress not only the absorption effect, become dominant determinants of the system’s behavior. Our analyses reinforce this physically based deduction: The distribution of gaps through which photons escape the canopy is the dominant mechanism that generates a positive correlation between observed NIR canopy reflectance and %N. The distribution of gaps can be characterized by the DASF, which is an estimate of the ratio of the leaf area that forms the canopy upper boundary, as seen along a given direction, to the total leaf area. The DASF “distils” the positive relationship between reflectance and %N (Fig. 6), and the residual information in the reflectance that is not due to this structural variable is negatively related to foliar nitrogen in the PAR and NIR spectral regions (Fig. 7). This finding suggests that the observed NIR BRF vs. %N positive correlation conveys no information about %N. Thus, to infer leaf biochemical constituents, e.g., N content, from remotely sensed data, the DASF provides critical information for correction of canopy structural influences. For vegetation canopies with a dark background, or sufficiently dense vegetation where the impact of canopy background is negligible, the DASF can be directly retrieved from the BRF spectrum in the 710- to 790-nm interval, without involving canopy reflectance models, prior knowledge, or ancillary information regarding leaf scattering properties.

In addition, characteristics of the leaf surface are also important to remote sensing of foliage pigments. Radiation reflected from leaf surfaces does not penetrate the leaf and therefore conveys no information about its interior. Radiation reflected by the leaf surface can vary greatly between species (23, 29). The canopy reflectance therefore becomes sensitive to both species-specific canopy architecture and leaf surface features. This further decreases the ability to remotely sense canopy foliar nitrogen content from hyperspectral data. Reflectance measurements alone cannot distinguish radiation scattered from leaf surface and interior tissue (24). Polarization measurements may be useful to correct for this additional source of uncertainty because radiation reflected from the leaf surface is partly polarized whereas that from the leaf interior is not.

Hyperspectral remote sensing of leaf biochemical constituents relies on the fact that scattering from a leaf responds differently at different wavelengths to changes in leaf properties such as pigment concentrations, other chemical constituents, internal structures, and leaf surface characteristics. Three-dimensional radiative transfer theory provides the most physically consistent linkage between leaf scattering and canopy reflectance. Most of the existing approaches to interpret reflectance spectra, however, neglect this fundamental linkage. This can lead to misinterpretation of satellite data. Three-dimensional radiative transfer should therefore be an integral part of hyperspectral remote sensing to ensure success of hyperspectral missions, e.g., the planned NASA Hyperspectral Infrared Imager (51) mission recommended for implementation by the US National Research Council (52).

Materials and Methods

Field Data.

This research is focused on six sites located in the eastern United States and Washington State (Table 1). The sites represent closed-canopy forests and are characterized by a strong gradient in the proportion of needle- and broadleaf species. Their detailed description can be found in ref. 12. Data used in our research were sampled between 2001 and 2006 during the peak growing season on 85 plots across the six research sites (Table 1) according to a protocol documented in refs. 11, 12, and 53. At each 20 × 20-m plot green leaves were sampled from several heights in the canopy and their mass-based foliar nitrogen concentration (in grams per 100 g of dry foliage mass) and dry mass per foliage area (in g⋅m⁻²) were measured under laboratory conditions. Foliage area was defined as one-sided leaf area for deciduous species and as the projected needle area for conifers (11, 12, 53). Foliar biomass distribution by species was determined using an optical camera point-quadrat method combined with leaf mass per area measurements (53). Plot level foliar %N is calculated as the mean of foliar N concentration among all species, weighted by species canopy foliar mass fraction (11, 12). The accuracy of the methodology was assessed with data collected at the Bartlett Experimental Forest. The estimated foliar mass-based nitrogen concentrations compared well with values derived from litter-fall collection (11, 12, 53). A detailed description of the approach and its validation can be found in refs. 12 and 53.

Species Composition and %N.

In our analysis we stratified trees into needle- and broadleaf species. An equation for plot-level foliar %N takes the form

where %n _N and %n _L represent the mass-based nitrogen concentration of an average needle and leaf, respectively, and BfM is the broadleaf fraction of the canopy leaf dry mass (in g/g). This variable can be expressed as

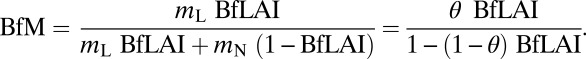Here m _L and m _N are the dry mass per foliage area of an average leaf and needle (in g⋅m⁻²), θ = m _L/m _N, and BfLAI is the broadleaf fraction of leaf area. Note that the BfM is an increasing function of BfLAI. The ratio θ determines its convexity. For the Bartlett Forest, %n _L = 2.17 (SD = 0.4), m _L = 66.3 (SD = 14.2), %n _N = 1.24 (SD = 0.26), m _N = 224.2 (SD = 67.8), and θ = 0.30. These estimates are based on data reported in ref. 53. A solid line in Fig. 2 shows plot-level %N as a function of BfLAI.

Data available to this research included the canopy foliar %N (all sites) and its portions, %BN, from broadleaf species (all sites except Wind River Experimental Forest); i.e., %BN = %n _L⋅BfM. For the Bartlett Forest, distribution of the species canopy foliar dry mass fraction for 14 plots was also available. These data and species leaf mass per area (53) were used to obtain BfM and BfLAI for 13 plots in the Bartlett Forest for which AVIRIS BRF data (next section) were available. A Tikhonov regularization technique (54) is used to reconstruct field BfLAI from %BN data for the remaining sites (SI Text 1). LAI data collected in August of 2002, at 25 m resolution as part of the Bigfoot MODIS validation campaign, were used for the Harvard Forest (55). LAI values of all sites except Austin Cary Memorial Forest (LAI = 2.9) exceeded 4.5 (11).

Airborne Data.

Hyperspectral data were acquired by NASA’s AVIRIS in May–June 2002 and August 2003. AVIRIS is a nadir-viewing sensor that registers radiance in 224 spectral bands, from 400 to 2,500 nm, with a 10-nm nominal bandwidth (56). Data spatial resolution is ∼17 m. A standard processing system (12) is used to obtain atmospherically corrected BRF. We excluded noisy data below 423 nm and used data from the 423- to 855-nm spectral region. The AVIRIS includes four sensors, two of which overlap at ∼655 nm. Duplicate bands at 655.09, 664.79, and 675.78 nm were not used. Mean AVIRIS BRF over [800, 850 nm] weighted by a normalized solar radiance spectrum is taken as NIR BRF (11).

To account for geolocation uncertainties, we calculated the mean BRFs and their SDs over a 3 × 3 pixel patch (51 × 51 m) centered on plot locations. We used the mean spectral BRF to characterize the reflectance of a plot. The most probable value of the coefficient of variation (SD-to-mean ratio) was taken as the relative precision of the observations. Its value was specified from the histogram of the coefficient over all plots and wavelengths between 440 nm and 1,000 nm. The histogram has a sharp peak at 4.8% (SD = 2.1%); 78% of the values are around the peak and below 10%. The relative precision of AVIRIS BRFs is set to 4.8%.

Airborne Laser Vegetation Imaging Sensor (LVIS) data were acquired in the summer of 2003 over Howland, Harvard, and Bartlett Forests (57). We use the LVIS H100 product as the height measure. Point data collected from the H100 height measures are sampled into a raster grid dataset at a 28-m nominal resolution, using a window average scheme (42). The Bigfoot LAI data and LVIS H100 height are used to generate Fig. 1.

Accuracy Metrics.

We used the relative root mean square error (RRMSE) to quantify the proximity between observed, X, and estimated, Y, vectors; i.e.,

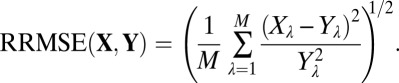Here X _λ and Y _λ represent components of X and Y. A value of RRMSE below the relative precision indicates a good accuracy.