Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions

Abstract

Recent methods have revealed that cells on planar substrates exert both shear (in-plane) and normal (out-of-plane) tractions against the extracellular matrix (ECM). However, the location and origin of the normal tractions with respect to the adhesive and cytoskeletal elements of cells have not been elucidated. We developed a high-spatiotemporal-resolution, multidimensional (2.5D) traction force microscopy to measure and model the full 3D nature of cellular forces on planar 2D surfaces. We show that shear tractions are centered under elongated focal adhesions whereas upward and downward normal tractions are detected on distal (toward the cell edge) and proximal (toward the cell body) ends of adhesions, respectively. Together, these forces produce significant rotational moments about focal adhesions in both protruding and retracting peripheral regions. Temporal 2.5D traction force microscopy analysis of migrating and spreading cells shows that these rotational moments are highly dynamic, propagating outward with the leading edge of the cell. Finally, we developed a finite element model to examine how rotational moments could be generated about focal adhesions in a thin lamella. Our model suggests that rotational moments can be generated largely via shear lag transfer to the underlying ECM from actomyosin contractility applied at the intracellular surface of a rigid adhesion of finite thickness. Together, these data demonstrate and probe the origin of a previously unappreciated multidimensional stress profile associated with adhesions and highlight the importance of new approaches to characterize cellular forces.

Understanding how cells generate and respond to mechanical forces is critical in cell biology. In anchorage-dependent cells, myosin-II cross-links and contracts actin filaments to generate tension, which is transmitted to the extracellular matrix (ECM) via integrin-mediated adhesions (1–4). The traction stresses (force per area) exerted between adhesions and the ECM drive cell spreading and migration in morphogenesis (5, 6), wound healing (7), and tumor metastasis (8, 9). In addition, these stresses induce changes in adhesion signaling, cytoskeletal reorganization, and gene expression (4, 10–13), thereby regulating functions such as proliferation (14, 15) and differentiation (16, 17).

Measurements of cellular traction stresses have advanced our understanding of mechanotransduction and enabled quantitative modeling of cellular interactions with the ECM (18–20). These measurements reveal that cells exert inwardly oriented tractions at their periphery, where focal adhesions grow centripetally (3, 4, 21). However, the vast majority of methods (collectively termed traction force microscopy, TFM) have assumed that cells exert only shear forces (parallel to the plane of the substrate). Interestingly, recent studies have demonstrated that cells on planar substrata exert significant vertical (normal) tractions, indicating that patterns of cellular force generation are more complex than previously thought (22–25). However, mapping these multidimensional traction stresses with a high spatiotemporal resolution has been challenging, and there is no clear agreement on the dynamics and the location of the normal stresses. Thus, how normal and shear traction stresses are integrated and what type of net forces are produced relative to focal adhesions and the actin cytoskeleton remain poorly understood.

In this study, we developed a high-resolution 2.5D TFM [measurement of 3D forces exerted by cells on 2D planar surfaces, as opposed to cells fully encapsulated within a 3D matrix (26)] to explore the precise nature of cellular forces applied to the ECM. After fully characterizing the resolution of both the shear and normal tractions using numerical simulations, we applied this approach to mouse embryo fibroblasts (MEFs) expressing EGFP-tagged paxillin, actin, or plasma membrane to measure the multidimensional traction stresses associated with focal adhesions and the actin cytoskeleton. In addition, we generated a finite element model (FEM) of the focal adhesion and pliable substrate and performed 3D super-resolution imaging to explore the most plausible means by which such moments may be generated subject to geometrical constraints within a very thin (200–300 nm) cellular lamella.

Results

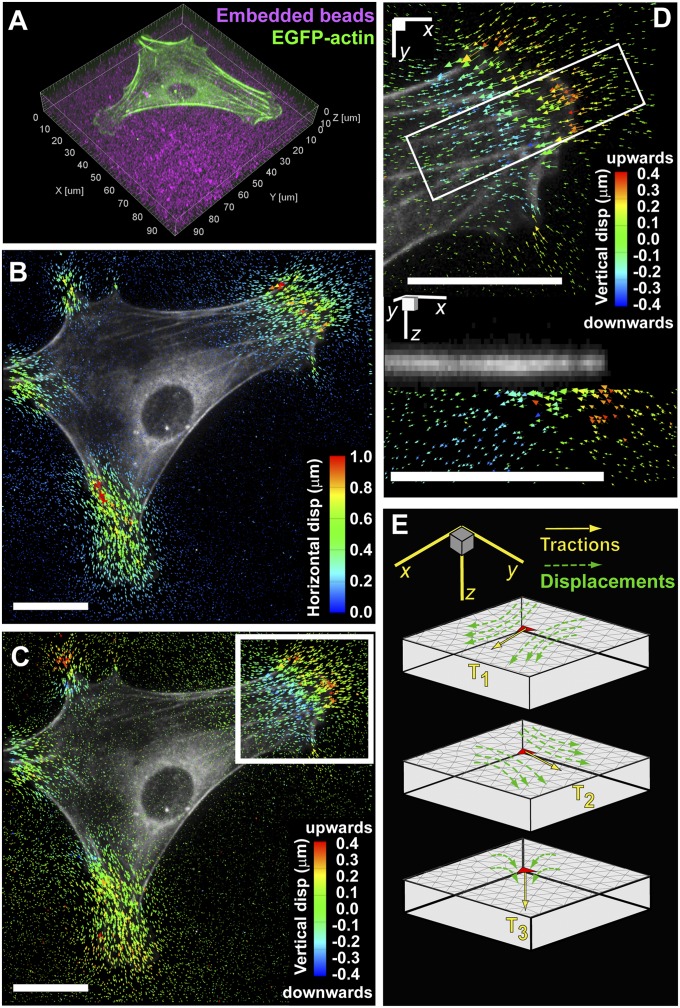
To observe the distribution of 3D substrate deformations relative to cytoskeletal structures, we investigated MEFs expressing EGFP-actin cultured on arginine-glycine-aspartic acid-serine (RGDS)–conjugated PEG hydrogels containing fluorescent beads (Fig. 1A and Movie S1). The elastic modulus of hydrogels used in this study was 6,500 Pa, unless specified otherwise. MEFs on PEG hydrogels assumed morphologies comparable to those on traditional culture substrates (e.g., glass or plastic), exhibiting anisotropic protrusions and polarization. Cells were flat; super-resolution structured illumination microscopy (SIM) showed that lamellae are ∼180–280 nm tall, whereas the primary increase in height (up to 2–3 μm) occurs only near the nucleus (SI Appendix, Fig. S1). The 3D displacement field within the substrate was determined by tracking beads before and after lysing the cell with detergent. We observed significant in-plane and out-of-plane displacements underneath the thin cell periphery, whereas no displacements (neither in-plane nor out-of-plane) could be detected under the cell nucleus (Fig. 1 B and C and Movie S2). In agreement with previous implementations of 2D traction force microscopy (2D TFM), the shear components of the displacements were also present only at the cell periphery (3, 21). Closer inspection of the vertical displacements revealed that cells pull the hydrogel upward under the leading edge and push downward ∼10 μm behind the leading edge (Fig. 1D).

Fig. 1.

Experimental setup and computational methods. (A) Volume rendering of an EGFP-actin–expressing mouse embryonic fibroblast (MEF) fully spread and polarized on a planar PEG hydrogel with fluorescent beads imbedded (magenta). (B and C) Shear and normal components of bead displacement trajectories color-coded by magnitude. (D) Inset outlined in C magnified showing the normal component of bead displacement trajectories. The bottom figure is the cross-sectional view of the inset outlined above showing the multidimensional bead displacement trajectories. (E) Schematic of the finite element model to reconstruct the Green’s function. (All scale bars, 20 μm.)

To quantify the traction stress from the displacement field, we followed a previously described procedure (26). Briefly, a tetrahedral mesh of the hydrogel volume under the cell was generated. Unit tractions were then applied in each of the Cartesian directions at each facet on the surface, and the induced displacement fields were recorded after solving the forward problem for stress equilibrium (Fig. 1E). These traction-displacement mappings were then used to generate a discretized Green’s function for the hydrogel volume that can be inverted and regularized [through use of the L-curve criterion (27)] to solve for cell tractions. We characterized both the resolution and sensitivity limits of the shear and normal traction reconstructions under experimentally relevant levels of noise, bead density, and material properties (SI Appendix, Figs. S2–S12). Our approach was able to capture spatially isolated loadings with a full-width half-maximum of ∼10 μm and traction magnitudes down to 300 Pa. Tractions distributed over smaller spatial regions were significantly underestimated and spatially averaged (SI Appendix, Figs. S5–S8). We also investigated our ability to recover sinusoidally oscillating loadings with wavelengths between 5 and 20 μm (SI Appendix, Figs. S9–S12) and were able recover oscillatory loadings of 130 Pa at wavelengths of 14 μm. Although the average element area of the grid on which tractions are computed is significantly smaller (∼0.9 μm²), this information does not fully capture the traction resolution (analogous to how the pixel size of a camera does not necessarily reflect the resolution to optically resolve two point sources in an image). In contrast, the combination of simulated loadings and an experimentally relevant recovery process accurately captures both the spatial resolution and sensitivity of the reported tractions. It should be noted that for sinusoidally oscillating loadings the traction resolution is anisotropic; recovered normal tractions and shear tractions that are directed orthogonal to the spatial axis of variation had ∼25% lower errors than shear tractions directed parallel to the axis of spatial variation (SI Appendix, Fig. S10). Finally, reported tractions in the range of 100–300 Pa that are near the 10-µm resolution limit likely represent an underestimated and spatially blurred description of the true traction field but are still statistically significant (as confirmed by a bootstrap analysis of the reported tractions) (SI Appendix, Fig. S13). SI Appendix contains a complete discussion of resolution, sensitivity, and significance.

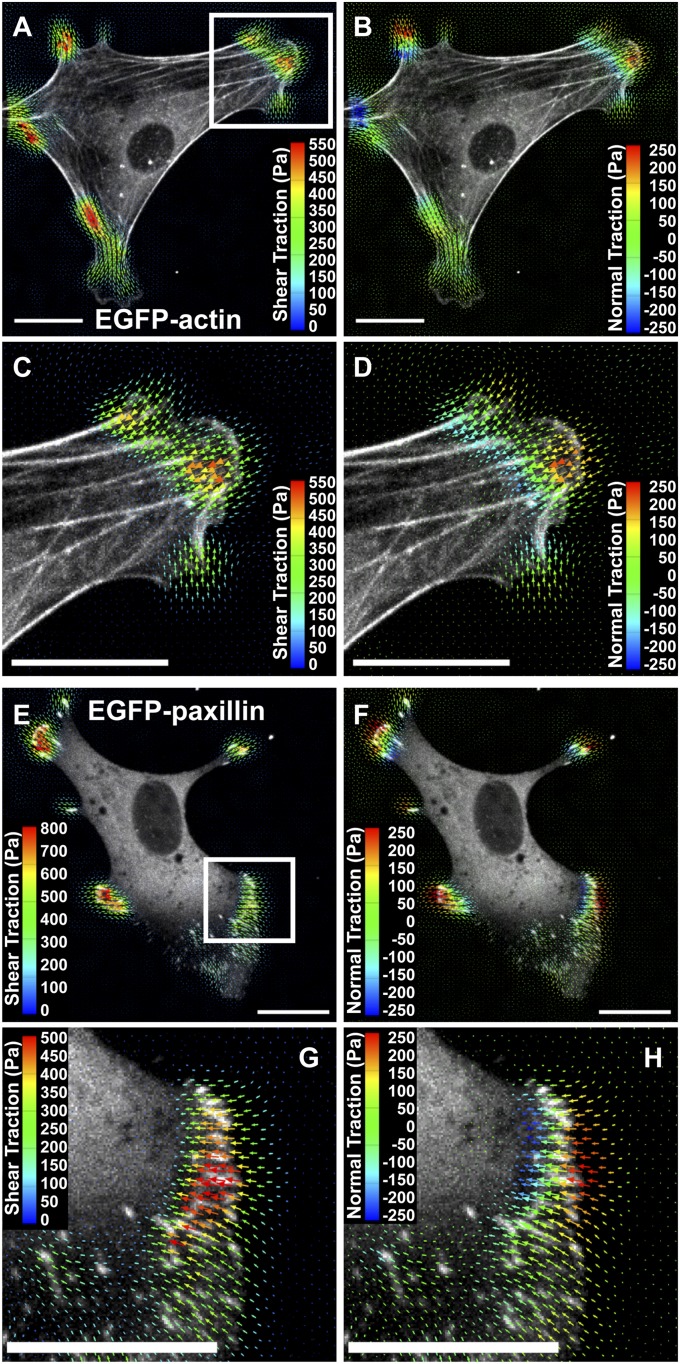
Applying this approach to cell-induced displacement fields, we found that both shear and normal cellular traction stresses were limited to the cell periphery, whereas negligible tractions were detected in the perinuclear and nuclear regions (Fig. 2 A and B and Movie S3). Maximum shear tractions (550 Pa) occurred at the termini of stress fibers (Fig. 2C); however, highest upward and downward normal tractions were concentrated ∼5 μm distal (toward the cell periphery) and 5 μm proximal (toward the cell center) to the stress fiber ends, respectively (Fig. 2D and Movie S3). These normal tractions (±250 Pa) were typically 30–50% of shear values. Variation of the regularization parameter used for traction reconstruction changed the overall magnitude of both shear and normal forces but did not alter the general conclusions (SI Appendix, Fig. S14). These findings suggested that torque was being applied to the substrate in the vicinity of focal adhesions, which anchor the ends of stress fibers and serve as the primary force-transmitting structure to the ECM. To investigate this possibility, we transfected MEFs with paxillin-EGFP, an adapter protein that localizes to integrin-mediated adhesions (28). We observed paxillin-EGFP–containing focal adhesions near the cell periphery and maximal shear tractions directly under the adhesions (Fig. 2 E and G). Moreover, we detected upward and downward traction stresses just distal and proximal of the adhesions, respectively, indicating that focal adhesions indeed served as pivot points for rotational moments (Fig. 2 F and H). These moments were present at focal adhesions in both the leading lamella and in retracting extensions of cells (Fig. 2 E and F), and their magnitudes mirrored changes in adhesion density (number of adhesions per unit area) due to growth and disassembly (Movies S4 and S5). Taken together, these results reveal that shear tractions and rotational moments are generated under and around focal adhesions, respectively, demonstrating a more complex and intrinsic force distribution than described previously (3, 19, 29).

Fig. 2.

Multidimensional traction stress and cytoskeletal localization. (A and B) Shear and vertical traction stress vectors generated by a MEF expressing EGFP-actin. The vectors are color-coded by magnitude. Both components of traction stresses are localized to the cell periphery. (C and D) Inset outlined in A magnified showing traction stress vectors color-coded by shear and normal components. Maximum shear tractions are detected at the termini of actin stress fibers, whereas the upward and downward normal tractions are applied in front of and behind the fiber ends, respectively. (E and F) Shear and normal traction stress vectors generated by a MEF expressing paxillin-EGFP are localized to focal adhesions in broad peripheral regions and a narrow retracting tail. (G and H) Inset outlined in E magnified showing shear and normal traction stress vectors relative to focal adhesions. Maximum shear stresses are detected directly over elongated focal adhesions, whereas the upward-to-downward gradient of normal stresses forms a rotational moment around the adhesions. (All scale bars, 20 μm.)

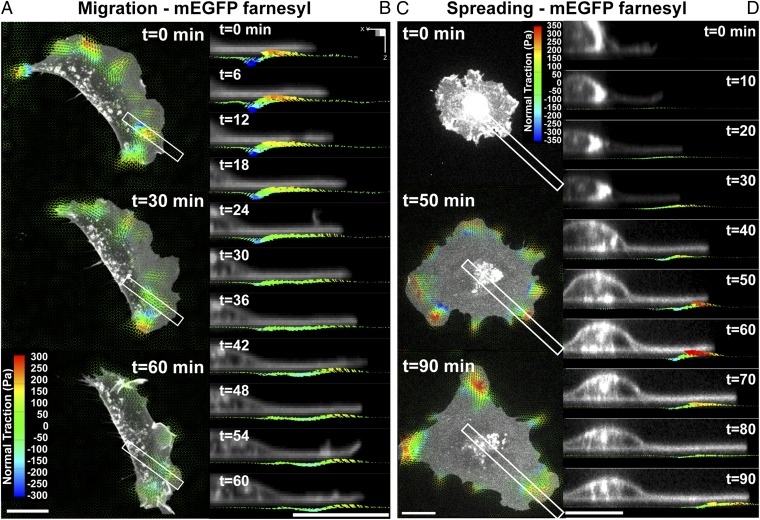
To examine how rotational moments around focal adhesions evolved during dynamic cellular processes, we acquired time-lapse volumetric stacks during migration and initial spreading. MEFs were transfected with mEGFP-farnesyl to visualize cell morphology dynamics (Movie S6). Similar to stationary cells, both migrating and spreading cells generated rotational moments localized to both protruding and retracting regions with normal tractions reaching ∼±350 Pa. In migrating cells, we found that both shear and normal tractions moved with the extending leading edge (Fig. 3 A and B and Movies S7 and S8). This dynamic colocalization of force distributions at the cell periphery was also observed during cell spreading. Cells spread initially in an isotropic manner and flatten against the substrate as they become polarized, similar to what has been previously described (30). We observed the simultaneous emergence of both shear and normal tractions shortly (∼20 min) after cells adhered to the substrate (Fig. 3 C and D). Both the shear and normal tractions were restricted to the leading lamella and increased substantially during the first hour of spreading. In contrast to previous studies that showed substantial downward compression under the nucleus, we found no tractions under the cell nucleus, but observed instead the presence of outward “waves” of rotational tractions that perhaps emerged initially in the perinuclear region but quickly propagated outward, remaining localized with the leading edge (Fig. 3D and Movies S9 and S10).

Fig. 3.

Dynamic measurements of 2.5D traction stress. (A) Time-lapse images depicting traction stress vectors color-coded by the normal component generated by a migrating MEF expressing mEGFP-farnesyl. As the cell moves (toward right), rotational moments are applied in the protruding front as well as the sides. (B) Time-lapse cross-sectional views of the inset outlined in A showing dynamic rotational moments that move with the thin protruding cellular body during cell migration. (C) Time-lapse images of mEGFP-farnesyl–expressing MEF undergoing spreading. No significant vertical traction stresses are detected until the cell extends thin protrusions and flattens against the substratum. Minimal tractions are detected under the nucleus. (D) Time-lapse cross-sectional views of the inset outlined in C. Comparable to migrating cells, rotating moments progress outward with the leading edge and remain localized to the cell periphery. (All scale bars, 20 μm.)

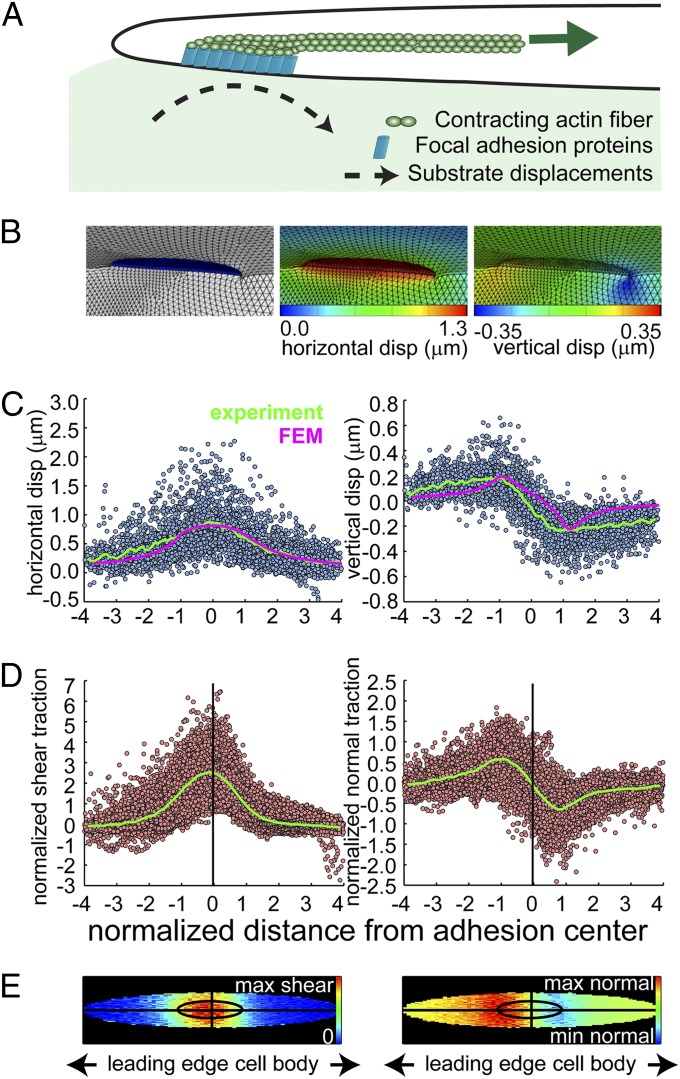
Because it was not immediately apparent how focal adhesions in a thin (∼200 nm tall) cellular lamella could generate substantial out-of-plane moments, we generated a FEM derived from our current knowledge of cell adhesions. Based on a recent interferometric photoactivated localization microscopy (iPALM) study (31) and our SIM data (SI Appendix, Fig. S1), the focal adhesion was set at 150 nm in height and physically coupled to the elastic PEG hydrogel, which was modeled as a Neo-Hookean solid (SI Appendix, Fig. S15). In the simplest scenario, we applied a uniform shear load to the top surface of the adhesion plate to mimic actin-myosin filaments pulling on adhesions (1, 4, 12, 20) (Fig. 4A). The magnitude of this load was then scaled to induce a lateral ECM displacement of similar magnitude (∼0.5 μm) to what was observed experimentally. We found that rotational moments could be generated only if the adhesion were significantly stiffer than the underlying substrate (SI Appendix). In this setting, as the material adjacent to the adhesion is compressed, shear lag from the top of the adhesion to the substrate causes the plate to rotate, thereby generating a moment (Fig. 4B). With this model, a lateral ECM displacement of 0.5 μm corresponded to ∼200 nm vertical displacements generated at the distal and proximal ends of the adhesion (Fig. 4 B and C). These vertical displacements matched well with the experimentally observed results (averaged over 120 focal adhesions in 10 different cells), consistent with a model in which the focal adhesion rotation is generated primarily by horizontal tension transmitted by actin stress fibers at the intracellular surface of adhesions. Interestingly, the experimental vertical displacements recovered slowly at the proximal end, which may indicate that other cytoskeletal structures, such as cortical actin, are also contributing to the compression into the ECM, a phenomenon that was not modeled. The nature of shear and normal traction stresses relative to the focal adhesion was highly consistent. Compiling the data from the multiple adhesions, we found that the maximum shear traction is applied symmetrically about the adhesion center (Fig. 4 D and E). In addition, the maximum upward and downward tractions localized to the distal and proximal ends of adhesions, respectively, demonstrating the characteristic rotational moment. Both the shear and normal tractions spread slightly beyond the adhesion boundaries, although it is currently unclear whether this spread is mediated by additional adhesions in the lamellipodium distal to focal adhesions, and/or whether it is due to the smoothing nature of the Green’s function that relates substrate displacements to surface tractions (Discussion and SI Appendix).

Fig. 4.

Finite element models of focal adhesion rotations. (A) Cartoon depicting the key elements in the FEM model. A contracting actin fiber generates shear traction on the upper surface of a focal adhesion (FA), which is modeled as a rigid plate connected to the PEG hydrogel. The shear load is applied uniformly on the top side of the FA, which is sufficient to induce both the horizontal and vertical substrate displacements comparable to experimental data. (B) Finite element renderings showing deformed configurations of the PEG hydrogel and focal adhesion. Contour maps along the symmetry plane show both horizontal and vertical displacements within the hydrogel. (C) Scatter plots of the measured hydrogel displacements from individual FAs (n = 121, 10 cells) with the average (green lines). Only beads residing within the first 0–2 μm of the hydrogel are shown. The x axis was normalized by the major axis of the fitted ellipse to each adhesion, so the adhesion itself spans from −1 to 1 (SI Appendix). The average FEM simulated hydrogel displacements within 0–2 μm from the hydrogel surface are shown for comparison (magenta lines, with the x axis normalized by the modeled FA length). (D) Scatter plots of the normalized experimental traction stresses from individual FAs with the average (green lines). The x axis is normalized by the fitted major axis length and the y axis of both plots is normalized by the mean shear traction surrounding each adhesion. (E) Top-down graphical maps of the averaged experimentally measured traction stresses from D with the same spatial dimensions. The inner ellipse depicts the normalized area of the FA, and the average shear and normal tractions within and outside of the FA are shown. The shape of the inner ellipse is scaled to match the mean major and minor axis lengths of the ellipses fit to the adhesions (8.3 ± 3.9 μm and 2.17 ± 0.9 μm, respectively). Note that the maximum shear traction stress is centered on the FA, whereas the maximum upward and downward traction stresses are at the distal and proximal ends of the FA, respectively.

Discussion

In this study, we developed high-resolution 2.5D TFM to investigate the multidimensional nature of cellular tractions. The spatial resolution and traction sensitivity are inherently interdependent in TFM, and we performed an extensive analysis of this key relationship, including a sensitivity curve that characterizes our method under multiple different loading conditions (SI Appendix, Fig. S8). We anticipate that providing such a curve for each TFM method will allow for comparisons of resolution and sensitivity across methods. We use our 2.5D TFM to demonstrate that cells exert dynamic rotational moments at focal adhesions and associated actin stress fibers. Cells exerted upward forces that were distal and downward forces proximal to focal adhesions, which thereby served as pivots to mediate a torque on the ECM. The locations, magnitude, and dynamics of these tractions were consistent in polarized cells, migrating cells, and spreading cells. Moreover, the normal tractions occurred at focal adhesions both in protrusions and retracting tails, suggesting that the rotational moment about adhesions is intrinsic to the structural organization of the cell–matrix interface.

Previous studies have reported downward pushing forces into the substrate that suggested a role for nuclear compression (22, 25), but we find minimal forces exerted in the nuclear and perinuclear regions. This discrepancy may result from differences in cell type (fibroblasts vs. endothelial cells or Dictyostelium), cell shape (spread vs. round), hydrogel rigidity (∼6.5 kPa in this study vs. 400 Pa, ∼4 kPa for previous studies), or spatial resolution of the different TFM methods. Indeed, we observed that downward tractions are localized in the nuclear region in cells that are in the early phase of spreading (i.e., cells that are relatively round). A similar pattern of substrate deformation has been reported from a round fluid droplet adhered to a flexible substrate (32, 33), suggesting that surface tension could contribute to this type of deformation. However, as cells spread and flatten out against the substrate, their shape departs dramatically from that of a fluid droplet and normal tractions propagate outward to localize to the cell periphery. When substrate rigidity was decreased, we found that both shear and normal tractions also decreased. Interestingly, the relative magnitude of the normal tractions compared with the shear tractions increased on less rigid hydrogels, indicating that substrate rigidity may modify how the two traction components are transmitted. On all substrate rigidities, however, shear and normal tractions were exerted primarily near the cell periphery (SI Appendix, Fig. S16). We also found in multiple cell types that the shear and normal tractions are exerted at focal adhesions, demonstrating the coupling of focal adhesions and multidimensional traction stresses (SI Appendix, Figs. S17 and S18).

The measurements of rotational moments around focal adhesions suggest a more complex pattern of stresses at the cell–ECM interface than is currently appreciated. Cell-generated tension at adhesions has been described largely as in-plane, whereby adhesion growth, actin flow, and traction stresses are coupled and exhibit correlated directional dynamics (2, 3, 21, 34). As a result, mechanotransduction processes at adhesions are proposed to be regulated predominantly by shear forces that stretch adhesion proteins and induce protein–protein interactions and signaling events (13, 19, 20, 29). Our analysis of subadhesion, multidimensional traction stress introduces additional factors to consider. These distinct mechanical loads within a single focal adhesion could contribute to the spatial structure of adhesions, for example by differentially regulating protein binding, conformational changes, and force-induced signaling (35). Tension in the distal end could promote protein unfolding and interactions (e.g., between vinculin, talin, and actin) to mediate a molecular clutch (36–39) or phosphorylation (40), whereas shearing and compression in the proximal end may induce the rapid protein exchanges that mediate focal adhesion elongation (41–44). Adhesion dynamics (turnover and lifetime) and strengthening may also be regulated differently by vertical extension, shear, and compression, depending on the size and the molecular composition of adhesions (4, 20, 45, 46). Thus, in addition to the magnitude and the rate of applied force, knowing how molecules respond to different types of stress will lead to a more complete understanding of adhesion-mediated mechanotransduction.

It is interesting to note that rotational moments have not been observed in cells encapsulated within a 3D hydrogel (26), suggesting that the moments about focal adhesions are characteristic phenomena induced by a 2D ECM. Actin is a key cytoskeletal element that transmits tension to the cell–ECM interface to generate traction stress, and its architecture is dramatically different in 2D and 3D ECMs (47). More recently, 3D super-resolution, stochastic optical reconstruction microscopy showed directly that the dorsal and ventral actin layers have dramatically different architectures in the vicinity of focal adhesions (48). This study also shows the ventral cortex can be buckled, whereas the dorsal layer is relatively smooth. These findings support a model of ventral buckling under compressive loading due to a dorsal contractile element and would agree with the slower ECM displacement recovery observed in our data (compared with our FEM model) measured near the proximal end of focal adhesions. In addition, subresolution nascent adhesions assemble in the lamellipodium and mediate attachment to the substratum at the leading edge (42). These structures may also serve as traction point sources near the distal edge of focal adhesions as actin ruffles and polymerizes, but resolving precise tractions resulting from these structures is beyond our current resolution limits. This 2D-specific organization could contribute to mechanotransduction, migration, and signaling responses uniquely observed in 2D settings (49, 50). In summary, the mappings of multidimensional cellular forces and cytoskeletal structures presented here offer another dimension to current models of cell migration and adhesion mechanobiology (10, 51–54). Future improvements to the spatial and temporal resolution of cell traction measurements in 2.5D and fully 3D settings (26), combined with subdiffraction limit imaging of the 3D cytoskeletal and adhesion architecture (31, 48), will be a critical path toward understanding how cells generate, sense, and respond to mechanical forces in a variety of physiological settings.

Materials and Methods

Cell Culture and Plasmids.

Spontaneously immortalized MEFs were cultured in DMEM (Mediatech, Inc.) with 5% (vol/vol) FBS (55) (Richard Assoian, University of Pennsylvania, Philadelphia, PA). MEFs were transfected transiently with paxillin-EGFP [Clare Waterman, National Institutes of Health (NIH), Bethesda, MD], EGFP-actin, and mEGFP-farnesyl-5 [a plasma membrane localized GFP-tagged 20-amino-acid farnesylation signal from c-Ha-Ras (56)] (Michael Davidson, Florida State University, Tallahassee, FL) using Lipofectamine 2000 (Invitrogen) or TransIT-LT1 (Mirus). Cells were plated on hydrogels for at least 3 h to allow spreading before imaging.

Preparation of Deformable Substrates and Mechanical Characterization.

PEG-based hydrogels with RGDS were synthesized as described previously (57) and flexible 2D substrates for TFM experiments were polymerized between glass coverslips with UV light. After removal of the top coverslip, the substrates were incubated in PBS at 37 °C for at least 24 h to allow swelling (SI Appendix). The Poisson ratio of 0.34 and shear modulus of 2,431 ± 87 Pa for the PEG-based hydrogels was measured as described in (SI Appendix, Fig S3). The Young’s modulus of 6,517 Pa was calculated from the shear modulus using the Poisson ratio of 0.34 and assuming linearly elastic, isotropic material properties.

Image Acquisition.

Cells were imaged with a 60×, 1.2 numerical aperture (NA), water immersion objective (UPLSAPO 60XW; Olympus) attached to an Olympus IX71 inverted microscope equipped with a CSU10 spinning disk confocal scan head (Yokogawa Electric Corp.), live cell incubator (Pathology Devices), and an ImagEM 16-bit EMCCD camera (Hamamatsu Photonics) or a LD C-Apochromat 63×, 1.15 NA, water immersion objective attached to a Zeiss Axiovert 200M inverted microscope equipped with a CSU10 spinning disk confocal scan head, live cell incubator, and a Photometrics Evolve EMCCD camera. A 98- × 98- × 15-μm volume was imaged around each cell to incorporate the entire cell volume and ∼10 μm of hydrogel below the cell. These parameters corresponded to voxel dimensions of 0.1917 × 0.1917 × 0.5 μm or 0.1808 × 0.1808 × 0.5 μm in the horizontal and axial planes on the Olympus and Zeiss systems, respectively. After the stressed image was acquired, the cells were treated with 0.5% (wt/vol) SDS detergent (JT Baker), reequilibrated for 10 min, and then reimaged to acquire a reference image of the nonstressed hydrogel. Time-lapse datasets were acquired at time intervals ranging from 30 s to 5 min. Super-resolution structured illumination images were acquired as described previously (58) (SI Appendix, Fig S1).

Calculation of Bead Displacements and Cell Tractions.

Images were imported into Matlab (MathWorks) and bead centroids were identified using a 3D Gaussian maximum likelihood estimator. After centroid identification, beads in the stressed (subject to cell-generated tractions) dataset were matched to beads in the relaxed (after cell lysis) dataset using a previously described feature vector-based algorithm relating the relative position of each bead to its local neighbors (26). Cell tractions were calculated from the measured bead displacements via a discretized Green’s function as described previously (26) and in detail in SI Appendix.

Finite Element Modeling.

FEM simulations of adhesions were carried out in Abaqus using the finite strain option (NLGEOM) to account for any geometric nonlinearities. The assumptions, parameters and material properties for each condition are detailed in SI Appendix.