Modulation of hippocampal rhythms by subthreshold electric fields and network topology

Abstract

Theta (4–12 Hz) and gamma (30–80 Hz) rhythms are considered important for cortical and hippocampal function. Although several neuron types are implicated in rhythmogenesis, the exact cellular mechanisms remain unknown. Subthreshold electric fields provide a flexible, area-specific tool to modulate neural activity and directly test functional hypotheses. Here we present experimental and computational evidence of the interplay among hippocampal synaptic circuitry, neuronal morphology, external electric fields, and network activity. Electrophysiological data are used to constrain and validate an anatomically and biophysically realistic model of area CA1 containing pyramidal cells and two interneuron types: dendritic- and perisomatic-targeting. We report two lines of results: addressing the network structure capable of generating theta-modulated gamma rhythms, and demonstrating electric field effects on those rhythms. First, theta-modulated gamma rhythms require specific inhibitory connectivity. In one configuration, GABAergic axo-dendritic feedback on pyramidal cells is only effective in proximal but not distal layers. An alternative configuration requires two distinct perisomatic interneuron classes, one exclusively receiving excitatory contacts, the other additionally targeted by inhibition. These observations suggest novel roles for particular classes of oriens and basket cells. The second major finding is that subthreshold electric fields robustly alter the balance between different rhythms. Independent of network configuration, positive electric fields decrease, while negative fields increase the theta/gamma ratio. Moreover, electric fields differentially affect average theta frequency depending on specific synaptic connectivity. These results support the testable prediction that subthreshold electric fields can alter hippocampal rhythms, suggesting new approaches to explore their cognitive functions and underlying circuitry.

Introduction

Subthreshold electric fields, by definition, do not evoke spiking in individual neurons at rest in the absence of other stimulation (for review see Schiff 2012). However, constant (DC) fields suppress (Gluckman et al. 1996, 2001; Richardson et al. 2003) and entrain (Sunderam et al. 2009) epileptiform discharges, and affect cortical wave propagation (Richardson et al. 2005). At the single cell level subthreshold DC fields only produce weak somatic polarization (Bikson et al. 2004; Deans et al. 2007). Such small perturbations can nevertheless influence network rhythms and synchronization (Berzhanskaya et al. 2007; Park et al. 2005). Subthreshold alternating (AC) fields produce similar size effects at the single cell level and can shift frequencies of hippocampal oscillations in vitro (Deans et al. 2007; Fröhlich et al. 2010) and in vivo (Ozen et al. 2010).

While the ultimate goal of electric field modulation of theta and gamma rhythms would be to affect brain activity and behavior in vivo (Buzsaki, 2002), here we concentrate on the in vitro network to generate more directly testable predictions. Oscillatory rhythms can be evoked in hippocampal slices with agonists of muscarinic (Oren et al. 2006), kainate (Gloveli et al. 2005b) or metabotropic glutamate receptors (Gillies et al. 2002). Rhythms are also observed in the whole hippocampus preparation (Goutagny et al. 2009; Wong et al. 2005), and have been associated with both excitatory and inhibitory synaptic potentials in the slice and whole hippocampus in vitro. From dozens of hippocampal interneuron types (Freund and Buzsaki 1996; Somogyi and Klausberger 2005), few have been systematically studied in the context of theta or gamma rhythms. Phase relationships and preferential firing frequencies of perisomatic and dendritic-targeting interneurons generally differ. Perisomatic interneurons fire with higher (30–80 Hz) while dendrite-targeting interneurons fire with lower (4–12 Hz) frequencies. Similar observations in vivo (Csicsvari et al. 1999, 2003, Klausberger et al. 2003) suggest a strong contribution of intrinsic rhythmicity to hippocampal oscillations. In addition to membrane properties of neurons (Cobb et al. 2003; Gillies et al. 2002), network connectivity is critical in rhythm generation (Fischer et al. 2002; Fisahn et al. 2004; Oren et al. 2006; Kullmann 2011). The ratio between theta and gamma rhythms, which in vivo changes based on behavioral state, depends in vitro on slicing orientation (Gloveli et al. 2005a).

While experimentally identifying the specific contribution of individual neuron types to hippocampal rhythm generation remains to date an open challenge, computer simulations have fostered the mechanistic exploration of hippocampal theta and gamma oscillations. A model with two-compartment pyramidal cells and one-compartment basket and oriens/lacunosum-moleculare (OLM) cells (Gloveli et al. 2005a) generated rhythms by both inhibitory and excitatory interactions (Börgers et al. 2005). More biophysically complex models investigated rhythms, learning and retrieval in hippocampus relative to theta phase and synchronization across cell assemblies (Kunec et al. 2005; Orbán et al. 2006; Tort et al. 2007). Biophysically and morphologically realistic pyramidal cells in our model are instrumental to simulating electric field effects.

We combined experiments and computational modeling to investigate the effect of electric fields on hippocampal rhythms. First, we applied subthreshold electric fields in vitro, recording intracellularly the somatic polarization in pyramidal cells and interneurons, as well as effects on spike latency and synaptic response. Next, based on these data, we constructed a CA1 circuit model with morphologically and biophysically realistic pyramidal cells (Li and Ascoli 2006), several perisomatic and dendrite-targeting interneuron types, and simulated electric fields. Specific network connectivity allows activity propagation within and across lamellae.. Synaptic weights were constrained using experimental data on both intracellular recordings (Magee and Cook 2000) and differences in rhythm generation in alternative slicing orientations (Gloveli et al. 2005a). Rhythm generation involves interplay between pyramidal cells and interneurons. Our simulation results implicate additional interneuron classes and connectivity configurations, and support the experimentally testable prediction that subthreshold electric fields can robustly switch between theta- and gamma-dominated regimes. Moreover, the ability to discriminate between alternative network topologies by the resulting field effects on input/output function suggests the design of new model-guided experiments to uncover functional network connectivity.

Materials and Methods

Experimental Methodology and Procedures

Slice Preparation

All experimental procedures were performed in agreement with George Mason University IACUC protocol. Sprague–Dawley rats (18–30 day old) were anesthetized with diethyl-ether. After decapitation, brains were removed, hippocampi isolated, and transverse 400 µm sections cut from the middle part of the hippocampus in a cold (4°C) dissection buffer perfused with 95% O2 - 5% CO2 (concentration in mM: 2.6 KCl, 1.23 NaH2PO4, 24 NaHCO3, 0.1 CaCl2, 2 MgCl2, 205 sucrose, 20 glucose) using a vibratome. Slices were incubated for at least 1 hr at 30°C in artificial cerebrospinal fluid (ACSF; pH 7.3; in mM: 130 NaCl, 1.2 MgSO4, 3.5 KCl, 1.2 CaCl2, 10 glucose, 2.5 NaH2PO4, 24 NaHCO3) saturated with 95% O2 - 5% CO2, before being transferred to a submersion recording chamber (modified from RC 22, Warner Instruments). The chamber was modified with AgCl pellets to apply and control electric fields (detailed below), and perfused with ACSF (~1 ml/min, 32°C). No synaptic blockers were used. Borosilicate glass micropipettes (4–8 MΩ) for current-clamp recordings contained (in mM): 116 K gluconate, 6 KCl, 0.5 EGTA, 20 HEPES, 10 phosphocreatine, 0.3 NaGTP, 2 NaCl, 4 MgATP, and 0.5% neurobiotin (pH 7.25, 295 mOsm). Either an AgCl pellet (without an applied electric field) or a glass micropipette (1–3 MΩ, filled with 0.9% NaCl, in the electric field application) was used as an extracellular reference.

Electric Field Protocol

Uniform electric fields were applied with a customized electronic circuit using a 4-electrode technique (Berzhanskaya et al. 2005; Gluckman et al. 1996a, 1996b, 2001). Briefly, one of two pairs of AgCl pellets created the field (Figure 2A, F1 and F2), and a separate pair of AgCl pellets in the middle of the chamber was used to measure this field (Figure 2A, S1 and S2). The electronic control circuit automatically adjusted the electric field to preset values and waveforms by comparing the measured signal against the command signal. Because of this design, for a given input signal, field strength was unaffected by electrode degradation or ongoing neuronal activity. Uniformity of electric field both within and outside the hippocampal slice was characterized in a similar chamber (Gluckman et al. 1996a). Charge-balanced waveforms of up to 60 mV/mm (as measured in the chamber) were employed. Although not systematically measured in these experiments, the currents applied to generate these fields were below 0.1 mA. Cell responses to the electric field were measured using a square-wave alternating negative, zero, and positive field levels, 250 ms each, for a total trial length of 1 s (Figure 2B) repeated for 10–16 cycles and averaged across repetitions. “Negative” electric field direction is defined here as one created by a pair of field electrodes when the positive electrode is next to the alveus of CA1 (Figure 1A, Figure 2A, electrodes F1 and F2). “Positive” field direction is obtained with the negative electrode next to the alveus. For purposes of data processing and visualization, both positive and negative capacitive transients were truncated (Figure 2B). Before the start of the whole cell recordings a patch pipette was positioned on the equipotential line of the applied electric field with the glass reference electrode. Equipotentiality was tested by minimizing the response to the electric field, and the glass reference electrode was moved if necessary (Figure 2A). The patch electrode was then lowered vertically onto the cell surface without violating equipotentiality. Transmembrane polarization response to a field application measured in this way would include a negligible contamination by any potential difference due to the distance between recording and refrence electrodes. In several cells the effect of the electric field on subthreshold synaptic responses, cell input resistance, and latency of the first spike was tested by applying Schaffer collateral stimulation every 250 ms, or by delivering a short negative (for measuring input resistance) or positive (for measuring spike latency) whole-cell current pulse (Figure 3). The timing of either synaptic stimulation or whole-cell current pulse was chosen around 100 ms after the field level change to take into account typical time constants for polarizing pyramidal cells (approximately 25 ms: Bikson et al. 2004). Spike latency was calculated as the time of maximum membrane depolarization relative to the whole-cell current injection onset, and plotted as a function of the applied electric field. Synaptic potentials were measured as peak values. Cell and synaptic properties were measured for 10–16 cycles of charge-balanced field waveforms (see above) and averaged across repetitions. We observed no long-lasting changes in extracellular media, cell or network properties at the end of the field protocol.

Figure 2.

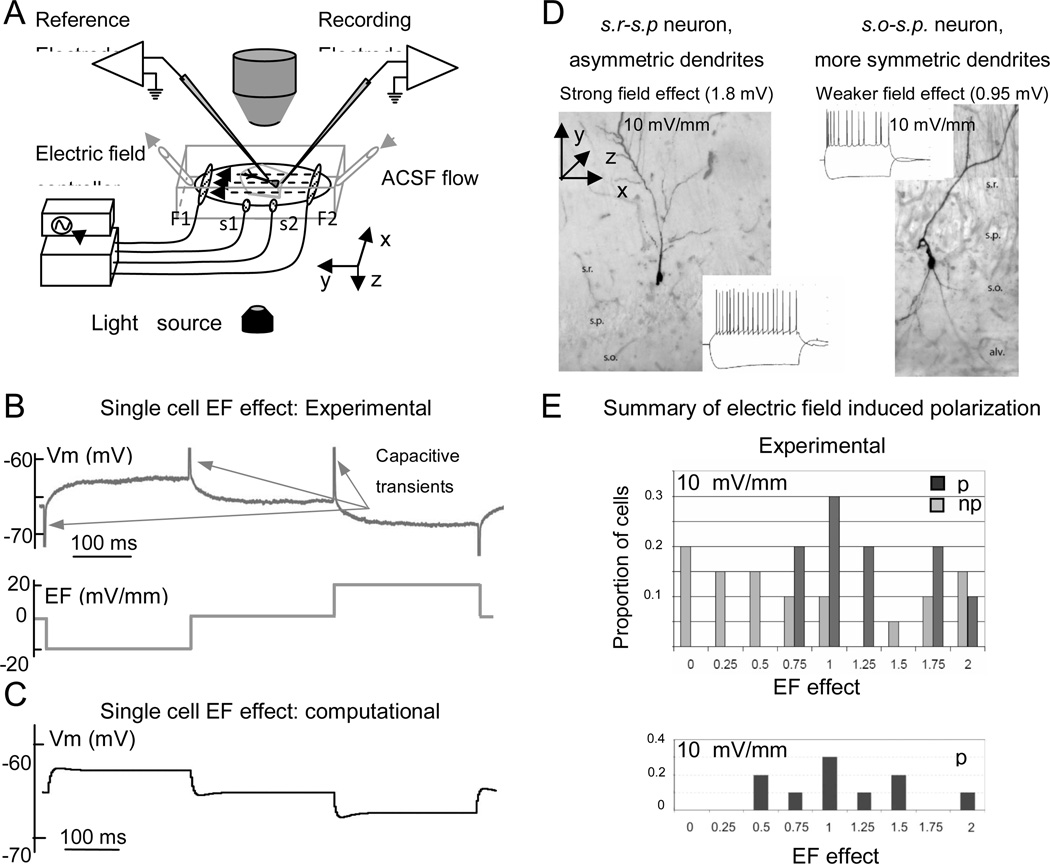
Single cell electric field effects: experiments and model. A. Schematics of experimental setup. Dashed arrows indicate electric field direction. B. Somatic recording (Vm, above) and externally applied electric field (below) showing the small effect of subthreshold fields (20 mV/mm) on cell body polarization. Positive and negative capacitive transients upon field switching (arrows) are truncated. C. Simulated somatic recording from a model pyramidal cell at 20 mV/mm electric field corresponding to the experimental design of panel B. D. Effect of electric field on single cells depends on the dendritic arbor-balance between apical and basal trees in various cell types. Two non-pyramidal cells with different dendritic tree imbalance and somatic polarization effects. Insets show the response of these cells to current injections. E. Histograms of somatic polarization values for pyramidal (p) and non-pyramidal (np) cell populations in experiments (top) and for pyramidal cells in the computational model (bottom). Abbreviations: s.r. stratum radiatum, s.p. stratum pyramidale, s.o. stratum oriens, alv. alveus.

Figure 1.

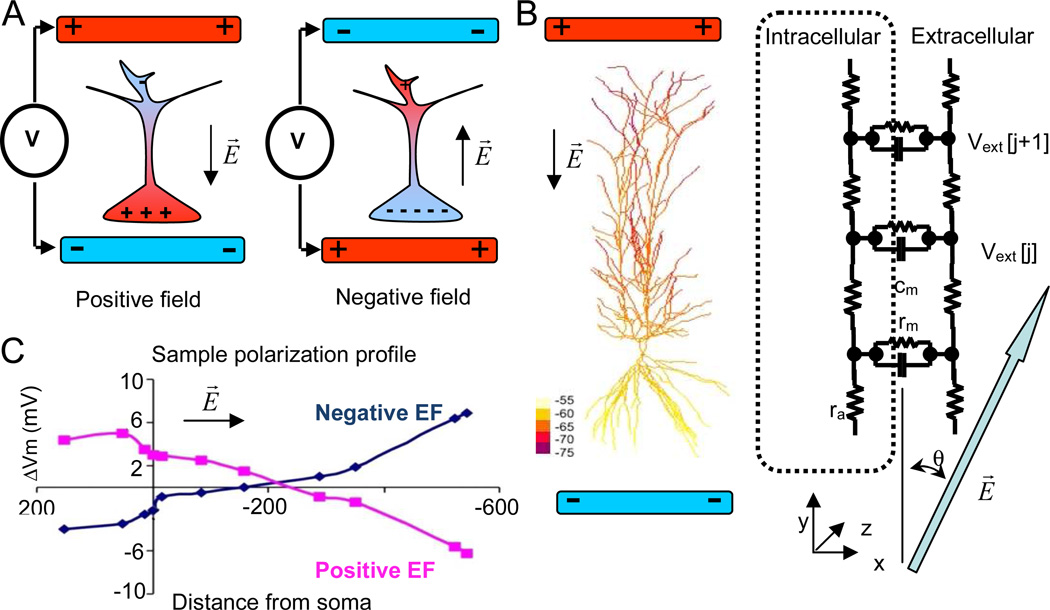
A. Simplified schematic view of neuronal polarization by subthreshold electric fields. “Positive” electric fields aligned with somato-dendritic axis, and created by positioning a negative electrode next to the soma and a positive electrode next to the dendrites, depolarize the cell body (left); “negative” electric fields, created by positioning a positive electrode next to the soma, hyperpolarize the cell body (right). Black arrows indicate the direction of the electric field B. A sample pyramidal cell from the model color-coded by the computed polarization profile. A black arrow indicates the direction of the electric field E (30 mV/mm). Schematic representation of “extracellular” mechanism implementation in NEURON for subthreshold electric field effects. The large blue arrow (gray in hardcopy) indicates the direction of the electric field. C. Polarization profiles (Vm) for positive and negative electric fields aligned with the longest cell axis (y axis) in the model plotted as a function of the distance from the soma along the dendrites (negative values refer to the basal tree). Electric field is 20 mV/mm.

Figure 3.

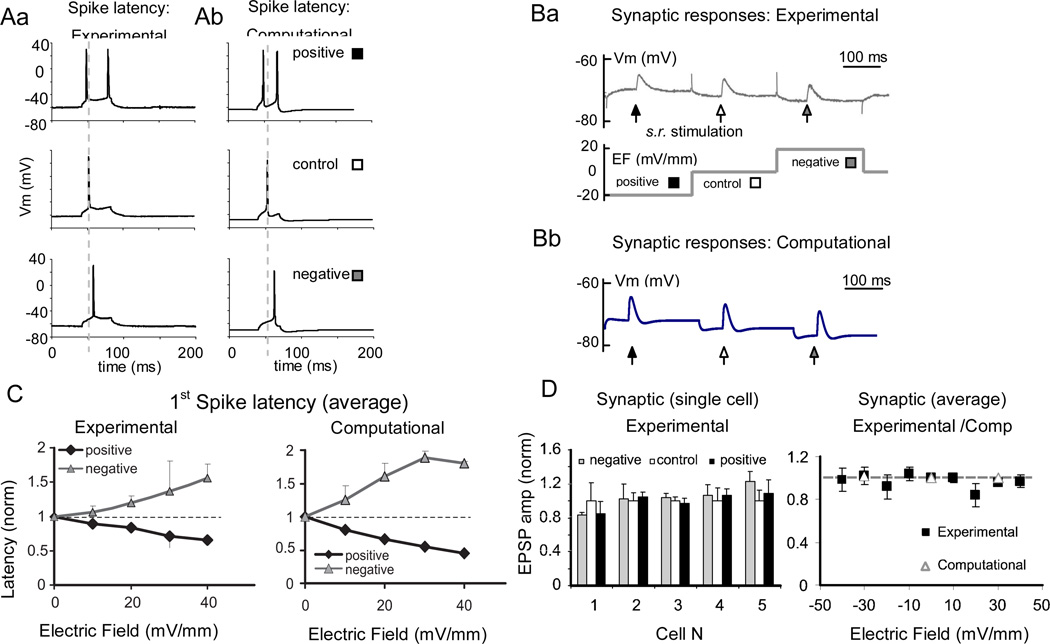
Effect of electric field on spike latency and synaptic responses. A. The latency of the first spike evoked by a square depolarizing current pulse is oppositely affected by positive (black square) and negative (gray square) electric fields compared to control (white square): experiments (Aa) and model (Ab). B. Sample synaptic responses evoked by stratum radiatum stimulation at positive, neutral, and negative electric fields: experiments (Ba) and model (Bb). C. Spike latency effect scales with the strength of the electric field. First spike latencies for positive (black) and negative (gray line) fields are normalized to the control (0 mV/mm) and averaged across recorded cells. Error bars represent standard error of mean. Left: experimental (n=8); right: computational (n=9). Dashed horizontal line represents control level (y=1). D. Left: summary of the experimental synaptic effects of a ± 10mV/mm electric field, normalized to the 0 mV/mm control. Right: most cells show a non-significant synaptic effect that does not depend consistently on the sign of the field. The summary plot of these 5 experimental cells between −40 mV/mm and 40 mV/mm (solid line) of electric field and 9 computational cells (open triangles) at 30 mV/ mm of electric field shows that the synaptic effect remains negligible at the higher strengths of electric field in both experiments and simulations. Gray line (y=1) represents control level.

Morphological Cell Identification

After completing the electrophysiological protocol, the cell was held attached to the neurobiotin-filled pipette for at least 30 min. The slice was then fixed in 4% paraformaldehyde and stored at 4°C. Neurobiotin was later developed using either a diaminobenzidine or an Alexa-conjugated strepavidin (Morozov et al. 2002) protocol, Figure 2D. Fluorescent images were taken using a Cooke camera and IPLab (BD Biosciences) or two-photon microscopy (courtesy of Dr. T. Haydar, Children’s National Medical Center, Washington, DC).

Computational Modeling

A network model of hippocampal area CA1 was implemented in the NEURON simulation environment (version 5.9; Carnevale and Hines 2006) under the Windows XP operating system, running on a 1.7 GHz Athlon or Intel 2.4 GHz Core2 Quad computer. The code is available through the ModelDB database (senselab.med.yale.edu/ModelDB - accession number: 144589). The network model included CA1 pyramidal cells and several types of interneurons. We adopted a pyramidal cell model from area CA1 since more is known about these cells compared to those in CA3. In particular, many ion channel parameters have been validated (see below), and our own single cell experiments have also been performed in CA1 (see above).

Pyramidal cells had realistic morphology imported from the NeuroMorpho.Org database (Ascoli et al. 2007), but did not include axonal compartments; interneurons had a simplified compartmental structure. Below we describe the details of passive and active membrane biophysics, synaptic properties and connectivity, network embedding in the extracellular electric field, and the stimulation protocol. A typical simulation with 60 neurons, 1000 synapses, and 4,000 compartments, with a fixed time step of 0.025 ms, required approximately 8 hours of run time for 1 s of virtual recording.

Cable Properties and Voltage-gated Distributions

The CA1 pyramidal cell model follows previously described biophysics (Migliore et al. 1999, 2004, 2005; Watanabe et al. 2002; Li and Ascoli, 2006, 2008), and is based on minor modifications of a publicly available implementation (http://senselab.med.yale.edu/modeldb, access number 55035). Passive and active membrane properties are summarized in Table 1. Voltage-dependent mechanisms included transient sodium, delayed rectifier potassium (K_DR), rapidly inactivating potassium (K_A), and non-specific hyperpolarizing cation (Ih) currents. The sodium conductance (200 pS/µm²) and K_DR (100 pS/µm²) were uniform throughout the whole neuron. K_A had a somatic density of 250 pS/µm², which in the dendrites increased linearly with the distance from the soma by 250 pS/µm² per 100 µm (Hoffman et al. 1997). As in previous models, the activation curve of this channel was shifted +12 mV in the proximity (< 100 µm) of the soma. Ih density also increased from 0.5 pS/µm2 in the soma by 1.5 pS/µm² per 100 µm in the dendrites (corresponding to “type I” model in Li and Ascoli 2006; see also Magee 1998; Poolos et al. 2002). Specific membrane capacitance (Cm), axial resistance (Ra), and membrane resistance (Rm) were 1 µF/cm², 80 Ω·cm, and 28 kΩ·cm², respectively. Passive and active properties of interneurons (also reported in Table 1) did not vary with the distance from the soma.

Table1.

Passive and active membrane properties of pyramidal (P) cells and interneurons (O and B/B2). Rm is in KΩ*cm²; Ra is in Ω*cm, Cm is in µF/cm². Channel conductances gNa and others are in pS/µm².

	Rm	Ra	Cm	gNa	gKdr	gKa	gIh
P	28	80	1	200	100	250*	0.5*
O	28	80	1	200	100	250	0.5
B/B2	28	80	1	200	50	0	0

^*gKa and gIh values are given for the somatic compartment, and increase with distance (d) from soma as gKa·(A·d²+B) or gIh·(A·d²+B) (see Methods). A values ranged from 0.0012 to 0.0065 (pS/µm²), B values from 14 to 155pS (Li and Ascoli 2006).

Morphology and Synapses

The three-dimensional dendritic morphology of CA1 pyramidal neurons was sampled from the same ten digital reconstructions used in our previous models (Li and Ascoli 2006: neurons c20466, c30465, c70863, c72965, c62564, c70963, c73162, c80761, c91662, cd1152 from NeuroMorpho.Org). Each cell was divided into isopotential compartments shorter than one-tenth of the space constant at 100 Hz, resulting in 1000–2000 compartments per neuron. In the network model, the somato-dendritic axis of pyramidal cells was aligned with the vertical (radial) coordinate, parallel to the electric field (see below). Interneurons were modeled as one-compartment cells except for a subset of simulations designed to investigate the effect of interneuron geometry. In that case interneuron morphology consisted of a soma and two linear dendrites of 300 µm total length, oriented either vertically (parallel to the electric field) or horizontally (orthogonal to the electric field).

All synapses were created as NEURON point process mechanism (exp2syn). Each pyramidal cell received between 30 and 160 excitatory synapses, with rise and decay time constants τ1 = 0.2 ms and τ2 = 10 ms, respectively, and reversal potentials of 0 mV (Table 2). These synapses were randomly distributed throughout the apical and basal dendrites, up to a distance along the dendritic path of 350 µm from the soma, corresponding to CA1 strata radiatum and oriens. NMDA synapses were not included to avoid accounting for calcium dynamics which would substantially increase model complexity. Experimental data suggest that blocking NMDA receptors produces weak effects on self-generated rhythms (Goutagny et al. 2009). Moreover, NMDA currents only mildly affect firing frequency input/output curves in CA1 pyramidal neurons (Li and Ascoli 2006). Each pyramidal cell also received one inhibitory synapse at the soma (τ1 = 0.5 ms and τ2 = 10 ms) modeling perisomatic inhibition from basket cells, and 20 inhibitory synapses on the dendrites (τ1 = 1 ms and τ2 = 20 ms) from oriens interneurons, all with reversal potentials of −85 mV. Dendritic-targeting inhibition was distributed either proximally (within 350 µm from the soma) or distally (farther than 350 µm) corresponding to inputs from oriens/bistratified (O-bi) and oriens/lacunosum-moleculare (OLM) interneurons, respectively (Maccaferri et al. 2000; Maccaferri 2005). All interneurons had excitatory synapses positioned on the soma.

Table 2.

Synaptic properties. Reversal potentials (Erev) are in mV, time constants (tau) in ms.

	Ereve	Erevi	Tau1e	Tau2e	Tau1i (from B)	Tau2i (from B)	Tau1i (from O)	Tau2i (from O)
P	0	−85	0.2	10	0.5	10	1	20
O	0		0.2	10
B	0		0.05	5
B2	0	−85	0.05	5			0.5	10

Synaptic parameters were selected to generate excitatory and inhibitory postsynaptic potentials consistent with those measured in vitro (Cossart et al. 2006; Hájos and Mody 1997, Otmakhova et al. 2002; Patenaude et al. 2001; Williams and Johnston 1991). Synaptic conductances, reported in Table 3, were manually tuned to yield results of transverse/longitudinal cut simulations consistent with experimental observations. The conductance of excitatory synapses on pyramidal cells increased from 50–80 pS next to the soma as a quadratic function (A·d²+B) of the distance (d) along the dendritic tree (for values see Li and Ascoli 2006). The parameters (A and B) were fitted for each pyramidal cell individually to provide constant somatic EPSPs of 0.2 mV in agreement with experimental data (Magee and Cook 2000; Smith et al. 2003). Each pyramidal-pyramidal cell connection consisted of 10 synapses.

Table 3.

Connectivity between cell types in the basic network configuration (OPb) in nS. Connections from cell type “X” to cell type “Y” are in row X and column Y. For computational efficiency, each pyramidal cell had 30 excitatory point processes, 30 inhibitory point processes in the dendrites and 1 inhibitory point process at the soma (using NEURON exp2syn capability to accept multiple synaptic projections).

Synaptic weight (nS)	P (intralam.)	P (crosslam.)	O (intralam.)	O (crosslam.)	B (1-to-1)
P	0.5–0.8*	0.5–0.8*	0.02	0.01	0.8
O	1.5	1.2	0	0	0
B	15	0	0	0	0

^*P-P values represent the range over all pyramidal morphologies for the somatic compartment, and increase with distance from soma (see Methods).

Network Connectivity

The network was connected to mimic the core hippocampal circuit. In the basic configuration, 20 pyramidal (P), 20 oriens (O), and 20 basket (B) cells were assembled into 5 transverse sections (“lamellae”) each containing 4 cells of each type (Figure 4A; for clarity, only 3 lamellae are depicted). Thus, the lamellar organization corresponds to the longitudinal arrangement of adjacent transverse sections. Excitatory P-P connectivity was all-to-all within each lamella (convergence 3:1, divergence 1:3) and all-to-one (to an individual “input” cell) between lamellae (convergence between 1:1 and 16:1, divergence 1:1 to 1:4). Maximum convergence/divergence ratios are higher than those estimated in real rat hippocampus because of excitatory drive constraints due to the limited number of pyramidal cells. Lower convergence/divergence ratios could have been achieved by increasing the number of pyramidal cells. In that case, however, computational constraints would have forced simplified dendritic structure, which would not be practical for biophysically realistic exploration of electric field effects. Connections between P and O cells (both P-O and O-P) were all-to-all both within and across lamellae. Oriens interneurons corresponded to either OLM or O-bi cells depending on whether they inhibited pyramidal cells on distal or proximal dendrites, respectively. Only one of the two types of O interneurons was used in any one simulation. Basket cells received one-to-one projection from pyramidal cells (P-B) and projected back to the soma of the same cell (B-P) providing individual inhibitory feedback. We refer to this basic network configuration as OPb, indicating that the oriens-to-pyramidal connection is sufficiently strong to modulate theta rhythms by itself.

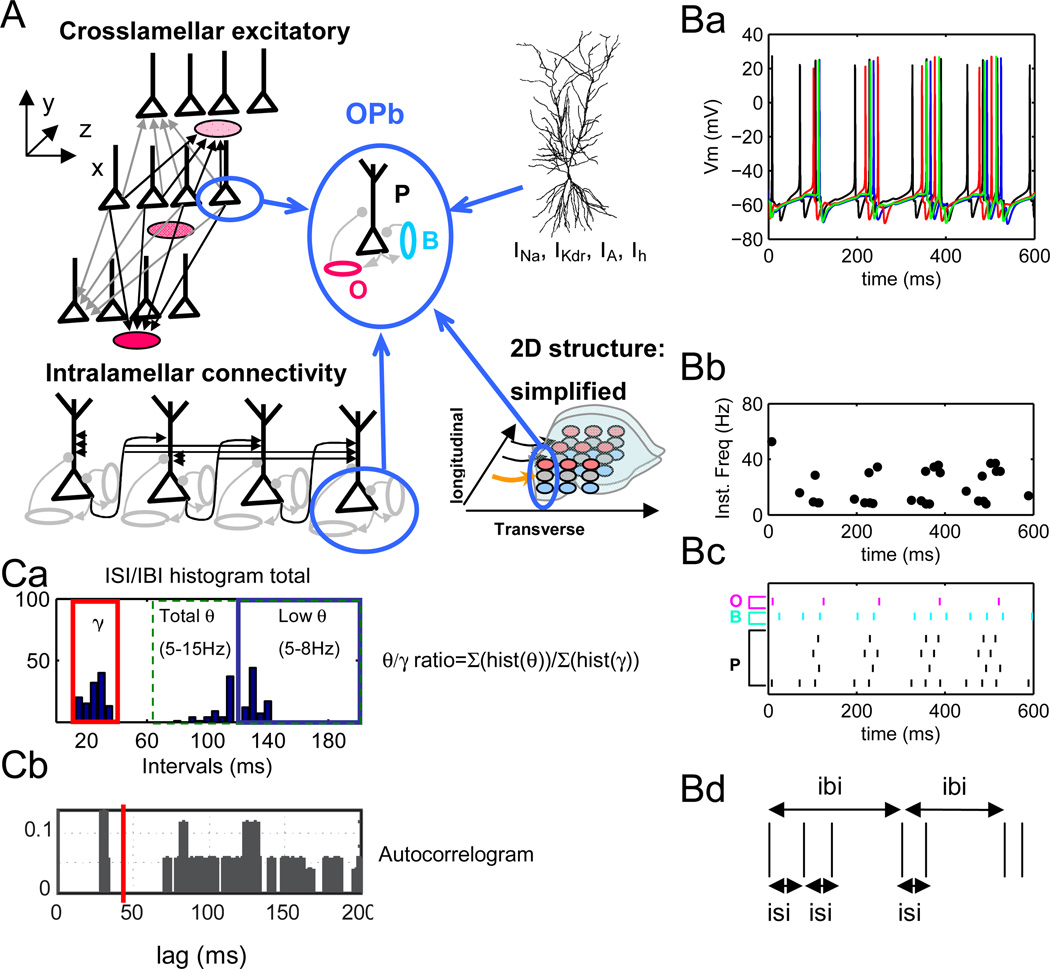
Figure 4.

A. Basic network configuration (OPb) consisting of realistic pyramidal cells (P) and reduced oriens (O) and basket cells (B) assembled in several lamellae (three out of five lamellae are shown for simplicity). Pyramidal cells have full morphology (cf. Figure 1). B cells provide perisomatic inhibitory feedback to pyramidal cells, and O cells provide direct dendritic modulation. O-B inhibition is not present. Unless noted otherwise, O-P connections correspond to inhibitory synapses on proximal dendrites. Arrows and dots indicate excitatory and inhibitory connections, respectively. Network is arranged in a 2-dimensional layout to simulate excitation propagation within (transverse, x axis) and between (longitudinal, z axis) lamellae. B. Simulation results (no electric field). Ba. Spike trains generated by 4 P cells in one lamella demonstrate theta-modulated gamma frequency firing. Bb. Instantaneous firing rate plot for 4 P cells in one lamella. Bc. Raster plots of 4 P (black, bottom four rows), 1 B (blue, 2^nd row from the top) and 1 O (magenta, top row) cells. Bd. Schematics of interburst (IBI) and intra-burst interspike interval (ISI) calculation. Ca. Histogram of IBI and ISI distribution over all 5 lamellae from simulations in Ba-Bc. Both “low theta” (5–8 Hz) and “high theta” (9–15 Hz) are observed. Theta/gamma ratios are computed as the number of intervals in the 5–15 Hz (“total”) or 5–8 Hz (“low”) divided by the number of intervals in the 30–80 Hz range.

Cb. Autocorrelogram of data averaged across all pyramidal cells showing two frequency groups, one in gamma (~30 ms) and one in theta (~110 ms) range.

The absence of the direct oriens to basket input in the OPb configuration is motivated by relatively scarce anatomical evidence for OLM cells (Gulyas et al. 1999; Katona et al. 1999; Sik et al. 1995). Only 8%–15% of synapses on parvalbumin-positive cells are inhibitory, with the largest percentage of inhibitory synapses on the soma (outside of the area of OLM axonal branching). Conversely, only a minute proportion of the contacts received by parvalbumin-positive cells are inhibitory synapses on thin dendrites in stratum lacunosum-moleculare. Connectivity between oriens/bistratified (O-bi) and basket cells, to our knowledge, has not been investigated. In contrast, OLM cells form about 75% of their connections on pyramidal cells (Katona et al. 1999), as demonstrated by somatostatin-positive reactivity in stratum lacunosum-moleculare. Both oriens (O-bi and OLM) and basket cells receive functional projections from pyramidal cells (Ali et al. 1998a,b). The strength of connections in the intact OPb network was tuned to produce a mix of theta and gamma rhythms in conjunction with selective rhythm generation in different slice orientations.

The relative balance of theta and gamma rhythms changes in vitro depending on the slicing angle of the hippocampus (Gloveli et al. 2005b). We used these experimental data to constrain the model synaptic weights (Table 3). A transverse slice was simulated by “cutting out” four pyramidal cells at the same septo-temporal level (z axis, Figure 4A; only 3 out of 5 lamellae depicted for clarity), i.e. preserving intralamellar connections and setting the strengths of crosslamellar connections to zero. Thus the transverse slice effectively consisted of four P, four B, and four O cells. A “longitudinal slice” was produced by “cutting out” three P, three B, and three O cells across each of the five lamellae. This “longitudinal slice” therefore consisted of 15 P, 15 B and 15 O cells. Both crosslamellar and intralamellar connections among remaining cells were left unchanged as in the full model. These slice definitions only account for axonal cuts, and not possible changes in individual cell biophysics due to cut dendrites. In other words, the remaining pyramidal cells have intact dendritic morphology.

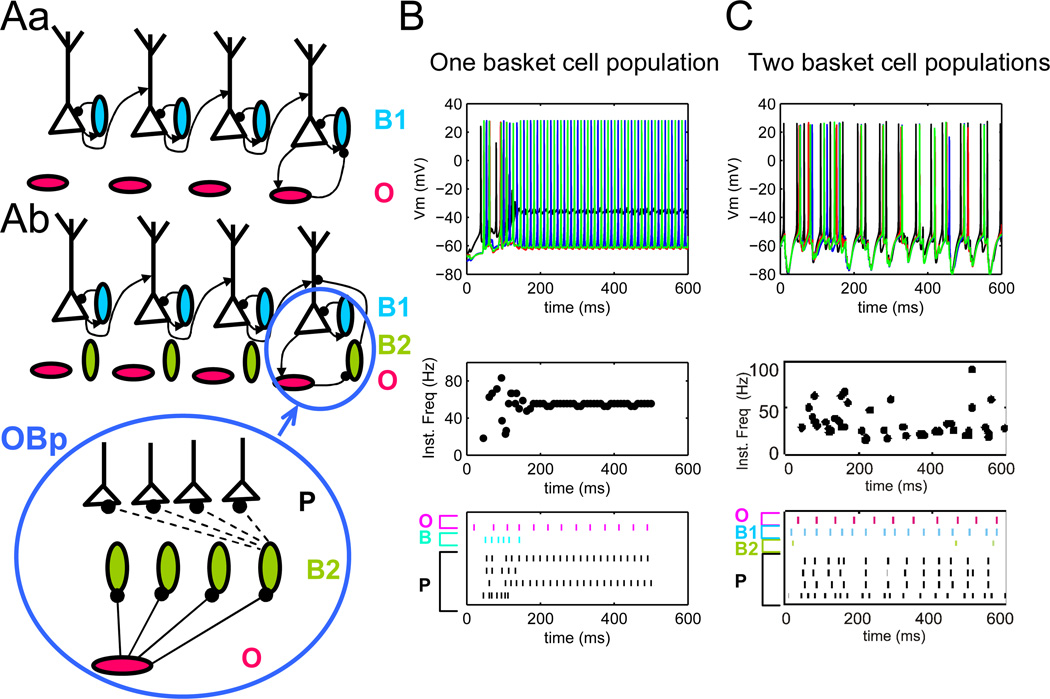
Because the strength of inhibitory connections in the theta/gamma generating circuitry is not known, we also explored an alternative network configuration. In this circuit variation (Figure 6Ab), in addition to the “feedback” basket cells described above, a separate group of basket cells (“population” basket cells) received projections from all pyramidal cells in the lamella and projected back to all pyramidal cells in the same lamella. In this network, the oriens projection to pyramidal cells (O-P) was weaker than in the basic configuration, but oriens interneurons also provided inhibition to population basket cells (B2 in Table 4). Thus, these B2 cells had an inhibitory synapse in addition to the excitatory one, and both of these synapses received connections from multiple O and P cells, respectively. This alternative network configuration is referred to as OBp, indicating that theta modulation in pyramidal cells is achieved indirectly through suppression of basket cell activity (Klausberger et al. 2005).

Figure 6.

A. OBp network configuration: strong O-B inhibition requires two basket cell populations to produce theta/gamma rhythms. Aa OP, OB and BP connectivity with one basket cell population. Ab OP, OB and BP connectivity with two basket cell populations. B. Network activity with one B population is unstable. C. Network activity with two B cells populations demonstrates a combination of theta/gamma rhythms. One population of basket cells (B1) provides local inhibitory feedback to P cells, while the second (B2) is modulated with theta frequency via O cells. Top to bottom: spike trains from one lamella, instantaneous firing rate for pyramidal cells in one lamella, raster of P cells and sample O and B cells.

4.

Connectivity between cell types in the alternative network configuration (OBp) in nS. For computational efficiency, each pyramidal cell had 30 excitatory point processes, 30 inhibitory point processes in the dendrites and 1 inhibitory point process at the soma (using NEURON exp2syn capability to accept multiple synaptic projections).

Synaptic weight (nS)	P (intralam.)	P (crosslam.)	O (intralam.)	O (crosslam.)	B (1- to-1)	B2 (intralam.)	B2 (crosslam.)
P	0.5–0.8*	0.5–0.8*	0.03	0.015	0.8	0.15	0
O	0	0	0	0	0	1	0.5
B	15	0	0	0	0	0	0
B2	10	0	0	0	0	0	0

^*P-P values represent the range over all pyramidal morphologies for the somatic compartment, and increase with distance from soma (see Methods).

Stimulation Protocol and Network Randomization

The network was typically stimulated by small constant somatic current injections. The range of current amplitudes was adjusted during network tune-up in the whole hippocampus/transverse/longitudinal simulations (Figure 5). This paradigm simulates the activation of individual cells in the experimental CA1 and CA3 slice models of theta and gamma rhythms (see Gillies et al. 2002 for isolated CA1 oscillation; Widmer et al. 2006; Williams and Kauer 1997) and is similar to existing modeling studies (e.g. Gloveli et al. 2005a). A range of rhythms can be evoked in the isolated hippocampus or slice preparations (Fellous and Sejnowski 2000; Wong et al. 2005; Wu et al. 2002). Correspondingly, our model explored intrinsic hippocampal dynamics without accounting for external inputs. Each simulation run was rendered unique by stochastic selection of synapse positions on the dendritic trees. Somatic current injections were chosen from uniform distribution and did not change from simulation to simulation. The ranges of current injections for P and O cells were 210–260 pA and 100–120 pA, respectively. Of the basket cells, only those of the “population” sub-type in the alternative network configuration were stimulated with a current injections range of 100–140 pA. The same basket cell population can be modulated in theta rhythm by external input in vivo (Freund and Antal 1988; Freund 2003; Klausberger et al. 2005). In the simulations modeling transverse and longitudinal slices, somatic current injections to the remaining cells were unchanged from the full model.

Figure 5.

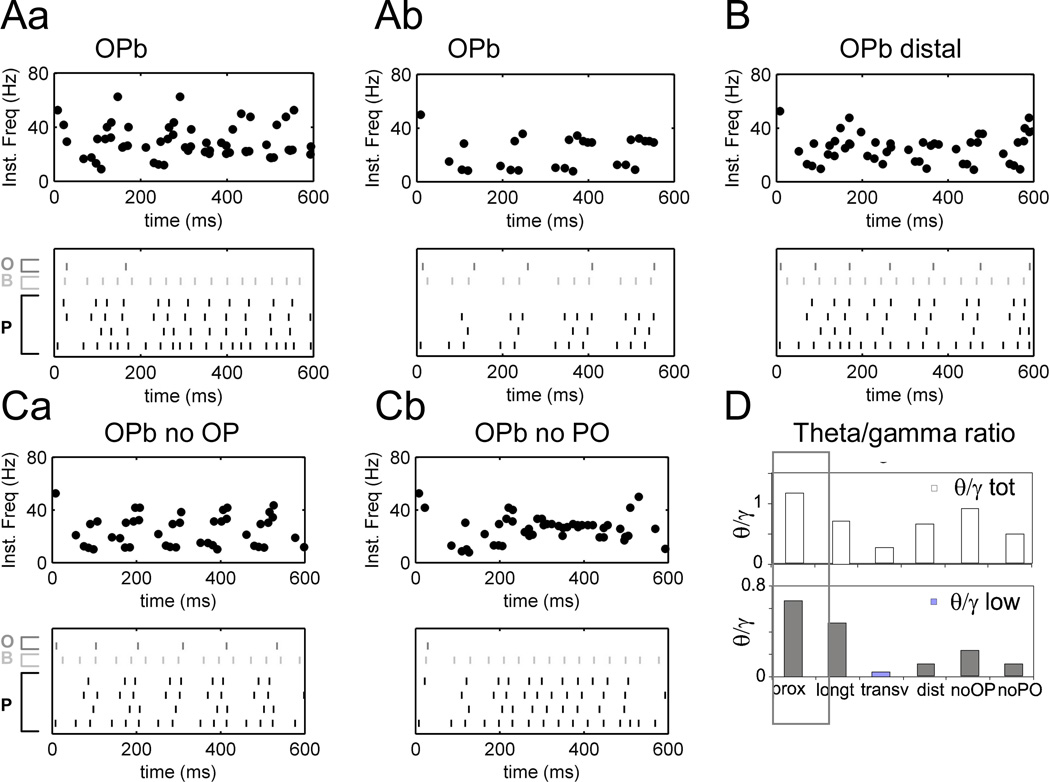
A. Cuts in transverse (Aa) and longitudinal (Ab) dimensions of OPb network produce different rhythms in agreement with Gloveli et al. (2005). Top: instantaneous firing rate for pyramidal cells; bottom: raster of P cells and sample O and B cells with O-P connections on proximal dendrites. B. Network with distal O-P connections (>350 µm in apical dendrites) demonstrates weak theta. C. Both cross-lamellar O-P (Ca) and P-O projections (Cb) are important for theta-modulated gamma rhythms. D. Theta/gamma ratio summary for “total theta” (5–15 Hz) and “low theta” (5–8 Hz) ranges corresponding to simulations in Figure 4A (proximal, control, marked by black box), Figure 5A, B and C.

Electric Field and Modulation of Network Acitivity

Effects of constant electric fields were modeled using the NEURON extracellular mechanism and its modification by McIntyre and colleagues (Bikson et al. 2002; see also Anastassiou et al. 2010). Briefly, the potential of each extracellular node j, Vext[j], was set using

$$\mathit{\text{Vext}}\mathit{[}j\mathit{]}=E^{*}\mathit{\text{cos}}{\mathit{(}\theta \mathit{)}}^{*}y\mathit{[}j\mathit{]}+E^{*}\mathit{\text{sin}}{\mathit{(}\theta \mathit{)}}^{*}x\mathit{[}j\mathit{]},$$ (1)

where θ is the angle of the electric field E relatively to the y axis (Figure 1B), and x[j] and y[j] are coordinates of compartment j. The NEURON simulator then numerically solves the cable

$$\text{equation }{g}_{\mathit{\text{in}}}\partial V\mathit{(}t,x\mathit{)}/\partial x^2=I_m\mathit{(}t,x\mathit{)}=C\partial V\mathit{(}t,x\mathit{)}/\partial t+g_{m}V\mathit{(}t,x\mathit{)},$$ (2)

$$\text{where }V\text{ is }\mathrm{a}\text{ transmembrane potential }V=\mathit{\text{Vext}}-\mathit{\text{Vin}},$$ (3)

g_in is intracellular (axial) conductance, and g_m is membrane conductance. Details on compartmentalization techniques and numerical methods can be found in the NEURON book (Carnevale and Hines 2006).

In (1) the potential difference between two extracellular compartments j and j+1 can be expressed

$$\text{as}\mathit{\text{Vext}}\mathit{[}j+\mathit{1}\mathit{]}-\mathit{\text{Vext}}\mathit{[}j\mathit{]}={\mathit{\text{dl}}}^{*}{E}^{*}\mathit{\text{cos}}\mathit{(}\theta -\gamma \mathit{)}$$ (4)

where dl is the distance between the compartments, and γ is the angle of the dendrite relatively to the y axis. In this model, the field effect is proportional to the cosine of the angle between the dendrite and the field, as suggested from previous studies (e.g. Rushton 1927; Tranchina and Nicholson 1986). While in the actual experimental chamber a potential difference between field electrodes results in a steady current flow through extracellular media, in the model only the resulting potential differences between neighboring extracellular compartments are used. Model responses at the single cell level, including electric field effects on somatic polarization and whole-cell current-injection induced spikes, are then compared with those experimentally measured. The axial extracellular resistance was kept at the default NEURON value of 10⁹ MΩ/cm in all parts of the model (Carnevale and Hines 2006). The conductance between extracellular and intracellular nodes everywhere was 10⁶ S/cm². Capacitive extracellular mechanisms are not simulated by default, but because we use DC as opposed to AC electric fields, only brief simulation transients immediately following field switches are affected by this simplification. Model simplifications listed above might be important while simulating extracellular potentials (Bédard et al. 2010; Gold et al. 2006) but not in the context of this study.

Modulation of the hippocampal network in this model is geometrically similar to modulation of the whole hippocampus by an electric field applied with axial hippocampal electrodes in vivo (Richardson et al. 2003; Sunderam et al. 2009), which create a radial electric field polarizing pyramidal cells. We use the same geometrical approach here, namely, subthreshold electric fields aligned with the somato-dendritic axis of pyramidal cells to modulate hippocampal rhythms. Periods of constant negative (hyperpolarizing) and positive (depolarizing) electric fields were applied for the whole duration of the network activity period (1–2 s) and compared to control conditions (zero field). In particular, theta/gamma ratios were computed for each period (except the initial 100 ms to avoid possible fast and slow transient effects, as also reported in Bikson et al. 2004) and plotted as a function of the electric field. Figures 4–8 display shorter simulation periods for illustration clarity. In the main set of simulations, the electric field did not affect basket and oriens cells, because they had a single compartment. The same held true when interneurons were modeled with four dendritic compartments that were either horizontal or radially arbor-balanced (i.e. with equal basal and apical extent), so that soma polarization was absent. To explore further the effects of electric fields on interneuron populations and network dynamics, in one set of simulations oriens and/or basket cells had unbalanced basal/apical dendrites aligned with the electric field.

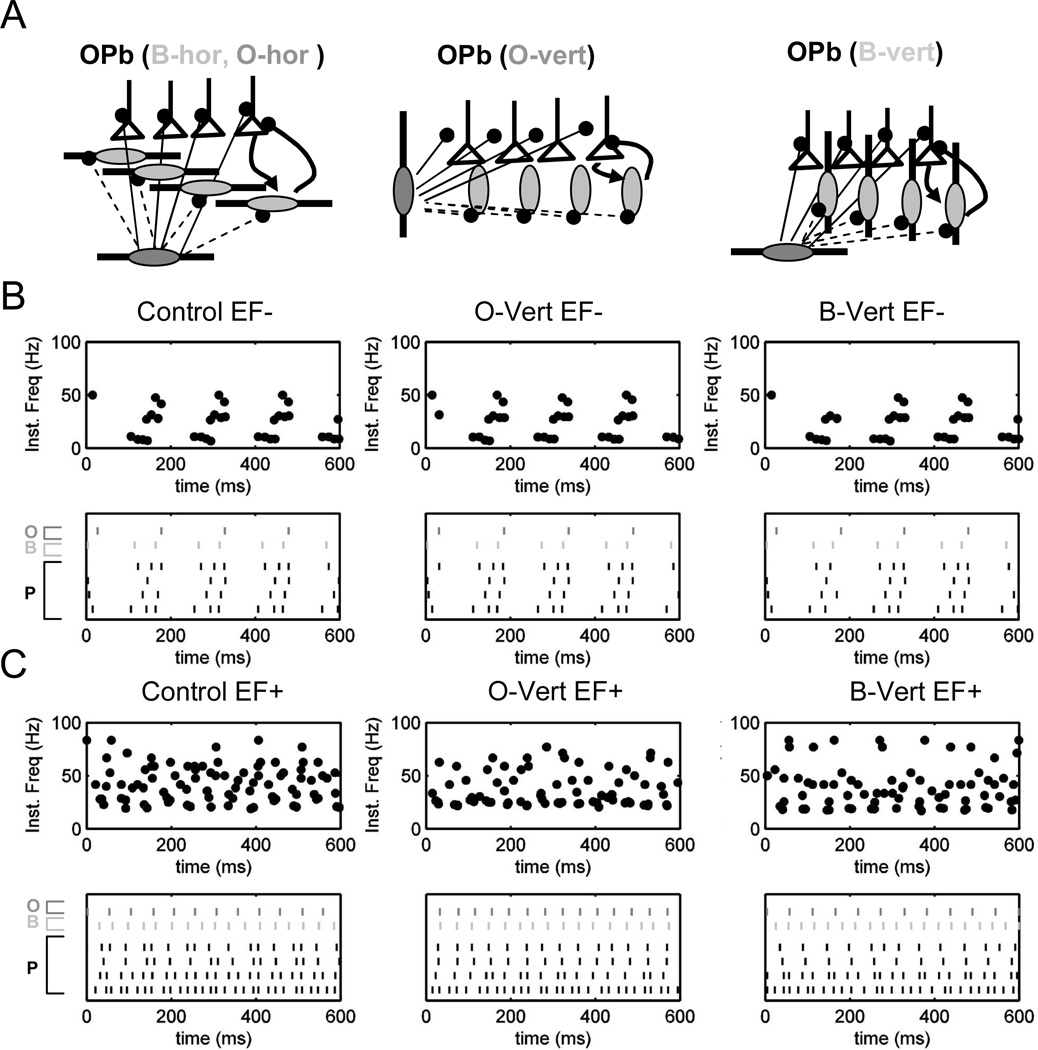
Figure 8.

Network modulation in theta/gamma rhythms is not substantially affected by interneuronal geometry. A. Three network structures including O and B cells with horizontal dendrites (control, left), vertically imbalanced O cells (O-vert, middle) and vertically imbalanced B cells (B-vert, right). B. Similar effects of negative electric field on control, O-vert and B-vert OPb networks (top to bottom: instantaneous frequency plots, rasters). C. Similar effects of positive electric field on control, O-vert and B-vert OPb networks (top to bottom: instantaneous frequency plots, rasters).

Computational Data Processing

Membrane voltage values were stored for pyramidal, oriens, and basket cells from the lamellae of interest. Spike timing and interspike interval (ISI) distributions were extracted for each cell using custom Matlab scripts and displayed as raster and histogram plots (for a representative lamella). Instantaneous firing rate (FR) was computed as the inverse of the raw ISI. We used theta/gamma ratios computed for the whole network (described below) to quantify occurrence of theta-bursts, i.e. high-frequency firing (gamma, 30–80 Hz) modulated by lower frequency (theta, 5–15 Hz). This notion does not refer to intrinsically bursting cells that can fire at much higher rates (e.g. Harris et al. 2001, Colling et al. 1998). Inter-burst intervals (IBIs) were determined as time differences between the first spikes in consecutive theta-bursts. The start of a new burst was identified by an ISI larger than 40 ms, and all following spikes with ISI less than 40 ms were defined as within-burst (Figure 4Bd: single pyramidal cell, 4Ca: whole network “ISI/IBI histogram total”). Autocorrelograms of pyramidal cells were typically bimodal (e.g. Figure 4Cb), with peaks at time lags around 30 ms and 115 ms, separated by the 40 ms threshold (red line, Figure 4Cb). Histograms of ISI and IBI for all pyramidal cells in the network were binned at 5 ms (Figure 4Ca, “ISI/IBI histogram total”). The theta/gamma ratio is computed as the ratio of the total number of theta (5–15 Hz) range intervals between bursts to the total number of gamma (30–80 Hz) range intervals within bursts (Figure 4B and 4C).

Results

The application of a constant electric field results in membrane polarization such that positive and negative ions inside the cell are attracted to the negative and positive electrodes, respectively. If the dendritic distribution around the soma is anisotropic, as in the case of unbalanced basal/apical arbors in pyramidal cells, an external electric field aligned with the neuronal somato-dendritic axis results in somatic polarization (Figure 1). In particular, a negative electrode next to the cell body (or to the basal dendrites) would depolarize the soma and hyperpolarize the distal apical tuft (Figure 1A). Conversely, a positive electrode next to cell body would hyperpolarize it. Accordingly, we refer to electric fields that depolarize soma and basal dendrites as “positive” and to those that hyperpolarize them as “negative”. This phenomenon can be clearly demonstrated by computing the membrane polarization (“recorded” using NEURON current clamp) throughout the dendritic morphology of a representative pyramidal cell under simulated application of a subthreshold electric field (Figure 1B). The resulting polarization profile as a function of position along the somato-dendritic axis (Figure 1C) is consistent with the passive cable prediction (Tranchina and Nicholson 1986). A subthreshold somatic depolarization of ~3 mV corresponds to a peak hyperpolarization in the most distal apical dendrites of ~−7 mV, with the equipotential location in the apical tree at a distance from the soma of ~200 µm along the dendritic path.

Experimental observations and model validation

While the dendritic polarization profile is difficult to measure experimentally, our experimental set-up (Figure 2A) allows recording of somatic membrane potential upon application of subthreshold electric fields (<30–40 mV/mm). Both the sign and the amplitude of single cell response at the steady state level are consistent with the computational predictions (Figure 2B and 2C) although individual cell traces may differ between model and experiments in minor details (time constants of membrane response at field onset. Positive fields (with the negative electrode close to the soma and the positive electrode close to the apical dendrites) depolarize the soma, while negative fields (reversed electrode polarity) hyperpolarize the soma. The typical somatic polarization of pyramidal cells was 1–2 mV per 10 mV/mm electric field (consistent with Bikson et al. 2004; Reato et al. 2010). These and all subsequent observations derive from experiments performed under subthreshold electric field strength.

The experimental effect of subthreshold electric fields on somatic polarization was measured in both pyramidal and non-pyramidal cells. The two types were distinguished morphologically and electrophysiologically (Figure 2D). The average polarization for pyramidal cells in response to a 10 mV/mm field was 1.35±0.50 mV (mean±SD, n=8). Both the mean and variance of this effect were consistent with the values produced in the model (p>0.95, Kolmogorov-Smirnov test) under the same conditions across the ten morphologies used in network simulations (Figure 2E). The experimental average recorded for non-pyramidal cells was 0.89±0.81 mV (n=17). Both the smaller polarization effect and greater variability observed in non-pyramidal compared to pyramidal cells (p<0.05, Kolmogorov-Smirnov test) are expected on the basis of their dendritic morphology. Pyramidal cells have a more consistently imbalanced dendritic arbor around the soma, with larger apical than basal trees. Hippocampal interneurons display a more diverse morphology. Non-pyramidal cells with higher dendritic imbalance showed larger polarization effect than interneurons with a more uniform distribution of dendrites (e.g. 1.8 mV vs. 0.95 mV of somatic depolarization in the examples of Figure 2D), consistent with previous work on neuronal polarization (Chan and Nicholson, 1986; Chan et al. 1988). Some non-pyramidal cells had a somatic polarization in response to electric fields comparable to that of pyramidal cells, and the maximum value was also similar for the two groups. However, other interneurons (but none of the pyramidal cells) displayed almost no polarization effect. Half of the tested interneurons showed a smaller somatic polarization (0.5 mV or less) than the minimum value observed for pyramidal cells (0.75 mV).The input resistance of the pyramidal cells in the model varied from 32 to 58 MΩ. These values were consistent with our experimental measurements, which ranged from 29 to 95 MΩ. Electric fields up to 30 mV/ mm did not significantly alter input resistance in either experiments or simulations. Only at 40mV/mm some experimental cells had up to 8% changes in input resistance that were statistically significant (p<0.05, ANOVA).

Additional experiments demonstrated a significant effect on the latency of the first spike evoked by somatic current injection in the presence of a polarizing electrical field (p<0.05, ANOVA, Figure 3Aa). In particular, positive and negative fields decrease and increase spike latency, respectively, consistent with previous results (Parra and Bikson 2004; Radman et al. 2007). As expected, latency scales with electric field amplitude within the subthreshold range (Figure 3C, left), with some asymmetry in both means and variability between positive and negative electric fields. Latency shift is reproduced in our model cell (Figure 3Ab, 3C, right).

In another set of experiments, most cells showed no significant effect of electric fields on the synaptic response evoked by Schaffer collateral stimulation (p>0.05, ANOVA, Figure 3Ba). Recorded EPSPs were larger than those evoked by minimal stimulation (Dobrunz et al., 1997) and likely involved synapses at multiple positions along the dendritic tree. Responses evoked on opposite sides of an equipotential point (Figure 1C) would be slightly increased or decreased by electric field-induced polarization. The net result can be expected to be close to zero. Indeed in individual cells, a 10 mV/mm electric field elicited small changes and no systematic trend (Figure 3D, left). The lack of significant effect persisted for stronger electric fields throughout the subthreshold range (Figure 3D, right). These results, also confirmed by simulations at the single cell level (Figure 3Bb), are consistent with the range of positions of Schaffer collateral synapses around an equipotential point along the dendritic tree of pyramidal cells.

Theta/gamma Modulation Depends on Connectivity

Most existing models of hippocampal theta and gamma rhythms are based on simplified neuronal structures (e.g. Gloveli et al. 2005a; Rotstein et al. 2005; Tiesinga et al. 2001; Tort et al. 2007). Several of these models involve the neuron types that fire in phase with theta and gamma rhythms both in vitro (Gillies et al. 2002; Gloveli et al. 2005b) and in vivo (Klausberger et al. 2003, 2005), namely pyramidal (P), basket (B), and oriens (O) cells. Using a similarly reduced model, we recently demonstrated that small somatic polarization mimicking subthreshold electric field effect could in principle switch network rhythms between theta and gamma (Berzhanskaya et al. 2007). The explicit representation of pyramidal cell morphology in the present work enables more detailed explorations of the specific cellular connectivity underlying theta-modulated gamma rhythms. Using realistic dendritic morphology also allows more biophysically accurate simulation of electric field effects.

In the basic circuit configuration (OPb), basket cells provide inhibitory feedback to pyramidal cells and oriens cells connect directly to pyramidal cells (Figure 4A). Gamma rhythmicity in this circuit is determined by passive and active properties of pyramidal and basket cells, the current injections representing pharmacological network activation (Gloveli et al. 2005, Rotstein et al. 2005, Traub et al. 2000), as well as time constants and strength of P-P and P-B/B-P connectivity (see Tables 1–4 for parameter values). Theta rhythmicity depends on pyramidal cell activation, the properties of O cells, and the time constants and strength of the reciprocal P-O/O-P connectivity. OPb network displays a stable mixture of theta and gamma rhythms (Figure 4B) when oriens neurons contact pyramidal cells in the proximal dendrites, corresponding to the connectivity typical of oriens/bistratified cells (Maccaferri et al. 2005). Rhythms remained stable over several seconds of simulated time. In a typical simulation, this phenomenon can be illustrated by displaying a representative portion of the voltage traces from four pyramidal cells in one lamella (Figure 4 Ba), their instantaneous spiking frequency (Figure 4 Bb), and a raster plot for the same set of pyramidal cells as well as one representative B cell and O cell in the same lamella (Figure 4 Bc). Inspection of the raster from the P cells (bottom 4 rows) and O cell (top row) demonstrates that the O cell fires after accumulating enough excitatory input from P cells in the lamella (and across the lamellae). The B cell (5^th row), in contrast, rapidly fires after P cell in the 1^st row at the bottom, demonstrating the role of B-P feedback.

These rhythms can be quantified in terms of interburst intervals (IBI) and interspike intervals (ISI) within bursts (Figure 4Bd). The resulting combined histogram of IBI and ISI over the whole 1 s simulation period and all 5 lamellae (Figure 4Ca, “total IBI/ISI histogram”) demonstrates the presence of two frequency ranges in the absence of electric fields: gamma (30–80 Hz; mode 35.6 Hz) and theta (5–15 Hz; mode 8.7 Hz). These spike trains or theta-bursts are not the same as found in bursting cells in CA1 in vivo (Harris et al. 2001), and under special conditions in CA1 (Magee and Carruth 1999) or in subiculum (Colling et al. 1998) in vitro. No ISI in the model was shorter than 10 ms. Bimodality of ISI distribution is demonstrated by two peaks on a representative pyramidal cell autocorrelogram (around 30 ms and 115 ms, Figure 4Cb). Other studies exploring in vitro models of rhythm generation found similar autocorrelograms (Chapman and Lacaille 1999; Colling et al. 1998). We quantify the relative prevalence of theta vs. gamma in the network as a ratio between the count of IBIs and ISIs (summed over all pyramidal cells). We further analyze a frequency sub-range corresponding to “low” or “classic” theta (5–8 Hz). The theta/gamma ratio in these control conditions were 1.17 and 0.67 for total and low theta, respectively, indicating a balanced combination of both rhythmic modes.

Cutting “transverse slices” in the model (Figure 5Aa) removes both cross-lamellar oriens inhibition of pyramidal cells and cross-lamellar pyramidal activation of oriens cells, which results in both increased firing rate and decreased theta modulation (total theta/gamma ratio 0.2). In contrast, cutting “longitudinal slices” in the model decreases excitatory connectivity within the lamella while preserving crosslamellar oriens modulation, and therefore largely preserves the theta component of oscillations (Figure 5Ab). The consistency of these trends with experimental observations (Gloveli et al. 2005b) is not an emergent property of the model, since synaptic parameters (Table 3) were tuned to reproduce this behavior. Nevertheless, the existence of a plausible parameter range compatible with this constraint is non-trivial. In particular, placing the inhibitory synapses from oriens cells distally (>350 µm) instead of proximally (150–350 µm) on the pyramidal cell dendrites, resulted in decreased theta/gamma ratio (Figure 5B, D). We did not find any combination of synaptic values enabling robust theta modulation by O interneurons with distal synapses on P cells. Proximal and distal locations correspond respectively to oriens/bistratified (O-bi) and oriens/lacunosum-moleculare (OLM) projections to P cells. These results suggest that O-bi rather than OLM interneurons might be involved in the generation of theta rhythm in the hippocampus. Further exploration of OPb network dynamics indicates that both crosslamellar O-P and P-O projections are required for stable oscillations (Figure 5C). Partial crosslamellar connectivity resulted in much lower theta/gamma ratios (~0.4–0.8) than in the full model (Figure 5D). While the septo-temporal extent of OLM axonal branching was previously proposed to be responsible for the higher theta power in longitudinal slices (Gloveli et al. 2005b), our results suggest a prominent role of both excitatory and inhibitory cross-lamellar connectivity (Figure 5C).

An alternative mechanism for theta oscillations in the hippocampus involves rhythmic disinhibition of tonically firing basket cells by either oriens cells or external GABAergic input (Kunec et al. 2005). Patterns of basket and pyramidal cell firing consistent with this hypothesis have been observed during theta rhythms in vivo (Ylinen et al. 1995). To explore this mechanism, we simulated an alternative network configuration (OBp) in which oriens cells project to the existing population of “feedback” basket cells, and the O-P connection is weak (Figure 6Aa). Although our model does not implement external (medium septal, entorhinal) projections, tonic activation of basket cells has been demonstrated in the slice (Widmer et al. 2006). Accordingly, B cells in this network are depolarized by a small constant current injection to provide inhibitory tone. Interestingly, direct O-B suppression in this circuit configuration resulted in excessive disinhibition of certain pyramidal cells, depolarization block of others, and no combination of synaptic parameters could be found to provide stable firing regimes producing continuous periods of theta-modulated gamma rhythms (Figure 6B). In particular, oriens-driven suppression systematically prevented B cells from limiting the firing rate of P cells via inhibitory feedback.

However, experimental data suggest that the basket cell population is not homogeneous. Some (CCK-containing) basket cells fire before pyramidal cells in the theta cycle, and some after (Klausberger et al. 2005). Up to 50% of the synapses from CCK-positive basket cells target interneurons. These observations are compatible with oriens-basket activation loop generating rhythms (see Rotstein et al. 2005). To investigate this possibility, we added a second class of “population” basket cells (B2) to the OBp structure, resulting in a stable combination of theta and gamma rhythms (Figure 6Ab). These B2 cells receive input from and project back to all P cells within the lamella. They also receive inhibitory input from all O cells within and across lamellae (Table 4). The results of these simulations (Figure 6C) suggest that smooth modulation of pyramidal cell firing via oriens-mediated basket cell inhibition requires dissociating the feedback role and the tonic (dis)inhibition of basket cells receiving oriens cell suppression. Inspection of the raster (Figure 6C) from the P cells (bottom 4 rows) and O cell (top row) demonstrates that the O cell fires after accumulating enough excitatory input from P cells in the lamella (and across the lamellae). The B1 cell in OBp (2^nd row from the top) rapidly fires after the P cell in the last row at the bottom, demonstrating the role of B-P feedback similar to the B cell in OPb network (Figure 4). O cells modulate (suppress) B2 cells and allow gamma rate firing of the P ensemble (only one B2 cell plotted in Figure 6C). Unlike in Figure 6B, theta- gamma modulation was stable in the presence of P-O projection.

Electric Field Modulation of Theta and Gamma Rhythms

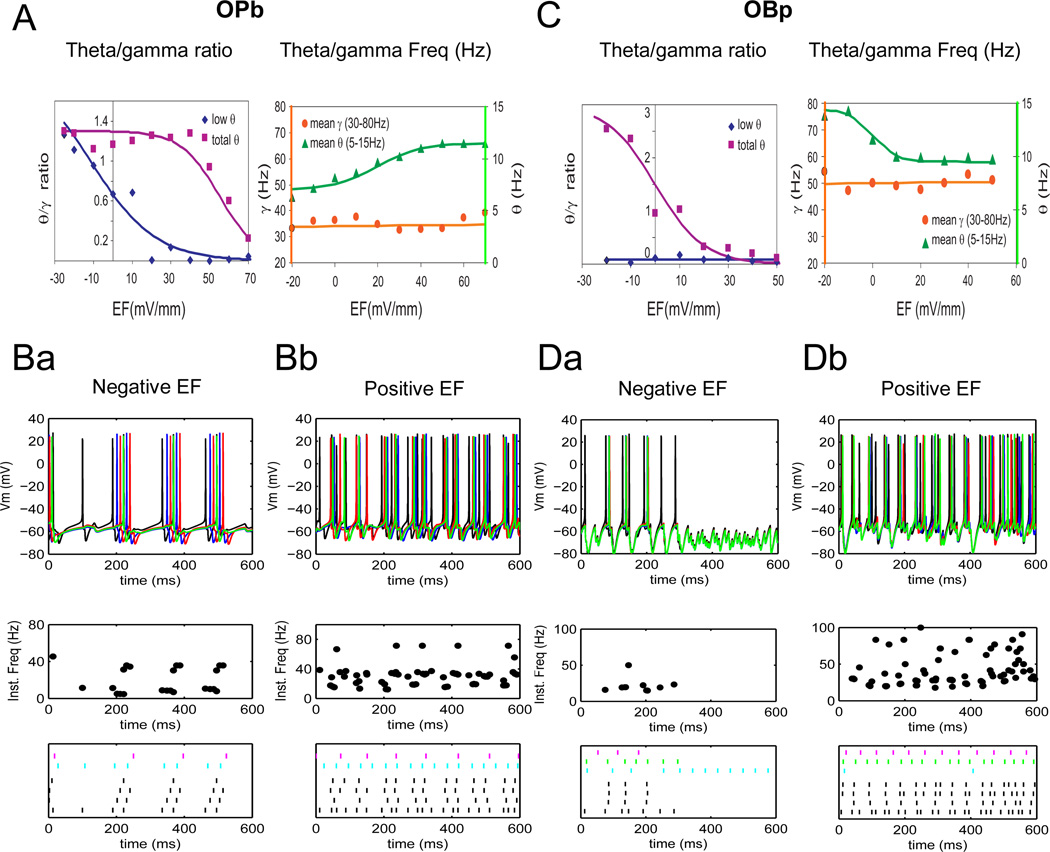
The application of external electric fields substantially altered theta-modulated gamma rhythms in both OPb and OBp networks (Figure 7). Specifically, positive fields shifted the oscillation frequency towards gamma, while negative fields shifted it towards theta (Figure 7B, D). These effects generally increased with the field intensity within the subthreshold range, in agreement with previous results from a less detailed model that mimicked electric fields with current injections (Berzhanskaya et al. 2007). This similarity with a simplified modeling approach may indicate that interactions between intrinsic (local) rhythms and electric field can be simulated using reduced models, allowing for scaling up network size. Interestingly, on top of these consistently robust predictions, the simulations also suggest distinctive differences between the alternative network configurations. When considering the classic “low” range of theta rhythms (5–8 Hz), the OPb network showed a decrease in theta/gamma ratio at positive electric fields, and a moderate increase as electric fields become more negative (Figure 7A, left). When the broader (5–15 Hz) theta range was analyzed, this circuit configuration still demonstrated a reduction of the theta/gamma ratio at the most positive fields, but no effect from reverse polarity. The electric field response of the OBp network was different. This configuration displayed significant modulation of the theta/gamma ratio computed with the total theta frequency by both positive (ratio decrease) and negative (ratio increase) electric fields (Figure 7C, left). In contrast, no parameter combination resulted in the lower theta range. Moreover, the average theta frequency, corresponding to inter-burst intervals, increased from negative to positive electric fields in the OPb network, but decreased in OBp. In both configurations, the average gamma frequency, corresponding to interspike intervals within bursts, remained unaffected throughout the entire subthreshold range of external electric fields (Figure 7A, right, vs. Figure 7C, right).

Figure 7.

Both network configurations (OPb, left and OBp, right) are modulated between theta, gamma and theta/gamma regimes by electric fields, albeit in different manners. A. Left. Summary of OPb theta/gamma ratio changes with electric field. While the “low theta”/gamma ratio (diamonds) changes from stronger theta at negative fields, through mixed theta/gamma at zero electric field, to mostly gamma at positive electric fields, the “total theta”/gamma ratio (squares) shows significant decrease only at higher positive fields. Right. Average theta (5–15 Hz, triangles) frequency shows significant increase with electric field while gamma (30–80 Hz, circles) remains nearly constant. B. Top to bottom: spike trains, instantaneous frequency plots and rasters for negative, −20 mV/mm (Ba) and positive (+40 mV/mm) electric field (Bb) in OPb network. C. Left. Summary of OBp theta/gamma ratio changes with electric field. The “total theta”/gamma ratio (diamonds) changes from stronger theta at negative fields, through mixed theta/gamma at zero electric field, to mostly gamma at positive electric fields. Note that OBp network produces higher theta frequencies and “low theta” is negligible. Right. Average theta (5–15 Hz, triangles) frequency shows significant decrease with electric field while gamma (30–80 Hz, circles) remains nearly constant. D. Spike trains, instantaneous frequency plots and rasters for negative (Da) and positive electric field (Db) in OBp network.

The theta/gamma ratio can decrease both because of lower incidence of theta-range intervals (as seen in Fig. 7Ba/b, bottom) and increase of gamma-range intervals (as in Fig. 7Da/b, bottom). While the mechanisms of theta/gamma decrease in the OPb and OBp networks may be different, this simple measure alone cannot distinguish them. However, the model predicts that the two networks can be distinguished based on their frequency response. As described above, average theta frequency increased with increasing electric field in OPb network, and decreased in OBp network. Theta or gamma could also appear as a consequence of increased population coherence (Tort et al. 2007; Goutagny et al. 2009), but the theta/gamma ratio is not sensitive to this phenomenon. Moreover, because the intervals are counted for each pyramidal neuron in the model and then summed across the cells, the effects of possible correlations between the cells cannot be considered. At the same time, the number of pyramidal cells in each lamella, limited by the use of their full morphology to explore the influence of electric fields, is insufficient to address gamma coherence meaningfully. A more resistant approach in this regard would in principle consist of simulating field potentials from the sum of membrane potentials across the population, then filtering them in the theta or gamma range. Unfortunately, however, extracellular potentials are too computationally expensive to be computed explicitly with electric fields (see also Bikson et al. 2004 and Anastassiou et al. 2010).

Lastly, we explored the possible effects of different geometries of interneurons on network dynamics. The wide variation of electric field effects on somatic polarization of non-pyramidal cells suggests a broad range of dendritic arbor balance, from nearly isotropic arborizations to a basal/apical arbor imbalance similar to pyramidal cells (Figure 2D, E). The dendritic morphologies of O and B cells known to participate in the creation of theta and gamma rhythms have not yet been digitally reconstructed and deposited in publicly shared archives. Thus, we used simplified units with 4 dendritic compartments forming 2 opposing branches. Basal to apical branch length ratio was 1:1 for arbor-balanced dendrites and 1:2 for arbor-imbalanced dendrites. At the single cell level, interneurons with balanced trees and interneurons with imbalanced dendrites aligned “horizontally” (i.e., perpendicular to the electric field) unsurprisingly resulted in no somatic polarization. As expected, in contrast, both basket and oriens cells with vertically imbalanced dendrites responded to subthreshold electric fields with a somatic polarization as strong as pyramidal cells, in agreement with our experimental data. In our simulations, however, this strong effect in individual interneurons did not qualitatively alter the general influence of subthreshold electric fields on theta-modulated gamma activity at the network level (Figure 8). In particular, we tested three variants of the OPb configuration containing interneurons with imbalanced dendrites (Figure 8A): one control with horizontal O and B cells, one with vertical O cells (O-vert), and one with vertical B cells (B-vert). Negative and positive electric field had the same effects on all three variants (as in the native OPb network), namely shifting rhythms towards theta and gamma, respectively (Figure 8B, C). Different interneuronal geometries resulted in only minor changes of the theta/gamma ratio.

Discussion

Modulation of Theta and Gamma Rhythms

In the hippocampus, the relative position and spatial orientation of dendritic trees affect both synaptic circuitry and the interaction with electric fields. The presented work investigated how subthreshold electric fields could alter hippocampal dynamics toward theta or gamma regimes, relating the underlying mechanisms to specific aspects of network connectivity.

The Role of Specific Cells

Two different network configurations were analyzed for production of theta and gamma rhythms. Both include morphologically detailed pyramidal cells and simplified oriens and basket cells. Network connectivity is consistent with the location of axonal arborization of the corresponding cell types. The exact strength of connections between different cell types in the hippocampus is unknown. Parameter ranges were constrained by the experimental observations that transverse hippocampal slices generate more gamma rhythms, while longitudinal slices generate more theta rhythms (Gloveli et al. 2005b). The resulting networks generated a range of regimes from theta, through mixed theta/gamma, to gamma, simulating several in vitro models (Fisahn et al. 2004; Gillies et al. 2002; Gloveli et al. 2005b; Oren et al. 2006). However, our specific predictions of cell types underlying these oscillations differ from previous proposals. Although oscillations can be generated in isolated CA1 (e.g. Gillies et al., 2002), the majority of experimental studies to date has explored CA3 oscillations. We adopted a pyramidal cell model from area CA1 since more is known about these cells compared to those in CA3. Due to the relatively scarce experimental data in CA3, a model of this area would have many free parameters. This suggests that the model synaptic weights could be also adjusted in CA3 so as to robustly generate theta and gamma rhythms in the whole hippocampus and different slice orientations. While theta-gamma modulation by electric fields could likely also be simulated in CA3, the lack of constraints might have reduced confidence in the interpretation of results.

It was suggested that theta oscillations can be generated in vitro by periodically changing inhibitory drive. Interneurons in both oriens and lacunosum-moleculare layers have subthreshold oscillations in the theta range (Chapman and Lacaille 1999). Oriens cells projecting to lacunosum-molecular (OLM) were previously hypothesized to critically contribute to theta rhythms (Kunec et al. 2005), consistent with the septo-temporal elongation of their axonal arborization and the prevalence of theta rhythms in longitudinal slices (Gloveli et al. 2005a). In contrast to these predictions, we found that the distal inhibitory input of OLM cells is too weak to directly modulate pyramidal cells firing induced by more proximal excitation. Instead, other interneurons capable of theta oscillations that project to the proximal dendrites of pyramidal cells, such as oriens-bistratified (O-bi) cells (Klausberger et al. 2004; Maccaferri 2005) could modulate network firing in theta rhythm in the OPb network. We predict that during pharmacologically induced theta or theta-gamma rhythms in vitro O-bi neurons will fire in the theta frequency range following the peak of pyramidal cell firing. In this framework, basket cells crucially maintain fast gamma oscillations via negative feedback (Fuchs et al. 2007) and are predicted to fire in theta phase with pyramidal cells or shortly thereafter. OLM interneurons are likely to affect entorhinally driven inputs in vivo, a prediction testable with an expanded version of our model.

The discovery of a subset of basket cells firing in the opposite half of theta than pyramidal cells (Klausberger et al. 2005) suggested an alternative configuration, OBp. In this network, basket cells fire tonically upon activation by current injections (mimicking agonist application). Suppression of this activity in theta rhythm releases pyramidal cells from inhibition, bringing them above firing threshold. Similar models involving direct oriens inhibition of basket cells were previously formulated (Gloveli et al. 2005a; Tort et al. 2007). Nonetheless, our simulations suggest novel critical constraints. Specifically, two distinct basket cell types are needed in OBp for stable theta-modulated gamma rhythms. We predict that one population of basket cells (likely parvalbumin-positive), modulated in gamma rather than theta rhythm, provides inhibitory feedback to pyramidal cells. A second basket population (possibly CCKcontaining), modulated by oriens cells in theta, is predicted to fire in anti-phase relative to pyramidal theta. Suppression of this second type of basket cells was suggested to be produced by either external sources in vivo or OLM cells in vitro (Freund and Antal 1998; Gloveli et al. 2005a; Rotstein et al. 2005). Direct reciprocal inhibition between perisomatic basket cells and OLM interneurons is unlikely. Basket axons are far from OLM dendrites, and OLM axons only reach distal basket dendrites. However, as in the OBp network, basket cells can also receive O-bi connections. Although direct projections from oriens to basket cells are not yet demonstrated, other known interneuron-specific cells (Gulyas et al. 1996) might play similar roles.

Electric Field Effects

Both network configurations can be modulated by subthreshold electric fields. These results extend our previous network study with simplified morphology modeling cell polarization by electric fields with somatic current injections (Berzhanskaya et al. 2007). The work presented here adopts a more anatomically and biophysically realistic approach to model electric fields effects using the extracellular NEURON mechanism (Bikson et al. 2005, Carnevale and Hines 2006) modified for application of uniform extracellular fields. At the single cell level, positive and negative fields aligned with the pyramidal somato-dendritic axis resulted in somatic depolarization and hyperpolarization, respectively, in agreement with both our experimental data (Figure 2, 3) and previous studies (Anastassou et al. 2010; Bikson et al. 2004).

An applied electric field can shift rhythmic activity between theta, theta/gamma and gamma regimes in both OPb and OBp networks, as well as when either B or O cells are also polarized. The ability of electric fields to shift networks between regimes could be used to test cognitive correlates of theta and gamma rhythms. Similar experimental modulation of carbachol-induced oscillations with positive/negative DC electric fields was recently observed (Reato et al. 2010). This model and experiments represent the closest match to our paradigm in the way they use subthreshold electric fields. Converging experimental and computational evidence at the single cell level (Figure 3) indicate that, at least for proximal apical inputs, electric field modulation of population activity is likely to be mediated by changes in spike latency rather than in synaptic responses. In addition, the distinct dependence of field modulation function on synaptic circuitry, including opposite electric field effects on theta frequency in OPb and OBp, opens the unexplored opportunity to use electric fields as probes to specifically discriminate between alternative network connectivities.

The adopted electric field implementation is a simplification of brain slice physics. Specifically, extracellular nodes are only weakly connected to nearest neighbors along the chain of NEURON cellular compartments. Thus, ephaptic interactions between neurons or dendritic branches are omitted. Coupling through the extracellular fluid can play role in network synchronization (Park et al. 2005), but such implementation in NEURON would be computationally expensive and beyond the scope of this project.

Comparison with Other Network Models

Simplified

Several previous approaches included reduced pyramidal cells and one-compartment interneurons. One network in particular (Gloveli et al. 2005a) used the same set of experimental data we selected to constrain model parameters, namely agonist-activated theta/gamma rhythms in hippocampal slices of different orientations. The more realistic dendritic morphology of our model allows predicting a specific role for O-bi (as distinct from OLM) cells. The realistic lamellar structure of our network also enables testing rhythm generation in different slice orientations directly, rather than approximated as lumped excitatory and inhibitory conductance changes (as in Gloveli et al. 2005a). Although gamma (and theta) rhythms are possible in networks composed just of interneurons (Rotstein et al. 2005), inclusion of pyramidal cells ensures greater rhythm stability (PING or Pyramidal/INterneuron-Generated rhythms: Börgers et al. 2005). Because both oriens and basket cells receive strong input from pyramidal neurons, we did not explore pure interneuronal connectivity as a basis for rhythmogenesis. Another simplified model addressed electric field modulation of network activity (Park et al. 2005). Using more complex morphology, our network explored different configurations of pyramidal-interneuron connectivity, but could not test for ephaptic interactions.

More complex network models

A larger-scale network of hippocampal area CA3 simulated different oscillations evoked by carbachol with one-compartment neurons and a complex set of currents (Tiesinga et al. 2001). Although this study, like ours, implemented inhomogeneous connectivity, inhibitory neurons fired in gamma similarly to the feedback basket cells in our model, and lacked the critical role played by oriens neurons in theta rhythm organization. We did not explore B-B connectivity included in this previous model, as cell-specific loss of B-B inhibition was recently found not to affect hippocampal gamma rhythms (Wulff et al. 2009).

An even larger simulation of gamma rhythms in recurrent CA3 network included 3072 pyramidal cells, each with 63 compartments, and 384 muticompartmental, but not as detailed, interneurons of 4 different types based on connectivity (Traub et al. 2000). Such size allowed simulating realistic convergence divergence ratios and low pyramidal cell firing rates, but did not investigate theta rhythmogenesis, similar to other studies (Mann et al. 2005). As in this model, both GABAA and AMPA played a role in our simulations, and pyramidal cell firing increased upon GABAA blockage.

Previous attempts simulated the CA1 circuitry with realistic pyramidal cells, one-compartment interneurons, and signal transfer properties similar to our model (Orbán et al. 2006), but without validating parameters against rhythms in different orientations of hippocampal slices. Our use of more complex interneuronal geometry enabled a detailed study of the effect of electric fields on network activity, which can be tested in the future both in vivo and in vitro. Recent work had demonstrated the ability of applied electrical fields to modulate hippocampal activity (Annastasiou et al. 2010; Reato et al. 2010; Sunderam et al. 2009). Our models will form a link to experimental model-based observation and control of such network dynamics.

Notation

CA1

cornus ammonis area 1

CA3

cornus ammonis area 3

SC

Schaffer Collateral

alv

alveus

s.o

stratum oriens

s.p

stratum pyramidale

s.r

stratum radiatum

s.l.m

stratum lacunosum moleculare

O-bi

Oriens-bistratified

OLM

Oriens-lacunosum moleculare

ISI

interspike interval

IBI

interburst interval

CCK

Cholecystokinin

IPSC/IPSP

Inhibitory postsynaptic currents/potentials

EPSC/EPSP

Excitatory postsynaptic currents/potentials

GABA

gamma-Aminobutyric acid

AMPA

alpha- Amino -3 hydroxyl -5 Methyl-4- isoxazole-Propionate

NMDA

N-Methyl-D-aspartic acid

Network model

P

pyramidal cell (excitatory)

O

oriens cell (inhibitory, dendritic targeting, O-Bi /OLM)

B

basket cell (inhibitory, perisomatic targeting, B1/ B2)

OBp

Network configuration with strong O-B connections and weak O-P connections

OPb

Network configuration with weak O-B connections and strong O-P connections

B-vert

basket cell with vertically oriented dendrites

O-vert

oriens cell with vertically oriented dendrites