Abstract
The detection of moons orbiting extrasolar planets (“exomoons”) has now become feasible. Once they are discovered in the circumstellar habitable zone, questions about their habitability will emerge. Exomoons are likely to be tidally locked to their planet and hence experience days much shorter than their orbital period around the star and have seasons, all of which works in favor of habitability. These satellites can receive more illumination per area than their host planets, as the planet reflects stellar light and emits thermal photons. On the contrary, eclipses can significantly alter local climates on exomoons by reducing stellar illumination. In addition to radiative heating, tidal heating can be very large on exomoons, possibly even large enough for sterilization. We identify combinations of physical and orbital parameters for which radiative and tidal heating are strong enough to trigger a runaway greenhouse. By analogy with the circumstellar habitable zone, these constraints define a circumplanetary “habitable edge.” We apply our model to hypothetical moons around the recently discovered exoplanet Kepler-22b and the giant planet candidate KOI211.01 and describe, for the first time, the orbits of habitable exomoons. If either planet hosted a satellite at a distance greater than 10 planetary radii, then this could indicate the presence of a habitable moon. Key Words: Astrobiology—Extrasolar planets—Habitability—Habitable zone—Tides. Astrobiology 13, 18–46.
1. Introduction
The question whether life has evolved outside Earth has prompted scientists to consider habitability of the terrestrial planets in the Solar System, their moons, and planets outside the Solar System, that is, extrasolar planets. Since the discovery of the first exoplanet almost two decades ago (Mayor and Queloz, 1995), roughly 800 more have been found, and research on exoplanet habitability has culminated in the targeted space mission Kepler, specifically designed to detect Earth-sized planets in the circumstellar irradiation habitable zones (IHZs; Huang, 1959; Kasting et al., 1993; Selsis et al., 2007; Barnes et al., 2009)1 around Sun-like stars. No such Earth analogue has been confirmed so far. Among the 2312 exoplanet candidates detected with Kepler (Batalha et al., 2012), more than 50 are indeed in the IHZ (Borucki et al., 2011; Kaltenegger and Sasselov, 2011; Batalha et al., 2012), yet most of them are significantly larger and likely more massive than Earth. Habitability of the moons around these planets has received little attention. We argue here that it will be possible to constrain their habitability on the data available at the time they will be discovered.
Various astrophysical effects distinguish investigations of exomoon habitability from studies on exoplanet habitability. On a moon, there will be eclipses of the star by the planet (Dole, 1964), the planet's stellar reflected light, as well as the planet's thermal emission, all of which might affect the moon's climate. Tidal heating can also provide an additional energy source, which must be considered for evaluations of exomoon habitability (Reynolds et al., 1987; Scharf, 2006; Debes and Sigurdsson, 2007; Cassidy et al., 2009; Henning et al., 2009). Moreover, tidal processes between the moon and its parent planet will determine the orbit and spin evolution of the moon. Earth-sized planets in the IHZ around low-mass stars tend to become tidally locked, that is, one hemisphere permanently faces the star (Dole, 1964; Goldreich, 1966; Kasting et al., 1993), and they will not have seasons because their obliquities are eroded (Heller et al., 2011a,b). On moons, however, tides from the star are mostly negligible compared to the tidal drag from the planet. Thus, in most cases exomoons will be tidally locked to their host planet rather than to the star (Dole, 1964; Gonzalez, 2005; Henning et al., 2009; Kaltenegger, 2010; Kipping et al., 2010) so that (i.) a satellite's rotation period will equal its orbital period about the planet, (ii.) a moon will orbit the planet in its equatorial plane (due to the Kozai mechanism and tidal evolution, Porter and Grundy, 2011), and (iii.) a moon's rotation axis will be perpendicular to its orbit about the planet. A combination of (ii.) and (iii.) will cause the satellite to have the same obliquity with respect to the circumstellar orbit as the planet.
More massive planets are more resistive against the tidal erosion of their obliquities (Heller et al., 2011b); thus massive host planets of exomoons can maintain significant obliquities on timescales much larger than those for single terrestrial planets. Consequently, satellites of massive exoplanets could be located in the IHZ of low-mass stars while, firstly, their rotation would not be locked to their orbit around the star (but to the planet) and, secondly, they could experience seasons if the equator of their host planet is tilted against the orbital plane. Both aspects tend to reduce seasonal amplitudes of stellar irradiation (Cowan et al., 2012) and thereby stabilize exomoon climates.
An example is given by a potentially habitable moon in the Solar System, Titan. It is the only moon known to have a substantial atmosphere. Tides exerted by the Sun on Titan's host planet, Saturn, are relatively weak, which is why the planet could maintain its spin-orbit misalignment, or obliquity, ψp of 26.7° (Norman, 2011). Titan orbits Saturn in the planet's equatorial plane with no significant tilt of its rotation axis with respect to its circumplanetary orbit. Thus, the satellite shows a similar obliquity with respect to the Sun as Saturn and experiences strong seasonal modulations of insolation as a function of latitude, which leads to an alternation in the extents and localizations of its lakes and potential habitats (Wall et al., 2010). While tides from the Sun are negligible, Titan is tidally synchronized with Saturn (Lemmon et al., 1993) and has a rotation and an orbital period of ≈16 d. Uranus, where ψp≈97.9° (Harris and Ward, 1982), illustrates that even more extreme scenarios are possible.
No exomoon has been detected so far, but it has been shown that exomoons with masses down to 20% the mass of Earth (M⊕) are detectable with the space-based Kepler telescope (Kipping et al., 2009). Combined measurements of a planet's transit timing variation (TTV) and transit duration variation (TDV) can provide information about the satellite's mass (Ms), its semimajor axis around the planet (aps) (Sartoretti and Schneider, 1999; Simon et al., 2007; Kipping, 2009a), and possibly about the inclination (i) of the satellite's orbit with respect to the orbit around the star (Kipping, 2009b). Photometric transits of a moon in front of the star (Szabó et al., 2006; Lewis, 2011; Kipping, 2011a; Tusnski and Valio, 2011), as well as mutual eclipses of a planet and its moon (Cabrera and Schneider, 2007; Pál, 2012), can provide information about its radius (Rs), and the photometric scatter peak analysis (Simon et al., 2012) can offer further evidence for the exomoon nature of candidate objects. Finally, spectroscopic investigations of the Rossiter-McLaughlin effect can yield information about the satellite's orbital geometry (Simon et al., 2010; Zhuang et al., 2012), although relevant effects require accuracies in stellar radial velocity of the order of a few centimeters per second (see also Kipping, 2011a). Beyond, Peters and Turner (personal communication) suggest that direct imaging of extremely tidally heated exomoons will be possible with next-generation space telescopes. It was only recently that Kipping et al. (2012) initiated the first dedicated hunt for exomoons, based on Kepler observations. While we are waiting for their first discoveries, hints to exomoon-forming regions around planets have already been found (Mamajek et al., 2012).
In Section 2 of this paper, we consider general aspects of exomoon habitability to provide a basis for our work, while Section 3 is devoted to the description of the exomoon illumination plus tidal heating model. Section 4 presents a derivation of the critical orbit-averaged global flux and the description of habitable exomoon orbits, ultimately leading to the concept of the “habitable edge.” In Section 5, we apply our model to putative exomoons around the first Neptune-sized1 planet in the IHZ of a Sun-like star, Kepler-22b, and a much more massive, still to be confirmed planet candidate, the “Kepler Object of Interest” (KOI) 211.013, also supposed to orbit in the IHZ. We summarize our results with a discussion in Section 6. Detailed illustrations on how we derive our model are placed into the appendices.
2. Habitability of Exomoons
So far, there have been only a few published investigations on exomoon habitability (Reynolds et al., 1987; Williams et al., 1997; Kaltenegger, 2000; Scharf, 2006; Porter and Grundy, 2011). Other studies were mainly concerned with the observational aspects of exomoons (for a review see Kipping et al., 2012), their orbital stability (Barnes and O'Brien, 2002; Domingos et al., 2006; Donnison, 2010; Weidner and Horne, 2010; Quarles et al., 2012; Sasaki et al., 2012), and eventually with the detection of biosignatures (Kaltenegger, 2010). Thus, we provide here a brief overview of some important physical and biological aspects that must be accounted for when considering exomoon habitability.
Williams et al. (1997) were some of the first who proposed that habitable exomoons could be orbiting giant planets. At the time of their writing, only nine extrasolar planets, all of which are giant gaseous objects, were known. Although these bodies are not supposed to be habitable, Williams et al. argued that possible satellites of the jovian planets 16 Cygni B and 47 Ursae Majoris could offer habitats, because they orbit their respective host star at the outer edge of the habitable zone (Kasting et al., 1993). The main counter arguments against habitable exomoons were (i.) tidal locking of the moon with respect to the planet, (ii.) a volatile endowment of those moons, which would have formed in a circumplanetary disk, that is different from the abundances available for planets forming in a circumstellar disk, and (iii.) bombardment of high-energy ions and electrons within the magnetic fields of the jovian host planet and subsequent loss of the satellite's atmosphere. Moreover, (iv.) stellar forcing of a moon's upper atmosphere will constrain its habitability.
Point (i.), in fact, turns out as an advantage for Earth-sized satellites of giant planets over terrestrial planets in terms of habitability, by the following reasoning: Application of tidal theories shows that the rotation of extrasolar planets in the IHZ around low-mass stars will be synchronized on timescales ≪ 1 Gyr (Dole, 1964; Goldreich, 1966; Kasting et al., 1993). This means one hemisphere of the planet will permanently face the star, while the other hemisphere will freeze in eternal darkness. Such planets might still be habitable (Joshi et al., 1997), but extreme weather conditions would strongly constrain the extent of habitable regions on the planetary surface (Heath and Doyle, 2004; Spiegel et al., 2008; Edson et al., 2011; Heng and Vogt, 2011; Wordsworth et al., 2011). However, considering an Earth-mass exomoon around a Jupiter-like host planet, within a few million years at most the satellite should be tidally locked to the planet—rather than to the star (Porter and Grundy, 2011). This configuration would not only prevent a primordial atmosphere from evaporating on the illuminated side or freezing out on the dark side (i.) but might also sustain its internal dynamo (iii.). The synchronized rotation periods of putative Earth-mass exomoons around giant planets could be in the same range as the orbital periods of the Galilean moons around Jupiter (1.7–16.7 d) and as Titan's orbital period around Saturn (≈16 d) (NASA/JPL planetary satellite ephemerides)4. The longest possible length of a satellite's day compatible with Hill stability has been shown to be about P*p/9, P*p being the planet's orbital period about the star (Kipping, 2009a). Since the satellite's rotation period also depends on its orbital eccentricity around the planet and since the gravitational drag of further moons or a close host star could pump the satellite's eccentricity (Cassidy et al., 2009; Porter and Grundy, 2011), exomoons might rotate even faster than their orbital period.
Finally, from what we know about the moons of the giant planets in the Solar System, the satellite's enrichment with volatiles (ii.) should not be a problem. Cometary bombardment has been proposed as a source for the dense atmosphere of Saturn's moon Titan, and it has been shown that even the currently atmosphere-free jovian moons Ganymede and Callisto should initially have been supplied with enough volatiles for an atmosphere (Griffith and Zahnle, 1995). Moreover, as giant planets in the IHZ likely formed farther away from their star, that is, outside the snow line (Kennedy and Kenyon, 2008), their satellites will be rich in liquid water and eventually be surrounded by substantial atmospheres.
The stability of a satellite's atmosphere (iv.) will critically depend on its composition, the intensity of stellar extreme ultraviolet radiation (EUV), and the moon's surface gravity. Nitrogen-dominated atmospheres may be stripped away by ionizing EUV radiation, which is a critical issue to consider for young (Lichtenegger et al., 2010) and late-type (Lammer et al., 2009) stars. Intense EUV flux could heat and expand a moon's upper atmosphere so that it can thermally escape due to highly energetic radiation (iii.), and if the atmosphere is thermally expanded beyond the satellite's magnetosphere, then the surrounding plasma may strip away the atmosphere nonthermally. If Titan were to be moved from its roughly 10 AU orbit around the Sun to a distance of 1 AU (AU being an astronomical unit, i.e., the average distance between the Sun and Earth), then it would receive about 100 times more EUV radiation, leading to a rapid loss of its atmosphere due to the moon's smaller mass, compared to Earth. For an Earth-mass moon at 1 AU from the Sun, EUV radiation would need to be less than 7 times the Sun's present-day EUV emission to allow for a long-term stability of a nitrogen atmosphere. CO2 provides substantial cooling of an atmosphere by IR radiation, thereby counteracting thermal expansion and protecting an atmosphere's nitrogen inventory (Tian, 2009).
A minimum mass of an exomoon is required to drive a magnetic shield on a billion-year timescale (Ms≳0.1M⊕; Tachinami et al., 2011); to sustain a substantial, long-lived atmosphere (Ms≳0.12M⊕; Williams et al., 1997; Kaltenegger, 2000); and to drive tectonic activity (Ms≳0.23M⊕; Williams et al., 1997), which is necessary to maintain plate tectonics and to support the carbon-silicate cycle. Weak internal dynamos have been detected in Mercury and Ganymede (Gurnett et al., 1996; Kivelson et al., 1996), suggesting that satellite masses>0.25M⊕ will be adequate for considerations of exomoon habitability. This lower limit, however, is not a fixed number. Further sources of energy—such as radiogenic and tidal heating, and the effect of a moon's composition and structure—can alter the limit in either direction. An upper mass limit is given by the fact that increasing mass leads to high pressures in the planet's interior, which will increase the mantle viscosity and depress heat transfer throughout the mantle as well as in the core. Above a critical mass, the dynamo is strongly suppressed and becomes too weak to generate a magnetic field or sustain plate tectonics. This maximum mass can be placed around 2M⊕ (Gaidos et al., 2010; Noack and Breuer, 2011; Stamenković et al., 2011). Summing up these conditions, we expect approximately Earth-mass moons to be habitable, and these objects could be detectable with the newly started Hunt for Exomoons with Kepler (HEK) project (Kipping et al., 2012).
2.1. Formation of massive satellites
The largest and most massive moon in the Solar System, Ganymede, has a radius of only≈0.4R⊕ (R⊕ being the radius of Earth) and a mass of≈0.025M⊕. The question as to whether much more massive moons could have formed around extrasolar planets is an active area of research. Canup and Ward (2006) showed that moons formed in the circumplanetary disk of giant planets have masses ≲10−4 times that of the planet's mass. Assuming satellites formed around Kepler-22b, their masses will thus be 2.5×10−3 M⊕ at most, and around KOI211.01 they will still weigh less than Earth's Moon. Mass-constrained in situ formation becomes critical for exomoons around planets in the IHZ of low-mass stars because of the observational lack of such giant planets. An excellent study on the formation of the Jupiter and the Saturn satellite systems is given by Sasaki et al. (2010), who showed that moons of sizes similar to Io, Europa, Ganymede, Callisto, and Titan should build up around most gas giants. What is more, according to their Fig. 5 and private communication with Takanori Sasaki, formation of Mars- or even Earth-mass moons around giant planets is possible. Depending on whether or not a planet accretes enough mass to open up a gap in the protostellar disk, these satellite systems will likely be multiple and resonant (as in the case of Jupiter) or contain only one major moon (see Saturn). Ogihara and Ida (2012) extended these studies to explain the compositional gradient of the jovian satellites. Their results explain why moons rich in water are farther away from their giant host planet and imply that capture in 2:1 orbital resonances should be common.
FIG. 5.
Stellar and planetary contributions to the illumination of our prototype moon as in Fig. 4 but at a stellar orbital phase 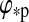 =0.5 in an eccentric orbit (
=0.5 in an eccentric orbit (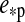 =0.3) and with an inclination
=0.3) and with an inclination 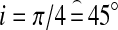 of the moon's orbit against the circumstellar orbit.
of the moon's orbit against the circumstellar orbit.
Ways to circumvent the impasse of insufficient satellite mass are the gravitational capture of massive moons (Debes and Sigurdsson, 2007; Porter and Grundy, 2011; Quarles et al., 2012), which seems to have worked for Triton around Neptune (Goldreich et al., 1989; Agnor and Hamilton, 2006); the capture of Trojans (Eberle et al., 2011); gas drag in primordial circumplanetary envelopes (Pollack et al., 1979); pull-down capture trapping temporary satellites or bodies near the Lagrangian points into stable orbits (Heppenheimer and Porco, 1977; Jewitt and Haghighipour, 2007); the coalescence of moons (Mosqueira and Estrada, 2003); and impacts on terrestrial planets (Canup, 2004; Withers and Barnes, 2010; Elser et al., 2011). Such moons would correspond to the irregular satellites in the Solar System, as opposed to regular satellites that form in situ. Irregular satellites often follow distant, inclined, and often eccentric or even retrograde orbits about their planet (Carruba et al., 2002). For now, we assume that Earth-mass extrasolar moons—be they regular or irregular—exist.
2.2. Deflection of harmful radiation
A prominent argument against the habitability of moons involves high-energy particles, which a satellite meets in the planet's radiation belt. Firstly, this ionizing radiation could strip away a moon's atmosphere, and secondly it could avoid the buildup of complex molecules on its surface. In general, the process in which incident particles lose part of their energy to a planetary atmosphere or surface to excite the target atoms and molecules is called sputtering. The main sources for sputtering on Jupiter's satellites are the energetic, heavy ions O+ and S+, as well as H+, which give rise to a steady flux of H2O, OH, O2, H2, O, and H from Ganymede's surface (Marconi, 2007). A moon therefore requires a substantial magnetic field that is strong enough to embed the satellite in a protective bubble inside the planet's powerful magnetosphere. The only satellite in the Solar System with a substantial magnetic shield of roughly 750 nT is Ganymede (Kivelson et al., 1996). The origin of this field is still subject to debate because it can only be explained by a very specific set of initial and compositional configurations (Bland et al., 2008), assuming that it is generated in the moon's core.
For terrestrial planets, various models for the strength of global dipolar magnetic fields Bdip as a function of planetary mass and rotation rate exist, but none has proven exclusively valid. Simulations of planetary thermal evolution have shown that Bdip increases with mass (Tachinami et al., 2011; Zuluaga and Cuartas, 2012) and rotation frequency (López-Morales et al., 2011). The spin of exomoons will be determined by tides from the planet, and rotation of an Earth-sized exomoon in the IHZ can be much faster than rotation of an Earth-sized planet orbiting a star. Thus, an exomoon could be prevented from tidal synchronization with the host star—in support of an internal dynamo and thus magnetic shielding against energetic irradiation from the planet and the star. Some studies suggest that even extremely slow rotation would allow for substantial magnetic shielding, provided convection in the planet's or moon's mantle is strong enough (Olson and Christensen, 2006). In this case, tidal locking would not be an issue for magnetic shielding.
The picture of magnetic shielding gets even more complicated when tidal heating is considered, which again depends on the orbital parameters. In the Moon, tidal heating, mostly induced by the Moon's obliquity of 6.68° against its orbit around Earth, occurs dominantly in the core (Kaula, 1964; Peale and Cassen, 1978). On Io, however, where tidal heating stems from Jupiter's effect on the satellite's eccentricity, dissipation occurs mostly in the mantle (Segatz et al., 1988). In the former case, tidal heating might enhance the temperature gradient between the core and the mantle and thereby also enhance convection and finally the strength of the magnetic shielding; in the latter case, tidal heating might decrease convection. Of course, the magnetic properties of terrestrial worlds will evolve and, when combined with the evolution of EUV radiation and stellar wind from the host star, define a time-dependent magnetically restricted habitable zone (Khodachenko et al., 2007; Zuluaga et al., 2012).
We conclude that radiation of highly energetic particles does not ultimately preclude exomoon habitability. In view of possible deflection due to magnetic fields on a massive satellite, it is still reasonable to consider the habitability of exomoons.
2.3. Runaway greenhouse
On Earth, the thermal equilibrium temperature of incoming and outgoing radiation is 255 K. However, the mean surface temperature is 289 K. The additional heating is driven by the greenhouse effect (Kasting, 1988), which is a crucial phenomenon to the habitability of terrestrial bodies. The strength of the greenhouse effect depends on numerous variables—most importantly on the inventory of greenhouse gases, the albedo effect of clouds, the amount of liquid surface water, and the spectral energy distribution of the host star.
Simulations have shown that, as the globally absorbed irradiation on a water-rich planetary body increases, the atmosphere gets enriched in water vapor until it gets opaque. For an Earth-like body, this imposes a limit of about 300 W/m2 to the thermal radiation that can be emitted to space. If the global flux exceeds this limit, the body is said to be a runaway greenhouse. Water vapor can then leave the troposphere through the tropopause and reach the stratosphere, where photodissociation by stellar UV radiation allows the hydrogen to escape to space, thereby desiccating the planetary body. While boiling oceans, high surface temperatures, or high pressures can make a satellite uninhabitable, water loss does by definition. Hence, we will use the criterion of a runaway greenhouse to define an exomoon's habitability.
Surface temperatures strongly depend on the inventory of greenhouse gases, for example, CO2. The critical energy flux FRG for a runaway greenhouse, however, does not (Kasting, 1988; Goldblatt and Watson, 2012). As in the work of Barnes et al. (2013), who discussed how the interplay of stellar irradiation and tidal heating can trigger a runaway greenhouse on exoplanets, we will use the semi-analytical approach of Pierrehumbert (2010) for the computation of FRG:
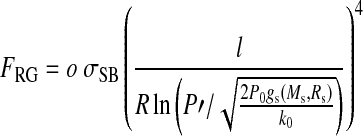 |
(1) |
with
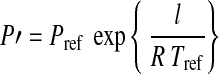 |
(2) |
Pref=610.616 Pa, l is the latent heat capacity of water, R is the universal gas constant, Tref=273.13 K, o=0.7344 is a constant designed to match radiative transfer simulations, σSB is the Stefan-Boltzmann constant, P0=104 Pa is the pressure at which the absorption line strengths of water vapor are evaluated, 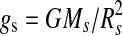 is the gravitational acceleration at the satellite's surface, and k0=0.055 is the gray absorption coefficient at standard temperature and pressure. Recall that the runaway greenhouse does not depend on the composition of the atmosphere, other than that it contains water. As habitability requires water and Eq. 1 defines a limit above which the satellite will lose it, the formula provides a conservative limit to habitability.
is the gravitational acceleration at the satellite's surface, and k0=0.055 is the gray absorption coefficient at standard temperature and pressure. Recall that the runaway greenhouse does not depend on the composition of the atmosphere, other than that it contains water. As habitability requires water and Eq. 1 defines a limit above which the satellite will lose it, the formula provides a conservative limit to habitability.
In addition to the maximum flux FRG to allow for a moon to be habitable, one may think of a minimum flux required to prevent the surface water from freezing. On terrestrial exoplanets, this freezing defines the outer limit of the stellar IHZ. On exomoons, the extra light from the planetary reflection and thermal emission as well as tidal heating in the moon will move the circumstellar habitable zone away from the star, whereas eclipses will somewhat counterbalance this effect. While it is clear that a moon under strong tidal heating will not be habitable, it is not clear to what extent it might actually support habitability (Jackson et al., 2008). Even a relatively small tidal heating flux of a few watts per square meter could render an exomoon inhospitable; see Io's global volcanism, where tidal heating is a mere 2 W/m2 (Spencer et al., 2000). Without applying sophisticated models for the moon's tidal heating, we must stick to the irradiation aspect to define an exomoon's circumstellar habitable zone. At the outer edge of the stellar IHZ, the host planet will be cool and reflect little stellar flux. Neglecting tidal heating as well as thermal emission and reflection from the planet, the minimum flux for an Earth-like moon to be habitable will thus be similar to that of an Earth-like planet at the same orbital distance to the star. Below, we will only use the upper flux limit from Eq. 1 to constrain the orbits of habitable exomoons. This leads to the concept of the circumplanetary “habitable edge.”
3. Energy Reservoirs on Exomoons
Life needs liquid water and energy, but an oversupply of energy can push a planet or an exomoon into a runaway greenhouse and thereby make it uninhabitable. The critical, orbit-averaged energy flux for an exomoon to turn into a runaway greenhouse is around 300 W/m2, depending on the moon's surface gravity and atmospheric composition (Kasting, 1988; Kasting et al., 1993; Selsis et al., 2007; Pierrehumbert, 2010; Goldblatt and Watson, 2012). An exomoon will thus only be habitable in a certain range of summed irradiation and tidal heat flux (Barnes et al., 2013).
We consider four energy reservoirs and set them into context with the IHZ: (i.) stellar illumination, (ii.) stellar reflected light from the planet, (iii.) thermal radiation from the planet, and (iv.) tidal heating on the moon. Here, primordial heat from the moon's formation and radiogenic decay is neglected, and it is assumed that the moon's rotation is tidally locked to its host planet, as is the case for almost all the moons in the Solar System. Our irradiation model includes arbitrary orbital eccentricities 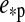 of the planet around the star5. While we compute tidal heating on the satellite as a function of its orbital eccentricity eps around the planet, we assume eps=0 in the parametrization of the moon's irradiation. This is appropriate because typically eps ≪ 0.1. Bolmont et al. (2011) studied the tidal evolution of Earth-mass objects around brown dwarfs, a problem which is similar to an Earth-mass moon orbiting a jovian planet, and found that tidal equilibrium occurs on very short timescales compared to the lifetime of the system. For non-zero eccentricities (eps≠0), the moon will not be tidally locked. But since eps ≪ 0.1, the moon's rotation will librate around an equilibrium orientation toward the planet, and the orbital mean motion will still be almost equal to the rotational mean motion (for a review on Titan's libration, see Sohl et al.,
1995). By reasons specified by Heller et al. (2011b), we also assume that the obliquity of the satellite with respect to its orbit around the planet has been eroded to 0°, but we allow for arbitrary inclinations i of the moon's orbit with respect to the orbit of the planet-moon barycenter around the star. If one assumed that the moon always orbits above the planet's equator, that would imply that i is equal to the planetary obliquity ψp, which is measured with respect to the planet's orbit around the star. We do not need this assumption for the derivation of our equations, but since ψp≈i for all the large moons in the Solar System, except Triton, observations or numerical predictions of ψp (Heller et al.,
2011b) can provide reasonable assumptions for i.
of the planet around the star5. While we compute tidal heating on the satellite as a function of its orbital eccentricity eps around the planet, we assume eps=0 in the parametrization of the moon's irradiation. This is appropriate because typically eps ≪ 0.1. Bolmont et al. (2011) studied the tidal evolution of Earth-mass objects around brown dwarfs, a problem which is similar to an Earth-mass moon orbiting a jovian planet, and found that tidal equilibrium occurs on very short timescales compared to the lifetime of the system. For non-zero eccentricities (eps≠0), the moon will not be tidally locked. But since eps ≪ 0.1, the moon's rotation will librate around an equilibrium orientation toward the planet, and the orbital mean motion will still be almost equal to the rotational mean motion (for a review on Titan's libration, see Sohl et al.,
1995). By reasons specified by Heller et al. (2011b), we also assume that the obliquity of the satellite with respect to its orbit around the planet has been eroded to 0°, but we allow for arbitrary inclinations i of the moon's orbit with respect to the orbit of the planet-moon barycenter around the star. If one assumed that the moon always orbits above the planet's equator, that would imply that i is equal to the planetary obliquity ψp, which is measured with respect to the planet's orbit around the star. We do not need this assumption for the derivation of our equations, but since ψp≈i for all the large moons in the Solar System, except Triton, observations or numerical predictions of ψp (Heller et al.,
2011b) can provide reasonable assumptions for i.
In our simulations, we consider two prototype moons: one rocky Earth-mass satellite with a rock-to-mass fraction of 68% (similar to Earth) and one water-rich satellite with the tenfold mass of Ganymede and an ice-to-mass fraction of 25% (Fortney et al., 2007). The remaining constituents are assumed to be iron for the Earth-mass moon and silicates for the Super-Ganymede. The more massive and relatively dry moon represents what we guess a captured, Earth-like exomoon could be like, while the latter one corresponds to a satellite that has formed in situ. Note that a mass of 10 MG (MG being the mass of Ganymede) corresponds to roughly 0.25 M⊕, which is slightly above the detection limit for combined TTV and TDV with Kepler (Kipping et al., 2009). Our assumptions for the Super-Ganymede composition are backed up by observations of the Jupiter and Saturn satellite systems (Showman and Malhotra, 1999; Grasset et al., 2000) as well as terrestrial planet and satellite formation studies (Kuchner, 2003; Ogihara and Ida, 2012). These papers show that in situ formation naturally generates water-rich moons and that such objects can retain their water reservoir for billions of years against steady hydrodynamic escape. Concerning the habitability of the water-rich Super-Ganymede, we do not rely on any assumptions concerning possible life-forms in such water worlds. Except for the possible strong heating in a water-rich atmosphere (Matsui and Abe, 1986; Kuchner, 2003), we see no reason why ocean moons should not be hospitable, in particular against the background that life on Earth arose in (possibly hot) oceans or freshwater seas.
For the sake of consistency, we derive the satellites' radii Rs from planetary structure models (Fortney et al., 2007). In the case of the Earth-mass moon, we obtain Rs=1R⊕, and for the much lighter but water-dominated Super-Ganymede Rs=1.235R⊕. Equation 1 yields a critical flux of 295 W/m2 for the Earth-mass moon and 243 W/m2 for the Super-Ganymede satellite. The bond albedo of both moons is assumed to be 0.3, similar to the mean albedo of Earth and of the Galilean satellites (Clark, 1980). In the following, we call our Earth-like and Super-Ganymede satellites our “prototype moons.” Based on the summary of observations and the model for giant planet atmospheres provided by Madhusudhan and Burrows (2012), we also use a bond albedo of 0.3 for the host planet, although higher values might be reasonable due to the formation of water clouds at distances 1 AU from the host star (Burrows et al., 2006a). Mass and radius of the planet are not fixed in our model, but we will mostly refer to Jupiter-sized host planets.
3.1. Illumination
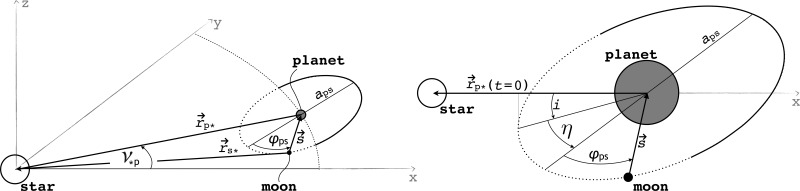
The total bolometric illumination on a moon is given by the stellar flux (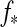 ), the reflection of the stellar light from the planet (fr), and the planetary thermal emission (ft). Their variation will be a function of the satellite's orbital phase 0≤φps(t)=(t−t0)/Pps≤1 around the planet [with t being time, t0 as the starting time (0 in our simulations), and Pps as the period of the planet-moon orbit], the orbital phase of the planet-moon duet around the star (
), the reflection of the stellar light from the planet (fr), and the planetary thermal emission (ft). Their variation will be a function of the satellite's orbital phase 0≤φps(t)=(t−t0)/Pps≤1 around the planet [with t being time, t0 as the starting time (0 in our simulations), and Pps as the period of the planet-moon orbit], the orbital phase of the planet-moon duet around the star (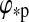 , which is equivalent to the mean anomaly
, which is equivalent to the mean anomaly 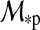 divided by 2π), and will depend on the eccentricity of the planet around the star (
divided by 2π), and will depend on the eccentricity of the planet around the star (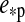 ), on the inclination (i) of the two orbits, on the orientation of the periapses (η), as well as on longitude and latitude on the moon's surface (φ and θ).
), on the inclination (i) of the two orbits, on the orientation of the periapses (η), as well as on longitude and latitude on the moon's surface (φ and θ).
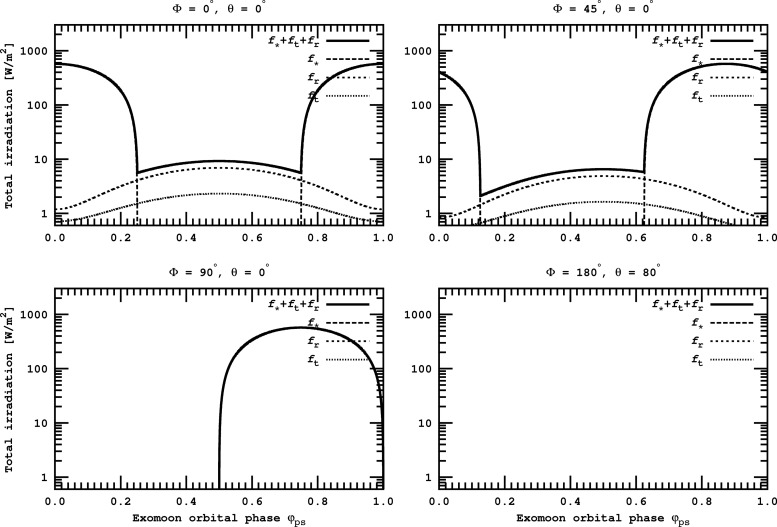
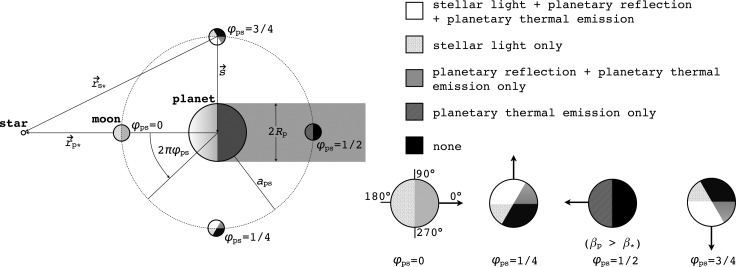
In Fig. 1, we show the variation of the satellite's illumination as a function of the satellite's orbital phase φps. For this plot, the orbital phase of the planet-moon pair around the star 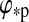 =0 and i=0. Projection effects due to latitudinal variation have been neglected, starlight is assumed to be plane-parallel, and radii and distances are not to scale.
=0 and i=0. Projection effects due to latitudinal variation have been neglected, starlight is assumed to be plane-parallel, and radii and distances are not to scale.
FIG. 1.
Geometry of the triple system of a star, a planet, and a moon with illuminations indicated by different shadings (pole view). For ease of visualization, the moon's orbit is coplanar with the planet's orbit about the star, and the planet's orbital position with respect to the star is fixed. Combined stellar and planetary irradiation on the moon is shown for four orbital phases. Projection effects as a function of longitude φ and latitude θ are ignored, and we neglect effects of a penumbra. Radii and distances are not to scale, and starlight is assumed to be plane-parallel. In the right panel, the surface normal on the subplanetary point is indicated by an arrow. For a tidally locked moon this spot is a fixed point on the moon's surface. For ϕps=0 four longitudes are indicated.
In our irradiation model of a tidally locked satellite, we neglect clouds, radiative transfer, atmospheric circulation, geothermal flux6, thermal inertia, and so on, and we make use of four simplifications:
(i.) We assume the planet casts no penumbra on the moon. There is either total illumination from the star or none. This assumption is appropriate since we are primarily interested in the key contributions to the moon's climate.
(ii.) The planet is assumed to be much more massive than the moon, and the barycenter of the planet-moon binary is placed at the center of the planet. Even if the planet and the moon had equal masses, corrections would be small since the range between the planet-moon barycenter and the star ≫ aps.
(iii.) For the computation of the irradiation, we treat the moon's orbit around the planet as a circle. The small eccentricities which we will consider later for tidal heating will not modify our results significantly.
(iv.) The distance between the planet-satellite binary and the star does not change significantly over one satellite orbit, which is granted when either
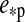 is small or Pps ≪
is small or Pps ≪ 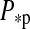 .
.
In the following, we present the general results of our mathematical derivation. For a more thorough description and discussions of some simple cases, see Appendices A and B.
3.1.1. Illumination from the star
The stellar flux on the substellar point on the moon's surface will have a magnitude 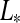 /(4π
/(4π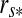 (t)2), where
(t)2), where 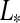 is stellar luminosity and
is stellar luminosity and 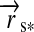 is the vector from the satellite to the star. We multiply this quantity with the surface normal
is the vector from the satellite to the star. We multiply this quantity with the surface normal 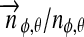 on the moon and
on the moon and 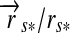 to include projection effects on a location (φ, θ). This yields
to include projection effects on a location (φ, θ). This yields
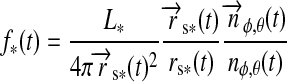 |
(3) |
If 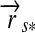 and
and 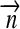 have an antiparallel part, then
have an antiparallel part, then 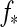 <0, which is meaningless in our context, and we set
<0, which is meaningless in our context, and we set 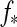 to zero. The task is now to find
to zero. The task is now to find 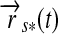 and
and 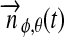 . Therefore, we introduce the surface vector from the subplanetary point on the satellite to the planet,
. Therefore, we introduce the surface vector from the subplanetary point on the satellite to the planet, 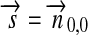 , and the vector from the planet to the star,
, and the vector from the planet to the star, 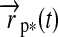 , which gives
, which gives 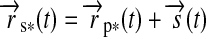 (see Fig. 1). Applying Kepler's equations of motion, we deduce
(see Fig. 1). Applying Kepler's equations of motion, we deduce 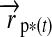 ; and with a few geometric operations (see Appendix A), we obtain
; and with a few geometric operations (see Appendix A), we obtain 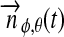 :
:
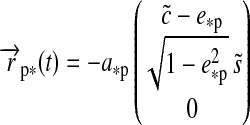 |
(4) |
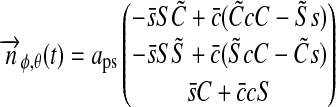 |
(5) |
with
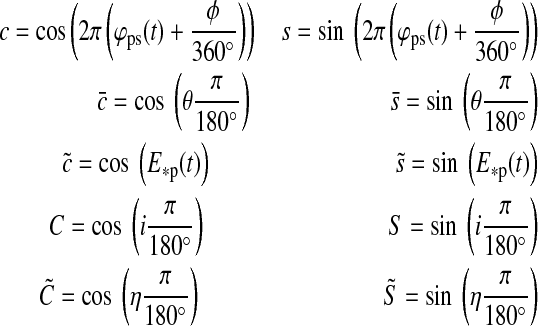 |
(6) |
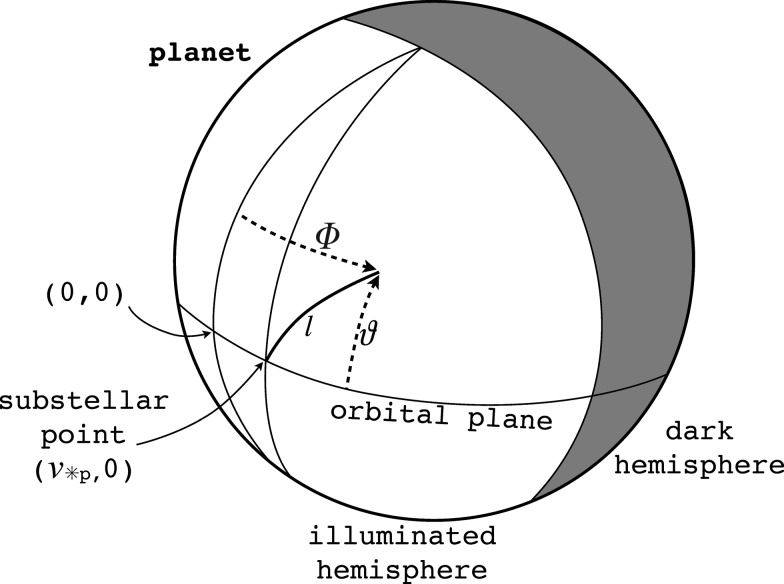
where i, η, 0≤φ≤360°, and 0≤θ≤90° are provided in degrees, and φ and θ are measured from the subplanetary point (see Fig. 1).
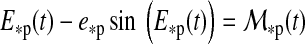 |
(7) |
defines the eccentric anomaly E*p and
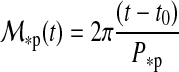 |
(8) |
is the mean anomaly. The angle η is the orientation of the lowest point of the moon's inclined orbit with respect to the star at periastron (see Appendix A). Kepler's equation (Eq. 7) is a transcendental function which we solve numerically.
To compute the stellar flux over one revolution of the moon around the planet, we put the planet-moon duet at numerous orbital phases around the star (using a fixed time step dt), where 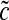 and
and 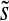 will be given. At each of these positions, we then evolve φps from 0 to 1. With this parametrization, the moon's orbit around the planet will always start at the left, corresponding to Fig. 1, and it will be more facile to interpret the phase functions. If we were to evolve the moon's orbit consistently, 2π
will be given. At each of these positions, we then evolve φps from 0 to 1. With this parametrization, the moon's orbit around the planet will always start at the left, corresponding to Fig. 1, and it will be more facile to interpret the phase functions. If we were to evolve the moon's orbit consistently, 2π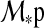 would have to be added to the arguments of c and s. Our simplification is appropriate as long as
would have to be added to the arguments of c and s. Our simplification is appropriate as long as 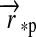 does not change significantly over one satellite orbit. Depending on the orientation of an eventual inclination between the two orbits and depending on the orbital position of the planet-moon system around the star, the star can be eclipsed by the planet for a certain fraction of φps as seen from the moon. This phenomenon might have significant impacts on exomoon climates. Eclipses occur if the perpendicular part
does not change significantly over one satellite orbit. Depending on the orientation of an eventual inclination between the two orbits and depending on the orbital position of the planet-moon system around the star, the star can be eclipsed by the planet for a certain fraction of φps as seen from the moon. This phenomenon might have significant impacts on exomoon climates. Eclipses occur if the perpendicular part
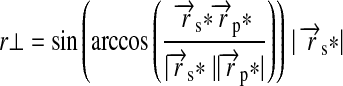 |
(9) |
of 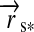 with respect to
with respect to 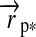 is smaller than the radius of the planet and if
is smaller than the radius of the planet and if 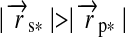 , that is, if the moon is behind the planet as seen from the star and not in front of it. The angular diameters of the star and the planet,
, that is, if the moon is behind the planet as seen from the star and not in front of it. The angular diameters of the star and the planet, 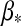 and βp, respectively, are given by
and βp, respectively, are given by
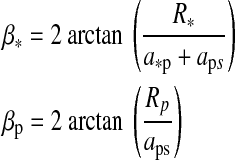 |
(10) |
If βp>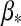 then the eclipse will be total. Otherwise the stellar flux will be diminished by a factor [1−(βp/
then the eclipse will be total. Otherwise the stellar flux will be diminished by a factor [1−(βp/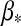 )2].
)2].
3.1.2. Illumination from the planet
We now consider two contributions to exomoon illumination from the planet, namely, reflection of stellar light (fr) and thermal radiation (ft). If the planet's rotation period is ≲1 d, then the stellar irradiation will be distributed somewhat smoothly over longitude. However, for a planet which is tidally locked to the star, the illuminated hemisphere will be significantly warmer than the back side. In our model, the bright side of the planet has a temperature 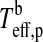 , and the dark back side has a temperature
, and the dark back side has a temperature 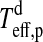 (see Appendix B). With
(see Appendix B). With 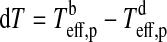 as the temperature difference between the hemispheres and αp as the planet's bond albedo, that is, the fraction of power at all wavelengths scattered back into space, thermal equilibrium yields
as the temperature difference between the hemispheres and αp as the planet's bond albedo, that is, the fraction of power at all wavelengths scattered back into space, thermal equilibrium yields
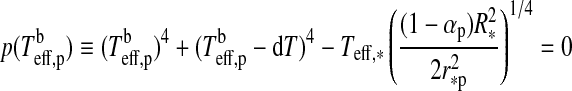 |
(11) |
For a given dT, we search for the zero points of the polynomial 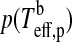 numerically. In our prototype system at 1 AU from a Sun-like star and choosing dT=100 K, Eq. 11 yields
numerically. In our prototype system at 1 AU from a Sun-like star and choosing dT=100 K, Eq. 11 yields 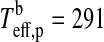 K and
K and 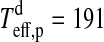 K. Finally, the thermal flux received by the moon from the planet turns out as
K. Finally, the thermal flux received by the moon from the planet turns out as
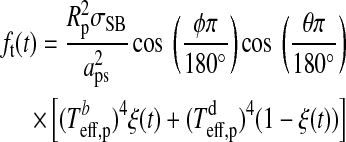 |
(12) |
where
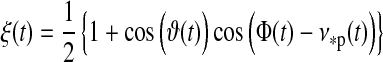 |
(13) |
weighs the contributions from the two hemispheres,
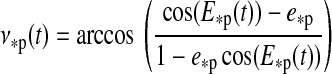 |
(14) |
is the true anomaly,
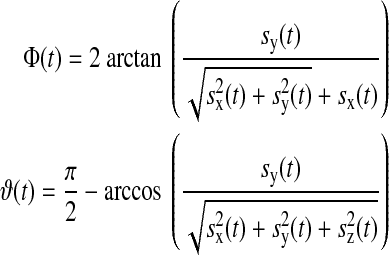 |
(15) |
and sx,y,z are the components of 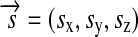 (see Appendix B).
(see Appendix B).
Additionally, the planet reflects a portion 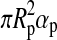 of the incoming stellar light. Neglecting that the moon blocks a small fraction of the starlight when it passes between the planet and the star (<1% for an Earth-sized satellite around a Jupiter-sized planet), we find that the moon receives a stellar flux
of the incoming stellar light. Neglecting that the moon blocks a small fraction of the starlight when it passes between the planet and the star (<1% for an Earth-sized satellite around a Jupiter-sized planet), we find that the moon receives a stellar flux
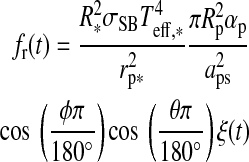 |
(16) |
from the planet.
In Fig. 2, we show how the amplitudes of ft(t) and fr(t) compare. Therefore, we neglect the time dependence and compute simply the maximum possible irradiation on the moon's subplanetary point as a function of the moon's orbit around the planet, which occurs in our model when the moon is over the substellar point of the planet. Then it receives maximum reflection and thermal flux at the same time. For our prototype system, it turns out that ft>fr at a given planet-moon distance only if the planet has an albedo≲0.1, which means that it needs to be almost black. The exact value, αp=0.093 in this case, can be obtained by comparing Eqs. 12 and 16 (see Appendix B). For increasing αp, stellar reflected flux dominates more and more; and for αp≳0.6, 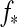 is over a magnitude stronger than ft.
is over a magnitude stronger than ft.
FIG. 2.
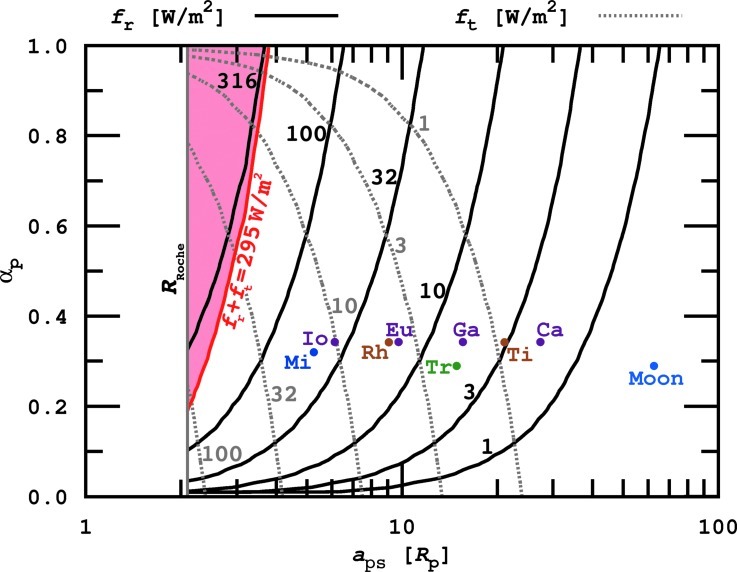
Contours of constant planetary flux on an exomoon as a function of the planet-satellite semimajor axis aps and the planet's bond albedo αp. The planet-moon binary orbits at 1 AU from a Sun-like host star. Values depict the maximum possible irradiation in terms of orbital alignment, i.e., on the subplanetary point on the moon, and when the moon is over the substellar point of the planet. For αp≈0.1 contours of equal fr and ft intersect; i.e., both contributions are equal. An additional contour is added at 295 W/m2, where the sum of fr and ft induces a runaway greenhouse on an Earth-sized moon. Some examples from the Solar System are given: Miranda (Mi), Io, Rhea (Rh), Europa (Eu), Triton (Tr), Ganymede (Ga), Titan (Ti), Callisto (Ca), and Earth's moon (Moon). Color images available online at www.liebertonline.com/ast
The shapes of the curves can be understood intuitively, if one imagines that at a fixed semimajor axis (abscissa) the reflected flux received on the moon increases with increasing albedo (ordinate), whereas the planet's thermal flux increases when it absorbs more stellar light, which happens for decreasing albedo.
The shaded area in the upper left corner of the figure indicates where the sum of maximum ft and fr exceed the limit of 295 W/m2 for a runaway greenhouse on an Earth-sized moon. Yet a satellite in this part of the parameter space would not necessarily be uninhabitable, because firstly it would only be subject to intense planetary radiation for less than about half its orbit, and secondly eclipses could cool the satellite half an orbit later. Moons at aps≲4Rp are very likely to experience eclipses. Note that a moon's orbital eccentricity eps will have to be almost perfectly zero to avoid intense tidal heating in such close orbits (see Section 3.2).
Since we use aps in units of planetary radii, ft and fr are independent of Rp. We also show a few examples of Solar System moons, where we adopted 0.343 for Jupiter's bond albedo (Hanel et al., 1981), 0.342 for Saturn (Hanel et al., 1983), 0.32 for Uranus (Neff et al., 1985; Pollack et al., 1986; Pearl et al., 1990), 0.29 for Neptune (Neff et al., 1985; Pollack et al., 1986; Pearl and Conrath, 1991), and 0.3 for Earth. Flux contours are not directly applicable to the indicated moons because the host planets Jupiter, Saturn, Uranus, and Neptune do not orbit the Sun at 1 AU, as assumed for our prototype exomoon system7. Only the position of Earth's moon, which receives a maximum of 0.35 W/m2 reflected light from Earth, reproduces the true Solar System values. The Roche radius for a fluid-like body (Weidner and Horne, 2010, and references therein) is indicated with a gray line at 2.07Rp.
3.1.3. The circumstellar habitable zone of exomoons
We next transform the combined stellar and planetary flux into a correction for the IHZ, for which the boundaries are proportional to 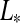 1/2 (Selsis et al.,
2007). This correction is easily derived if we restrict the problem to just the direct and the reflected starlight. Then we can define an “effective luminosity” Leff that is the sum of the direct starlight plus the orbit-averaged reflected light. We ignore the thermal contribution as its spectral energy distribution will be much different from the star and, as shown below, the thermal component is the smallest for most cases. Our IHZ corrections are therefore only lower limits. From Eqs. 3, 13, and 16 one can show that
1/2 (Selsis et al.,
2007). This correction is easily derived if we restrict the problem to just the direct and the reflected starlight. Then we can define an “effective luminosity” Leff that is the sum of the direct starlight plus the orbit-averaged reflected light. We ignore the thermal contribution as its spectral energy distribution will be much different from the star and, as shown below, the thermal component is the smallest for most cases. Our IHZ corrections are therefore only lower limits. From Eqs. 3, 13, and 16 one can show that
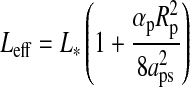 |
(17) |
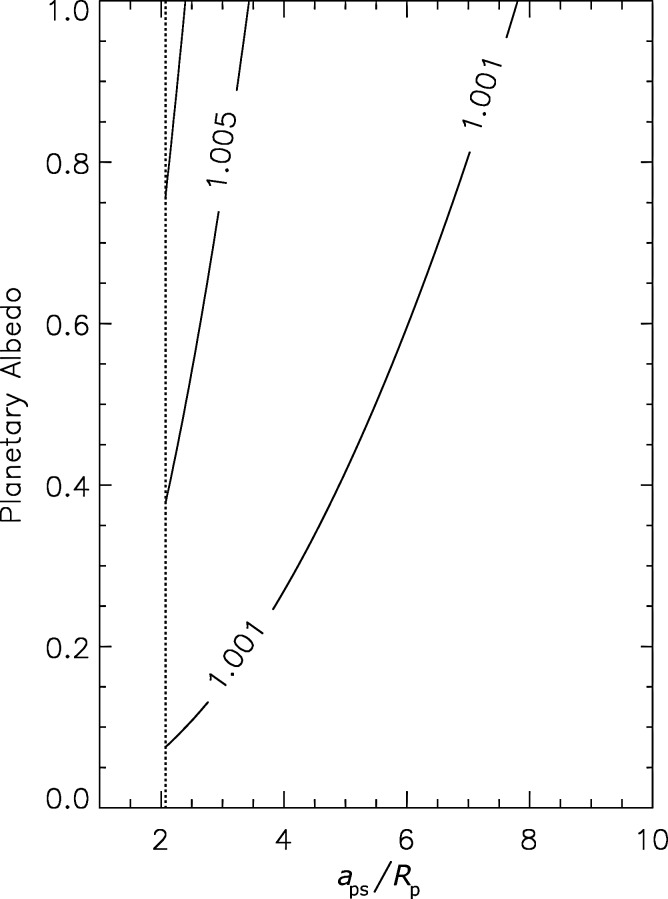
where we have averaged over the moon's orbital period. For realistic moon orbits, this correction amounts to 1% at most for high αp and small aps. For planets orbiting F dwarfs near the outer edge of the IHZ, a moon could be habitable about 0.05 AU farther out due to the reflected planetary light. In Fig. 3, we show the correction factor for the inner and outer boundaries of the IHZ due to reflected light as a function of αp and aps.
FIG. 3.
Contours of the correction factor for the limits of the IHZ for exomoons, induced by the star's reflected light from the planet. Since we neglect the thermal component, values are lower limits. The left-most contour signifies 1.01. The dotted vertical line denotes the Roche lobe.
3.1.4. Combined stellar and planetary illumination
With Eqs. 3, 12, and 16, we have derived the stellar and planetary contributions to the irradiation of a tidally locked moon in an inclined, circular orbit around the planet, where the orbit of the planet-moon duet around the star is eccentric. Now, we consider a satellite's total illumination
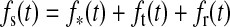 |
(18) |
For an illustration of Eq. 18, we choose a moon that orbits its Jupiter-sized host planet at the same distance as Europa orbits Jupiter. The planet-moon duet is in a 1 AU orbit around a Sun-like star, and we arbitrarily choose a temperature difference of dT=100 K between the two planetary hemispheres. Equation 18 does not depend on Ms or Rs, so our irradiation model is not restricted to either the Earth-sized or the Super-Ganymede prototype moon.
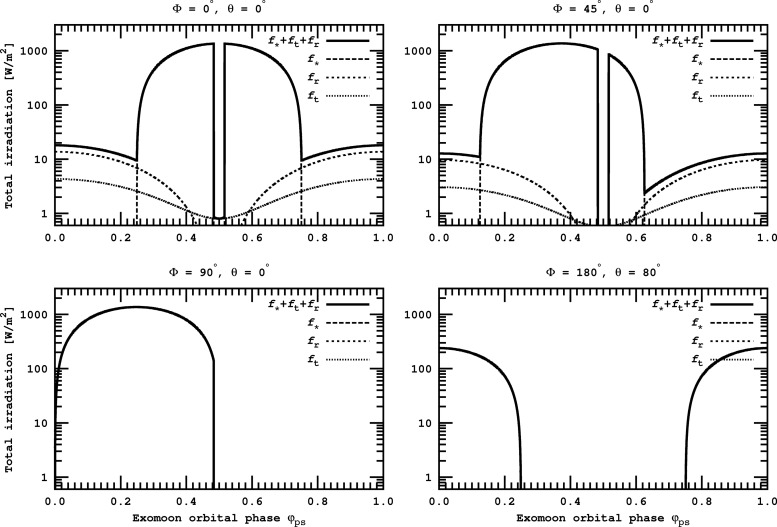
In Fig. 4, we show fs(t) as well as the stellar and planetary contributions for four different locations on the moon's surface. For all panels, the planet-moon duet is at the beginning of its revolution around the star, hence  =0, and we set i=0. Although
=0, and we set i=0. Although 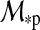 would slightly increase during one orbit of the moon around the planet, we fix it to zero, so the moon starts and finishes over the illuminated hemisphere of the planet (similar to Fig. 1). The upper left panel depicts the subplanetary point, with a pronounced eclipse around φps=0.5. At a position 45° counterclockwise along the equator (upper right panel), the stellar contribution is shifted in phase, and ft as well as fr are diminished in magnitude (note the logarithmic scale!) by a factor cos(45°). In the lower row, where φ=90°, θ=0° (lower left panel) and φ=180°, θ=80° (lower right panel), there are no planetary contributions. The eclipse trough has also disappeared because the star's occultation by the planet cannot be seen from the antiplanetary hemisphere.
would slightly increase during one orbit of the moon around the planet, we fix it to zero, so the moon starts and finishes over the illuminated hemisphere of the planet (similar to Fig. 1). The upper left panel depicts the subplanetary point, with a pronounced eclipse around φps=0.5. At a position 45° counterclockwise along the equator (upper right panel), the stellar contribution is shifted in phase, and ft as well as fr are diminished in magnitude (note the logarithmic scale!) by a factor cos(45°). In the lower row, where φ=90°, θ=0° (lower left panel) and φ=180°, θ=80° (lower right panel), there are no planetary contributions. The eclipse trough has also disappeared because the star's occultation by the planet cannot be seen from the antiplanetary hemisphere.
FIG. 4.
Stellar and planetary contributions to the illumination of our prototype moon as a function of orbital phase φps. Tiny dots label the thermal flux from the planet (ft), normal dots the reflected stellar light from the planet (fr), dashes the stellar light (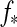 ), and the solid line is their sum. The panels depict different longitudes and latitudes on the moon's surface. The upper left panel is for the subplanetary point, the upper right 45° counterclockwise along the equator, the lower left panel shows a position 90° counterclockwise from the subplanetary point, and the lower right is the antiplanetary point.
), and the solid line is their sum. The panels depict different longitudes and latitudes on the moon's surface. The upper left panel is for the subplanetary point, the upper right 45° counterclockwise along the equator, the lower left panel shows a position 90° counterclockwise from the subplanetary point, and the lower right is the antiplanetary point.
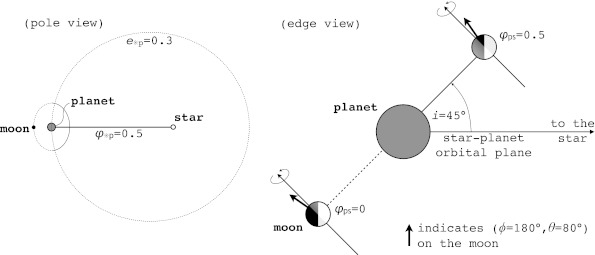
For Fig. 5, we assume a similar system, but now the planet-moon binary is at an orbital phase 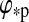 =0.5, corresponding to
=0.5, corresponding to 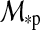 =π, around the star. We introduce an eccentricity
=π, around the star. We introduce an eccentricity 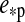 =0.3 as well as an inclination of 45° between the two orbital planes. The first aspect shifts the stellar and planetary contributions by half an orbital phase with respect to Fig. 4. Considering the top view of the system in Fig. 1, this means eclipses should now occur when the moon is to the left of the planet because the star is to the right, “left” here meaning φps=0. However, the non-zero inclination lifts the moon out of the planet's shadow (at least for this particular orbital phase around the star), which is why the eclipse trough disappears. Due to the eccentricity, stellar irradiation is now lower because the planet-moon binary is at apastron. An illustration of the corresponding star-planet orbital configuration is shown in the pole view (left panel) of Fig. 6.
=0.3 as well as an inclination of 45° between the two orbital planes. The first aspect shifts the stellar and planetary contributions by half an orbital phase with respect to Fig. 4. Considering the top view of the system in Fig. 1, this means eclipses should now occur when the moon is to the left of the planet because the star is to the right, “left” here meaning φps=0. However, the non-zero inclination lifts the moon out of the planet's shadow (at least for this particular orbital phase around the star), which is why the eclipse trough disappears. Due to the eccentricity, stellar irradiation is now lower because the planet-moon binary is at apastron. An illustration of the corresponding star-planet orbital configuration is shown in the pole view (left panel) of Fig. 6.
FIG. 6.
Illustration of the antiplanetary winter on the moon with the same orbital elements as in Fig. 5. The arrow in the edge view panel indicates the surface normal at φ=180°, θ=80°, i.e., close to pole and on the antiplanetary side of the moon. For all orbital constellations of the moon around the planet (φps going from 0 to 1), this location on the moon receives neither irradiation from the star nor from the planet (see lower right panel in Fig. 5). Shadings correspond to the same irradiation patterns as in Fig. 1.
The eccentricity-driven cooling of the moon is enhanced on its northern hemisphere, where the inclination induces a winter. Besides, our assumption that the moon is in the planet's equatorial plane is equivalent to i=ψp; thus the planet also experiences northern winter. The lower right panel of Fig. 5, where φ=180° and θ=80°, demonstrates a novel phenomenon, which we call an “antiplanetary winter on the moon.” On the satellite's antiplanetary side there is no illumination from the planet (as in the lower two panels of Fig. 4); and being close enough to the pole, at θ>90° – i for this occasion of northern winter, there will be no irradiation from the star either, during the whole orbit of the moon around the planet. In Fig. 6, we depict this constellation in the edge view (right panel). Note that antiplanetary locations close to the moon's northern pole receive no irradiation at all, as indicated by an example at φ=180°, θ=80° (see arrow). Of course there is also a “proplanetary winter” on the moon, which takes place just at the same epoch but on the proplanetary hemisphere on the moon. The opposite effects are the “proplanetary summer,” which occurs on the proplanetary side of the moon at 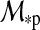 =0, at least for this specific configuration in Fig. 5, and the “antiplanetary summer.”
=0, at least for this specific configuration in Fig. 5, and the “antiplanetary summer.”
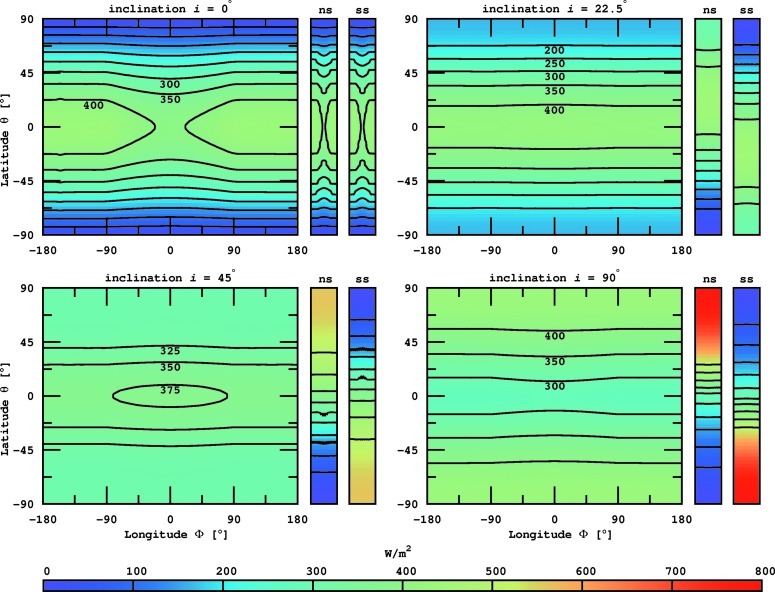
Finally, we compute the average surface flux on the moon during one stellar orbit. Therefore, we first integrate dφps
fs(φps) over 0≤φps≤1 at an initial phase in the planet's orbit about the star (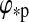 =0), which yields the area under the solid lines in Fig. 4. We then step through≈50 values for
=0), which yields the area under the solid lines in Fig. 4. We then step through≈50 values for 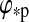 and again integrate the total flux. Finally, we average the flux over one orbit of the planet around the star, which gives the orbit-averaged flux Fs(φ, θ) on the moon. In Fig. 7, we plot these values as surface maps of a moon in four scenarios. The two narrow panels to the right of each of the four major panels show the averaged flux for −1/4≤
and again integrate the total flux. Finally, we average the flux over one orbit of the planet around the star, which gives the orbit-averaged flux Fs(φ, θ) on the moon. In Fig. 7, we plot these values as surface maps of a moon in four scenarios. The two narrow panels to the right of each of the four major panels show the averaged flux for −1/4≤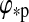 ≤+1/4 and +1/4≤
≤+1/4 and +1/4≤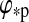 ≤+3/4, corresponding to northern summer (ns) and southern summer (ss) on the moon, respectively.
≤+3/4, corresponding to northern summer (ns) and southern summer (ss) on the moon, respectively.
FIG. 7.
Illumination of our prototype exomoon (in W/m2) averaged over the orbit of the planet-moon duet around their host star. Major panels present four different orbital inclinations: i=0° (upper left), i=22.5° (upper right), i=45° (lower left), and i=90° (lower right). The two bars beside each major panel indicate averaged flux for the northern summer (ns) and southern summer (ss) on the moon. Contours of constant irradiation are symmetric about the equator; some values are given. Color images available online at www.liebertonline.com/ast
In the upper left panel, the two orbits are coplanar. Interestingly, the subplanetary point at φ=0=θ is the “coldest” spot along the equator (if we convert the flux into a temperature) because the moon passes into the shadow of the planet when the star would be at zenith over the subplanetary point. Thus, the stellar irradiation maximum is reduced (see the upper left panel in Fig. 4). The contrast between polar and equatorial irradiation, reaching from 0 to≈440 W/m2, is strongest in this panel. In the upper right panel, the subplanetary point has turned into the “warmest” location along the equator. On the one hand, this is due to the inclination of 22.5°, which is why the moon does not transit behind the planet for most of the orbital phase around the star. On the other hand, this location gets slightly more irradiation from the planet than any other place on the moon. In the lower left panel, the average flux contrast between equatorial and polar illumination has decreased further. Again, the subplanetary point is slightly warmer than the rest of the surface. In the lower right panel, finally, where the moon's orbital inclination is set to 90°, the equator has become the coldest region of the moon, with the subplanetary point still being the warmest location along 0° latitude.
While the major panels show that the orbit-averaged flux contrast decreases with increasing inclination, the side panels indicate an increasing irradiation contrast between seasons. Exomoons around host planets with obliquities similar to that of Jupiter with respect to the Sun (ψp≈0) are subject to an irradiation pattern corresponding to the upper left panel of Fig. 7. The upper right panel depicts an irradiation pattern of exomoons around planets with obliquities similar to that of Saturn (26.7°) and is qualitatively in good agreement with the yearly illumination pattern of Titan as simulated by Mitchell (2012, see his Fig. 1c). Exomoons around a planet with a Uranus-like obliquity (97.9°) will have an irradiation similar to the lower right panel.
The typical orbit-averaged flux between 300 and 400 W/m2 in Fig. 7 is about a quarter of the solar constant. This is equivalent to an energy redistribution factor of 4 over the moon's surface (Selsis et al., 2007), indicating that climates on exomoons with orbital periods of a few days (in this case 3.55 d, corresponding to Europa's orbit about Jupiter) may be more similar to those of freely rotating planets rather than to those of planets that are tidally locked to their host star.
3.2. Tidal heating
Tidal heating is an additional source of energy on moons. Various approaches for the description of tidal processes have been established. Two of the most prominent tidal theories are the “constant-time-lag” (CTL) and the “constant-phase-lag” (CPL) models. Their merits and perils have been treated extensively in the literature (Ferraz-Mello et al., 2008; Efroimsky and Williams, 2009; Greenberg, 2009; Hansen, 2010; Heller et al., 2010, 2011b; Lai, 2012), and it turns out that they agree for low eccentricities. To begin with, we arbitrarily choose the CTL model developed by Hut (1981) and Leconte et al. (2010) for the computation of the moon's instantaneous tidal heating, but we will compare predictions of both CPL and CTL theory below. We consider a tidal time lag τs=638 s, similar to that of Earth (Lambeck, 1977; Neron de Surgy and Laskar, 1997), and an appropriate second-order potential Love number of k2,s=0.3 (Henning et al., 2009).
In our two-body system of the planet and the moon, tidal heating on the satellite, which is assumed to be in equilibrium rotation and to have zero obliquity against the orbit around the planet, is given by
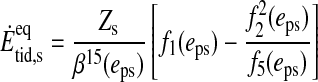 |
(19) |
where
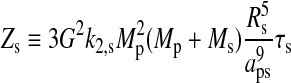 |
(20) |
and
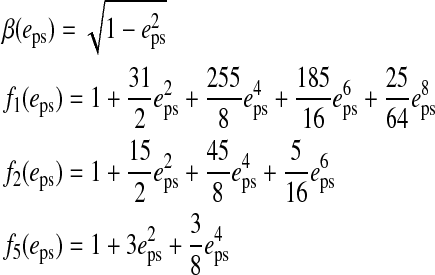 |
(21) |
Here, G is Newton's gravitational constant, and Mp is the planet's mass. The contribution of tidal heating to the moon's energy flux can be compared to the incoming irradiation when we divide 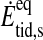 by the surface of the moon and define its surface tidal heating
by the surface of the moon and define its surface tidal heating 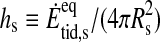 . We assume that hs is emitted uniformly through the satellite's surface.
. We assume that hs is emitted uniformly through the satellite's surface.
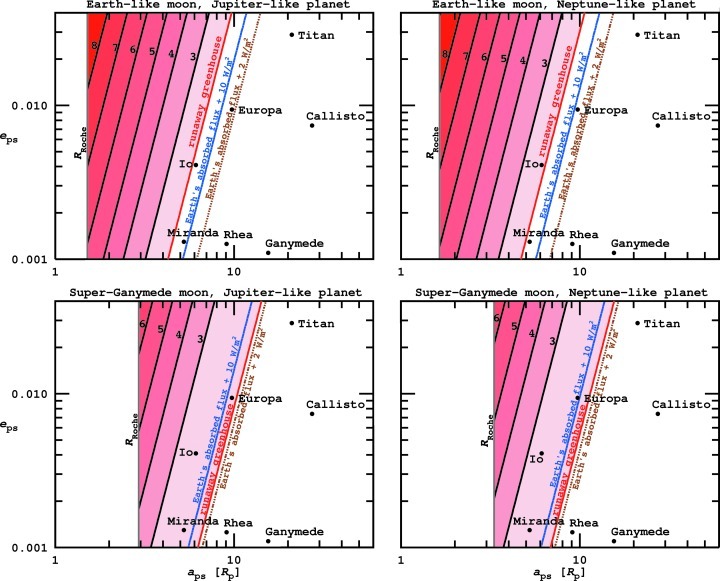
To stress the importance of tidal heating on exomoons, we show the sum of hs and the absorbed stellar flux for four star-planet-moon constellations as a function of eps and aps in Fig. 8. In the upper row, we consider our Earth-like prototype moon, in the lower row the Super-Ganymede. The left column corresponds to a Jupiter-like host planet, the right column to a Neptune-like planet, both at 1 AU from a Sun-like star. Contours indicate regions of constant energy flux as a function of aps and eps. Far from the planet, illustrated by a white area at the right in each plot, tidal heating is negligible, and the total heat flux on the moon corresponds to an absorbed stellar flux of 239 W/m2, which is equal to Earth's absorbed flux. The right-most contour in each panel depicts a contribution by tidal heating of 2 W/m2, which corresponds to Io's tidal heat flux (Spencer et al., 2000). Satellites left of this line will not necessarily experience enhanced volcanic activity, since most of the dissipated energy would go into water oceans of our prototype moons, rather than into the crust as on Io. The blue contour corresponds to a tidal heating of 10 W/m2, and the red line demarcates the transition into a runaway greenhouse, which occurs at 295 W/m2 for the Earth-mass satellite and at 243 W/m2 for the Super-Ganymede. Note that in the lower panels a runaway greenhouse occurs for less than 10 W/m2 of tidal heating. That is, the Super-Ganymede satellite must be farther away from the planet to be habitable. For comparison, we show the positions of some prominent moons in the Solar System, where aps is measured in radii of the host planet. Intriguingly, an Earth-like exomoon orbiting a Jupiter- or a Neptune-mass planet would be habitable in a Europa- or Miranda-like orbit (in terms of fractional planetary radius and eccentricity), while the Super-Ganymede would not.
FIG. 8.
Contours of summed absorbed stellar irradiation and tidal heating (in logarithmic units of W/m2) as a function of semimajor axis aps and eccentricity eps on an Earth-like (upper row) and a Super-Ganymede (lower row) exomoon. In the left panels, the satellite orbits a Jupiter-like planet, in the right panels a Neptune-mass planet, in both cases at 1 AU from a Sun-like host star. In the white area at the right, tidal heating is negligible and absorbed stellar flux is 239 W/m2. The right-most contours in each panel indicate Io's tidal heat flux of 2 W/m2, a tidal heating of 10 W/m2, and the critical flux for the runaway greenhouse (295 W/m2 for the Earth-like moon and 243 W/m2 for the Super-Ganymede). Positions of some massive satellites in the Solar System are shown for comparison. Color images available online at www.liebertonline.com/ast
The Roche radii are≈1.5Rp for an Earth-type moon about a Jupiter-like planet (upper left panel in Fig. 8), ≈1.6Rp for an Earth-type moon about a Neptune-mass planet (upper right), ≈2.9Rp for the Super-Ganymede about a Jupiter-class host (lower left), and≈3.2Rp for the Super-Ganymede orbiting a Neptune-like planet (lower right). The extreme tidal heating rates in the red areas may not be realistic because we assume a constant time lag τs of the satellite's tidal bulge and ignore its dependence on the driving frequency as well as its variation due to the geological processes that should appear at such enormous heat fluxes.
In Fig. 8, irradiation from the planet is neglected; thus decreasing distance between planet and moon goes along with increasing tidal heating only. An Earth-like exomoon (upper panels) could orbit as close as≈5Rp, and tidal heating would not induce a runaway greenhouse if eps≲0.001. If its orbit has an eccentricity similar to Titan (eps≈0.03), then the orbital separation needed to be≳10Rp to prevent a runaway greenhouse. Comparison of the left and right panels shows that for a more massive host planet (left) satellites can be slightly closer and still be habitable. This is because we draw contours over the fractional orbital separation aps/Rp on the abscissa. In the left panels 10Rp≈7×105 km, whereas in the right panel 10Rp≈2.5×105 km. When plotting over aps/Rp, this discrepancy is somewhat balanced by the much higher mass of the host planet in the left panel and the strong dependence of tidal heating on Mp (see Eq. 20).
3.2.1. Planet-moon orbital eccentricity
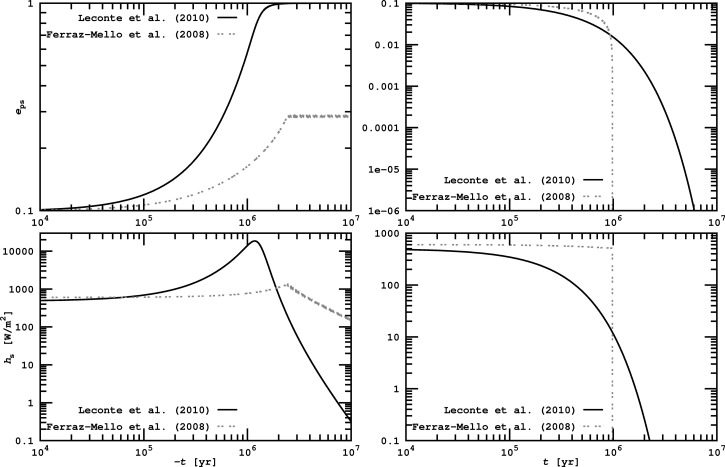
Tidal heating on the moon will only be significant if eps≠0. If the eccentricity is free, that is, the moon is not significantly perturbed by other bodies, then eps will change with time due to tidal damping, and orbit-averaged equations can be applied to simulate the tidal evolution. For those cases considered here, deps/dt<0. Similar to the approach used by Heller et al. (2011b), we apply a CTL model (Leconte et al., 2010) and a CPL model (Ferraz-Mello et al., 2008) to compute the tidal evolution, albeit here with a focus on exomoons rather than on exoplanets.
In Fig. 9, we show the evolution of our Earth-sized prototype moon in orbit around a Jupiter-like planet. The upper two panels show the change of eccentricity eps(t), the lower two panels of tidal surface heating hs(t). In the left panels, evolution is backward until −107 yr; in the right panels evolution is forward until +107 yr. The initial eccentricity is set to 0.1, and for the distance between the planet and the moon we choose the semimajor axis of Europa around Jupiter. Going backward, eccentricity increases8 as does tidal heating. When eps→1 at≈− 1 Myr, the moon is almost moving on a line around the planet, which would lead to a collision (or rather to an ejection because we go backward in time). At this time, tidal heating has increased from initially 600 W/m2 to 1300 W/m2. The right panels show that free eccentricities will be damped to zero within <10 Myr and that tidal heating becomes negligible after≈2 Myr.
FIG. 9.
Evolution of the orbital eccentricity (upper row) and the moon's tidal heating (lower row) following the two-body tidal models of Leconte et al. (2010) (a “constant-time-lag” model, solid line) and Ferraz-Mello et al. (2008) (a “constant-phase-lag” model, dashed line). Initially, an Earth-sized moon is set in an eccentric orbit (eps=0.1) around a Jupiter-mass planet at the distance in which Europa orbits Jupiter. In the left panels evolution is backward, in the right panel into the future. Both tidal models predict that free eccentricities are eroded and tidal heating ceases after <10 Myr.
Although eps is eroded in <10 Myr in these two-body simulations, eccentricities can persist much longer, as the cases of Io around Jupiter and Titan around Saturn show. Their eccentricities are not free, but they are forced, because they are excited by interaction with other bodies. The origin of Titan's eccentricity eps=0.0288 is still subject to debate. As shown by Sohl et al. (1995), tidal dissipation would damp it on timescales shorter than the age of the Solar System. It could only be primordial if the moon had a methane or hydrocarbon ocean that is deeper than a few kilometers. However, surface observations by the Cassini Huygens lander negated this assumption. Various other possibilities have been discussed, such as collisions or close encounters with massive bodies (Smith et al., 1982; Farinella et al., 1990) and a capture of Titan by Saturn≪ 4.5 Gyr ago. The origin of Io's eccentricity eps=0.0041 lies in the moon's resonances with Ganymede and Callisto (Yoder, 1979). Such resonances may also appear among exomoons.
Using the publicly available N-body code Mercury (Chambers, 1999)9, we performed N-body experiments of a hypothetical satellite system to find out whether forced eccentricities can drive a tidal greenhouse in a manner analogous to the volcanic activity of Io. We chose a Jupiter-mass planet with an Earth-mass exomoon at the same distance as Europa orbits Jupiter, placed a second exomoon at the 2:1 external resonance, and integrated the resulting orbital evolution. In one case, the second moon had a mass equal to that of Earth, in the other case a mass equal to that of Mars. For the former case, we find the inner satellite could have its eccentricity pumped to 0.09 with a typical value of 0.05. For the latter, the maximum eccentricity is 0.05 with a typical value near 0.03. Although these studies are preliminary, they suggest that massive exomoons in multiple configurations could trigger a runaway greenhouse, especially if the moons are of Earth mass, and that their circumstellar IHZ could lie farther away from the star. A comprehensive study of configurations that should also include Cassini states and damping to the fixed-point solution is beyond the scope of this study but could provide insight into the likelihood that exomoons are susceptible to a tidal greenhouse.
4. Orbits of Habitable Exomoons
By analogy with the circumstellar habitable zone for planets, we can imagine a minimum orbital separation between a planet and a moon to let the satellite be habitable. The range of orbits for habitable moons has no outer edge, except that Hill stability must be ensured. Consequently, habitability of moons is only constrained by the inner edge of a circumplanetary habitable zone, which we call the “habitable edge.” Moons inside the habitable edge are in danger of running into a greenhouse by stellar and planetary illumination and/or tidal heating. Satellites outside the habitable edge with their host planet in the circumstellar IHZ are habitable by definition.
Combining the limit for the runaway greenhouse from Section 2.2 with our model for the energy flux budget of extrasolar moons from Section 3, we compute the orbit-averaged global flux 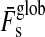 received by a satellite, which is the sum of the averaged stellar
received by a satellite, which is the sum of the averaged stellar 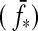 , reflected
, reflected 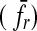 , thermal
, thermal 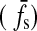 , and tidal heat flux (hs). Thus, in order for the moon to be habitable
, and tidal heat flux (hs). Thus, in order for the moon to be habitable
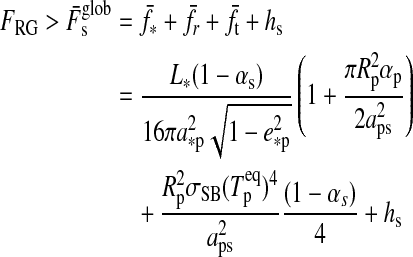 |
(22) |
where the critical flux for a runaway greenhouse FRG is given by Eq. 1, the tidal heating rate 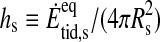 by Eq. 19, and the planet's thermal equilibrium temperature
by Eq. 19, and the planet's thermal equilibrium temperature 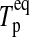 can be determined with Eq. 11 and using dT=0. Note that the addend “1” in brackets implies that we do not consider reduction of stellar illumination due to eclipses. This effect is treated in a forthcoming paper (Heller, 2012).
can be determined with Eq. 11 and using dT=0. Note that the addend “1” in brackets implies that we do not consider reduction of stellar illumination due to eclipses. This effect is treated in a forthcoming paper (Heller, 2012).
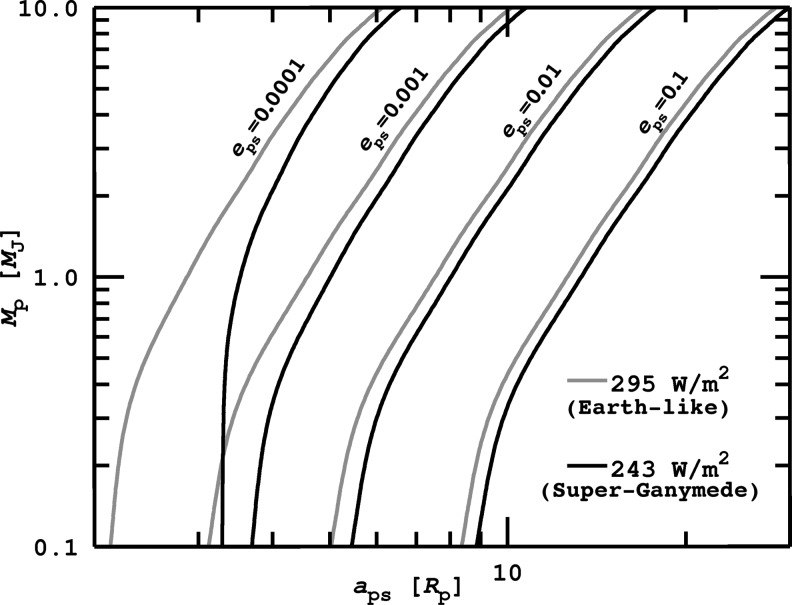
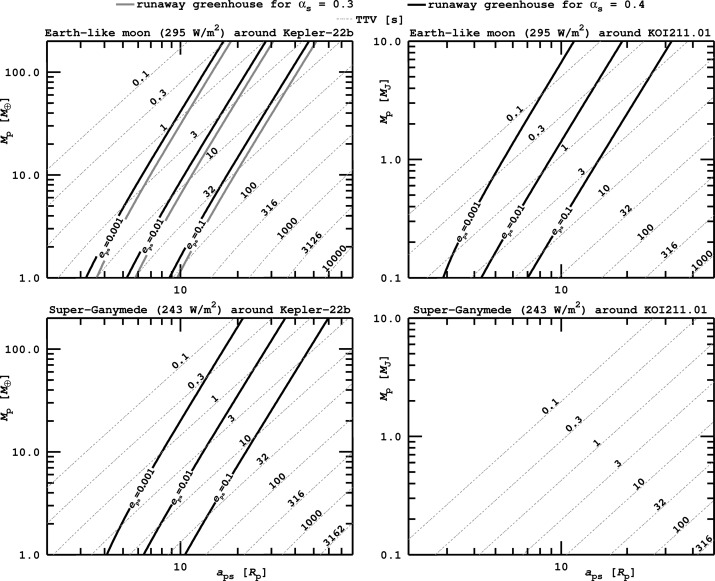
In Fig. 10, we show the 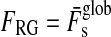 orbits of both the Earth-like (gray lines) and the Super-Ganymede (black lines) prototype moon as a function of the planet-moon semimajor axis and the mass of the giant host planet, which orbits the Sun-like star at a distance of 1 AU.10 Contours are plotted for various values of the orbital eccentricity, which means that orbits to the left of a line induce a runaway greenhouse for the respective eccentricity of the actual moon. These innermost, limiting orbits constitute the circumplanetary habitable edges.
orbits of both the Earth-like (gray lines) and the Super-Ganymede (black lines) prototype moon as a function of the planet-moon semimajor axis and the mass of the giant host planet, which orbits the Sun-like star at a distance of 1 AU.10 Contours are plotted for various values of the orbital eccentricity, which means that orbits to the left of a line induce a runaway greenhouse for the respective eccentricity of the actual moon. These innermost, limiting orbits constitute the circumplanetary habitable edges.
FIG. 10.
Innermost orbits to prevent a runaway greenhouse, i.e., the “habitable edges” of an Earth-like (gray lines) and a Super-Ganymede (black lines) exomoon. Their host planet is at 1 AU from a Sun-like star. Flux contours for four eccentricities of the moons' orbits from eps=10−4 to eps=10−1 are indicated. The larger eps, the stronger tidal heating and the more distant from the planet will the critical flux be reached.
When the moon is virtually shifted toward the planet, then illumination from the planet and tidal heating increase, reaching FRG at some point. With increasing eccentricity, tidal heating also increases; thus FRG will be reached farther away from the planet. Gray lines appear closer to the planet than black contours for the same eccentricity, showing that more massive moons can orbit more closely to the planet and be prevented from becoming a runaway greenhouse. This is a purely atmospheric effect, determined only by the moon's surface gravity gs(Ms, Rs) in Eq. 1. We also see that, for a fixed eccentricity, moons can orbit closer to the planet—both in terms of fractional and absolute units—if the planet's mass is smaller.
Estimating an exomoon's habitability with this model requires a well-parametrized system. With the current state of technology, stellar luminosity 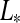 and mass
and mass 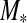 can be estimated by spectral analysis and by using stellar evolution models. In combination with the planet's orbital period
can be estimated by spectral analysis and by using stellar evolution models. In combination with the planet's orbital period 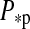 , this yields
, this yields 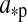 by means of Kepler's third law. The planetary mass Mp could be measured with the radial velocity method and assuming it is sufficiently larger than the moon's mass. Alternatively, photometry could determine the mass ratios Mp/
by means of Kepler's third law. The planetary mass Mp could be measured with the radial velocity method and assuming it is sufficiently larger than the moon's mass. Alternatively, photometry could determine the mass ratios Mp/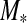 and Ms/Mp. Thus, if Ms were known from spectroscopy and stellar evolution models, then all masses were accessible (Kipping, 2010). Combining radial velocity and photometry, the star-planet orbital eccentricity
and Ms/Mp. Thus, if Ms were known from spectroscopy and stellar evolution models, then all masses were accessible (Kipping, 2010). Combining radial velocity and photometry, the star-planet orbital eccentricity 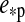 can be deduced (Mislis et al.,
2012); and by combination of TTV and TDV, it is possible to determine Ms as well as aps (Kipping, 2009a). Just like the planetary radius, the moon's radius Rs can be determined from photometric transit observations if its transit can directly be observed. The satellite's second-order tidal Love number k2,s and its tidal time lag τs, however, would have to be assumed. For this purpose, Earth or Solar System moons could serve as reference bodies. If the age of the system (i.e., of the star) was known or if the evolution of the satellite's orbit due to tides could be observed, then tidal theory could give a constraint on the product of k2,s and τs (or k2,s/Qs in CPL theory) (Lainey et al.,
2009; Ferraz-Mello, 2012). Then the remaining free parameters would be the satellite's albedo αs and the orbital eccentricity of the planet-moon orbit eps. N-body simulations of the system would allow for an average value of eps.
can be deduced (Mislis et al.,
2012); and by combination of TTV and TDV, it is possible to determine Ms as well as aps (Kipping, 2009a). Just like the planetary radius, the moon's radius Rs can be determined from photometric transit observations if its transit can directly be observed. The satellite's second-order tidal Love number k2,s and its tidal time lag τs, however, would have to be assumed. For this purpose, Earth or Solar System moons could serve as reference bodies. If the age of the system (i.e., of the star) was known or if the evolution of the satellite's orbit due to tides could be observed, then tidal theory could give a constraint on the product of k2,s and τs (or k2,s/Qs in CPL theory) (Lainey et al.,
2009; Ferraz-Mello, 2012). Then the remaining free parameters would be the satellite's albedo αs and the orbital eccentricity of the planet-moon orbit eps. N-body simulations of the system would allow for an average value of eps.
We conclude that a combination of all currently available observational and theoretical techniques can, in principle, yield an estimation of an exomoon's habitability. To that end, the satellite's global average energy flux  (Eq. 22) needs to be compared to the critical flux for a runaway greenhouse FRG (Eq. 1).
(Eq. 22) needs to be compared to the critical flux for a runaway greenhouse FRG (Eq. 1).
5. Application to Kepler-22b and KOI211.01
We now apply our stellar-planetary irradiation plus tidal heating model to putative exomoons around Kepler-22b and KOI211.01, both in the habitable zone around their host stars. The former is a confirmed transiting Neptune-sized planet (Borucki et al., 2012), while the latter is a much more massive planet candidate (Borucki et al., 2011). We choose these two planets that likely have very different masses to study the dependence of exomoon habitability on Mp.
For the moon, we take our prototype Earth-sized moon and place it in various orbits around the two test planets to investigate a parameter space as broad as possible. We consider two planet-moon semimajor axes: aps=5Rp, which is similar to Miranda's orbit around Uranus, and aps=20Rp, which is similar to Titan's orbit around Saturn11. We also choose two eccentricities, namely, eps=0.001 (similar to Miranda) and eps=0.05 (somewhat larger than Titan's value). With this parametrization, we cover a parameter space of which the diagonal is spanned by Miranda's close, low-eccentricity orbit around Uranus and Titan's far but significantly eccentric orbit around Saturn (see Fig. 8). We must keep in mind, however, that strong additional forces, such as the interaction with further moons, are required to maintain eccentricities of 0.05 in the assumed close orbits for a long time, because tidal dissipation will damp eps. Finally, we consider two orbital inclinations for the moon, i=0° and i=45°.
5.1. Surface irradiation of putative exomoons about Kepler-22b
Orbiting its solar-mass, solar-luminosity (Teff, =5518 K,
=5518 K,  =0.979R⊙, R⊙ being the radius of the Sun) host star at a distance of ≈0.85 AU, Kepler-22b is in the IHZ of a Sun-like star and has a radius 2.38±0.13 times the radius of Earth (Borucki et al.,
2012). For the computation of tidal heating on Kepler-22b's moons, we take the parametrization presented by Borucki et al. (2012), and we assume a planetary mass of 25M⊕, consistent with their photometric and radial-velocity follow-up measurements but not yet well constrained by observations. This ambiguity leaves open the question whether Kepler-22b is a terrestrial, gaseous, or transitional object.
=0.979R⊙, R⊙ being the radius of the Sun) host star at a distance of ≈0.85 AU, Kepler-22b is in the IHZ of a Sun-like star and has a radius 2.38±0.13 times the radius of Earth (Borucki et al.,
2012). For the computation of tidal heating on Kepler-22b's moons, we take the parametrization presented by Borucki et al. (2012), and we assume a planetary mass of 25M⊕, consistent with their photometric and radial-velocity follow-up measurements but not yet well constrained by observations. This ambiguity leaves open the question whether Kepler-22b is a terrestrial, gaseous, or transitional object.
In Fig. 11, we show the photon flux, coming both from the absorbed and re-emitted illumination as well as from tidal heating, at the upper atmosphere for an Earth-sized exomoon in various orbital configurations around Kepler-22b. Illumination is averaged over one orbit of the planet-moon binary around the star. In the upper four panels aps=5Rp (similar to the Uranus-Miranda semimajor axis), while in the lower four panels aps=20Rp (similar to the Saturn-Titan semimajor axis). The left column shows co-orbital simulations (i=0°); in the right column i=45°. In the first and the third line eps=0.001; in the second and fourth line eps=0.05.
FIG. 11.
Orbit-averaged flux (in units of W/m2) at the top of an Earth-sized exomoon's atmosphere around Kepler-22b for eight different orbital configurations. Computations include irradiation from the star and the planet as well as tidal heating. The color bar refers only to the lower two rows with moderate flux. Color images available online at www.liebertonline.com/ast
In orbits closer than ≈5Rp even very small eccentricities induce strong tidal heating of exomoons around Kepler-22b. For eps=0.001 (upper row), a surface heating flux of roughly 6250 W/m2 should induce surface temperatures well above the surface temperatures of Venus, and for eps=0.05 (second row), tidal heating is beyond 107 W/m2, probably melting the whole hypothetical moon (Léger et al., 2011). For orbital distances of 20Rp, tidal heating is 0.017 W/m2 for the low-eccentricity scenario; thus the total flux is determined by stellar irradiation (third line). However, tidal heating is significant for the eps=0.05 case (lower line), namely, roughly 42 W/m2.
Non-inclined orbits induce strong variations of irradiation over latitude (left column), while for high inclinations, seasons smooth the distribution (right column). As explained in Section 3.1.4, the subplanetary point for co-planar orbits is slightly cooler than the maximum temperature due to the eclipses behind the planet once per orbit. But for tilted orbits, the subplanetary point becomes the warmest spot.
We apply the tidal model presented by Heller et al. (2011b) to compute the planet's tilt erosion time tero and assess whether its primordial obliquity ψp could still persist today. Due to its weakly constrained mass, the value of the planet's tidal quality factor Qp is subject to huge uncertainties. Using a stellar mass of 1M⊙ and trying three values Qp=102, 103, and 104, we find tero=0.5, 5, and 50 Gyr, respectively. The lowest Qp value is similar to that of Earth, while the highest value corresponds approximately to that of Neptune.12 Thus, if Kepler-22b turns out mostly gaseous and provided that it had a significant primordial obliquity, the planet and its satellites can experience seasons today. But if Kepler-22b is terrestrial and planet-planet perturbations in this system can be neglected, it will have no seasons; and if its moons orbit above the planet's equator, they would share this tilt erosion.
5.2. Surface irradiation of putative exomoons about KOI211.01
KOI211.01 is a Saturn- to Jupiter-class planet candidate (Borucki et al., 2011). In the following, we consider it as a planet. Its radius corresponds to 0.88RJ, and it has an orbital period of 372.11 d around a 6072 K main-sequence host star, which yields an estimate for the stellar mass and then a semimajor axis of 1.05 AU. The stellar radius is 1.09R⊙, and using models for planet evolution (Fortney et al., 2007), we estimate the planet's mass to be 0.3MJ. This value is subject to various uncertainties because little is known about the planet's composition, the mass of a putative core, the planet's atmospheric opacity and structure, and the age of the system. Thus, our investigations will serve as a case study rather than a detailed prediction of exomoon scenarios around this particular planet. Besides KOI211.01, some 10 gas giants have been confirmed in the IHZ of their host stars, all of which are not transiting. Thus, detection of their putative moons will not be feasible in the foreseeable future.
In Fig. 12, we present the flux distribution on our prototype Earth-like exomoon around KOI211.01 in the same orbital configurations as in the previous subsection. Tidal heating in orbits with aps≲5Rp can be strong, depending on eccentricity, and make the moon uninhabitable. For eps=0.001, tidal heating is of the order of 1 W/m2 and thereby almost negligible for the moderate flux distribution (first line). However, it increases to over 3200 W/m2 for eps=0.05 and makes the moon uninhabitable (second line). Tidal heating is negligible at semimajor axes≳20Rp even for a significant eccentricity of 0.05.
FIG. 12.
Orbit-averaged flux (in units of W/m2) at the top of an Earth-sized exomoon's atmosphere around KOI211.01 for eight different orbital configurations. Computations include irradiation from the star and the planet as well as tidal heating. The color bar refers only to the first and the lower two rows with moderate flux. Color images available online at www.liebertonline.com/ast
By comparison of Fig. 11 with Fig. 12, we see that in those cases where tidal heating can be neglected and stellar irradiation dominates the energy flux, namely, in the third line of both figures, irradiation is higher on comparable moons around KOI211.01. But in the lower panel line, the total flux on our Kepler-22b prototype satellite becomes comparable to the one around KOI211.01, which is because of the extra heat from tidal dissipation. Surface flux distributions in the low-eccentricity and the moderate-eccentricity state on our KOI211.01 exomoons are virtually the same at aps=20Rp.
Since KOI211.01 is a gaseous object, we apply a tidal quality factor of Qp=105, which is similar to, but still lower than, the tidal response of Jupiter. We find that tero of KOI211.01 is much higher than the age of the Universe. Thus, satellites of KOI211.01 will experience seasons, provided the planet had a primordial obliquity and planet-planet perturbations can be neglected.
The radius of KOI211.01 is about 4 times greater than the radius of Kepler-22b; thus moons at a certain multitude of planetary radii distance from the planet, say 5Rp or 20Rp as we considered, will be effectively much farther away from KOI211.01 than from Kepler-22b. As tidal heating strongly depends on aps and on the planet's mass, a quick comparison between tidal heating on exomoons around Kepler-22b and KOI211.01 can be helpful. For equal eccentricities, the fraction of tidal heating in two moons about Kepler-22b and KOI211.01 will be equal to a fraction of Zs from Eq. 20. By taking the planet masses assumed above, thus MKOI≈3.81MKe, and assuming that the satellite mass is much smaller than the planets' masses, respectively, we deduce
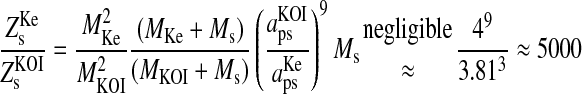 |
(23) |
where indices “Ke” and “KOI” refer to Kepler-22b and KOI211.01, respectively. The translation of tidal heating from any panel in Fig. 11 to the corresponding panel in Fig. 12 can be done with a division by this factor.
5.3. Orbits of habitable exomoons
We now set our results in context with observables to obtain a first estimate for the magnitude of the TTV amplitude induced by habitable moons around Kepler-22b and KOI211.01. For the time being, we will neglect the actual detectability of such signals with Kepler but discuss it in Section 6 (see also Kipping et al., 2009).
To begin with, we apply our method from Section 4 and add the orbit-averaged stellar irradiation on the moon to the averaged stellar-reflected light, the averaged thermal irradiation from the planet, and the tidal heating (in the CTL theory). We then compare their sum 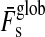 (see Eq. 22) to the critical flux for a runaway greenhouse FRG on the respective moon. In Fig. 13, we show the limiting orbits
(see Eq. 22) to the critical flux for a runaway greenhouse FRG on the respective moon. In Fig. 13, we show the limiting orbits 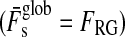 for a runaway greenhouse of an Earth-like (upper row) exomoon and a Super-Ganymede (lower row) exomoon around Kepler-22b (left column) and KOI211.01 (right column). For both moons, we consider two albedos (αs=0.3, gray solid lines; and αs=0.4, black solid lines) and three orbital eccentricities (eps=0.001, 0.01, 0.1). Solid lines define the habitable edge as described in Section 4. Moons in orbits to the left of a habitable edge are uninhabitable, respectively, because the sum of stellar and planetary irradiation plus tidal heating exceeds the runaway greenhouse limit. Dashed lines correspond to TTV amplitudes and will be discussed below.
for a runaway greenhouse of an Earth-like (upper row) exomoon and a Super-Ganymede (lower row) exomoon around Kepler-22b (left column) and KOI211.01 (right column). For both moons, we consider two albedos (αs=0.3, gray solid lines; and αs=0.4, black solid lines) and three orbital eccentricities (eps=0.001, 0.01, 0.1). Solid lines define the habitable edge as described in Section 4. Moons in orbits to the left of a habitable edge are uninhabitable, respectively, because the sum of stellar and planetary irradiation plus tidal heating exceeds the runaway greenhouse limit. Dashed lines correspond to TTV amplitudes and will be discussed below.
FIG. 13.
Habitable edges for an Earth-like (upper row) and a Super-Ganymede (lower row) exomoon in orbit around Kepler-22b (left column) and KOI211.01 (right column). Masses of both host planets are not well constrained; thus abscissae run over several decades (in units of M⊕ for Kepler-22b and MJ for KOI211.01). We consider two albedos αs=0.3 (gray solid lines) and αs=0.4 (black solid lines) and three eccentricities (eps=0.001, 0.01, 0.1) for both moons. No gray solid lines are in the right column because both prototype moons would not be habitable with αs=0.3 around KOI211.01. TTVs (in units of seconds) for coplanar orbits are plotted with dashed lines.
5.3.1. Orbit-averaged global flux
We first consider the three black solid lines in the upper left panel, corresponding to an Earth-like satellite with αs=0.4 about Kepler-22b. Each contour represents a habitable edge for a certain orbital eccentricity of the moon; that is, in these orbits the average energy flux on the moon is equal to FRG=295 W/m2. Assuming a circular orbit around the star (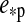 =0), the orbit-averaged stellar flux absorbed by a moon with αs=0.4 is
=0), the orbit-averaged stellar flux absorbed by a moon with αs=0.4 is
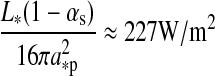 |
(24) |
using the parametrization presented in Sect 5.1. Thus, black contours indicate an additional heating of≈68 W/m2. The indicated eccentricities increase from left to right. This is mainly due to tidal heating, which increases for larger eccentricities but decreases at larger separations aps. Thus, the larger eps, the farther away from the planet the moon needs to be to avoid becoming a greenhouse. If a moon is close to the planet and shall be habitable, then its eccentricity must be small enough.
Next, we compare the black lines to the gray lines, which assume an albedo of 0.3 for an Earth-like satellite. With this albedo, it absorbs≈265 W/m2 of stellar irradiation. Consequently, a smaller amount of additional heat is required to push it into a runaway greenhouse, so the corresponding habitable edges are farther away from the planet, where both tidal heating and irradiation from the planet are lower.
In the lower left panel, we consider a Super-Ganymede around Kepler-22b. Its critical flux of 243 W/m2 is smaller than that for an Earth-like moon, so for an albedo of 0.4 only 16 W/m2 of additional heating is required for the moon to turn into a runaway greenhouse. Compared to the Earth-like satellite in the upper left panel, the habitable edges (black lines) will thus be farther from the planet. More important, gray lines are absent from this panel because with an albedo of 0.3 the satellite would absorb more stellar flux (265 W/m2) than its critical flux (243 W/m2). This is irrespective of whether our Ganymede-like object is orbiting a planet.
Next, we consider moons in orbit about KOI211.01, shown in the right column of Fig. 13. First note the absence of gray solid lines. For moons with an albedo of αs=0.3, the orbit-averaged stellar irradiation will be 315 W/m2, with the parametrization presented in Section 5.2. This means that stellar irradiation alone is larger than the critical flux of both our Earth-like (295 W/m2, upper panel) and Super-Ganymede (243 W/m2, lower panel) prototype moons. Thus, both moons with αs=0.3 around KOI211.01 are not habitable, irrespective of their distance to the planet.
Moons with αs=0.4 around KOI211.01 absorb 270 W/m2, which is less than the critical flux for the Earth-like moon (upper right panel) but more than the Super-Ganymede moon could bear (lower right panel). Thus, the black lines are absent from the latter plot but show up in the upper right. Contours for given eccentricities are closer to the planet than their counterparts in the case of Kepler-22b. This is because we plot the semimajor axis in units of planetary radii—while KOI211.01 has a much larger radius than Kepler-22b—and tidal heating, which strongly depends on the absolute distance between the planet and the moon.
5.3.2. Transit timing variations of habitable exomoons
Now we compare the habitable edges as defined by Eq. 22 to the amplitude of the TTV induced by the moon on the planet. TTV amplitudes Δ in units of seconds are plotted with dashed lines in Fig. 13. Recall, however, that Δ would not directly be measured by transit observations. Rather the root-mean-square of the TTV wave would be observed (Kipping, 2009a). We apply the Kipping et al. (2012) equations, assuming that the moon's orbit is circular and that both the circumstellar and the circumplanetary orbit are seen edge-on from Earth.
Each panel of Fig. 13 shows how the TTV amplitude decreases with decreasing semimajor axis of the satellite (from right to left) and with increasing planetary mass (from bottom to top). Thus, for a given planetary mass, a moon could be habitable if its TTV signal is sufficiently large. Comparison of the upper and the lower panels in each column shows how much larger the TTV amplitude of an Earth-like moon is with respect to our Super-Ganymede moon.
Corrections due to an inclination of the moon's orbit and an accidental alignment of the moon's longitude of the periapses are not included but would be small in most cases. For non-zero inclinations, the TTV amplitude Δ will be decreased. This decrease is proportional to 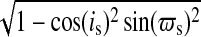 where is is measured from the circumstellar orbital plane normal to the orbital plane of the planet-moon orbit, and
where is is measured from the circumstellar orbital plane normal to the orbital plane of the planet-moon orbit, and 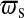 denotes the orientation of the longitude of the periapses (see Eq. 6.46 in Kipping, 2011b). Thus, corrections to our picture will only be relevant if both the moon's orbit is significantly tilted and
denotes the orientation of the longitude of the periapses (see Eq. 6.46 in Kipping, 2011b). Thus, corrections to our picture will only be relevant if both the moon's orbit is significantly tilted and 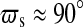 . In the worst case of
. In the worst case of 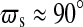 , an inclination of 25° reduces Δ by<10%, while for
, an inclination of 25° reduces Δ by<10%, while for 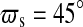 , is could be as large as 40° to produce a similar correction. Simulations of the planet's and the satellite's tilt erosion can help assess whether substantial misalignments are likely (Heller et al.,
2011b). While such geometric blurring should be small for most systems, prediction of the individual TTV signal for a satellite in an exoplanet system—as we suggest in Fig. 13—is hard because perturbations of other planets, moons, or Trojans could affect the TTV.
, is could be as large as 40° to produce a similar correction. Simulations of the planet's and the satellite's tilt erosion can help assess whether substantial misalignments are likely (Heller et al.,
2011b). While such geometric blurring should be small for most systems, prediction of the individual TTV signal for a satellite in an exoplanet system—as we suggest in Fig. 13—is hard because perturbations of other planets, moons, or Trojans could affect the TTV.
6. Summary and Discussion
Our work yields the first translation from observables to exomoon habitability. Using a scaling relation for the onset of the runaway greenhouse effect, we have deduced constraints on exomoon habitability from stellar and planetary irradiation as well as from tidal heating. We determined the orbit-averaged global energy budget 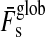 for exomoons to avoid a runaway greenhouse and found that for a well-parametrized system of a star, a host planet, and a moon, Eq. 22 can be used to evaluate the habitability of a moon. By analogy with the circumstellar habitable zone (Kasting et al.,
1993), these rules define a circumplanetary “habitable edge.” To be habitable, moons must orbit their planets outside the habitable edge.
for exomoons to avoid a runaway greenhouse and found that for a well-parametrized system of a star, a host planet, and a moon, Eq. 22 can be used to evaluate the habitability of a moon. By analogy with the circumstellar habitable zone (Kasting et al.,
1993), these rules define a circumplanetary “habitable edge.” To be habitable, moons must orbit their planets outside the habitable edge.
Application of our illumination plus tidal heating model shows that an Earth-sized exomoon about Kepler-22b with a bond albedo of 0.3 or higher would be habitable if (i.) the planet's mass is≈10M⊕, (ii.) the satellite would orbit Kepler-22b with a semimajor axis ≳10Rp, and (iii.) the moon's orbital eccentricity eps would be <0.01 (see Fig. 13). If Kepler-22b turns out more massive, then such a putative moon would need to be farther away to be habitable. Super-Ganymede satellites of Kepler-22b meet similar requirements, but beyond that their bond albedo needs to be ≳0.4.
Super-Ganymede or smaller moons around KOI211.01 will not be habitable, since their critical flux for a runaway greenhouse effect (≤243 W/m2) is less than the orbit-averaged irradiation received by the star (270 W/m2). But Earth-like or more massive moons can be habitable if (i.) the planet's mass≈MJ, (ii.) the satellite's bond albedo≳0.4, (iii.) the satellite orbits Kepler-22b with a semimajor axis≳10Rp, and (iv.) the moon's orbital eccentricity eps<0.01. If the planet turns out less massive, then its moons could be closer and have higher eccentricities and still be habitable.
Kepler-22 and KOI211 both are mid-G-type stars, with Kepler magnitudes 11.664 (Borucki et al., 2012) and 14.99 (Borucki et al., 2011), respectively. As shown by Kipping et al. (2009), the maximum Kepler magnitude to allow for the detection of an Earth-like moon is about 12.5. We conclude that such moons around Kepler-22b are detectable if they exist, and their habitability could be evaluated with the methods provided in this communication. Moons around KOI211.01 will not be detectable within the 7 yr duty cycle of Kepler. Nevertheless, our investigation of this giant planet's putative moons serves as a case study for comparably massive planets in the IHZ of their parent stars.
Stellar flux on potentially habitable exomoons is much stronger than the contribution from the planet. Nevertheless, the sum of thermal emission and stellar reflected light from the planet can have a significant impact on exomoon climates. Stellar reflection dominates over thermal emission as long as the planet's bond albedo αp≳0.1 and can reach some 10 or even 100 W/m2 once the moon is in a close orbit (aps≲10Rp) and the planet has a high albedo (αp≳0.3) (Section 3.1.2). Precise values depend on stellar luminosity and the distance of the planet-moon duet from the star. Our calculations for Kepler-22b and KOI211.01 show that the limiting orbits for exomoons to be habitable are very sensitive to the satellite's albedo.
Due to the weak tides from its host star, KOI211.01 can still have a significant obliquity, and if its moons orbit the planet in the equatorial plane they could have seasons and are more likely to be discovered by transit duration variations of the transit impact parameter (TDV-TIP, Kipping, 2009b). For Kepler-22b, the issue of tilt erosion cannot be answered unambiguously until more about the planet's mass and composition is known.
If a moon's orbital inclination is small enough, then it will be in the shadow of the planet for a certain time once per planet-moon orbit (see also Heller, 2012). For low inclinations, eclipses can occur about once every revolution of the moon around the planet, preferentially when the subplanetary hemisphere on the moon would experience stellar irradiation maximum (depending on 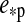 ). Eclipses have a profound impact on the surface distribution of the moon's irradiation. For low inclinations, the subplanetary point on the moon will be the “coldest” location along the equator, whereas for moderate inclinations it will be the “warmest” spot on the moon due to the additional irradiation from the planet. Future investigations will clarify whether this may result in enhanced subplanetary weathering instabilities, that is, runaway CO2 drawdown rates eventually leading to very strong greenhouse forcing, or subplanetary dissolution feedbacks of volatiles in subplanetary oceans, as has been proposed for exoplanets that are tidally locked to their host stars and thus experience such effects at the fixed substellar point (Kite et al.,
2011).
). Eclipses have a profound impact on the surface distribution of the moon's irradiation. For low inclinations, the subplanetary point on the moon will be the “coldest” location along the equator, whereas for moderate inclinations it will be the “warmest” spot on the moon due to the additional irradiation from the planet. Future investigations will clarify whether this may result in enhanced subplanetary weathering instabilities, that is, runaway CO2 drawdown rates eventually leading to very strong greenhouse forcing, or subplanetary dissolution feedbacks of volatiles in subplanetary oceans, as has been proposed for exoplanets that are tidally locked to their host stars and thus experience such effects at the fixed substellar point (Kite et al.,
2011).
We predict seasonal illumination phenomena on the moon, which emerge from the circumstellar season and planetary illumination. They depend on the location on the satellite and appear in four versions, which we call the “proplanetary summer,” “proplanetary winter,” “antiplanetary summer,” and “antiplanetary winter.” The former two describe seasons due to the moon's obliquity with respect to the star with an additional illumination from the planet; the latter two depict the permanent absence of planetary illumination during the seasons.
For massive exomoons with aps≲10Rp around Kepler-22b and around KOI211.01, tidal heating can be immense, presumably making them uninhabitable if the orbits are substantially noncircular. On the one hand, tidal heating can be a threat to life on exomoons, in particular when they are in close orbits with significant eccentricities around their planets. If the planet-moon duet is at the inner edge of the circumstellar IHZ, small contributions of tidal heat can render an exomoon uninhabitable. Tidal heating can also induce a thermal runaway, producing intense magmatism and rapid resurfacing on the moon (Běhounková et al., 2011). On the other hand, we can imagine scenarios where a moon becomes habitable only because of tidal heating. If the host planet has an obliquity similar to that of Uranus, then one polar region will not be illuminated for half the orbit around the star. Moderate tidal heating of some tens of watts per square meter might be just adequate to prevent the atmosphere from freezing out. Or if the planet and its moon orbit their host star somewhat beyond the outer edge of the IHZ, then tidal heating might be necessary to make the moon habitable in the first place. Tidal heating could also drive long-lived plate tectonics, thereby enhancing the moon's habitability (Jackson et al., 2008). An example is given by Jupiter's moon Europa, where insolation is weak but tides provide enough heat to sustain a subsurface ocean of liquid water (Greenberg et al., 1998; Schmidt et al., 2011). On the downside, too much tidal heating can render the body uninhabitable due to enhanced volcanic activity, as it is observed on Io.
Tidal heating has a strong dependence on the moon's eccentricity. Eccentricities of exomoons will hardly be measurable even with telescopes available in the next decade, but it will be possible to constrain eps by simulations. Therefore, once exomoon systems are discovered, it will be necessary to search for further moons around the same planet to consistently simulate the N-body (N>2) evolution with multiple-moon interaction, gravitational perturbations from other planets, and the gravitational effects of the star. Such simulations will also be necessary to simulate the long-term evolution of the orientation η of the moon's inclination i with respect to the periastron of the star-related orbit, because for significant eccentricities 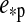 it will make a big difference whether the summer of either the northern or southern hemisphere coincides with minimum or maximum distance to the star. Technically, these variations refer to the apsidal precession (the orientation of the star-related eccentricity, i.e., of
it will make a big difference whether the summer of either the northern or southern hemisphere coincides with minimum or maximum distance to the star. Technically, these variations refer to the apsidal precession (the orientation of the star-related eccentricity, i.e., of 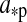 ) and the precession of the planet's rotation axis, both of which determine η. For Saturn, and thus Titan, the corresponding timescale is of order 1 Myr (French et al.,
1993), mainly induced by solar torques on both Saturn's oblate figure and the equatorial satellites. Habitable exomoons might preferably be irregular satellites (see Section 2) for which Carruba et al. (2002) showed that their orbital parameters are subject to particularly rapid changes, driven by stellar perturbations.
) and the precession of the planet's rotation axis, both of which determine η. For Saturn, and thus Titan, the corresponding timescale is of order 1 Myr (French et al.,
1993), mainly induced by solar torques on both Saturn's oblate figure and the equatorial satellites. Habitable exomoons might preferably be irregular satellites (see Section 2) for which Carruba et al. (2002) showed that their orbital parameters are subject to particularly rapid changes, driven by stellar perturbations.
We find that more massive moons can orbit more closely to the planet and be prevented from becoming a runaway greenhouse (Section 2.2). This purely atmospheric effect is shared by all terrestrial bodies. Similar to the circumstellar habitable zone of extrasolar planets (Kasting et al., 1993), we conclude that more massive exomoons may have somewhat wider habitable zones around their host planets—of which the inner boundary is defined by the habitable edge and the outer boundary by Hill stability—than do less massive satellites. In future investigations, it will be necessary to include simulations of the moons' putative atmospheres and their responses to irradiation and tidal heating. Thus, our irradiation plus tidal heating model should be coupled to an energy balance or global climate model to allow for more realistic descriptions of exomoon habitability. As indicated by our basal considerations, the impact of eclipses and planetary irradiation on exomoon climates can be substantial. In addition to the orbital parameters that we have simulated here, the moons' climates will depend on a myriad of bodily characteristics.
Spectroscopic signatures of life, so-called “biosignatures,” in the atmospheres of inhabited exomoons will only be detectable with next-generation, several-meter-class space telescopes (Kaltenegger, 2010; Kipping et al., 2010). Until then, we may primarily use our knowledge about the orbital configurations and composition of those worlds when assessing their habitability. Our method allows for an evaluation of exomoon habitability based on the data available at the time they will be discovered. The recent detection of an Earth-sized and a sub-Earth-sized planet around a G-type star (Fressin et al., 2012) suggests that not only the moons' masses and semimajor axes around their planets can be measured (e.g., by combined TTV and TDV, Kipping, 2009a) but also their radii by direct photometry. A combination of these techniques might finally pin down the moon's inclination (Kipping, 2009b) and thus allow for precise modeling of its habitability based on the model presented here.
Results of ESA's Jupiter Icy Moons Explorer (“JUICE”) will be of great value for characterization of exomoons. With launch in 2022 and arrival at Jupiter in 2030, one of the mission's two key goals will be to explore Ganymede, Europa, and Callisto as possible habitats. Therefore, the probe will acquire precise measurements of their topographic distortions due to tides on a centimeter level; determine their dynamical rotation states (i.e., forced libation and nutation); characterize their surface chemistry; and study their cores, rocky mantles, and icy shells. The search for water reservoirs on Europa, exploration of Ganymede's magnetic field, and monitoring of Io's volcanic activity will deliver fundamentally new insights into the planetology of massive moons.
Although our assumptions about the moons' orbital characteristics are moderate, that is, they are taken from the parameter space mainly occupied by the most massive satellites in the Solar System, our results imply that exomoons might exist in various habitable or extremely tidally heated configurations. We conclude that the advent of exomoon observations and characterization will permit new insights into planetary physics and reveal so far unknown phenomena, analogous to the staggering impact of the first exoplanet observations 17 yr ago. If observers feel animated to use the available Kepler data, the Hubble Space Telescope, or meter-sized ground-based instruments to search for evidence of exomoons, then one aim of this communication has been achieved.
Appendix A: Stellar Irradiation
We include here a thorough explanation for the stellar flux 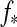 (t) presented in Section 3.1.1. To begin with, we assume that the irradiation on the moon at a longitude φ and latitude θ will be
(t) presented in Section 3.1.1. To begin with, we assume that the irradiation on the moon at a longitude φ and latitude θ will be
 |
(A1) |
with 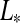 as the stellar luminosity and
as the stellar luminosity and 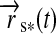 as the vector from the moon to the star (see Fig. A1). The product of the surface normal
as the vector from the moon to the star (see Fig. A1). The product of the surface normal 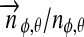 on the moon and
on the moon and 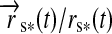 accounts for projection effects on the location (φ, θ), and we set
accounts for projection effects on the location (φ, θ), and we set 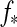 to zero in those cases where the star shines from the back. Figure A1 shows that
to zero in those cases where the star shines from the back. Figure A1 shows that 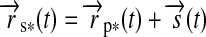 . While the Keplerian motion, encapsulated in
. While the Keplerian motion, encapsulated in 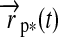 , is deduced in Section 3.1.1, we focus here on the moon's surface normal
, is deduced in Section 3.1.1, we focus here on the moon's surface normal 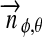 .
.
FIG. A1.
Geometry of the triple system of a star, a planet, and a moon. In the left panel the planet-moon duet has advanced by an angle ν around the star, and the moon has progressed by an angle 2πϕps. The right panel shows a zoom-in to the planet-moon binary. As in the left panel, time has proceeded, and a projection of
around the star, and the moon has progressed by an angle 2πϕps. The right panel shows a zoom-in to the planet-moon binary. As in the left panel, time has proceeded, and a projection of 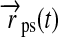 at time t=0 has been included to explain the orientation of the moon's orbit, which is inclined by an angle i and rotated against the star-moon periapses by an angle η.
at time t=0 has been included to explain the orientation of the moon's orbit, which is inclined by an angle i and rotated against the star-moon periapses by an angle η.
In the right panel of Fig. A1, we show a close-up of the star-planet-moon geometry at t=0, which corresponds to the initial configuration of the orbit evolution. The planet is at periastron (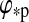 =0) and for the case where η=0 the vector
=0) and for the case where η=0 the vector 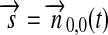 from the subplanetary point on the moon to the planet would have the form
from the subplanetary point on the moon to the planet would have the form
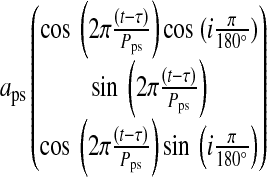 |
(A2) |
where all angles are provided in degrees. The angle η depicts the orientation of the lowest point of the moon's orbit with respect to the projection of 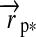 on the moon's orbital plane at t=0. At summer solstice on the moon's northern hemisphere, the true anomaly ν
on the moon's orbital plane at t=0. At summer solstice on the moon's northern hemisphere, the true anomaly ν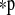 equals η (see Eq. B8). This makes η a critical parameter for the seasonal variation of stellar irradiation on the moon because it determines how seasons, induced by orbital inclination i, relate to the changing distance to the star, induced by star-planet eccentricity
equals η (see Eq. B8). This makes η a critical parameter for the seasonal variation of stellar irradiation on the moon because it determines how seasons, induced by orbital inclination i, relate to the changing distance to the star, induced by star-planet eccentricity 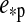 . In particular, if η=0, then northern summer coincides with the periastron passage about the star and northern winter occurs at apastron, inducing distinctly hot summers and cold winters. It relates to the conventional orientation of the ascending node Ω as η=Ω+270° and can be considered as the climate-precession parameter.
. In particular, if η=0, then northern summer coincides with the periastron passage about the star and northern winter occurs at apastron, inducing distinctly hot summers and cold winters. It relates to the conventional orientation of the ascending node Ω as η=Ω+270° and can be considered as the climate-precession parameter.
For η≠0, we have to apply a rotation M(η):  3→
3→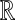 3 of around the z axis (0,0,1), which is performed by the rotation matrix
3 of around the z axis (0,0,1), which is performed by the rotation matrix
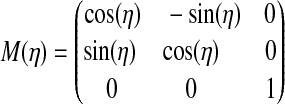 |
(A3) |
With the abbreviations introduced in Eq. 6 (with φ=0 for the time being), we obtain
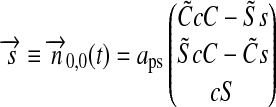 |
(A4) |
This allows us to parametrize the surface normal  of the subplanetary point on the moon for arbitrary i and η.
of the subplanetary point on the moon for arbitrary i and η.
Finally, we want to find the surface normal 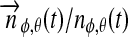 for any location (φ,θ) on the moon's surface. Therefore, we have to go two steps on the moon's surface, each one parametrized by one angle: one in longitudinal direction φ and one in latitudinal direction θ. The former one can be walked easily, just by adding 2πφ/360° in the sine and cosine arguments in Eq. A2 (see first line in Eq. 6), thus
for any location (φ,θ) on the moon's surface. Therefore, we have to go two steps on the moon's surface, each one parametrized by one angle: one in longitudinal direction φ and one in latitudinal direction θ. The former one can be walked easily, just by adding 2πφ/360° in the sine and cosine arguments in Eq. A2 (see first line in Eq. 6), thus 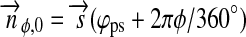 . This is equivalent to a shift along the moon's equator. For the second step, we know that if θ=90°, then the surface normal will be along the rotation axis
. This is equivalent to a shift along the moon's equator. For the second step, we know that if θ=90°, then the surface normal will be along the rotation axis
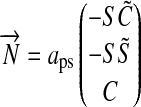 |
(A5) |
of the satellite; that is, we are standing on the north pole. The vector  can then be obtained by tilting
can then be obtained by tilting 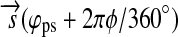 by an angle θ toward
by an angle θ toward  . With N=aps=s, we then derive
. With N=aps=s, we then derive
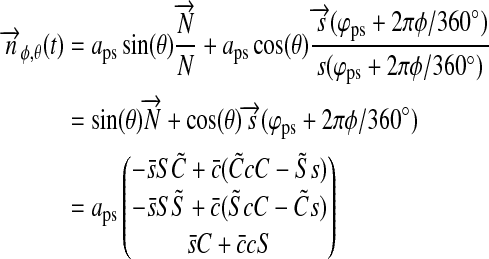 |
(A6) |
which solves Eq. A1.
Appendix B: Planetary Irradiation
In addition to stellar light, the moon will receive thermal and stellar-reflected irradiation from the planet, ft(t) and fr(t), respectively. One hemisphere on the planet will be illuminated by the star, and the other one will be dark. On the bright side of the planet, there will be both thermal emission from the planet as well as starlight reflection, while on the dark side the planet will only emit thermal radiation, though with a lower intensity than on the bright side due to the lower temperature.
We begin with the thermal part. The planet's total thermal luminosity Lth,p will be the sum of the radiation from the bright side and from the dark side. On the bright side, the planet shall have a uniform temperature  , and on the dark side its temperature shall be
, and on the dark side its temperature shall be 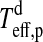 . Then thermal equilibrium between outgoing thermal radiation and incoming stellar radiation yields
. Then thermal equilibrium between outgoing thermal radiation and incoming stellar radiation yields
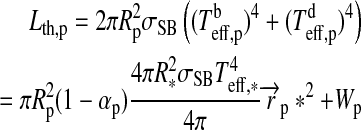 |
(B1) |
where the first term in the second line describes the absorbed radiation from the star and the second term (Wp) can be any additional heat source, for example, the energy released by the gravitation-induced shrinking of the gaseous planet. For Jupiter, Saturn, and Neptune, which orbit the Sun at distances >5 AU, Wp is greater than the incoming radiation. However, for gaseous planets in the IHZ it will be negligible once the planet has reached an age≳100 Myr (Baraffe et al., 2003).13 Owed to the negligibility for our purpose and for simplicity we set Wp=0.
In our model, we want to parametrize the two hemispheres by a temperature difference 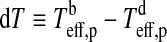 . We define
. We define
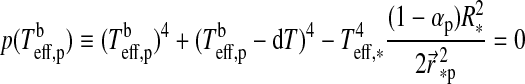 |
(B2) |
and, once dT is given, search for the first zero point of 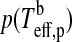 above
above
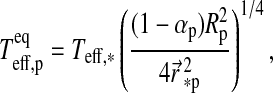 |
(B3) |
which yields 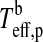 and
and 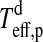 . In our prototype exomoon system, we assume dT=100 K, which is equivalent to fixing the efficiency of heat redistribution from the bright to the dark hemisphere on the planet (Burrows et al.,
2006b; Budaj et al.,
2012).
. In our prototype exomoon system, we assume dT=100 K, which is equivalent to fixing the efficiency of heat redistribution from the bright to the dark hemisphere on the planet (Burrows et al.,
2006b; Budaj et al.,
2012).
From Eq. B1, we can deduce the thermal flux on the subplanetary point on the moon. With increasing angular distance from the subplanetary point, ft will decrease. We can parametrize this distance on the moon's surface by longitude φ and latitude θ, which gives
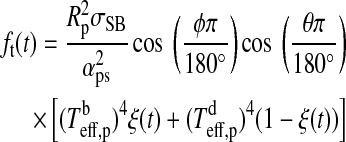 |
(B4) |
The time dependence of the irradiation is now packed into ξ(t), which serves as a weighting function for the two contributions from the bright and the dark side. It is given by
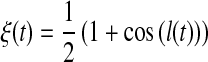 |
(B5) |
where
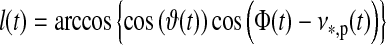 |
(B6) |
is the angular distance between the moon's projection on the planetary surface and the substellar point on the planet. In other words, l(t) is an orthodrome on the planet's surface, determined by Φ(t) and ϑ(t) (see Fig. B1). This yields
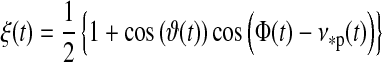 |
(B7) |
FIG. B1.
Geometry of the planetary illumination. The subsatellite point on the planetary surface is at (φ,ϑ). The angular distance l of the moon from the substellar point (ν , 0) determines the amount of light received by the moon from the two different hemispheres.
, 0) determines the amount of light received by the moon from the two different hemispheres.
Since the subplanetary point lies in the orbital plane of the planet, it will be at a position (ν ,0(t)) on the planetary surface, where
,0(t)) on the planetary surface, where
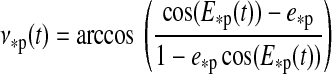 |
(B8) |
is the true anomaly. Moreover, with sx, sy, and sz as the components of  =(sx, sy, sz), we have
=(sx, sy, sz), we have
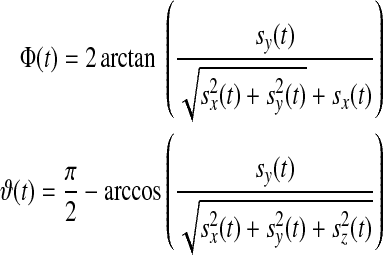 |
(B9) |
and thus determined ft(t).
We now consider the reflected stellar light from the planet. For the derivation of ft(t), we assumed that the planet is divided in two hemispheres, one of which is the bright side and one the dark side. Now the bright part coincides with the hemisphere from which the planet receives stellar reflected light, while there is no contribution to the reflectance from the dark side. Thus, the deduction of the geometrical part of fr(t), represented by ξ(t), goes analogously to ft(t). We only have to multiply the stellar flux received by the planet 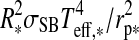 with the amount
with the amount 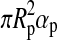 that is reflected from the planet and weigh it with the squared distance decrease
that is reflected from the planet and weigh it with the squared distance decrease  between the planet and its satellite. Consideration of projectional effects of longitude and latitude yields
between the planet and its satellite. Consideration of projectional effects of longitude and latitude yields
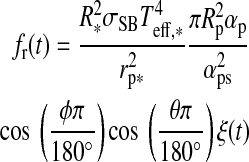 |
(B10) |
In Section 3.1.2, we compared thermal radiation and stellar reflection from the planet as a function of the planet-moon distance aps and the planet's albedo αp (see Fig. 2). To compute the amplitudes of ft and fr over the moon's orbit around the planet, we assume that the moon is over the substellar point on the planet where the satellite receives both maximum reflected and thermal radiation from the planet. Then ξ(t)=1, and equating Eq. B4 with B10 allows us to compute that value of αp for which the two contributions will be similar. We neglect projectional effects of longitude and latitude and derive
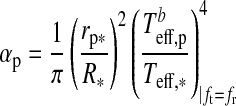 |
(B11) |
For our prototype system this yields αp=0.093. For higher planetary albedo, stellar reflected light will dominate irradiation on the moon.
Appendix C: Computer Code of Our Model: exomoon.py
Finally, we make the computer code exomoon.py, which we set up to calculate the phase curves (Figs. 4 and 5) and surface maps (Figs. 7, 11, and 12), publicly available. It can be downloaded from www.aip.de/People/RHeller or requested via e-mail. The code is written in the programming language python and optimized for use with ipython (Pérez and Granger, 2007). Care has been taken to make it easily human-readable, and a downloadable manual will be available, so it can be modified by non-expert users. The output format are ascii tables, which can be accessed with gnuplot and other plotting software.
In brief, the program has three operation modes, which allow the user to compute (i.) phase curves of  (φps), fr(φps), and ft(φps), (ii.) orbit-averaged flux maps of exomoon surfaces, and (iii.) the orbit of the planet-moon duet around their common host star. In Fig. C1, we show an example for such an orbit calculation. The moon's orbit is inclined by 45° against the planet spanned by the planet and the star, and the stellar orbit has an eccentricity
(φps), fr(φps), and ft(φps), (ii.) orbit-averaged flux maps of exomoon surfaces, and (iii.) the orbit of the planet-moon duet around their common host star. In Fig. C1, we show an example for such an orbit calculation. The moon's orbit is inclined by 45° against the planet spanned by the planet and the star, and the stellar orbit has an eccentricity  =0.3. Near periastron (at the right of the plot), where
=0.3. Near periastron (at the right of the plot), where 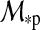 =0, the orbital velocity of the planet-moon duet is greater than at apastron. This is why the moon's path is more curly at the left, where
=0, the orbital velocity of the planet-moon duet is greater than at apastron. This is why the moon's path is more curly at the left, where 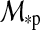 =π. Note that the starting point and the final point of the moon's orbit at the very right of the figure do not coincide! This effect induces TTVs of the planet.
=π. Note that the starting point and the final point of the moon's orbit at the very right of the figure do not coincide! This effect induces TTVs of the planet.
FIG. C1.
Orbits of an exomoon and an exoplanet around their common host star as computed with our exomoon.py software. Color images available online at www.liebertonline.com/ast
Footnotes
A related but more anthropocentric circumstellar zone, termed “ecosphere,” has been defined by Dole (1964, p 64 therein). Whewell (1853, Chapter X, Section 4 therein) presented a more qualitative discussion of the so-called “Temperate Zone of the Solar System.”
Planets with radii between 2R⊕ and 6R⊕ are designated Neptune-sized planets by the Kepler team (Batalha et al., 2012).
Although KOI211.01 is merely a planet candidate, we talk of it as a planet, for simplicity; but keep in mind its unconfirmed status.
Maintained by Robert Jacobson, http://ssd.jpl.nasa.gov.
In the following, a parameter index “ ” will refer to the star, “p” to the planet, and “s” to the satellite. The combinations “
” will refer to the star, “p” to the planet, and “s” to the satellite. The combinations “ ” and “ps,” e.g., for the orbital eccentricities
” and “ps,” e.g., for the orbital eccentricities 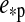 and eps, refer to systems of a star plus a planet and a planet plus a satellite, respectively. For a vector, e.g.,
and eps, refer to systems of a star plus a planet and a planet plus a satellite, respectively. For a vector, e.g., 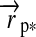 , the first letter indicates the starting point (in this case the planet), and the second index locates the endpoint (here the star).
, the first letter indicates the starting point (in this case the planet), and the second index locates the endpoint (here the star).
Tidal heating will be included below, but we will neglect geothermal feedback between tidal heating and irradiation.
At a distance of 5.2 AU from the Sun, Europa receives roughly 0.5 W/m2 reflected light from Jupiter, when it passes the planet's subsolar point. Jupiter's thermal flux on Europa is negligible.
For the CPL model, eps converges to 0.285 for −t ≳ 2 Myr. This result is not physical but owed to the discontinuities induced by the phase lags, in particular by ɛ1,s and ɛ1,p (for details, see Ferraz-Mello et al., 2008; Heller et al., 2011b). We have tried other initial eccentricities, which all led to this convergence.
Download via www.arm.ac.uk/∼jec.
For consistency, we computed the planetary radius (used to scale the abscissa) as a function of the planet's mass (ordinate) by fitting a high-order polynomial to the Fortney et al. (2007) models for a giant planet at 1 AU from a Sun-like star (see line 17 in their Table 4).
Note that in planet-moon binaries close to the star Hill stability requires that the satellite's orbit is a few planetary radii at most. Hence, if they exist, moons about planets in the IHZ around M dwarfs will be close to the planet (Barnes and O'Brien, 2002; Domingos et al., 2006; Donnison, 2010; Weidner and Horne, 2010).
See Gavrilov and Zharkov (1977) and Heller et al. (2010) for discussions of Q values and Love numbers for gaseous substellar objects.
Note that Barnes et al. (2013) identified 100 Myr as the time required for a runaway greenhouse to sterilize a planet.
Acknowledgments
R.B. acknowledges support from the NASA Astrobiology Institute's Cooperative agreement No. NNH05ZDA001C that supports the Virtual Planetary Lab, as well as NSF grant AST-1108882. This work has made use of NASA's Astrophysics Data System Bibliographic Services and of Jean Schneider's exoplanet database (www.exoplanet.eu). Computations have been performed with ipython 0.13 on python 2.7.2 and figures have been prepared with gnuplot 4.4 (www.gnuplot.info) as well as with gimp 2.6 (www.gimp.org). We thank the two anonymous referees for their expert counsel.
Author Disclosure Statement
No competing financial interests exist.
Abbreviations
CPL, constant-phase-lag; CTL, constant-time-lag; EUV, extreme ultraviolet radiation; IHZ, irradiation habitable zone; KOI, Kepler Object of Interest; TDV, transit duration variation; TTV, transit timing variation.
References
- Agnor C.B. Hamilton D.P. Neptune's capture of its moon Triton in a binary-planet gravitational encounter. Nature. 2006;441:192–194. doi: 10.1038/nature04792. [DOI] [PubMed] [Google Scholar]
- Baraffe I. Chabrier G. Barman T.S. Allard F. Hauschildt P.H. Evolutionary models for cool brown dwarfs and extrasolar giant planets. The case of HD 209458. Astron Astrophys. 2003;402:701–712. [Google Scholar]
- Barnes J.W. O'Brien D.P. Stability of satellites around close-in extrasolar giant planets. Astrophys J. 2002;575:1087–1093. [Google Scholar]
- Barnes R. Jackson B. Greenberg R. Raymond S.N. Tidal limits to planetary habitability. Astrophys J. 2009;700:L30–L33. [Google Scholar]
- Barnes R. Mullins K. Goldblatt C. Meadows V.S. Kasting J.F. Heller R. Tidal Venuses: triggering a climate catastrophe via tidal heating. Astrobiology. 2013;13 doi: 10.1089/ast.2012.0851. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batalha N.M. Rowe J.F. Bryson S.T. Barclay T. Burke C.J. Caldwell D.A. Christiansen J.L. Mullally F. Thompson S.E. Brown T.M. Dupree A.K. Fabrycky D.C. Ford E.B. Fortney J.J. Gilliland R.L. Isaacson H. Latham D.W. Marcy G.W. Quinn S. Ragozzine D. Shporer A. Borucki W.J. Ciardi D.R. Gautier T.N., III Haas M.R. Jenkins J.M. Koch D.G. Lissauer J.J. Rapin W. Basri G.S. Boss A.P. Buchhave L.A. Charbonneau D. Christensen-Dalsgaard J. Clarke B.D. Cochran W.D. Demory B.-O. Devore E. Esquerdo G.A. Everett M. Fressin F. Geary J.C. Girouard F.R. Gould A. Hall J.R. Holman M.J. Howard A.W. Howell S.B. Ibrahim K.A. Kinemuchi K. Kjeldsen H. Klaus T.C. Li J. Lucas P.W. Morris R.L. Prsa A. Quintana E. Sanderfer D.T. Sasselov D. Seader S.E. Smith J.C. Steffen J.H. Still M. Stumpe M.C. Tarter J.C. Tenenbaum P. Torres G. Twicken J.D. Uddin K. Van Cleve J. Walkowicz L. Welsh W.F. Planetary candidates observed by Kepler, III: analysis of the first 16 months of data. 2012. arXiv:1202.5852.
- Běhounková M. Tobie G. Choblet G. Čadek O. Tidally induced thermal runaways on extrasolar Earths: impact on habitability. Astrophys J. 2011;728 doi: 10.1088/0004-637X/728/2/89. [DOI] [Google Scholar]
- Bland M.T. Showman A.P. Tobie G. The production of Ganymede's magnetic field. Icarus. 2008;198:384–399. [Google Scholar]
- Bolmont E. Raymond S.N. Leconte J. Tidal evolution of planets around brown dwarfs. Astron Astrophys. 2011;535:A94. [Google Scholar]
- Borucki W.J. Koch D.G. Basri G. Batalha N. Brown T.M. Bryson S.T. Caldwell D. Christensen-Dalsgaard J. Cochran W.D. DeVore E. Dunham E.W. Gautier T.N., III Geary J.C. Gilliland R. Gould A. Howell S.B. Jenkins J.M. Latham D.W. Lissauer J.J. Marcy G.W. Rowe J. Sasselov D. Boss A. Charbonneau D. Ciardi D. Doyle L. Dupree A.K. Ford E.B. Fortney J. Holman M.J. Seager S. Steffen J.H. Tarter J. Welsh W.F. Allen C. Buchhave L.A. Christiansen J.L. Clarke B.D. Das S. Désert J.-M. Endl M. Fabrycky D. Fressin F. Haas M. Horch E. Howard A. Isaacson H. Kjeldsen H. Kolodziejczak J. Kulesa C. Li J. Lucas P.W. Machalek P. McCarthy D. MacQueen P. Meibom S. Miquel T. Prsa A. Quinn S.N. Quintana E.V. Ragozzine D. Sherry W. Shporer A. Tenenbaum P. Torres G. Twicken J.D. Van Cleve J. Walkowicz L. Witteborn F.C. Still M. Characteristics of planetary candidates observed by Kepler. II. Analysis of the first four months of data. Astrophys J. 2011;736 doi: 10.1088/0004-637X/736/1/19. [DOI] [Google Scholar]
- Borucki W.J. Koch D.G. Batalha N. Bryson S.T. Rowe J. Fressin F. Torres G. Caldwell D.A. Christensen-Dalsgaard J. Cochran W.D. DeVore E. Gautier T.N. Geary J.C. Gilliland R. Gould A. Howell S.B. Jenkins J.M. Latham D.W. Lissauer J.J. Marcy G.W. Sasselov D. Boss A. Charbonneau D. Ciardi D. Kaltenegger L. Doyle L. Dupree A.K. Ford E.B. Fortney J. Holman M.J. Steffen J.H. Mullally F. Still M. Tarter J. Ballard S. Buchhave L.A. Carter J. Christiansen J.L. Demory B.-O. Désert J.-M. Dressing C. Endl M. Fabrycky D. Fischer D. Haas M.R. Henze C. Horch E. Howard A.W. Isaacson H. Kjeldsen H. Johnson J.A. Klaus T. Kolodziejczak J. Barclay T. Li J. Meibom S. Prsa A. Quinn S.N. Quintana E.V. Robertson P. Sherry W. Shporer A. Tenenbaum P. Thompson S.E. Twicken J.D. Van Cleve J. Welsh W.F. Basu S. Chaplin W. Miglio A. Kawaler S.D. Arentoft T. Stello D. Metcalfe T.S. Verner G.A. Karoff C. Lundkvist M. Lund M.N. Handberg R. Elsworth Y. Hekker S. Huber D. Bedding T.R. Rapin W. Kepler-22b: a 2.4 Earth-radius planet in the habitable zone of a Sun-like star. Astrophys J. 2012;745 doi: 10.1088/0004-637X/745/2/120. [DOI] [Google Scholar]
- Budaj J. Hubeny I. Burrows A. Day and night side core cooling of a strongly irradiated giant planet. Astron Astrophys. 2012;537:A115. [Google Scholar]
- Burrows A. Sudarsky D. Hubney I. L and T dwarf models and the L to T transition. Astrophys J. 2006a;640:1063–1077. [Google Scholar]
- Burrows A. Sudarsky D. Hubney I. Theory for the secondary eclipse fluxes, spectra, atmospheres, and light curves of transiting extrasolar giant planets. Astrophys J. 2006b;650:1140–1149. [Google Scholar]
- Cabrera J. Schneider J. Detecting companions to extrasolar planets using mutual events. Astron Astrophys. 2007;464:1133–1138. [Google Scholar]
- Canup R.M. Simulations of a late lunar-forming impact. Icarus. 2004;168:433–456. [Google Scholar]
- Canup R.M. Ward W.R. A common mass scaling for satellite systems of gaseous planets. Nature. 2006;441:834–839. doi: 10.1038/nature04860. [DOI] [PubMed] [Google Scholar]
- Carruba V. Burns J.A. Nicholson P.D. Gladman B.J. On the inclination distribution of the jovian irregular satellites. Icarus. 2002;158:434–449. [Google Scholar]
- Cassidy T.A. Mendez R. Arras P. Johnson R.E. Skrutskie M.F. Massive satellites of close-in gas giant exoplanets. Astrophys J. 2009;704:1341–1348. [Google Scholar]
- Chambers J.E. A hybrid symplectic integrator that permits close encounters between massive bodies. Mon Not R Astron Soc. 1999;304:793–799. [Google Scholar]
- Clark R.N. Ganymede, Europa, Callisto, and Saturn's rings—compositional analysis from reflectance spectroscopy. Icarus. 1980;44:388–409. [Google Scholar]
- Cowan N.B. Voigt A. Abbot D.S. A false positive for ocean glint of exoplanets: the latitude-albedo effect. Astrophys J. 2012;752:L3. [Google Scholar]
- Debes J.H. Sigurdsson S. The survival rate of ejected terrestrial planets with moons. Astrophys J. 2007;668:L167–L170. [Google Scholar]
- Dole S.H. Habitable Planets for Man. 1st. Blaisdell; New York: 1964. [Google Scholar]
- Domingos R.C. Winter O.C. Yokoyama T. Stable satellites around extrasolar planets. Mon Not R Astron Soc. 2006;373:1227–1234. [Google Scholar]
- Donnison J.R. The Hill stability of the possible moons of extrasolar planets. Mon Not R Astron Soc. 2010;406:1918–1934. [Google Scholar]
- Eberle J. Cuntz M. Quarles B. Musielak Z.E. Case studies of habitable Trojan planets in the system of HD 23079. International Journal of Astrobiology. 2011;10:325–334. [Google Scholar]
- Edson A. Lee S. Bannon P. Kasting J.F. Pollard D. Atmospheric circulations of terrestrial planets orbiting low-mass stars. Icarus. 2011;212:1–13. [Google Scholar]
- Efroimsky M. Williams J.G. Tidal torques: a critical review of some techniques. Celestial Mechanics and Dynamical Astronomy. 2009;104:257–289. [Google Scholar]
- Elser S. Moore B. Stadel J. Morishima R. Icarus. 2011;214:357–365. [Google Scholar]
- Farinella P. Paolicchi P. Strom R.G. Kargel J.S. Zappala V. The fate of Hyperion's fragments. Icarus. 1990;83:186–204. [Google Scholar]
- Ferraz-Mello S. Tidal synchronization of close-in satellites and exoplanets. A rheophysical approach. 2012. arXiv:1204.3957.
- Ferraz-Mello S. Rodríguez A. Hussmann H. Tidal friction in close-in satellites and exoplanets: the Darwin theory re-visited. Celestial Mechanics and Dynamical Astronomy. 2008;101:171–201. [Google Scholar]
- Fortney J.J. Marley M.S. Barnes J.W. Planetary radii across five orders of magnitude in mass and stellar insolation: application to transits. Astrophys J. 2007;659:1661–1672. [Google Scholar]
- French R.G. Nicholson P.D. Cooke M.L. Elliot J.L. Matthews K. Perkovic O. Tollestrup E. Harvey P. Chanover N.J. Clark M.A. Dunham E.W. Forrest W. Harrington J. Pipher J. Brahic A. Grenier I. Roques F. Arndt M. Geometry of the Saturn system from the 3 July 1989 occultation of 28 SGR and Voyager observation. Icarus. 1993;103:163–214. [Google Scholar]
- Fressin F. Torres G. Rowe J.F. Charbonneau D. Rogers L.A. Ballard S. Batalha N.M. Borucki W.J. Bryson S.T. Buchhave L.A. Ciardi D.R. Désert J.M. Dressing C.D. Fabrycky D.C. Ford E.B. Gautier T.N., III Henze C.E. Holman M.J. Howard A. Howell S.B. Jenkins J.M. Koch D.G. Latham D.W. Lissauer J.J. Marcy G.W. Quinn S.N. Ragozzine D. Sasselov D.D. Seager S. Barclay T. Mullally F. Seader S.E. Still M. Twicken J.D. Thompson S.E. Uddin K. Two Earth-sized planets orbiting Kepler-20. Nature. 2012;482:195–198. doi: 10.1038/nature10780. [DOI] [PubMed] [Google Scholar]
- Gaidos E. Conrad C.P. Manga M. Hernlund J. Thermodynamics limits on magnetodynamos in rocky exoplanets. Astrophys J. 2010;718:596–609. [Google Scholar]
- Gavrilov S.V. Zharkov V.N. Love numbers of the giant planets. Icarus. 1977;32:443–449. [Google Scholar]
- Goldblatt C. Watson A.J. The runaway greenhouse: implications for future climate change, geoengineering and planetary atmospheres. Philos Transact A Math Phys Eng Sci. 2012;370:4197–4216. doi: 10.1098/rsta.2012.0004. [DOI] [PubMed] [Google Scholar]
- Goldreich P. Final spin states of planets and satellites. Astron J. 1966;71:1–7. [Google Scholar]
- Goldreich P. Murray N. Longaretti P.Y. Banfield D. Neptune's story. Science. 1989;245:500–504. doi: 10.1126/science.245.4917.500. [DOI] [PubMed] [Google Scholar]
- Gonzalez G. Habitable zones in the Universe. Orig Life Evol Biosph. 2005;35:555–606. doi: 10.1007/s11084-005-5010-8. [DOI] [PubMed] [Google Scholar]
- Grasset O. Sotin C. Deschamps F. On the internal structure and dynamics of Titan. Planet Space Sci. 2000;48:617–636. [Google Scholar]
- Greenberg R. Frequency dependence of Tidal q. Astrophys J. 2009;698:L42–L45. [Google Scholar]
- Greenberg R. Geissler P. Hoppa G. Tufts B.R. Durda D.D. Pappalardo R. Head J.W. Greeley R. Sullivan R. Carr M.H. Tectonic processes on Europa: tidal stress, mechanical response, and visible features. Icarus. 1998;135:64–78. [Google Scholar]
- Griffith C.A. Zahnle K. Influx of cometary volatiles to planetary moons: the atmospheres of 1000 possible Titans. J Geophys Res. 1995;100:16907–16922. doi: 10.1029/95je01135. [DOI] [PubMed] [Google Scholar]
- Gurnett D.A. Kurth W.S. Roux A. Bolton S.J. Kennel C.F. Evidence for a magnetosphere at Ganymede from plasma-wave observations by the Galileo spacecraft. Nature. 1996;384:535–537. [Google Scholar]
- Hanel R. Conrath B. Herath L. Kunde V. Pirraglia J. Albedo, internal heat, and energy balance of Jupiter—preliminary results of the Voyager infrared investigation. J Geophys Res. 1981;86:8705–8712. [Google Scholar]
- Hanel R.A. Conrath B.J. Kunde V.G. Pearl J.C. Pirraglia J.A. Albedo, internal heat flux, and energy balance of Saturn. Icarus. 1983;53:262–285. [Google Scholar]
- Hansen B.M.S. Calibration of equilibrium tide theory for extrasolar planet systems. Astrophys J. 2010;723:285–299. [Google Scholar]
- Harris A.W. Ward W.R. Dynamical constraints on the formation and evolution of planetary bodies. Annu Rev Earth Planet Sci. 1982;10:61–108. [Google Scholar]
- Heath M.J. Doyle L.R. From near-synchronously rotating planets to tidal lock: a new class of habitable planets examined for forest habitability. In: Norris R., editor; Stootman F., editor. Bioastronomy 2002: Life Among the Stars, IAU Symposium 213. International Astronomical Union; Paris: 2004. pp. 225–229. [Google Scholar]
- Heller R. Exomoon habitability constrained by energy flux and orbital stability. Astron Astrophys. 2012;545:L8. [Google Scholar]
- Heller R. Jackson B. Barnes R. Greenberg R. Homeier D. Tidal effects on brown dwarfs: application to the eclipsing binary 2MASS J05352184-0546085—the anomalous temperature reversal in the context of tidal heating. Astron Astrophys. 2010;514:A22. [Google Scholar]
- Heller R. Barnes R. Leconte J. Habitability of extrasolar planets and tidal spin evolution. Orig Life Evol Biosph. 2011a;41:539–543. doi: 10.1007/s11084-011-9252-3. [DOI] [PubMed] [Google Scholar]
- Heller R. Leconte J. Barnes R. Tidal obliquity evolution of potentially habitable planets. Astron Astrophys. 2011b;528:A27. [Google Scholar]
- Heng K. Vogt S.S. Gliese 581g as a scaled-up version of Earth: atmospheric circulation simulations. Mon Not R Astron Soc. 2011;415:2145–2157. [Google Scholar]
- Henning W.G. O'Connell R.J. Sasselov D.D. Tidally heated terrestrial exoplanets: viscoelastic response models. Astrophys J. 2009;707:1000–1015. [Google Scholar]
- Heppenheimer T.A. Porco C. New contributions to the problem of capture. Icarus. 1977;30:385–401. [Google Scholar]
- Huang S.S. Occurrence of life in the Universe. Am Sci. 1959;47:397–402. [Google Scholar]
- Hut P. Tidal evolution in close binary systems. Astron Astrophys. 1981;99:126–140. [Google Scholar]
- Jackson B. Barnes R. Greenberg R. Tidal heating of terrestrial extrasolar planets and implications for their habitability. Mon Not R Astron Soc. 2008;391:237–245. [Google Scholar]
- Jewitt D. Haghighipour N. Irregular satellites of the planets: products of capture in the early Solar System. Annu Rev Astron Astrophys. 2007;45:261–295. [Google Scholar]
- Joshi M.M. Haberle R.M. Reynolds R.T. Simulations of the atmospheres of synchronously rotating terrestrial planets orbiting M dwarfs: conditions for atmospheric collapse and the implications for habitability. Icarus. 1997;129:450–465. [Google Scholar]
- Kaltenegger L. What does it take for a moon to support life?. In: Foing B.H., editor; Perry M., editor. Proceedings of the Fourth International Conference on Exploration and Utilisation of the Moon: ICEUM 4, ESA SP-462; Noordwijk, the Netherlands: European Space Agency, ESTEC; 2000. pp. 199–201. [Google Scholar]
- Kaltenegger L. Characterizing habitable exomoons. Astrophys J. 2010;712:L125–L130. [Google Scholar]
- Kaltenegger L. Sasselov D. Exploring the habitable zone for Kepler planetary candidates. Astrophys J. 2011;736:L25. [Google Scholar]
- Kasting J.F. Runaway and moist greenhouse atmospheres and the evolution of Earth and Venus. Icarus. 1988;74:472–494. doi: 10.1016/0019-1035(88)90116-9. [DOI] [PubMed] [Google Scholar]
- Kasting J.F. Whitmire D.P. Reynolds R.T. Habitable zones around main sequence stars. Icarus. 1993;101:108–128. doi: 10.1006/icar.1993.1010. [DOI] [PubMed] [Google Scholar]
- Kaula W.M. Tidal dissipation by solid friction and the resulting orbital evolution. Rev Geophys. 1964;2:661–685. [Google Scholar]
- Kennedy G.M. Kenyon S.J. Planet formation around stars of various masses: the snow line and the frequency of giant planets. Astrophys J. 2008;673:502–512. [Google Scholar]
- Khodachenko M.L. Ribas I. Lammer H. Griessmeier J.M. Leitner M. Selsis F. Eiroa C. Hanslmeier A. Biernat H.K. Farrugia C.J. Rucker H.O. Coronal mass ejection (CME) activity of low mass M stars as an important factor for the habitability of terrestrial planets. I. CME impact on expected magnetospheres of Earth-like exoplanets in close-in habitable zones. Astrobiology. 2007;7:167–184. doi: 10.1089/ast.2006.0127. [DOI] [PubMed] [Google Scholar]
- Kipping D.M. Transit timing effects due to an exomoon. Mon Not R Astron Soc. 2009a;392:181–189. [Google Scholar]
- Kipping D.M. Transit timing effects due to an exomoon—II. Mon Not R Astron Soc. 2009b;396:1797–1804. [Google Scholar]
- Kipping D.M. How to weigh a star using a moon. Mon Not R Astron Soc. 2010;409:L119–L123. [Google Scholar]
- Kipping D.M. LUNA: an algorithm for generating dynamic planet-moon transits. Mon Not R Astron Soc. 2011a;416:689–709. [Google Scholar]
- Kipping D.M. The Transits of Extrasolar Planets with Moon. Springer; Berlin: 2011b. [Google Scholar]
- Kipping D.M. Fossey S.J. Campanella G. On the detectability of habitable exomoons with Kepler-class photometry. Mon Not R Astron Soc. 2009;400:398–405. [Google Scholar]
- Kipping D.M. Fossey S.J. Campanella G. Schneider J. Tinetti G. Pathways towards habitable moons. ASPC. 2010;430:139–144. [Google Scholar]
- Kipping D.M. Bakos G.Á. Buchhave L.A. Nesvorny D. Schmitt A. The hunt for exomoons with Kepler (HEK). I. Description of a new observational project. Astrophys J. 2012;750 doi: 10.1088/0004-637X/750/2/115. [DOI] [Google Scholar]
- Kite E.S. Gaidos E. Manga M. Climate instability on tidally locked exoplanets. Astrophys J. 2011;743 doi: 10.1088/0004-637X/743/1/41. [DOI] [Google Scholar]
- Kivelson M.G. Khurana K.K. Russell C.T. Walker R.J. Warnecke J. Coroniti F.V. Polanskey C. Southwood D.J. Schubert G. Discovery of Ganymede's magnetic field by the Galileo spacecraft. Nature. 1996;384:537–541. [Google Scholar]
- Kuchner M.J. Volatile-rich Earth-mass planets in the habitable zone. Astrophys J. 2003;596:L105–L108. [Google Scholar]
- Lai D. Tidal dissipation in planet-hosting stars: damping of spin-orbit misalignment and survival of hot Jupiters. Mon Not R Astron Soc. 2012;423:486–492. [Google Scholar]
- Lainey V. Arlot J.-E. Karatekin Ö. van Hoolst T. Strong tidal dissipation in Io and Jupiter from astrometric observations. Nature. 2009;459:957–959. doi: 10.1038/nature08108. [DOI] [PubMed] [Google Scholar]
- Lambeck K. Tidal dissipation in the oceans: astronomical, geophysical and oceanographic consequences. Philos Transact A Math Phys Eng Sci. 1977;287:545–594. [Google Scholar]
- Lammer H. Bredehöft J.H. Coustenis A. Khodachenko M.L. Kaltenegger L. Grasset O. Prieur D. Raulin F. Ehrenfreund P. Yamauchi M. Wahlund J.-E. Grießmeier J.-M. Stangl G. Cockell C.S. Kulikov Yu.N. Grenfell J.L. Rauer H. What makes a planet habitable? Astronomy & Astrophysics Review. 2009;17:181–249. [Google Scholar]
- Leconte J. Chabrier G. Baraffe I. Levrard B. Is tidal heating sufficient to explain bloated exoplanets? Consistent calculations accounting for finite initial eccentricity. Astron Astrophys. 2010;516:A64. [Google Scholar]
- Léger A. Grasset O. Fegley B. Codron F. Albarede A.F. Barge P. Barnes R. Cance P. Carpy S. Catalano F. Cavarroc C. Demangeon O. Ferraz-Mello S. Gabor P. Grießmeier J.-M. Leibacher J. Libourel G. Maurin A.-S. Raymond S.N. Rouan D. Samuel B. Schaefer L. Schneider J. Schuller P.A. Selsis F. Sotin C. The extreme properties of the CoRoT-7b super-Earth. Icarus. 2011;213:1–11. [Google Scholar]
- Lemmon M.T. Karkoschka E. Tomasko M. Titan's rotation—surface feature observed. Icarus. 1993;103:329–332. [Google Scholar]
- Lewis K. Effect of realistic and filtered stellar photometric noise on the detection of moons using photometric transit timing [ID 01009] In: Bouchy F., editor; Díaz R., editor; Moutou C., editor. Detection and Dynamics of Transiting Exoplanets, EPJ Web of Conferences Vol. 11. EDP Sciences; Les Ulis, France: 2011. [Google Scholar]
- Lichtenegger H.I.M. Lammer H. Grießmeier J.-M. Kulikov Yu.N. von Paris P. Hausleitner W. Krauss S. Rauer H. Aeronomical evidence for higher CO2 levels during Earth's Hadean epoch. Icarus. 2010;210:1–7. [Google Scholar]
- López-Morales M. Gómez-Perez N. Ruedas T. Magnetic fields in Earth-like exoplanets and implications for habitability around M-dwarfs. Orig Life Evol Biosph. 2011;41:533–537. doi: 10.1007/s11084-012-9263-8. [DOI] [PubMed] [Google Scholar]
- Madhusudhan N. Burrows A. Analytic models for albedos, phase curves, and polarization of reflected light from exoplanets. Astrophys J. 2012;747 doi: 10.1088/0004-637X/747/1/25. [DOI] [Google Scholar]
- Mamajek E.E. Quillen A.C. Pecaut M.J. Moolekamp F. Scott E.L. Kenworthy M.A. Cameron A.C. Parley N.R. Planetary construction zones in occultation: discovery of an extrasolar ring system transiting a young Sun-like star and future prospects for detecting eclipses by circumsecondary and circumplanetary disks. Astron J. 2012;143 doi: 10.1088/0004-6256/143/3/72. [DOI] [Google Scholar]
- Marconi M.L. A kinetic model of Ganymede's atmosphere. Icarus. 2007;190:155–174. [Google Scholar]
- Matsui T. Abe Y. Impact-induced atmospheres and oceans on Earth and Venus. Nature. 1986;322:526–528. [Google Scholar]
- Mayor M. Queloz D. A Jupiter-mass companion to a solar-type star. Nature. 1995;378:355–359. [Google Scholar]
- Mislis D. Heller R. Schmitt J.H.M.M. Hodgkin S. Estimating transiting exoplanet masses from precise optical photometry. Astron Astrophys. 2012;538 doi: 10.1051/0004-6361/201116711. [DOI] [Google Scholar]
- Mitchell J.L. Titan's transport-driven methane cycle. Astrophys J. 2012;756:L26. [Google Scholar]
- Mosqueira I. Estrada P.R. Formation of the regular satellites of giant planets in an extended gaseous nebula II: satellite migration and survival. Icarus. 2003;163:232–255. [Google Scholar]
- Neff J.S. Ellis T.A. Apt J. Bergstralh J.T. Bolometric albedos of Titan, Uranus, and Neptune. Icarus. 1985;62:425–432. [Google Scholar]
- Neron de Surgy O. Laskar J. On the long term evolution of the spin of the Earth. Astron Astrophys. 1997;318:975–989. [Google Scholar]
- Noack L. Breuer D. Plate tectonics on Earth-like planets [EPSC-DPS2011-890]. EPSC-DPS Joint Meeting 2011, European Planetary Science Congress and Division for Planetary Sciences of the American Astronomical Society; 2011. [Google Scholar]
- Norman L.H. Is there life on…Titan? Astronomy & Geophysics. 2011;52:39–42. [Google Scholar]
- Ogihara M. Ida S. N-body simulations of satellite formation around giant planets: origin of orbital configuration of the Galilean moons. Astrophys J. 2012;753 doi: 10.1088/0004-637X/753/1/60. [DOI] [Google Scholar]
- Olson P. Christensen U.R. Dipole moment scaling for convection-driven planetary dynamos. Earth Planet Sci Lett. 2006;250:561–571. [Google Scholar]
- Pál A. Light-curve modelling for mutual transits. Mon Not R Astron Soc. 2012;420:1630–1635. [Google Scholar]
- Peale S.J. Cassen P. Contribution of tidal dissipation to lunar thermal history. Icarus. 1978;36:245–269. [Google Scholar]
- Pearl J.C. Conrath B.J. The albedo, effective temperature, and energy balance of Neptune, as determined from Voyager data. J Geophys Res. 1991;96:18921–18930. [Google Scholar]
- Pearl J.C. Conrath B.J. Hanel R.A. Pirraglia J.A. The albedo, effective temperature, and energy balance of Uranus, as determined from Voyager IRIS data. Icarus. 1990;84:12–28. [Google Scholar]
- Pérez F. Granger B.E. IPython: a system for interactive scientific computing. Comput Sci Eng. 2007;9:21–23. [Google Scholar]
- Pierrehumbert R.T. Principles of Planetary Climate. Cambridge, Cambridge University Press; UK: 2010. [Google Scholar]
- Pollack J.B. Burns J.A. Tauber M.E. Gas drag in primordial circumplanetary envelopes—a mechanism for satellite capture. Icarus. 1979;37:587–611. [Google Scholar]
- Pollack J.B. Rages K. Baines K.H. Bergstralh J.T. Wenkert D. Danielson G.E. Estimates of the bolometric albedos and radiation balance of Uranus and Neptune. Icarus. 1986;65:442–466. [Google Scholar]
- Porter S.B. Grundy W.M. Post-capture evolution of potentially habitable exomoons. Astrophys J. 2011;736:L14. [Google Scholar]
- Quarles B. Musielak Z.E. Cuntz M. Habitability of Earth-mass planets and moons in the Kepler-16 system. Astrophys J. 2012;750 doi: 10.1088/0004-637X/750/1/14. [DOI] [Google Scholar]
- Reynolds R.T. McKay C.P. Kasting J.F. Europa, tidally heated oceans, and habitable zones around giant planets. Adv Space Res. 1987;7:125–132. doi: 10.1016/0273-1177(87)90364-4. [DOI] [PubMed] [Google Scholar]
- Sartoretti P. Schneider J. On the detection of satellites of extrasolar planets with the method of transits. Astron Astrophys (Supplement) 1999;134:553–560. [Google Scholar]
- Sasaki T. Stewart G.R. Ida S. Origin of the different architectures of the jovian saturnian satellite systems. Astrophys J. 2010;714:1052–1064. [Google Scholar]
- Sasaki T. Barnes J.W. O'Brien D.P. Outcomes and duration of tidal evolution in a star-planet-moon system. Astrophys J. 2012;754 doi: 10.1088/0004-637X/754/1/51. [DOI] [Google Scholar]
- Scharf C.A. The potential for tidally heated icy and temperate moons around exoplanets. Astrophys J. 2006;648:1196–1205. [Google Scholar]
- Schmidt B.E. Blankenship D.D. Patterson G.W. Schenk P.M. Active formation of ‘chaos terrain’ over shallow subsurface water on Europa. Nature. 2011;479:502–505. doi: 10.1038/nature10608. [DOI] [PubMed] [Google Scholar]
- Segatz M. Spohn T. Ross M.N. Schubert G. Tidal dissipation, surface heat flow, and figure of viscoelastic models of Io. Icarus. 1988;75:187–206. [Google Scholar]
- Selsis F. Kasting J.F. Levrard B. Paillet J. Ribas I. Delfosse X. Habitable planets around the star Gliese 581? Astron Astrophys. 2007;476:1373–1387. [Google Scholar]
- Showman A.P. Malhotra R. The Galilean satellites. Science. 1999;296:77–84. doi: 10.1126/science.286.5437.77. [DOI] [PubMed] [Google Scholar]
- Simon A.E. Szatmáry K. Szabó G.M. Determination of the size, mass, and density of “exomoons” from photometric transit timing variations. Astron Astrophys. 2007;470:727–731. [Google Scholar]
- Simon A.E. Szabó G.M. Szatmáry K. Kiss L.L. Methods for exomoon characterization: combining transit photometry and the Rossiter-McLaughlin effect. Mon Not R Astron Soc. 2010;406:2038–2046. [Google Scholar]
- Simon A.E. Szabó G.M. Kiss L.L. Szatmáry K. Signals of exomoons in averaged light curves of exoplanets. Mon Not R Astron Soc. 2012;419:164–171. [Google Scholar]
- Smith B.A. Soderblom L. Batson R.M. Bridges P. Inge J. Masursky H. Shoemaker E. Beebe R. Boyce J. Briggs G. Bunker A. Collins S.A. Hansen C.J. Johnson T.V. Mitchell J.L. Terrile R.J. Cook A.F., II Cuzzi J. Pollack J.B. Danielson G.E. Ingersoll A.P. Davies M.E. Hunt G.E. Morrison D. Owen T. Sagan C. Veverka J. Strom R. Suomi V.E. A new look at the Saturn system—the Voyager 2 images. Science. 1982;215:504–537. doi: 10.1126/science.215.4532.504. [DOI] [PubMed] [Google Scholar]
- Sohl F. Sears W.D. Lorenz R.D. Tidal dissipation on Titan. Icarus. 1995;115:278–294. [Google Scholar]
- Spencer J.R. Rathbun J.A. Travis L.D. Tamppari L.K. Barnard L. Martin T.Z. McEwen A.S. Io's thermal emission from the Galileo photopolarimeter-radiometer. Science. 2000;288:1198–1201. doi: 10.1126/science.288.5469.1198. [DOI] [PubMed] [Google Scholar]
- Spiegel D.S. Menou K. Scharf C.A. Habitable climates. Astrophys J. 2008;681:1609–1623. [Google Scholar]
- Stamenković V. Breuer D. Spohn T. Thermal and transport properties of mantle rock at high pressure: applications to super-Earths. Icarus. 2011;216:572–596. [Google Scholar]
- Szabó G.M. Szatmáry K. Divéki Z. Simon A. Possibility of a photometric detection of an “exomoon.”. Astron Astrophys. 2006;450:395–398. [Google Scholar]
- Tachinami C. Senshu H. Ida S. Thermal evolution and lifetime of intrinsic magnetic fields of super-Earths in habitable zones. Astrophys J. 2011;726 doi: 10.1088/0004-637X/726/2/70. [DOI] [Google Scholar]
- Tian F. Thermal escape from super Earth atmospheres in the habitable zones of M stars. Astrophys J. 2009;703:905–909. [Google Scholar]
- Tusnski L.R.M. Valio A. Transit model of planets with moon and ring systems. Astrophys J. 2011;743 doi: 10.1088/0004-637X/743/1/97. [DOI] [Google Scholar]
- Wall S. Hayes A. Bristow C. Lorenz R. Stofan E. Lunine J. Le Gall A. Janssen M. Lopes R. Wye L. Soderblom L. Paillou P. Aharonson O. Zebker H. Farr T. Mitri G. Kirk R. Mitchell K. Notarnicola C. Casarano D. Ventura B. Active shoreline of Ontario Lacus, Titan: a morphological study of the lake and its surroundings. Geophys. Res Lett. 2010;37 doi: 10.1029/2009GL041821. [DOI] [Google Scholar]
- Weidner C. Horne K. Limits on the orbits and masses of moons around currently-known transiting exoplanets. Astron Astrophys. 2010;521:A76. [Google Scholar]
- Whewell W. On the Plurality of Worlds. J.W. Parker and Son; London: 1853. [Google Scholar]
- Williams D.M. Kasting J.F. Wade R.A. Habitable moons around extrasolar giant planets. Nature. 1997;385:234–236. doi: 10.1038/385234a0. [DOI] [PubMed] [Google Scholar]
- Withers P. Barnes J.W. Using satellites to probe extrasolar planet formation. Proceedings of the International Astronomical Union. 2010;6 doi: 10.1017/S1743921312000038. [DOI] [Google Scholar]
- Wordsworth R.D. Forget F. Selsis F. Millour E. Charnay B. Madeleine J.-B. Gliese 581d is the first discovered terrestrial-mass exoplanet in the habitable zone. Astrophys J. 2011;733:L48. [Google Scholar]
- Yoder C.F. How tidal heating in Io drives the Galilean orbital resonance locks. Nature. 1979;279:767–770. [Google Scholar]
- Zhuang Q. Gao X. Yu Q. The Rossiter-McLaughlin effect for exomoons or binary planets. Astrophys J. 2012;758 doi: 10.1088/0004-637X/758/2/111. [DOI] [Google Scholar]
- Zuluaga J.I. Cuartas P.A. The role of rotation in the evolution of dynamo-generated magnetic fields in super-Earths. Icarus. 2012;217:88–102. [Google Scholar]
- Zuluaga J.I. Cuartas P.A. Hoyos J.H. Evolution of magnetic protection in potentially habitable terrestrial planets. 2012. arXiv:1204.0275.