Measurement of Microchannel Fluidic Resistance with a Standard Voltage Meter

Abstract

A simplified method for measuring the fluidic resistance (R_fluidic) of microfluidic channels is presented, in which the electrical resistance (R_elec) of a channel filled with a conductivity standard solution can be measured and directly correlated to R_fluidic using a simple equation. Although a slight correction factor could be applied in this system to improve accuracy, results showed that a standard voltage meter could be used without calibration to determine R_fluidic to within 12% error. Results accurate to within 2% were obtained when a geometric correction factor was applied using these particular channels. When compared to standard flow rate measurements, such as meniscus tracking in outlet tubing, this approach provided a more straightforward alternative and resulted in lower measurement error. The method was validated using 9 different fluidic resistance values (from ~40 – 600 kPa s mm⁻³) and over 30 separately fabricated microfluidic devices. Furthermore, since the method is analogous to resistance measurements with a voltage meter in electrical circuits, dynamic R_fluidic measurements were possible in more complex microfluidic designs. Microchannel R_elec was shown to dynamically mimic pressure waveforms applied to a membrane in a variable microfluidic resistor. The variable resistor was then used to dynamically control aqueous-in-oil droplet sizes and spacing, providing a unique and convenient control system for droplet-generating devices. This conductivity-based method for fluidic resistance measurement is thus a useful tool for static or real-time characterization of microfluidic systems.

1. Introduction

Microfluidic technology provides an attractive platform for a variety of purposes, with devices that can be tailored for many chemical and biological applications. One unique capability is to integrate processing and analysis functionalities onto the same chip, creating micro-total analysis systems (μTAS) [1–6]. A key aspect to any microfluidic system is proper flow control. Most systems use high-voltage electrical power supplies or syringe pumps to control flow through microdevices. Analytically, these systems are capable of high performance assays, biological sample preparation, and electrophoretic separations, among other applications; although, the disadvantages to these systems are the highly specialized equipment and expertise needed to operate [3–6].

One way to make these systems more amenable to point-of-care analysis is by implementing passive flow control to simplify operation, where little to no external power sources are needed to operate devices [3,4,5–11]. Passive flow control employs everyday forces such as gravity, suction, and capillary action to manipulate fluids in microdevices [12]. For example, microfluidic channel resistance can be exploited to tune fluidic flow rates passively, so that no external syringe pumps or power supplies are needed in the operation of these devices [4,5,9,11,13]. Fluidic resistances of microchannels can be designed to automatically modulate flow rates through individual parts of the device, analogous to the design of differential impedances in electrical circuits. Relatively simple fluid dynamics equations have been used successfully to predict fluidic resistances of microfluidic channels [5,7]. Yet, as is the case in the electrical counterpart, errors introduced during fabrication can significantly deviate resistance values from the ideal. During photolithography, slight imperfections such as errors in the depth of spin-coated layers of photoresist can cause changes in channel depths, and thus significant changes in channel resistances. As such, there is a clear need for methodology to directly measure fluidic resistances of microfluidic channels. Such methods have been presented, including measurement of the pressure drop across a series fluidic circuit [7]. However, this approach requires precisely controlled pressurized reservoirs, solenoids, and series fluidic circuits with rigid components that possess significant dead volume. Another approach is to directly measure the fluidic flow rate through microfluidic circuits while controlling the applied pressure. One of the most facile methods, meniscus tracking through outlet tubing, requires only water, a pressure source, and a timer [4,14], yet this approach requires ~15 minutes for each measurement and is highly sensitive to user error. Another method is to quantify flux of colored solutions through devices [15], but this approach requires syringe pumps and UV spectroscopy to accomplish. These examples highlight the need to further simplify the measurement of fluidic resistance, ideally reducing the measurement system to the analogous electrical voltage meter.

In this work, we provide a fast and convenient method to measure fluidic resistance directly using solution conductivity. By using commercially available conductivity standards, an electrical resistor, and a standard voltage meter, we measure the electrical resistance of a microfluidic channel. We then provide a simple equation that can be used to calculate the fluidic resistance from this electrical resistance measurement. We show that the equation holds true for 9 different fluidic resistance values tested on over 30 microfluidic devices and that the method can be used to measure dynamic changes in electrical resistance in real time. The simplicity of this approach permits the use of a standard voltage meter to directly measure fluidic resistance. Although a slight correction factor for fluidic resistance can be applied in our system, relatively accurate results can even be obtained without requiring calibration or correction factors, providing users with the option to further simplify the measurements.

2. Experimental

2.1. Reagents and Materials

Polydimethylsiloxane (PDMS) precursors, Sylgard^® 184 elastomer base and curing agent, were obtained from Dow Corning (Midland, Maryland, USA). NIST traceable conductivity standards of 200 000, 150 000, and 100 000 μS cm⁻¹ were purchased from VWR (West Chester, Pennsylvania, USA). Silicon wafers were obtained from (Boise, ID, USA), SU-8 photoresist and developer were purchased from Microchem (Newton, Massachusetts, USA), and trichloromethysilane was purchased from Sigma-Aldrich. HFE-7500 perfluorocarbon oil was obtained from 3M, and Krytox 157-FSH carboxylated perfluorocarbon surfactant was purchased from DuPont. The ammonium salt of the Krytox surfactant was made as described previously [11]. Aquapel for channel coating was purchased from Pittsburgh Glass Works. Tubing for interfacing syringes and devices was obtained from Small Parts (TGY-020-5C; 0.02 in. ID, 0.06 in. OD, 0.02 in. wall), as were blunt ended needles (NE-223PL-C 22G).

2.2. Microfluidic device fabrication

All devices were fabricated using PDMS as the channeled substrate and No. 1 glass coverslips as the floor substrate. In brief, PDMS was mixed in a 10:1 elastomer to curing agent ratio, poured over the silicon master, and allowed to cure overnight at 60 °C [16]. The microfluidic channel layout (Figure 1A) was designed in Adobe Illustrator software and sent to Fineline Imaging (Colorado Springs, CO) for photomask printing at 65 024 DPI resolution (negative image). The SU-8/silicon master was fabricated using standard photolithography with channels that varied in length (17, 35, and 71 mm) and depth (33, 52, and 78 μm).

Figure 1.

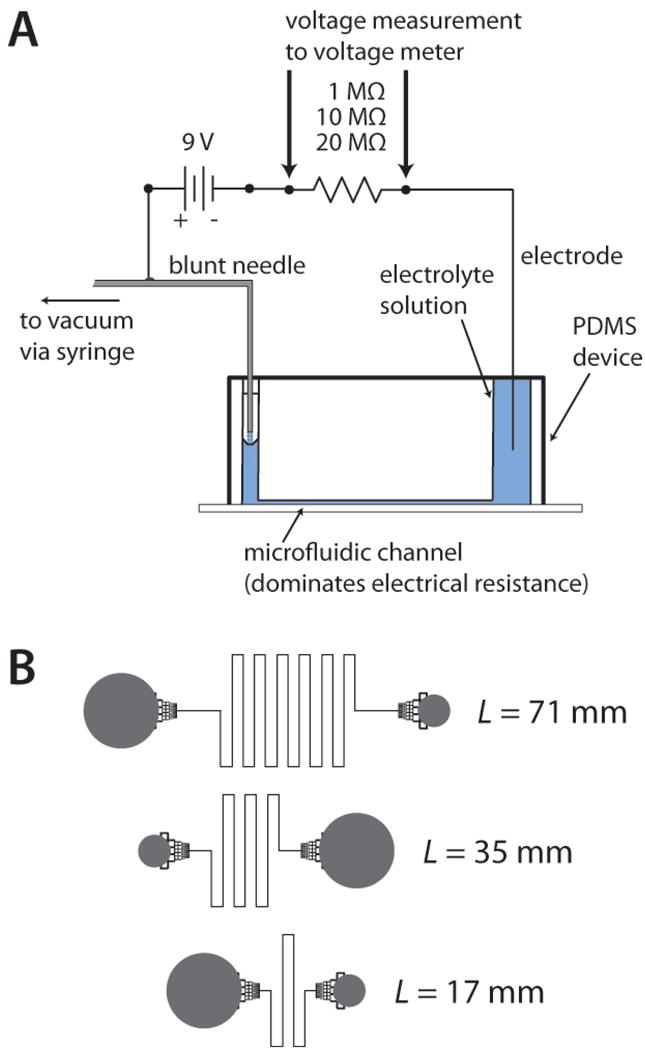
A) System used for conductivity measurements. Electrical resistors of 1, 10, or 20 MΩ, in series with the microchannel, were interchanged based on the length and depth of the microchannel. B) Design of the fluidic channels, or fluidic resistors, used to make the conductivity measurements. Channel lengths of 17, 35, and 71 mm were fabricated with channel depths of 33, 52, and 78 μm, resulting in nine different values of fluidic resistance for this study. Fluidic reservoirs (gray) were interfaced to channels using monolithic debris filters, which had negligible effect on fluidic resistance values.

2.3. Fluidic Flow Rate Measurements

A meniscus tracking method was used to measure the linear velocity of fluid in outlet tubes of microdevices from which volumetric flow rate and fluidic resistance could be calculated [4,14]. Water was placed into the large inlet reservoir of the device, and a vacuum was applied at the outlet. Tracking the meniscus in the outlet tubing, a distance measurement was made every 1 min for 15 min. For each measurement, linear velocity, volumetric flow rate, and fluidic resistance were calculated.

2.4. Electrical Resistance Measurements

Electrical resistances of the microfluidic channels were measured using the circuit shown in Fig. 1A. The voltage drop was measured across an electrical resistor in series with the microfluidic channel (fluidic resistor). This voltage was then used to calculate the electrical resistance of the microchannel through the relationship below.

$$R_{\mathit{elec}}=\frac{R_{\mathit{div}}{V}_{\mathit{bat}}}{V_{\mathit{meas}}}-R_{\mathit{div}}-R_{\mathit{sys}}$$ (1)

In Eq. 1, R_elec is the electrical resistance of the microchannel, V_bat is the voltage of the battery powering the circuit, V_meas is the measured voltage across the series resistor, and R_sys is the relatively small system resistance introduced by interfacing to the microdevice. R_div, the total resistance of the voltage divider, also incorporated the resistance of the voltage measurement system, such that in Eq. 1, R_div = 1/(1/R_resistor + 1/R_voltmeter). R_resistor was either 20, 10, or 1 MΩ, and R_voltmeter was measured to be 9.86 ± 0.01 × 10⁵ Ω for the standard voltage meter and 2.95 ± 0.03 × 10⁵ Ω for the USB-DAQ interface to LabVIEW. R_sys was measured at the beginning of each set of measurements on a new device by removing the microdevice from the circuit, and the value was consistently 4.6 × 10⁴ Ω. To allow application of vacuum during conductivity measurements, an electrode/outlet tube hybrid was made in house using a blunt needle (Small Parts) with a piece of copper wire soldered to one end, and the needle was interfaced with the outlet tubing. Using the supplier provided correction factors, conductivity values of the NIST standards were adjusted based on the average temperature of the measurements (21.6 ± 0.6 °C); standards labeled 200 000, 150 000, and 100 000 μS cm⁻¹ were temperature corrected to 188 480, 142 080, and 93 390 μS cm⁻¹ (or 0.018848, 0.014208, and 0.009339 S mm⁻¹). These standard solutions were added to the large inlet reservoir, and a vacuum was applied at the outlet tubing using a handheld syringe. V_meas was allowed to equilibrate, and a reading was taken every 1 min for 5 min for each conductivity standard in each fluidic resistor. Care was taken to ensure no air bubbles were blocking channels during the experiment, and there was no evidence of significant electroosmotic flow or electrolysis in this configuration.

A push-down version of the variable fluidic resistor—made for droplet microfluidics—was fabricated using partial curing and bonding of PDMS, without plasma oxidation. Briefly, PDMS was mixed in a 7:1 ratio and placed in a vacuum chamber to remove any trapped air bubbles. It was then poured over a blank silicon wafer and cured for ~45 min in an oven at 60 °C, or just until it was rigid enough to handle. Another batch of PDMS was mixed at a 15:1 ratio and placed in a vacuum chamber. This batch was poured over a silicon master with 39 μm deep channel patterns, spin coated to a height of 60 μm, then allowed to cure in an oven at 60 °C for 15 min. The blank PDMS portion was then taken from the oven and removed from the wafer, and the valve input was punched. The blank portion was then aligned with the spin coated portion to ensure that the valve input was in the correct position over the oil inlet channel. The two portions were then placed back in the oven and allowed to cure overnight at 60 °C. Devices were then removed from the oven, and a scalpel was used to score around each chip to cut the membrane to the size of the chip. Devices were then carefully peeled from the silicon wafer to prevent tearing of the thin membrane portion. Reservoirs for oil and aqueous phases and a fluidic outlet were then punched. Some devices were then exposed to an air plasma (Harrick Plasma, Ithaca, New York, USA) for 45 s and bonded to a glass slide for stability. Channels were coated with Aquapel (Pittsburgh Glass Works) to induce hydrophobicity. After rinsing the chip with methanol, drying with air, and placing in the oven at 60 °C for 10–15 min to remove any remaining solvent, the chip was filled with carrier oil and was ready for aqueous-in-oil droplet formation.

2.5. Image Analysis

Data analysis for droplet fluidics was performed on video images of the droplets downstream of the droplet generator, with or without valve actuation. Video was collected at 40 fps using a Nikon Ti-E inverted fluorescence microscope in DIC mode. To measure droplet and flow properties, a region of interest (ROI) was selected in the Nikon Elements software to monitor the intensity of transmitted light in a small area as droplets passed by. A time trace of transmitted light intensity was generated for each experiment, and this trace was fed into an in-house written LabView application for frequency analysis. ImageJ [17], a freeware image analysis program, was also used to analyze the raw video images to determine droplet volumes, spacing, and oil volumes.

3. Results and Discussion

3.1. Fluidic Resistance Measurements

As shown by the fluidic channel schematics in Fig. 1B, devices were designed to encompass a range of fluidic resistances. Three different lengths (17, 35, and 71 mm) and depths (33, 52, and 78 μm) were fabricated from an inverted version of these mask designs, resulting in 9 different values of fluidic resistance ranging from ~40 to ~600 kPa s mm⁻³. First, we confirmed the fluidic resistances using the simple but tedious meniscus tracking method [4,14]. From the linear velocity of the meniscus in the tubing connecting the syringe to the device, the volumetric flow rate was calculated using the cross-sectional area of the tubing. The vacuum pressure applied by the 100-mL glass syringe was determined using the ideal gas law, as previously described and validated with ~2% error [4,15]. From the volumetric flow rate (Q) and pressure (ΔP) measurements, the fluidic resistance (R_fluidic) was determined with the equation $R_{\mathit{fluidic}}=\frac{\mathrm{\Delta }P}{Q}$. These measured R_fluidic values are shown in Fig. S1 as a function of channel length. As expected, R_fluidic increased linearly with channel length as depth was held constant, and R_fluidic decreased with increasing depth. The meniscus linear velocity was measured over a range of vacuum pressures from 4 – 10 kPa, and the velocity varied linearly over this entire range, suggesting that there was no increase in resistance caused by channel wall distortion from the modest vacuum applied. The measurements were done at least 3 times at each pressure to determine the error. As expected, the shallowest channel showed the highest slope versus channel length, and as the channel depth increased, the slope decreased (Fig. S1).

The theoretical fluidic resistance can also be calculated, as shown previously by other researchers using microfluidics [5,7,8,13]. For a rectangular channel, R_fluidic can be determined using geometric parameters and the solution viscosity, as in Eq. 2 below.

$$R_{\mathit{fluidic}\mid \mathit{calc}}=\frac{12\eta L}{w{h}^{3}F}$$ (2)

In this equation, η represents the solution viscosity, L the channel length, w the channel width, h the channel height, and F represents a geometric form factor related to the rectangular shape. Calculation of F requires only h and w, and this calculation is described by Eq. S2 in Supporting Information. As shown in Fig. 2A, measured R_fluidic values correlated well with calculated R_fluidic|calc values, showing a slope of 1.12 ± 0.02 and an R² of 0.998. Interestingly, R_fluidic values were progressively higher than R_fluidic|calc values, as indicated by the slope of 1.12 ± 0.02 in Fig. 2A; this observed discrepancy is likely due to the assumption of a perfectly rectangular channel cross-section for Eq. 2, while the photolithographic process often resulted in slightly distorted rectangular cross-sections, as shown in Fig. 2B, which would result in higher measured resistance. It should be noted that although we corrected the measurements to include the resistance of the measurement system, i.e. the fluidic resistance of the tubing and needle interfacing with the glass syringe, this resistance was found to be a negligible 0.6 kPa s mm⁻³. These results (Fig. 2A–B, Fig. S1) indicate that a more accurate equation to calculate fluidic resistance for our system would incorporate the distorted rectangular cross-section, which would pose a significant mathematical challenge. Alternatively, it sufficed to apply a correction factor, k, to Eq. 2, as shown in Eq. 3 below.

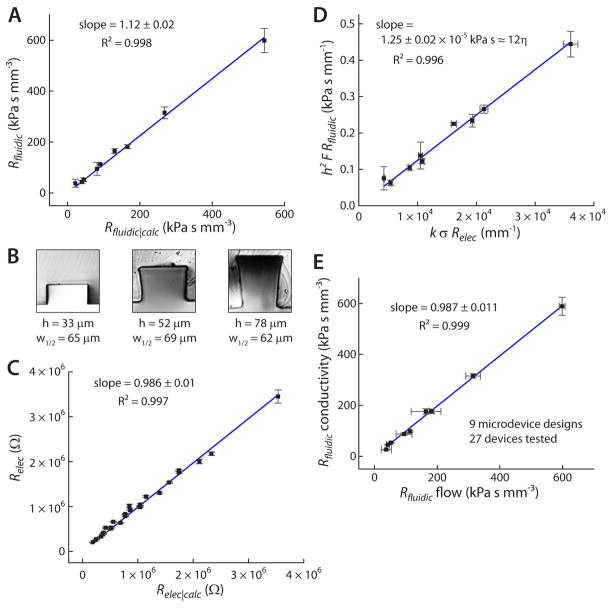
Figure 2.

A) R_fluidic (measured) was shown to be well-correlated with R_fluidic|calc for all of the nine tested fluidic resistors. B) Cross-sections of PDMS channels were sliced with a razor and imaged, revealing the slightly distorted rectangular cross-section, particularly in the deeper channels. C) Measured R_elec was well-correlated with R_elec|calc for all nine fluidic resistors and with three different conductivity standards (27 values of R_elec). D) A plot of h² F R_fluidic versus k σ R_elec gave a slope of 1.25 × 10⁻⁵ ± 0.02 kPa s⁻¹, essentially equal to 12 η = 1.21 × 10⁻⁵ kPa s⁻¹, as expected from Eq. 5. This result was obtained after triplicate measurements on 27 different microdevices. E) A comparison between the meniscus tracking method (R_fluidic flow) and the new conductivity-based method (R_fluidic conductivity) showed excellent correlation, with lower error rates associated with the more straightforward conductivity-based method.

$$R_{\mathit{fluidic}\mid \mathit{calc}}=k\frac{12\eta L}{w{h}^{3}F}$$ (3)

In our system, k = 1.12 was obtained from the slope of the best-fit line in Fig. 2A. This slight (12%) deviation from Eq. 2 suggests that fairly accurate results can even be obtained without applying a correction factor.

3.2. Electrical Resistance Measurements

To check whether standard electrical resistance calculations would be suitable for our system, first it was necessary to ensure that the measured electrical resistance, R_elec, correlated with the expected electrical resistance given by the simple relationship, $R_{\mathit{elec}\mid \mathit{calc}}=\frac{L}{\sigma A}$, where σ is the solution conductivity and A the cross-sectional area of the channel. The widths, w, and heights, h, of each channel were measured by using a razor blade to slice a cross-section of a representative PDMS device, then imaging that cross-section using a Nikon TiE inverted microscope with Nikon Elements software. These cross-sections are shown as insets to Fig. 2B. Channel heights were determined to be 33, 52, and 78 μm. Particularly for the 52 and 78 μm depths, the channels were not perfectly rectangular, but slightly trapezoidal. This distortion is attributed to an artifact of the photolithographic process, likely due to non-uniformity in cross-linking the photoresist with the masked UV beam; and, as discussed above, the distortion is the most reasonable explanation for the slight discrepancy observed between R_fluidic and R_fluidic|calc in Fig. 2A. The assigned widths, w, for each channel were determined by the widths at half-height (w_1/2). Values of w were found to be 65, 69, and 62 μm for channels with h = 33, 52, and 78 μm, respectively. These values of h and w were used to calculate R_elec|calc for all nine fluidic resistors, and they were also used in the above calculations of R_fluidic|calc.

Next, R_elec values were measured for each fluidic resistor (i.e. microchannel). To do so, the measurement system shown in Fig. 1A was used, as described in the Experimental section. The internal resistance of the voltage meter was first determined to be 9.86 ± 0.01 × 10⁵ Ω, by referencing it to a series of resistors in the kΩ to MΩ range. The voltage meter was treated as a resistor in parallel to the circuit voltage divider. For each measurement, the voltage meter was used to determine the voltage of the battery (V_bat) and the electrical resistance of the system (R_sys), and the temperature was recorded. Measurements showed a consistent internal electrical resistance of the system, R_sys = 4.6 × 10⁴ Ω, which was significant enough to include into Eq. 1. To measure R_elec of each fluidic resistor, an appropriate resistor was chosen for the voltage divider. Guided by the predicted R_elec|calc for each channel, a divider resistor was chosen to optimize measurement sensitivity. 20 MΩ, 10 MΩ, and 1 MΩ resistors were used in the voltage dividers for the 33, 52, and 78 μm deep channels, respectively. Approximately 9 V was applied across the microchannel and voltage divider, while the voltage meter was set to measure the voltage drop across the divider resistor, as shown in Fig. 1A. Thus, when a high conductivity solution was placed into the device, the electrical resistance of the channel was relatively low, and the divider resistance dominated the circuit to give a high voltage reading. When a low conductivity solution was placed into the device, the channel’s electrical resistance was high, and most of the voltage was dropped across it to give a low voltage reading. In this way, R_elec was determined in triplicate for each of the nine different device geometries. Fig. 2C shows that these values correlated very well with the calculated electrical resistances, R_elec|calc; the correlation coefficient of R_elec versus R_elec|calc was R² = 0.997, and the slope was 0.986 ± 0.01. These data were recorded in triplicate with 3 different NIST conductivity standards (200 000, 150 000, and 100 000 μS cm⁻¹) for each of the 9 channel geometries, giving 27 average values of R_elec (n = 81), as shown in Fig. 2C. The resultant high correlation validated the use of the basic equation, $R_{\mathit{elec}\mid \mathit{calc}}=\frac{L}{\sigma A}$, for our microfluidic channels.

3.3. Relating Fluidic Resistance and Electrical Resistance in Microfluidic Channels

Using Eq. 2 in concert with the definition of the electrical resistance of a tube of solution ( $R_{\mathit{elec}}=\frac{L}{\sigma A}$), a substitution gives the following relationship,

$$R_{\mathit{fluidic}}=\frac{12\eta \sigma }{h^{2}F}{R}_{\mathit{elec}}$$ (4)

where R_elec is the measured electrical resistance, η is the viscosity of the solution, and σ is the conductivity of the solution. As before, this equation can be slightly modified by including the correction factor of k = 1.12 for our system.

$$R_{\mathit{fluidic}}=k\frac{12\eta \sigma }{h^{2}F}{R}_{\mathit{elec}}$$ (5)

Eq.s 4 and 5 imply that a simple measurement of electrical resistance could be made to determine the fluidic resistance. The conversion would simply require the value of R_elec to be multiplied by a set of constants related to the properties of the solution (η, σ) and the geometric parameters of the microchannel (h, w), with the optional correction factor, k, to adjust for any observed discrepancies in the fluidic resistance calculation from Eq. 2. This is an elegant approach that can greatly simplify the measurement of fluidic resistance in microfluidic devices.

To validate the use of Eq. 4 or Eq. 5, a rearrangement was applied to Eq. 5, and all measurements of R_fluidic and R_elec were compiled into one plot, shown in Fig. 2D. By plotting h² F R_fluidic versus k σ R_elec, the slope of the best-fit line was expected to be proportional to the solution viscosity, η. Specifically, since the solution viscosity at the average measurement temperature (21.6 ± 0.6 °C) should be η = 1.01 × 10⁻⁶ kPa s⁻¹, the slope was expected to equal 12 η = 1.21 × 10⁻⁵ kPa s⁻¹. Indeed, a regression line of the compiled data in Fig. 2D gave a slope of 1.25 × 10⁻⁵ ± 0.02 kPa s⁻¹, essentially equal to the expected value (~3% error). Since this result was obtained using multiple replicates of 9 different device geometries (more than 30 separately fabricated microdevices tested), and these were tested with three different NIST conductivity standards, the accuracy of Eqs. 4 and 5 were considered to be validated.

As a final validation, the correlation between fluidic resistances measured by our proposed method (Eq. 4 or 5) and those measured by the meniscus tracking method was determined (Fig. 2E). Our method was labeled as “R_fluidic conductivity,” while the standard meniscus tracking approach was labeled “R_fluidic flow.” The methods showed excellent correlation, with R² = 0.999 and a slope of 0.987 ± 0.011. Thus, Fig. 2E proves directly that a microchannel’s electrical resistance can be measured, then plugged into Eq. 4 or 5 to determine the fluidic resistance. The only requirement for a user is to ensure that their microchannels’ fluidic resistances can be accurately described by Eq. 2, which has worked well in other studies [5,7,8]. If so, Eq. 4 can be used directly to determine R_fluidic. If there is a discrepancy between R_fluidic and R_fluidic|calc from Eq. 2, as in our case, a correction factor can be applied, and Eq. 5 can be used. Even when our data was used without the correction factor (Eq. 4), the methods were still very well correlated at R² = 0.999 with a slope of 0.881 ± 0.012, meaning that without any type of calibration, Eq. 4 could be used to give accurate values of R_fluidic to < 12 % error.

This conductivity-based method for measuring R_fluidic provides significant advantages over the flow-based, meniscus-tracking method. First, the measurement can be made with a standard voltage meter and conductivity standards, thus the system is extremely simple-to-use and inexpensive. In fact, the measurement system shown in Fig. 1A is more complex than is necessary; the blunt needle interface was put in place only to simplify switching of conductivity standards over the many measurements made to validate the technique. In a minimized embodiment, standard voltage meter leads can be inserted into microfluidic reservoirs, with or without a parallel resistor, and the voltage measurement can be made directly without requiring flowing solution. Secondly, each measurement requires only a few seconds, akin to a voltage measurement in an electrical circuit. By comparison, meniscus-tracking requires ~15 min for each measurement to ensure precision of the measurement of distance traveled by the solution’s meniscus. Third, our conductivity-based approach showed greater than three-fold improvement in measurement precision compared to the flow-based method. As evident from the error bars in Fig. 2E, the average percent relative standard deviation (%RSD) for our system was 4.6 % (y-error bars), while the meniscus-tracking approach showed an average of 15 % error (x-error bars). Finally, this method of R_fluidic measurement with direct voltage readout affords connectivity to computerized systems for dynamic measurement or control systems, as elaborated on below. Consequently, at this stage it can be concluded that the conductivity-based approach presented here is a faster, simpler, more flexible, and more precise approach for determining R_fluidic of microfluidic channels.

3.4. Dynamic Fluidic Resistance Measurements

One of the noted advantages of the conductivity-based approach is that it gives direct voltage readout. In this way, the system shown in Fig. 1A can be interfaced with a digital data acquisition (DAQ, National Instruments, Austin, Texas, USA) system to allow dynamic measurements of fluidic resistance. This could be particularly useful for characterization or real-time monitoring of systems with deformable channel walls, such as valved microfluidic systems which can be described as digital fluidic circuits [14,18,20]. In particular, dynamic fluidic resistance measurement would be ideal to monitor microfluidic variable resistors or analog fluidic circuits [9,10,19,21–23]. Recent work has described the use of conductivity of ionic liquids for a similar purpose, although in that work the measured channels were aligned parallel to the primary channels to serve as pressure sensors [23]; in fact, this work further highlights the usefulness of our approach. Here, we have shown the proof-of-concept of making dynamic fluidic resistance measurements using the system in Fig. 1A to continuously monitor R_fluidic of microfluidic variable resistors.

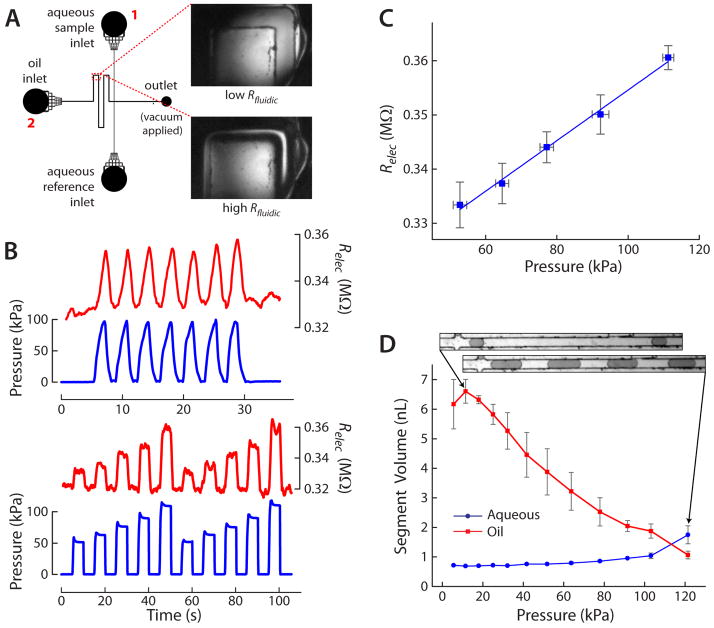
The upper portion of Fig. 3A shows the microchannel design for a previously-developed microfluidic droplet generator [11]. This design was modified by inclusion of a variable fluidic resistor, i.e. a rectangular microchannel with a deformable PDMS membrane as the channel ceiling. As shown in Fig. 3A, the PDMS membrane did not serve as a digital valve, since by design it only partially blocked flow through the fluidic channel of rectangular cross-section. Rather, the membrane served to increase the fluidic resistance of the flow channel as pressure was applied from above, creating a variable microfluidic resistor. The variable resistor was included on the oil input channel to allow dynamic control of droplet formation. As shown in Fig. 3B, dynamic increases in pressure resulted in increases in electrical resistance, R_elec, of the microfluidic channel. Pressure (blue traces) was measured with pressure sensors (Honeywell 26PCCFB6G, Allied Electronics), while R_elec (red traces) was dynamically measured—as discussed previously—by monitoring the voltage drop across a series resistor with the system from Fig. 1A and with conductivity standards filling the device. Voltages were measured between the reservoirs labeled with 1 and 2 in Fig. 3A. The traces in Fig. 3B show clearly that the measured R_elec waveforms (red traces) closely mimicked the input membrane pressure waveforms (blue traces), with an approximate sawtooth waveform shown in the upper plot and square waves of varying intensity in the lower plot. These data highlight some of the major advantages of the presented conductivity-based method, specifically that fluidic resistance can be dynamically monitored, and that this can be achieved in more complex microfluidic devices.

Figure 3.

A) Channel layout of droplet generating microfluidic device. The inset images show the variable resistor region at low R_fluidic (upper image) and high R_fluidic (lower image) after pressure is applied. B) Different pressure waveforms (blue traces) were applied to the variable resistor, and R_elec of the channel (red traces) varied similarly, as expected. C) A linear relationship was observed between the pressures applied to the variable resistor and the oil channel’s R_elec value. D) Plot of segment volume of the oil and aqueous phases over a range of pressures applied to the variable resistor. Increasing pressure (i.e. increasing R_fluidic of the oil channel) resulted in increased aqueous droplet volume and decreased oil segment volume between droplets, providing dynamic control of droplet size and spacing. Inset images show examples of droplet sizes and spacing. Microchannels in all inset images (parts A and D) are 100 μm wide.

It was clear that R_fluidic increased with R_elec in an essentially equal pattern. However, in the case of the variable fluidic resistor, prior assumptions about rectangular cross-section no longer held true; thus, Eq. 4 (or 5) was not valid for translating from R_elec to R_fluidic. Accurate determination of R_fluidic from these dynamic data would likely require measurement of the cross-section of the variable resistor region during operation followed by numerical predictions. Nonetheless, R_elec varied linearly with pressure (Fig. 3C), suggesting that R_fluidic was varying in a predictable manner. This assumption was confirmed by operation of the droplet generator with added control using the variable fluidic resistor. It was possible to dynamically vary the oil segment volume by more than 6-fold from 6.61 to 1.07 nL, while the aqueous segment volume was also varied by approximately 2.5-fold from 0.71 to 1.75 nL (Fig. 3D). Thus, the aqueous-to-oil segment volume ratio was varied over sixteen-fold from 0.10 to 1.64 using the variable fluidic resistor, as further highlighted by the inset images in Fig. 3D. The dye-filled aqueous droplet segments could be significantly increased in size by applying pressure to the membrane, thereby increasing R_fluidic of the oil input channel. Since flow through the device was accomplished using vacuum at a single outlet reservoir, the pressure distribution was varying dynamically, allowing larger aqueous flow rates to accompany the smaller oil flow rates. This type of dynamic control using a single pressure input is novel in itself and could have implications on future droplet generating microfluidic systems due to its simplicity of operation and accessibility to a wide range of segment volumes.

4. Conclusions

We have developed a new, simpler method for measuring microchannel fluidic resistances using the electrical conductivity of solutions in the channels. Existing methods for measuring fluidic resistance can require bulk equipment, such as syringe pumps and high voltage suppliers, as well as significant time and effort. Our approach can be accomplished with a standard voltage meter, and calibration can be omitted with minimal loss of accuracy. Major advantages shown by our approach are simplicity, speed, flexibility, and precision. In particular, the flexibility of the method was highlighted by dynamically monitoring the resistance of a variable fluidic resistor, which was then used to provide dynamic control over a droplet-generating microfluidic system. As future microfluidic devices move toward easier-to-operate interfacing through passive flow control [4–11], this conductivity-based method for fluidic resistance measurement should provide users with a useful tool for static or real-time characterization of the their microfluidic systems.

Highlights.

• Standard voltage meter used to measure fluidic resistance

• Manual measurement takes a few seconds, akin to electrical resistance measurements

• Measurement error is reduced compared to other approaches

• Amenable to dynamic measurement of fluidic resistance