Searching microsatellites in DNA sequences: approaches used and tools developed

Abstract

Microsatellite instability associated genomic activities and evolutionary changes have led to a renewed focus on microsatellite research. In last decade, a number of microsatellite mining tools have been introduced based on different computational approaches. The choice is generally made between slow but exhaustive dynamic programming based approaches, or fast and incomplete heuristic methods. Tools based on stochastic approaches are more popular due to their simplicity and added ornamental features. We have performed a comparative evaluation of the relative efficiency of some microsatellite search tools with their default settings. The graphical user interface, the statistical analysis of the output and ability to mine imperfect repeats are the most important criteria in selecting a tool for a particular investigation. However, none of the available tools alone provides complete and accurate information about microsatellites, and a lot depends on the discretion of the user.

Microsatellites, also known as Simple Sequence Repeats (SSRs), represent specific sequences in genomic DNA composed of short motifs (typically 1–6 bp) repeated for many number of times. Such sequences are abundant and distributed all over the eukaryotic genomes with variable frequency (Sharma et al. 2007; Guo et al. 2009). Higher rates of mutations at these loci (Eckert and Hile 2009) compared to other regions of genomic DNA, often generate inter- and intra-specific genetic variation (Agarwal et al. 2008), allowing their wide exploitation as genetic markers. In addition to their time–tested utility as an efficient molecular marker system, recent evidences in favour of structural and functional significance (Hammock and Young 2005; Bagshaw et al. 2006; 2008; Huda et al. 2009; Sureshkumar et al. 2009) of microsatellites have made it an important subject in contemporary research.

Traditionally, microsatellites are isolated from size-selected or enriched genomic libraries of the species under investigation, by screening several thousands of clones through hybridization with microsatellite probes (Zane et al. 2002). Such methods yield only fractional representation of the genomic microsatellites and are biased towards particular motifs used for screening. With the revolution in sequencing technologies, it has now become feasible to screen the entire genome(s) using bioinformatics tools for the presence of microsatellites even in case of non model organisms (Davey et al. 2011). Such methods have been found to be extremely successful in molecular marker development for the purpose of gene tagging, marker assisted selection, molecular mapping, etc. (Varshney et al. 2005; Sharma et al. 2007; Grover and Sharma 2011). However, the choice of microsatellite mining criteria and algorithms adopted for the purpose of screening genomic sequences for identifying microsatellites therein offer a lot of diversity (Toth et al. 2000; Katti et al. 2001; Dieringer and Schlotterer 2003; La Rota et al. 2005). Each of the algorithm used in these studies fulfills a certain criteria and accordingly is based on a different principle. An unfortunate outcome of this flexibility is inconsistent mathematical and biological definitions of the term microsatellite and non-uniformity in the usage of other related terms (Table 1). This review paper thus attempts to outline the underlying logistics used so far for designing different search tools and software which can be used for the identification of microsatellites. We have taken a drop down approach for classification of underlying algorithms into deterministic and stochastic ones, and further sub-classified those considering the approach used to identify a string/signal. We see this information as a significant step in pursuing biologists to develop a consensus for defining the microsatellites biologically as well as mathematically and use this information for detecting microsatellites in the vast resources of genomic sequences currently available in the public and private domains.

Table 1.

Synonyms for the basic microsatellite features from published literature

Microsatellite feature	Synonyms
Microsatellite	Simple sequence repeat (SSR), short tandem repeat (STR), tandem repeat (TR), exact tandem repeat (ETR), perfect tandem repeat (PTR)
Pattern size	Motif size, Array size, Periodicity
Pattern structure	Motif, microsatellite sequence
Number of copies	Repeat number, period, array
Position of pattern	Genomic position
Imperfect repeat	Approximate tandem repeat, degenerate repeat, inexact repeats

Problem solving approaches and algorithms

An algorithm is a set of finite and well-defined instructions for completing a task. The instructions together work as a method, which will start from an initial state, proceed through well-defined successive states (transitions) and would terminate at a final state. Fundamentally, depending on the nature of the transition, an algorithm can either be deterministic or probabilistic. A deterministic algorithm behaves predictably i.e., it will necessarily produce the same output with a given input passing through the same sequence of states. A probabilistic algorithm (or randomized algorithm) on the other hand allows a degree of logical randomness. The algorithms that have been applied for finding microsatellites in genomic sequences have been based both on the deterministic models and stochastic (or probabilistic) models (Brodzik 2007). Fundamentally, the deterministic model uses single estimates to represent the values of all the variables, but a stochastic model uses a range of values for each variable.

Deterministic methods

Deterministic approach determines more number of repeats, and has frequently been applied as a signal processing (SP) method for identification of microsatellite repeats (Gupta et al. 2006; 2007). In genomics, nucleotide bases (A, T, C and G) act as signals while their transformation and mapping into the numeric domain is referred to as signal processing (Pop 2006).

SP-based algorithms for microsatellite identification offer sensitivity towards detection of inexact repeats and application of faster signal processing tool like discrete Fourier transformation (DFT) under spectral analysis. Under Fourier analysis, a given function or object is broken down into smaller basic pieces in order to understand the central theme. Thus, under DFT, periodic trends in the signal and their associated strength are analyzed. The approach has been implemented using a web server called Spectral Repeat Finder (SRF) available at http://www.imtech.res.in/raghava/srf. This method first identifies the length of the potential repeat unit present in the DNA sequence and subsequently, the sequence is scanned to locate the approximate region(s) where the repeat units are contained. Potential seed patterns from these regions are then used to identify repeats through an exact method (Sharma et al. 2004). However, DFT is also known to cause data truncation artifacts (Zhou et al. 2009). Within spectral analysis, two different approaches can be employed for the identification of approximate repeats (hidden periodicity)- sum spectrum and Fourier product spectrum (FPS). According to Emanuele et al. (2005), FPS identifies more number of repeats. Autoregressive (AR) model, as implemented in optimized moving window spectral analysis (OMWSA) (Du et al. 2007; Zhou et al. 2009) overcomes this problem, and is claimed to be more accurate and has higher resolution (Zhou et al. 2009).

As the spectral analysis relies on visualization on a spectrogram, the smaller frequencies as produced by smaller motifs can sometimes go undetected. Therefore, a repeat sequence with smaller motif may go undetected or falsely detected (Gupta et al. 2007; Zhou et al. 2009). For example, a sequence (AT)₂₄ may be falsely detected as (ATATAT)₈. Leese et al. (2008) have used deterministic tool “Phobos” that relies on the alignment scores for the identification of tandem repeats in genome. The tool has also been integrated into the Staden package for sequence analysis (Kraemer et al. 2009).”

An alternative to spectral analysis is periodicity transform (PT) that detects repetitive regions in a given sequence as periodicities by decomposing the sequence onto a set of periodic subspaces which represent a sum of periodicities (Sethares and Staley 1999; Muresan and Parks 2003). To biologists, this simply means pictorial presentation of DNA, where a given nucleotide in combination with neighbouring nucleotides constitutes a separate entity. Many such entitites are compared to check if two or more adjacent entities are same. If so, they are reported as repeats. Historically, this approach has been used for the detection of repeats in short-time periodicity transform (STPT) (Buchner and Janjarasjitt 2003), quaternionic periodicity transform (QPT) (Brodzik 2007) and as exactly periodic subspace decomposition (EPSD) (Gupta et al. 2006; 2007).

Stochastic (probabilistic) methods

In stochastic model, even if the starting point is known, there may be many possibilities the process may transit into, but some paths are more probable than others. Sequence alignment following stochastic models is one of the most straightforward approaches for microsatellite finding, either using a slow and optimizing method like dot plot or dynamic programming, or using a heuristic approach. Other more advanced approaches that have been used for finding microsatellites include ‘sliding window’ approach, dictionary approach using keyword and suffix trees.

Mining tools based on sequence alignments

When aligning to the subject sequences themselves, the algorithms of local alignments do provide powerful tandem repeat finding tools. For alignment of microsatellites, wraparound dynamic programming (Fischetti et al. 1993) is generally used to minimize calculations (Benson 1999; 2005). Dynamic programming in combination with compression algorithms has effectively been used for the identification of approximate tandem repeats in a mining tool called search for tandem approximate repeats (STAR) (Delgrange and Rivals 2004). STAR based on Kolmogorov complexity theory carries a motif specific search (Merkel and Gemmell 2008). Kolmogorov complexity of an object is defined as the number of computational resources required to specify the object. When DNA sequences are read as text symbols, Kolmogorov complexity will be the measure of shortest description of the sequence string. STAR identifies the approximate tandem repeats from the matrix of alignment matches as the regions of ‘compression’, where a motif is picked up as a parameter, and wraparound dynamic programming is implemented to align it to the query sequence. Reneker et al. (2004) effectively overcame the inherent disadvantage of longer processing times using dynamic programming in ACEMS, which is a web server for extraction of repetitive sequences from large query files. At the server end, each of the sequence files are converted into integers, and are effectively stored and accessed through the index file, which direct the information precisely to the desired integer file.

The methods mentioned above are exhaustive but relatively slower. In the current genomic scenario, users are not exactly looking for a complete compilation, but rather a ‘near complete’ dataset. Certain heuristics can be employed to pre-determine what to be aligned, and which can help creating a consensus pattern of repeated arrays (Coward and Dablos 1998). Most popularly, k-tuple match detection is used in combination with wraparound dynamic programming as seen in Adplot (Taneda 2004) and tandem repeats finder (TRF) (Benson 2005). k-tuple may be defined as a sequence of ‘k’ similar items, where it is a positive number. The Adplot is similar to the dot plot except that instead of diagonal bands in dot plot, Adplot uses horizontal bands presented in form of ladder steps. The dots in horizontal direction on a plot are screened and filtered later based on their inclusion into the ‘windows’ designed to coincide with the logical start of the repeat sequence. The latter step is performed using the method followed by tandem repeats finder (TRF) (Benson 2005) involving Bernoulli trials. TRF is capable of finding the repeats with larger patterns. The searching ability of TRF is based on the comparative values of the matching probabilities and indel probabilities. TRF has also become part of many other online or downloadable utilities to be utilized for varied purposes, for example, VNTRfinder (O’Dushlaine and Shields 2006). Tandem Repeats Analysis Program (TRAP) classifies, quantifies and selects candidate microsatellite markers from the output of TRF (Sobreira et al. 2006). ATRhunter (Wexler et al. 2004) is similar in function to TRF, being a two-phased algorithm taking a heuristic approach for detection of approximate tandem repeats of multiple periods. This has been made possible by adopting multiple definitions of tandem repeats and underlying algorithm for counting the repeats. ATRhunter is capable of indexing the position of the approximate repeat, distance between the two arms of an approximate repeat and the quality of the repeat. Another approach for finding approximate repeats is to find all perfect repeats first and then using these as seeds to find imperfect (approximate) repeats, as implemented in Mreps (Kolpakov et al. 2003). Other algorithms based on the same principles are exemplified by Karlin et al. (1988), Benson and Waterman (1994) and Sagot and Myers (1998).

Sokol et al. (2007) implemented the use of ‘edit-distance’ to define the tandem repeats, and designed an algorithm to find the repeats in a genome. Their model assumed that each copy of the repeat is derived from its previous copy through zero or more mutations, and hence each copy being similar to its predecessor as well as successor (Sokol et al. 2007). Krishnan and Tang (2004) explained a similar strategy to find approximate tandem repeats but relied on mismatch ratio instead of fixed mismatch score. Thus, longer interruptions could be tolerated in longer repeats and shorter in shorter repeats. Another heuristic tool called Search for Tandem Repeats IN Genomes (STRING) uses dynamic programming to autoalign the genomic sequences (Parisi et al. 2003). The sequence regions which return a score above a given threshold are further analyzed so that only ‘promising candidates’ among the returned values are read (Parisi et al. 2003).

Mining tools based on sliding window approach

For the extraction of microsatellites, sliding window approach may determine the periodicity of any motif of size ‘n’. This principle has been implemented by a number of investigators, but the most widely known example is that of Exact Tandem Repeats Analyzer (E-TRA) (Karaca et al. 2005), which considers each of the nucleotide to be potentially a part of microsatellite and scans for the motif type as well as the length up to which it extends. Compound microsatellites are identified by measuring the distance between the two microsatellites with distance equaling zero. The same approach was previously described in Sputnik, by Katti et al. (2001) and Bilgen et al. (2004). Imperfect Microsatellite Extractor (IMEx) allows harbouring k mismatches (point mutations) at each of the iterations due to indels or substitutions (Mudunuri and Nagarajaram 2007). Other tools based on the same approach include Poly (Bizzaro and Marx 2003) and SciRoKo (Kofler et al. 2007).

Mining tools based on dictionary approach

In dictionary approach, a microsatellite is considered as a pattern (or word) and the entire genomic sequence is treated as a sentence in the form of a text string containing multiple patterns. This approach calls for construction of special data type structures called keyword- and suffix-trees, allowing fast implementation of string matching operations. A tree has several nodes, and on a given node in a keyword tree the existing label is a concatenation of characters on the path from root till the node. In a keyword tree, each edge is labeled with exactly one character and any two edges out of the same node have distinct characters. Suffix trees which are essentially the keywords tree only, are relatively complicated data structures and offer the benefit of data compression. Suffix trees also allow fast implementation of the string operations. Identification of imperfect repeats is also faster as suffix trees implement locating a substring with certain number of mistakes allowed mush faster. A well known example of implementation of dictionary approach for repeat mining is Repeatmasker (Smit and Green; unpublished), where alignment of the pattern with the target sequence is based on Smith-Waterman method.

TROLL (Castelo et al. 2002) based on Aho-Corasick Algorithm, uses a keyword-tree adapted bibliographic searching and attempts to match the exact keywords. A widely used microsatellite finding tool MISA (Thiel et al. 2003) is also based on the same approach. RepeatFinder (Volfovsky et al. 2001) uses a set of exact repeats in the form of suffix trees for the identification of repeat classes. In the first step all the repeats are identified, and in the second step repeats are clustered into various repeat classes. Other computational tools falling into the same category include RepeatMatch (Delcher et al. 1999) and REPuter (Kurtz and Schleiermacher 1999; Kurtz et al. 2001; Boeva et al. 2006). In REPuter, it is implemented using the search engine REPfind (Kurtz and Schleiermacher 1999), which uses exact repeats as seeds, and approximate repeats are predicted allowing mismatches, insertions and deletions. The results are returned to the user in order of their E-value. REPfind is coupled to REPvis, which allows the visualization of the repeats. The latter versions of REPuter not only exploit suffix trees approach, rather also make use of dot plots and edit distance approaches for finding approximate repeats (Kurtz and Schleiermacher 1999).

Comparative performance of selected tools

We have performed a comparative evaluation of the relative efficiency of E-TRA, IMEx, MISA, Mreps, REPuter, SciRoko, STAR, SRF, TRF and TROLL (Table 2) initially with their default settings, thus defining microsatellites with ten distinct mathematical and biological logics and variable amount of complexity (or simplicity).

Table 2.

Details of the microsatellite mining tools analyzed in the 150 kb long genomic sequence

Tool/Algorithm	Underlying principle	Remarks	Repeats identified
Exact Tandem Repeats Analyzer (E-TRA) (Karaca et al. 2005)	Sliding Window	Suitable for mining of EST-SSRs; facilitates key-word mining	17
Imperfect Microsatellite Extractor (IMEx) (Mudunuri and Nagarajaram 2007)	Sliding Window	Easy-to-use tool for mining of imperfect repeats	146
MISA (Thiel et al. 2003)	Dictionary approach	Mining of simple and compound repeats	31
Mreps (Kolpakov et al. 2003)	k-tuple matching	Mining of perfect and imperfect repeats	158
REPuter (Kurtz and Schleiermacher 1999)	Dictionary approach	General purpose repeat mining tool	460
SciRoko(Kofler et al. 2007)	Sliding Window	Fast and efficient	3,185
Search for Tandem Approximate Repeats (STAR) (Merkel and Gemmell 2008)	Dynamic programming based sequence alignment	Mining of approximate repeats	450
Spectral Repeat Finder (SRF) (Zhou et al. 2009)	Discrete Fourier Transformation	Mining of perfect repeats	>1,000
Tandem Repeat Finder (TRF) (Benson 2005)	K-tuple matching	Mining of perfect and imperfect tandem repeats	36
Tandem Repeat Occurrence Locator (TROLL) (Castelo et al. 2002)	Dictionary approach	Mining of perfect and imperfect tandem repeats	850

Choice of input DNA sequences

We initially selected 21 Mb long chromosome 4 of Arabidopsis thaliana, for the detection of microsatellites using various tools. As a number of tools including SRF and E-TRA have a size limit up to which they can accept the input, smaller sized files were picked up to carryout further analysis. Standardizations were performed with various file sizes and ultimately a DNA sequence of length 150 Kb was found suitable for analysis, interpretation of results and subsequent comparison of performance of the above mentioned tools (Table 2).

Search parameters

Depending upon the tool and its interface, a few parameters are left to the user to select, and thus the user keeps the power to change the definition of a microsatellite to some extent. Initially, default parameters were selected for each of the ten tools. This helped us to gain basic understanding of the working of the tools, and also worked as a reference set of the microsatellites. Later, the parameters were adjusted using various criteria to study the impact on the amount and quality of the output sets.

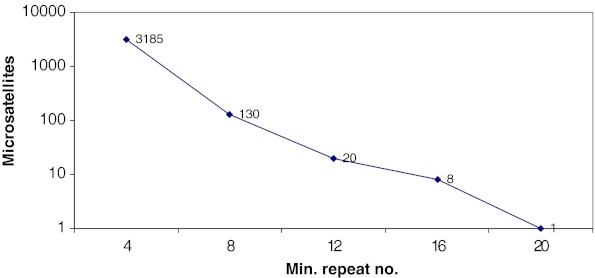
In general, a steep fall is seen when the minimum repeat number was increased in the search criteria, which corresponded to the general behaviour of microsatellite repeats in the genome that the frequency of microsatellites falls with an increase in microsatellite motif length. For example, in SciRoko, when the minimum repeat number is changed from 4 to any of its higher multiple, the number of microsatellites detected showed a characteristic fall (Fig. 1). However, a gradual negative correlation was seen when SciRoKo was used to scan the same file with adjusted parameters of minimum repeat length (MR)/minimum total length (MTL) and on raising the required alignment score, the number of detections expectedly came drastically down (Table 3).

Fig. 1.

Number of microsatellites detected using different length parameters in SciRoko

Table 3.

Effect of parameter adjustments on the number of complex microsatellite detections under mismatch (fixed penalty) mode in SciRoko

Required alignment score	Mismatch penalty	SSR seed length	Minimum repeat number	Mismatch at once	Microsatellites detected
15	5	8	3	3	39
25	5	8	3	3	11
15	3	8	3	3	43
15	5	12	3	3	38
15	5	8	5	3	27
15	5	8	3	5	39
20	8	10	5	5	20

Output

When the search tools were classified based on their underlying principles, all the tools based on sequence alignment returned relatively lesser number of repeats under similar search criteria. Among all the tools picked up for analysis, TRF, STAR and mreps belonged to this class. While, TRF detected only 36 repeats, mreps could identify 158 (Table 2).

In the second category of tools based on sliding window approach, there was a large difference in the number of repeats identified. SciRoKo as described above identified maximum number of repeats. IMEx identified 35 perfect and 111 imperfect repeats, while E-TRA identified only 17 perfect repeats.

REPuter created a highly attractive graphical output generated by REPvis, which also provides position of occurrence of these repeats. However, a disadvantage of using REPuter is that even a sequence of 150,000 bp was also too large for the software to scan through. In comparison to each of these, MISA returned only 67 microsatellite repeats. The benefit of using MISA over other tools is that it gives a proper summary and statistics of the output alongwith the position of repeats on the genomic sequence.

SRF is similar to TROLL in terms of output, that is, it highlights the repeat region in the sequence. However, no statistics are provided and output is generated in a considerably longer time period.

Desired characteristics in a microsatellite search tool

Whichever the approach used, a microsatellite search tool is expected to find the microsatellite motif size, motif sequence, repeat number and the position of the microsatellite in the given sequence. A good tool is expected to handle (i) directionality and repeatability, relative to the underlying sequence (forward/reverse) as well as to each other (complementarity/reverse complementarity), and (ii) identification of imperfect repeats as a special case in tandem repeats. The imperfect microsatellite repeats may be considered as extensions in the definitions of ETRs incorporating certain editing operations (Volfovsky et al. 2001) or sequences with lesser degree of periodicity and spaced from another island showing periodic sequence (Fischetti et al. 1993). As most of the repeats are rendered imperfect by frequent point mutations, the contemporary research is oriented towards increasing the efficiency of detection of such repeats. Besides that, a good software or tool is expected to provide efficiency, flexibility, visualization and compositionality in identification and analysis of repeats (Kurtz et al. 2001). Recently, handling of redundancy has also been recognized as a useful property in a good microsatellite finding tool (Reneker et al. 2004). Further, ease in use, particularly for a non-expert makes the tool more popular, even if it compromises with any of other desired characteristics. A tool must have a graphical user interface (GUI) to gain popularity among non experts at least. Similarly, an average user is only concerned with the amount of the output generated, the type of repeats searched for and the ease with which these could be visualized (Table 4).

Table 4.

User-friendliness of various microsatellite mining tools in terms of the output generated

Tool	Statistics	Graphic visualization	Sequence display
E-TRA	+	−	+
IMEx	+	−	−
MISA	+	−	−
Mreps	−	−	+
REPuter	−	+	−
SciRoKo	+	−	−
SSRIT	+	−	+
STAR	+	−	−
SRF	−	−	+
TRF	+	−	−
TROLL	−	−	+

The choice of microsatellite tool for a user is often dictated by ornamental features and not exactly by the underlying algorithm. As the microsatellites are ubiquitous in the eukaryotic genomes, a ‘near complete’ compilation of microsatellites pleases a user equally well, as a complete list would have. Further, because each of the tools is based on a different logic and different definition (biological as well as mathematical) of microsatellites, the set of microsatellites reported are always different by different tools. The two of the most popular microsatellite finding tools differ in this regards, i.e. while TRF can identify perfect, imperfect and complex type repeats, MISA can scan perfect, interrupted and compound repeats. Thus, a programmer’s perspective of putting up a mathematical definition for microsatellites differs a great deal and may reflect into the actual usage and output of the tool.

When in addition to microsatellites, other types of repeats are also targeted, tools like repeatmasker, repeatfinder, REPuter, ACEMS, etc. should be adopted. While it is easy to use all of these tools on the world wide web, their use on a stand-alone computer might require the UNIX platform. This may restrict their use as a popular tool. When different type of microsatellites are required to be screened, any heuristic tool using dynamic programming may be used online or offline, depending upon how much time is consumed by these tools. As discussed above, the time lapse for such tools increases linearly with the size of input files. When EST files are to be executed, a tool like E-TRA becomes more useful. Some of the genomic sequence scanning tools like MISA are linked to primer designing utilities also. MISA, SciRoKo, msatminer and STRING are additionally powered to provide statistical analysis/graphical representation of the output also.

Microsatellite discovery in the context of next generation sequencing (NGS)

Next generation sequencing technologies like 454 Life Sciences (Roche GS-FLX genome), Solexa (Illumina), SoLiD (Applied Biosystems), Helicos, Pacific Biosciecnes or Nanopore Technology can generate enormous genomic or transcriptomic sequence data in no time. These technologies have proved valuable for the discovery, validation and assessment of genetic markers including microsatellites in populations also (Davey et al. 2011). Moreover, the microsatellite isolation via NGS technologies is rapid and inexpensive as well (Bai et al. 2010; Guichoux et al. 2011). In the last 3 years, next generation sequencing data has increasingly been used for development of microsatellite markers by integrating the microsatellite finding tools with Primer3 software. Microsatellite finding tools that have popularly been applied on next generation sequencing data include msatfinder (Santana et al. 2009, Bai et al. 2010), E-TRA (Perry and Rowe 2010), msatcommander (Faircloth 2008, Magain et al. 2010) and MISA (Garg et al. 2011). Mikheyev et al. (2010) used a customized Python script for the identification of microsatellites in RNA seq data. Moreover, this enables mining of microsatellites with equal ease in non-model species also (Davey et al. 2011). Microsatellite mining tools like QDD developed in recent past have specifically been designed keeping the technological requirements of NGS data Choosing among the sequencing technologies and NGS tool to maximize information content however depends primarily on the research interests of the scientist, as described elsewhere as well. Using assembled next-generation sequencing derived sequences offers more possibilities for primer design, as contigs tend to be longer than the individual reads.

Microsatellite search approaches and tools: user’s perspective

From the point of view of an analyst, an important consideration is to choose between an exhaustive search for low complexity DNA microsatellite sequence or heuristics based faster search. Most of the present day microsatellite scanning tools are based on heuristic approaches. The statistical approaches are all the more important for a logical identification of imperfect repeats. For example, in TandemSwan (Boeva et al. 2006), adjacent windows are compared to each other, which might contribute to matrices of varying sizes.

A good microsatellite search tool should produce a dataset of non redundant microsatellite repeats. This demands the use of an analysis filter to be embedded within the programme, and the entire exercise is vital for accurate counts of microsatellite repeats. In the absence of such a filter, the microsatellite frequency may be over-represented in the genomes. Still, motif-identification can be erroneous in case of complex and interrupted repeats, and may contribute to the redundancy in the output. Such problems are also associated with statistical analysis of the repeats. For example, for a repeat sequence like (CA)n(TA)m, MISA reports the number of counts as 2, while SciRoko counts it as one. TRF further reports up to three possible motifs per locus, and that poses actual difficulties in computing total repeat counts. Conveniently, in many tools like MISA, SciRoko, Sputnik, etc., permutations of a motif and their complementary motif sequences are grouped together. While such a grouping for SciRoko and Sputnik can be called as natural (Reneker et al. 2004), as it groups reverse complementary sequences together, the grouping in the output of MISA may be called as artificial due to the grouping of motifs which are considered complementary due to the readability from left to right on paper. Such results should be dealt with caution especially when strand specificities of microsatellite motifs are under consideration (Fujimori et al. 2003).

Differences in the count of microsatellites generated by different mining tools are the outcome of different computational approaches. However, the discrepancies may also emerge out of their use, i.e., the definition adopted for identification of microsatellites, and the stringency followed. In the present study, a vast variation was seen in terms of the number of repeats identified, which in turn depended on the parameters selected for their identification. The output of TRF, in general, was a unique dataset, without or little overlapping with the output of other tools. On the contrary, the output of IMEx overlapped with the output of many other tools like Mreps, MISA, etc. Merkel and Gemmell (2008) suggested that parameter settings can also cause a nonproportional change in relative frequencies of different type of repeats, as different motif size classes harbour imperfections to different degrees.

We, however, observed that by adjustment of parameters, one can obtain a consensus dataset representing most of the repeats present in the given genomic sequence. Mining of imperfect repeats was found more difficult to be reached to any consensus. Adjustment of minimum repeats number is an important criterion for the identification of repeats due to inherent length properties of microsatellites and has little to do with the usage of the tool.

Microsatellite mining is a challenging field of computational biology research. The mining efficiency may determine the efficiency of various models and hypothesis derived from these datasets. Over the last 15 years, there have been global attempts in designing the tools for mining of microsatellites using different approaches and definitions. However, neither any of the approach could be found complete, nor could a consensus be reached among the biologists for these issues. The use of a specific tool also gets limited by other factors, for example, the input file format and input sequence information may change the choice of a tool. While a particular tool might be suitable for a kind of input file with a standard output, it might not hold true when the type of input file would change, and output would be desired in a different format. The choice of tool may also have an effect on concluding the genome cover made by microsatellites. For example, International Human Genome Sequencing Consortium concluded that microsatellites represent 1.5 % of the human genome using TRF with modified parameters (International Human Genome Sequencing Consortium 2001). When the same genome was scanned with the same tool by default parameters, this proportion was raised to 3.9 % (International Human Genome Sequencing Consortium 2001). Further, Sharma et al. (2007) used MISA to obtain a value ~1 % in the same genome. Thus, a good practice would be to use more than one tool and find the common set of microsatellites detected by the two. The advantage of such an approach would be more realistic for mining of imperfect repeats, when depending upon the tool and definition adopted, microsatellite screened might have different formations. TReaDS (Tandem repeats discovery service) available at http://bioalgo.iit.cnr.it/treads is a useful tool that allows microsatellite mining using TRF, mreps and ATRhunter, compares their results and finds the common microsatellite repeats among the three tools used. Nevertheless, any individual tool is capable of providing meaningful information on global distribution of microsatellites in a given genome, and hence can be used for most of the genomic or evolutionary studies.

Considering the various discrepancies and problems generated during mining of microsatellites, a future line of research should focus on the standardization of definitions, tools, and algorithms that can integrate the mining of perfect with imperfect repeats and can simulate the evolutionary models on the resulting dataset. We recommend that microsatellite detection be based on both its sequence and the evolutionary model that fits in. This would guide to integrate interrupted repeats into a single repeat or not, especially in case of complex repeats.