Skip to main content
PMC home page
Journal of Food Science and Technology logoLink to Journal of Food Science and Technology
. 2011 Feb 6;49(5):547–555. doi: 10.1007/s13197-011-0298-z

Optimization of osmotic dehydration conditions of peach slices in sucrose solution using response surface methodology

Baljeet Singh Yadav 2,✉, Ritika B Yadav 2, Monika Jatain 1
PMCID: PMC3550838  PMID: 24082265

Abstract

Osmotic dehydration (OD) conditions of peach slices were optimized using response surface methodology (RSM) with respect to sucrose concentration (50–70°B), immersion time (2–4 h) and process temperature (35–55 °C) for maximum water loss (WL), minimum solute gain (SG) and maximum rehydration ratio (RR) as response variables. A central composite rotatable design (CCRD) was used as experimental design. The models developed for all responses were significant. All model terms were significant in WL except the quadratic levels of sucrose concentration and temperature whereas in SG, linear terms of time and linear and quadratic terms of temperature were significant. All the terms except linear term of time and interaction term of time and sucrose concentration, were significant in RR. The optimized conditions were sucrose concentration = 69.9°B, time = 3.97 h and temperature = 37.63 °C in order to obtain WL of 28.42 (g/100 g of fresh weight), SG of 8.39 (g/100 g of fresh weight) and RR of 3.38.

Keywords: Osmotic dehydration, Peach, Optimization, Response surface methodology, Sucrose solution

Peach (Prunus persica) is believed to be the native of China. It is cultivated throughout warm temperate and subtropical regions of the world. The fruit has yellow and white flesh, a delicate aroma and velvety skin in some cultivars. Peach is considered as sodium free, fat free, cholesterol free and rich source of vitamin A and C (Sharma 2010). The processing of peach can maintain its freshness and increase its shelf-life leading to increased commercialization of peach. Among the various methods of processing intended for extended shelf life and freshness, freeze- drying produces highest quality products, but it is expensive method of preservation. Therefore, to save the perishable products like peach and maintain their freshness, osmotic dehydration is considered as one of the new, simple and inexpensive pretreatment method with low capital investment. Osmotic dehydration, due to its energy and quality related advantages, is gaining popularity as a complimentary processing step in the chain of integrated food processing. However, since osmotic dehydration is a slow process, various methods to increase the rate of mass transfer, such as application of high hydrostatic pressure, high electrical field pulses, ultrasound, vacuum and centrifugal force can also be used in osmotic dehydration systems (Rastogi et al. 2002).

Osmotic dehydration (OD) is a method for the partial dehydration of water-rich foods, such as fruits and vegetables, by immersing them in concentrated solutions of sugar or salt (Raoult-wack 2002; Spiazzi and Mascheroni 1997). OD processes are normally designed with the aim of maximizing water removal meanwhile restraining solids uptake. The parameters which represent adequately the OD process are the water loss (WL) and solute gain (SG). The amount of water which diffuses from the fruit to the solution is the WL while the SG indicates the solids which diffuse from the solution to the fruit less the solids of the fruit which are migrated to the solution. The third stream is connected with the elution of low molecular weight substances like saccharides, organic acids, vitamins, minerals and salts. The quantity and rate of water removal depend on several variables and processing parameters like the weight loss, immersion time, agitation of solution, temperature, solution/food ratio and specific surface area of the food (Singh et al. 2008; Ozdemir et al. 2008; EL-aouar et al. 2006; Lenart and Flink 1984). Osmotic agents that are used include sugar, glucose, corn syrup and sodium chloride.

Osmotic dehydration of fruits has recently received a lot of attention as a potential pre-treatment to conventional drying and freezing for improving the quality of fruit products and reducing energy consumption (Raoult-wack 2002; Nieto et al. 1998). This pre-treatment minimizes the thermal degradation of color and flavor, prevents enzymatic browning and thus limits the use of SO2 (Lenart and Grodeka 1989). Additionally, it has been found to improve nutrient retention during the subsequent convective drying process (Islam and Flink 1982).

Statistical designs are powerful tools used to study the main as well as the interactive effects of different process variables on a process. Among them, response surface methodology (RSM) is a collection of certain statistical techniques for designing experiments, building models, evaluating the effects of factors and searching for optimal conditions of desirable responses. RSM is an effective tool for optimization of a number of food processes including OD (Corzo and Gomez 2004). The main advantage of RSM is the reduced number of experimental runs that provide sufficient information for statistically valid results.

Osmotic dehydration process has been investigated for various fruits and vegetables like papaya (Kaleemullah et al. 2002), mushroom (Kar and Gupta 2003), beetroot (Manivannan and Rajasimman 2008), carrot (Sodhi et al. 2006) onion (Sutar and Gupta 2007) pineapple (Parjoko et al. 1996; Kumar and Devi 2010) apple (Conway et al. 1983; Janowicz and Lenart 2010), banana (Pokharkar and Prasad 1998). The process variables for the osmotic dehydration of pomegranate arils were successfully optimized using response surface methodology (central composite rotatable design) by Mundada et al. (2010). In the optimization of the osmotic dehydration process of the carrot cubes in mixtures of sucrose and sodium chloride by response surface methodology, using face-centered central composite design (CCF), the optimum osmotic dehydration process conditions for maximum water loss and minimum solute gain were: 50°Brix + 15% w/v sodium chloride solution, 54.8 °C solution temperature and 120 min process time (Singh et al. 2010). Shedame and Patil (2009) studied the effect of osmotic dehydration on the drying characteristics of grapes. Response surface methodology was also used to investigate the effect of sugar concentration (50–70° Brix), solution temperature (30–60 °C), solution to fruit ratio (4:1–8:1) and immersion time (60–180 min) on the water loss, solute gain, rehydration ratio, vitamin-C loss, colour change and sensory overall acceptability of Indian gooseberry (aonla) slices (Alam et al. 2010). Rastogi and Raghavarao (2003) studied the osmotic dehydration kinetics of pineapple cubes over a range of concentration (40–70°B) and temperature (30–50 °C) of osmotic solution. Although there have been very few studies on the osmotic dehydration of peach also (Sahari et al. 2006; Giangiecome et al. 1987) but the studies on the optimization of process conditions for osmotic dehydration of peach are scanty. Therefore, the purpose of the present study was to investigate the effect of process variables of sucrose concentration, process duration and process temperature on WL, SG and RR during OD of peach slices and to establish optimum OD conditions.

Materials and methods

Sample preparation

Fresh, fully ripened peaches (Prunus perica) (5 kg) of Red heaven cultivar were purchased from a local market. The initial moisture content of the fresh peach was 88.5 ± 0.90.0%. The fruits were washed, peeled, destoned and sliced into pieces of 20 × 20 × 5 mm before immersing them in different osmotic solutions.

Osmotic solutions preparation

Food grade sucrose was used as osmotic dehydrating agent and osmotic solutions of 50, 60 and 70°B were prepared.

Osmotic dehydration process

The prepared fruit slices were immersed in desired osmotic solutions at 35, 45 and 55 °C for 2, 3 and 4 h. For each experiment, 50 g of peach slices were put in to 500 ml beakers containing 250 ml of osmotic solutions of different concentrations preset at the desired temperature in a precision hot water bath (±1 °C). The sample/solution ratio was kept as 1:5 (Kar and Gupta 2003). After the specified immersion time, the osmotically dehydrated samples were quickly rinsed, gently blotted dry with absorbing paper in order to remove adhering osmotic solution and later weighed and analyzed. Triplicate samples were used for each experiment. The water content was determined by drying the samples in a hot air oven at 65 °C and 1.6 m/sec air velocity. The same hot air drying conditions were used for dehydrating the osmotically dehydrated samples used for rehydration studies.

Water loss, solute gain and rehydration ratio

The equations given by Ozen et al. (2002) were used to calculate the water loss and solid gain during the osmotic dehydration process.

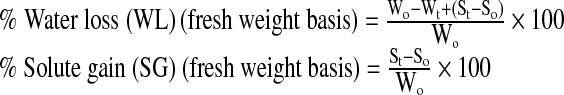graphic file with name M1.gif

Where, Wo is the initial weight (g) of the peach slices, Wt is the weight (g) of the peach slices after osmotic dehydration for time t in hours, So is the initial weight of solids (dry matter) in the peach slices (g), and St is the weight of solids (dry matter) of peach slices after osmotic dehydration for time t(h).

Rehydration ratio (RR), which is used to measure water absorption by osmotically dehydrated and dried product was determined by soaking 15 g of each sample in a sufficient volume of water (approximately 30 times of weight of dried peaches) at room temperature for 12 h. The slices were weighed after removing excess water with the help of absorbent paper.

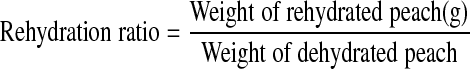graphic file with name M2.gif

Theoretical considerations

Factors affecting the osmotic dehydration of peach slices were investigated with a face centered central composite design (FCC) as used by Singh et al. (2008), the only difference being the consideration of three variables with three levels in the present study. The information provided by the FCC was used in the experimental design chosen to optimize the osmotic dehydration of sliced peaches. Three independent variables used were sucrose concentration (°B), process temperature (°C) and time (h). The responses measured were water loss, solid gain and rehydration ratio. The low and high levels of constraints in the actual (uncoded) form were taken as 50–70°B for sucrose concentration, 35–55 °C for temperature and 2–4 h for immersion time. Three different levels for each experiment in coded form were –1, 0 and +1. The levels of input variables in coded and uncoded form are given in Table 1. Further, it was assumed that three functions exist between each response and the input factors. A second order polynomial equation was fitted to the experimental data of each independent variable as given below.

graphic file with name M3.gif

where Yk = response variable (Y1 = water loss; Y2 = solute gain; Y3 = rehydration ratio) and xi represent the coded independent variables (i = 1,2,3 = A, B, C respectively, where, A = solute concentration; B = process duration; C = process temperature), Bk0 is the value of the fitted response at the center point of the design, Bki, Bkii and Bkij are the linear, quadratic and interaction regression coefficients, respectively.

Table 1.

Coded and uncoded values of variables and their levels

Independent variables Coded levels −1 0 +1
Sucrose concentration (°B) A 50 60 70
Time (h) B 2 3 4
Temperature(°C) C 35 45 55
Open in a new tab

Experimental design

The experimental design along with values of various responses is given in Table 2. A face centered central composite design (FCC) with three independent variables at three levels was used to study the response pattern and optimum combinations of variables. RSM was applied to the experimental data using commercial statistical package (Design expert. 7.1.6 version, Statease USA). Twenty runs were defined using the above software.

Table 2.

Outline of the experimental design (FCC) matrix and observed values of response variables

Standards Run Sucrose Conc.(°B) Time (h) Temp. (°C) WLa SLa RR
7 1 −1 +1 +1 24.78 9.33 3.34
9 2 −1 0 0 19.38 8.36 3.28
16 3 0 0 0 23.83 9.73 3.52
20 4 0 0 0 23.83 9.73 3.54
14 5 0 0 +1 28.75 8.49 3.33
5 6 −1 −1 +1 24.46 9.11 3.49
12 7 0 +1 0 28.94 9.26 3.41
1 8 −1 −1 −1 17.22 8.09 2.84
13 9 0 0 −1 18.95 6.84 2.71
11 10 0 −1 0 20.19 8.16 3.47
10 11 +1 0 0 27.33 8.89 3.55
8 12 +1 +1 +1 31.34 10.65 3.54
4 13 +1 +1 −1 28.42 8.36 3.4
17 14 0 0 0 23.83 9.97 3.58
15 15 0 0 0 23.92 9.12 3.47
18 16 0 0 0 23.22 9.84 3.53
19 17 0 0 0 23.87 9.85 3.56
3 18 −1 +1 −1 20.21 8.66 2.92
2 19 +1 −1 −1 20.35 7.83 3.21
6 20 +1 −1 +1 25.13 9.73 3.54
Open in a new tab

ag/100 g of fresh weight

The statistical significance of the terms in the regression equation was examined by analysis of variance (ANOVA). Three dimensional response models were generated. The response surface plots were generated for different variables, while holding the values of third variable as constant (at the central value). Such response surface plots give accurate geometrical representation and provide useful information about the behavioral system with experimental design. The models obtained were used to interpret the effect of various variables on the responses i.e. WL, SG and RR. The optimization of the osmotic dehydration process was aimed at finding the levels of three independent factors (sucrose concentration, time and temperature) which would give maximum possible WL, minimum SG and maximum RR.

Results and discussion

ANOVA was used to assess the effect of variables on the responses. The results of the second-order response surface model in the form of ANOVA are given in Table 3. The second order polynomial equation was regressed for all the responses at different processing conditions.

Table 3.

Analysis of variance for response variable

Source df Water loss Solute gain Rehydration ratio
SS p-value SS p-value SS p-value
Modela 9 267.36 <0.0001 13.29 0.0043 1.22 <0.0001
A 1 74.7 <0.0001 0.38 0.2366 0.18 <0.0001
B 1 76.42 <0.0001 1.22 0.0468 2.67 0.9148
C 1 94.85 <0.0001 5.49 0.0007 0.49 <0.0001
AB 1 15.04 <0.0001 0.054 0.6429 8.45 0.0795
AC 1 2.11 0.0057 0.78 0.1003 0.045 0.0011
BC 1 2.57 0.0032 2.00 0.9775 0.022 0.0103
A2 1 0.24 0.2689 0.77 0.1033 0.023 0.0089
B2 1 1.29 0.0209 0.58 0.1501 0.014 0.0302
C2 1 0.032 0.677 4.68 0.0013 0.47 <0.0001
Residual 10 1.73 2.38 0.022
Lack of fitb 5 1.38 0.0764 1.93 0.0688 0.015 0.22
Pure error 5 0.34 5 0.45 5 7.03
Total 19 269.09 19 15.67 19 1.24
Open in a new tab

A: Sucrose concentration; B: Process time; C: Process temperature

aSignificant

bNon significant

The response surface plots were generated to visualize the combined effect of two variables on a particular response. The sign and magnitude of the coefficients as given in Table 4 indicated the effect of variables on the responses. Negative sign of a coefficient at linear level indicated decrease in response value with an increase in level of the variable, whereas, at interactive level, the level of one variable increased while that of other decreased to give similar response values.

Table 4.

Regression coefficients of different responses

Factor Coefficients
WL SG RR
Intercept 23.75 9.68 3.53
β1 2.34**** 0.17 0.11****
β2 2.37**** 0.30* 1.398E-003
β3 2.64**** 0.63*** 0.19****
β12 1.37**** 0.08 0.03
β13 −0.51*** 0.31 −0.08**
β23 −0.57*** 5.000E-003 −0.05**
β11 −0.13 −0.23 −0.04**
β22 0.30* −0.20 −0.03*
β33 0.05 −0.57** −0.18****
Adeq Precision 49.98 9.20 27.15
R2 0.99 0.85 0.98
Adjusted R2 0.98 0.71 0.96
Predicted R2 0.96 0.61 0.89
PRESS 11.12 15.34 0.12
Open in a new tab

A: Sucrose concentration; B: Process time; C: Process temperature

****p < 0.0001, ***p < 0.005, **p < 0.01, *p < 0.05

Water loss (WL)

As shown in Table 2, the maximum WL in osmotically dehydrated fruit slices observed was 31.3%, while the minimum was 17.2%. Table 3 indicated that model was significant and the lack of fit was non-significant showing the significance of model at both 1 and 5% level of significance. The coefficient of determination (R2) was 0.99 and the predicted R2 of 0.96 was in reasonable agreement with adjusted R2 of 0.98 in case of WL (Table 4). All the model terms were significant in WL except the quadratic levels of sugar concentration and temperature. As shown in Table 4, all the process variables at linear level and solute concentration and process time at interaction level had positive effect on WL (p < 0.0001). The sugar concentration-temperature and time-temperature at interaction level affected the WL negatively at 0.5% level of significance. At quadratic level, only process time affected the WL at 5% level of significance.

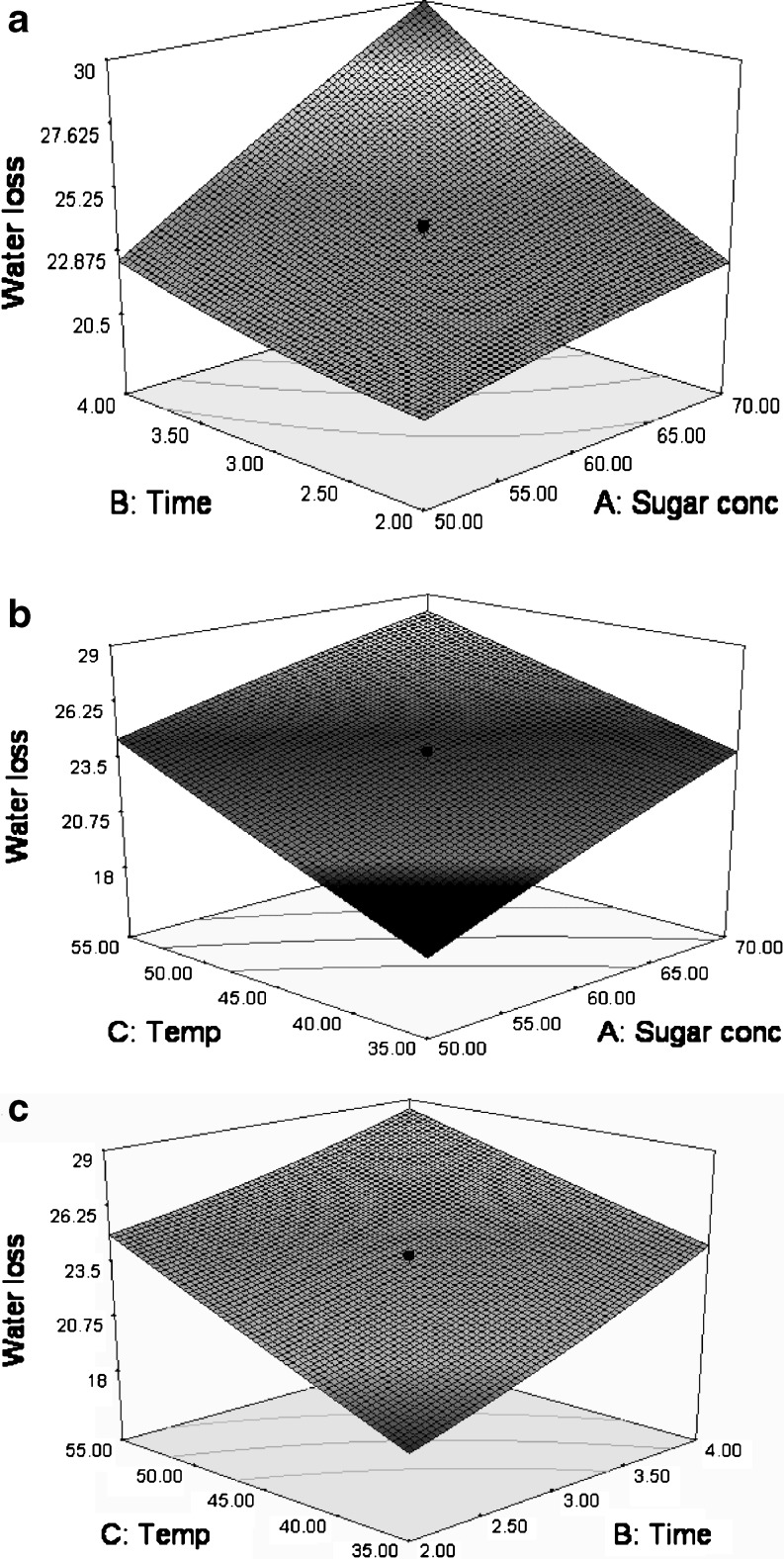
The response surface plots for WL scores in relation to time-sucrose concentration; temperature-sucrose concentration and temperature-time have been shown in Fig. 1. As the immersion time increased, there was a continuous increase in the WL at a specific sucrose concentration and with increase in sucrose concentration from 50 to 70°B at constant time, the water loss again increased (Fig. 1a). These results are in agreement with Park et al. (2002) who also observed an increase in water loss with increase in concentration of the osmotic agent. As the sucrose concentration was increased, water loss was more pronounced with increase in time showing the positive interaction effect of process time and sucrose concentration on WL. Increased concentration showed it pronounced effect on WL taking more time as further increase of sugar concentration reduces the water loss that might have lead to the sugar gain by the fruits which was not desirable (Rahman and Lamb 1990). This is attributed to the diffusion of water from dilute medium to the concentrated hypertonic solution developed in the fruit. As the temperature was increased at a specific sucrose concentration, there was a continuous increase in water loss. However, this increase was less pronounced at 70° B as compared to 50°B (Fig. 1b). The interactive effect of temperature and sucrose concentration showed a decreasing effect on WL after a certain level. However, the interactive effect of time and temperature showed a decreasing effect on WL after a certain level (Fig. 1c). These results indicate an increase in WL with increase in osmotic solution temperature for specific immersion time. However, this increase was less pronounced when immersion time was increased to 4 h (Fig. 1c). The less pronounced increase in WL at high temperature maintained for higher time can be explained by the fact that further increase in temperature affects the semi-permeability of the cell walls and reduces the rate of osmosis. This may be due to reduction in viscosity of hypertonic solution and increase in diffusion coefficient of water increased at high temperature (Shahabuddin et al. 1990; Yao and Le Maguer 1996; Park et al. 2002).When immersion time was increased at a constant temperature, there was again an increase in water loss. Kim (1990) also reported an increase in the WL with increase in temperature during OD of apples as the rate of diffusion of water increased through semi permeable membrane with increase in temperature.

Fig. 1.

Fig. 1

Open in a new tab

Response surface and contour plots showing effect of processing variables on the WL a time v/s sucrose concentration (temperature = 45 °C); b temperature v/s sucrose concentration (time = 3 h) and c temperature v/s time (sucrose concentration = 60°B)

The present results are also in agreement with those of Singh et al. (2007) who observed increase in WL with increase in osmotic solution temperature and process time but very slight increase with increase in osmotic solution concentration. Sahari et al. (2006) also observed higher water removal using more concentrated solution of sucrose (50 and 60%) during osmotic dehydration of peach slices The concentration gradient between the intracellular fluid and solute solution caused the osmotic pressure, which lead to diffusion of water and solid molecules through semi-permeable membrane to achieve osmotic equilibrium. So the increase in solute concentration led to, increase in SG and WL.

Solute gain (SG)

It is evident from Table 3, the model was significant and lack of fit was non significant for SG, which again confirms that the model was significant at 1 and 5% levels of significance. The regression coefficients of SG with different terms of process variables are given in Table 4. In linear terms, time and temperature were found to be significant model terms with an increasing effect on SG (p < 0.05 and <0.005 respectively) whereas, sucrose concentration was non-significant model term.

However, effect of all the interactive terms on solute gain was non-significantly positive or negligible. These results are in agreement with findings of Singh et al. (2007) obtained during the optimization of the osmotic dehydration process for carrots. The quadratic effect of all the process variables was decreasing on SG with only temperature showing significant effect at 1% level of significance. The coefficient of determination (R2) was 0.85 showing 85% variability in the data. The maximum SG attained during OD was 10.65 whereas the minimum was 6.84 (Table 2).

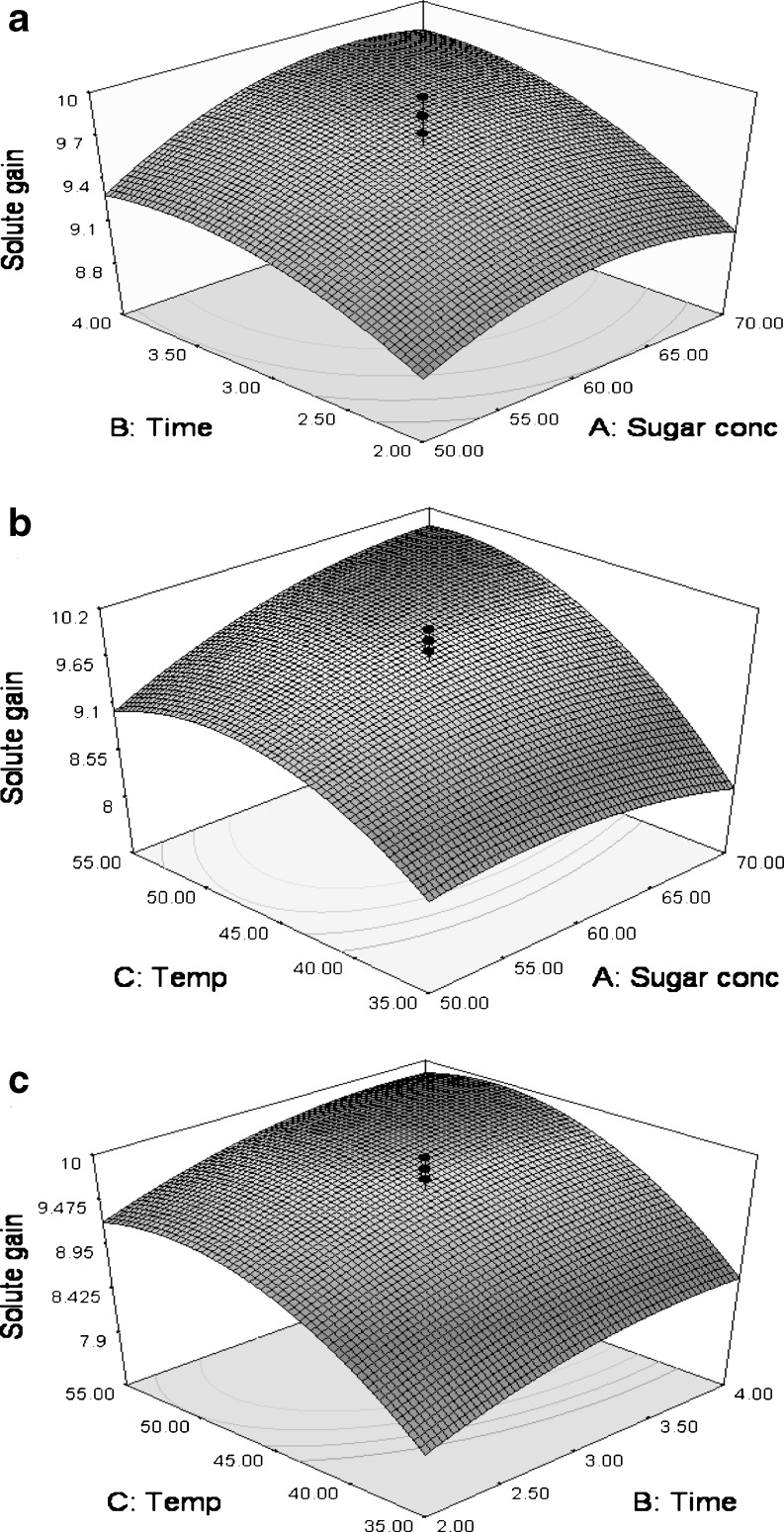
The SG increased with increase in immersion temperature and immersion time up to a level at a specific sucrose concentration and after it decreased. However, when the sucrose concentration increased from 50–70°B, the increase in SG was more pronounced with increase in time as compared to increase in temperature (Fig. 2a and b). This positive interaction between process time and osmotic agent concentration was also reported by Manivannan and Rajasimman (2008) during the osmotic dehydration studies on beetroot in salt solution. When temperature was increased from 35–55 °C, the increase in SG was more pronounced after 4 h as compared to 2 h (Fig. 2c). The SG showed an initial increasing trend with increase in sucrose concentration and then declined when sucrose concentration reached to maximum level. The decrease in SG with increase osmotic solution concentration might be attributed to high viscosity of more concentrated osmotic solution imparting resistance to solute penetration at solution and peach slice interface. These results are in agreement with those of Singh et al. (2007), who also observed an increase in SG with increase in osmotic solution temperature and process time, and a decrease in SG with increase in osmotic solution concentration.

Fig. 2.

Fig. 2

Open in a new tab

Response surface and contour plots showing effect of processing variables on the SG a time v/s sucrose concentration (temperature = 45 °C); b temperature v/s sucrose concentration (time = 3 h) and c temperature v/s time (sucrose concentration = 60°B)

Rehydration ratio (RR)

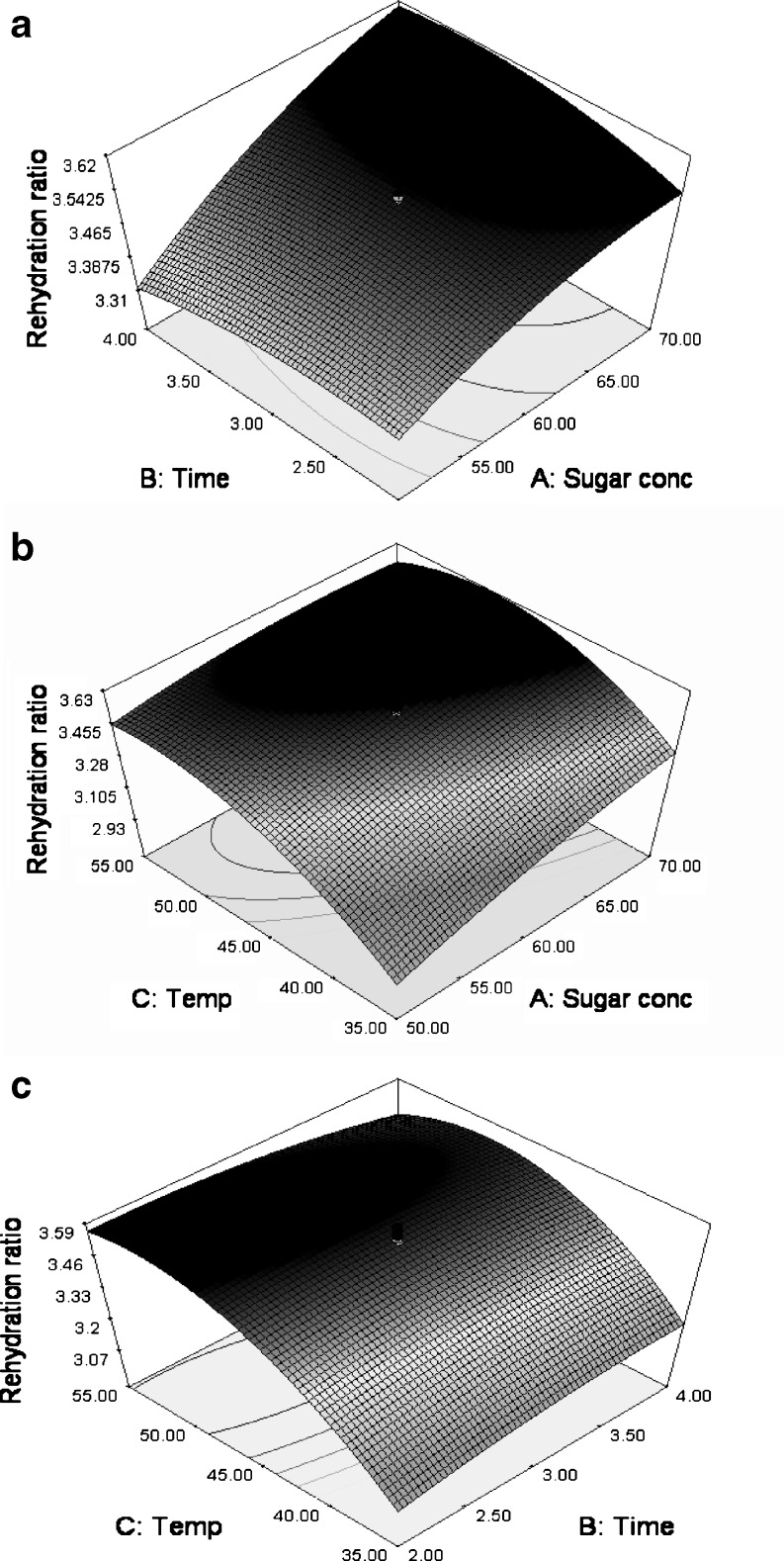
RR is used to measure water absorption by dehydrated product. Table 3 shows that model was significant and lack of fit was non significant for RR. The regression coefficients of RR with different terms of process variables are given in Table 4. In the linear terms, sucrose concentration and temperature were found to be significant model terms (p < 0.0001) having increasing effect on RR of the osmotically dehydrated product where as time was non significant model term. However, in the interactive terms, all terms were found significant (p < 0.01) with decreasing effect on RR except sucrose concentration-time interaction term which had positive but non-significant effect. The quadratic level of all the three process variables had significant decreasing effect on RR at 1, 5 and 0.01% levels of significance for sucrose concentration, time and temperature respectively. Variability in the data was observed to be 98% (R2 = 0.98).

The maximum RR attained during OD was 3.58 whereas minimum was 2.71 (Table 2). RR increased with increase in sucrose concentration at a constant time. However, the increase in RR with increase in sugar concentration was more pronounced with increase in time (Fig. 3a). The increase in temperature resulted in increase in RR at a particular sucrose concentration up to 45 °C, after which a decline in RR was observed (Fig. 3b). However, this increasing effect of temperature on RR was less pronounced with increase in sucrose concentration. Similarly, the increase in temperature had an increasing effect on RR at a constant time with maximum increase at about 45 °C. However, when immersion time was increased from 2 to 4 h, the RR was less pronounced with increase in temperature at 4 h (Fig. 3c).

Fig. 3.

Fig. 3

Open in a new tab

Response surface and contour plots showing effect of processing variables on the RR a time v/s sucrose concentration (temperature = 45 °C); b temperature v/s sucrose concentration (time = 3 h) and c temperature v/s time (sucrose concentration = 60°B)

Optimization

Responses were numerically optimized in combination with design expert software. In order to optimize the process of osmotic dehydration the maximization of WL, RR and minimization of SG were the considerations. Two solutions were obtained by RSM and depending upon the desirability of the process variables with observed and predicted values, one of the two solutions was selected for optimization of the process variables. The constraint criteria for optimization, solution along with predicted and actual values are shown in Table 5. Using the given criteria, process conditions were optimized at sucrose concentration of 69.9°B, time 3.97 h and temperature 37.63 °C in order to obtain WL of 28.42%, SG of 8.39% and RR of 3.38. Experiments were conducted based upon solution obtained. The predicted and actual values for all responses were not statistically different at 5% level of significance as verified from t-test. The results showed that coefficient of variance (CV) of the responses were less than 5.6%, which confirmed that the predicted and actual values of all the responses were in close agreement with each other. Therefore, optimum conditions obtained in the model may be recommended for osmotic dehydration of peaches.

Table 5.

Constraints, criteria for optimization, solution along with predicted and actual response values

Constraints Goal Lower limit Upper limit Importance Solution ARV CV%
Sucrose concentration (°B) In range 50 70 3 69.9 – –
Time (h) In range 2 4 3 3.97 – –
Temperature (°C) In range 35 55 3 37.63 – –
WL Maximize 17.22 31.34 3 28.42 28.00 5.60
SG Minimize 6.84 10.65 3 8.39 8.10 2.68
RR Maximize 2.71 3.58 3 3.38 3.32 1.88
Open in a new tab

ARV Actual response values

The predicted values and actual reported values for any response differed non-significantly (p < 0.05)

Conclusion

Response surface methodology was effective in identifying the optimum processing conditions for OD of peach slices in osmotic aqueous solutions of sucrose having concentration in range of 50–70°B, temperature of 35–55 °C and process duration of 2–4 h. The results clearly showed that models developed were appropriate to be used for predicting WL, SG and RR of peach slices within the experimental study. The OD of peach slices at optimum conditions of 69.9°B sucrose concentration, 3.97 h process duration and 37.63 °C process temperature would reduce the original water content of the peach slices by about 28.42% with a rehydration ratio of 3.38. Therefore, OD of peach could effectively be used as a pretreatment prior to freezing or air drying to reduce energy costs and maintain the naturalness of the product.

References

  1. Alam MS, Singh A, Sawhney BK. Response surface optimization of osmotic dehydration process for aonla slices. J Food Sci Technol. 2010;47(1):47–54. doi: 10.1007/s13197-010-0014-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Conway J, Castaigne F, Picard C, Vovan X. Mass transfer considerations in the osmotic dehydration of apples. Can Inst Food Sci Technol J. 1983;16:25–29. [Google Scholar]
  3. Corzo O, Gomez ER. Optimization of osmotic dehydration of cantaloupe using desired function methodology. J Food Eng. 2004;64:213–219. doi: 10.1016/j.jfoodeng.2003.09.035. [DOI] [Google Scholar]
  4. EL-aouar AA, Azoubel PM, Jr B, Murr FEX. Influence of the osmotic agent on the osmotic dehydration of papaya (Carica papaya) J Food Eng. 2006;75:267–274. doi: 10.1016/j.jfoodeng.2005.04.016. [DOI] [Google Scholar]
  5. Giangiecome R, Torreggiani D, Abbe E. Osmotic dehydration of fruit, part I. Sugar exchange between fruit and extraction syrups. J Food Process Preserv. 1987;11:83. doi: 10.1111/j.1745-4549.1987.tb00038.x. [DOI] [Google Scholar]
  6. Islam MN, Flink JM. Dehydration of potato II. Osmotic concentration and its effect on air drying behavior. J Food Technol. 1982;17:387–403. doi: 10.1111/j.1365-2621.1982.tb00194.x. [DOI] [Google Scholar]
  7. Janowicz M, Lenart A. Some physical properties of apples after low pressure osmotic dehydration and convective drying. Chem Process Eng. 2010;31:237–252. [Google Scholar]
  8. Kaleemullah S, Kailappan R, Varadharaju N, Devdas CT. Mathematical modelling of osmotic dehydration kinetics of papaya. Agricultural mechanization in Asia, Africa, Latin America. 2002;33:30–34. [Google Scholar]
  9. Kar A, Gupta DK. Air drying of osmosed button mushrooms. J Food Sci Technol. 2003;40:23–27. [Google Scholar]
  10. Kim MH. Osmotic concentration of apples and its effects on browning reaction during air dehydration. J Korean Sci Nutri. 1990;9:121–125. [Google Scholar]
  11. Kumar PS, Devi P (2010) Optimization of some process variables in mass transfer kinetics of osmotic dehydration of pineapple slices. Int Food Res J (In press).
  12. Lenart A, Flink JM. Osmotic concentration of potato II. Spatial distribution of the osmotic effect. J Food Technol. 1984;19:65–89. doi: 10.1111/j.1365-2621.1984.tb00327.x. [DOI] [Google Scholar]
  13. Lenart A, Grodeka E. Influence of the kind of osmotic substance on the kinetics of convection drying of apples and carrots. Food Tech Nutr. 1989;18:27–35. [Google Scholar]
  14. Manivannan P, Rajasimman M. Osmotic dehydration of beetroot in salt solution: optimization of parameters through statistical experimental design. Int J Chem Biomol Eng. 2008;1(4):215–222. [Google Scholar]
  15. Mundada M, Singh B, Maske S. Optimization of processing variables affecting the osmotic dehydration of pomegranate arils. Int J Food Sci Technol. 2010;45:1732–1738. doi: 10.1111/j.1365-2621.2010.02328.x. [DOI] [Google Scholar]
  16. Nieto A, Salvatori D, Castro MA, Alzamora SM. Air drying behavior of apples as affected by blanching and glucose impregnation. J Food Eng. 1998;36:63–79. doi: 10.1016/S0260-8774(98)00043-0. [DOI] [Google Scholar]
  17. Ozdemir M, Ozen BF, Dock LL, Floros LD. Optimization of osmotic dehydration of diced green peppers by response surface methodology. LWT Food Sci Technol. 2008;41:2044–2050. doi: 10.1016/j.lwt.2008.01.010. [DOI] [Google Scholar]
  18. Ozen BF, Dock LL, Ozdenir M, Floros JD. Processing factors affecting the osmotic dehydration of diced green peppers. Inter J Food Sci Technol. 2002;37:497–502. doi: 10.1046/j.1365-2621.2002.00606.x. [DOI] [Google Scholar]
  19. Parjoko, Rahman MS, Buckle KA. Osmotic dehydration kinetics of pineapple wedges using palm sugar. LWT - Food Sci Technol. 1996;29:452–459. doi: 10.1006/fstl.1996.0069. [DOI] [Google Scholar]
  20. Park KJ, Bin A, Brod FPR, Park THKB. Osmotic dehydration kinetics of pear d’Anjou (Pyrus communis) J Food Eng. 2002;52:293–298. doi: 10.1016/S0260-8774(01)00118-2. [DOI] [Google Scholar]
  21. Pokharkar SM, Prasad S. Mass transfer during osmotic dehydration of banana slices. J Food Sci Technol. 1998;35:336–338. [Google Scholar]
  22. Rahman MS, Lamb J. Osmotic dehydration of pineapple. J Food Sci Technol. 1990;27:150–152. [Google Scholar]
  23. Raoult-wack AL. Recent advances in the osmotic dehydration of foods. Trends Food Sci Technol. 2002;5:46–51. [Google Scholar]
  24. Rastogi NK, Raghavarao KSMS. Mass transfer during osmotic dehydration of pineapple: considering Fickian diffusion in cubical configuration. LWT Food Sc Technol. 2003;37(1):43–47. doi: 10.1016/S0023-6438(03)00131-2. [DOI] [Google Scholar]
  25. Rastogi NK, Raghavarao KSMS, Niranjan K, Knorr D. Recent developments in osmotiv dehydration: methods to enhance mass transfer. Trends Food Sci Technol. 2002;13(2):48–59. doi: 10.1016/S0924-2244(02)00032-8. [DOI] [Google Scholar]
  26. Sahari MA, Souti M, Emam-jomeh Z. Improving the dehydration of dried peach osmotic method. J Food Technol. 2006;4(3):189–193. [Google Scholar]
  27. Shahabuddin M, Hawader MNA, Rahman SMD. Evaluation of characteristics of pineapple in the production of pineapple powder. J Food Process Preserv. 1990;14:375–391. doi: 10.1111/j.1745-4549.1990.tb00141.x. [DOI] [Google Scholar]
  28. Sharma R (2010) Nutrients and functional components in fruits and vegetables. Retrieved from http://www.ozscientific.com on May 12, 2010.
  29. Shedame BM, Patil NB. Effect of osmotic dehydration on drying characteristics. Int J Agric Eng. 2009;2(1):107–109. [Google Scholar]
  30. Singh B, Panesar PS, Gupta AK, Kennedy JF. Optimization of osmotic dehydration of carrot cubes in sucrose-salt solutions using response surface methodology. Eur Food Res Technol. 2007;25:157–165. doi: 10.1007/s00217-006-0395-9. [DOI] [Google Scholar]
  31. Singh B, Panesar PS, Nanda V. Optimization of osmotic dehydration process of carrot cubes in sucrose solution. J Food Process Eng. 2008;31:1–20. doi: 10.1111/j.1745-4530.2007.00173.x. [DOI] [Google Scholar]
  32. Singh B, Panesar PS, Gupta AK, Kennedy JF. Optimization of osmotic dehydration process of carrot cubes in mixtures of sucrose and sodium chloride solutions. Food Chem. 2010;123(3):590–600. doi: 10.1016/j.foodchem.2010.04.075. [DOI] [Google Scholar]
  33. Sodhi NS, Singh N, Komal Osmotic dehydration kinetics of carrots. J Food Sci Technol. 2006;43(4):374–376. [Google Scholar]
  34. Spiazzi E, Mascheroni RH. Mass transfer model for osmotic dehydration of fruits and vegetables I. Development of the simulation model. J Food Eng. 1997;34:387–410. doi: 10.1016/S0260-8774(97)00102-7. [DOI] [Google Scholar]
  35. Sutar PP, Gupta DK. Mathematical modeling of mass transfer in osmotic dehydration of onion slices. J Food Eng. 2007;78:90–97. doi: 10.1016/j.jfoodeng.2005.09.008. [DOI] [Google Scholar]
  36. Yao Z, Le Maguer M. Mathematical modeling and simulation of mass transfer in osmotic dehydration process. Part I: Conceptual and mathematical models. J Food Eng. 1996;29:349–360. doi: 10.1016/0260-8774(95)00045-3. [DOI] [Google Scholar]

Articles from Journal of food science and technology are provided here courtesy of Springer

RESOURCES