Skip to main content
NCBI home page
Journal of Food Science and Technology logoLink to Journal of Food Science and Technology
. 2011 Feb 14;49(2):214–220. doi: 10.1007/s13197-011-0272-9

Sun drying of seedless and seeded grapes

İbrahim Doymaz 1,✉
PMCID: PMC3550863  PMID: 23572844

Abstract

In this study, sun drying behaviour of seedless and seeded grapes was investigated. The drying study showed that the times taken for drying of seedless and seeded grapes of berry size of 1.72 cm and 2.20 cm thicknesses from the initial moisture contents of 78.2% and 79.5% (w.b.) to final moisture content of around 22% (w.b.) were 176 and 228 h in open sun drying, respectively. The drying data were fitted to 12 thin-layer drying models. The performance of these models were compared using the determination of coefficient (R2), mean relative percent error (P), reduced chi-square (χ2) and root mean square error (RMSE) between the observed and predicted moisture ratios. The results showed that Midilli et al. model was found to satisfactorily describe the sun drying curves of seedless and seeded grapes. The effective moisture diffusivity values were estimated from Fick’s diffusion model by 1.02 × 10−11 and 1.66 × 10−11 m2/s for seeded and seedless grapes.

Keywords: Sun drying, Seedless and seeded grapes, Thin-layer drying models, Non-linear regression, Effective moisture diffusivity

Introduction

Drying of fruit and vegetable is one of the oldest forms of food preservation methods known to man and is the most important process to preserve food since it has a great effect on the quality of the dried products. The major objective in drying agricultural products is the reduction of the moisture content to a level, which allows safe storage over an extended period. Also, it brings about substantial reduction in weight and volume, minimising packaging, storage and transportation costs (Okos et al. 1992; Zomorodian and Dadashzadeh 2009). In spite of many disadvantages such as long drying times, contamination of the product and product losses, sun drying is still practised in many places throughout the world. Solar energy is an important alternative source of energy and preferred to other energy sources because it is abundant, inexhaustible, renewable, cheap and non-pollutant (Basunia and Abe 2001; Akbulut and Durmus 2009; Chong et al. 2009).

Grape is one of the world’s largest fruit crops. According to FAO data for 2007, grape production all over the world was about 67,221 million tones. The major producer countries include Italy, China, United States of America, France, Spain, Turkey, and Iran (FAO 2008). Turkey exported 240 600 tones dried grapes (raisin) in 2007 and income was about 240 599 000 US$ (IGEME 2007). Most of the grapes in Turkey are produced in the Aegean region. In general, the fresh grapes are untreated or pre-treated with traditional solution (5% K2CO3 + 1.5% olive oil) and left for sun drying. Drying process usually takes 15 to 20 days for untreated grapes and 7 to 12 days for pre-treated grapes, depending on the relative humidity and temperature of ambient air (Pala et al. 1993). Grapes are covered naturally with a thin-layer of wax; hence, it is necessary to increase water transport from grape berries during drying process. Dipping in hot water or the use of chemicals such as sulphur, potassium meta bisulphide (KMS), potassium hydroxide (KOH), sodium hydroxide (NaOH), potassium carbonate (K2CO3), and ethyl or methyl oleate emulsions are some of pretreatments widely used for fruit drying to increase drying rate and improve the colour quality of products (Mahmutoglu et al. 1996; Di Matteo et al. 2000; Kingsly et al. 2007; Serratosa et al. 2008; Bingol et al. 2008; Shi et al. 2008).

Drying is a complex thermal process in which unsteady heat and moisture transfer occur simultaneously (Sahin and Dincer 2005). From an engineering point of view, it is important to develop a better understanding of the controlling parameters of this complex process. Mathematical models of the drying processes are used for designing new or improving existing drying systems or even for the control of the drying process. Many mathematical models have been proposed to describe the drying process, of them thin-layer drying models have been widely in use. These models can be categorized as theoretical, semi-theoretical, and empirical (Ozdemir and Devres 1999; McMinn 2006). Recently, there have been many research on the mathematical modelling and experimental studies of the drying behaviour of various fruits, such as grapes (Kostaropoulos and Saravacos 1995; Sawhney et al. 2009), apricots (Togrul and Pehlivan 2004), figs (Babalis and Belessiotis 2004; Doymaz 2005), plum (Sabarez and Price 1999), and mulberry (Akpinar 2008; Akbulut and Durmus 2009). Studies on the sun drying of seedless and seeded grapes are scarce in the literature. Therefore, the present study was undertaken to study the drying kinetics of seedless and seeded grapes in direct exposure to the sun, to calculate the effective diffusivity of the samples, and to fit the drying curves with 12 thin-layer drying models.

Material and methods

Materials

Fresh ripe hand harvested grapes (seedless and seeded) from Iskenderun region, Hatay, were used for the drying tests. Hatay is a province of southern Turkey, situated between the Mediterranean Sea to the west and Syria to the South-East. Its geographic coordinates are 35° 52′ to 37° 04′ North, 35° 40′ to 36° 35′ West and is hot and dry in summer. For ensuring the uniformity of the physical characteristics of the grapes dried. The average berry diameters of seedless and seeded grapes were kept at 1.72 ± 0.1 and 2.20 ± 0.1 cm, respectively.

Drying procedure

The selected samples were cleaned with tap water to make samples free from dust and foreign materials. The grapes were then subjected to dipping in order to remove wax layer on the grapes so as to increase drying rate. For this reason, seedless and seeded grapes are dipped for 1 min into the solution of potassium carbonate and olive oil (2.5% K2CO3 + 0.5% olive oil). Pre-treated samples, about 300 ± 0.5 g, were distributed uniformly in a single layer in the sample tray, and then sun dried by direct exposure to solar radiation in August 2007 in the Iskenderun, Hatay. The grapes were exposed to sunlight for 12 h daily. Moisture loss was measured at 4-h intervals during drying for determination of the drying curves by a Mettler balance (model BB3000), which has 0–3000 g measurement range with an accuracy of ±0.1 g. No measurement was made during the night. Drying was continued until the sample reached the desired moisture level of 22 ± 0.5% (w.b). Dried samples were packed in Low Density Polyethylene (LDPE) bags. The experiments were conducted in triplicate and the average values were reported.

Initial moisture content

The average initial moisture contents of the seedless and seeded grape samples were found to be 78.2 ± 0.2% and 79.5 ± 0.2% (w.b.), respectively, as determined by using vacuum oven at 70°C for 24 h following the Association of Official Analytical Chemists (AOAC 1990).

Ambient air temperature

Ambient air temperature during drying was measured by an iron-constantan thermocouple, with a manually controlled 8-channel automatic digital thermometer, with reading accuracy of ±0.1°C (Meter Electronic, Turkey).

Mathematical modeling of drying curves

Moisture ratio (MR) of grapes was obtained using the equation below:

graphic file with name M1.gif 1

where Mt is the moisture content at anytime (kg water/kg dry matter), M0 is the initial moisture content (kg water/kg dry matter) and Me is the equilibrium moisture content of samples (kg water/kg dry matter). The moisture ratio (MR) was simplified to Mt/M0 instead of (Mt-Me)/(M0-Me) by some investigators (Diamante and Munro 1993; Yaldiz et al. 2001; Doymaz 2005; Kingsly et al. 2007; Akpinar 2008) because of the continuous fluctuation of relative humidity of the drying air during sun drying.

Drying curves were fitted to 12 thin-layer drying models, which are widely used in the scientific literature to describe the kinetics of the drying process. The selected thin-layer drying models are identified in Table 1. A nonlinear estimation package (Statistica 6.0) was used to estimate the coefficients of the given models. The four criteria of statistic analysis have been used to evaluate the fitting of the experimental data to the different models; the coefficient of determination (R2), mean relative percent error (P), reduced chi-square (χ2) and root mean square error (RMSE). These parameters can be calculated as:

graphic file with name M2.gif 2
graphic file with name M3.gif 3
graphic file with name M4.gif 4

where MRexp,i and MRpre,i are experimental and predicted dimensionless moisture ratios, respectively; N is number of observations; z is number of constants. For quality fit, R2 value should be higher and P, χ2 and RMSE values should be lower (Kingsly et al. 2007; Vega-Gálvez et al. 2009).

Table 1.

Proposed thin-layer drying models for seedless and seeded grapes

Model no Model name Model equation References
1 Lewis 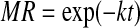Inline graphic Ayensu (1997)
2 Henderson and Pabis 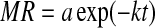Inline graphic Henderson and Pabis (1961)
3 Modified Henderson and Pabis Inline graphic Karathanos (1999)
4 Logarithmic 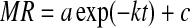Inline graphic Kingsly et al. (2007), Akpinar (2008), Vega-Gálvez et al. (2009).
5 Two-term Inline graphic Yaldiz et al. (2001), Togrul and Pehlivan (2004)
6 Two-term exponential 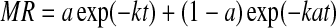Inline graphic Midilli and Kucuk (2003)
7 Verma et al. Inline graphic Verma et al. (1985)
8 Approximation of diffusion 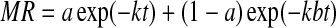Inline graphic Yaldiz and Ertekin (2001)
9 Page 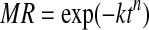Inline graphic Rajkumar et al. (2007), Sawhney et al. (2009).
10 Midilli et al. Inline graphic Midilli et al. (2002), Bingol et al. (2008), Boughali et al. (2009).
11 Parabolic 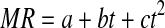Inline graphic Sharma and Prasad (2004)
12 Wang and Singh Inline graphic Wang and Singh (1978)
Open in a new tab

Determination of effective moisture diffusivity

Fick’s second law of diffusion equation was used to fit the experimental data for the determination of effective moisture diffusivity:

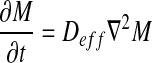graphic file with name M17.gif 5

The analytical solution of Fick’s second law (Eq. 5) unsteady state diffusion in a spherical coordinates with the assumptions of moisture migration being by diffusion, negligible shrinkage, constant effective moisture diffusivity and temperature during the drying process is given as follows (Crank 1975):

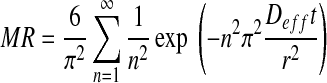graphic file with name M18.gif 6

where, Deff is the effective moisture diffusivity in m2/s, r is the radius of samples in m, and n is a positive integer. For long drying periods, Eq. (6) can be further simplified to only the first term of the series. Thus, Eq. (6) is written in a logarithmic form as follows:

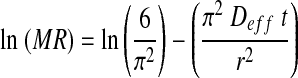graphic file with name M19.gif 7

The effective moisture diffusivity is obtained by plotting the experimental drying data in terms of ln (MR) versus time. From Eq. (7), a plot of ln MR versus time gives a straight line with a slope of (K), in which:

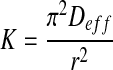graphic file with name M20.gif 8

Results and discussion

Ambient temperature

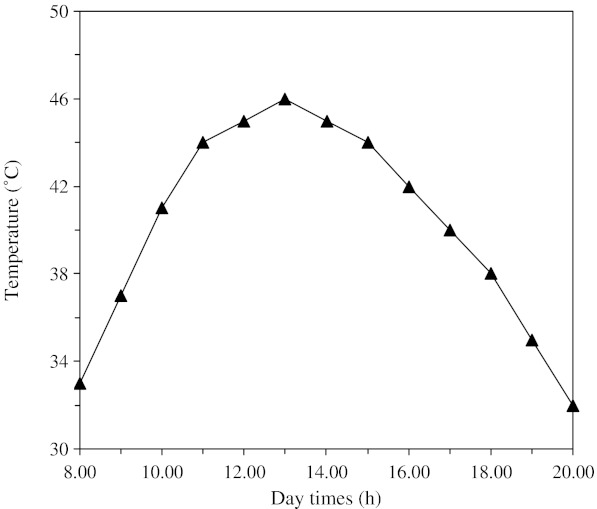
The experiments were performed in August 2007, in Iskenderun, Hatay, Turkey. The variation of ambient air temperatures during sun drying of grape samples under natural convection in a typical day is shown in Fig. 1. During the drying experiments, the weather was generally sunny and no rain appeared. From Fig. 1, the temperature of ambient air ranged from 32 to 46 °C. The ambient air temperature increased to reach 46 °C at 13:00, which was considered the maximum ambient temperature during the day time.

Fig. 1.

Fig. 1

Open in a new tab

Variation of ambient temperature during sun drying of seedless and seeded grapes on a typical day of August 2007 at Iskenderun, Hatay

Drying curves

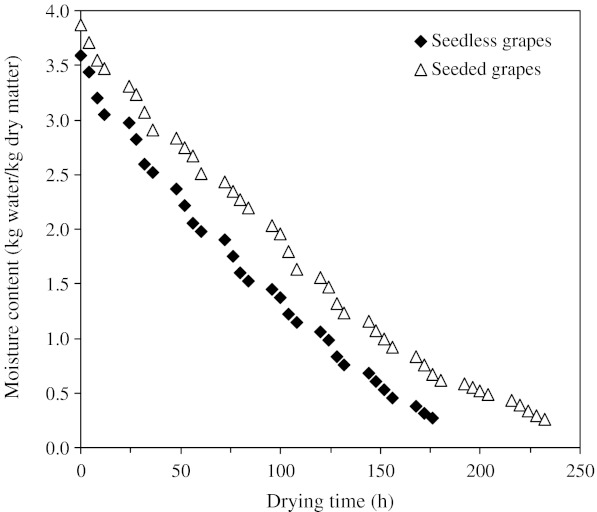
The changes in moisture content with drying time of samples in open sun drying are presented in Fig. 2. The interruptions of the line in this figure represent the night periods of the drying process. The seedless and seeded grapes of average initial moisture content of around 78.2% and 79.5% (w.b.), respectively, were reduced to the final moisture content of 22% (w.b.). It is apparent that moisture ratio decreases continuously with drying time. It is seen from Fig. 2 that the time required to dry the seedless and seeded grapes was 176 and 228 h, respectively. As expected, drying time increased with increase in berry size when diameters increased from 1.72 to 2.20 cm. It observed that small grapes (1.72 cm) could be heated up more quickly than large ones (2.20 cm). Therefore, small fruits showed high drying rates. Similar results have been reported by Shi et al. (2008).

Fig. 2.

Fig. 2

Open in a new tab

Experimentally moisture contents of seedless and seeded grapes versus drying time

Evaluation of the models

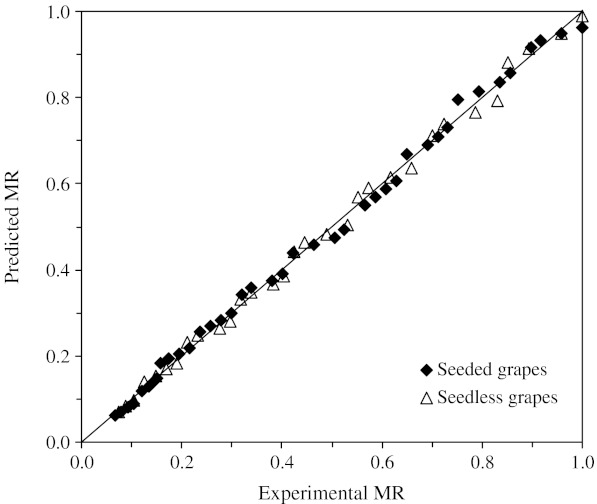
Non-linear regression analyses were performed to thin-layer drying models (Table 1) regarding moisture ratio versus drying time data. The models were evaluated based on the determination of coefficient (R2), mean relative percent error (P), reduced chi-square (χ2) and root mean square error (RMSE). R2, P, χ2 and RMSE values obtained are summarised in Tables 2 and 3. The best model describing the thin-layer drying characteristics of seedless and seeded grapes was chosen as the one with the highest R2 values and the lowest P, χ2 and RMSE values. In all cases, the R2 values for the models were greater than 0.96, indicating a good fit. From Tables 2 and 3, the statistical parameter estimations showed that R2, P, χ2 and RMSE values ranged from 0.9684 to 0.9964, 3.4653 to 21.1572, 0.00031 to 0.0026 and 0.07967 to 0.27813, respectively. As expected, the Midilli et al. model gives the highest value of R2 and lowest of P, χ2 and RMSE values (Tables 2 and 3). Thus, Midilli et al. model may be assumed to represent sun drying characteristics of seedless and seeded grapes in thin-layers. Figure 3 compares the experimental data with the predicted ones using Midilli et al. model for seedless and seeded grapes. The prediction using the model showed MR values banded along a straight line, which proved the suitability of these models in describing the drying characteristics of samples. This observation is in agreement with the result reported by Midilli et al. (2002), and Akbulut and Durmus (2009).

Table 2.

Curve fitting criteria for the various models and parameters for drying of seedless grapes

Model no Constants R2 P χ2 RMSE
1 k: 0.0105 0.9788 16.4944 0.00165 0.18409
2 a: 1.0269, k: 0.0108 0.9802 15.6052 0.00159 0.18392
3 a: −18.1370, k: 0.0290, b:7.7622, g: 0.0359, c: 11.3748, h: 0.0230 0.9951 5.8843 0.00045 0.08916
4 a: 1.4712, k: 0.0054, c: −0.4945 0.9962 3.7993 0.00031 0.08037
5 a: −16.1182, k0: 0.0192, b: 17.0797, k1: 0.0184 0.9916 8.8371 0.00072 0.11677
6 a: 0.0017, k: 6.0812 0.9786 16.6194 0.00172 0.18403
7 a: −4.620, k: 0.0191, g: 0.0169 0.9900 9.5772 0.00083 0.12219
8 a: −5.6006, k: 0.0188, b: 0.9063 0.9900 9.5619 0.00083 0.12219
9 k: 0.0043, n: 1.1939 0.9888 9.7126 0.00089 0.12822
10 a: 0.9894, k: 0.0098, n: 0.9069, b: −0.0015 0.9964 3.4653 0.00031 0.07967
11 a: 0.9703, b: −0.0074, c: 0.0001 0.9959 3.7892 0.00033 0.08382
12 a: −0.0080, b: 0.0001 0.9943 4.4772 0.00045 0.08841
Open in a new tab

Table 3.

Curve fitting criteria for the various models and parameters for drying of seeded grapes

Model no Constants R2 P χ2 RMSE
1 k: 0.0082 0.9687 20.9432 0.00258 0.27709
2 a: 1.0503, k: 0.0087 0.9731 18.5239 0.00227 0.25875
3 a: 9.5141, k: 0.0154, b: −3.4207, g: 0.0169, c: −5.1432, h: 0.0169 0.9931 7.6239 0.00064 0.12351
4 a: 1.6033, k: 0.0038, c: −0.6135 0.9956 6.1286 0.00037 0.10278
5 a: 25.2698, k0: 0.0158, b: −24.3196, k1: 0.0164 0.9931 7.5937 0.00061 0.12321
6 a: 0.0012 ; k: 6.4832 0.9684 21.1572 0.00267 0.27813
7 a: −4.2613, k: 0.0166, g: 0.0143 0.9910 8.7674 0.00078 0.14037
8 a: −5.8401, k: 0.0163, b: 0.8906 0.9910 8.7426 0.00078 0.14013
9 k: 0.0018; n: 1.3089 0.9908 7.6445 0.00078 0.13904
10 a: 0.9616, k: 0.0019, n: 1.2489, b: −0.0005 0.9963 4.3141 0.00032 0.08614
11 a: 0.9875, b: −0.0059, c: 0.0001 0.9962 4.9585 0.00033 0.09270
12 a: −0.0061, b: 0.0001 0.9960 4.4775 0.00033 0.09059
Open in a new tab

Fig. 3.

Fig. 3

Open in a new tab

Experimental vs. predicted moisture ratio (MR) values for seedless and seeded grapes drying

Effective moisture diffusivity

The values of effective moisture diffusivity were calculated using Eq. (8) and found as 1.02 × 10−11 m2/s for seeded grapes and 1.66 × 10−11 m2/s for seedless grapes. As expected, Deff values increased with decrease in berry size from 2.20 to 1.72 cm. Table 4 shows the Deff values of the present study as well as information available in the literature. Obviously, the effective moisture diffusivity values in sun drying are smaller, mainly because the daytime temperature was below 46 °C most of the time. The temperature is the most important factor affecting the drying process of grape samples. The Deff values reported herein are within the general range of 10−11 to 10−9 m2/s for food materials (Madamba et al. 1996). The differences between the results could be due to the differences in fruits and varieties, pretreatments and drying equipments.

Table 4.

Effective moisture diffusivity values of seedless and seeded grapes and other products

Fruits Drying type Effective moisture diffusivity (m2/s) References
Seedless grapes Sun drying 1.66 × 10−11 Present work
Seeded grapes Sun drying 1.02 × 10−11 Present work
Seedless grapes Solar drying 0.95–1.05 × 10−10 Raouzeos and Saravacos (1986)
Seedless grapes Hot-air drying 2.40–6.22 × 10−10 Pahlavanzadeh et al. (2001)
Seedless grapes Air-impingement drying 1.82–5.84 × 10−10 Xiao et al. (2010)
Seedless grapes Hot-air drying 7.91–24.5 × 10−10 Ismail et al. (2008)
Fig Sun drying 2.47 × 10−10 Doymaz (2005)
Prune Hot-air drying 4.30 × 10−10–7.60 × 10−10 Sabarez and Price (1999)
Ciku Sun drying 1.95 × 10−10–2.08 × 10−10 Chong et al. (2009)
Chempedak Hot-air drying 3.29 × 10−10–4.53 × 10−10 Chong et al. (2008)
Apple Hot-air drying 2.27 × 10−10–4.97 × 10−10 Sacilik and Elicin (2006)
Open in a new tab

Conclusions

In this study, sun drying characteristics of seedless and seeded grapes were investigated under open sun. Results showed that the drying time increased with increased berry size. To explain the drying characteristics of grapes 12 thin-layer drying models were applied. The Midilli et al. model showed better fit with high R2, and low P, χ2 and RMSE values. The resulting model gave values of parameters for samples in the thin layer sun drying process: R2: 0.9963–0.9964, P: 3.4653–4.3141, χ2: 0.00031–0.00032, and RMSE: 0.07967–0.08614. The effective moisture diffusivity values for seeded and seedless grapes estimated using Fick’s diffusion model were 1.02 × 10−11 and 1.66 × 10−11 m2/s, respectively.

Nomenclature

a, b, c, g, h

Empirical constants in drying models

Deff

Effective diffusivity (m2/s)

K, k0, k1

Empirical coefficients in the drying models (1/h)

K

Slope

MRexp,i

Experimental moisture ratio

MRpre,i

Predicted moisture ratio

M

Moisture content at time t (kg water/kg dry matter)

Me

Equilibrium moisture content (kg water/kg dry matter)

M0

Initial moisture content (kg water/kg dry matter)

N

Number of observations

n

Constant, positive integer

P

Mean relative percent error

R2

Determination of coefficient

RMSE

Root mean square error

r

Radius (m)

t

Drying time (h)

χ2

Reduced chi-square

z

Number of constants

References

  1. Akbulut A, Durmus A. Thin layer solar drying and mathematical modeling of mulberry. Int J Energy Res. 2009;33:687–695. doi: 10.1002/er.1504. [DOI] [Google Scholar]
  2. Akpinar EK. Mathematical modeling and experimental investigation on sun and solar drying of white mulberry. J Mec Sci Technol. 2008;22:1544–1553. doi: 10.1007/s12206-008-0508-4. [DOI] [Google Scholar]
  3. Official methods of analysis. 15. Arlington: Association of Official Analytical Chemists; 1990. [Google Scholar]
  4. Ayensu A. Dehydration of food crops using a solar dryer with convective heat flow. Sol Energy. 1997;59:121–126. doi: 10.1016/S0038-092X(96)00130-2. [DOI] [Google Scholar]
  5. Babalis SJ, Belessiotis VG. Influence of the drying conditions on the drying constants and moisture diffusivity during the thin-layer drying of figs. J Food Eng. 2004;65:449–458. doi: 10.1016/j.jfoodeng.2004.02.005. [DOI] [Google Scholar]
  6. Basunia MA, Abe T. Thin-layer solar drying characteristics of rough rice under natural convection. J Food Eng. 2001;47:295–301. doi: 10.1016/S0260-8774(00)00133-3. [DOI] [Google Scholar]
  7. Bingol G, Pan Z, Roberts JS, Devres O, Balaban M. Mathematical modeling of microwave-assisted convective heating and drying of grapes. Int J Agric Biol Eng. 2008;1(2):46–54. [Google Scholar]
  8. Boughali S, Benmoussa H, Bouchekima B, Mennouche D, Bouguettaia H, Bechki D. Crop drying by indirect active hybrid solar – Electrical dryer in the Eastern Algerian Septentrional Sahara. Sol Energy. 2009;83:2223–2232. doi: 10.1016/j.solener.2009.09.006. [DOI] [Google Scholar]
  9. Chong CH, Law CL, Cloke M, Hii CL, Luqman Chuah A, Daud WRW. Drying kinetics and quality of dried chempedak. J Food Eng. 2008;88:522–527. doi: 10.1016/j.jfoodeng.2008.03.013. [DOI] [Google Scholar]
  10. Chong CH, Law CL, Cloke M, Abdullah LC, Daud WRW. Drying models and quality analysis of sun-dried ciku. Dry Technol. 2009;27:985–992. doi: 10.1080/07373930902904491. [DOI] [Google Scholar]
  11. Crank J. The mathematics of diffusion. Oxford: Clarendon; 1975. [Google Scholar]
  12. Di Matteo M, Cinquanta L, Galiero G, Crescitelli S. Effect of a novel physical pretreatment process on the drying kinetics of seedless grapes. J Food Eng. 2000;46:83–89. doi: 10.1016/S0260-8774(00)00071-6. [DOI] [Google Scholar]
  13. Diamante LM, Munro PA. Mathematical modelling of thin layer solar drying of sweet potato slices. Sol Energy. 1993;51:271–276. doi: 10.1016/0038-092X(93)90122-5. [DOI] [Google Scholar]
  14. Doymaz I. Sun drying of figs: an experimental study. J Food Eng. 2005;71:403–407. doi: 10.1016/j.jfoodeng.2004.11.003. [DOI] [Google Scholar]
  15. FAO (2008) Statistical database. Available: http://www.fao.org
  16. Henderson SM, Pabis S. Grain drying theory I: temperature effect on drying coefficient. J Agric Eng Res. 1961;6:169–174. [Google Scholar]
  17. IGEME (2007) Undersecretariet of the Prime Ministry for Foreign Trade, Turkey. Available from http://www.igeme.gov.tr
  18. Ismail O, Keyf S, Beyribey B, Corbacioglu B. Effects of dipping solutions on air-drying rates of the seedless grapes. Food Sci Technol Res. 2008;14:547–552. doi: 10.3136/fstr.14.547. [DOI] [Google Scholar]
  19. Karathanos VT. Determination of water content of dried fruits by drying kinetics. J Food Eng. 1999;39:337–344. doi: 10.1016/S0260-8774(98)00132-0. [DOI] [Google Scholar]
  20. Kingsly RP, Goyal RK, Manikantan MR, Ilyas SM. Effects of pretreatments and drying air temperature on drying behavior of peach slice. Int J Food Sci Technol. 2007;42:65–69. doi: 10.1111/j.1365-2621.2006.01210.x. [DOI] [Google Scholar]
  21. Kostaropoulos AE, Saravacos GD. Microwave pre-treatment for sun-dried raisins. J Food Sci. 1995;60:344–347. doi: 10.1111/j.1365-2621.1995.tb05669.x. [DOI] [Google Scholar]
  22. Madamba PS, Driscoll RH, Buckle KA. The thin-layer drying characteristics of garlic slices. J Food Eng. 1996;29:75–97. doi: 10.1016/0260-8774(95)00062-3. [DOI] [Google Scholar]
  23. Mahmutoglu T, Emir F, Saygi YB. Sun/solar drying of differently treated grapes and storage stability of dried grapes. J Food Eng. 1996;29:289–300. doi: 10.1016/0260-8774(96)00006-4. [DOI] [Google Scholar]
  24. McMinn WAM. Thin-layer modeling of the convective, microwave, microwave-convective and microwave-vacuum drying of lactose powder. J Food Eng. 2006;72:113–123. doi: 10.1016/j.jfoodeng.2004.11.025. [DOI] [Google Scholar]
  25. Midilli A, Kucuk H. Mathematical modelling of thin layer drying of pistachio by using solar energy. Energy Convers Manage. 2003;44:1111–1122. doi: 10.1016/S0196-8904(02)00099-7. [DOI] [Google Scholar]
  26. Midilli A, Kucuk H, Yapar Z. A new model for single layer drying. Dry Technol. 2002;20:1503–1513. doi: 10.1081/DRT-120005864. [DOI] [Google Scholar]
  27. Okos MR, Narsimhan G, Singh RK, Witnauer AC. Food dehydration. In: Heldman DR, Lund DB, editors. Handbook of food engineering. New York: Marcel Dekker; 1992. [Google Scholar]
  28. Ozdemir M, Devres YO. The thin layer drying characteristics of hazelnuts during roasting. J Food Eng. 1999;42:225–233. doi: 10.1016/S0260-8774(99)00126-0. [DOI] [Google Scholar]
  29. Pahlavanzadeh H, Basiri A, Zarrabi M. Determination of parameters and pretreatment solution for grape drying. Dry Technol. 2001;19:217–226. doi: 10.1081/DRT-100001363. [DOI] [Google Scholar]
  30. Pala M, Saygi YB, Sadikoglu H (1993) A study on the drying of sultana grapes by different techniques and effective parameters. In: Charalambous G (ed) In Developments in Food Science 32: food flavors, ingredients and composition. Elsevier Science Publishers, Amsterdam, pp 437–444
  31. Rajkumar P, Kulanthaisami S, Raghavan GSV, Gariépy Y, Orsat V. Drying kinetics of tomato slices in vacuum assisted solar and open sun drying methods. Drying Technol. 2007;25:1349–1357. doi: 10.1080/07373930701438931. [DOI] [Google Scholar]
  32. Raouzeos GS, Saravacos GD. Solar drying of raisins. Dry Technol. 1986;4:633–649. doi: 10.1080/07373938608916353. [DOI] [Google Scholar]
  33. Sabarez HT, Price WE. A diffusion model for prune dehydration. J Food Eng. 1999;42:167–172. doi: 10.1016/S0260-8774(99)00115-6. [DOI] [Google Scholar]
  34. Sacilik K, Elicin AK. The thin layer drying characteristics of organic apple slices. J Food Eng. 2006;73:281–289. doi: 10.1016/j.jfoodeng.2005.03.024. [DOI] [Google Scholar]
  35. Sahin AZ, Dincer I. Prediction of drying times for irregular shaped multi-dimensional moist solids. J Food Eng. 2005;71:119–126. doi: 10.1016/j.jfoodeng.2004.10.024. [DOI] [Google Scholar]
  36. Sawhney RL, Pangavhane DR, Sarsavadia PN (2009) Drying studies of single layer Thomson seedless grapes. International Solar Food Processing Conference, January 14–16, 2009, Indore, India
  37. Serratosa MP, Lopez-Toledano A, Medina M, Merida J. Drying of Pedro Ximenez grapes in chamber at controlled temperature and with dipping pretreatments. Changes in the color fraction. J Agric Food Chem. 2008;56:10739–10746. doi: 10.1021/jf8021767. [DOI] [PubMed] [Google Scholar]
  38. Sharma GP, Prasad S. Effective moisture diffusivity of garlic cloves undergoing microwave-convective drying. J Food Eng. 2004;65:609–617. doi: 10.1016/j.jfoodeng.2004.02.027. [DOI] [Google Scholar]
  39. Shi J, Pan Z, McHugh TH, Wood D, Zhu Y, Avena-Bustillos RJ, Hirschberg E. Effect of berry size and sodium hydroxide pretreatment on the drying characteristics of blueberries under infrared radiation heating. J Food Sci. 2008;73:259–265. doi: 10.1111/j.1750-3841.2008.00816.x. [DOI] [PubMed] [Google Scholar]
  40. Togrul IT, Pehlivan D. Modelling of thin layer drying kinetics of some fruits under open-air sun drying process. J Food Eng. 2004;65:413–425. doi: 10.1016/j.jfoodeng.2004.02.001. [DOI] [Google Scholar]
  41. Vega-Gálvez A, Lemus-Mondaca R, Tello-Ireland C, Miranda M, Yagnam F. Kinetic study of convective drying of blueberry variety O’Neil (Vacccinium corymbosum L.) Chilean J Agric Res. 2009;69:171–178. doi: 10.4067/S0718-58392009000200006. [DOI] [Google Scholar]
  42. Verma LR, Bucklin RA, Endan JB, Wratten FT. Effects of drying air parameters on rice drying models. Trans ASAE. 1985;28:296–301. [Google Scholar]
  43. Wang CY, Singh RP (1978) Use of variable equilibrium moisture content in modeling rice drying. ASAE Meeting Paper No. 78–6505, ASAE, St. Joseph.
  44. Xiao HW, Pang CL, Wang LH, Bai JW, Yang WX, Gao ZJ. Drying kinetics and quality of Monukka seedless grapes dried in an air-impingement jet dryer. Biosyst Eng. 2010;105:233–240. doi: 10.1016/j.biosystemseng.2009.11.001. [DOI] [Google Scholar]
  45. Yaldiz O, Ertekin C. Thin layer solar drying of some vegetables. Drying Technol. 2001;19:583–597. doi: 10.1081/DRT-100103936. [DOI] [Google Scholar]
  46. Yaldiz O, Ertekin C, Uzun HI. Mathematical modeling of thin layer solar drying of sultana grapes. Energy. 2001;26:457–465. doi: 10.1016/S0360-5442(01)00018-4. [DOI] [Google Scholar]
  47. Zomorodian AA, Dadashzadeh M. Indirect and mixed mode solar drying mathematical models for Sultana grape. J Agric Sci Technol. 2009;11:391–400. [Google Scholar]

Articles from Journal of food science and technology are provided here courtesy of Springer

RESOURCES