Effect of drying methods on the moisture sorption isotherms and thermodynamic properties of mint leaves

Abstract

Mint leaves were dried by three different types of dryers, namely; tray, freeze and distributed (indirect)-type solar dryer. Sorption isotherms of fresh, solar, tray and freeze dried mint were determined at temperatures of 15 °C, 25 °C and 35 °C over a range of relative humidities (10–90%). The effect of drying method on the water sorption isotherms of dried mint samples was evaluated. Experimental data were used to determine the best models for predicting the moisture sorption content of mint. Among nine sorption models tested, Peleg, GAB, Lewicki and modified Mizrahi equations gave the best fit to experimental data. The sorption data were analyzed for determination of monolayer moisture content, density of sorbed water, number of adsorbed monolayers, percent bound water, and surface area of adsorbance. The experimental data were also used to determine some thermodynamic properties of mint.

Introduction

Drying has a long time tradition as a conservation method and use of dried medicinal and aromatic plants in traditional medicine has been well-known. The pharmacology and food industry handle these crops as raw materials to produce drugs, spices and essential oils. Mint has been used both as a medicinal and aromatic plant since ancient times. Its leaves are used for flavoring, tea infusions and spicing. In order to preserve this seasonal plant, and make it to available to consumers during the whole year, it undergoes specific technological treatments, such as drying. Several methods have been used in drying process. Final product characteristics such as water sorption, porosity, color, and texture depend on drying methods used (Ekechukwu 1999). Tray drying is frequently used in food industry and tray dried foods usually have some undesirable effects due to use of high temperature and long time. Freeze drying provides better porous structure but operational costs are higher. In order to minimize drying cost and to improve the nutritional value, drying methods have to be optimized. One way is to introduce a solar drying system (Ekechukwu and Norton 1999). It is particularly important for countries which have more sun throughout the year. Most suitable drying methods and their operating conditions have to be determined to control the product quality.

The moisture sorption isotherm is an extremely valuable tool for food scientists and technologists because it can be used to predict potential changes in food stability; determination of storing method, and packaging selection (Basu et al. 2006).

There are many works on moisture sorption isotherms of foods. Some of these works are related to the determination of moisture sorption isotherms and their temperature dependence some are related to the mathematical expressions to represent the moisture sorption isotherms. Many empirical and semi empirical models have been proposed to describe the sorption characteristics of foods. The mostly applied models are GAB, Halsey, BET, Oswin, Henderson, Peleg, Caurie, and Lewicki (Ayranci and Duman 2005; Rao et al. 2006; Chirife and Iglesias 1978; Lomauro et al. 1985a, b; Peleg 1993).

Information on moisture sorption isotherms of various herbs and aromatical/medicinal plants including peppermint, daphne, marjoram, muscat, cardamom, chamomile, cloves, coriander, thyme, cinnamon, ginger fennel and anise (Soysal and Öztekin 2001), saffron (Tsimidou and Biliaderis 1997), mint, sage, and verbena (Kouhila et al. 2001), rosemary (Timoumi and Zagrouba 2005), green tea powder (Sinija and Mishra 2008), chitosan (Rosa et al. 2010) are available. Henderson equation was found to be an adequate model for mint (Kouhila et al. 2001). The influence of temperature and velocity of tray drying on the sorption isotherms of garden mint was studied, and BET, Oswin and Peleg models were found to be the best models to describe the mint desorption isotherms (Park et al. 2002). Effect of drying method on the moisture sorption isotherms for mushroom was studied and the maximum monolayer moisture content has been found for freeze-dried samples (Lee and Lee 2008).

In recent years, there have been many contributions in the field of thermodynamics to understand the properties of water in relation to a biological system. The thermodynamic functions can be easily calculated from moisture sorption isotherms (Rizvi and Benado 1984). Thermodynamic functions include free energy, heat of vaporization, integral enthalpy and entropy. Thermodynamic functions are important for understanding the properties of water and calculating the energy requirements of heat and mass transfer in biological systems (Iglesias et al. 1976). Park et al. 2002 were studied drying parameters and sorption isotherms of garden mint leaves. Tray drying of mint leaves at different temperatures and air velocities were only studied in this work.

The objectives of this study were to determine the moisture sorption isotherms of fresh, solar, tray and freeze dried mint at three temperatures, 15, 25, and 35 °C, and to find the most suitable model describing the isotherms of mint leaves. The second part of this study deals with determination the monolayer moisture content and some thermodynamic functions (heat of sorption and entropy of sorption) of mint leaves.

Materials and methods

Materials

Fresh garden mint bunches were supplied from local greengrocers (Gaziantep, TURKEY). The leaves of mint bunches were separated from the stalk and cleaned. Nine saturated salt solutions (NaOH, CH₃COOK, MgCl₂, K₂CO₃, Mg(NO₃)₂, KI, NaCl, KCl and KNO₃) in different closed containers were prepared to obtain constant relative humidity environments. All salt solutions were reagent grade.

Drying procedures

The leaves of fresh garden mint bunches were dried by passing heated air over the drying trays. A tray dryer (Armfield UOP 8-Tray dryer, ENGLAND) was used. Mint leaves were placed into the trays and drying was started. The weight of the sample was measured periodically. It was continued until the constant weight of the sample obtained. Operating conditions of driers are given in Table 1.

Table 1.

Experimantal conditions for dried mint process

Drying method	Initial moisture content,% (wb)	Drying temperature, °C	Air velocity, m/s	Drying time to reach EMCa, min
Tray drying	87.20	65	1.00	75
Freeze drying	87.20	−50	–	300
Solar drying	87.20	65	1.00	75

^aEMC Equilibrium Moisture Content

The leaves of fresh garden mint were also dried by a freeze-dryer (Eyela Model FD-1, JAPAN). The leaves were placed into the sample flask and frozen by the anti-freeze liquid (ethanol) bath at −50 °C. Frozen sample was attached to the drying chamber and dried under vacuum.

A typical distributed (indirect) type solar dryer (Designed and built at University of Gaziantep) was used to dry mint leaves. It consists of four basic components; a fan, an air-heating solar-energy collector, a drying chamber and appropriately insulated ducting. The system was active solar drying system because of the use of motorized fan for forced air circulation. Drying air was heated through solar-energy collector. The sample placed into the removable tray was dried by hot and dry air. The weight of the sample was measured periodically and drying was stopped when the weight of the sample was being unchanged.

Determination of moisture sorption isotherms

A gravimetric method was used in this work. The method was based on the use of saturated salt solutions to maintain a fixed relative humidity (RH). Nine salts were chosen so as to have a range of relative humidities of 10–90%.

Nine saturated salt solutions were used to provide water activities ranging from 0.06 to 0.98. The salts used were NaOH, KAc,MgCl2, K2CO3,MgNO3,KI, KCl,KNO3, and NaCl. Saturated solutions of them were prepared at each temperature studied. They were placed into separate jars in an amount to occupy a space of about 1 cm deep at the bottom. A small amount of solid salt was also added to make sure that solutions remain saturated. A tripod was also placed in each jar. Duplicate samples of 1 g of the solar-, tray-, freeze-dried mint leaves, and fresh mint leaves were weighed into small crucibles of aluminum foil and placed on tripods in the jars, which were then tightly closed.

The samples were kept in ovens at 15, 25 and 35 ± 1 °C for equilibration. This required about 4 weeks. Moisture content of the mint leaves was determined using the oven method at 105 °C after the final equilibrium moisture content was reached (AOAC 1990). The equilibrium moisture content of the samples was given as g/100 g dry solids.

Analysis of sorption data

Isotherm models

A large number of models have been proposed in the literature for the sorption isotherms (Basu et al. 2006; Ayranci and Duman 2005). In this study, Peleg, GAB, Lewicki, BET, Halsey, Oswin, Henderson, Modified Mizrahi, and Caurie equations were applied to determine the best fit for the experimental data. The mathematical expressions of the nine models are presented in Table 2. The parameters of equations (Halsey, Oswin, BET, Henderson, Caurie and Lewicki) were obtained by linear regression analysis while those of equations (GAB, Peleg and Modified Mizrahi) were obtained by non-linear regression analysis using the SigmaPlot 2000 (SPSS Inc., Chicago, IL, USA).

Table 2.

Mathematical models for the sorption isotherm curves

Model	Expression	Number of constants
GAB		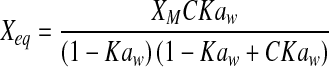3
Halsey		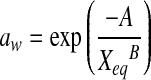2
Peleg		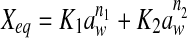4
Oswin		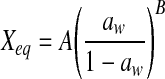2
BET		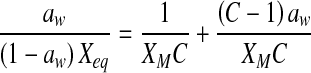2
Henderson		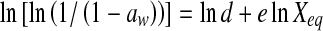2
Lewicki		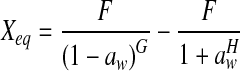3
Modified Mizrahi		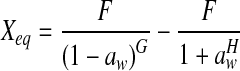3
Caurie		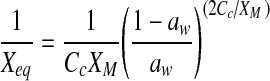2

The nonlinear regression analysis was carried with the Marquardt-Levenberg algorithm; this is a search method to minimize the sum of squares of the differences between the predicted and experimental data. In order to compare the precision of fit of the sorption models, mean relative percent deviation modulus (P) and coefficient of determination (R²) were used.

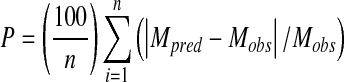1

where M_obs, M_pred, and n are observed moisture content at any water activity, predicted moisture content according to the equation under study with best fitted parameters, and number of observations, respectively.

The BET equation was applied to sorption data below a_w of 0.5 as it was reported to be successful only in this range (Labuza 1984). The statistical parameters of BET equation were therefore not determined as the applicability of this equation is limited below a_w of 0.5.

Monolayer moisture content

The monolayer moisture content M₀, can be determined from the equilibrium sorption isotherm data by fitting BET, GAB and Caurie expressions. The prediction of M₀ has a significant importance for physical and chemical stability of foods. Below M₀ values, food deterioration is expected to be extremely small, because water is strongly bound to the food and water is not involved in any deteriorative reaction. Treatment of sorption data to Caurie equation allows the evaluation of the number of binding sites, the influence of temperature on monolayer, density of sorbed water, surface area of absorbent and per cent non-freezable or bound water. The number of adsorbed monolayers (N) (Rao et al. 2006) was calculated using;

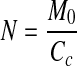2

where M₀ is the monolayer moisture content from Caurie’s equation and C_c is Caurie’s constant. Assuming that the magnitude of C_c equals the density of adsorbed water in the monolayer, the surface area of adsorbent (A) was calculated as

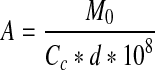3

where d is the diameter of water molecule (d = 3.673*10⁻¹⁰ m).

Isosteric heat of sorption

The isosteric heat of sorption Q_st, is the energy per unit mass required to remove water from a material and incorporates the binding energy between water molecules and the food dry matter. The heat of sorption was obtained from the slopes of lna_w vs. 1/T plots by linear regression analysis using the Clausius-Clapeyron equation (Labuza 1984).

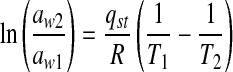4

where a_w1 and a_w2 are the water activities at temperatures T₁ and T₂ respectively and R is the gas constant (8.314 J mol⁻¹ K⁻¹). q_st is the net heat of sorption, which is equal to the difference between the isosteric heat of sorption, Q_st and the enthalpy of vaporization of water, ΔH_vap (H₂O). Q_st is logically related to the amount of energy required in a dehydration process.

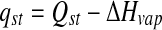5

Q_st is logically related to the amount of energy required in a dehydration process.

Enthalpy entropy compensation theory

The relationship between the isosteric heat (Q_st) and the differential entropy (ΔS_d) of sorption is given by

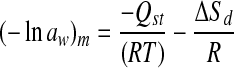6

by plotting ln(a_w) versus 1/T, for a given moisture content (m), Q_st was determined from the slope (−Q_st/R), and ΔS_d from intercept (ΔS_d/R) (McMinn and Magee 2003). The dependence of Q_st and ΔS_d with moisture at different moisture content is therefore, determined.

The compensation theory proposes a linear relationship between Q_st and ΔS_d (McMinn and Magee 2003):

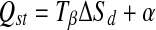7

The isokinetic temperature (T_β) and constant (α) were calculated using linear regression.

The isokinetic temperature has an important physical meaning as it represents the temperature at which all reactions in a given series have the same reactivity. Since there is a high degree of linear correlation between enthalpy and entropy, the compensation theory was assumed to be valid for sorption. It was recommended a test for the compensation theory (Telis et al. 2000), which involves comparing the isokinetic temperature with the harmonic mean temperature T_hm that is defined as:

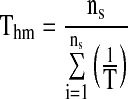8

where n_s is number of isotherms. If T_β > T_hm the process is enthalpy driven, while if the opposite condition is observed (T_β < T_hm), the process is considered to be entropy-controlled (Lefler 1955; Telis et al. 2000; McMinn et al. 2005).

Results and discussion

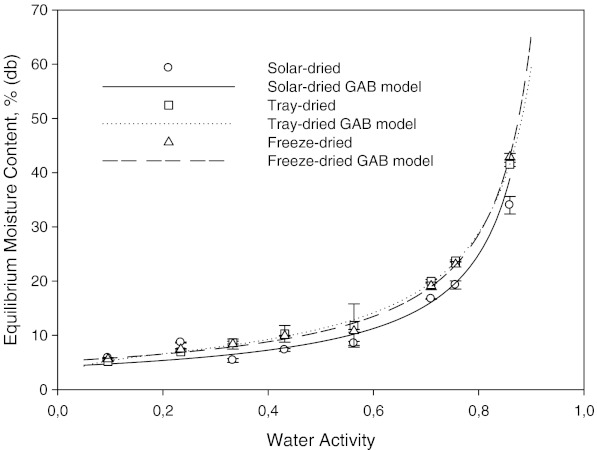
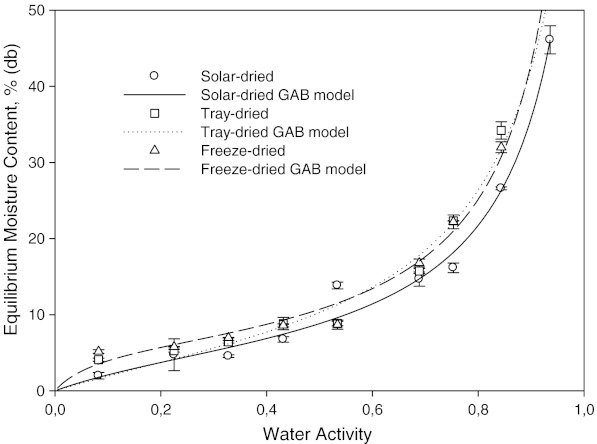
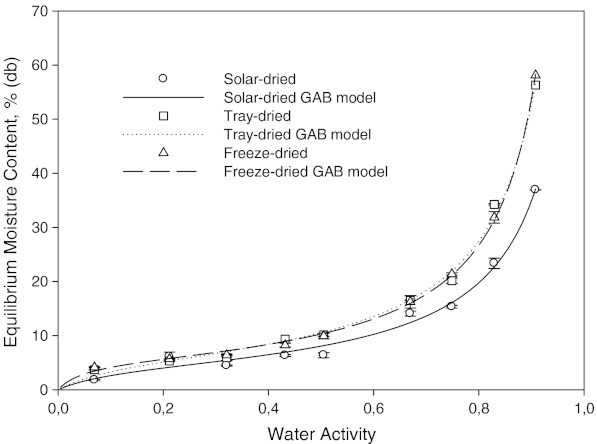
Initial moisture content (IMC) of fresh mint leaves was found to be 4,672 ± 0,031 g/g dry matter. Experimental equilibrium moisture content (EMC) values of fresh and dried mint leaves are presented in Table 3. The moisture sorption isotherms for solar, tray and freeze dried mint are shown in Figs. 1, 2 and 3 respectively. Each point of the curves represents the mean value of two replications. The sorption isotherms obtained were generally showed characteristics of BET III type isotherm. This type isotherm is common for many foods having rich soluble components (Labuza 1984). This is probably due to the higher carbohydrate content. Mint has approximately 70% (db) of carbohydrates (Whfoods 2006).

Table 3.

Experimental EMC values (% dry basis) of fresh and dried mint at selected temperatures

Temperature (°C)	aw	Desorption	Adsorption
		Fresh mint	Solar-dried	Tray-dried	Freze-dried
15	0.096	6.944 ± 0.007	5.839 ± 0.038	5.187 ± 0.035	5.619 ± 0.125
	0.234	9.134 ± 0.130	8.676 ± 0.069	6.962 ± 0.010	7.432 ± 0.092
	0.333	10.136 ± 0.136	5.377 ± 0.247	8.665 ± 0.181	8.411 ± 0.659
	0.432	12.219 ± 0.127	7.305 ± 0.184	10.279 ± 1.088	9.920 ± 0.045
	0.563	12.418 ± 0.141	8.526 ± 0.260	11.819 ± 2.829	10.825 ± 0.169
	0.710	20.916 ± 0.320	16.726 ± 0.042	19.957 ± 0.249	19.132 ± 0.496
	0.756	22.613 ± 0.380	19.292 ± 0.527	23.715 ± 0.145	23.103 ± 0.354
	0.859	43.217 ± 1.175	38.991 ± 6.151	41.532 ± 0.273	42.951 ± 0.427
25	0.082	2.824 ± 0.522	1.971 ± 0.304	4.080 ± 0.142	5.169 ± 0.163
	0.225	7.478 ± 0.147	4.739 ± 1.480	5.270 ± 0.133	5.784 ± 0.024
	0.328	9.622 ± 0.059	4.558 ± 0.127	6.426 ± 0.111	6.976 ± 0.019
	0.432	10.865 ± 0.421	6.746 ± 0.253	8.830 ± 0.574	8.602 ± 0.144
	0.689	15.216 ± 2.107	14.685 ± 0.659	15.738 ± 0.239	16.796 ± 0.368
	0.534	12.280 ± 1.014	13.836 ± 0.306	8.840 ± 0.200	8.698 ± 0.426
	0.753	21.340 ± 3.975	16.162 ± 0.443	22.332 ± 0.017	22.201 ± 0.642
	0.843	30.275 ± 0.146	26.596 ± 0.134	34.221 ± 0.809	32.004 ± 0.502
	0.936	52.064 ± 1.413	46.114 ± 1.308	52.343 ± 1.513	56.937 ± 0.952
35	0.069	5.014 ± 0.346	1.802 ± 0.097	3.698 ± 0.032	4.158 ± 0.063
	0.212	6.232 ± 0.204	6.109 ± 0.606	5.327 ± 0.029	5.676 ± 0.032
	0.321	8.929 ± 0.284	4.474 ± 0.087	5.941 ± 0.373	6.416 ± 0.124
	0.432	10.421 ± 0.064	6.325 ± 0.138	9.347 ± 0.089	8.257 ± 0.240
	0.505	10.815 ± 0.074	6.393 ± 0.333	10.154 ± 0.199	9.928 ± 0.370
	0.670	15.342 ± 3.604	14.077 ± 0.331	16.522 ± 0.026	16.244 ± 0.811
	0.749	19.365 ± 0.100	15.348 ± 0.176	20.169 ± 0.351	21.391 ± 0.146
	0.830	22.952 ± 0.918	23.364 ± 0.672	34.259 ± 0.101	31.852 ± 0.752
	0.908	36.250 ± 1.125	36.939 ± 0.013	56.261 ± 0.132	58.122 ± 0.100

Fig. 1.

Moisture sorption isotherm of solar, tray, and freeze dried mint at 15 °C

Fig. 2.

Moisture sorption isotherm of solar, tray, and freeze dried mint at 25 °C

Fig. 3.

Moisture sorption isotherm of solar, tray, and freeze dried mint at 35 °C

At low water activities, water can be absorbed only at the surface sites. As the water activity increases the dissolution of soluble components (mostly carbohydrates) bring about increasing the moisture content. In general, at water activities higher than 0.80, there is a sharp increase in moisture content.

Fitting of sorption equations to experimental data

The sorption data were fitted to nine well-known sorption isotherm equations. These equations and number of constants are presented in Table 2. Non-linear regression analysis was used for evaluating the best-fitted values of constants. The isotherm models, equation constants, R² and ‘P’ values are summarized in Table 4. The higher R² and the lower ‘P’ values represent the goodness of fit. Generally, Peleg, GAB, Lewicki and Modified Mizrahi equations have the lowest ‘P’ and hihger R² values. The best fit was obtained by the model of Peleg for fresh mint, tray and freeze dried mint at 15 °C and for tray dried mint at 25 °C; by the models of GAB for fresh mint, at 35 °C, and for tray dried mint at 15 °C and for freeze dried mint both at 15 °C and 35 °C; by the model of Lewicki for fresh mint at 35 °C and for freeze dried mint both at 15 °C and 35 °C; by the model of Halsey for fresh mint, at 35 °C and finally by the model of Modified Mizrahi for fresh mint at 35 °C and for tray dried mint at 15 °C and for freeze dried mint at 35 °C.

Table 4.

Parameters of sorption isotherm equations, R² (coefficient of determination), and mean relative deviation modulus (P) for isotherms of fresh and dried mint at 15, 25, and 35 °C

Equation		Fresh mint			Solar dried			Tray dried			Freeze dried
		15 °C	25 °C	35 °C	15 °C	25 °C	35 °C	15 °C	25 °C	35 °C	15 °C	25 °C	35 °C
Peleg	n1	8.2772	6.0264	7.1082	6.9201	12.1467	6.5761	6.9117	5.3027	7.9907	7.2857	6.3111	8.7836
	n2	0.3383	−0.0455	0.5353	0.0561	1.2507	0.5383	0.4284	0.3139	0.6321	0.3247	0.3127	0.6281
	K1	100.9339	61.3048	40.2993	90.4382	56.2305	51.1580	81.7882	62.3201	91.5972	95.0581	70.6742	101.5043
	K2	15.1294	9.2093	16.2918	7.3000	22.9642	10.0267	13.7206	8.9164	14.9023	12.0528	10.1549	15.2066
	R2	0.9948	0.9928	0.9892	0.9904	0.9880	0.9878	0.9991	0.9984	0.9973	0.9990	0.9968	0.9968
	P	3.9664	7.8311	7.4588	9.4428	15.8264	14.5081	2.7059	4.2138	8.2378	2.1564	6.4516	8.5978
GAB	Mo	6.0079	6.3006	6.2833	4.2587	5.8295	4.6302	5.7006	7.9363	5.9391	5.2111	6.0282	5.4212
	C1	3.19E + 07	7.18E + 07	3.89E + 01	3.07E + 07	4.67E + 00	9.73E + 00	4.88E + 01	2.78E + 00	9.15E + 00	1.47E + 07	1.36E + 01	1.96E + 01
	K	1.0000	0.9354	0.9092	0.9909	0.9372	0.9660	1.0000	0.9174	0.9875	0.9998	0.9571	0.9995
	R2	0.9879	0.9825	0.9929	0.9828	0.9846	0.9881	0.9983	0.9884	0.9954	0.9971	0.9936	0.9991
	P	8.1310	8.1840	5.0338	13.3802	12.7752	13.8124	2.9023	15.5526	8.2735	4.6631	10.8089	5.3774
Lewicki	F	6.6533	11.0946	13.5310	4.5731	11.7202	7.5327	7.8691	14.2084	8.2035	5.3833	10.7504	7.2316
	G	0.9789	0.5946	0.4835	1.1130	0.5438	0.7110	0.8924	0.5297	0.8408	1.0847	0.6446	0.8992
	H	−2.5443	−0.4926	0.2939	−1.5721	1.0475	0.4051	−0.2405	1.0337	0.2161	−2.3800	0.3348	−0.0173
	R2	0.9920	0.9879	0.9949	0.9838	0.9857	0.9878	0.9974	0.9817	0.9961	0.9976	0.9924	0.9999
	P	6.4611	9.3033	4.6466	12.5781	14.4761	15.1675	5.0866	16.3609	5.2492	4.5745	10.5012	1.5863
BETa	Mo	7.0551	6.6971	5.7116	4.6845	4.6712	3.6401	6.0867	4.9481	5.2225	5.7843	4.7631	4.8527
Halsey	A	18.0137	49.4374	44.1144	6.7913	16.9874	9.9744	12.5117	24.1004	10.3272	10.1660	19.7446	9.1614
	B	1.2840	1.6860	1.7052	1.0465	1.4405	1.2802	1.1893	1.4752	1.1566	1.1260	1.4034	1.1216
	R2	0.9690	0.9729	0.9944	0.9583	0.9772	0.9870	0.9933	0.9743	0.9960	0.9843	0.9911	0.9990
	P	14.4991	10.6822	4.6352	18.7158	30.1324	18.3399	8.8426	16.0855	6.1995	14.1668	10.8312	5.4740
Oswin	A	12.9762	12.4979	11.7438	8.7224	9.1816	8.0056	11.5961	10.9804	10.0969	10.9452	10.6638	9.6749
	B	0.6251	0.5151	0.4822	0.8023	0.6044	0.6669	0.6846	0.5932	0.7491	0.7309	0.6273	0.7765
	R2	0.9379	0.9501	0.9908	0.9306	0.9849	0.9859	0.9772	0.9819	0.9924	0.9624	0.9912	0.9926
	P	21.0540	14.9029	7.2517	24.6150	14.7886	14.0552	16.8860	13.3034	14.1929	22.0334	13.6265	15.9941
Henderson	d	0.0570	0.0668	0.0368	0.1700	0.1245	0.1460	0.0856	0.1089	0.1615	0.1093	0.1297	0.1800
	e	0.9702	0.9608	1.1865	0.6799	0.8138	0.7819	0.8573	0.8153	0.6733	0.7839	0.7591	0.6427
	R2	0.8791	0.8971	0.9611	0.8861	0.9757	0.9693	0.9404	0.9831	0.9746	0.9195	0.9789	0.9706
	P	29.0169	25.9026	16.3683	34.6530	19.3741	25.0165	26.8017	23.8013	30.2048	31.9018	26.5288	32.1741
Modified Mizrahi	a	−7.8188	−7.1443	−3.4970	−7.0660	0.5021	−1.4282	−4.9502	−0.0716	−2.4979	−6.1379	−1.7945	−3.3474
	b	5.9053	−1.6853	−10.9643	11.8025	−18.6894	−9.2723	−1.4914	−20.3700	−8.4673	4.4004	−14.1882	−4.8118
	c	−4.4332	6.1652	12.2711	−11.6176	15.9969	7.7650	0.5245	17.9009	5.9864	−4.9807	12.9637	2.8486
	R2	0.9916	0.9745	0.9957	0.9898	0.9854	0.9858	0.9980	0.9727	0.9953	0.9971	0.9871	0.9997
	P	7.3891	13.4188	4.4546	10.1939	17.6281	15.4615	4.0263	18.4600	6.2663	5.7546	13.8096	2.9002
Caurie	Mo	6.4447	6.9673	6.9794	4.6621	5.5118	4.8998	5.8206	6.0846	5.1924	5.4721	5.8307	4.9921
	Cc	2.0139	1.7941	1.6827	1.8706	1.6658	1.6339	1.9924	1.8046	1.9447	1.9999	1.8289	1.9381
	R2	0.9379	0.9501	0.9908	0.9306	0.9849	0.9860	0.9772	0.9819	0.9924	0.9624	0.9913	0.9926
	P	21.0463	14.9033	7.2488	24.6195	14.7872	14.0554	16.8839	13.3036	14.1910	22.0374	13.6263	15.9927

^aThe BET equation was applied to the sorption data below a_w of 0.5

The sorption data for all mint samples at all temperatures were not fit to Oswin, Henderson and Caurie models. Overall, Peleg, GAB, Lewicki and Modified Mizrahi could be used to describe the mint desorption isotherms. It was reported that BET, GAB, Oswin and Peleg models were best fit for mint (Park et al. 2002). Henderson’s equation was found to be satisfactory for the prediction of the sorption isotherms of aromatic plants including mint (Kouhila et al. 2001). However, in this study neither Henderson model nor Oswin model was indicated a good fit for the entire range of water activity.

Hysteresis

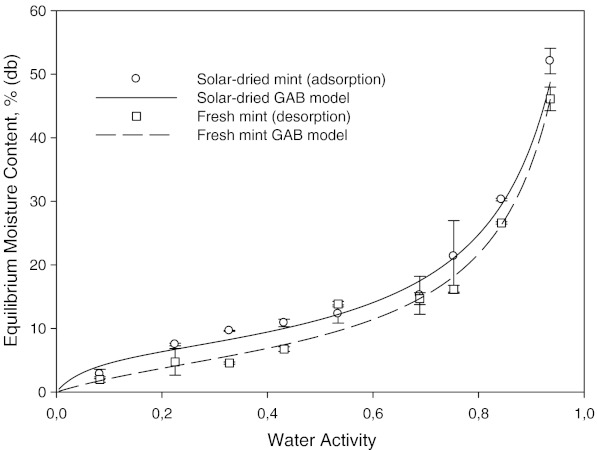
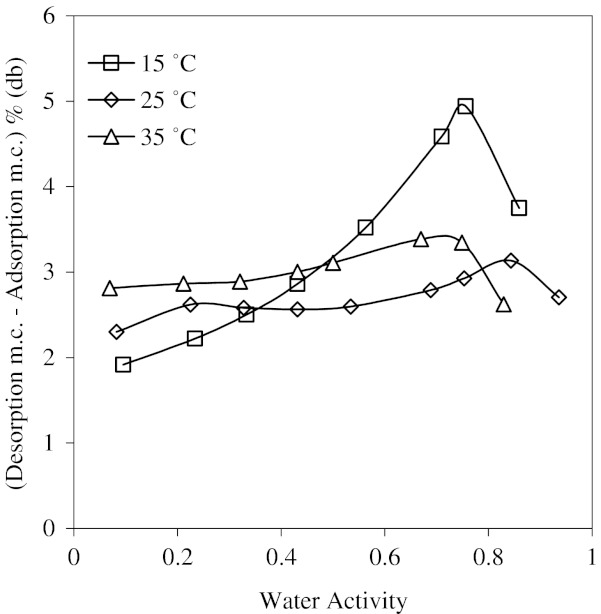
The behavior of adsorption and desorption experiments was different and hysteresis was observed. Equilibrium moisture content was higher at a particular water activity for the desorption curve than that of adsorption (Figs. 4, 5 and 6). The hysteresis existed over the entire range water activity range. Similar type of hysteresis was observed on various foods (Okubayashi et al. 2004).

Fig. 4.

Adsorption (solar-dried) and desorption (fresh) isotherms of mint at 25 °C

Fig. 5.

Sorption hysterisis values

Fig. 6.

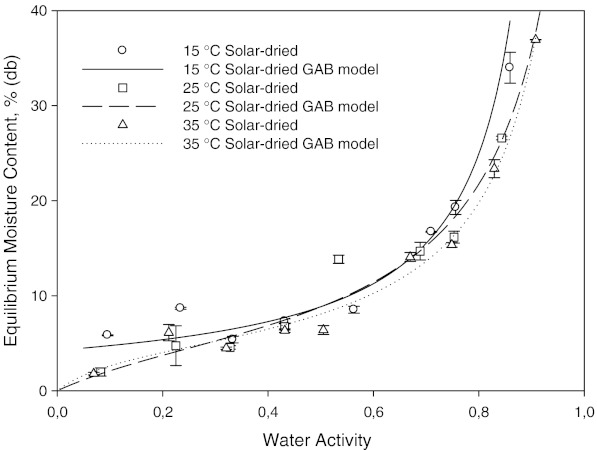
Change of moisture sorption isotherm of solar dried mint at 15, 25, and 35 °C

In order to see the hysteresis more clearly desorption moisture content minus adsorption moisture content vs. water activity was plotted (Fig. 6). This figure shows that the hysteresis values increased gradually up to water activity of 0.75 at 25 °C. After this value, the difference was decreased. The magnitude of the hysteresis decreased with an increase in temperature.

Temperature dependence of isotherms

The influence of the temperature on desorption isotherms for the range of water activities studied can be observed. (Fig. 6). It can be seen that moisture contents decrease while the temperature increases at constant water activity. This is possibly due to the state of carbohydrate and proteins which are having more water binding (Ayranci and Dalgic 1992). This is typical for many foodstuffs (Ayranci et al. 1990; Mohamed et al. 2005).

The water activity region above about 0.55, equilibrium moisture content of solar dried samples were lower than equilibrium moisture contents of tray and freeze dried mint samples at 25 °C. This is possibly due to the state of some components such as carbohydrate. Carbohydrates and proteins are known to have more water-binding capacity than at high temperatures. For freeze dried samples less components were being dissolved and thus less water.

The effect of drying method on sorption characteristics of mint

The effect of drying method on the sorption isotherm at 15, 25 and 35 °C can be seen in Figs. 1, 2 and 3, respectively. It is well known that freeze drying provides a dry-product with more porous structure and little shrinkage. At the same time, high retention of nutrients and flavor/aroma can be obtained. Freeze dried samples showed a lower water sorption potential. The higher adsorptive capacities of freeze dried and tray dried samples were more pronounced at higher water activities, especially at 35 °C (Fig. 3). Fast evaporation of water in freeze and tray dried mint samples possibly created more porous structures. The sorbed moisture was low for water activities of up to 0.4 at all temperatures. From this point, the slope of equilibrium moisture content vs. a_w curve changed slightly. After this point, there was steep increase in equilibrium moisture content vs. a_w curve, indicating gradual dissolution of carbohydrates (Tsami et al. 1998).

Properties of sorbed water

Monolayer moisture contents of mints calculated from GAB, BET and Caurie equations were shown in Table 5. Although Caurie model was not fit very well, it was further analyzed to get fairly accurate information about monolayer moisture content, percent bound water, density of sorbed water, number of adsorbed mono layers and surface area of adsorbent. Caurie model has been used successfully by other workers (Rao et al. 2006) for chhana pado. M_o values are particularly important for determining the storage and preserving conditions above which deteriorative changes may occur. It was observed that the monolayer moisture content was not constant in the range of temperature employed. The value of parameters is in the same range as for other similar products (Ayranci and Duman 2005). The M_o values of various foods are in the range of 4–11% (Karel 1975). M_o values in this work are among 3.6–7%. The M_o values of mints were decreased with increasing temperature. The M_o values of mint obtained using BET model were lower than those obtained using GAB and Caurie models particularly at 25 and 35 °C. The converse was the case at 15 °C.

Table 5.

Properties of sorbed water in mint

Mint sample	Temperature	Monolayer moisture content. M0.%			Caurie’s equation
	°C	BET	GAB	Caurie	N	Bound water%	Cc. g/cm3	A m2/g
Fresh	15	7.0551	6.0079	6.4447	3.20	20.62	2.0139	87.13
	25	6.6971	6.3006	6.9673	3.88	27.03	1.7941	105.73
	35	5.7116	6.2833	6.9794	4.15	28.96	1.6827	112.92
Solar- dried	15	4.6845	4.2587	4.6621	2.49	11.61	1.8706	67.86
	25	4.6712	5.8295	5.5118	3.31	18.24	1.6658	90.08
	35	3.6401	4.6302	4.8998	3.00	14.70	1.6339	81.65
Tray-dried	15	6.0867	5.7006	5.8206	2.92	17.00	1.9924	79.54
	25	4.9481	7.9363	6.0846	3.37	20.51	1.8046	91.79
	35	5.2225	5.9391	5.1924	2.67	13.86	1.9447	72.69
Freeze- dried	15	5.7843	5.2111	5.4721	2.74	14.99	1.9999	74.49
	25	4.7631	6.0282	5.8307	3.19	18.60	1.8289	86.80
	35	4.8527	5.4212	4.9921	2.58	12.88	1.9381	70.13

The number of adsorbed monolayers (N) for fresh mint samples was increased with increasing temperature (Table 5). For all dried mint samples, the value of N increased with increase in temperature from 15 to 25 °C. N value was decreased when the temperature was increased from 25 to 35 °C (except for the BET model).

The increase in the number of adsorbed monolayers with an increase in temperature for fresh mint is possibly due to increase in polar groups (Singh et al. 2006). Bound water and surface area of absorbance showed different characteristics for fresh and dried mint samples. Both bound water and area of absorbance increased with increased temperature for fresh mint. No trend has been observed for dried samples.

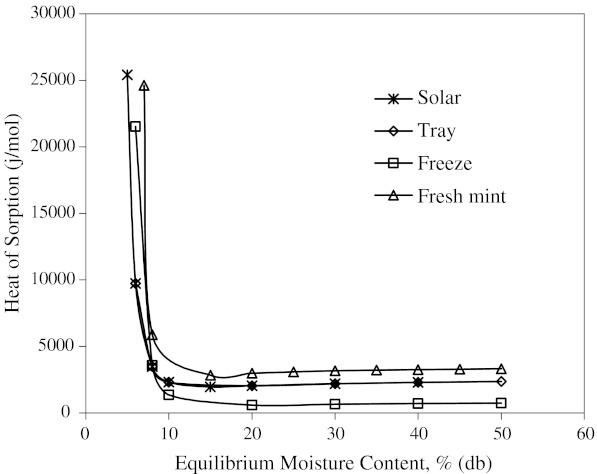
Heat of sorption is of interest to food scientists because it determines the temperature dependence of water activity. Isosteric sorption heat (Q_st) plotted as a function of moisture content is presented in Fig. 7. Q_st decreased exponentially with increasing moisture content, initially rapidly up to (10%) and later slowly. This kind of behavior has been observed for many foods (Mohamed et al. 2005). The Q_st values reached a plateau after the moisture content about 10%. This plateau lies in the range of heat of vaporization of pure water. The rapid increase in Q_st values at low moisture content is due to existence of highly active polar sites on the surface of food material, which are covered with water molecules forming a mono molecular layer (Hossain et al. 2001). Higher heat of sorption also indicates that there is a need for the highest binding energy for removal of water. Increasing moisture content decreases the heat of sorption and therefore binding energy for removal of water.

Fig. 7.

Effect of moisture content on the isosteric heat of sorption of mint samples

The Q_st values are below 40 kJ/mol. This is called physisorption where the sorption involves weak bonding to the surface (Moore 1972). Here, Van der Waals interactions are usually involved and absorbed molecules can often move across the surface. The molecules remain intact, and can be freed easily (the forces are small, and short-range).

The relation between isosteric heat of sorption and equilibrium moisture content was accurately described by a two parameter exponential model and shown in Table 6. Exponential (Adam et al. 2000) and power law (McMinn and Magee 2003) models for onion and potato, respectively were used to express the relationships between isosteric heat of sorption and moisture content.

Table 6.

Thermodynamic properties of mint

Heat of sorption	qst		R2
Fresh		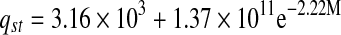	0.988
Solar-dried		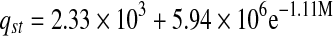	0.999
Tray-dried		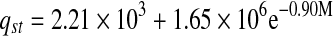	0.998
Freeze-dried		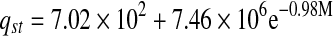	0.999
Entropy of sorption	ΔSd		R2
Fresh		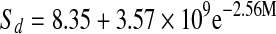	0.986
Solar-dried		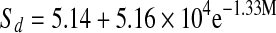	0.996
Tray-dried		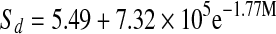	0.956
Freeze-dried		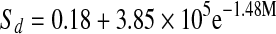	0.997
qst & ΔSd relationship	Tβ (K)	α	R2
Fresh	368.51	214.95	0.978
Solar-dried	342.02	687.07	0.992
Tray-dried	307.28	977.15	1.000
Freeze-dried	352.56	1004.61	0.988

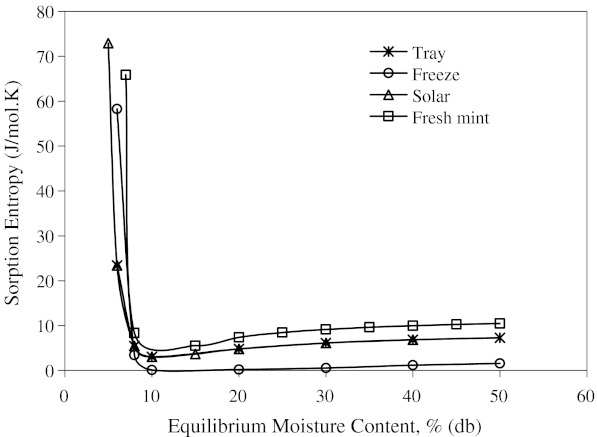
The entropies plotted as a function of water content are presented in Fig. 8. Entropies for all mint samples had minimum values at 10% moisture content. All mint samples showed a decrease in entropy, reaching a minimum and than slightly increasing and reaching a plateau as water content increased. After reaching plateau, entropy values remained practically constant at higher moisture contents. Fresh mint showed minimum sorption entropy at higher moisture content compared to that of dried mint samples. The relation between differential entropy of sorption and equilibrium moisture content was accurately described by a two parameter exponential model and also shown in Table 6.

Fig. 8.

Differential entropy change of mint samples with moisture content

The relation between differential entropy and isosteric heat was determined by linear regression analysis (Eq. 7). Very high values of correlation coefficients (R²) between 0.978 and 1.000 have been observed (Table 5). This indicates a high degree of linearity between differential entropy and isosteric heat, the compensation theory is assumed to exit (McMinn et al. 2005). The harmonic mean temperature (T_hm) was calculated from Eq. 8 and found as 297.93 K. According to Leffler, if T_β > T_hm the process is enthalpy driven, the reverse is valid for entropy driven. T_β values of mint samples were higher than T_hm (Table 5). The water sorption process is therefore considered to be enthalpy controlled.

Conclusions

The moisture sorption isotherms of fresh, tray-, solar-, and freeze-dried mint leaves at different temperatures were determined by a standard gravimetric method. The equilibrium moisture content increased decreasing temperature at constant water activity. The hysteresis between adsorption and desorption was observed. The experimental data were fitted to nine sorption models. Among them, GAB, Lewicki, Peleg, and modified Mizrahi equations described the sorption data well over the range of temperatures and water activities investigated. Isosteric heat of sorption of mint leaves decreased with increasing moisture content. Exponential model can be used to characterize heat of sorption and entropy of sorption.