Abstract
The thin-layer vacuum drying behavior of Zizyphus jujuba Miller slices was experimentally investigated at the temperature of 50, 60, and 70 °C and the mathematical models were used to fit the thin-layer vacuum drying of Z. jujuba slices. The increase in drying air temperature resulted in a decrease in drying time. The drying rate was found to increase with temperature, thereby reducing the total drying time. It was found that Z. jujuba slices with thickness of 4 mm would be dried up to 0.08 kg water/kg dry matter in the range of 180–600 min in the vacuum dryer at the studied temperature range from 70 to 50 °C. The Midilli et al. model was selected as the most appropriate model to describe the thin-layer drying of Z. jujuba slices. The diffusivity coefficient increased linearly over the temperature range from 1.47 × 10−10 to 3.27 × 10−10 m2/s, as obtained using Fick’s second law. The temperature dependence of the effective diffusivity coefficient followed an Arrhenius-type relationship. The activation energy for the moisture diffusion was determined to be 36.76 kJ/mol.
Keywords: Drying kinetics, Vacuum drying, Zizyphus jujuba Miller slices, Modeling, Effective diffusivity, Activation energy
Introduction
Zizyphus jujuba Miller, belonging to the family Rhamnaceae, is found in many countries especially in the subtropical and tropical regions of Asia and America (Li et al. 2007). The plant has been important in traditional Oriental medicine for many years, and is known to effectively prevent some diseases, such as tumors and cardiovascular disease, related to the production of radical species resulting from oxidative stress (Zhang et al. 2010). Fresh Z. jujuba contains abundant amounts of nutrients, especially vitamin C: 10-fold as much as that in other fruits (Li et al. 2007).
Most of the Z. jujuba produced annually has been consumed in dried forms. The traditional drying methods for Z. jujuba have been natural drying in the sun and air-drying (Fang et al. 2009). Sun-drying takes 15 days or more and is climate-dependent; moreover, it may result in lower economic efficiency (Fang et al. 2009). Recently, whole-fruit Chinese jujube was dried using hot air, and its drying dynamics were reported.
Hot-air drying is a relatively simple and economic procedure, having several advantages over sun drying, but also has disadvantages, including shrinkage, darkening in color, loss of flavor, and decrease in rehydration ability (Cho et al. 1989; Lee et al. 2004). Freeze-drying produces a high-quality product, but being an expensive process, its application is limited. Vacuum-drying is another alternative method, and is especially suitable for products that are prone to heat damage such as, fruits and vegetables (Giri and Prasad 2007).
Despite plentiful drying studies that have previously been undertaken, little information is available about differences in drying rate, diffusivity, and mathematical models to describe the drying process of Z. jujuba slices, which can be used as a guideline toward optimal design of drying methods and conditions. Drying kinetics is often used to describe the combined macroscopic and microscopic mechanisms of heat and mass transfer during drying, which is affected by drying conditions, types of dryers, and characteristics of materials to be dried. Drying-kinetics models are essential for equipment design, process optimization and product quality improvement. It is also vital to know the drying characteristics of the material to be dried under a range of conditions (McLoughlin et al. 2003; Giri and Prasad 2007).
The objectives of this work were to determine the effect of drying temperature on drying characteristics of Z. jujuba slices, to evaluate a suitable drying model for describing the vacuum drying process, and to compute the effective moisture diffusivity and activation energy of samples.
Materials and methods
Materials
Fresh Z. jujuba samples were procured from a local market and stored at 4 °C in a refrigerator before use. Samples were selected in terms of hard texture, smooth skin, and uniform size. Z. jujuba was cut into slices in ellipsoidal shape with diameters about 2.5 cm in minor axis and 3 cm in major axis and thickness of 4 mm using a stainless steel knife. The initial moisture content of the fresh samples was 76.68% (wet basis, wb), which was determined in triplicate by using a convection oven at 105 °C for 24 h.
Drying experiment
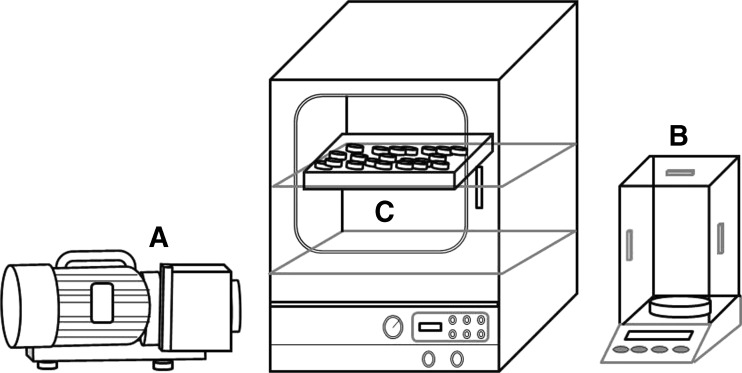
The Z. jujuba slices was dried in a vacuum oven with vacuum pressure of 0.1 MPa (VOS-301SD, Tokyo Rikakikai Co., Ltd., Japan; temperature variation: ±1.5 °C at 240 °C setting), consisting of a temperature control unit, a vacuum gauge, a heating chamber, and a vacuum pumpas shown in Fig. 1. An approximate mass of 0.10 kg of fruits was chosen for each batch. The fruits were spread in a single layer on a tray. The batch of samples was retrieved from the dryer and weighed every 30 min using an electronic balance (CP423S, Satorius AG, Göttingen, Germany; repeatability: ±0.001 g, linearity: ±0.002 g, stabilization time: 1 s) with a sensitivity of 0.001 g. The content of dry solid of the dry samples after drying experiment was determined (AOAC 2002) and used to convert the weight of Z. jujuba samples collected during drying tests into moisture content in dry basis (M, kg water/kg dry solid). Equilibrium moisture content (Me) at each drying temperature was determined by monitoring the weight change for extended drying until it remained constant. Drying experiments were performed in duplicate. The three different drying temperatures used for this study were 50, 60, and 70 °C, based on the actual industrial application range.
Fig. 1.
Schematic diagram of vacuum dryer used in this study. a. Vacuum pump, b. Electronic balance, c. Vacuum oven consisting of a temperature control unit, a vacuum gauge, a heating chamber
Modeling of drying data
The experimental drying data were used to calculate the moisture ratio (MR, dimensionless) and drying rate using the following equations:
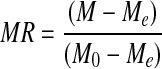 |
1 |
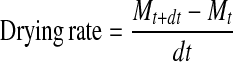 |
2 |
where, M, Mo, Me, Mt and 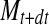 are the moisture content at any time, initial moisture content, equilibrium moisture content, moisture content at t and moisture content at t + dt (kg water/kg dry matter), respectively, where t is the drying time (s). Eight well-known thin-layer drying models in Table 1 were tested to select the best model for describing the drying curve of the Z. jujuba slices. Non-linear least square regression analysis was performed using the Levenberg-Marquardt procedure in the SigmaPlot computer program. The coefficient of determination (R2) was the primary criterion for selecting the best model to describe the drying curve. In addition, root mean square error (RMSE) and the reduced chi-square (χ2) were used to determine the goodness of fit. The reduced chi-square (χ2) is the chi-square divided by degrees of freedom. These parameters can be calculated as follows:
are the moisture content at any time, initial moisture content, equilibrium moisture content, moisture content at t and moisture content at t + dt (kg water/kg dry matter), respectively, where t is the drying time (s). Eight well-known thin-layer drying models in Table 1 were tested to select the best model for describing the drying curve of the Z. jujuba slices. Non-linear least square regression analysis was performed using the Levenberg-Marquardt procedure in the SigmaPlot computer program. The coefficient of determination (R2) was the primary criterion for selecting the best model to describe the drying curve. In addition, root mean square error (RMSE) and the reduced chi-square (χ2) were used to determine the goodness of fit. The reduced chi-square (χ2) is the chi-square divided by degrees of freedom. These parameters can be calculated as follows:
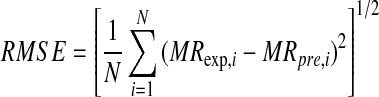 |
3 |
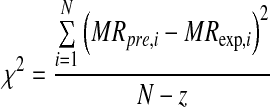 |
4 |
where, MRexp,i is the ith experimentally observed moisture ratio, MRpre,i the ith predicted moisture ratio, N the number of observations, and z is the number of constants in the model (Madamba et al. 1996; Martin et al. 2001). The model was considered best when RMSE and χ2 were at a minimum value and R2 at a maximum value (Sacilik and Elicin 2006; Giri and Prasad 2007).
Table 1.
Thin layer drying models used for mathematical modeling
| No. | Model name | Model | References |
|---|---|---|---|
| 1 | Newton | MR = exp(−kt) | Ayensu (1997) |
| 2 | Page | MR = exp(−kt)m | Agrawal and Singh (1977) |
| 3 | Henderson and Pabis | MR = a exp(−kt) | Westerman et al. (1973) |
| 4 | Logarithmic | 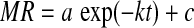 |
Yagcioglu et al. (1999) |
| 5 | Two term exponential | 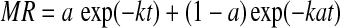 |
Sharaf-Eldeen et al. (1980) |
| 6 | Wang and Singh | 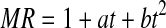 |
Wang and Singh (1978) |
| 7 | Modified Henderson and Pabis | 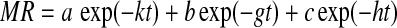 |
Karathanos (1999) |
| 8 | Midilli et al. | 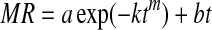 |
Midilli et al. (2002) |
Moisture diffusivity and activation energy
The dehydration of biological materials normally follows a falling-rate drying period. The moisture and/or vapor migration during this period is controlled by diffusion. The moisture diffusivity for an infinite slab was calculated by using the following equation (Crank 1975; Ramesh et al. 2001; Sacilik and Unal 2005; Sacilik and Elicin 2006):
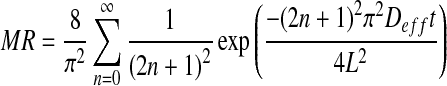 |
5 |
where, Deff is the effective diffusivity (m2/s) and L is the half thickness of the slab (m).
For long drying times, only the first term (n = 0) in the series expansion of the above equation can give good estimate of the solution (Saravacos and Raouzeos 1986), which is expressed in logarithmic forms as follows (Madamba 2003):
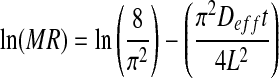 |
6 |
The diffusion coefficients are typically determined by plotting experimental drying data in terms of ln(MR) versus drying time (t) and noting the slope of straight line.
The effective moisture diffusivity can be related to temperature by a simple Arrhenius-type relationship:
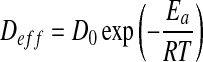 |
7 |
where, D0 is the pre-exponential factor of the Arrhenius equation (m2/s), Ea the activation energy (kJ/mol), R the universal gas constant (8.314 J/mol K), and T the absolute temperature (K).
The activation energy was calculated by plotting the natural logarithm of Deff versus the reciprocal of the absolute temperature.
Results and discussion
Drying kinetics
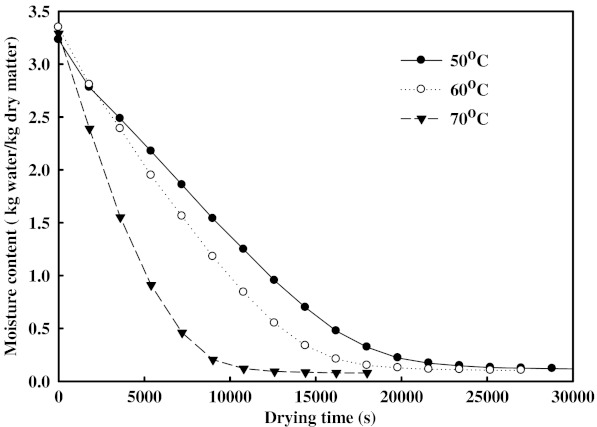
The Z. jujuba slices were dried as a single layer with thickness of 4 mm at the drying air temperature of 50, 60 and 70 °C in a vacuum dryer. The variations in moisture content of the Z. jujuba slices as a function of drying time at different temperatures are presented in Fig. 2. It can be seen that the moisture content of the Z. jujuba samples decreased with the increase in drying time. It only took 3 h to dry Z. jujuba samples from an initial moisture content of 3.288 kg water/kg dry matter to a final moisture content of 0.08 kg water/kg dry matter at 70 °C of drying air temperature, and it took 6 h at 60 °C and 10 h at 50 °C, respectively. It indicated that increasing the drying temperature decreases the drying time (Akpinar 2006; Fang et al. 2009). The decrease in drying time with an increase in the drying air temperature have been reported for many food-stuffs, such as eggplant (Ertekin and Yaldiz 2004; Wu et al. 2007), apple pomace (Wang et al. 2007), pumpkin slices (Doymaz 2007), and Asian white radish (Lee and Kim 2009).
Fig. 2.
Effect of drying air temperature on the moisture content of Z. jujuba slices
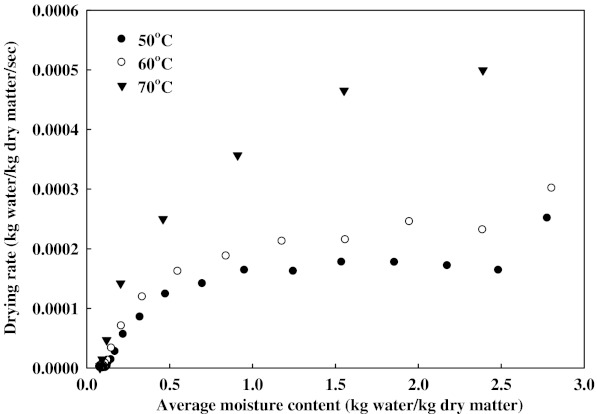
The drying rates versus average moisture content curve of Z. jujuba samples are illustrated in Fig. 3. The drying rates decreased continually with the decrease in moisture content and increased with the temperature. It was observed that there was no period with a constant drying rate; the whole drying process represented a falling-rate drying period. Similar results have been shown in thin-layer drying of other biomaterials, such as Asian white radish (Lee and Kim 2009), whole-fruit Chinese jujube (Fang et al. 2009), and Monukka seedless grapes (Xiao et al. 2010). Similar result was quoted in the case of apricot (Toğrul and Pehlivan 2003) and carrot (Prakash et al. 2004; Singh and Gupta 2007). The drying rates at high temperatures were always higher than that at low temperature when the moisture ratio was the same.
Fig. 3.
Drying rate curves of Z. jujuba slices determined at different temperatures
Modeling of the drying curves
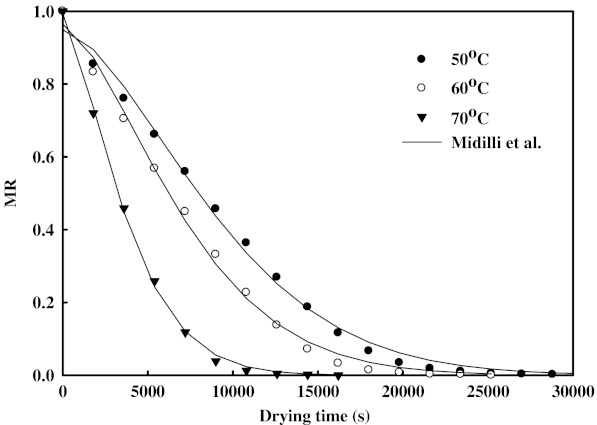
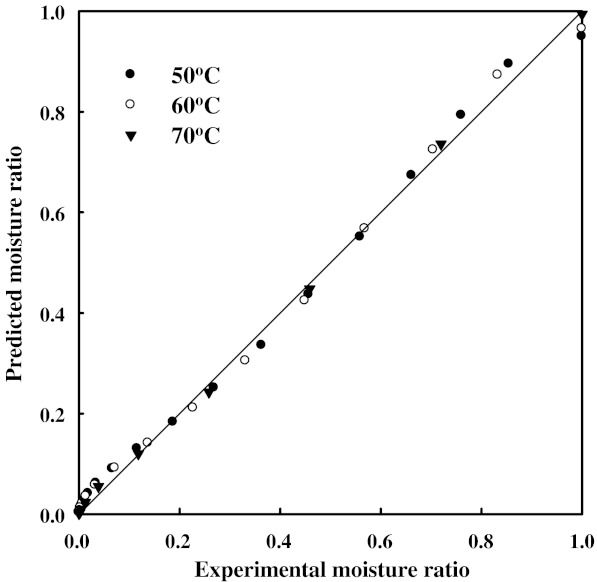
The moisture contents of Z. jujuba slices at different drying temperatures were converted to the moisture ratio (MR) and fitted to the 8 selected thin-layer drying models listed in Table 1. Table 2 shows the results of statistical tests (R2, RMSE, and χ2) performed in the proposed models. These statistical tests evaluate the goodness of fit on the experimental data and have been used in various food drying studies (Lee and Kim 2009; Vega-Gálvez et al. 2009; Mota et al. 2010). The values of mentioned tests were in the range of 0.9622–0.9988 for R2, 0.0125–0.0695 for RMSE, 0.00016–0.02459 for χ2. Based on the criteria of the highest R2 and the lowest RMSE, and χ2, the model of Midilli et al. was selected as the most suitable model to represent the thin-layer drying behavior of Z. jujuba slices as shown in Fig. 4. Figure 5 shows the comparison of the predicted moisture ratios obtained by Midilli et al. model and the experimental moisture ratio values at various drying air temperatures 50, 60, and 70 °C.
Table 2.
Statistical results obtained from various thin layer drying models
| No. | Model name | T (°C) | Model coefficients | R2 | RMSE | χ2 |
|---|---|---|---|---|---|---|
| 1 | Newton | 50 |
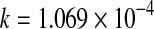 *** *** |
0.9622 | 0.0649 | 0.00460 |
| 60 |
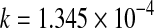 *** *** |
0.9678 | 0.0610 | 0.01171 | ||
| 70 |
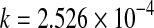 *** *** |
0.9809 | 0.0490 | 0.00431 | ||
| 2 | Page | 50 |
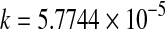 ***; m = 1.8516*** ***; m = 1.8516*** |
0.9622 | 0.0668 | 0.00447 |
| 60 |
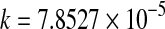 ; m = 1.7118 ; m = 1.7118 |
0.9678 | 0.0633 | 0.00401 | ||
| 70 | k = 0.0002***; m = 1.5265*** | 0.9809 | 0.0519 | 0.00528 | ||
| 3 | Henderson and Pabis | 50 | a = 1.0820***; k = 0.0001*** | 0.9688 | 0.0608 | 0.00550 |
| 60 | a = 1.0723***; k = 0.0001*** | 0.9733 | 0.0578 | 0.01702 | ||
| 70 | a = 1.0463***; k = 0.0003*** | 0.9832 | 0.0486 | 0.00376 | ||
| 4 | Logarithmic | 50 |
a = 1.1751***; 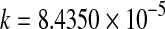 ***; c = −0.1326 ***; c = −0.1326 |
0.9866 | 0.0411 | 0.00169 |
| 60 | a = 1.1665***; k = 0.0001***; c = −0.1288 | 0.9894 | 0.0378 | 0.00197 | ||
| 70 | a = 1.0976***; k = 0.0002***; c = −0.0660 | 0.9910 | 0.0381 | 0.00267 | ||
| 5 | Two term exponential | 50 | a = 1.9348***; k = 0.0002*** | 0.9890 | 0.0361 | 0.00693 |
| 60 | a = 1.9200***; k = 0.0002*** | 0.9916 | 0.0324 | 0.00108 | ||
| 70 | a = 1.0000; k = 0.0002 | 0.9808 | 0.0521 | 0.00737 | ||
| 6 | Wang and Singh | 50 |
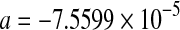 ***; ***; 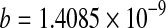 *** *** |
0.9969 | 0.0190 | 0.00032 |
| 60 |
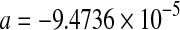 ***; ***; 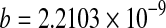 *** *** |
0.9982 | 0.0149 | 0.00016 | ||
| 70 |
a = −0.0002***; 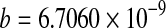 *** *** |
0.9921 | 0.0334 | 0.00403 | ||
| 7 | Modified Henderson and Pabis | 50 | a = 0.3826; b = 0.3601; c = 0.3355; g = h=k = 0.0001 | 0.9688 | 0.0695 | 0.00719 |
| 60 | a = 0.3757; b = 0.3611***; c = 0.3355***; g*** = h*** = k=0.0001 | 0.9733 | 0.0694 | 0.02459 | ||
| 70 | a = 0.3597; b = 0.3536; c = 0.3330; g = h*** = k = 0.0003 | 0.9832 | 0.0688 | 0.00751 | ||
| 8 | Midilli et al. | 50 |
a = 0.9497***; 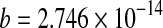 ; ; 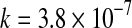 *, m = 1.596*** *, m = 1.596*** |
0.9953 | 0.0236 | 0.00063 |
| 60 |
a = 0.9651***; 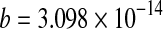 ; ; 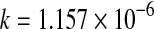 *, m = 1.517*** *, m = 1.517*** |
0.9959 | 0.0225 | 0.00061 | ||
| 70 |
a = 0.994***; 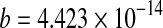 ; ; 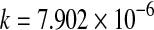 **, m = 1.407*** **, m = 1.407*** |
0.9988 | 0.0125 | 0.00018 |
***p < 0.0001, **p < 0.01, *p < 0.05
Fig. 4.
Drying curves of Z. jujuba slices determined at different temperatures. Solid line represents curve fitting using Midilli et al. model
Fig. 5.
Comparison of moisture ratios determined by experimentation and prediction using the Midilli et al. model for Z. jujuba slices
As seen in Fig. 5, the proposed model provided conformity between the experimental and predicted moisture ratios. There was a very good agreement between the experimental and predicted moisture ratio values, which closely band around a 45° straight line. The Midilli et al. model has also been suggested by others to describe the infrared drying of fresh apple slices (Toğrul 2005), thin layer drying of potato, apple, and pumpkin slices (Akpinar 2006), hot-air drying of eggplant (Ertekin and Yaldiz 2004), dill and parsley leaves (Doymaz et al. 2006), and the natural sun drying of long green pepper (Akpinar and Bicer 2008).
Moisture diffusivity and activation energy
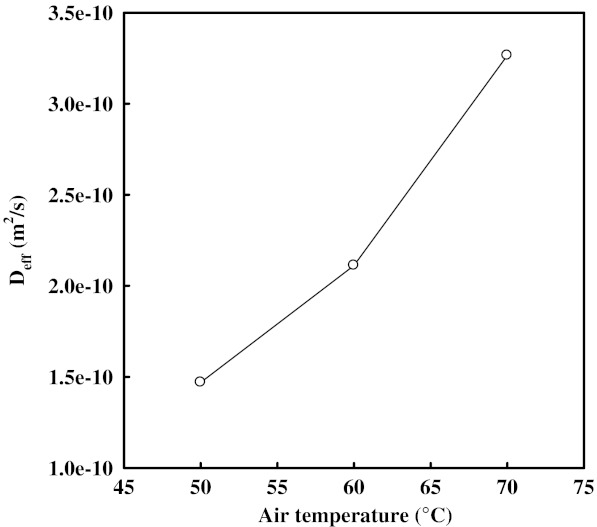
The effective moisture diffusivity values were 1.47 × 10−10, 2.11 × 10−10, and 3.27 × 10−10 m2/s for the samples dried at 50, 60, and 70 °C drying air temperatures, respectively. The values for Deff obtained from this study lie within the general range 10−11–10−9 m2/s for drying of food materials (Madamba et al. 1996; Kaleemullah and Kailappan 2006; Sacilik et al. 2006) and comparable with other reported values. In Fig. 6, it was noted that Deff increased progressively with the increase of drying air temperature. This might be explained by the increased heating energy, which would increase the activity of the water molecules leading to higher moisture diffusivity when samples were dried at higher temperature (Xiao et al. 2010). This finding agrees well with those of Hayaloglu et al. (2007) for drying strained yogurt using a convective type tray-dryer, Celma et al. (2008) for thin-layer infrared drying of wet olive husk, Celma et al. (2009) for infrared drying of industrial grape by-products, Lee and Kim (2009) for vacuum drying of Asian white radish, and Swasdisevi et al. (2009) for drying banana slices using combined far-infrared and vacuum drying.
Fig. 6.
Influence of the drying air temperature on the diffusion coefficient
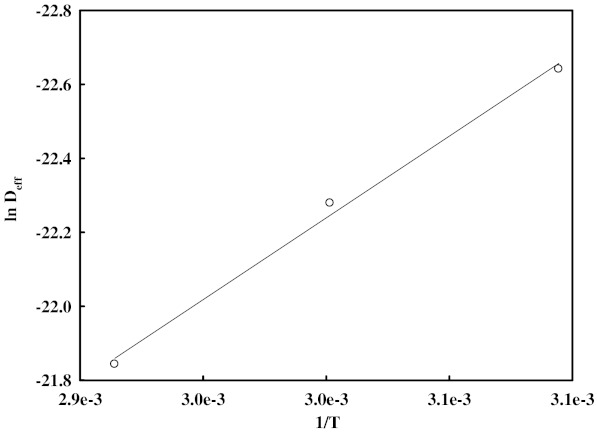
The activation energy value of Eq. (7) was determined as 36.76 kJ/mol by plotting ln Deff versus 1/T as shown in Fig. 7. The value obtained in this study is in agreement within the range of 15–40 kJ/mol for various foods reported by Rizvi (1986). The Ea of Z. jujuba slices is close to that of green beans (35.43 kJ/mol) (Doymaz 2005) and beans (39.41–39.47 kJ/mol) (Senadeera et al. 2003) but more than that of lettuce and cauliflower leaves (19.82 kJ/mol) (Lopez et al. 2000), red chillies (24.47 kJ/mol) (Kaleemullah and Kailappan 2005), apple slices (19.96–22.62 kJ/mol) (Kaya et al. 2007), and Asian white radish (16.49–20.26 kJ/mol) (Lee and Kim 2009).
Fig. 7.
Plot of ln Deff versus 1/T for calculating the active energy (Ea)
Conclusion
The drying kinetics of the Z. jujuba slices was investigated in a vacuum dryer as a single layer at the drying air temperatures of 50, 60, and 70 °C. Z. jujuba did not exhibit a constant drying rate period. The entire drying took place in a falling rate period. The moisture content and drying rate were influenced by the drying air temperature. Increases in drying air temperature caused decreases in drying time and increases in the drying rate. The effective diffusivity increased with the increase in the drying air temperature. Based on non-linear regression analysis, the Midilli et al. model was considered adequate to describe the thin-layer drying behavior of Z. jujuba slices. The effective diffusivity varied from 1.47 × 10−10 to 3.27 × 10−10 m2/s over the temperature range from 50 °C to 70 °C. The effective diffusivity increased with increasing temperature and it followed an Arrhenius relationship. The activation energy for moisture diffusion was found to be 36.76 kJ/mol. This information can be used to simulate vacuum drying process of Z. jujuba slices and improve efficiency of the drying process.
Acknowledgement
This research was supported by the Daegu University Research Grant, 2009.
Nomenclature
- a, b, c, g, h, m
coefficients in models
- Deff
effective diffusivity (m2/s)
- L
half thickness of the slab in sample (m)
- k
empirical constant in drying models
- M
moisture content (kg water/kg dry matter) at time t
- t
drying time (s)
- Me
equilibrium moisture content (kg water/kg dry matter)
- M0
initial moisture constant (kg water/kg dry matter) at time t = 0
- MR
moisture ratio
- MRexp
experimental moisture ratio
- MRpre
predicted moisture ratio
- n
number of constants in the model
- N
number of observations
- R
universal gas constant (J/mol K)
- R2
coefficient of determination
- RMSE
root mean square error
- χ2
reduced chi-square
- T
the absolute temperature (K)
References
- Agrawal YC, Singh RD (1977) Thin layer drying studies on short grain rice. ASAE Paper No. 3531, ASAE, St. Joseph, MI
- Akpinar EK. Determination of suitable thin layer drying curve model for some vegetables and fruits. J Food Eng. 2006;73:75–84. doi: 10.1016/j.jfoodeng.2005.01.007. [DOI] [Google Scholar]
- Akpinar EK, Bicer Y. Mathematical modelling of thin layer drying process of long green pepper in solar dryer and under open sun. Energy Convers Manag. 2008;49:1367–1375. doi: 10.1016/j.enconman.2008.01.004. [DOI] [Google Scholar]
- Official methods of analysis. 16. Washington: Association of Official Analytical Chemists; 2002. [Google Scholar]
- Ayensu A. Dehydration of food crops using a solar dryer with convective heat flow. Sol Energy. 1997;59:121–126. doi: 10.1016/S0038-092X(96)00130-2. [DOI] [Google Scholar]
- Celma AR, Rojas S, López-Rodríguez FL. Mathematical modelling of thin-layer infrared drying of wet olive husk. Chem Eng Process. 2008;47:1810–1818. doi: 10.1016/j.cep.2007.10.003. [DOI] [Google Scholar]
- Celma AR, López-Rodríguez FL, Blázquez FC. Experimental modelling of infrared drying of industrial grape by-products. Food Bioprod Process. 2009;87:247–253. doi: 10.1016/j.fbp.2008.10.005. [DOI] [Google Scholar]
- Cho DJ, Hur JW, Kim HY. Influencing factors in drying and shrinking characteristics of root vegetables. Korean J Food Sci Technol. 1989;21:203–211. [Google Scholar]
- Crank J. The mathematics of diffusion. 2. Oxford: Clarendon; 1975. [Google Scholar]
- Doymaz İ. Drying behavior of green beans. J Food Eng. 2005;69:161–165. doi: 10.1016/j.jfoodeng.2004.08.009. [DOI] [Google Scholar]
- Doymaz İ. The kinetics of forced convective air-drying of pumpkin slices. J Food Eng. 2007;79:243–248. doi: 10.1016/j.jfoodeng.2006.01.049. [DOI] [Google Scholar]
- Doymaz İ, Tugrul N, Pala M. Drying characteristics of dill and parsley leaves. J Food Eng. 2006;77:559–565. doi: 10.1016/j.jfoodeng.2005.06.070. [DOI] [Google Scholar]
- Ertekin C, Yaldiz O. Drying of eggplant and selection of a suitable thin layer drying model. J Food Eng. 2004;63:349–359. doi: 10.1016/j.jfoodeng.2003.08.007. [DOI] [Google Scholar]
- Fang S, Wang Z, Hu X. Hot air drying of whole fruit Chinese jujube (Zizyphus jujuba Miller): thin-layer mathematical modelling. Int J Food Sci Technol. 2009;44:1818–1824. doi: 10.1111/j.1365-2621.2009.02005.x. [DOI] [Google Scholar]
- Giri SK, Prasad S. Drying kinetics and rehydration characteristics of microwave-vacuum and convective hot-air dried mushrooms. J Food Eng. 2007;78:512–521. doi: 10.1016/j.jfoodeng.2005.10.021. [DOI] [Google Scholar]
- Hayaloglu AA, Karabulut I, Alpaslan M, Kelbaliyev G. Mathematical modeling of drying characteristics of strained yoghurt in a convective type tray-dryer. J Food Eng. 2007;78:109–117. doi: 10.1016/j.jfoodeng.2005.09.006. [DOI] [Google Scholar]
- Kaleemullah S, Kailappan R. Drying kinetics of red chillies in rotary dryer. Biosys Eng. 2005;92:15–23. doi: 10.1016/j.biosystemseng.2005.05.015. [DOI] [Google Scholar]
- Kaleemullah S, Kailappan R. Modelling of thin-layer drying kinetics of red chillies. J Food Eng. 2006;76:531–537. doi: 10.1016/j.jfoodeng.2005.05.049. [DOI] [Google Scholar]
- Karathanos VT. Determination of water content of dried fruits by drying kinetics. J Food Eng. 1999;39:337–344. doi: 10.1016/S0260-8774(98)00132-0. [DOI] [Google Scholar]
- Kaya A, Aydin O, Demirtas C. Drying kinetics of red delicious apple. Biosys Eng. 2007;96:517–524. doi: 10.1016/j.biosystemseng.2006.12.009. [DOI] [Google Scholar]
- Lee JH, Kim HJ. Vacuum drying kinetics of Asian white radish (Raphanus sativus L.) slices. LWT Food Sci Technol. 2009;42:180–186. doi: 10.1016/j.lwt.2008.05.017. [DOI] [Google Scholar]
- Lee JH, Park JW, Ha YS. Modeling drying characteristics of mushroom (Agaricus bisporus) depending on drying methods. Food Sci Biotechnol. 2004;10:677–681. [Google Scholar]
- Li JW, Fan LP, Ding SD, Ding XL. Nutritional composition of five cultivars of Chinese jujube. Food Chem. 2007;103:454–460. doi: 10.1016/j.foodchem.2006.08.016. [DOI] [Google Scholar]
- Lopez A, Iguaz A, Esnoz A, Virseda P. Thin-layer drying behavior of vegetable wastes from wholesale market. Drying Technol. 2000;18:995–1006. doi: 10.1080/07373930008917749. [DOI] [Google Scholar]
- Madamba PS. Thin layer drying models for osmotically pre-dried young coconut. Drying Technol. 2003;21:1759–1780. doi: 10.1081/DRT-120025507. [DOI] [Google Scholar]
- Madamba PS, Driscoll RH, Buckle KA. The thin layer drying characteristics of garlic slices. J Food Eng. 1996;29:75–97. doi: 10.1016/0260-8774(95)00062-3. [DOI] [Google Scholar]
- Martin MBS, Mate JI, Fernandez T, Virseda P. Modelling adsorption equilibrium moisture characteristics of rough rice. Dry Technol. 2001;19:681–690. doi: 10.1081/DRT-100103944. [DOI] [Google Scholar]
- McLoughlin CM, McMinn WAM, Magee TRA. Microwave-vacuum drying of pharmaceutical powders. Dry Technol. 2003;21:1719–1733. doi: 10.1081/DRT-120025505. [DOI] [Google Scholar]
- Midilli A, Kucuk H, Yapar Z. A new model for single layer drying. Dry Technol. 2002;20:1503–1513. doi: 10.1081/DRT-120005864. [DOI] [Google Scholar]
- Mota CL, Luciano C, Dias A, Barroca MJ, Guiné RPF. Convective drying of onion: kinetics and nutritional evaluation. Food Bioprod Process. 2010;88:115–123. doi: 10.1016/j.fbp.2009.09.004. [DOI] [Google Scholar]
- Prakash S, Jha SK, Datta N. Performance evaluation of blanched carrots dried by three different driers. J Food Eng. 2004;62:305–313. doi: 10.1016/S0260-8774(03)00244-9. [DOI] [Google Scholar]
- Ramesh MN, Wolf W, Tevini D, Jung G. Influence of processing parameters on the drying of spice paprika. J Food Eng. 2001;49:63–72. doi: 10.1016/S0260-8774(00)00185-0. [DOI] [Google Scholar]
- Rizvi SSH. Thermodynamic properties of foods in dehydration. In: Rao MA, Rizvi SSH, editors. Engineering properties of foods. New York: Marcel Dekker; 1986. pp. 190–193. [Google Scholar]
- Sacilik K, Elicin AK. The thin layer drying characteristics of organic apple slices. J Food Eng. 2006;73:281–289. doi: 10.1016/j.jfoodeng.2005.03.024. [DOI] [Google Scholar]
- Sacilik K, Unal G. Dehydration characteristics of Kastamonu garlic slices. Biosys Eng. 2005;92:207–215. doi: 10.1016/j.biosystemseng.2005.06.006. [DOI] [Google Scholar]
- Sacilik K, Elicin AK, Unal G. Drying kinetics of Uryani plum in a convective hot-air dryer. J Food Eng. 2006;76:362–368. doi: 10.1016/j.jfoodeng.2005.05.031. [DOI] [Google Scholar]
- Saravacos GD, Raouzeos GS. Diffusivity of moisture in air-drying of raisins. In: Mujumdar AS, editor. Drying 86, vol. 2. New York: Hemisphere Publishing Co; 1986. pp. 487–491. [Google Scholar]
- Senadeera W, Bhandari B, Young G, Wijesinghe B. Influence of shapes of selected vegetable materials on drying kinetics during fluidized bed drying. J Food Eng. 2003;58:277–283. doi: 10.1016/S0260-8774(02)00386-2. [DOI] [Google Scholar]
- Sharaf-Eldeen YI, Blaisdell JL, Hamdy MY. A model for ear corn drying. Trans ASAE. 1980;23:1261–1271. [Google Scholar]
- Singh B, Gupta AK. Mass transfer kinetics and determination of effective diffusivity during convective dehydration of pre-osmosed carrot cubes. J Food Eng. 2007;79:459–470. doi: 10.1016/j.jfoodeng.2006.01.073. [DOI] [Google Scholar]
- Swasdisevi T, Devahastin S, Sa-Adchom P, Soponronnarit S. Mathematical modeling of combined far-infrared and vacuum drying banana slice. J Food Eng. 2009;92:100–106. doi: 10.1016/j.jfoodeng.2008.10.030. [DOI] [Google Scholar]
- Toğrul H. Simple modeling of infrared drying of fresh apple slices. J Food Eng. 2005;71:311–323. doi: 10.1016/j.jfoodeng.2005.03.031. [DOI] [Google Scholar]
- Toğrul IT, Pehlivan D. Modelling of drying kinetics of single apricot. J Food Eng. 2003;58:23–32. doi: 10.1016/S0260-8774(02)00329-1. [DOI] [Google Scholar]
- Vega-Gálvez A, Andres A, Gonzalez E, Notte-Cuello E, Chacana M, Lemus-Mondaca R. Mathematical modelling on the drying process of yellow squat lobster (Cervimunida jhoni) fishery waste for animal feed. Anim Feed Sci Technol. 2009;151:268–279. doi: 10.1016/j.anifeedsci.2009.01.003. [DOI] [Google Scholar]
- Wang CY, Singh RP (1978) A single layer drying equation for rough rice. ASAE Paper No. 78-3001, ASAE, St. Joseph, MI
- Wang J, Sun J, Liao X, Chen F, Zhao G, Wu J, Hu X. Mathematical modeling on hot air drying of thin layer apple pomace. Food Res Int. 2007;40:39–46. doi: 10.1016/j.foodres.2006.07.017. [DOI] [Google Scholar]
- Westerman PW, White GM, Ross IJ. Relative humidity effect on the high temperature drying of shelled corn. Trans ASAE. 1973;16:1136–1139. [Google Scholar]
- Wu L, Orikasa T, Ogawa Y, Tagawa A. Vacuum drying characteristics of eggplants. J Food Eng. 2007;83:422–429. doi: 10.1016/j.jfoodeng.2007.03.030. [DOI] [Google Scholar]
- Xiao HW, Pang CL, Wang LH, Bai JW, Yang WX, Gao ZJ. Drying kinetics and quality of Monukka seedless grapes dried in an air-impingement jet dryer. Biosys Eng. 2010;105:233–240. doi: 10.1016/j.biosystemseng.2009.11.001. [DOI] [Google Scholar]
- Yagcioglu A, Degirmencioglu A, Cagatay F (1999) Drying characteristics of laurel leaves under different drying conditions. In Proceedings of the 7th international congress on agricultural mechanization and energy. Adana, Turkey, pp 565–569, May 26–27
- Zhang H, Jiang L, Ye S, Ye Y, Ren F. Systematic evaluation of antioxidant capacities of the ethanolic extract of different tissues of jujube (Ziziphus jujuba Mill.) from China. Food Chem Toxicol. 2010;48:1461–1465. doi: 10.1016/j.fct.2010.03.011. [DOI] [PubMed] [Google Scholar]