Optimization of process parameters for osmotic dehydration of papaya cubes

Abstract

Process temperature (30, 40 and 50 °C), syrup concentration (50, 60 and 70^o Brix) and process time (4, 5 and 6 h) for osmotic dehydration of papaya (Carica papaya) cubes were optimized for the maximum water loss and optimum sugar gain by using response surface methodology. The peeled and pre-processed papaya cubes of 1 cm size were immersed in sugar syrup at constant temperature water bath having syrup to papaya cubes ratio of 4:1 (w/w). The cubes were removed from bath at pre-decided time, rinsed with water and weighed. Initial moisture content of papaya samples were 87.5–88.5% (wb), which was reduced to 67.6–81.1% after osmotic dehydration in various experiments showing mass reduction, water loss and sugar gain in the range of 20.6–36.4, 23.2–44.5 and 2.5–8.1%, respectively. The weight reduction, water loss and sugar gain data were statistically analyzed and regression equation of second order were found the best fit for all the experimental data. Maximum water loss of 28% with optimum sugar gain of 4% was predicted for the 60^oBrix syrup concentration at 37 °C for syrup to fruit ratio as 4:1 in 4.25 h of osmotic dehydration.

Introduction

Fruits dried using hot air in conventional tray, cabinet or vacuum dryers have not much popular acceptance due to poor product quality. The problems associated with products obtained by air dehydration of fruits include “woody texture”, slow or incomplete rehydration of developed product, loss of juiciness and considerable shrinkage caused by collapsing of cells due to substantial amount of water loss (Rosa and Giroux 2001). It also brings about undesirable changes in colour, flavour and loss in nutritional quality (Jain and Verma 2003).

Osmotic dehydration is one of the potential preservation techniques for producing high quality products. This provides minimum thermal degradation of nutrients due to low temperature water removal process (Kar and Gupta 2001, Rastogi et al 2002, Sodhi et al 2006). Water removal in case of osmotic dehydration is influenced by many factors such as type and concentration of osmotic agents, temperature, agitation/circulation of solution, solution to sample ratio, thickness of food material and pre-treatment (Rosa and Giroux 2001). An attempt was made to optimize the selected 3 process parameters for maximum water loss and optimum sugar gain during the osmotic dehydration of papaya cubes.

Materials and methods

A widely grown ‘Taiwan Red’ variety of papaya (Carica papaya) was selected for the osmotic dehydration experiments. Physiologically matured papaya fruits were procured from local market. They were allowed to ripen at room temperature. Ripened papaya of uniform size, colour and firm texture were washed, peeled and cut in two halves. Seeds along with supporting fibres and layer of flesh were scrapped off. The peeled and prepared segments were further cut into 1 × 1 × 1 cm pieces.

Osmotic dehydration of papaya cubes

The initial moisture content of raw and pre-treated papaya cubes was determined by oven drying as described by Ranganna (1986). The cubes of 1 cm size were osmotically dehydrated using sugar syrup with syrup to fruit ratio of 4:1. The beakers were placed inside the constant temperature water bath. The syrup in the beakers was manually stirred at regular intervals to maintain uniform temperature. One beaker was removed from water bath at pre-decided time and the samples were immediately rinsed in flowing water and placed on tissue paper to remove surface moisture. The samples were weighed and their moisture contents determined.

The selection of the levels for processing parameters was made by preliminary experiments in which 5 levels of each process parameters viz., syrup concentration (40, 50, 60, 70, 80^o Brix), temperature (30, 40, 50, 60, 70 °C) and osmotic duration (2, 4, 6, 8, 10 h) were studied as suggested by earlier workers (Rosa and Giroux 2001, Torreggiani and Bertolo 2001, Nieto et al 2001, Ozen et al 2002, Jain and Verma 2003) for various fruits. The results of preliminary experiments revealed the levels of process variables and the same are given in Table 1.

Table 1.

Experimental layout for 3 variables and 3 levels response surface analysis

Treatment No	Syrup temp, °C	Syrup concentration, oBrix	Duration of osmosis, h
	T	C	θ
1	1 (50)	1 (70)	0 (5)
2	1 (50)	−1 (50)	0 (5)
3	−1 (30)	1 (70)	0 (5)
4	−1 (30)	−1 (50)	0 (5)
5	1 (50)	0 (60)	1 (6)
6	1 (50)	0 (60)	−1 (4)
7	−1 (30)	0 (60)	1 (6)
8	−1 (30)	0 (60)	−1 (4)
9	0 (40)	1 (70)	1 (6)
10	0 (40)	1 (70)	−1 (4)
11	0 (40)	−1 (50)	1 (6)
12	0 (40)	−1 (50)	−1 (4)
13	0 (40)	0 (60)	0 (5)
14	0 (40)	0 (60)	0 (5)
15	0 (40)	0 (60)	0 (5)

The data in parentheses indicate actual variables

Determination of water loss and sugar gain

The overall mass transport data namely, mass reduction, water loss (WL), sugar gain (SG) and soluble solid concentration were used to indicate the overall exchange of solute and water between papaya cubes and sugar syrup. The WL and SG were calculated using the following mass balance equations. The WL can be defined as the net loss of water from papaya cubes at time (θ) on the initial mass basis.

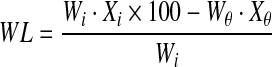1

The dry matter gain is related to SG and hence, the SG was the net gain in total solids by papaya cubes on initial mass basis.

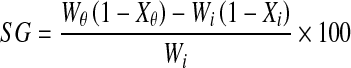2

and mass reduction can be defined as the net mass reduction of the food material on initial mass basis.

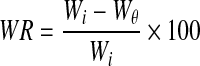3

Where

WL

water loss (g water/ 100 g initial mass of papaya cubes), %

SG

sugar gain (g/100 g initial mass of papaya cubes), %

W_θ

mass of papaya cubes after time θ , g

X_θ

water content as a fraction of mass of papaya cubes at time θ

W_i

initial mass of papaya cubes, g

X_i

water content as a fraction of initial mass of papaya cubes.

Experimental design

Fifteen experiments were performed as enumerated in Table 1 for obtaining WL and SG as responses for each treatment. To avoid bias, 15 runs were performed in a random order for estimation of the constants of Eq. 7. The decision for the range and centre points of the variables was taken through preliminary trial experiments.

The osmotic dehydration was assumed to be affected by 3 independent variables (regressor or factors), r_i, viz., sugar syrup temperature (T), sugar syrup concentration (C) and duration of osmosis (θ). The experimental design of input variables and layout are shown in Table 1 for these 3 levels and 3 variables under the response surface methodology (Floros and Chinnan 1987, Mudhar et al 1989, Saba 1994). All these variables were closely controlled and accurately measured during experimentation. The dependent variables, also referred as responses, Y_k (% WL and % SG) were measured experimentally.

It is assumed that the mathematical function f_k (k = 1, 2, 3,...n), exists for each response variable, Y_k in terms of the processing factors, r_i (i = 1, 2, 3,...m), such as

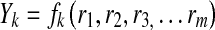The exact mathematical representation of the function (f) is either unknown or extremely complex. However, second order polynomial equation of the following form was assumed to relate the response, Y_k and the factors, r_i

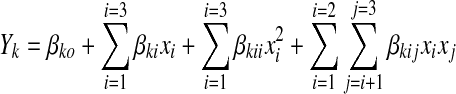4

where, β_ko, β_ki, β_kii and β_kij are constant coefficients and x_i, the coded independent variables are linearly related to T, C and θ In practice, the levels of independent variables change from one application to another. Therefore, the general designs are given in terms of standardized coded variables (x_i), which in any particular application are linearly related to r_i by the following equations:

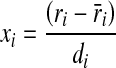5

where,

r_i

actual value in original units

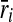
mean of high and low levels of r_i

d_i

spacing between the low and high levels of r_i.

In the present study, n = 2 and m = 3 and hence Eq. 3 can be written as

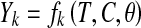6

where, T is the syrup temperature in °C; C is the syrup concentration in ^oBrix; θ is the duration of osmotic dehydration; h and k are WL and SG in %, respectively during osmotic dehydration process. Therefore, Eq. 4 takes the following form

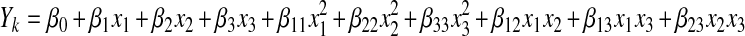7

Optimization of process variables

The response surface analysis involved fitting experimental values of WL/SG to general quadratic polynomial equation and subsequently optimizing the values with suitable optimization software (SAS). SAS statistical software was used to evaluate coefficients of the Eq. 7. The sum of squares for the models (regression) and total error were computed. The regression sums of squares were divided into 3 parts, namely, linear, quadratic and cross products as the terms appeared in Eq. 7. The significance of these sources of sum of squares was determined by computing the F-ratio and comparing with the tabulated value for respective degrees of freedom under particular probability level.

Determination of optimum condition of independent variables viz. syrup temperature, syrup concentration and duration of osmosis involved calculation of stationary points and exploration of the nature (shape) of the surface around these points. At the stationary point, the slope of response surface is zero in all directions (Box and Draper 1959).

Optimum level of SG

Dehydrated papaya should have a typical taste, flavour, colour and texture. To test these organoleptic characteristics, sensory evaluation was done on the basis of numerical sensory card based on BIS (1971).

The osmo-dehydrated products were prepared having 1, 2, 3, 4, 5 and 6% SG. The product was served for the evaluation to 20 panelists in the age range of 18 to 45 years. The over all acceptability of the dehydrated product is mainly governed by the taste of the product, so it was used to obtain the desired level of SG in the osmo-dehydrated products. The SG in osmotic dehydrated papaya cubes were given to the consumer panel and paired “t test” was conducted by assuming null hypothesis (H_o) as there is no significant difference between the mean score due to variation in SG of 2 levels.

Results and discussion

Optimum level of SG

During the preliminary experiments it was found that WL and SG during osmotic dehydration depend on temperature and concentration of syrup and duration of osmotic process. However, equilibrium could not be reached even after 10 h of osmotic dehydration. Although, the SG in samples increased with increase in initial concentration of syrup, at higher concentrations WL was not much. Therefore, it can be inferred that sweetness of the product was enhanced at higher concentration of sugar syrup without much advantage of WL. For this reason it was felt necessary to optimize SG in the final product for better acceptability.

To decide the optimum level of SG in the final product, the samples with varied SG levels were given to the consumers and they were asked to mention the quality grade scores as suggested in BIS (1971). The effect of SG in osmo-dehydrated papaya cubes on acceptability by the consumers is shown in Table 2. It can be observed from Table 2 that with increase in SG from 1 to 3%, the t-value was non-significant i.e., there was no significant change in the taste of the product. When SG was increased from 4 to 6%, there was significant change in the taste at 4 and 5% level. Therefore, it was concluded that SG of 4% was superior to 5%, since the mean score of 4% was 82.3, while the mean sensory score of 5% SG was 78.9.

Table 2.

Effect of sugar gain in osmo-dehydrated papaya cubes on sensory score

Sugar gain, %	Score	Consumer panel remarks	t-value
1	71.5	Good
2	72.3	Good	2.49 ns
3	73.2	Good	2.71 ns
4	82.3	Excellent	11.96*
5	78.9	Good	3.94*
6	72.4	Good	15.60*

ns non significant * significant at 5% level, Tabulated value at 5% level of significance t_0.05 (19)=2.86

Effect of process variables on mass reduction, WL and SG

Initial mass of papaya cubes taken in the study was in the range of 50.0–51.5 g. The final mass after osmotic dehydration was in the range of 32.1–40.9 g showing mass reduction in the range of 20.6 to 36.4% in the experimental range of study (Table 3). Similarly initial moisture content of papaya cubes was 87.5–88.5% (wb) which was reduced to 67.6–81.1% after osmotic dehydration in various experiments causing WL and SG of 23.2–44.5% and 2.56–8.1%, respectively.

Table 3.

Experimental data for water loss (WL) and sugar gain (SG) under different treatment conditions (IMC=initial moisture content, FMC=final moisture content)

Syrup temp, °C	Syrup concentration, oBrix	Duration of osmosis, h	IMC (wb), %	FMC (wb), %	Mass reduction, %	Water loss, %	Sugar gain, %
50	70	5	87.5	67.6	36.4	44.5	8.1
50	50	5	88.0	75.1	29.7	35.2	5.5
30	70	5	88.5	78.0	27.2	31.7	4.5
30	50	5	88.0	81.0	20.6	23.6	3.0
50	60	6	88.5	69.1	36.3	44.5	8.2
50	60	4	88.5	72.6	32.6	39.6	7.0
30	60	6	87.5	78.6	23.3	27.2	3.9
30	60	4	87.5	81.1	20.8	23.2	2.5
40	70	6	88.0	74.9	33.0	37.8	4.8
40	70	4	88.5	77.2	30.5	34.8	4.3
40	50	6	88.0	78.4	24.1	28.4	4.4
40	50	4	88.5	80.8	22.3	25.7	3.4
40	60	5	87.5	77.5	25.4	29.7	4.3
40	60	5	88.0	78.0	25.6	30.0	4.3
40	60	5	88.5	78.4	25.8	30.2	4.4

Optimization for WL

A second order polynomial equation (Eq. 7) was fitted with the experimental data presented in Table 3. Equation 8 gives the predicted WL % as a function of syrup temperature (x₁), concentration (x₂) and duration of osmosis (x₃) expressed in coded form. This equation was obtained using step-down regression method where factors with F-values less than one were rejected as suggested by Snedecor and Cochran (1967). High value of coefficient of determination (R² = 0.9902) obtained for response variable indicated that the developed model for WL accounted for and adequately explained 99.0% of the total variation.

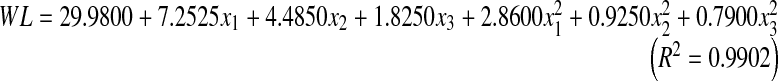8

Replacing x₁, x₂ and x₃ with 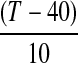, 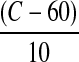and 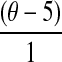, respectively (Eq. 5) in Eq. 8, the water loss in real terms of syrup temperature, concentration and duration of osmosis can be given by

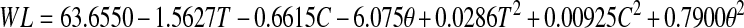9

The result of analysis of variance of Eq. 8 indicated that linear terms of syrup temperature, concentration and duration of osmosis were highly significant at 1% level of significance (Table 4). The quadratic terms of the syrup temperature was also highly significant, while the quadratic terms of syrup concentration and duration were not significant.

Table 4.

Analysis of variance (F-value calculated) for regression coefficient of Eqs. 8 and 10

	Linear terms		Quadratic terms		Interaction terms
	Water loss	Sugar gain	Water loss	Sugar gain		Sugar gain
X1	264.1379*	115.2418*	18.95812*	17.47208*	x1 x2	1.334578 ns
X 2	101.0137*	15.52209*	1.983110 ns
X 3	16.72558*	8.784654*	1.44649 ns

* Significant p ≤ 0.01 ns not significant

The effect of individual variables and their interactions on WL can be explained with the help of coefficients of Eq. 8. It was observed that the duration of osmosis contributed maximum for WL, followed by temperature and concentration of syrup. The presence of quadratic terms of the variables in Eq. 9 indicated curvilinear nature of the response surface (i.e. observed WL). Negative coefficient for syrup temperature, concentration and duration indicated that increase in the level of these 3 variables decreased WL. However, the positive coefficients for their quadratic terms suggested that an excessive increase in the levels of these variables resulted in significant increase in WL %.

Optimization for SG

A second order polynomial equation (Eq. 7) was fitted with the experimental data presented in Table 3. Equation 10 gives the predicted SG % as a function of syrup temperature (x₁), concentration (x₂) and duration of osmosis (x₃) expressed in coded form. This equation was obtained using step-down regression method where factors with F-values less than one were rejected as suggested by Snedecor and Cochran (1967). High value of coefficient of determination (R² = 0.9727) obtained for response variable indicated that the developed model for SG accounted for and adequately explained 97.3% of the total variation.

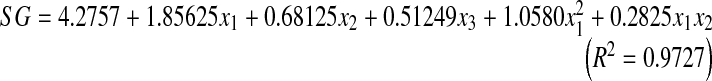10

and SG in real process parameters is given by

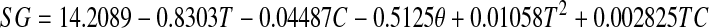11

The result of analysis of variance of Eq. 10 indicated that linear terms of syrup temperature, concentration and duration of osmosis were highly significant at 1% level (Table 4). The quadratic terms of the syrup temperature was also highly significant, while the interaction term of syrup concentration and temperature was not significant.

The effect of individual variables and their interactions on SG can be explained with the help of coefficients of Eq. 10. It was observed that the syrup temperature contributed maximum for SG, followed by duration of osmosis and concentration of syrup. The presence of quadratic terms of the variable in Eq. 11 indicated curvilinear nature of the response surface (i.e. observed SG). Negative coefficient for syrup temperature, concentration and duration indicated that increase in the level of these 3 variables decreased SG. However, the positive coefficients for the quadratic and interaction term suggested that an excessive increase in the levels of these variables resulted in significant increase in SG %.

Localization of optimum conditions

Table 5 shows the statistical analysis for the overall effects of process variables on 2 parameters. This analysis revealed that syrup temperature and concentration both had most significant effect, whereas the third variable i.e. duration of osmosis had no significant overall effect for WL and SG. However, for SG only syrup temperature showed significant effect. Thus, the syrup temperature (x₁) showed a significant effect on the osmotic dehydration process and can be considered as the most sensitive factor influencing the osmotic process.

Table 5.

Analysis of variance (sum of squares) for the overall effect of process variables on two responses

Process variable	Water loss	Sugar gain
Syrup temperature (x1)	283.09602**	134.048458**
Syrup concentration(x2)	102.99681**	16.856668 ns
Duration of osmosis(x3)	18.172076 ns	8.784654 ns

** Significant at p ≤ 0.01 ns not significant

Syrup temperature, °C

The optimum level of these variables was established using a procedure described by Myers (1971). The stationary points show the specific combination of input variables for yielding the optimum values of responses (37 °C syrup temperature, 60 ^oBrix syrup concentration for 4.25 h of osmotic dehydration). It could be seen that optimum response for each variable did not fall exactly in the experimental region. Hence, constraints were set such that the selected variables (temperature and time) would be minimum for the most important product attribute and close to the optimum for others. The SG, the most important quality (sweetness attribute) was considered for optimization.

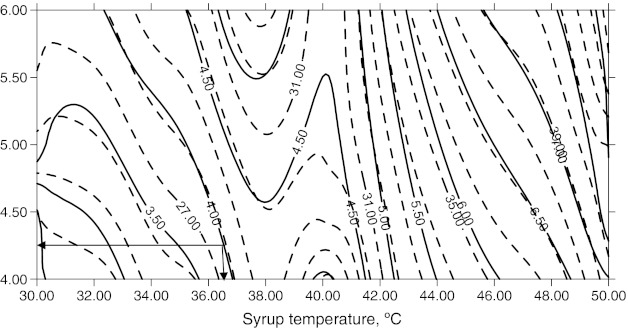
The contours were plotted for WL and SG as responses and the syrup temperature, (x₁) and duration of osmosis (x₃) as variables with syrup concentration (x₂) as constant. The super imposed contour plots for WL and SG are shown in Fig. 1 for constant syrup concentration 60 ^oBrix (x₂ = −0.01, rounded). The contour line of 4% sugar gain is observed in Fig. 1, at which the optimum sugar level was assessed by organoleptic evaluation.

Fig. 1.

Superimposed contour plots of water loss and sugar gain at constant syrup concentration of 60 ^oBrix

The contour interval of 1 and 0.5% was taken for WL and SG, respectively. It can be seen that corresponding to the 4% SG, the WL was ~ 28%. Considering the input variables, syrup temperature and osmosis time (x₁ and x₃) both should have a minimum possible value from economic point of view. Thus, the optimum temperature of the syrup was ~37 °C where the 4% SG contour intersected contour of WL, the corresponding time of osmosis is about 4.25 h. Hence, the co-ordinates of 37 °C and 4.25 h, for temperature and time, respectively, yielded SG of 4% with corresponding WL of 28%.

Conclusion

The effect of sugar syrup concentration, syrup temperature and duration of osmosis during the osmotic dehydration process was investigated and these were optimized. The regression equations of second order polynomial were found to predict the behaviour of osmotic dehydration process of papaya cube. If the papaya cubes were osmo-dehydrated in sugar syrup having 37 °C syrup temperature, 60^oBrix syrup concentration for 4.25 h then 28% of WL could take place with 4% SG which would be the good quality market acceptable product. Further, the developed model can also be used to predict WL and SG in papaya cubes during osmotic dehydration process, which can also be helpful to the food processing industry.