Abstract
A ready-to-reconstitute formulation of Basundi, a popular Indian dairy dessert was subjected to storage at various temperatures (10, 25 and 40 °C) and deteriorative changes in the Basundi mix were monitored using quality indices like pH, hydroxyl methyl furfural (HMF), bulk density (BD) and insolubility index (II). The multiple regression equations and the Arrhenius functions that describe the parameters’ dependence on temperature for the four physico-chemical parameters were integrated to develop mathematical models for predicting sensory quality of Basundi mix. Connectionist model using multilayer feed forward neural network with back propagation algorithm was also developed for predicting the storage life of the product employing artificial neural network (ANN) tool box of MATLAB software. The quality indices served as the input parameters whereas the output parameters were the sensorily evaluated flavour and total sensory score. A total of 140 observations were used and the prediction performance was judged on the basis of per cent root mean square error. The results obtained from the two approaches were compared. Relatively lower magnitudes of percent root mean square error for both the sensory parameters indicated that the connectionist models were better fitted than kinetic models for predicting storage life.
Keywords: Kinetics, Connectionist, ANN models, Basundi, Dairy products, Shelf life prediction
Introduction
Basundi is a dairy dessert extremely popular in western parts of India. The product represents sweetened concentrated milk with caramel flavour, creamy consistency and soft textured flakes distributed uniformly in the liquid (Aneja et al. 2002). However one of the major limitations for its marketing over long distances is its relatively limited shelf life which is less than a week at room temperature. To overcome this, a ready-to-reconstitute formulation was developed using osmo-air drying (dehydration in sugar syrup followed by air drying) process. Although the process was intended for longer shelf life, it was expected that like most other dried milk products, certain deteriorative reactions may continue to progress over prolonged storage time. These could be monitored by following the change in pH, hydroxyl methyl furfural (HMF) concentration, bulk density and insolubility index as a function of storage time and temperature. These physico-chemical events occurring in the product may thus also significantly affect the sensory quality of the product.
Shelf life prediction using mathematical models based on kinetic concept is one of the widely researched areas in food science. A kinetic model represents a series of differential equations which are integrated to give, with time, the concentrations of reaction intermediates and products. These mathematical models provide an output (such as quantitative estimate of a quality parameter) based on a set of input data (time, temperature) and can be successfully employed to predict quality parameters and shelf life of a wide range of processed foods (Albanesea et al. 2007; Corradini and Peleg 2007; Singh et al. 2009). Shelf life prediction models help the manufacturers and also the food quality regulating agencies to critically evaluate the quality of such foods in the marketing chain.
Connectionist model also known as artificial neural network (ANN) is a computational technique which mimics the structure and function of human brain to some extent (Mehrotra et al. 1996). It is capable of solving extremely complex problems with self-reliant investigation of relationship between input and output variables based on a given set of data values. The ability of learning through examples makes the ANN more versatile and has shown its merit in solving the problems dealing with uncertainties, non linear approximation and noisy data environment. It has found wide application in diverse areas of food science research viz., changes in physical properties of dried carrots (Kerdpiboon et al. 2007), food quality evaluation in production ovens (Lewis et al. 2008), sensory quality of meat (Vestergaard et al. 2007), noodles (Tulbek et al. 2003) and Ultra-high-temperature (UHT) milk ( Singh et al. 2009). The objective of this paper is therefore to develop mathematical models based on kinetic concept and connectionist model using back propagation neural network and subsequently evaluate the two for accuracy of prediction of sensory parameters of Basundi mix.
Materials and methods
Data generation
Ready-to-reconstitute Basundi mix was manufactured in the experimental dairy of National Dairy Research Institute. The product was stored at three temperatures viz. 10, 25 and 40 °C and analysed at periodic intervals for various physico-chemical and sensory attributes. Out of the several attributes evaluated during storage of the product, the quality parameters which statistically showed higher magnitude of correlation coefficients with sensory parameters were used as the input parameters for model building exercise. Besides pH, hydroxy methyl furfural (HMF) - extent of browning measured by the method of Keeney and Bassette (1959), bulk density (BD) - measure of volume of powder measured as per method recommended by Sjollema (1963) and insolubility index (II) - quantity of suspended or settled solids upon reconstitution measured by the method of ADMI (1971), the other input parameters were temperature (°C) and storage period (weeks). A sensory panel consisting of 5 trained judges drawn from the faculty of Dairy Technology Division evaluated the samples of Basundi mix. The judges were served with 30–40 ml. of reconstituted and cooled Basundi mix. A 9-point hedonic scale was used for evaluating sensory parameters namely flavour, colour and appearance, consistency and overall acceptability.
Kinetic models
Changes in the quality of foods are often described by applying fundamental principles of chemical kinetics. These changes are generally modeled by means of a zero-, 1st-, or 2nd-order reaction (Labuza 1984; Saguy and Karel 1980; Singh 2000). The general rate law for a single reactant at concentration ‘c’ can be written as:
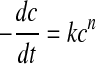 |
1 |
Linear decrease in ‘c’ implies that the rate change in the concentration of the reactant is constant throughout the period of study and it does not depend on the concentration of ‘c’, this linear relationship between the reactant and treatment time will be a zero order reaction. It follows that for n = 0 for a decomposition reaction:
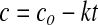 |
2 |
Where ‘co’ represents initial value of the reactant and ‘c’ is the amount of that reactant at time ‘t’.
First-order reactions have also been frequently reported for many reactions in foods. It relates concentration of the reactant ‘c’ that increases in an exponential manner with storage time. The rate of change in the reaction is thus dependent on the concentration of reactant ‘c’ implying that with the progression of time, the concentration of the reactant decreases and so does the rate of reaction. Thus the equation where n = 1 can be written as:
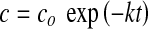 |
3 |
Where c is the quantitative estimate of reactant remaining at time ‘t’.
The influence of temperature on the reaction rate may be described by using the Arrhenius relationship:
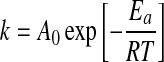 |
4 |
Where, AO is “pre-exponential factor” (sometimes called the frequency factor or Arrhenius constant), Ea is the activation energy (kJ/mol), R is gas constant (8.314 J/mol K) and T is the absolute temperature (K = 273 + °C).
The model for prediction of shelf life of Basundi mix was based on development of multiple regression equations with deteriorative changes such as pH, HMF, BD and II as explanatory variables while the sensory flavour (FS) and total sensory scores (TS) were the dependent variables. These equations were then integrated with the function of temperature dependence for the four explanatory variables. The performances of the two models were tested by per cent root mean square error (RMS) as described later in Eq. 8.
Connectionist model
Connectionist model is an intelligent data processing system. The predictive ability of connectionist model automatically comes from the data set presented while training the network. It consists of a set of neurons, known as processing units and these units are arranged in several parallel layers for solving complex unstructured non linear problems with high speed. Several architecture and algorithms have been proposed to address complex cognitive problems related to prediction, classification, pattern recognition etc. A multilayer feed forward network with backpropagation of error learning mechanism is the most commonly used neural network architecture and have shown excellent results in dealing with functional approximation problems (Huang et al. 2007). Such neural network consists of input layer, hidden layer(s) and output layer. Each layer has a specific role in execution of the neural network.
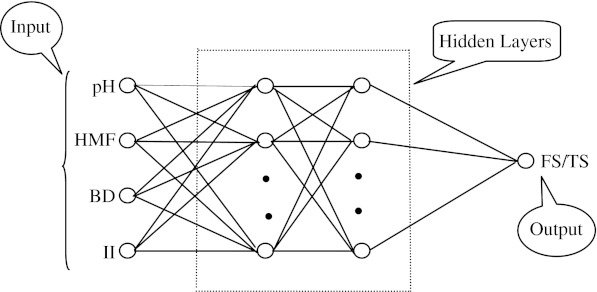
The backpropagation is a method to train a multilayer feed forward network for performing a given task in supervisory learning mode with a given set of input data and known results. At each iteration the output response of the network is compared with desired output and then the difference of network response and desired output is computed. This error propagates backwards from the output layer to input layer through hidden layers and in this process weights and biases of different layers are adjusted accordingly. This process continues until the number of iterations are completed or algorithm converges i.e. the error goal is achieved. A well trained neural network produces reasonable output response when given a new set of data. General architecture of a multilayer feed forward network with two hidden layers developed for this study is shown in Fig. 1.
Fig. 1.
Neural network model for prediction of sensory parameters
Network architecture
In the present study a multilayer feed forward network with backpropagation algorithm was developed with 4 nodes in input layer and the one node in output layer for producing the network response. The network was tested with 1 and 2 hidden layers with 3 to 20 nodes in each hidden layer. Initial weights and bias matrix was randomly initialized between −1 and 1. Learning rate and performance goal were set automatically by the training algorithms. A non linear transformation (or activation) function tangent sigmoid (Eq. 5) was used to compute the output from summation of weighted inputs of neurons in each hidden layer. A pure linear transformation function was used at output for getting network response.
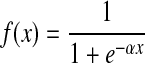 |
5 |
where, x is weighted sum of inputs and α is a constant
The performance of neural network model was evaluated using the relative percent root mean square (RMS) given as under:
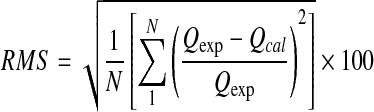 |
6 |
where,
- Qexp
Observed value
- Qcal
Predicted value
- N
Number of observations
The input and output layer of the network included the following variables. The network was simulated separately for predicting FS (Flavor Score) and TS (Total Sensory Score). Experimentally, 140 records were generated for input/ output data sets for modeling the network.
Input parameters
pH – pH Value
HMF – Hydroxy Methyl Furfural
BD – Bulk Density
II – Insolubility Index
Output parameters
FS – Flavor Score
TS – Total Sensory Score
Training and simulation
The modeled multilayer feed forward neural network was trained in a supervisory mode and several variant of backpropagation algorithm like Gradient descent, Widrow Hoff learning rule, Conjugate gradient, Quasi-Newton, Levenberg-Marquardt, Resilient backpropagation and Bayesian regularization were tested for a given set of input/ output data. Data set of 140 records was partitioned at random into two subsets namely training subset comprising of 112 records (80% of total records) to train the neural network and the test subset comprising of 28 records (20% of total records) to validate the network. As per the requirement of algorithms to get the best results, the data was preprocessed to scale the input and output data in the range [−1 1] using the feature prestd of neural network tool box of MATLAB 7.0. The network response was again converted to its normal values using poststd feature of neural network tool box of MATLAB 7.0.
The network was trained using the above mentioned learning algorithms for up to 2000 epochs or till the algorithms truly converged. The parameters like learning rate, performance/ error goal and learning rate increment were used at the default setting of the algorithms in the MATLAB. The number of hidden layers and number of neurons in each layer were judiciously selected based on the experience of earlier workers (Mehrotra et al. 1996; Singh et al. 2009) as very small number of nodes may not be powerful enough to learn the task whereas a large number of nodes could lead to often a cumbersome algorithm. In the present study the network was simulated with one and two hidden layers and number of neurons in each layer varied from 3 to 20. Weights and biases were adjusted automatically by the back-propagation training algorithm. Most of the time the algorithms were observed to truly converge which means that performance/ error goal was achieved. The network was trained a number of times with training data set to get consistent results. The prediction performance was tested using a new data set (test data).
One of the main problems associated with neural network is over prediction while training the network with back-propagation algorithm. The error in the training data set is computed to a very small value but when a new data set is employed to the network the error becomes large. In this situation, network memorizes the training examples but it does not learn to apply it to new situation (Mittal and Zhang 2000). To overcome the problem of over prediction, MATLAB 7.0 provides a Bayesian regularization method. This method optimizes the regularization parameters in an automated fashion.
Results and discussion
Modeling of data using reaction kinetics concept
The deteriorative changes in the ready-to-reconstitute Basundi mix represented by pH, HMF, BD and II served as the explanatory variables whereas sensory properties of the stored product evaluated in terms of flavour and total score were the dependent variables. Fitness of the data sets for the order of the reactions was determined based on r2 values obtained for each of the reactions. The results revealed that changes in pH, BD and II were best described by zero order reactions while HMF formation followed first order reaction kinetics (Table 1). Reaction rate constants of the selected reaction orders were then modeled using Arrhenius model to determine their temperature dependence over the temperature range of 10–40 °C. The Arrhenius relationship of the rate constants of pH, BD and II with temperatures of storage showed very high coefficients of determination (0.93, 0.95 and 0.99 respectively), while HMF showed a fairly acceptable fit (r2 = 0.79). Activation energy for pH, BD and II were 447.49, 896.18 and 757.77 kJ/mol respectively whereas for HMF it was 686.20 kJ/mol. The Arrhenius equations (Eq. 7–10) for each of the quality parameters are given below
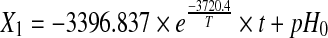 |
7 |
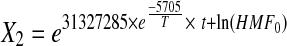 |
8 |
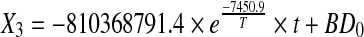 |
9 |
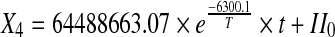 |
10 |
Table 1.
Summary of kinetic parameters for stored Basundi mix
| Order of reaction | Physico-chemical parameters | Activation energy (Ea, kJ/mol) | Arrhenius Constant (A0) | r2 |
|---|---|---|---|---|
| Zero | pH | 447.49 | 3.3968 × 103 | 0.93 |
| First | HMF | 686.20 | 3.1327 × 107 | 0.79 |
| Zero | Bulk density (BD) | 896.18 | 8.1037 × 108 | 0.95 |
| Zero | Insolubility Index (II) | 757.77 | 6.4489 × 107 | 0.99 |
The following multiple regression equations were developed for predicting flavour score (FS) and total sensory score (TS) using the four quality parameters from experimental data:
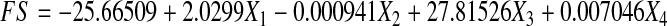 |
11 |
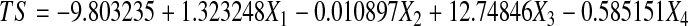 |
12 |
The multiple regression equations derived with FS (Eq. 11) and TS (Eq. 12) as dependent variables were then integrated with kinetic equations (Eq. 7–10) of the four explanatory variables (pH, HMF, BD and II) and the following prediction models were developed.
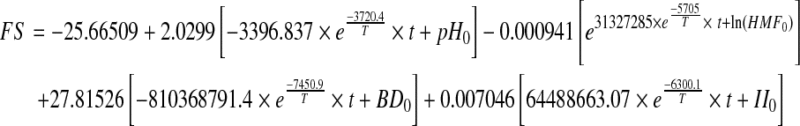 |
13 |
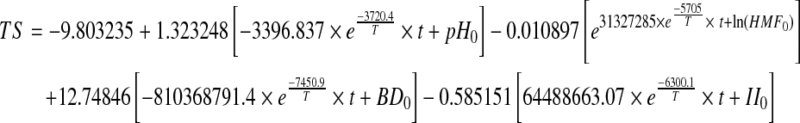 |
14 |
Where t = Storage period in weeks, T = Storage temperature (K), and pH0, HMF0, BD0 and II0 are the initial values of respective input parameters.
The flavour and total sensory scores were predicted and the observed values were plotted against the predicted values. The scatter plots for flavour score (Fig. 2a) and total sensory score (Fig. 2b) showed a certain degree of spread. These observations are supported by other performance parameters listed in Table 2. The MSE and RMS for Kinetic model for flavour score (FS) were 0.38 and 12.22 respectively while in case of total sensory scores (TS), MSE and RMS were relatively lower at 0.08 and 4.28 respectively. This variation was also corroborated well by the low correlation coefficient (0.74) in case of FS as compared to value of correlation coefficient (0.80) for TS.
Fig. 2.
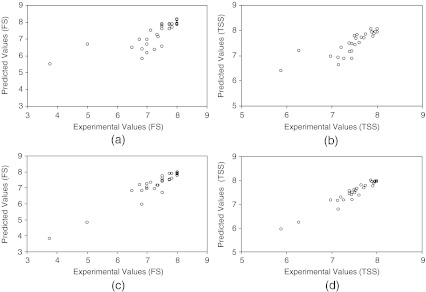
Predictability of the kinetic {(a) and (b)} and ANN {(c) and (d)} models for sensory scores of Basundi mix
Table 2.
Performance matrix for kinetic and ANN models
| Performance parameters | Flavour score | Total sensory score | ||
|---|---|---|---|---|
| Kinetic | ANN | Kinetic | ANN | |
| MSE | 0.38 | 0.09 | 0.08 | 0.02 |
| RMS | 12.22 | 4.13 | 4.28 | 1.71 |
| r | 0.74 | 0.94 | 0.80 | 0.96 |
ANN based modelling of data
Among all the algorithms mentioned above in materials and methods section, Bayesian regularization algorithm gave low error (RMS) and consistent results during training of the network. It has the ability to adjust the network performance parameter for improving generalisation (i.e. to avoid over fitting and under fitting) of network automatically as per the situation. Therefore only the results of this algorithm are being discussed here. Values for network parameters such as learning rate, momentum factor, performance goal etc. were set to the default values of the algorithm. The best performance of the Bayesian regularization algorithm for FS as well as TS was obtained at 280 and 340 epochs respectively with 2 hidden layers of 3 neurons in each hidden layer. The final weights and biases matrices of trained neural networks for the flavour and total sensory scores have been given in Tables 3 and 4 respectively. The observed values of the data when plotted against ANN predicted values showed high correlation coefficients (r) of 0.94 and 0.96 respectively for the FS and TSS (Table 2). The scatter plots for observed and predicted values of flavour score (Fig. 2c) and total sensory score (Fig. 2d) showed very narrow spread of data. Other performance parameters viz., MSE and RMS were 0.09 and 4.13 for FS and 0.02 and 1.71 for TSS models respectively indicating high goodness of fit for the data (Table 2). These performance parameters thus clearly established that ANN based prediction models are better positioned to predict the sensory quality as compared to the mathematical models developed using kinetic functions.
Table 3.
Final weights and biases matrices for Flavour score using ANN model
| Layer | Neuron No. | Weights | Biases | |||
|---|---|---|---|---|---|---|
| 1st Hidden | 1 | 0.4045 | −0.0052 | −0.2904 | −0.3547 | 1.6018 |
| 2 | 1.1821 | −0.0738 | −0.4721 | 0.2534 | −0.5505 | |
| 3 | −0.4934 | 0.7955 | 0.0386 | −0.6275 | 0.0371 | |
| 2nd Hidden | 1 | 1.9133 | −1.2134 | 1.6758 | 0.0255 | |
| 2 | 0.4447 | −0.4731 | −0.9426 | 0.6999 | ||
| 3 | −0.1969 | −0.0115 | −0.2678 | −0.2801 | ||
| Output | 1 | 2.0880 | −1.0488 | 0.4663 | −0.8070 | |
Table 4.
Final weights and biases matrices for Total Sensory score using ANN models
| Layers | Neuron No. | Weights | Biases | |||
|---|---|---|---|---|---|---|
| 1st Hidden | 1 | −0.4189 | 0.0707 | −0.1598 | 0.2799 | −0.1758 |
| 2 | −1.4888 | −0.0929 | 0.2794 | −0.2164 | −0.2404 | |
| 3 | 0.0177 | −0.4635 | 0.6930 | −0.5784 | −0.6718 | |
| 2nd Hidden | 1 | 1.2384 | −0.3350 | 0.2977 | −0.0781 | |
| 2 | −0.6004 | 1.0949 | −1.3462 | −0.7860 | ||
| 3 | 1.2384 | −0.3350 | 0.2977 | −0.0781 | ||
| Output | 1 | −1.6520 | 1.8077 | −1.6521 | −0.4348 | |
Conclusion
Mathematical models for prediction of sensory quality of Basundi Mix, an Indian dairy product were developed using two approaches: chemical kinetics and artificial neural network. The kinetic models were constructed based on the kinetic functions of the four physico-chemical indices of deteriorative changes. The connectionist models were developed using ANN back-propagation algorithms with four input parameters. The output parameters for both types of models were flavour and total sensory scores. The correlation between experimental and predicted values was worked out both in case of kinetic and ANN model for flavour and total sensory score in order to judge the performance of both the models. It was revealed that the magnitude of correlations coefficient for ANN model were 0.94 for flavour score and 0.96 for total sensory score which were relatively higher than kinetic model (0.74 for flavour score and 0.80 for total sensory score), suggesting superiority of ANN model over kinetic model. This fact is also corroborated by the relatively lower values of percent per cent root mean square and MSE for the ANN models.
Nomenclature
- c
Concentration of the reactant
- k
Rate constant
- n
Order of reaction
- R
Gas constant (8.314 J K−1 mol−1)
- T
Absolute temperature (K)
- RMS
Root mean square per cent
- t
Time, min
- Ea
Activation energy (kJ/mol)
- A0
Pre-exponential factor
- Qexp
Experimental value
- Qcal
Calculated value
- N
Number of observations
- ANN
Artificial neural network
- FS
Flavour score
- TS
Total sensory score
- HMF
Hydroxyl methyl furfural
- BD
Bulk density
- II
Insolubility index
References
- ADMI (1971) Determination of solubility index standards for grades of dry milks including methods of analysis, Bull 916 (revised). Chicago: USA
- Albanesea D, Russoa L, Cinquantab L, Brasielloa A, Di Matteo M. Chemical changes in minimally processed green asparagus during cold-storage. Food Chem. 2007;101:274–280. doi: 10.1016/j.foodchem.2006.01.048. [DOI] [Google Scholar]
- Aneja RP, Mathur BN, Chandan RC, Banerjee AK. Technology of Indian milk products. Delhi: Dairy India Publication; 2002. [Google Scholar]
- Corradini MG, Peleg M. Shelf-life estimation from accelerated storage data. Trends Food Sci Technol. 2007;18:37–47. doi: 10.1016/j.tifs.2006.07.011. [DOI] [Google Scholar]
- Huang Y, Kangas LJ, Rasco BA. Applications of artificial neural networks (ANNs) in food science. Crit Rev Food Sci Nutr. 2007;47:113–126. doi: 10.1080/10408390600626453. [DOI] [PubMed] [Google Scholar]
- Keeney M, Bassette R. Detection of intermediate compounds in the early stages of browning reaction in milk products. J Dairy Sci. 1959;42:945–960. doi: 10.3168/jds.S0022-0302(59)90678-2. [DOI] [Google Scholar]
- Kerdpiboon S, Kerr WL, Devahastin S. Neural network prediction of physical property changes of dried carrot as a function of fractal dimension and moisture content. Food Res Int. 2007;39:1110–1118. doi: 10.1016/j.foodres.2006.07.019. [DOI] [Google Scholar]
- Labuza TP. Application of chemical kinetics to deterioration of foods. J Chem Educ. 1984;61:348–358. doi: 10.1021/ed061p348. [DOI] [Google Scholar]
- Lewis E, Sheridan C, O’Farrell M, Flanagan C, Kerry JF, Jackman N. Optical fibre sensors for assessing food quality in full scale production ovens—a principal component analysis and artificial neural network based approach. Nonlinear Analysis: Hybrid Systems. 2008;2:51–57. doi: 10.1016/j.nahs.2006.05.008. [DOI] [Google Scholar]
- Mehrotra K, Mohan CK, Raka S. Elements of artificial neural networks. Cambridge: MIT Press; 1996. [Google Scholar]
- Mittal GS, Zhang J. Use of artificial neural network to predict, temperature, moisture and fat in slab-shaped foods with edible coatings during deep fat frying. J Food Sci. 2000;65:978–983. doi: 10.1111/j.1365-2621.2000.tb09403.x. [DOI] [Google Scholar]
- Saguy I, Karel M. Model of quality deterioration during food processing and storage. Food Tech. 1980;34:78–85. [Google Scholar]
- Singh RP (2000) Scientific principles of shelf life evaluation. In: Shelf life evaluation of foods. Aspen Publishers Inc, Maryland
- Singh RRB, Ruhil AP, Jain DK, Patel AA, Patil GR. Prediction of sensory quality of UHT milk: a comparison of kinetic and neural network approaches. J Food Eng. 2009;92:146–151. doi: 10.1016/j.jfoodeng.2008.10.032. [DOI] [Google Scholar]
- Sjollema A. Some investigation on the free flowing properties and porosity of milk powders. Neth Milk Dairy J. 1963;17:45–253. [Google Scholar]
- Tulbek MC, Panigrahi S, Borhan S, Boyacioglu MH, Boyacioglu D, Clifford H (2003) Prediction of alkaline noodle sensory attributes by multiple regression and neural network models. In: Proc IFT Annual Meetings, Chicago, USA
- Vestergaard JS, Martens M, Turkki P. Application of an electronic nose system for prediction of sensory quality changes of a meat product (pizza topping) during storage. Food Sci Technol. 2007;40:1095–1101. [Google Scholar]