Q-learning for estimating optimal dynamic treatment rules from observational data

Abstract

The area of dynamic treatment regimes (DTR) aims to make inference about adaptive, multistage decision-making in clinical practice. A DTR is a set of decision rules, one per interval of treatment, where each decision is a function of treatment and covariate history that returns a recommended treatment. Q-learning is a popular method from the reinforcement learning literature that has recently been applied to estimate DTRs. While, in principle, Q-learning can be used for both randomized and observational data, the focus in the literature thus far has been exclusively on the randomized treatment setting. We extend the method to incorporate measured confounding covariates, using direct adjustment and a variety of propensity score approaches. The methods are examined under various settings including non-regular scenarios. We illustrate the methods in examining the effect of breastfeeding on vocabulary testing, based on data from the Promotion of Breastfeeding Intervention Trial.

1. INTRODUCTION

Dynamic treatment regimes present a framework for developing individually tailored treatment policies that are particularly useful for chronic disorders like mental illnesses, substance abuse, HIV infection, cancer, and so on. More precisely, a dynamic treatment regime (DTR), or adaptive treatment strategy, is a sequence of decision rules where each decision rule takes a patient’s treatment and covariate history at each interval of clinical intervention as inputs, and outputs a recommended treatment. The ultimate goal of research in this arena is to come up with a DTR that leads to maximum benefit to the participants, that is, to formulate an “optimal” DTR in some well-defined sense. Formally, a DTR is often said to be optimal if it optimizes the mean outcome at the end of the final interval of treatment.

There are a number of methods of analysis and inference that have been developed to estimate the optimal dynamic treatment regime. Parametric and Bayesian approaches have been proposed (Bellman, 1957; Bertsekas & Tsitsiklis, 1996; Thall, Millikan, & Sung, 2000; Arjas & Saarela, 2010), however it is the semi-parametric methods that have gained the widest use in the statistical community, with techniques such as iterative minimization of regrets (Murphy, 2003), G-estimation (Robins, 2004), machine-learning methods (Pineau et al., 2007), regret-regression (Henderson, Ansell, & Alshibani, 2010), and even marginal structural models (Robins, Hernán, & Brumback, 2000; Hernán et al., 2006; van der Laan & Petersen, 2007; Robins, Orellana, & Rotnitzky, 2008). In particular, Q-learning (Murphy, 2005; Chakraborty, 2011) is a popular choice because of the ease of implementation and its connections with other methods such as G-estimation (Chakraborty, Murphy, & Strecher, 2010).

One important limitation of Q-learning is that it has been studied and implemented only in the context of randomized trials (Zhao, Kosorok, & Zeng, 2009; Chakraborty, Murphy, & Strecher, 2010; Zhao et al., 2011; Shortreed et al., 2011; Song et al., 2012; Chakraborty & Moodie, 2012; Laber et al., 2012). However, the development of DTRs is often exploratory, and it is useful to explore potentially optimal DTRs using large samples with observational data, which may later be assessed in a confirmatory study in which individuals are randomized to one of a small number of regimes of interest. It has been assumed that, in principle, Q-learning can be used for observational data. We examine several approaches to Q-learning in an observational (non-randomized) treatment setting, where all confounding covariates are assumed to be measured. In particular, we use direct adjustment and a variety of propensity score approaches, including regression and inverse probability weighting. We illustrate the methods by applying Q-learning to determine whether there is an optimal strategy for breastfeeding which will maximize a vocabulary score using data from the Promotion of Breastfeeding Intervention Trial. In the trial, subjects were randomized to a breastfeeding encouragement program or standard care, but all women in the study initiated breastfeeding and weaning time was not randomized. While the “treatment” of interest (breastfeeding) was influenced by the randomization status, it was by no means determined by it.

2. ESTIMATING TREATMENT RULES BY Q-LEARNING

2.1. Notation and Data Structure

We frame this work in a two-interval setting, however the methods considered extend naturally to any finite number of treatment intervals. Longitudinal data on a single patient are given by the trajectory (C₁, O₁, A₁, C₂, O₂, A₂, Y), where C_j and O_j (j = 1, 2) denote the covariates measured prior to treatment at the beginning of the jth interval, Y is the observation at the end of interval 2, and A_j (j = 1, 2) is the treatment assigned at the jth interval subsequent to observing O_j. We distinguish two types of covariates: those variables O_j that interact with treatment, called tailoring or prescriptive variables, and those variables C_j that do not interact with treatment but that potentially confound the relationship between the treatment and outcome. Note that O_j may also be a confounding variable, that is, a common cause of both treatment and the outcome. We do not consider that case in this work since tailoring variables are typically included in the models used for Q-learning, and so any confounding effects of tailoring variables are naturally accounted for in this way.

The data set consists of a random sample of n patients. Define the history at each interval as: H₁ = (C₁, O₁), H₂ = (C₁, O₁, A₁, C₂, O₂). We consider studies in which there are two possible treatments at each interval, A_j ∈ {−1, 1}, and the receipt of treatment A_j depends on the observed value of covariates C_j. The outcome Y observed at the end of the second treatment interval may be a single measurement or a known function, f (·), of some or all covariates measured throughout the study. A two-interval DTR consists of two decision rules, (d₁, d₂), with d_j ≡ d_j(H_j) ∈ 𝒜_j, where 𝒜_j is the set of possible treatments at the jth interval.

2.2. Basic Q-learning With Linear Regression Models

Q-learning is closely related to dynamic programming, in that estimation begins at the last interval, and the optimal treatment at each interval is then found by estimating the impact of treatment in that interval on a “pseudo-outcome" which is constructed by assuming all subsequent treatments are optimal; the pseudo-outcome is simply a predicted counterfactual outcome under optimal treatment in the future intervals. We begin by describing the basic implementation of Q-learning, that assumes randomized treatment. That is, we suppose that there are no confounding variables C_j, so that H₁ = O₁, H₂ = (O₁, A₁, O₂). Define the Q-functions (Sutton & Barto, 1998; Murphy, 2005) for the two intervals as follows:

$$Q_2(H_2,A_2)=E[Y|H_2,A_2],$$

$$Q_1(H_1,A_1)=E[\underset{a_2}{\text{max }}{Q}_2(H_2,a_2)|H_1,A_1].$$

If perfect knowledge were available to the analyst, the true multivariate distribution of the data would be known, which would in turn imply known Q-functions. Were that the case, the optimal DTR (d₁, d₂) could be deduced using backwards induction, so that

$$d_j(h_j)=\text{arg }\underset{a_j}{\text{max }}{Q}_j(h_j,a_j),j=1,2.$$

In practice, however, the true Q-functions are not known, and hence must be estimated from the data. A simple and often reasonable approach is to assume a linear model for the Q-functions, so that the interval-j (j = 1, 2) Q-function is modelled as

$$Q_j(H_j,A_j;{\beta }_j,{\psi }_j)={\beta }_j^T{H}_{j0}+({\psi }_j^T{H}_{j1})A_j,$$ (1)

where H_j0 and H_j1 are two (possibly different) summaries of the historyH_j. We use H_j0 to contain the collection of variables that have a predictive effect on the outcome that is not modified by the treatment, and H_j1 to denote the components of the history that do interact with treatment. Both H_j0 and H_j1 include a constant, or intercept, term. Then the Q-learning algorithm consists of the following steps:

1. Interval 2 parameter estimation: Using regression, find

   $$({\mathrm{\beta ̂}}_2,{\mathrm{\psi ̂}}_2)=\text{arg }\underset{{\beta }_2,{\psi }_2}{\text{min}}\frac{1}{n}{\displaystyle \sum _{i=1}^n}{(Y_i-Q_2(H_{2i},A_{2i};{\beta }_2,{\psi }_2))}^2.$$

2. Interval 2 optimal rule: By substitution, d̂₂(h₂) = argmax_a2 Q₂(h₂, a₂; β̂₂, ψ̂₂).

3. Interval 1 pseudo-outcome: By substitution,

   $${Ŷ}_{1i}=\underset{a_2}{\text{max}}{Q}_2(H_{2i},a_2;{\mathrm{\beta ̂}}_2,{\mathrm{\psi ̂}}_2),i=1,\dots ,n.$$
4. Interval 1 parameter estimation: Using regression, find

   $$({\mathrm{\beta ̂}}_1,{\mathrm{\psi ̂}}_1)=\text{arg}\underset{{\beta }_1,{\psi }_1}{\text{min}}\frac{1}{n}{\displaystyle \sum _{i=1}^n}{({Ŷ}_{1i}-Q_1(H_{1i},A_{1i};{\beta }_1,{\psi }_1))}^2.$$

5. Interval 1 optimal rule: By substitution, d̂₁(h₁) = argmax_a1 Q₁(h₁, a₁; β̂₁, ψ̂₁).

The estimated optimal DTR using Q-learning is given by (d̂₁, d̂₂). Note that the pseudo-outcome, Ŷ_1i, is the (expected) value of the second-interval Q-function under the optimal treatment.

2.3. Q-Learning in Non-Regular Settings

It is now well-understood (Robins, 2004; Moodie & Richardson, 2010; Chakraborty, Murphy, & Strecher, 2010; Chakraborty & Moodie, 2012; Song et al., 2012) that most estimators of DTR parameters, including those found by Q-learning and G-estimation, are non-regular. This phenomenon is a consequence of the non-differentiability of the pseudo-outcome ${Ŷ}_{1i}={\mathrm{\beta ̂}}_2^T{H}_{20,i}+|{\mathrm{\psi ̂}}_2^T{H}_{21,i}|$ with respect to the estimated second-interval parameters, ψ₂. The basic Q-learning algorithm is sometimes referred to as a “hard-max” estimator because of the sharp point of non-differentiability caused by employing a maximum operation, which in this case is the absolute value function.

The estimator ψ̂₁ is a function of the estimated pseudo-outcome, Ŷ_1i, and so it is also a non-smooth function of ψ̂₂. It is therefore the case that the asymptotic distribution of ψ̂₁ does not converge uniformly (Robins, 2004) over the space of the parameters ψ = (ψ₁, ψ₂). In fact, we can be more precise: the asymptotic distribution of $\sqrt{n}({\mathrm{\psi ̂}}_1-{\psi }_1)$ is normal (and the estimator is therefore regular) when ψ₂ is such that $P[H_2:{\psi }_2^T{H}_{21}=0]=0$, but is non-normal if $P[H_2:{\psi }_2^T{H}_{21}=0]>0$. Furthermore, the transition between the two asymptotic distributions is abrupt. This non-regularity results in bias in the estimator ψ̂₁, as well as poor coverage of Wald type confidence intervals (Robins, 2004; Moodie & Richardson, 2010). Even the usual bootstrap confidence intervals can perform badly (Chakraborty, Murphy, & Strecher, 2010).

A handful of approaches have been proposed to reduce the problems of bias and/or incorrect coverage (Moodie & Richardson, 2010; Chakraborty, Murphy, & Strecher, 2010; Song et al., 2012; Laber et al., 2012; Chakraborty et al., 2012). We focus on the soft-thresholding approach of Chakraborty, Murphy, & Strecher (2010), which has shown good performance in terms of both bias and coverage in non-regular settings. The basic idea of the soft-thresholding approach is to shrink the problematic term in the pseudo-outcome towards zero. Thus, the soft-thresholding implementation of Q-learning replaces the pseudo-outcome of the basic (hard-max) Q-learning algorithm with

$${Ŷ}_{1i}^{\mathit{\text{ST}}}={\mathrm{\beta ̂}}_2^T{H}_{20,i}+|{\mathrm{\psi ̂}}_2^T{H}_{21,i}|·{(1-\frac{{\lambda }_i}{{|{\mathrm{\psi ̂}}_2^T{H}_{21,i}|}^2})}^{+},i=1,\dots ,n,$$

where x⁺ = x𝕀[x > 0] stands for the positive part of a function, and λ_i (> 0) is a tuning parameter associated with the ith subject in the sample. A data-driven choice of the tuning parameter λ_i is obtained from a Bayesian approach to the problem: taking ${\lambda }_i=3H_{21,i}^{\mathrm{T}}{\mathrm{\Sigma ̂}}_2{H}_{21,i}/n,i=1,\dots ,n$, where Σ̂₂/n is the estimated covariance matrix of ψ̂₂ yields an approximate empirical Bayes estimator (Chakraborty, Murphy, & Strecher, 2010). The basic Q-learning algorithm is otherwise unchanged.

2.4. Q-Learning for Observational Data

In more general estimation problems where interest lies in assessing, for example, a treatment effect from a non-randomized study, many confounding-adjustment methods rely on the propensity score (PS). The basic approach requires the construction of a propensity score or treatment model—often a predicted probability resulting from a logistic regression of treatment on covariates—followed by some form of adjustment, such as regression or an unadjusted regression in a sample which uses inverse probability of treatment weights (IPTW).

Formally, the propensity score is defined to be

$$\pi (x)=P(A=1|X=x),$$

where A is a binary treatment and X is a collection of measured covariates (Rosenbaum & Rubin, 1983). The PS is said to be a balancing score, in that treatment received is independent of known covariates given the propensity score. This property is used to obtain unbiased estimates of the treatment effect based on conditional expectation modelling of the outcome given the propensity score. Common approaches include regression-based estimators, where some function of the propensity score is included as a covariate in the regression, or an estimate is obtained using a matched subsample of the data. Unbiasedness can be achieved if the PS is correctly specified; in particular, it is key that all confounding variables are available (measured) and included in the PS model.

In an inverse probability of treatment weighted analysis, weighting is used to achieve a pseudo-sample in which treatment is not confounded by the variables included in the PS, which is used to construct the weights (Robins, Hernán, & Brumback, 2000). That is, treatment receipt does not depend on confounders in the pseudo-sample. As with the propensity score adjustment methods and indeed all models for observational data, some assumptions are required for IPTW estimators of treatment effects to be unbiased. In particular, we require no unmeasured confounding, correct specification of the PS with respect to confounding variables and that the PS is neither 0 nor 1 to ensure the resulting weights are well-defined.

In what follows, we will compare the basic implementation of Q-learning with four approaches to confounder-adjustment. Recall that the basic Q-learning algorithm does not make any covariate adjustment, so that H₁ = O₁, H₂ = (O₁, A₁, O₂). Three of the adjustment methods adapt Q-learning by redefining the history vectors, H₁ and H₂. The fourth approach relies on weighting. Specifically, letting PS₁ = P(A₁ = 1|C₁), PS₂ = P(A₂ = 1|C₁, C₂) denote the interval-specific propensity scores, we consider accounting for confounding by:

1. including covariates as linear terms in the Q-function (we refer to this as linear adjustment): H₁ = (C₁, O₁), H₂ = (C₁, C₂, O₁, A₁, O₂),

2. including the propensity score as a linear term in the Q-function: H₁ = (PS₁, O₁), H₂ = (PS₂, O₁, A₁, O₂),

3. including quintiles of PS_j as covariates in the jth interval Q-function, and

4. inverse probability of treatment weighting with H₁, H₂ defined as in the basic Q-learning.

For simplicity, we focus on the IPTW estimator which uses unstabilized weights, defined as w₁ = 𝕀[A₁ = 1]/PS₁ + (1 −𝕀[A₁ = 1])/(1 − PS₁) at the first interval and w₂ = w₁ * {𝕀[A₂ = 1]/PS₂ + (1 −𝕀[A₂ = 1])/(1 − PS₂)} at the second interval.

3. SIMULATION STUDY

In this section, we consider a simulation study to compare the performances of several competing methods. In particular, we contrast no covariate adjustment (the basic Q-learning algorithm), with adjustment by (1) including covariates as linear terms in the Q-function; (2) including the PS directly in the Q-function; (3) including quintiles of the PS as covariates in the Q-function; and (4) IPTW.

The methods of adjustment are implemented using both the basic (hard-max) and the soft-thresholding versions of Q-learning. In addition to finding the performance of the point estimates, we will compute percentile bootstrap confidence intervals to assess coverage rates of 95% confidence intervals. The generative model and the analysis model are straightforward adaptations of the corresponding models described in Chakraborty et al. (2010), with the addition of time-varying confounding variables, C_j.

3.1. Generative Models: Primary Simulations for Confounding by Covariates

We consider a single continuous confounder, C_j, at each interval, where C₁ ~ 𝒩(0, 1) and C₂ ~ 𝒩(η₀ + η₁C₁, 1) for η₀ = −0.5, η₁ = 0.5. Treatment assignment is dependent on the value of the confounding variable: P[A_j = 1|C_j] = 1 − P[A_j = −1|C_j] = expit(ζ₀ + ζ₁C_j), j = 1, 2 where expit(x) = exp(x)/(1 + exp(x)). In simulations where treatment was randomly allocated, ζ₀ = ζ₁ = 0, while for confounded treatment, ζ₀ = −0.8, ζ₁ = 1.25. The binary covariates which interact with treatment to produce a personalized rule are generated via

$$P[O_1=1]=P[O_1=-1]=\frac{1}{2},$$

$$P[O_2=1|O_1,A_1]=1-P[O_2=-1|O_1,A_1]=\text{expit}({\delta }_1{O}_1+{\delta }_2{A}_1).$$

Let μ = E[Y|C₁, O₁, A₁, C₂, O₂, A₂], and ε ~ 𝒩(0, 1) be the error term. Then Y = μ + ε, with

$$\mu ={\gamma }_0+{\gamma }_1{C}_1+{\gamma }_2{O}_1+{\gamma }_3{A}_1+{\gamma }_4{O}_1{A}_1+{\gamma }_5{C}_2+{\gamma }_6{A}_2+{\gamma }_7{O}_2{A}_2+{\gamma }_8{A}_1{A}_2.$$

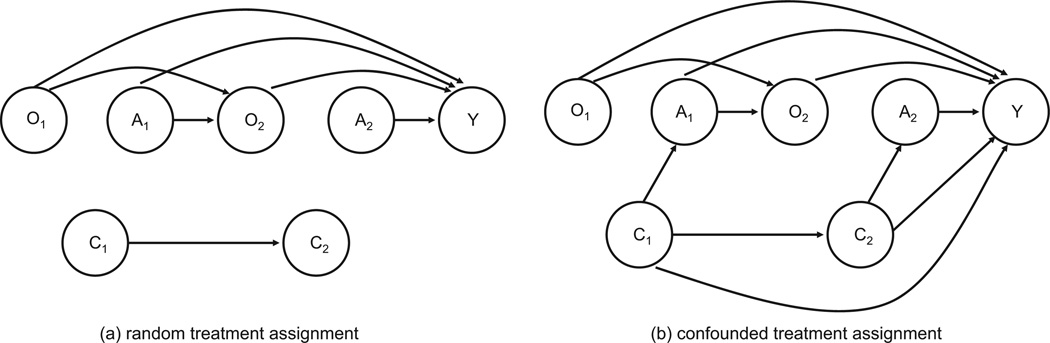
The parameters will be varied in the examples to follow. Note that confounding can be removed from the data generation by setting η₁ = 0 or γ₁ = γ₅ = 0. See Figure 1 for a depiction of the data generating mechanism using causal diagrams.

Figure 1.

Causal diagram for generative model for simulations: (a) random treatment assignment and (b) confounded treatment assignment.

Parameters were chosen to consider two regular settings and two non-regular settings. Non-regularity in interval 1 parameter estimators is a consequence of non-uniqueness in the optimal treatment at the second interval for some non-zero fraction of the population. In terms of the above data-generating model, non-regularity occurs when p = P[γ₆ + γ₇O₂ + γ₈A₁ = 0] > 0; we use p to describe the degree of non-regularity. Estimators also exhibit non-regular behaviour when γ₆ + γ₇O₂ + γ₈A₁ is near zero; we therefore also consider the standardized effect size, ϕ = E[γ₆ + γ₇O₂ + γ₈A₁]/var[γ₆ + γ₇O₂ + γ₈A₁] (Chakraborty, Murphy, & Strecher, 2010; Song et al., 2012).

The first regular setting was designed to have a large treatment effect, with γ = (0, γ₁, 0, −0.5, 0, γ₅, 0.25, 0.5, 0.5) and δ = (0.1, 0.1) so that p = 0 and ϕ = 0.3451. In the second regular setting, the treatment effect at the second interval is small (ϕ = 0.1/0) and first-interval estimators exhibit bias due to the near-non-regularity of the scenario: γ = (0, γ₁, 0, 0, 0, γ₅, 0.1, 0, 0) and δ = (0.5, 0.5). The two non-regular scenarios differed in both the degree of non-regularity and the standardized effect size. We considered non-regularity which was moderate (γ = (0, γ₁, 0, −0.5, 0, γ₅, 0.5, 0, 0.5) and δ = (0.5, 0.5) so that p = 0.5 and ϕ = 1) and severe (γ = (0, γ₁, 0, 0, 0, γ₅, 0, 0, 0) and δ = (0.5, 0.5) so that p = 1 and ϕ = 0/0). In the random treatment settings, we took γ₁ = γ₅ = 0, and in the confounded treatment settings, γ₁ = γ₅ = 1.

3.2. Generative Models: Additional Simulations for Confounding by Covariates

We considered three additional simulations, focusing on adjustment by inclusion of covariates in the Q-function model, inclusion of the PS as a linear term in the Q-function model, and IPTW. In the first simulation, treatment was randomly allocated, but the variables C₁ and C₂ both predicted the outcome, Y. As in the confounded scenarios, we set γ₁ = γ₅ = 1, but fixed ζ₀ = ζ₁ = 0. That is, in this setting, treatment was not confounded but the Q-function models were incorrectly specified for all methods of PS-adjustment and IPTW due to the omission of C₁ and C₂ from the models. This setting was considered to verify whether the results from the random treatment setting could be attributed to the lack of confounding or the lack of dependence of the outcome on the variables C₁ and C₂.

We also considered two confounded treatment settings where the confounders C₁ and C₂ were binary rather than continuous. For these scenarios, the data generation of Figure 1b was followed, but here P[C₁ = 1] = 1 − P[C₁ = −1] = 1/3 and P[C₂ = 1] = 1 − P[C₂ = −1] = expit(0.6C₁). In the first, γ₁ = γ₅ = 1 whereas in the second γ₅ = 1 but γ₁ = 0 so that C₂ was a predictor of Y, but C₁ was not.

3.3. Generative Models: Confounding by Counterfactuals

In the data-generating scenarios described above, only a model that includes the confounding variables as linear terms in the Q-function will be correctly specified. We therefore pursue an alternative approach to generating data that will allow us to examine the performance of the adjustment methods on a more even playing field by creating data for which all adjustment methods contain as a sub-model a correctly-specified model for the Q-function. We accomplish this by generating data in which the choice of treatment depends on the counterfactual outcomes.

In particular, the data are created by generating the outcome under each of the four potential treatment paths ((−1,−1), (−1,1), (1,−1), and (1,1)):

1. Generate the first-interval tailoring variable, O₁, using $P[O_1=1]=P[O_1=-1]=\frac{1}{2}$.

2. Generate the potential value of the second-interval tailoring variable, O₂(A₁), using P[O₂ = 1|O₁, A₁] = 1 − P[O₂ = −1|O₁, A₁] = expit(δ₁O₁ + δ₂A₁) for each possible value of A₁. Thus, we generate the potential second-interval value that would occur under A₁ = −1 and that which would occur under A₁ = 1.

3. Generate the vector of potential outcomes, Y = μ + ε, where ε is a multivariate normal error term with mean (0, 0, 0, 0)^T and a covariance matrix that takes the value 1 on its diagonal and 0.5 on all off-diagonals, and

   $$\mu ={\gamma }_0^{*}+{\gamma }_1^{*}{\mathbf{O}}_1+{\gamma }_2^{*}{\mathbf{A}}_1+{\gamma }_3^{*}{\mathbf{O}}_1{\mathbf{A}}_1+{\gamma }_4^{*}{\mathbf{A}}_2+{\gamma }_5^{*}{\mathbf{O}}_2{\mathbf{A}}_2+{\gamma }_6^{*}{\mathbf{A}}_1{\mathbf{A}}_2,$$ (2)

   where O₁ is the 4 × 1 vector consisting of O₁ from step (1) repeated four times, A₁ = (−1, −1, 1, 1), O₂ = (O₂(−1), O₂(−1), O₂(1), O₂(1)) using the potential values generated in step (2), and A₂ = (−1, 1, −1, 1).

4. Set the confounders to be C₁ = Y̅ and C₂ = max(Y).

5. From among the four possible treatment paths and corresponding potential outcomes, select the “observed” data using P[A_j = 1|C_j] = 1 − P[A_j = −1|C_j] = expit(ζ₀ + ζ₁C_j), j = 1, 2.

The vector of δs was set to (0.1, 0.1), while the vector of γs was taken to be (0, 0, −0.5, 0, 0.25, 0.5, 0.5), indicating a regular (large effect) scenario. In simulations where treatment was randomly allocated, ζ₀ = ζ₁ = 0, while for confounded treatment, ζ₀ = 0.2, ζ₁ = 1. As can be observed from Equation (2), the Q-functions will not depend on the values of C₁ and C₂ so that any model for the Q-function that includes O₁, A₁, O₂, A₂ and the appropriate interactions will be correctly specified. However the observed or selected treatment depends on C₁ and C₂, which are functions of the potential outcomes, hence the treatment-outcome relationship is confounded by these variables.

3.4. Results for Confounding by Covariates

We focus our attention on the parameter ψ₁₀, the parameter in the analytic model for the first-interval Q-function defined in Equation (1) which corresponds to the main effect of the treatment A₁. The true value of the parameter is fully determined by the γ and δ vectors (see Chakraborty, Murphy, & Strecher (2010) for the values, or Chakraborty & Moodie (2012) for the complete derivation).

Performance of the five different Q-learning approaches under random treatment allocation for both the hard-max and soft-thresholding implementations are given in Table 1, for a sample size of 250. Table 2 provides the results for the confounded treatment settings, and Table 3 provides the results from the additional scenarios considered. In Table 2, where we vary sample size, results are presented for the most appropriate analytic approach (hard-max for the regular, large effect setting, and soft-thresholding for the other three settings) to isolate the effects of confounding on the performance of the different methods of adjustment in Q-learning.

Table 1.

Performance of Q-learning adjustment methods for n = 250 when treatment is randomly assigned, as per Figure 1a: bias, Monte Carlo variance (MC var), mean squared error (MSE), and coverage of 95% bootstrap confidence intervals.

	Hard-max				Soft thresholding
Adjustment method	Bias	MC var	MSE	Cover	Bias	MC var	MSE	Cover
Regular setting (large effect)
None	0.0001	0.0076	0.0076	92.7	0.0028	0.0077	0.0077	95.2
Linear	0.0001	0.0076	0.0076	94.5	0.0028	0.0077	0.0077	95.4
PS (linear)	0.0000	0.0076	0.0076	94.2	0.0027	0.0076	0.0076	95.4
PS (quintiles)	0.0004	0.0077	0.0077	94.5	0.0029	0.0077	0.0077	95.4
IPW	−0.0001	0.0076	0.0076	93.9	−0.0011	0.0079	0.0078	95.5
Regular setting (small effect)
None	0.0071	0.0055	0.0056	96.6	0.0058	0.0045	0.0046	95.2
Linear	0.0070	0.0056	0.0056	96.5	0.0057	0.0046	0.0046	95.3
PS (linear)	0.0069	0.0055	0.0056	96.5	0.0057	0.0046	0.0046	95.7
PS (quintiles)	0.0072	0.0055	0.0055	96.9	0.0057	0.0046	0.0046	95.6
IPW	0.0070	0.0055	0.0056	96.4	0.0058	0.0046	0.0046	95.3
Non-regular (moderate) setting
None	−0.0420	0.0071	0.0088	89.2	−0.0202	0.0067	0.0071	92.8
Linear	−0.0423	0.0071	0.0086	89.3	−0.0204	0.0067	0.0071	92.7
PS (linear)	−0.0421	0.0071	0.0088	89.2	−0.0203	0.0067	0.0071	92.8
PS (quintiles)	−0.0425	0.0071	0.0089	89.5	−0.0206	0.0068	0.0071	93.1
IPW	−0.0420	0.0071	0.0088	89.5	−0.0202	0.0067	0.0071	93.1
Non-regular (severe) setting
None	−0.0015	0.0053	0.0053	95.7	−0.0005	0.0045	0.0045	94.5
Linear	−0.0011	0.0054	0.0054	95.7	−0.0003	0.0045	0.0045	94.7
PS (linear)	−0.0011	0.0054	0.0054	95.7	−0.0002	0.0045	0.0045	94.6
PS (quintiles)	−0.0007	0.0054	0.0054	95.8	−0.0003	0.0045	0.0046	94.8
IPW	−0.0013	0.0054	0.0054	95.4	−0.0002	0.0045	0.0045	94.1

Table 2.

Performance of Q-learning adjustment methods when treatment is confounded, as per Figure 1b: bias, Monte Carlo variance (MC var), mean squared error (MSE), and coverage of 95% bootstrap confidence intervals.

	n = 250				n = 500
Adjustment method	Bias	MC var	MSE	Cover	Bias	MC var	MSE	Cover
Regular setting (large effect)
None	−0.7201	0.0256	0.5441	0.2	−0.7194	0.0151	0.5325	0.0
Linear	−0.0027	0.0116	0.0116	95.6	0.0010	0.0065	0.0065	95.0
PS (linear)	−0.2534	0.0233	0.0875	64.0	−0.2594	0.0134	0.0809	35.5
PS (quintiles)	−0.3151	0.0213	0.1206	42.6	−0.3226	0.0121	0.1162	14.0
IPW	−0.4304	0.0189	0.2042	7.6	−0.4213	0.0109	0.1884	0.3
Regular setting (small effect)
None	−0.4365	0.0436	0.2341	38.0	−0.4427	0.0226	0.2186	12.2
Linear	0.0009	0.0095	0.0095	96.1	0.0036	0.0044	0.0044	95.9
PS (linear)	−0.2537	0.0207	0.0851	62.3	−0.2493	0.0105	0.0727	29.4
PS (quintiles)	−0.2892	0.0191	0.1028	48.2	−0.2872	0.0097	0.0923	17.2
IPW	−0.2544	0.0265	0.0912	59.0	−0.2563	0.0174	0.0831	44.9
Non-regular (moderate) setting
None	−0.9667	0.0337	0.9681	0.0	−0.9712	0.0184	0.9616	0.0
Linear	−0.0233	0.0121	0.0127	93.9	−0.0093	0.0058	0.0058	93.9
PS (linear)	−0.2988	0.0259	0.1152	47.8	−0.2704	0.0125	0.0856	25.2
PS (quintiles)	−0.3653	0.0237	0.1571	28.5	−0.3378	0.0111	0.1252	8.4
IPW	−0.5768	0.0251	0.3578	1.2	−0.5362	0.0128	0.3003	0.0
Non-regular (severe) setting
None	−0.4490	0.0380	0.2395	33.9	−0.4513	0.0226	0.2264	12.0
Linear	−0.0025	0.0090	0.0090	96.4	−0.0026	0.0045	0.0045	94.6
PS (linear)	−0.2517	0.0191	0.0824	60.7	−0.2555	0.0104	0.0757	28.3
PS (quintiles)	−0.2900	0.0169	0.1011	46.5	−0.2942	0.0097	0.0963	14.8
IPW	−0.2606	0.0301	0.0980	66.5	−0.2640	0.0171	0.0867	42.8

Soft-thresholding results are presented for all settings except the first; the hard-max results are shown for the regular setting with a large effect.

Table 3.

Performance of Q-learning adjustment methods under additional scenarios: bias, Monte Carlo variance (MC var), mean squared error (MSE), and coverage of 95% bootstrap confidence intervals.

	Hard-max				Soft thresholding
Adjustment method	Bias	MC var	MSE	Cover	Bias	MC var	MSE	Cover
Non-regular (severe) setting, random treatment
None	0.0015	0.0220	0.0220	96.9	0.0032	0.0185	0.0185	96.1
Linear	−0.0014	0.0094	0.0094	95.8	−0.0020	0.0086	0.0086	94.8
PS (linear)	−0.0018	0.0138	0.0138	97.4	−0.0012	0.0129	0.0129	97.2
IPW	−0.0001	0.0136	0.0136	96.9	0.0012	0.0115	0.0115	96.6
Non-regular (severe) setting, Cj binary
None	−0.3947	0.0265	0.1823	29.2	−0.3782	0.0278	0.1708	33.3
Linear	0.0010	0.0099	0.0099	96.2	0.0048	0.0092	0.0093	95.1
PS (linear)	−0.2739	0.0197	0.0947	51.0	−0.2692	0.0186	0.0911	50.2
IPW	−0.2145	0.0213	0.0673	63.5	−0.2026	0.0163	0.0573	62.6
Non-regular (severe) setting, Cj binary
None	−0.0839	0.0157	0.0227	90.0	−0.0774	0.0171	0.0231	90.8
Linear	−0.0029	0.0101	0.0101	95.6	0.0006	0.0092	0.0092	94.8
PS (linear)	−0.0043	0.0129	0.0129	95.8	−0.0006	0.0118	0.0118	94.7
IPW	−0.0505	0.0150	0.0176	92.5	−0.0465	0.0122	0.0144	92.7

In the first two scenarios, C₁ and C₂ predict Y, while in the third, C₂ predicts Y but C₁ does not.

As we might hope, all methods perform well when treatment is randomly allocated, whether or not the covariates C_j predict the outcome (Tables 1 and 3). In settings where treatment is confounded by the continuous confounders C₁ and C₂, only adjustment by the covariates themselves provides unbiased estimates with appropriate coverage by the percentile-based bootstrap confidence intervals (Table 2).

When the confounders are binary, all methods of adjustment except the correctly specified model which adjusts for confounders linearly in the Q-function model again exhibit bias. There is one situation in which this is not the case: if there exists a single confounder at each interval, and only C₂ but not C₁ affects Y (i.e., γ₁ = 0); in this case, including the PS in the Q-function model performs as well as including C₂ in the model, since the PS acts as a re-scaled version of C₂. Bias and undercoverage are exhibited by the unadjusted and IPTW estimators, however this is not as great as in other scenarios where there is a greater degree of confounding.

The question then arises as to whether these results are indeed as unexpected as they first appear: why is it that these classic methods of causal adjustment yield bias in the estimates of DTR parameters? We note that using these methods of adjustment, we do in fact obtain unbiased estimates of the data-generating parameters γ associated with the treatment A₂ (i.e., the variables contained in H₂₁), as is predicted by theory. However, we do not obtain unbiased estimators of the true pseudo-outcome (Figure 2) under the mis-specified (PS-based) models or, crucially, an accurate representation of the dependence of the pseudo-outcome on A₁. For example, in the sample corresponding to Figure 2a, the difference in the mean true pseudo-outcome for A₁ = 1 versus A₁ = −1 is 1.50; the difference in mean pseudo-outcome as estimated by linear adjustment, linear PS adjustment, and IPTW are, respectively, 1.49, 1.40, and 0.29. When treatment is randomly assigned—even when Y depends on C₁ and C₂—the observed dependence of the pseudo-outcome on A₁ does not vary widely, even though the pseudo-outcome is poorly estimated by some methods (Figure 2b): the difference in mean pseudo-outcome as estimated by linear adjustment, linear PS adjustment, and IPTW are, respectively, 0.03, 0.02, and −0.02 as compared to −0.01 for the true pseudo-outcome.

Figure 2.

True versus estimated pseudo-outcome in simulated data using linear adjustment, propensity-score (linear) adjustment, and inverse probability of treatment weighting, n = 10,000 in a regular (large effect) setting. (a) Confounding treatment (see Table 2, first scenario). (b) Randomly assigned treatment and C₁, C₂ predictive of Y.

3.5. Results for Confounding by Counterfactuals

Here again, we consider the estimates of the parameter ψ₁₀ under the counterfactual-based data generation approach described in Section 3.3. Performance of the five different Q-learning approaches under random and confounded treatment allocation for sample sizes 250 and 1,000 are given in Table 4. From these results, it is clear that ignoring the confounding variables results in significant bias. All methods of adjusting for confounding provide considerably improved estimates in terms of both bias and coverage for small samples, but in large samples, evidence points again to including the confounding covariate as a linear term as the optimal choice. This form of adjustment provides the best performance, perhaps because this approach does not require any additional model fitting (i.e., no additional variability is introduced to the estimation procedure due to the estimation of the propensity score), although IPTW performs well too in both small and large samples. These results suggest that many standard adjustment methods can be used to reduce or eliminate bias provided the Q-function can be correctly specified.

Table 4.

Performance of Q-learning adjustment methods under the confounding by counterfactuals simulations: bias, Monte Carlo variance (MC var), mean squared error (MSE), and coverage of 95% bootstrap confidence intervals.

	Randomized treatment				Confounded treatment
Adjustment method	Bias	MC var	MSE	Cover	Bias	MC var	MSE	Cover
n = 250
None	0.0020	0.0082	0.0082	94.0	0.2293	0.0080	0.0605	26.4
Linear	0.0011	0.0032	0.0032	95.1	0.0051	0.0039	0.0039	93.8
PS (linear)	0.0010	0.0052	0.0052	96.2	0.0548	0.0060	0.0090	89.4
PS (quintiles)	0.0008	0.0056	0.0056	96.1	0.0779	0.0061	0.0121	83.2
IPW	0.0004	0.0046	0.0046	93.9	0.0108	0.0075	0.0076	92.8
n = 1000
None	−0.0012	0.0022	0.0022	93.4	0.2246	0.0021	0.0525	0.5
Linear	0.0001	0.0009	0.0009	93.5	0.0037	0.0010	0.0010	93.5
PS (linear)	−0.0002	0.0014	0.0014	95.5	0.0446	0.0015	0.0035	77.0
PS (quintiles)	−0.0004	0.0015	0.0015	95.7	0.0699	0.0015	0.0064	55.0
IPW	−0.0008	0.0012	0.0012	93.6	0.0018	0.0018	0.0018	93.6

These simulations provide a useful demonstration of the methods of adjustment in principle, however it is not clear whether these results generalize to real-data scenarios as it is difficult to conceive of a situation in which counterfactual outcomes could be measured and used as covariates.

3.6. Additional Remarks

In addition to the regression and weighting approaches considered above, we considered propensity score matching. Caliper matching with replacement into pairs was accomplished using the Matching package in R (Sekhon, 2011); the matching was performed separately at each interval. We found that the estimators exhibited variability that was considerably larger than that of all other estimators. Furthermore, in the simulations where data generation was counterfactual-based, bias appeared to be of the same magnitude as the unadjusted Q-learning, however the origin of this bias is different: matching on the propensity score in this fashion targets estimation of the average treatment effect on treated (ATT) rather than the average treatment effect, which is the parameter of interest.

Finally, we note that it is typical to stabilize weights (Robins, 1999) in IPTW analyses to improve efficiency. We did implement this, but no substantial difference was noted in the estimators’ performance (results not shown).

4. BREASTFEEDING AND VOCABULARY TEST RESULTS: THE PROBIT STUDY

4.1. Background and Study Details

There have been a considerable number of studies from developed countries which have suggested higher cognitive scores on IQ and other tests among both children and adults who were breastfed compared with those who were formula-fed, although these findings have been nearly exclusively drawn from observational studies (Anderson, Johnstone, & Remley, 1999). Kramer and colleagues conducted the largest ever randomized trial assessing the impact of a breastfeeding promotion intervention on a variety of growth, infection, cognitive, and metabolic outcomes: the PROmotion of Breastfeeding Intervention Trial (PROBIT) (Kramer et al., 2001, 2002, 2003, 2004, 2007). Based on an intention-to-treat analysis, this trial produced strong evidence that prolonged and exclusive breastfeeding improves children’s cognitive development (Kramer et al., 2008). In our present analysis, we examine evidence that breastfeeding actually received—rather than the breastfeeding promotion intervention—increases verbal cognitive ability, and whether there is any advantage to tailoring breastfeeding habits to infant growth to improve this outcome.

In PROBIT, hospitals and affiliated polyclinics in the Republic of Belarus were randomized to a breastfeeding promotion intervention modelled on the WHO/UNICEF Baby-Friendly Hospital Initiative or to standard care. All study infants were born in one of 31 Belarusian maternity hospitals from June 17, 1996, to December 31, 1997, at term, weighing at least 2,500 g, initiated breastfeeding, and were enrolled during their postpartum stay. This resulted in the recruitment of 17,046 mother-infant pairs who were followed regularly for the first year of life. In a later wave of PROBIT, follow-up interviews and examinations were performed on 13,889 (81.5%) children at 6.5 years of age. One of the components of these visits was the administration of the Wechsler Abbreviated Scales of Intelligence (WASI), which consists of four subtests: vocabulary, similarities, block designs, and matrices. We focus our analysis on the vocabulary subtest.

4.2. Analysis

We focussed our attention on two key treatment intervals: birth to three months of age, and three to six months. The exposure of interest for our analysis is “any breastfeeding” measured in each of the intervals, which we will refer to as a “treatment” for consistency with the development of the previous sections. That is, A₁ takes the value 1 if the child was breastfed up to three months of age (and is set to −1 otherwise), and A₂ is the corresponding quantity for any breastfeeding up to six months of age. Note that any breastfeeding allows for exclusive breastfeeding, or breastfeeding with supplementation with formula or solid foods. The outcome, Y, is the vocabulary subtest score on the WASI measured at age 6.5 years.

We considered a single tailoring variable at each interval which measures the sex-specific size of the child. Specifically, we took O₁ to be the birthweight of the infant, and O₂ to be the infant’s three-month weight.

Four approaches were compared: no adjustment, adjustment via inclusion of potential confounders as linear terms in the Q_j model, adjusting for the propensity score as a linear term in the Q_j model, and inverse-probability weighting. Specifically, we fit the following Q-learning models:

$$Q_2={\beta }_{20}+{\beta }_{21}{A}_1+{\beta }_{22}{O}_1+{\beta }_{23}{O}_2+{\displaystyle \sum _{k=1}^K}{\beta }_{2k+3}{C}_{2k}+({\psi }_{20}+{\psi }_{21}{O}_2)*A_2,$$

$$Q_1={\beta }_{10}+{\beta }_{11}{O}_1+{\displaystyle \sum _{k=1}^K}{\beta }_{1k+1}{C}_{1k}+({\psi }_{10}+{\psi }_{11}{O}_1)*A_1,$$

where the matrix of confounders C_j (with columns C_j1, …, C_jK for j = 1, 2) was empty for both the no-adjustment and IPTW approach. In the direct adjustment approach, C_j consisted of intervention group, geographical region, maternal characteristics (education, smoking status, age and age-squared, whether previous children had been breastfed for three months), whether there was a family history of allergy, whether the birth was by caesarean section, and weight at the start of the interval. Finally, for the propensity-score adjustment approach, C_j was the propensity score, a one-dimensional summary of the confounders used in the direct adjustment approach.

To appropriately account for the variability of the complete estimation procedure, a non-parametric bootstrap procedure was employed.

4.3. Results

The decision rule parameter estimates are given in Table 5. With the exception of ψ₁₀, all four analytic approaches led to parameter estimates that agreed in terms of their sign, but in many cases differed with respect to statistical significance. Note that for a linear Q-function with a single variable used to tailor the treatment decision, the treatment rules at each interval can be characterized by the threshold −ψ_j0/ψ_j1. The optimal decision is determined by the rule: treat with A_j = 1 when (ψ_j0 + ψ_j1O_j) > 0, in other words, treat when O_j > −ψ_j0/ψ_j1 (for ψ_j1 > 0). For example, the PS-adjusted estimates yield the regime:

• breastfeed to 3 months if birthweight exceeds 2.60 kg,

• breastfeed to 6 months if 3-month weight exceeds 6.35 kg.

This corresponds to a rule which suggests that 98% of the infants in the study should be breastfed until 3 months to maximize vocabulary score at age 6.5, and 33% should be breastfed until 6 months (Figure 3). Note that ψ₂₀ and ψ₂₁ are not significantly different from zero, which suggests that breastfeeding decisions from 3 to 6 months will neither significantly increase nor decrease the vocabulary score.

Table 5.

Estimates (percentile bootstrap 95% CI) for decision rule parameters in the PROBIT example.

	None	Linear	PS	IPW
Hard-max
ψ10	0.612 (0.163, 0.996)	−0.556 (−0.971, −0.165)	−0.510 (−1.151, 0.201)	0.674 (0.160, 1.140)
ψ11	0.031 (−0.044, 0.142)	0.057 (−0.003, 0.139)	0.184 (0.020, 0.347)	0.046 (−0.037, 0.142)
ψ20	−2.493 (−7.829, 2.783)	−4.964 (−9.491, −0.533)	−3.366 (−8.622, 1.741)	−2.614 (−9.768, 4.615)
ψ21	0.648 (−0.188, 1.495)	0.790 (0.089, 1.515)	0.532 (−0.304, 1.357)	0.435 (−0.672, 1.554)
Soft thresholding
ψ10	0.649 (0.203, 1.052)	−0.428 (−0.875, −0.112)	−0.424 (−1.082, 0.248)	0.742 (0.187, 1.178)
ψ11	0.024 (−0.057, 0.144)	0.026 (−0.015, 0.121)	0.163 (0.003, 0.326)	0.029 (−0.040, 0.140)
ψ20	−2.493 (−7.829, 2.783)	−4.964 (−9.491, −0.533)	−3.366 (−8.622, 1.741)	−2.614 (−9.768, 4.615)
ψ21	0.648 (−0.188, 1.495)	0.790 (0.089, 1.515)	0.532 (−0.304, 1.357)	0.435 (−0.672, 1.554)

Figure 3.

Visualizing the optimal rule as a function of infant weight in the PROBIT study:—unadjusted; – – linear adjustment; … PS adjusted; · – · IPW. For values of infant weight where the line lies above 0, breastfeeding is considered optimal (zero is indicated by the horizontal grey line). Rugplot along x-axis indicates the observed distribution of the tailoring variable in the sample. (a) Interval 1: breastfeeding between 0 and 3 months as a function of birthweight. (b) Interval 2: breastfeeding between 3 and 6 months as a function of 3-month weight.

The unadjusted analysis suggests decision rules that would indicate breastfeeding all infants up to 3 months, and over 99% of the sample to 6 months. The linear adjustment analysis does not recommend breastfeeding for any infants in the sample up to 3 months, but suggests breastfeeding 38% of the sample from 3 to 6 months to maximize verbal IQ at 6.5 years. Note, however, that breastfeeding is such that infants do not recommence breastfeeding once weaned. Thus, for an infant to breastfeed from 3 to 6 months, it is necessary to have done so up until 6 months. The dependency of breastfeeding on not having already weaned an infant can be incorporated into the second-interval Q-function by including an interaction between A₁ and A₂; we did not pursue this in the current analysis as the simpler (fewer parameters) Q-function models did not suggest any significant or substantial findings. Finally, the IPTW analysis recommends breastfeeding all infants in the sample up to 3 months, and 49% from 3 to 6 months to maximize verbal IQ at 6.5 years. Estimates and decision rules from the hard-max estimation procedure were not substantially different. We also examined exclusive breastfeeding as the treatment of interest (i.e., no formula, other milks or liquids, or solid food supplementation); the results were similar.

5. CONCLUSION

In the care of virtually all conditions which are not acute, estimating the best sequence of actions or treatments should not be done in a series of single interval studies. Due to the complexity and cost of running a sequentially randomized trial, most complex regimes must first be explored through observational data, and hence it is key to develop inferential techniques that are easily interpreted and readily implemented. Q-learning is a particularly appealing approach due to the ease with which it can be implemented. However, as we have demonstrated, standard approaches to causal adjustment can lead to serious bias and unacceptably poor coverage if the model for the Q-function is not correctly specified. Where the dimension of the confounding variables permits, we therefore recommend directly including covariates into the models for the Q-functions. Where the relationships between the potential confounders and the outcome are poorly understood, it may be necessary to employ splines of polynomial functions to ensure an adequate model specification.