Toward optimal fragment generations for ab initio protein structure assembly

Abstract

Fragment assembly using structural motifs excised from other solved proteins has shown to be an efficient method for ab initio protein-structure prediction. However, how to construct accurate fragments, how to derive optimal restraints from fragments, and what the best fragment length is are the basic issues yet to be systematically examined. In this work, we developed a gapless-threading method to generate position-specific structure fragments. Distance profiles and torsion angle pairs are then derived from the fragments by statistical consistency analysis, which achieved comparable accuracy with the machine-learning-based methods although the fragments were taken from unrelated proteins. When measured by both accuracies of the derived distance profiles and torsion angle pairs, we come to a consistent conclusion that the optimal fragment length for structural assembly is around 10, and at least 100 fragments at each location are needed to achieve optimal structure assembly. The distant profiles and torsion angle pairs as derived by the fragments have been successfully used in QUARK for ab initio protein structure assembly and are provided by the QUARK online server at http://zhanglab.ccmb.med.umich.edu/QUARK/.

INTRODUCTION

Threading-based comparative modeling approaches^1-4 have demonstrated considerable success in the protein tertiary structure prediction. But the template-based comparative modeling methods cannot generate reliable models if there are no homologous structures in the Protein Data Bank (PDB)⁵ or if the query-template alignments cannot be appropriately identified. For the targets in the so-called midnight zone, ab initio folding is needed for constructing the protein models from scratch.

There have been a variety of methods that were developed for ab initio protein-structure construction, ranging from atomic-level molecular dynamic simulation^6,7 to reduced-level physics-based^8,9 and knowledge-based^10-12 Monte Carlo assembly, to topology-level fold enumeration,¹³ and to residue-contacts constrained conformational reconstruction.^14,15 Among these approaches, the fragment-based assembly method, as proposed by a number of authors^10,16-18 has demonstrated notable success, especially in the community-wide critical assessment of protein structure prediction (CASP) experiments. Compared to atomic-level simulations, the fragment insertion and replacing movements help reduce the entropy of conformational search and yet maintain the high quality of local structures, because the fragments are directly extracted from experimental structures. The lengths of the structural fragments are used differently by different methods. In both BE16 and Rosetta,¹⁰ 3 and 9 mer fragments were exploited. In QUARK,¹² fragments of continuous lengths in 1–20 residues were used.

Because ab initio modeling targets usually have no appropriate global templates, many authors tried to identify segmental substructures, which have various lengths following the nature of query-template alignments. For instance, SEGMER¹⁹ and chunk-TASSER²⁰ generated structural fragments for various sets of secondary structure (SS) elements, where more accurate spatial restraints can be derived from the local fragments than that from the global threading alignments. The position-specific structural fragments were also directly used by FRAGFOLD,²¹ TASSER,²² and I-TASSER²³ for structure assembly simulations.

There are two strategies for fragment generations. The first is to generate the position-specific fragments for each piece of query sequence by the query-to-template sequence/profile matches.^12,24 The second method is sequence-independent, which gathers fragments of various lengths and conformations by clustering the structures from the PDB library.^25,26 Because these fragments are independent of their residue types, they can be placed at any position of the query sequence for folding simulation. Although the total number of fragments generated in the second strategy is small, because the conformation at each location is more diverse, it can have the advantage in modeling the structurally variable regions such as loops where the threading-based methods may have a shortage of fragment conformations.

As a basic building block of the structure modeling, the quality of the fragments and the accuracy of the resultant restraints are essential for the success of ab initio structural predictions. Many open questions remain in the fragment generation and selection as well as their impact to the ab initio folding result, which have not been clearly studied and systematically answered, partly due to the lack of a clearly defined criterion to evaluate the quality of the fragment structures. For example, how to generate and select high-resolution fragments close to their native conformations? How to extract the optimal restraint information from (multiple) fragments? What is the optimal fragment length for ab initio structural assembly? How many fragments should be exploited at each position of the sequence? By now, existing works have partly addressed some of those problems. For instance, Handl et al.²⁷ analyzed the effects of fragment length and move size to the folding accuracy of different types of proteins. HHfrag focused on generating precise fragments with variable lengths by HMM profile comparison.²⁸ In this work, we aim to systematically address all the above-mentioned problems.

We first generate position-specific fragments of different lengths by using a multiple-feature gaplessthreading method. Distance profiles and clustered torsion angle pairs are then derived from the generated fragments via consensus analysis. The method is benchmarked on a set of 145 nonredundant proteins, where systematic analysis is performed to carefully examine the above-mentioned basic issues. Structural fragments, distance profile, and torsion angle pairs were also tested in the CASP9 experiment through the recently developed QUARK ab initio structural assembly algorithm.^12,18

MATERIALS AND METHODS

Template database construction

To generate the fragment structure library, we first downloaded all the protein-structure files from the PDB website and chose those having resolution better than 2.0 Å. Then, we split the PDB entries into chains and only keep the longest chain for each entry if chains in the entry are homologous to each other (sequence identity > 30%). We calculated the sequence identity I_ij between each pair of the remaining protein chains i and j by using NW-align (http://zhanglab.ccmb.med.umich.edu/NW-align/). Here, I_ij is defined as the number of identical residues between i and j divided by the length of sequence j. The accumulated identity AI_ij for chain i is defined by:

$$A{I}_i={\Sigma }_{j=1}^N{I}_{ij}$$ (1)

where N is the total number of protein chains for consideration.

The N chains are then sorted by the accumulated identities in a descending order, and the protein chains from the top to the bottom of the list are chosen to construct a nonhomologous structural library, with discarding the chains homologous (sequence identity > 30%) to the selected chains in the pool. Because the protein chains in the top are often longer and have more homologous neighbors than those in the bottom, this procedure helps to build a more representative library covering the majority of protein structures. As a result, 5637 protein chains are collected. If we build the database from the bottom of the list, protein chains that are first chosen belong to the outliers of the whole list.

Gapless-threading method for position-specific fragment generation

Fragment structures are generated by a gapless-threading algorithm, which aligns each fragment of the query sequence with the templates using multiple feature scores, which include sequence profiles, SS type, solvent accessibility, backbone torsion angles, and residue-based structure profile.

Sequence frequency profile for the query sequence is extracted from the multiple sequence alignment searched by PSI-BLAST²⁹ through a nonredundant sequence library (ftp://ftp.ncbi.nih.gov/blast/db). Henikoff and Henikoff³⁰ weighting is used to eliminate the redundant sequences. For each template protein, the sequence profile is constructed by a similar procedure but specified by the position-specific substitution matrix.

SS types of the query sequence are predicted by PSSpred (http://zhanglab.ccmb.med.umich.edu/PSSpred), a composite neural network (NN) training program based on the Rumelhart error backpropagation method.³¹ SSs for template proteins are assigned by DSSP.³²

Solvent accessibility and real-value phi and psi angles for the query sequence are predicted by separated two-layer NN programs, which were trained by PSI–BLAST checkpoint file and three-state SS types. The accuracy of torsion angle prediction by this program is higher than that of ANGLOR³³ on our benchmarking test set at http://zhanglab.ccmb.med.umich.edu/QUARK/list.txt, especially for the psi angle where the absolute error decreases from 44.76° to 37.84° (Table I). The solvent accessibility for template structures is calculated by EDTSurf,³⁴ which generates triangulated solvent-accessible surface using the fast Euclidean distance transform technique, where the solvent accessibility of each residue is defined as the ratio of the accessible surface area in protein to the maximum accessible surface area of this residue type. Solvent accessible surface area of each residue can also be estimated by DSSP. We find that it has a very high correlation (Pearson’s correlation coefficient = 0.994) with that calculated by EDTSurf based on the 145 test proteins.

Table I.

Real-Value Torsion Angle Prediction on 145 Test Proteins

Error	ANGLOR (°)	Two-layer NN (°)	First cluster center (°)	Best in top 30 cluster centers (°)
phi	23.79	23.46	24.70	6.42
psi	44.76	37.84	39.23	6.50
(phi, psi)	55.59	49.83	51.91	10.15

Note that the circular nature of the torsion angles has been considered in the calculation.

Finally, structural profile for each residue in the template is defined as the frequency matrix of 20 residue types at each position, calculated from the most similar fragments retrieved from the PDB, by matching multiple structural features of RMSD (root mean squared deviation), torsion angles, residue depth, SS, and solvent accessibility.^35,36

For each fragment of query sequence, we identify the best-fitting structural fragments by scanning the target sequence through the representative template library using gapless threading. Fragments of each length are probed along the sequence using a sliding window. Top 200 fragments of the highest alignment scores are retrieved by a composite scoring function at each position. The scoring function f(i,j) for aligning the ith residue in the query with the jth residue in the template is given by:

$$f(i,j)={\Sigma }_{k=1}^{20}{P}_q(i,k)L_t(j,k)+w_1\delta (s{s}_q\left(i\right),s{s}_t\left(j\right))-w_2\mid s{a}_q\left(i\right)-s{a}_t\left(j\right)\mid +w_3{\Sigma }_{k=1}^{20}S{P}_t(j,k)L_q(i,k)-w_4\mid {\phi }_q\left(i\right)-{\phi }_t\left(j\right)\mid -w_5\mid {\psi }_q\left(i\right)-{\psi }_t\left(j\right)\mid$$ (2)

Here, P_q(i,k) is the frequency profile of the query sequence while k runs through 20 amino acids. L_q(i,k) and L_t(j,k) represent the log-odds profiles (Position-Specific Substitution Matrix from PSI–BLAST) of query and template sequences, respectively. The first term in the scoring function is the dot-product of the frequency profile of the query sequence and the log-odds profile of the template. The higher the value is, the more consistent their profiles are. This profile–profile alignment score has been proved to be much better than sequence-profile alignment score for fold recognition.³⁷ ss_t(j), sa_t(j), φ_t(j), and ψ_t(j) stand for the SS type, solvent accessibility, phi, and psi torsion angles of the jth residue in the template. ss_q(i), sa_q(i), φ_q(i), and ψ_q(i) are those predicted for the ith residue of the query. Structure profile SP_t(j,k) is the frequency of having residue type k at the jth position of the template. δ(x,y) is the delta function. w_i (1 ≤ i ≤ 5) is the weighting factor of each feature. We performed an exhaustive search of the weighting parameters through a five-dimensional grid system and obtained w₁ = 2, w₂ = 6, w₃ = 2.5, w₄ = 12 and w₅ = 10, which resulted in the best average RMSD of fragments on 88 independent training proteins, which are also listed at http://zhanglab.ccmb.med.umich.edu/QUARK/list.txt.

Fragment-based distance profile derivation

Template-based residue–residue distance and contact maps have been frequently used to constrain the modeling simulations in protein structure prediction.^11,38 For the ab initio targets, however, there are generally no long-range distance/contact predictions due to the lack of homologous global templates. Here, we propose the concept of distance profile, which aims to derive long-range pair-wise distance and contact restraints from multiple fragments.

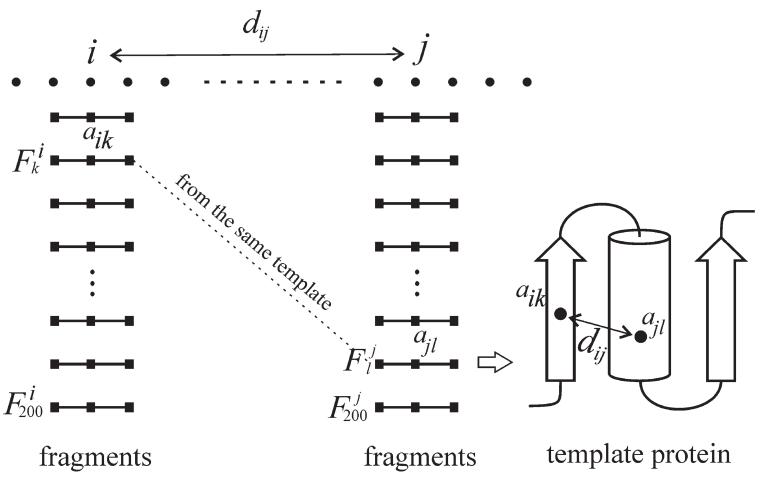
Let us consider two residues (i and j) at the query sequence, where top 200 fragments are generated for each position based on Eq. (2), that is, $F_k^i$ (k = 1, …, 200) corresponding to fragments at the position i, and $F_l^j$ (l = 1, …, 200) to that at j (Fig. 1). For the kth and lth fragments, the residues aligned with i and j are noted as a_ik and a_jl, respectively. Because the fragments at positions i and j were collected independently, most of the top scoring fragments at the two positions are from different template proteins. For those fragment pairs ($F_k^i$ and $F_l^j$), which come from the same PDB protein, we assume that it has a high probability that the distance (d_ij) between a_ik and a_jl on the template is similar to the distance between i and j in the query sequence, because these residue pairs are assumed to have similar local interaction environment on different proteins. Here, we only count the residue pairs with a distance below 9Å, because the short-distance interactions, for example, backbone and side-chain hydrogen bonding and disulfide bonds, tend to be more conserved than the long-distance ones in the local interaction environment.

Figure 1.

Fragments $F_k^i$ and $F_l^j$ coming from the same global template may have conserved contact interaction as that in the query residue pair.

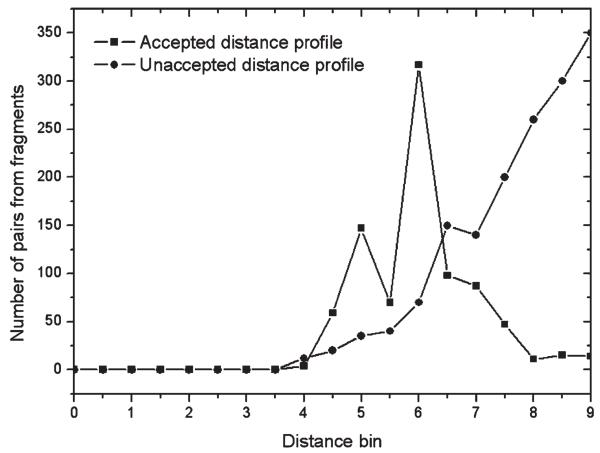
To construct the distance profiles, we generate a histogram for every residue pair in the query from the fragment pairs aligned with the target residue pair. The distance bin of the histograms is set to 0.5 Å. If the distance between a pair of residues in the template falls in a bin, the total number in the bin will increase by one. Figure 2 shows two typical examples of distance profiles. More often than not, the distance histogram increases monotonically with the distance, due to the trivial entropy increase of larger distances even if there is no interaction between the residue pairs (see the curve with circles in Fig. 2). To decrease the false-positive rate, we discard all residue pairs with such distance histogram from our consideration.

Figure 2.

Two typical distance profiles for a given residue pair.

The second curve with square in Figure 2 is of more interest to us, where a histogram peak appears in the middle range of the distance (d_ij = 6 Å in this example). The shape of this curve indicates that a large number of residue pairs from different template proteins have the same distances around 6 Å. These residue pairs in the template proteins may have different sequence separations, but their spatial distances are similar. Because all the residue pairs are aligned with the same residue pair in the query sequence, it should have a high possibility that the query residue pair may have this distance.

Because the distance profiles are specified with a broad range of distance distributions, they can provide more detailed spatial information than the traditional binary contact predictions, which only tell the distance below or above a distance cutoff.^39-41 When considered as energy constraints, they help avoid the inaccuracy of a single averaged distance. In the second profile of Figure 2, for instance, the average distance is near 5.5 Å. A restraint at this average distance represents actually an unfavorable channel of the distance histogram. In the QUARK ab initio-folding simulation,¹² we use negative logarithm of the counts in the distance profiles as the energy restraints, which can correctly simulate the multiple distance peaks in the profiles (at 5 and 6 Å in this example).

In addition to the middle-peak filter, several conditions are used for further filtering the distance profiles. First, residue pairs with a separation in the query sequence <5 amino acids are discarded. Second, if the total number of residue pairs appearing in the templates is <20, the distance profile for the corresponding residue pair is omitted. Third, sequence separation of the residue pair in the template should be comparable to that in the query sequence, that is, the sequence interval between the two residues in the template in Figure 1 should satisfy the condition 0.8 × |i − j| < |a_ik − a_jl| < 1.2 × |i − j|. On the basis of this condition, we ensure that long-range contacts (|i − j| is high) are predicted from residue pairs, which also have long sequence separations. Fourth, no cross alignment is considered, that is, (j − i)/(a_ik − a_jl) should be larger than 0.

Torsion angle pair clustering

For a given residue in the query sequence except for the N and C terminals, we can have M * N torsion angle pairs (phi and psi) extracted from the top M fragments of length N. In the fragment-based ab initio-folding simulations, the fragment replacement movement corresponds to the replacement of all the phi/psi angles and the associated bond-lengths and bond-angles of the decoy structure by those from the template structural fragments. Because the number of torsion angle pairs extracted from fragments is huge, it is impossible to cover all phi/psi phase space within a limited time of the ab initio simulations. To increase the efficiency of search, we prepare a lookup table, equipped with a nonredundant set of torsion angle pairs.

We use two clustering algorithms, SPICKER⁴² and k-means,⁴³ to generate the nonredundant (phi, psi) pairs at each position. SPICKER decides the number of clusters according to the distribution of data dynamically. k-means algorithm outputs converged k clusters in an iterative refinement from initial seeds. At most 30 cluster centers are chosen, which are also sorted based on their cluster sizes. Because the real-value torsion angle pairs are directly taken from template structures, the inherent correlations are automatically taken into account; this is different from the predictions by NN or Supporting Vector Machines where the phi/psi torsion angles are usually predicted separately.

RESULTS AND DISCUSSION

Benchmark test set

We collected 145 small to medium-sized proteins from the PDB with length between 70 and 150 residues as the test set. These proteins are assigned as hard targets by LOMETS⁴⁴ as no significant template alignments can be detected by any threading programs after excluding homologous templates with sequence identity > 30% to the query sequence. Even though, there are still some homologous proteins in the template library that have similar structure to the query but are not detected by threading. To make sure that these proteins are not been used in our testing, we added two additional strict filters to our library. First, we exclude all templates that have a TM-score > 0.3 to the target structure with the threading alignments by the MUSTER program.³⁵ Second, we run TM-align⁴⁵ to scan the target structure through the template library and exclude all the templates that have a TM-score > 0.5 to the target. Using these filters, we guarantee that there are no templates in the template library that may have similar sequences or structural folds to the query proteins.

Accuracy of fragment structures

To examine the impact of different alignment features to the accuracy of fragment identification, we include the six energy terms in Eq. (2), one by one, to the gapless-threading program and then compare the obtained fragments to the native conformations. Table II lists the average RMSD of the first and top 200 fragments. We only reported the RMSD of 9 mer fragments here on the purpose of comparing with Rosetta 9 mer fragments later. In the general case, the longer the fragments are, the higher average RMSD will be, due to the fact that RMSD is a sequence-length dependent measurement of protein structure similarity (see Fig. S1 in the Supporting Information).

Table II.

Fragment Accuracy by Different Scoring Terms in Eq. (2)

Features	〈RMSD1〉a (Å)	〈RMSD200〉b (Å)	σ〈RMSD200>〉c (Å)	〈RMSDB〉d (Å)	Ranke
1st	2.422	2.639	1.427	0.731	93
1-2nd	1.946	2.070	1.328	0.784	94
1-3rd	1.906	2.032	1.296	0.775	95
1-4th	1.868	1.987	1.279	0.772	95
1-5th	1.835	1.950	1.277	0.800	96
1-6th	1.811	1.907	1.265	0.864	98

^aAverage RMSD of the first 9 mer fragments.

^bAverage RMSD of the top 200 9 mer fragments.

^cStandard deviation of the top 200 9 mer fragments.

^dAverage RMSD of the best in the top 200 fragments.

^eAverage rank of the best fragment among the 200 9 mer fragments.

On average, all energy terms have positive effect to the fragment quality. The maximum RMSD improvement is obtained when the SS match is added to the sequence profile comparison, which results in a RMSD reduction from 2.422 to 1.946 Å for the first fragment and 2.639 to 2.070 Å for the top 200. The alignments of solvent accessibility and structure profile also have considerable contribution to the accuracy of fragments. But the last terms of phi/psi angles have the smallest contribution among all the terms, probably due to the relatively low accuracy of the prediction. Errors of the predicted features also affect the best retrieved fragments as shown in the table. However, performance of QUARK prediction is more correlated with the quality of all the top fragments than that of the best fragments, because fragment substitution movement can hardly identify and accept the best fragments. From Column 4, we find that the standard deviation of the top 200 fragments becomes smaller when we use more features. This is because the retrieved fragments are more restricted by using those features.

Columns 5 and 6 of Table II show the average RMSD and the relative rank of the best in the top 200 fragments. Although nearly perfect fragment (RMSD < 1.0 Å) exists in the template library for almost all sequences, the selection of the best fragment appears difficult, and the average rank of the best fragment is close to random (93–98th of 200). This is not unexpected, because all homologous templates have been excluded from the library, and most of the energy features in Eq. (2), which essentially originate from sequence or sequence profile comparisons, have no significant correlation with the similarity of the fragment to the native in the low-RMSD region. However, the overall quality of the top-scoring fragments is still much better than the random selection, which demonstrates that a general correlation of energyRMSD over the entire RMSD range still exists.

Rosetta program¹⁰ has two versions of template libraries of 2001 and 2006, which contain 2229 and 6025 protein chains, respectively. The protein chains in the libraries were idealized to contain only standard bond lengths and angles. We run the Rosetta program that generates fragments by matching the PSI–BLAST checkpoint file and SS types. For the same set of benchmark proteins, the average RMSD of the first 9 mer fragments is 1.966 and 1.987 Å, based on the small and large template library, respectively, which is close to (or only slightly worse than) our result 1.946 Å in Table II (Row 3), if we only use the top two features of profile alignment and SS match. The standard deviations of their top 200 9 mer fragments are 1.336 and 1.323 Å separately, which are also close to our result 1.328 Å.

Residue contact prediction derived from distance profiles

The fragment-based distance profiles can be used to deduce short-distance contact interactions of long-range separated residue pairs. It is of interest to examine the accuracy of these predictions compared to the traditional sequence-based contact predictions by machine learning.^39-41 For this purpose, we collect the residue contact predictions from the distance profiles, which have the peak corresponding to the distance bin < 8 Å, a distance cutoff most frequently used in the contact prediction assessments.⁴⁶ The contacts are sorted based on the accumulative number of residue pairs in all the distance bins < 8 Å. For each query sequence with length L, top 0.4L predicted contacts are selected for each of the three contact orders, that is, |i − j| in [6, 11], [12, 24], and >24, which result in 1.2L contact predictions in total for mixed-order contacts.

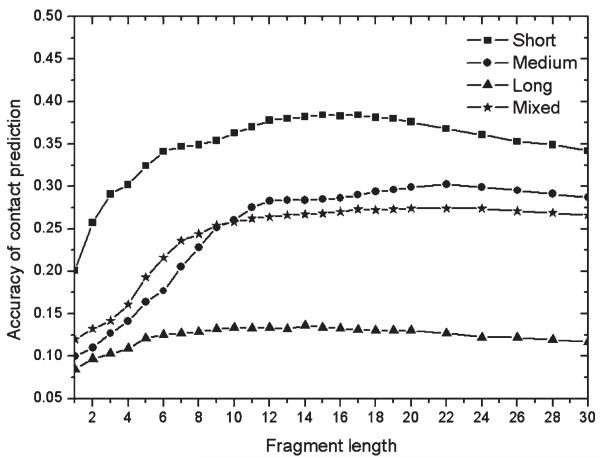
Figure 3 shows the accuracy of contact predictions by distance profile method using different lengths of fragment structures. Although no global templates were used, nontrivial contact predictions were achieved for all ranges of contact orders. Generally, the contact accuracy is higher when the sequence separation of the target residues is smaller. This is because more insertions and deletions are involved in the residue pairs of larger separation in both the query sequence and templates, which will induce larger variation of contact possibility and bigger error in contact prediction.

Figure 3.

Accuracy of contact prediction derived from nonhomologous fragments in terms of fragment lengths.

The trends of prediction accuracy regarding fragment lengths are different for the four types of contacts. The short-range contact prediction has the highest accuracy when the fragment length is around 16. For the medium-range contacts, the best fragment length is 22. For long-range contacts, fragments in the range of [9, 20] have the best accuracy. The overall mixed contact prediction is most stable and accurate when the fragment lengths are larger than 10.

Because no single fragment length is the best for all the contact types, distance contacts of each type are derived by fragments of the best length in each category. In Table III, we show a comparison of the contact predictions derived from the multiple fragments with that by the two representative machine-learning methods, SVMCON⁴⁰ and SVMSEQ,³⁹ both being publicly available software. The short and medium-range contact predictions from fragments have a comparable accuracy to the machine-learning-based method. However, the contact prediction in the long-range residue separation is still worse than the latter.

Table III.

Summary of Contact Predictions by Different Methods

Contact-range	SVMCON	SVMSEQ	QUARK filtered-Ia	QUARK filtered-IIb	Numc
145 benchmark proteins
Short	0.341	0.388	0.385	0.390	0.4L
Medium	0.288	0.299	0.300	0.307	0.4L
Long	0.211	0.212	0.136	0.214	0.4L
Mixed	0.292	0.297	0.274	0.300	1.2L
Contact-range	SVMCON	SVMSEQ	QUARK without fragment filter		Numc
31 FM proteins in CASP
Short	0.301	0.329	0.354		0.4L
Medium	0.267	0.256	0.280		0.4L
Long	0.134	0.138	0.135		0.4L
Mixed	0.239	0.244	0.249		1.2L

^aFilter template proteins of sequence identity > 30%, TM-score > 0.3 by MUSTER, and TM-score > 0.5 by TM-align.

^bFilter template proteins of sequence identity > 30%.

^cNumber of contact predictions with L being protein length.

The low accuracy of long-range contact prediction from fragments is mainly because of the lack of templates with similar fold to the query, because all homologous templates have been pre-excluded. In Column 5, we also list the accuracy of contact predictions only using the sequence filter, that is, sequence identity < 30%, which has been mostly often used for excluding homologous templates in protein structure-prediction studies.^22,47 The resultant contact accuracy of the fragments outperforms the machine-learning-based predictions for short- and medium-range contacts and becomes comparable for long-range contacts. The high accuracy of short- and medium-range contacts by the fragment-based method may partially benefit from the super-SSs of templates, which map to the short fragments at different positions. We also summarized the native contacts for all the structures in the template library. The ratios of residue pairs that are less than 8 Å to the total number of residue pairs are 4.8, 3.2, and 0.8% for the three types of contacts, which are much lower than the accuracies of predictions.

Because the performance of the contact prediction is sensitive to the manual setting of template filters, to examine the performance of the predictions in real case ab initio folding, we tested the algorithms on 31 Free Modeling (FM) targets/domains in CASP8 and CASP9 experiments. These targets were assigned in the FM category, because there were no global templates detected by any threading algorithms. The lower part of Table III shows the comparison of the fragment-based and machine-learning-based contact predictions. In the former case, no sequence or structure filters were implemented, but all templates solved after the CASP experiment were excluded to mimic the CASP ab initio predictions. To keep the consistency of the data, the SVMCON result in the table for those CASP targets is also calculated by its standalone program. It is slightly different to the result submitted to the CASP, which was evaluated as one of the best in CASP8 and CASP9.^46,48 In the table, distance profile-based method outperforms the machine-learning-based methods for short and medium-range contacts and has a similar performance for the long-range contact prediction. Here, although the sequences of FM targets are not homologous to any template structure, their folds may still be similar to some existing templates. Distance profile-based method makes use of the retrieved fragments from those templates and successfully predicts some of the long-range contacts. These data demonstrate the potential usefulness of the fragment-based methods in both contact and structure prediction for ab initio protein targets.

Finally, we examine the complementary of the fragment-based and machine-learning-based contact predictions. For the 31 FM targets, the total numbers of correct long-range contacts predicted by SVMCON and SVMSEQ are 192 and 198, among which 102 contacts are commonly predicted by both methods, that is, overlap rates of 53.1 and 51.5%. The high-overlap rates are expected, because the two predictors use similar algorithm although they were trained by different datasets. However, the overlap rates are 28.9 and 29.2% between the fragment-based method and SVMCON and 30.9 and 30.3% between the fragment-based method and SVMSEQ separately. Therefore, the fragment-based contact predictions are highly complementary to that of the machine-learning-based methods, and a combination of both should significantly increase the coverage of the contact prediction and the yield of ab initio folding. Overlap rates between the three methods are high (>60%) for short- and medium-range contacts.

Because distance profile also predicts the exact value for every residue pair, we further examine those correctly predicted pairs whose real distances are less than 8 Å. The average error between the exact distance and the distance in the distance profile that has the highest probability is 0.83 Å, while the error of distance prediction randomly chosen from [4 to 8 Å] is 1.24 Å.

Blind test of fragment-based distance profiles in CASP9

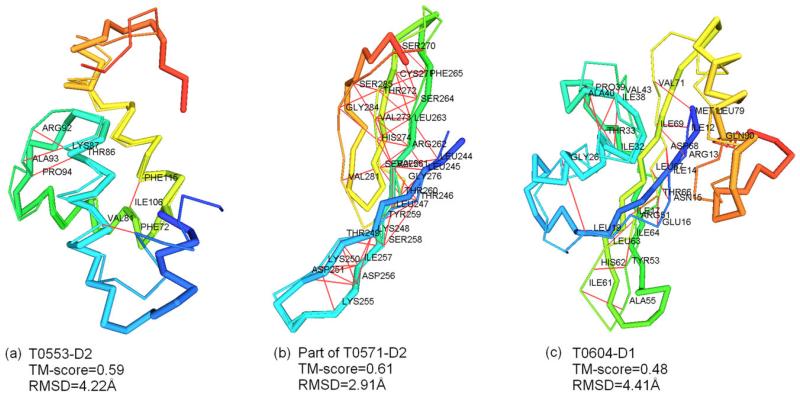
In CASP9, models in “Zhang_Ab_Initio” human group were generated by the QUARK ab initio program,¹² which exploits the distance profiles as restraint to guide the long-range atomic interactions. In Figure 4, we show three typical examples from the FM category, where pairwise distances predicted by the distance profiles played an important role in the successful QUARK ab initio structural assembly.

Figure 4.

Examples of successful QUARK predictions in CASP9 by incorporating distance profiles. Predicted model and native structure are represented by thick and thin backbones separately. Accurately predicted residue pairs are connected by red lines. (a) T0553-D2, TM-score = 0.59, and RMSD = 4.22 Å. (b) The middle part of T0571-D2, TM-score = 0.61 and RMSD = 2.91 Å. (c) T0604-D1, TM-score = 0.48, and RMSD = 4.41 Å.

First, Target T0553-D2 in Figure 4(a) is a small helical domain, which contains five α-helices. The QUARK model has TM-score = 0.59 and RMSD = 4.22 Å to the native structure, which is the best among all groups. The relative orientation of the five helices was correctly predicted in the model, which is mainly due to the fact that the pair-wise helix contacts, as specified by the short range distances [see red lines in Fig. 4(a) and data in Supporting Information Table SI], were precisely predicted in the fragment-based distance profiles. The C-terminal was however misplaced in the model, because there were no correct restraints between this terminal and the other helical region.

Second, T0571-D2 is a medium-sized β-protein of 135 amino acids where no group (including QUARK) correctly predicted the fold of the target for the entire sequence. The Zhang_Ab_Initio model by QUARK had the middle region of four β-strands correctly predicted, which has a TM-score = 0.61 and a RMSD = 2.91 Å [Fig. 4(b)]. From the distance profile data, QUARK obtained 50 accurate distance profiles between shortrange and medium-range residue pairs (Supporting Information Table SI), which is the major contribution to the success of modeling this difficult β-protein target.

Finally, T0604-D1 is the first domain of the VP0956 protein from vibrio parahaemolyticus. The Zhang_Ab_Initio model by QUARK has a TM-score = 0.48 and RMSD = 4.41 Å for the entire domain as illustrated in Figure 4(c). There are eight long-range distance restraints that were correctly identified by the distance profiles (see bottom rows of Supporting Information Table SI). These data help QUARK to generate hydrogen bonds between the first and the third β-strands. The two short helices in the model also have correct orientations due to the short-range distance restraints as predicted by the distance profiles. However, the C-terminal β-strand in the model did not form the antiparallel β-sheet with the N-terminal β-strand as the native structure, due to the lack of contact restraints between them.

The detailed information of the accurately predicted distance profiles in the above examples is provided in Table SI of the Supporting Information. Each predicted distance that corresponds to the maximum number in the distance profile has an error of <1 Å to the real distance in the native structure. It has the trend that when the sequence separation becomes bigger, the maximum number in the distance profile becomes smaller.

Torsion angle prediction derived from fragments

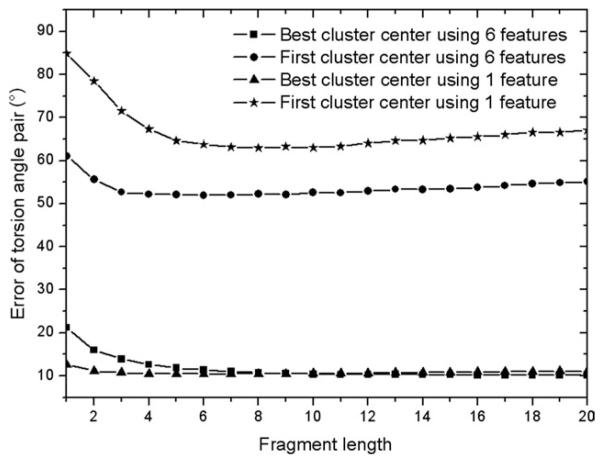
Using the clustering algorithms, we have collected up to 30 pairs of torsion angles for each residue. The accuracy of the first and the best cluster centers from the fragments of different lengths is shown in Figure 5. Here, the error between the native torsion pair (φ₀, ψ₀) and the prediction (φ_c, ψ_c) is calculated by the following formula. δ(x,y) is the absolute difference between two torsion angles with their periodicity considered.

$$\begin{array}{cc}\hfill E_t=& \sqrt{{\delta }^2({\phi }_c,{\phi }_0)+{\delta }^2({\psi }_c,{\psi }_0)}\hfill \\ \hfill & \delta (x,y)=\{\begin{array}{cc}\mid x-y\mid \hfill & if\mid x-y\mid <180\hfill \\ 360-\mid x-y\mid \hfill & \text{else}\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (3)

Figure 5.

Error of clustered torsion angle pairs using fragments of different lengths retrieved by 1 feature and 6 features. Note that the circular nature of the torsion angles has been considered in the calculation.

From the curves in the figure, it is shown that the best in top 30 torsion angle pairs is much better than that from the first pair of angles, which demonstrates the difficulty in the selection of the best fragments. However, using the complete set of alignment features in Eq. (2) still can considerably improve the accuracy of phi/psi predictions compared to that only using profile comparison.

For all four curves in the figure, we can see that the errors are high when the fragment length is too short (<5). This is understandable, because the scoring function based on too few residues does not contain sufficient co-operative information to pick up appropriate fragment structures. The error starts to increase when the length is larger than 13. This means that when the fragments become longer, there are fewer good fragments in template library that can match well with the target sequence. Overall, fragments with lengths around 10 have the best torsion angle pair prediction.

Finally, we collect at most 30 torsion angle pairs from fragments of length 10 by sorting their cluster sizes. Although the phi and psi angles from the first cluster are slightly worse than that of the machine-learning-based method (see Table I), the best torsion angles from this limited number of pairs are very close to the native values. In contrast, the best of the 30 randomly generated torsion angle pairs has an error around 16.43° for (phi, psi) pair, which is much worse than those by the clustering method.

SS prediction from fragments

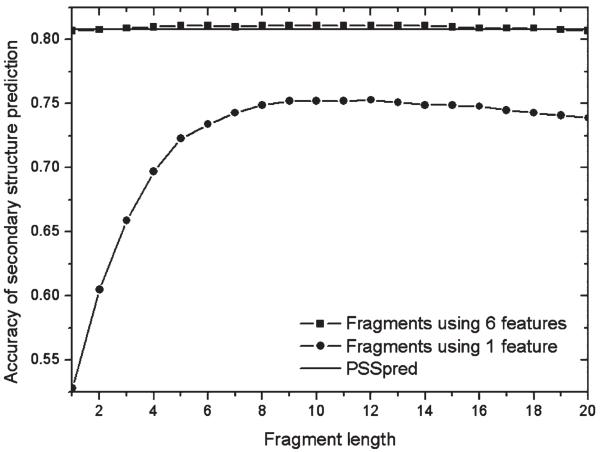
In the fragment file, for each position of the query sequence, we record the secondary structure (SS) types of the corresponding residues in the original templates. Accordingly, we can assign the SS type of each residue based on the consensus among the fragment templates. On the test set of 145 proteins, PSSpred has the Q₃ accuracy of 0.808 for the three-state SS prediction, which is slightly better than 0.800 by PSIPRED⁴⁹ prediction. If we only use the sequence profile match in Eq. (2) to generate the fragments, we can get the best prediction accuracy up to 0.752 from the single-size fragments, as shown in Figure 6. Again, because the profile information of short fragments is too arbitrary, the accuracy of SS prediction is low especially when the fragment size is below five.

Figure 6.

Comparison of secondary structure prediction in terms of fragment lengths.

By combining all six energy terms in the Eq. (2), we can achieve the best accuracy of 0.811 when the length is around 10, which is slightly better than that of PSSpred. Because the whole set of scoring function already includes the PSSpred prediction result, the accuracy of SS prediction is very stable no matter what the fragment length is. The NN-based SS prediction programs sometime predict mistakenly α-helix residues as β-strand or β-strand residues as α-helix. This type of errors is more serious than the errors caused by predicting helix/strand as coil or coil as helix/strand, because the conversion of helix and strand elements can misfold protein models into completely different topologies. A combination of the fragment-based and NN-based methods can considerably reduce the possibility of helix-strand mispredictions due to the complementary information provided by the fragment-based prediction. As a test, we simply combine the three-state probabilities of the two methods, which increases the Q₃ accuracy to 0.815 for those hard targets. The percentage of residues with helix-strand misconversion reduces from 3.0% in PSSpred to 2.3%.

Optimal number of fragments at each position

If some region of the query sequence has homologous alignments in the template library, the current scoring function can usually rank them at the top of the fragments. In this case, only a few fragments are sufficient to achieve the best accuracy of distance profile prediction and torsion angle prediction. However, for the hard proteins lack of homologous fragments in the library, which are exactly the targets of ab initio modeling, the ranking of the selected fragments becomes much worse. In this situation, more fragments are needed for achieving optimal structure predictions.

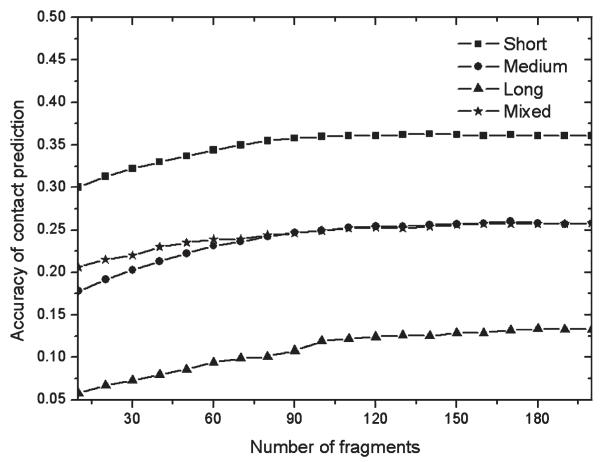
In Figure 7, we show the accuracy of the fragmentbased contact predictions versus the number of fragments used to collect the predictions. Here, we use fragments of a unified length of 10 residues, because it has achieved the best accuracy for most of the structural feature predictions. Indeed, the prediction accuracy becomes higher with the increase of the number of fragments. But after the number is above 100, there is no obvious difference on the data. Similar results are observed for the SS and torsion angle pair predictions (data not shown).

Figure 7.

Accuracy of contact prediction from 10 mer fragments versus the number of top fragments used for the counting of contact pairs in templates.

CONCLUSIONS

Assembling structural models using fragments extracted from unrelated proteins is one of the most efficient methods for template-free (or ab initio) proteinstructure prediction. As a critical step of the procedure, this work systematically examines a series of important issues involved in the fragment generation and selection as well as their impact to ab initio folding simulation.

We first developed a gapless-threading method to retrieve fragments of various sizes from a nonredundant protein structure library. Although all multiple features are shown to be useful to increase the accuracy of local fragments, the most important contributions come from the sequence profile alignment and the SS match. In contrast, the changes in the template library size and template protein sets have less important impact compared to the feature collections.

Second, we proposed a novel method to construct distance profiles from multiple fragments generated at different locations, which allows the derivation of longrange contact information from short local fragment structures. Using a peak cutoff of 8 Å in the distance histogram, the residue contact predictions by the fragments have accuracy better or comparable to that by the best machine-learning method depending on the contact orders. In the real-case ab initio folding, distance profile was also found advantageous over the traditional distance restraint predictions, which are usually specified by the average and the deviation of distances, because implementation of a continuous distance histogram rather than a single distance average helps tolerate distance errors.12 Distance profile can also be derived from multiple-threading alignments by different threading programs. It has shown encouraging results on modeling the remotely homologous protein targets when the strategy was used by QUARK in combination with the LOMETS alignments (data in preparation).

Finally, we examined the predictions of residue-residue contacts, torsion angles, and SS types as derived from different sets of fragment structures. It is found that the fragments of 10 residues in length can consistently result in the optimal results, and at least 100 fragments at each position are needed for the optimal modeling.

Abbreviations

NN

neural network

RMSD

root mean squared deviation

SS

secondary structure