Abstract
We study the electrochemistry of single layer graphene edges using a nanopore-based structure consisting of stacked graphene and Al2O3 dielectric layers. Nanopores, with diameters ranging from 5 to 20 nm, are formed by an electron beam sculpting process on the stacked layers. This leads to unique edge structure which, along with the atomically thin nature of the embedded graphene electrode, demonstrates electrochemical current densities as high as 1.2 × 104 A/cm2. The graphene edge embedded structure offers a unique capability to study the electrochemical exchange at an individual graphene edge, isolated from the basal plane electrochemical activity. We also report ionic current modulation in the nanopore by biasing the embedded graphene terminal with respect to the electrodes in the fluid. The high electrochemical specific current density for a graphene nanopore-based device can have many applications in sensitive chemical and biological sensing, and energy storage devices.
Keywords: Nanopores, graphene, graphene electrochemistry, nano-bio sensors, stacked graphene
Graphene has attracted tremendous interest in the scientific world over the recent years due to its unique electronic,1–2 thermal3 and optical4 properties. It has shown great promise in the field of electronics, biological and chemical sensing, and energy storage applications.5–6 Studies on graphene electrochemistry have suggested the ability of graphene based electrodes to carry a large amount of current at electron transfer rates superior to graphite and carbon nanotube (CNT) electrodes.5. The relative abundance of carbon on earth combined with widespread knowledge of carbon-based chemistries and stability makes the study of graphene based electrochemistry extremely exciting.5,7–8
Graphene is a single atom thick sheet of sp2 hybridized carbon atoms arranged in a honeycomb lattice structure. A graphene sheet has two types of electron transfer sites – edge and basal. Edge sites have already been demonstrated to possess enhanced electron transport rates and reactivity in studies of CNT ends.9 Graphene has a higher theoretical specific surface area (2630 m2/g) than graphite and CNTs (1315 m2/g) and provides motivation for study of heterogeneous electron transfer rates.8 In addition, graphene can carry significant current densities without degradation from electro-migration which typically causes significant damage in ultrathin metal films.10 Current densities as high as 2 × 109 A/cm2 have been reported for nanoscale interconnects based on graphene grown by chemical vapour deposition (CVD).11 The graphene edge plane atoms have been reported to have significantly higher electron transfer rate compared to basal planes in electrochemical studies on both highly ordered pyrolytic graphite as well as on multiple layers of graphene.12–13 Graphene modified glassy carbon electrodes have been reported to have much greater electrochemical response, than unadulterated glassy carbon electrodes, to molecules like paracetamol, hydrazine, glucose, ethanol dopamine as well as heavy metals.7,8 Zhou et al.14 demonstrated the ability of chemically reduced graphene oxide electrodes to distinguish the electrochemical current signal from the four bases of DNA, which could not be distinguished with graphite and glassy carbon electrodes. Another important application of graphene electrochemistry is in energy storage devices. The specific capacitance of chemically modified graphene was found to be up to 1352 F/g,5 and extremely high energy densities up to 85.6 Wh/kg at room temperature have been reported.15–16 Furthermore, graphene and hybrid graphene based electrodes have been used to increase specific capacities of Li+ ion based batteries, improving power density and cyclic performance, while maintaining mechanical integrity at high current densities.6
Despite extensive studies on graphene sheets and graphene doped electrodes, the electrochemical properties of isolated graphene edges remain relatively unexplored. Here, we demonstrate a graphene edge embedded nanopore (GEEN) structure to isolate graphene edge electrochemical activity from basal plane activity. Transmission electron microscopy (TEM) based sculpting offers potential for control on graphene edge structures.17 Furthermore, we demonstrate the use of the embedded graphene edge to modulate the ionic flux in the nanopore. Along with a conductive graphene terminal of thickness equivalent to the distance between two adjacent base pairs in dsDNA (~0.34 nm), this could provide a basis for single DNA molecule analysis with measurement methodologies like tunnelling or electrochemical redox reactions.
Results and Discussion
The fabrication of graphene nanopores using a TEM has been demonstrated previously and used to sense biomolecules like polynucleotides and DNA protein complexes.18–19 In this study, we fabricate GEENs in stacked graphene and dielectric layers using a focused electron beam in a TEM (200 keV), and measure the electrochemical current exchange at the graphene edge embedded within the nanopore. The top Al2O3 dielectric layer isolates the electrochemical basal plane activity. We demonstrate the very high electrochemical current density as well as the first known study of electrochemical current exchange at graphene (potentially as thin as single layer) edge in an ionic solution. The combination of non-linear diffusion at nanoscale electrodes, an enhanced concentration gradient of ions in the vicinity of the nanopore20 and high electron transfer rates at damaged edges of graphene12 creates a unique system with high electrochemical current densities.
The schematic of our test GEEN structures is shown in Fig. 1a.21 The fabrication process is further described in Fig. 1b–e (details in the Methods section). Initially, a suspended hydrophilic supporting membrane of stacked layers of 50 nm Al2O3, 200 nm SiNx and 50 nm Al2O3 is fabricated using deep reactive ion etching (DRIE). Subsequently, a hole of 300 ± 40 nm is formed in the supporting membrane using a focused ion beam (FIB) (Fig. 1b). The graphene – Al2O3 stack is then formed on the supporting membrane with the FIB hole by transferring graphene films grown by CVD (details in the Methods section). We note that the hydrophilic nature of the supporting membrane helps spread the water more evenly during the graphene transfer steps and improves the smoothness of the transferred graphene/PMMA stack.22 The Raman spectroscopy maps of the graphene 2D to G peak intensity ratios (I2D/IG) (Fig. 1g and Supplementary Fig. 4a–b) and the full-width at half maximum of the 2D peak (FWHM2D)23 (Supplementary Fig. 4e–f) show our growth process results in a mix of monolayer and bilayer graphene, similar to our previous work.21 The first graphene layer (G1) in our stack spans the FIB hole and acts as a mechanical support for deposition of the subsequent graphene and dielectric layers of our architecture. We note that subsequent to the graphene transfers, the membranes are annealed in an Ar/H2 atmosphere at 400 °C to remove PMMA residue remnant from the transfer process.24
Figure 1.
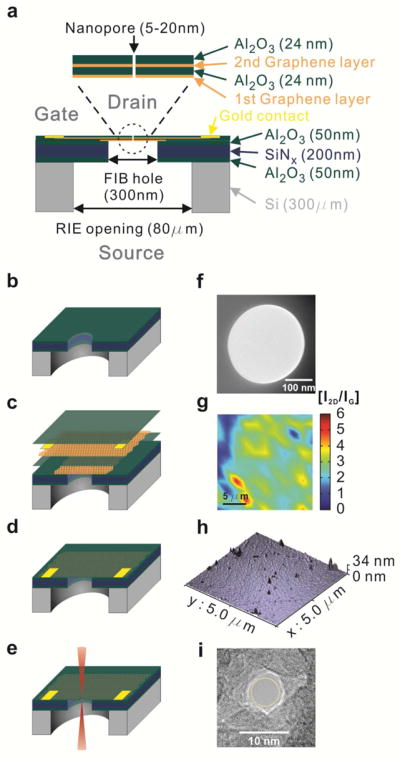
Schematic diagram of graphene-embedded stacked membrane structure and fabrication. (a) Schematic showing the thickness of each layer as well as diameters of RIE, FIB and nanopore holes (b) Supporting membrane consists of three layers of 50 nm of Al2O3, 200 nm of SiNx and 50 nm of Al2O3, deposited on 300 μm-thick double polished prime Si wafer. RIE is used to etch 80 μm-wide opening in Si wafer to supporting membrane and 300 nm through hole is fabricated in supporting membrane by FIB. (c) First graphene layer transferred onto the FIB hole acts as the support for subsequent layers. This is insulated from the second graphene layer by 24 nm of Al2O3 deposition. Second graphene layer, which is the active electrode at the middle of membrane, is transferred onto first Al2O3 layer. Ti/Au deposition enables the formation of contacts. A further layer of Al2O3 is deposited to insulate the electrode from the ionic solution. (d) Final structure of graphene embedded membrane suspended on 300 nm FIB hole. (e) Focused electron beam (CBED mode) in TEM is used to fabricate a single nanopore of 5 to 20 nm diameter. (f) TEM image of FIB hole of 300 nm diameter in supporting membrane. (g) Raman spectroscopy of I2D/IG obtained from graphene surface indicating predominantly monolayer coverage. (h) AFM image of membrane surface. Roughness (Ra = 1.89 ± 0.67 nm) is significantly reduced on deposition of Al2O3 on graphene compared to bare graphene surface (Ra = 0.84 ± 0.21 nm). (i) 5nm nanopore is fabricated by convergent electron beam in TEM.
To ensure uniform nucleation of the subsequent Al2O3 deposition (D1) onto the chemically inert graphene basal planes, a metallic seed layer of Al (2 nm thick) is evaporated onto the graphene.25 Al2O3 is a suitable choice as the dielectric due to its excellent mechanical stability26 and reduction in 1/f noise compared to Si3N4 and SiO2 membranes.27–28 The atomic force microscopy (AFM) images (Fig. 1h and Supplementary Fig. 4d) clearly show dense and uniform deposition of the dielectric due to the presence of the seed layer (Supplementary Fig. 5a–c and Supplementary Fig. 7) as compared to dielectric deposition without the Al seed layer (Supplementary Fig. 5a–b). ALD is chosen as it offers sub nanometer control over dielectric thickness in addition to being a conformal deposition technique and a low temperature process, making it compatible with the previously transferred graphene layers.21 The thickness of the dielectric deposited is 24 nm, a value established through extensive leakage testing in fluidic environments (Fig. 2 and Supplementary Fig. 1). Similar thicknesses of dielectric have been reported to provide effective isolation in ionic fluid environments in transistor based devices.29–30 A second graphene layer (G2) is transferred onto D1 and annealed in an Ar/H2 atmosphere. This layer is contacted using Ti/Au contacts and insulated by depositing another 24 nm of Al2O3 (D2) as described above (Details in the Methods section).
Figure 2.
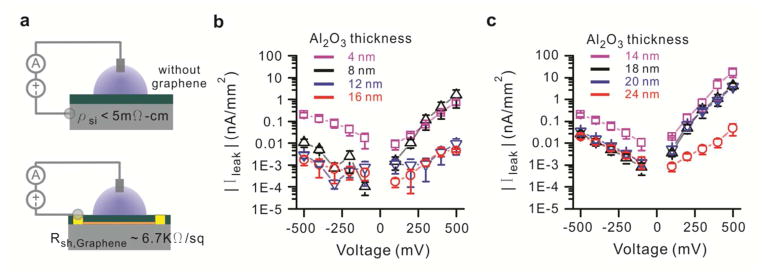
Leakage test on various thickness of Al2O3. (a-top) Schematics showing leakage measurement setup for Al2O3 on p++ Silicon (ρ < 5 mΩ-cm). Al2O3 of thickness 4 to 16 nm were deposited on the conductive Si wafer. Measurements are conducted with one electrode connected to Si wafer and the other attached to Ag/AgCl electrode in the solution (a-bottom) Schematic of leakage measurement setup for Al2O3 on graphene transferred onto Si surface with Al2O3 deposited on top. Al2O3 thickness in range of 14 to 24 nm is deposited on graphene (Rsh ≈ 6.7 kΩ/sq) transferred on Si wafer with a ALD deposited Al2O3 top surface. Measurements are conducted between the graphene film contacted with aluminium wires and the solution contacted with Ag/AgCl electrodes. All leakage experiments are performed in 1 M KCl, 10 mM Tris, 1 mM EDTA at pH 7.6 and at room temperature (22 ± 2 °C). (b) Leakage current density measured for Al2O3 on conductive Silicon. Al2O3 thickness less than 10 nm showed leakage current greater than 1 nA/mm2 at 500 mV, but thicker Al2O3 (>10 nm) showed much greater insulation over the voltage range of −500 mV to +500 mV. (c) Leakage current density for Al2O3 deposited on graphene. Leakage current is observed to be fairly high up to 20 nm-thick Al2O3. Also the leakage is significantly higher for positive voltage at Ag/AgCl electrode. 24 nm-thick Al2O3 displays decent insulation from leakage. Current leakage occurrence at relative thicker Al2O3 deposited on graphene is associated with wrinkles on graphene (Supplementary Fig. 9).
To explore the electrochemical current exchange at the graphene nanopore edges, it is essential to eliminate current exchange at the basal plane from affecting our measurements. In the embedded graphene membrane, the parasitic leakage current from gate to source and gate to drain (indicated in Fig. 1a) could adversely affect our experimental values. The active device area exposed to fluid on the backside (gate-source path) is just the area exposed to the FIB hole of 300 nm. This area is insulated from the fluid by the 24 nm Al2O3 under the graphene gate electrode. The rest of the graphene is well insulated by a total thickness of 300nm of stacked Al2O3 and SiNx layers of the supporting membrane structure. On the gate-drain path the entire encapsulated graphene sheet is shielded from the fluid by just the top layer of 24 nm Al2O3. The fluid area exposed at the top layer corresponds to the area exposed by the o-rings (diameter = 1.42 mm) used to seal the fluidic setup. To mimic our device structure and characterize leakage through the top dielectric, we fabricated the device as shown in Fig. 2a. We compared the leakage current through different thicknesses of Al2O3 deposited on a bare conductive silicon wafer and Al2O3 deposited on a graphene sheet transferred onto an Al2O3 coated (on Si wafer) top surface, similar to the D1/G2/D2 stack of our actual devices. The ALD dielectric deposition of Al2O3 on graphene is preceded by the seed layer Al (~ 2 nm thick) evaporation as described previously. The leakage is measured by attaching a PDMS well (2.75 mm in diameter) on top of the device to hold the fluid. The current is measured between the graphene electrode and Ag/AgCl electrode dipped in the electrolyte fluid. All leakage measurements were performed with a 1 M KCl solution. The conductive silicon and the graphene electrode are connected to ground in all measurements.
The leakage densities observed are presented on a logarithmic scale (absolute value) in Fig. 2b–c. On the bare silicon wafer, a slight asymmetry was observed in the I–V characteristics. For a positive Ag/AgCl electrode voltage a higher leakage current density was observed through the dielectric. The leakage current density reduces from −0.2 to −0.001 nA/mm2 at −500 mV, as the dielectric thickness is increased from 4 to 16 nm. Comparing these values to leakage currents on samples with the dielectric deposited on graphene we can see a significant increase in the leakage current of the latter (Fig. 2c). The electrochemical exchange at the dielectric-electrolyte interface has been reported in electrolyte-oxide-silicon (EOS) devices.31 Since the leakage current is high at positive electrode voltages, this could indicate electron tunnelling through the pinholes in the dielectric as shown in our AFM images (Supplementary Fig. 4d and Supplementary Fig. 9), similar to those reported in TiO2 coated CVD graphene membranes.18 On the other hand, at negative electrode voltages the leakage currents are significantly suppressed in the voltage range from 0 to −500 mV. Increasing the dielectric thickness from 14 to 24 nm decreases the leakage current density from −0.2 to −0.02 nA/mm2. For a 2.75 mm diameter PDMS well, that translates to a current of about 118.7 pA. Since the ionic current through the nanopore is usually in the range of nanoamperes, at least one order of magnitude lower leakage current is essential to maintain reliability of our electrochemical current measurements and to have gate current independent from interference due to leakages. Therefore, we use only the negative voltage range (0 to −500 mV) in our nanopore measurements to minimize and avoid leakage across D2.
On settling upon a dielectric thickness of 24 nm, nanopores are drilled in this stacked structure using convergent beam electron diffraction (CBED) mode in a TEM (Fig. 1e and 1i). We fabricated four different pore diameters (5, 9, 14, 20 nm) for our test structures. For a 5nm pore, the beam sputters through the membrane in about 30s. For larger pores, sculpting is needed by moving the beam on the edges of the pore to expand it. Control is achieved by in-situ monitoring of the nanopore dimension with imaging. Since TEM provides angstrom level precision we believe the nanopore dimensions are accurate within a tolerance of 1nm. Prior to assembly in the fluidic setup the backside (silicon trench side) (Fig. 1a) is O2 plasma treated to make the pore hydrophilic to facilitate wetting.18,21 The top graphene layer (G2) is contacted and the chip is encapsulated in a custom built fluidic setup (Supplementary Fig. 6). Ethanol is then flushed into both chambers to promote wetting as reported in previous nanopore studies.19,21 The ethanol is flushed away repeatedly with de-ionized (DI) water and the desired buffer solution is inserted into both chambers.
The schematics of drain-source, drain-gate and source-gate measurements are shown in Fig. 3a. An external resistor of 20 MΩ is placed in series with graphene. This helps ensure our graphene current measurements are not significantly affected by leakage. At 500 mV a 20 MΩ resistor conducts 25 nA of current. Since the currents observed are much less it indicates the electrochemical resistance at the graphene edge terminal is much higher and determines current in the series circuit. For a 1 M KCl solution used in these measurements, the drain-source conductance exhibits a squared dependence32 with pore diameter as indicated in Fig. 3c. The current values for the different pore diameters also seem to be in good agreement with our previous work on similar structures.21 For the source-gate and drain-gate measurements, the graphene gate is always connected to ground to maintain a positive voltage with respect to source or drain and ensure minimal leakage in accordance to our leakage measurements as described earlier. This is indicated in the I–V curves for a 5 nm pore showed in Fig. 3b (and Supplementary Fig. 2). The drain-gate and source-gate conductance is also plotted in Fig. 3c and is observed to be nearly identical for each of the four different pores diameters, indicating that the measured current is indeed only through the electrochemical exchange at the graphene terminal and the leakage contribution to these measurements on the drain side is indeed negligible. The o-rings used in these experiments are approximately 1.42 ± 0.1 mm in diameter. Based on the leakage measurements, for a 24 nm thick Al2O3 insulation layer, the maximum contribution of leakage at drain/source at potential of −500 mV should be approximately 30 pA, which is about two orders of magnitude less than the currents observed in these measurements. This is further confirmed by similar measurements in the same structure without a nanopore as currents in the range of 10 to 20 pA are observed across all three terminals. Furthermore, the conductance through the graphene terminal scales fairly linearly with pore diameter as seen in Fig. 3c. The slight variation from the linear dependence can be explained from the varying graphene sheet thickness (Fig. 1b) over the membrane, which affects pore sidewall area, since the pore region could consist of a mixture of mono and bi-layer graphene. Nonetheless, we do see an increase of conductance from 5 to 15 nS as the pore diameter is increased from 5 to 20 nm. This is expected and indeed proves that this current is due to electrochemical exchange on the cylindrical pore sidewalls.
Figure 3.
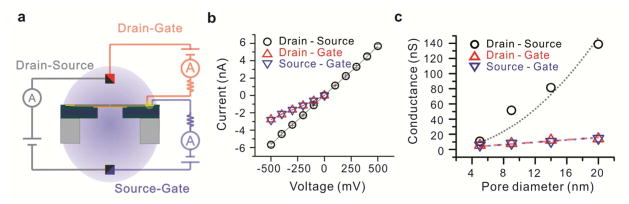
Electrochemical measurements for embedded graphene nanoelectrode. (a) Schematic diagram of measurement setup. For the drain-source measurement (gray), source is connected to ground and voltage applied at the drain. For drain-gate (red) and drain-source (blue) measurements, the gate is connected to ground and voltage is applied to the other terminal. (b) Current-voltage curve of nanopore ionic current and electrochemical behavior of graphene edge through 5 nm nanopore. Identical currents through the drain-gate and source-gate pathways indicate electrochemical exchange at the exposed graphene edge. (c) Conductance dependence on pore diameter. Drain-source conductance shows a square dependence on pore diameter, while gate current exchange shows a fairly linear dependence on pore diameter consistent with electrochemical exchange at cylindrical nanopore wall. The slight variation from linear dependence is may be attributed to varying graphene sheet thickness on various regions of the membrane. 5, 9, 14 and 20 nm diameter nanopores were used in this study. All experiments are performed in 1 M KCl, 10 mM Tris, 1 mM EDTA at pH 7.6
From the current values of electrochemical exchange at the 5nm pore edge, (Fig. 3b) and assuming a predominantly monolayer coverage of graphene, we calculate a current density of up to 1.2 × 104 A/cm2 at a drain voltage of −200mV. This current density is three orders of magnitude higher than electrochemical current densities reported for oxygen reduction on CNT electrodes.29 From electrochemistry studies on basal planes of individual monolayer sheets for CVD-grown graphene reported by Li et al.,33 a current density of about 6 × 10−8 A/cm2 is obtained. Thus a significant electrochemical current enhancement is observed using individual graphene edges as the active electrode material. Furthermore, we simulated the concentration of H+ and Cl− ions at the nanopore (details in the Methods section) and the Cl− ions are significantly higher in number. Thus, all redox couples based on H+/OH− ions can safely be ignored as it is highly unlikely they can contribute to such high currents. Thus, we conclude that the reaction at the positive graphene electrode (anode) edge is the oxidation of Cl− ions. The equilibrium oxidation potential for this reaction at room temperature is −1.36 V.34 However surface treatments enhancing the number of possible adsorption sites in diamond electrodes have been reported to lower the potential of chloride oxidation by as much as 0.5 V.35 A similar mechanism might explain high electron transfer rates observed on graphene edges at low voltages. Electrochemical studies on graphite edges have exhibited extremely high electrochemical reaction rates.12–13 Fast electron transfer kinetics reported on CNTs are also attributed to tube ends, identified as the reactive sites.9,36–37 For GEENs we expect all sites at the nanopore edge to be damaged. Girit et al.17 reported TEM drilled graphene nanopores which reconstruct and eventually exhibit a zigzag edge configuration due to its higher stability. For a graphene nanoribbon with zigzag edges, a large peak in the density of states is observed at the edges,38–39 as confirmed by Scanning tunnelling microscopy (STM) studies.40 An enhancement in the density of states at the graphene nanopore edges of our architecture may have a direct effect in enabling the high electrochemical current densities observed in our measurements.
We note an electrochemical reaction consists of mass transport of the reactive species to the electrode surface and electron exchange at the electrode surface.41 Since the dominant electrochemical exchange in our measurements occurs at the damaged graphene nanopore edges, it would appear that the electron exchange is not the rate limiting step. Diffusion limited electrochemical systems operate in the linear diffusion regime. For linear diffusion based systems, i.e. when the electro-active length is ≈ comparable to the diffusion layer thickness, the reaction is diffusion limited and the peak current ip is given by the Randles-Sevcik equation:9
| (1) |
where, n is the number of moles of electrons transferred in the reaction, A is the area of the electrode (cm2), C is the analyte concentration (in moles/cm3), D is the diffusion coefficient (cm2/s), and v is the scan rate (V/s) of the applied potential. For a chloride ion oxidation reaction n is assumed to be 1. The active area of the electrode is the cylindrical pore area, which for a 5 nm pore, is calculated to be 9.4 × 10−14 cm2. The concentration is taken as 10−3 mol/cm3 and the diffusion coefficient of Cl− is taken as 1.5 × 10−5 cm2/s.42 For a 5nm pore and a scan rate of 100 mV/10 s the peak current by the above equation gives ip = 9.6 × 10−7 nA, which is much smaller than observed current. Thus the reaction is not diffusion limited. It should be noted that our electrode size is in nanometers and is much smaller than the diffusion layer thickness (usually of the order of ,43 where t is the time period of each scan) and hence convergent diffusion effects are significant. For microelectrodes, convergent diffusion leads to significantly higher mass transport and thus higher current densities.9 We believe that with the graphene nanoelectrodes used in our experiments, this effect would be exacerbated. Furthermore, the local concentration of the electro-active species (Cl−) is much higher and a threefold increase has been reported when compared to microelectrodes of same electro-active area. This increase in concentration is in the vicinity of the nanopore as compared to the bulk solution, also results in faster mass transport,20 contributing to the large current densities measured in our GEEN structures. Our simulations report local (nanopore edge) concentration of Cl− as high as 8.5 M for bulk KCl concentration of 1 M (details in the Methods section).
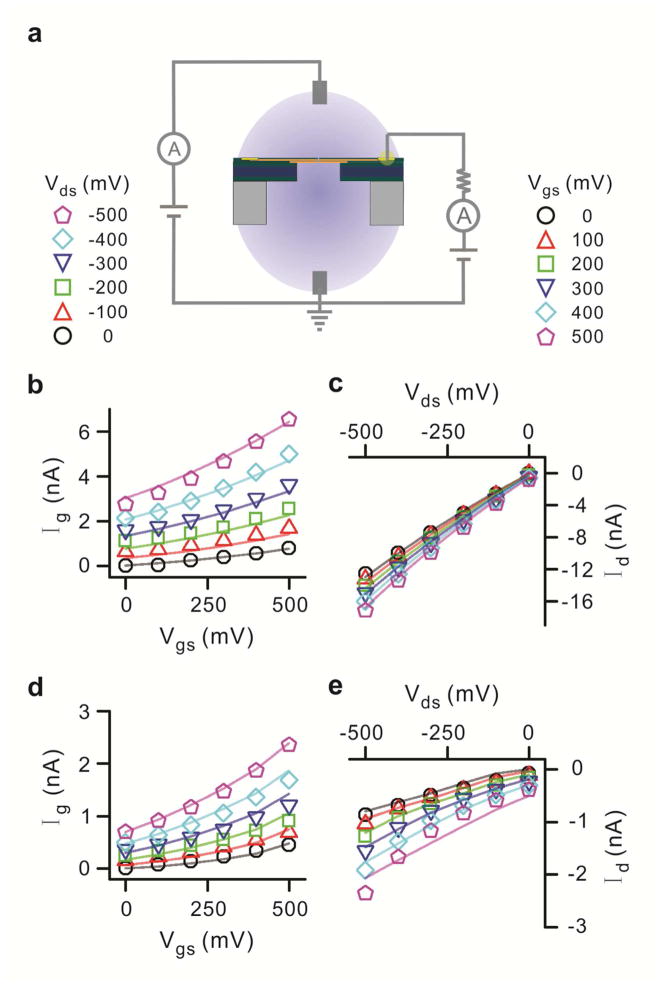
We further investigate the use of our structure as a 3 terminal device analogous to a transistor (Fig. 4a). The source terminal is always connected to ground in these measurements. The source current can be obtained by Kirchhoff’s law
Figure 4.
Three terminal measurement for the graphene embedded membrane. (a) Schematic diagram with source connected to ground while voltage is swept at the drain and gate terminals. (b) and (d) Gate current characteristics for 1 M KCl and 10 mM KCl respectively. The variation of gate current with gate source bias as drain voltage is varied is shown. The scatter points are experimental numbers while the straight lines are simulation fits. (c) and (e) Drain current characteristics for 1 M KCl and 10 mM KCl solution respectively. The variation of drain current with drain source bias as gate voltage is varied is recorded. Both solutions are prepared with 10 mM Tris and 1 mM EDTA for buffering at pH 7.6.
| (2) |
where, Id, Ig and Is are the drain, gate and source currents respectively. In accordance with our leakage results, the drain is always kept at a negative potential with respect to the gate for minimal interference from leakage. The graphene gate current characteristics (Ig vs. Vgs) for a 5 nm pore in 1 M KCl solution are shown in Fig. 4b. A shift in the gate current values is observed as the drain voltage is swept from 0 to −500 mV at a sweep rate of 100 mV/10 s (step function). Numerical simulations are used to explain gate current characteristics (details in the Methods section). The Ig dependence on Vgs and Vds voltage is estimated by an exponential function. This equation is coupled with the Poisson-Nernst-Plank equation and the Grahame equation and solved simultaneously to obtain both gate and drain current values. Fig. 4c shows the Id vs Vgs characteristics. As expected, a shift in the Id is seen as Vgs is swept. The simulation results are in good agreement with the experimental data at 1 M KCl.
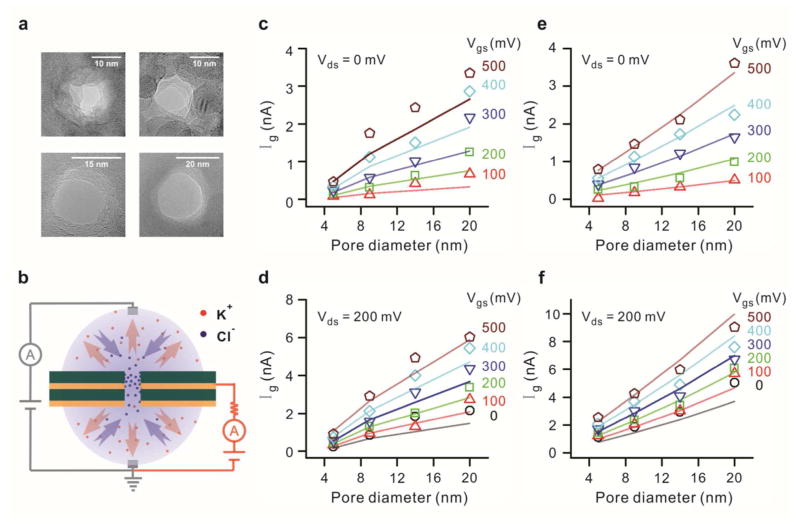
Further confirmation of observation of graphene edge currents is obtained by repeating these measurements for three more pores of 9, 15 and 20 nm diameters (Fig. 5a). Since the measured currents are due to electrochemical exchange at the pore walls, the active area is cylindrical. Thus linear dependence of Ig on pore diameter is expected. We previously noted this in our two-terminal measurements for currents due to electrochemical exchange at graphene electrodes (Fig. 3c). At 1 M KCl buffer solution the Ig values at two different Vds (0 and −200 mV) are shown in Fig. 5e and 5f, respectively, for Vgs swept between 0 to +500 mV. The simulated values (solid lines) show excellent agreement with experimental data (symbols) for all four pore diameters. We see a four-fold increase in the Ig value as the pore size is increased from 5 to 20 nm.
Figure 5.
Gate current dependence on pore diameter (a) TEM images of nanopores of four different diameters (5, 9, 14, 20 nm) nanopores drilled through an embedded graphene membrane. (b) Schematic diagram of electrochemistry. The positive gate bias leads to attraction of chloride ions to the nanopore and expulsion of potassium ions. Red dots and arrows represent potassium ions while blue dots and arrows are for chloride ions. (c–f) Scaling of gate current with pore size at drain bias of 0 and −200 mV for 4 different pore diameters. (c), (d) Gate current dependence on pore diameter using 10 mM KCl solution. Linear dependence on pore diameter is observed over gate bias ranging from 0 to +500 mV for both drain bias values. (e), (f) Gate current dependence on pore diameter using 1 M KCl solution. Similar linear dependence on pore diameter is observed entire voltage range. The scatter points are experimental numbers while the straight lines are simulation fits. Both solutions are prepared with 10 mM Tris and 1 mM EDTA for buffering at pH 7.6
Similar experiments were repeated in the 10 mM KCl solution. The (Ig vs. Vgs) and (Id vs. Vds) characteristics show a similar shift as expected (Fig. 4d and 4e). The simulation results (solid lines in both graphs) are in good agreement with the experimental results, although in this case the fitting parameters are altered for a 5 nm pore since the pore diameter is smaller than the Debye layer thickness (details in the Methods section).44 The Ig values do not scale linearly with concentration and this is attributed to enhanced ionic flux in the vicinity of the nanopore as shown in our simulations (details in the Methods section). The pore diameter dependence measurements in 10 mM KCl for all four pore diameters show fairly good agreement with simulated results and a linear increase of I g with pore diameter is displayed (Fig. 5c and 5d). Note that the values of Id and Ig are observed to be nearly the same for these measurements at 10mM, as illustrated in Supplementary Fig. 3. From equation (2), this implies an extremely low Is.
Our results confirm that the observation of electrochemical exchange at the graphene edge, isolated from any basal plane activity. An array of GEENs could potentially be used to harness extremely large value of energy density per unit mass. Methods like electron beam, nanoimprint lithography or Helium based focused ion beam45 techniques could be used to mass produce arrays of nanopores. Improvement in dielectric coverage of graphene by use of other materials like HfO246 and different dielectric seed layer materials47 like Titanium or 3,4,9,10-perylene tetracarboxylic acid dianhydride (PTCDA) would significantly enhance the voltage range used in these experiments by reducing parasitic leakage through the dielectric enabling higher current densities to be harnessed.
Furthermore, we note that the differential flux in ions on opposite sides of the nanopore could potentially have interesting applications in controlling the flux of bio-molecules to be sensed though electrochemical exchange at the graphene edge. The differential ion flow rate could potentially be used to trap molecules within the pore allowing for electrical interrogation using the conductive graphene terminal. Wanunu et al.48 reported the use of salt gradients as a means to enhance DNA capture rate to increase throughput of the detection scheme. Another major biosensing application of an embedded conductive terminal in a solid state nanopore is with regards to DNA sequencing.49 STM based studies have been demonstrated50 to distinguish deoxynucleotide monophosphates (dNMPs) and partially sequence DNA oligomers by using tunnelling current measurements. Tsutsui et al.51–52 demonstrated tunnelling current measurements to distinguish bases in deoxynucleotide triphosphate (dNTP) molecules. If an embedded conductive terminal, e.g. GEENs, can be combined with biological53 or electronic54 methods to slow DNA translocation rates, it could provide a pathway to DNA sequencing.
Conclusion
In summary, we present the investigation of electrochemical current exchange at a CVD-grown graphene edges within a nanopore. We demonstrate the ability of our graphene embedded nanopore structures to study electrochemistry at individual graphene layers in isolation from contribution from basal planes. We observed electrochemical current densities on the order of 104 A/cm2, three orders of magnitude higher than those reported for carbon nanotubes and much higher than those reported for graphene surface electrochemical studies. The high currents are attributed to a combination of the nanopore edge structures produced by electron beam sculpting along with the convergent diffusion mechanisms due to nanosized electrodes, which have been reported to enhance ionic flux of reactive species. We also demonstrated the modulation of ionic current by the use of the embedded conductive graphene terminal. Numerical simulations were performed to confirm the transistor like characteristics of the device. Extremely high electrochemical current densities have exciting applications for both chemical and biological sensing as well as energy storage. Scaling of these structures by producing arrays of nanopores could enable multiple applications.
Experimental Details
Graphene Growth and Transfer
Graphene is grown by chemical vapor deposition (CVD) on 1.4 mil copper foils purchased from Basic Copper.21,24,55 Copper foil is placed in an Atomate CVD system and annealed at ~1000 °C under Ar/H2 flow for 90 minutes at a base pressure of ≈ 4.4 Torr. Graphene is grown for 30 minutes at 1000 °C under 850 sccm of CH4 and 50 sccm of H2 at a base pressure of about 2.5 Torr. The resulting graphene and Cu substrates are cooled to 400 °C under 850 sccm of CH4, 50 sccm of H2 at a rate of ~ 10 °C/minute followed by cooling to room temperature under 500 sccm of Ar while the base pressure is ramped to 760 Torr (Supplementary Fig. 8a). Graphene is transferred to the receiving substrates by coating one side of the Cu foil with a bilayer of PMMA (495 K A2 and 950 K A4) (Supplementary Fig. 8b–i). Each layer of PMMA is coated at 3000 rpm followed by a 200 °C bake for 2 min. The backside graphene is removed by O2 plasma etching prior to etching the Cu foil (Supplementary Fig. 8b–ii) in etchant overnight (Transcene CE-100). The resultant PMMA/graphene film is transferred to a 10% HCl in deionized (DI) water solution to remove residual metal particles followed by a second DI rinse (Supplementary Fig. 8b–iii). The film is then transferred onto the receiving substrate (Supplementary Fig. 8b–iv) with predefined FIB holes (~ 300 nm in diameter) and PMMA is removed in a 1:1 methylene chloride/methanol solution for 30 min. The samples undergo a 400 °C anneal under Ar (500 sccm) and H2 (100 sccm) flow to remove residual PMMA.
Raman Spectroscopy and AFM Characterization
Raman mapping is performed using a scanning confocal Renishaw Raman microsope (inVia and WiRE 3.2 software). Data is collected using a 633 nm edge emitting laser (laser spot size ~ 1.3 μm and ~ 0.1 mW incident power), a 50× long working distance objective, a 1800 lines/mm grating, and 30 s acquisition time. 121 spectra is collected over 20 × 20 μm2 area at a 2 μm step size and analyzed by fitting mixed Gaussian and Lorentzian curves around the D, G, and 2D Raman peaks centered at ≈ 1340, 1590, and 2660 cm−1, respectively. A cubic spline interpolation is used to subtract the background before curve fitting. Atomic force microscope (AFM) data is collected using a Digital Instruments Dimension 3000 AFM in a tapping mode. Calculated root-mean-square (RMS) roughness values are obtained using Nanoscope Analysis v.1.4 software from Bruker Corporation. Three dimensional images are rendered using Gwyddion AFM analysis software.
Supporting Membranes
Membranes consisting of stacked layers of Al2O3 and SiNx is fabricated on 300 ± 2 μm thick double-side polished <100> silicon wafers purchased from Silicon Quest International. Wafers are piranha cleaned (1:1 H2SO4:H2O2) for 15 minutes before depositing Al2O3 via ALD (Cambridge Nanotech). 50 nm of Al2O3 was deposited at a platen temperature of 250 °C using tetramethyl-aluminum (TMA) and water vapor precursors. Subsequently, 200 nm of low-stress SiNx is deposited (STS Mesc PECVD System) using a mixed-frequency recipe (High Frequency: 6 s at 13.56 MHz, platen power of 20 W and Low Frequency: 2 s at 380 kHz, platen power of 60 W) with precursors SiH4 and NH3 at flow rates of 40 sccm and 55 sccm, respectively, at a platen temperature of 300 °C. Another 50 nm of Al2O3 (ALD) is deposited with the same parameters as described before. Optical lithography is used to define 80 μm square windows on the back of the wafer with the aid of plasma resistant Megaposit SPR-220 photoresist and an ABM Flood Exposure (Model 60) tool. The wafer is then placed inside a STS Pegasus ICP DRIE and 80 μm square membranes are suspended using a Bosch etching process. 300 to 350 nm holes are then formed in these membranes using a focused ion beam (FIB) (FEI DB235) operated at a beam current of 30 pA.
Nanopore Fabrication and Nanopore Fluidic Measurement
The graphene-Al2O3-graphene-Al2O3 stack is fabricated sequentially using the same graphene transfer and ALD process as described previously. The thickness of Al2O3 for both dielectric layers is 24 nm. A seed layer Al (2nm thick) is deposited on graphene using a CHA SEC-600 electron-beam evaporator prior to deposition of both dielectric layers. The second (top) graphene layer is contacted with Ti/Au contacts. Electrical contacts, Ti (2 nm thickness adhesion layer) and Au (300 nm thick), are deposited onto G2 by shadow masking and e-beam evaporation. The measured sheet resistance of graphene is 6.7 kΩ/sq. Single nanopores of 5–20 nm diameter are drilled in the graphene-embedded membrane using a JOEL 2010F field-emission gun TEM operated at 200 kV in CBED mode with focused electron probe of diameter = 1.6 nm. O2 plasma treatment at 50 W for 30 sec on source side facilitates wetting. Subsequently Al wires are attached on Ti/Au contacts using silver paint and the chip is assembled in a custom-built chamber. Ethanol is filled in both reservoirs initially to promote wetting. Subsequently the ethanol is flushed out and the reservoirs are filled with a solution of 1 M KCl, 10 mM Tris, 1 mM EDTA at pH 7.6. All nanopore experiments are performed with Axopatch 200B and Digidata 1440A at room temperature (22 ± 2 °C).
Electrostatic Simulations
The mathematical model for ion transport involves a set of equations governing ionic transport and the electric potential. 56
The total flux due to diffusion and electromigration of the ith species (ions) is given by the following expression
| (3) |
where F is the Faraday’s constant, zi is the valence, Di is the diffusion coefficient, Γi is the flux, ci is the concentration of the ith species, and φ is the electrical potential. The Nernst-Planck (NP) equation describes the reaction rate (ri) of dissolved species.
| (4) |
The electrical potential distribution is governed by the Poisson equation
| (5) |
where ε0 is the permittivity of vacuum and εr is the relative permittivity. The electric potential at the wall surface is governed by
| (6) |
where σs is the surface charge density and n is the normal to the wall.
The Poisson-Nernst-Planck equations (PNP) equations can be simplified by integrating equation (3) and (5) across the channel, which gives
| (7) |
and
| (8) |
where A is the cross-sectional area, x is the coordinate along the channel, d is the nanopore diameter, c̄i, r̄i, φ̄ are the cross-sectional averaged concentration, reaction rate, and electric potential, respectively.
From equation (7) and (8), we obtain the cross-sectional averaged electric potential, and ionic concentration. The drain current is calculated by multiplying the current density along the x direction (assumed normal to pore wall) with the cross-sectional area at drain.
| (9) |
where Γxi is the flux rate of ith species in the x direction.
The gate current is calculated from the reaction rate of the species near the graphene gate. The oxidation rate of Cl− is assumed as a function of the electrical potential bias and the local concentration.
| (10) |
where r0Cl−, a and b are fitting parameters. c̄Cl− is the cross-sectional averaged concentration of Cl− at pore surface (mM or mole/m3).
Near the graphene gate edge, water oxidation, which generated H+ ions.
| (11) |
The generation rate of H+ is assumed as
| (12) |
The gate current IG is calculated from
| (13) |
where lr is the length of reaction region. In the simulations, lr is taken as 2nm, r0Cl− = 5×107 s−1, and r0H+ = 2×107 mol/m3/s. The parameters a and b are correlated to the pore size and electrolyte concentrations. In these simulations, d > κ−1 where κ−1 is the debye layer thickness, we choose a = 0.66 V−1, and b = 2.05 V−1. However when d < κ−1, for d = 5nm and KCl concentration of 10 mM, we choose a = 0.625 V−1, and b = 1.25 V−1. The gate current from water oxidation is much smaller than that from Cl− oxidation. However water oxidation induces H+ ions in the nanopore, which affects the surface charge density of the Al2O3 layer.
The surface charge density of the Al2O3 layer is determined by the density difference of the sites attracting positive and negative charges.
| (14) |
| (15) |
where N+, N−, and N0 are the density of positively charged, negatively charged, and neutral sites, respectively.
The densities of the positively and negatively charged sites are related to the pH value and surface potential ψs.57
| (16) |
| (17) |
where ISP is the isoelectric point, cH+ is the H+ concentration in the nanopore. The surface charge density is obtained by the Grahame equation. 34
| (18) |
Given N, cH+ISP, and N0ISP, the surface charge density can be obtained by solving equations (14)–(18). In the simulations, cH+ISP is chosen as 10−8 mM, N = 6/nm2, and N0ISP = 2/nm2. We calculate c̄H+ = 0.01 mM in a 5 nm pore (for Vds = −500 mV and Vgs = 500 mV). We also calculate c̄Cl− = 5000 mM and c̄Cl− = 8500 mM for 10mM and 1000mM KCl solutions respectively.
Supplementary Material
Acknowledgments
The authors would like to acknowledge support from the National Institutes of Health (R21 CA155863) and Oxford Nanopore Technologies, U.K for supporting the effort. D. Estrada and E. Pop acknowledge support from the National Science Foundation (NSF) Graduate Research Fellowship Program and CAREER award ECCS 09-54423, respectively.
Footnotes
Leakage studies, additional graphene electrochemical studies, photographs of experimental setup, characterization of graphene transfer process and dielectric deposition. This material is available free of charge via the Internet at http://pubs.acs.org
References
- 1.Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, Grigorieva IV, Firsov AA. Electric Field Effect in Atomically Thin Carbon Films. Science. 2004;10 :306, 666–669. doi: 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- 2.Bolotin KI, Sikes KJ, Jiang Z, Klima M, Fudenberg G, Hone J, Kim P, Stormer HL. Ultrahigh Electron Mobility in Suspended Graphene. Solid State Commun. 2008;146:351–355. [Google Scholar]
- 3.Balandin AA. Thermal Properties of Graphene and Nanostructured Carbon Materials. Nat Mater. 2011;10:569–581. doi: 10.1038/nmat3064. [DOI] [PubMed] [Google Scholar]
- 4.Mak KF, Shan J, Heinz TF. Electronic Structure of Few-Layer Graphene: Experimental Demonstration of Strong Dependence on Stacking Sequence. Phys Rev Lett. 2010;104:176404. doi: 10.1103/PhysRevLett.104.176404. [DOI] [PubMed] [Google Scholar]
- 5.Pumera M. Electrochemistry of Graphene: New Horizons for Sensing and Energy Storage. Chem Rec. 2009;9:211–223. doi: 10.1002/tcr.200900008. [DOI] [PubMed] [Google Scholar]
- 6.Hou J, Shao Y, Ellis MW, Moore RB, Yi B. Graphene-Based Electrochemical Energy Conversion and Storage: Fuel Cells, Supercapacitors and Lithium Ion Batteries. Phys Chem Chem Phys. 2011;13:15384–15402. doi: 10.1039/c1cp21915d. [DOI] [PubMed] [Google Scholar]
- 7.Shao Y, Wang J, Wu H, Liu J, Aksay IA, Lin Y. Graphene Based Electrochemical Sensors and Biosensors: A Review. Electroanalysis. 2010;22:1027–1036. [Google Scholar]
- 8.Brownson DA, Banks CE. Graphene Electrochemistry: An Overview of Potential Applications. The Analyst. 2010;135:2768–2778. doi: 10.1039/c0an00590h. [DOI] [PubMed] [Google Scholar]
- 9.Banks CE, Davies TJ, Wildgoose GG, Compton RG. Electrocatalysis at Graphite and Carbon Nanotube Modified Electrodes: Edge-Plane Sites and Tube Ends Are the Reactive Sites. Chem Commun (Cambridge, UK) 2005:829–841. doi: 10.1039/b413177k. [DOI] [PubMed] [Google Scholar]
- 10.Durkan C, Welland ME. Analysis of Failure Mechanisms in Electrically Stressed Gold Nanowires. Ultramicroscopy. 2000;82:125–133. doi: 10.1016/s0304-3991(99)00133-3. [DOI] [PubMed] [Google Scholar]
- 11.Behnam A, Lyons AS, Bae MH, Chow EK, Islam S, Neumann CM, Pop E. Transport in Nanoribbon Interconnects Obtained from Graphene Grown by Chemical Vapor Deposition. Nano Lett. 2012;12:4424–4430. doi: 10.1021/nl300584r. [DOI] [PubMed] [Google Scholar]
- 12.Ambrosi A, Bonanni A, Pumera M. Electrochemistry of Folded Graphene Edges. Nanoscale. 2011;3:2256–2260. doi: 10.1039/c1nr10136f. [DOI] [PubMed] [Google Scholar]
- 13.Davies TJ, Hyde ME, Compton RG. Nanotrench Arrays Reveal Insight into Graphite Electrochemistry. Angew Chem, Int Ed Engl. 2005;44:5121–5126. doi: 10.1002/anie.200462750. [DOI] [PubMed] [Google Scholar]
- 14.Zhou M, Zhai Y, Dong S. Electrochemical Sensing and Biosensing Platform Based on Chemically Reduced Graphene Oxide. J Anal Chem. 2009;81:5603–5613. doi: 10.1021/ac900136z. [DOI] [PubMed] [Google Scholar]
- 15.Liu C, Yu Z, Neff D, Zhamu A, Jang BZ. Graphene-Based Supercapacitor with an Ultrahigh Energy Density. Nano Lett. 2010;10:4863–4868. doi: 10.1021/nl102661q. [DOI] [PubMed] [Google Scholar]
- 16.Yoo JJ, Balakrishnan K, Huang J, Meunier V, Sumpter BG, Srivastava A, Conway M, Reddy AL, Yu J, Vajtai R, et al. Ultrathin Planar Graphene Supercapacitors. Nano Lett. 2011;11:1423–1427. doi: 10.1021/nl200225j. [DOI] [PubMed] [Google Scholar]
- 17.Girit ÇÖ, Meyer JC, Erni R, Rossell MD, Kisielowski C, Yang L, Park CH, Crommie MF, Cohen ML, Louie SG, et al. Graphene at the Edge: Stability and Dynamics. Science. 2009;323:1705–1708. doi: 10.1126/science.1166999. [DOI] [PubMed] [Google Scholar]
- 18.Merchant CA, Healy K, Wanunu M, Ray V, Peterman N, Bartel J, Fischbein MD, Venta K, Luo Z, Johnson AT, et al. DNA Translocation through Graphene Nanopores. Nano Lett. 2010;10:2915–2921. doi: 10.1021/nl101046t. [DOI] [PubMed] [Google Scholar]
- 19.Schneider GF, Kowalczyk SW, Calado VE, Pandraud G, Zandbergen HW, Vandersypen LM, Dekker C. DNA Translocation through Graphene Nanopores. Nano Lett. 2010;10:3163–3167. doi: 10.1021/nl102069z. [DOI] [PubMed] [Google Scholar]
- 20.Zhang Y, Zhang B, White HS. Electrochemistry of Nanopore Electrodes in Low Ionic Strength Solutions. J Phys Chem B. 2006;110:1768–1774. doi: 10.1021/jp054704c. [DOI] [PubMed] [Google Scholar]
- 21.Venkatesan BM, Estrada D, Banerjee S, Jin X, Dorgan VE, Bae MH, Aluru NR, Pop E, Bashir R. Stacked Graphene-Al2O3 Nanopore Sensors for Sensitive Detection of DNA and DNA–Protein Complexes. ACS Nano. 2011;6:441–450. doi: 10.1021/nn203769e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liang X, Sperling BA, Calizo I, Cheng G, Hacker CA, Zhang Q, Obeng Y, Yan K, Peng H, Li Q, et al. Toward Clean and Crackless Transfer of Graphene. ACS Nano. 2011;5:9144–9153. doi: 10.1021/nn203377t. [DOI] [PubMed] [Google Scholar]
- 23.Lenski DR, Fuhrer MS. Raman and Optical Characterization of Multilayer Turbostratic Graphene Grown Via Chemical Vapor Deposition. J Appl Phys. 2011;110 [Google Scholar]
- 24.Salehi-Khojin A, Estrada D, Lin KY, Bae MH, Xiong F, Pop E, Masel RI. Polycrystalline Graphene Ribbons as Chemiresistors. Adv Mater. 2012;24:53–57. doi: 10.1002/adma.201102663. [DOI] [PubMed] [Google Scholar]
- 25.Kim S, Nah J, Jo I, Shahrjerdi D, Colombo L, Yao Z, Tutuc E, Banerjee SK. Realization of a High Mobility Dual-Gated Graphene Field-Effect Transistor with Al2O3 Dielectric. Appl Phys Lett. 2009;94:062107. [Google Scholar]
- 26.Wang L, Travis JJ, Cavanagh AS, Liu X, Koenig SP, Huang PY, George SM, Bunch JS. Ultrathin Oxide Films by Atomic Layer Deposition on Graphene. Nano Lett. 2012;12:3706–3710. doi: 10.1021/nl3014956. [DOI] [PubMed] [Google Scholar]
- 27.Venkatesan BM, Dorvel B, Yemenicioglu S, Watkins N, Petrov I, Bashir R. Highly Sensitive, Mechanically Stable Nanopore Sensors for DNA Analysis. Adv Mater. 2009;21:2771–2776. doi: 10.1002/adma.200803786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chen P, Mitsui T, Farmer DB, Golovchenko J, Gordon RG, Branton D. Atomic Layer Deposition to Fine-Tune the Surface Properties and Diameters of Fabricated Nanopores. Nano Lett. 2004;4:1333–1337. doi: 10.1021/nl0494001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Paik KH, Liu Y, Tabard-Cossa V, Waugh MJ, Huber DE, Provine J, Howe RT, Dutton RW, Davis RW. Control of DNA Capture by Nanofluidic Transistors. ACS Nano. 2012;6:6767–6775. doi: 10.1021/nn3014917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Reddy B, Jr, Dorvel B, Go J, Nair P, Elibol O, Credo G, Daniels J, Chow EC, Su X, Varma M, et al. High-K Dielectric Al2O3 Nanowire and Nanoplate Field Effect Sensors for Improved Ph Sensing. Biomed Microdevices. 2011;13:335–344. doi: 10.1007/s10544-010-9497-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wallrapp F, Fromherz P. TiO2 and HfO2 in Electrolyte-Oxide-Silicon Configuration for Applications in Bioelectronics. J Appl Phys. 2006;99:114103. [Google Scholar]
- 32.Smeets RMM, Keyser UF, Krapf D, Wu MY, Dekker NH, Dekker C. Salt Dependence of Ion Transport and DNA Translocation through Solid-State Nanopores. Nano Lett. 2005;6:89–95. doi: 10.1021/nl052107w. [DOI] [PubMed] [Google Scholar]
- 33.Li W, Tan C, Lowe MA, Abruña HcD, Ralph DC. Electrochemistry of Individual Monolayer Graphene Sheets. ACS Nano. 2011;5:2264–2270. doi: 10.1021/nn103537q. [DOI] [PubMed] [Google Scholar]
- 34.Bard AJ, Faulkner LR. Electrochemical Methods: Fundamentals and Applications. 2. Wiley; New York: 2001. p. 124.p. 546.p. 808. [Google Scholar]
- 35.McCreery RL. Advanced Carbon Electrode Materials for Molecular Electrochemistry. Chem Rev. 2008;108:2646–2687. doi: 10.1021/cr068076m. [DOI] [PubMed] [Google Scholar]
- 36.Britto PJ, Santhanam KSV, Rubio A, Alonso JA, Ajayan PM. Improved Charge Transfer at Carbon Nanotube Electrodes. Adv Mater. 1999;11:154–157. [Google Scholar]
- 37.Nugent JM, Santhanam KSV, Rubio A, Ajayan PM. Fast Electron Transfer Kinetics on Multiwalled Carbon Nanotube Microbundle Electrodes. Nano Lett. 2001;1:87–91. [Google Scholar]
- 38.Krauss B, Nemes-Incze P, Skakalova V, Biro LP, Klitzing K, Smet JH. Raman Scattering at Pure Graphene Zigzag Edges. Nano Lett. 2010;10:4544–4548. doi: 10.1021/nl102526s. [DOI] [PubMed] [Google Scholar]
- 39.Saha KK, Drndic M, Nikolic BK. DNA Base-Specific Modulation of Microampere Transverse Edge Currents through a Metallic Graphene Nanoribbon with a Nanopore. Nano Lett. 2012;12:50–55. doi: 10.1021/nl202870y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ritter KA, Lyding JW. The Influence of Edge Structure on the Electronic Properties of Graphene Quantum Dots and Nanoribbons. Nat Mater. 2009;8:235–242. doi: 10.1038/nmat2378. [DOI] [PubMed] [Google Scholar]
- 41.Rieger PH. Electrochemistry. 2. Chapman & Hall; New York: 1994. p. 152. [Google Scholar]
- 42.Liu J, Kvetny M, Feng J, Wang D, Wu B, Brown W, Wang G. Surface Charge Density Determination of Single Conical Nanopores Based on Normalized Ion Current Rectification. Langmuir. 2011;28:1588–1595. doi: 10.1021/la203106w. [DOI] [PubMed] [Google Scholar]
- 43.Bockris JOM, Reddy AKN. Modern Electrochemistry. 2. Plenum Press; New York: 1998. p. 1234. [Google Scholar]
- 44.Israelachvili JN. Intermolecular and Surface Forces. 2. Academic Press; London: 1991. p. 238. [Google Scholar]
- 45.Precision Material Modification Patterning with He Ions. J Vac Sci Technol B: Microelectron Nanometer Struct. 2009;27:2755. [Google Scholar]
- 46.Dorvel BR, Reddy B, Go J, Duarte Guevara C, Salm E, Alam MA, Bashir R. Silicon Nanowires with High-K Hafnium Oxide Dielectrics for Sensitive Detection of Small Nucleic Acid Oligomers. ACS Nano. 2012;6:6150–6164. doi: 10.1021/nn301495k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fallahazad B, Lee K, Lian G, Kim S, Corbet CM, Ferrer DA, Colombo L, Tutuc E. Scaling of Al2O3 Dielectric for Graphene Field-Effect Transistors. Appl Phys Lett. 2012;100:093112. [Google Scholar]
- 48.Wanunu M, Morrison W, Rabin Y, Grosberg AY, Meller A. Electrostatic Focusing of Unlabelled DNA into Nanoscale Pores Using a Salt Gradient. Nat Nanotechnol. 2010;5:160–165. doi: 10.1038/nnano.2009.379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Venkatesan BM, Bashir R. Nanopore Sensors for Nucleic Acid Analysis. Nat Nanotechnol. 2011;6:615–624. doi: 10.1038/nnano.2011.129. [DOI] [PubMed] [Google Scholar]
- 50.Huang S, He J, Chang S, Zhang P, Liang F, Li S, Tuchband M, Fuhrmann A, Ros R, Lindsay S. Identifying Single Bases in a DNA Oligomer with Electron Tunnelling. Nat Nanotechnol. 2010;5:868–873. doi: 10.1038/nnano.2010.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Tsutsui M, Taniguchi M, Yokota K, Kawai T. Identifying Single Nucleotides by Tunnelling Current. Nat Nanotechnol. 2010;5:286–290. doi: 10.1038/nnano.2010.42. [DOI] [PubMed] [Google Scholar]
- 52.Tsutsui M, Rahong S, Iizumi Y, Okazaki T, Taniguchi M, Kawai T. Single-Molecule Sensing Electrode Embedded in-Plane Nanopore. Sci Rep. 2011;1:46. doi: 10.1038/srep00046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Cherf GM, Lieberman KR, Rashid H, Lam CE, Karplus K, Akeson M. Automated Forward and Reverse Ratcheting of DNA in a Nanopore at 5-Å Precision. Nat Biotechnol. 2012;30:344–348. doi: 10.1038/nbt.2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.He Y, Tsutsui M, Fan C, Taniguchi M, Kawai T. Controlling DNA Translocation through Gate Modulation of Nanopore Wall Surface Charges. ACS Nano. 2011;5:5509–5518. doi: 10.1021/nn201883b. [DOI] [PubMed] [Google Scholar]
- 55.Kim RH, Bae MH, Kim DG, Cheng H, Kim BH, Kim DH, Li M, Wu J, Du F, Kim HS, et al. Stretchable, Transparent Graphene Interconnects for Arrays of Microscale Inorganic Light Emitting Diodes on Rubber Substrates. Nano Lett. 2011;11:3881–3886. doi: 10.1021/nl202000u. [DOI] [PubMed] [Google Scholar]
- 56.Karniadakis G, Beskök A, Aluru NR. Microflows and Nanoflows: Fundamentals and Simulation. Springer; New York, NY: 2005. pp. 255–304. [Google Scholar]
- 57.Mustafa S, Dilara B, Neelofer Z, Naeem A, Tasleem S. Temperature Effect on the Surface Charge Properties of γ-Al2o3. J Colloid Interface Sci. 1998;204:284–293. doi: 10.1006/jcis.1998.5572. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.