Abstract
Friction measurements of articular cartilage are important to determine the relative tribologic contributions made by synovial fluid or cartilage, and to assess the efficacy of therapies for preventing the development of post-traumatic osteoarthritis. Stanton’s equation is the most frequently used formula for estimating the whole joint friction coefficient (μ) of an articular pendulum, and assumes pendulum energy loss through a mass-independent mechanism. This study examines if articular pendulum energy loss is indeed mass independent, and compares Stanton’s model to an alternative model, which incorporates viscous damping, for calculating μ. Ten loads (25-100% body weight) were applied in a random order to an articular pendulum using the knees of adult male Hartley guinea pigs (n = 4) as the fulcrum. Motion of the decaying pendulum was recorded and μ was estimated using two models: Stanton’s equation, and an exponential decay function incorporating a viscous damping coefficient. μ estimates decreased as mass increased for both models. Exponential decay model fit error values were 82% less than the Stanton model. These results indicate that μ decreases with increasing mass, and that an exponential decay model provides a better fit for articular pendulum data at all mass values. In conclusion, inter-study comparisons of articular pendulum μ values should not be made without recognizing the loads used, as μ values are mass dependent.
Keywords: Friction, Mass, Cartilage, Pendulum, Lubrication
Introduction
Studies of articular cartilage have used whole joint pendulums or cartilage plugs to measure the friction coefficient (μ) of the articular surface (Jones, 1934; Tanaka et al., 2004; Wright and Dowson, 1976). Friction measurements are important to determine the relative tribologic contributions made by synovial fluid or cartilage, (Kawai et al., 2004; Mori et al., 2002; Tanaka et al., 2005) and/or to assess the efficacy of therapies for preventing the development of post-traumatic osteoarthritis (Jay et al., 2007; Kawano et al., 2003; Teeple et al., 2007). Whole joint pendulums have the benefit of allowing the joint to be examined as an intact system in that the opposing articular surfaces are matched as they would be in vivo, the endogenous synovial fluid is enclosed in the capsule, and trauma to the cartilage is eliminated.
Stanton’s equation (Stanton, 1923) is the most frequently used formula for calculating the whole joint μ:
| (1) |
where Δθ = change in the peak rotation of the pendulum per cycle about the flexion-extension (F-E) axis of the joint, L = distance between the pendulum center of gravity and the center of the F-E axis, and r = radius of the femoral condyles. This equation assumes that the peak F-E amplitude decays linearly with time, and thereby implies that energy loss is through a mass-independent mechanism (Crisco et al., 2007).
While the lubricating mechanisms of articular cartilage are not fully understood, it is likely that boundary lubrication (Charnley, 1960; Jay et al., 2001; Kumar et al., 2001), hydrodynamic lubrication (Jones, 1934; Kawano et al., 2003; Mori et al., 2002), fluid pressurization (Krishnan et al., 2003; Krishnan et al., 2004), and elastic deformation (Dowson and Jin, 1986) all contribute to the low μ in the knee joint. Whole knee experimental decay curves have been observed as being curvilinear (Jones, 1936; Teeple et al., 2007) which suggests energy loss via viscous damping, as well as energy loss due to capsular and ligamentous attachments (Charnley, 1960). We have previously published an alternative method for calculating μ of the articular pendulum (Eq. 2-7) (Crisco et al., 2007) that incorporates a viscous damping coefficient to separate non-linear contributions to energy loss from frictional damping in the articular pendulum. Crisco (2007) applied this calculation method to theoretical pendulum decay curves with a single decay time and mass, but only briefly postulated on how changes in mass might affect the model. Using our alternate calculation may provide an improved method for measuring joint friction in whole joint pendulum systems across a range of masses, allowing the advantages of a whole joint measurement while accounting for both linear and nonlinear modes of damping.
The objectives of this study were to determine if articular pendulum energy loss is mass independent, and to compare the two μ calculation models over a range of masses. To address these aims, articular pendulum data were collected from guinea pig knee joints loaded with ten separate masses. μ values were calculated using both Stanton’s equation and the exponential decay model.
Methods
Experimental data for an articular pendulum were obtained using four hind limbs from two adult male Hartley guinea pigs (ages 9 and 12 months). The animals were euthanized under a protocol approved by the Institutional Animal Care and Use Committee. After euthanasia, the hindlimbs were disarticulated at the hip, dissected to the knee joint capsule, wrapped in saline-soaked gauze, and frozen at −20° C degrees until the day of testing. On the day of testing, each specimen was thawed for 2 hours at room temperature and then mounted in the pendulum for friction testing.
The pendulum used for this study has been previously described (Fig. 1) (Teeple et al., 2007). A series of ten tibiofemoral compressive loads, ranging from 260-900g (25 - 100% average body weight), were applied in random order to each specimen. Motion of the tibia relative to the fixed femur was recorded using a motion analysis system (Optotrak, Northern Digital Inc., Waterloo, Ontario), which measures 3-D rigid body motion with an accuracy of 0.1 mm and 0.1 degrees. Three infrared light-emitting diodes were mounted to the tibia/pendulum and femur/base to define the rigid bodies and to measure rotational motion about the knee: flexion-extension, internal-external, and varus-valgus (Grood and Suntay, 1983). Rotations were referenced to an anatomic coordinate system established using the Optotrak digitizer prior to testing on each knee for each weight (Churchill et al., 1998; Teeple et al., 2007).
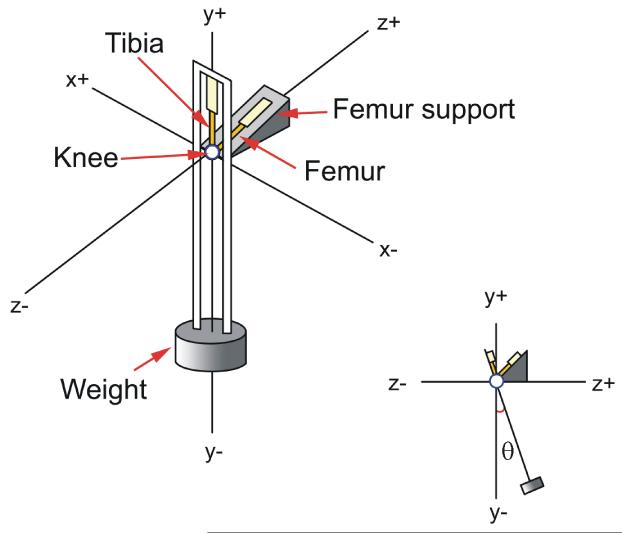
Figure 1.
Pendulum Apparatus. The pendulum utilizes the knee joint as the fulcrum, swinging the tibia relative to a fixed femur at a frequency of approximately 1 Hz while a compressive load is maintained across the tibiofemoral joint. The addition of load to the pendulum was done by screwing cylindrical masses into the base of the pendulum. The load’s effect on period, center of gravity, and effective length were calculated and accounted for in both calculation models (Used with permission, Teeple et al., 2007).
Peak amplitudes were plotted versus cycle number for each mass, and the resulting decay curve was used to calculate μ. Two models were used to fit the decay curve: Stanton’s equation, producing a linear fit (μL), and a previously published decay function incorporating a viscous damping coefficient (c), providing an exponential fit (μE) (Crisco et al., 2007). Root mean square error (RMSE) was used to determine the goodness of fit of each model to the experimental data curve.
Our previously published viscous damping model is briefly covered below. The equation for pendulum amplitude is
| (2) |
Where
| (3) |
| (4) |
| (5) |
therefore,
| (6) |
| (7) |
θn = peak displacement as a function of cycle number n, T = time between cycles, I = the moment of inertia about the joint centre, r = joint radius.
Statistical analyses were carried out using SAS version 9.3 (The SAS Institute, Cary, NC). Generalized linear mixed models for log-normal distributed data were used to model and compare μ and RMSE as a function of mass, model used, and their interaction. Models had random intercepts and slopes for mass nested within limb and grouped by equation. These parameters were permitted to have independent variances for slopes, intercepts, and covariances for each equation (unstructured variance-covariance structure block-diagonal by equation). A linear mixed model (Gaussian distribution) was used to model c from the exponential equation as a function of mass, with a random slope and intercept (unstructured variance-covariance structure). All models also used degree-of-freedom adjusted classical sandwich estimation to adjust for any model misspecification.
Results
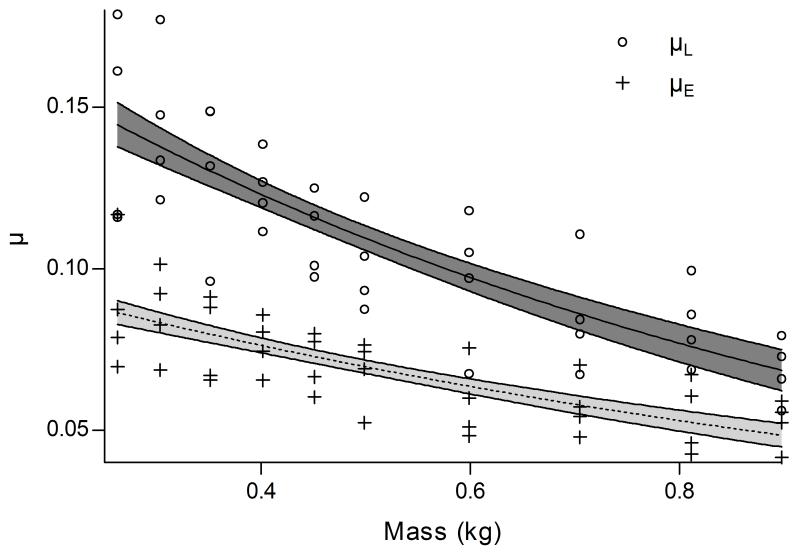
Both μL and μE declined proportionally as mass increased. μL declined significantly (p=0.0008) faster with approximately 68% (95%CI 57%-86%; p<.0001) decrease in value per kg, while μE decreased by 58% (95%CI 46%-67%; p<.0001) per kg (Fig. 2). At each mass, values of μL were significantly higher than those of μE (p<.0001). There was no significant effect of mass on c (p=0.4200).
Figure 2.
μ values calculated by Stanton’s Equation (μL) and our exponential decay model (μE). Mean parameter from models are presented with their 95% confidence intervals. The values of μL ranged from 0.056-0.179, while values of μE ranged from 0.042-0.117 across the range of mass. For the exponential decay model, the range of values for c was .00027-.00137.
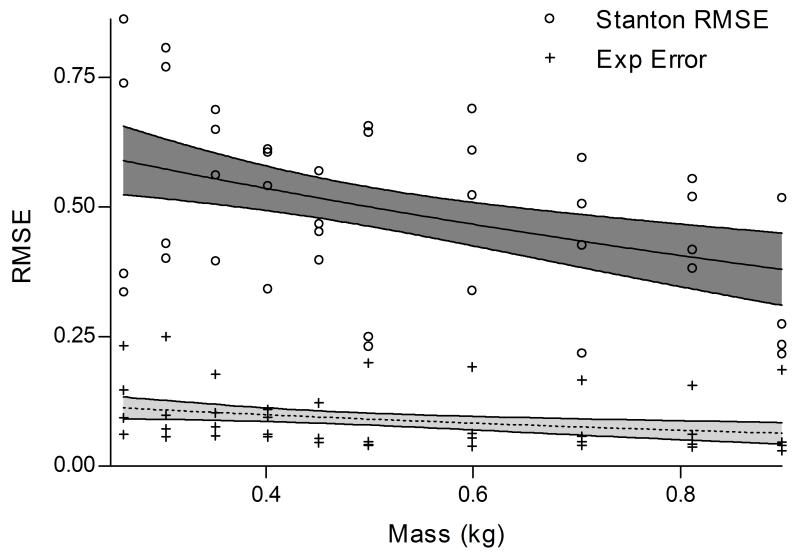
The RMSE decreased proportionally as mass increased for both models (56% per unit mass, 95%CI 34%-70%; p=0.0001), with no significant difference between slopes (p=0.3979) (Fig. 3). However, exponential decay model RMSE values (range: 0.03-0.25) were 82% (95%CI 78%-86%, p=0.0005) smaller than the Stanton model values (range: 0.21-0.86).
Figure 3.
RSME values for Stanton’s Equation and our exponential decay model. Mean parameters from models are presented with their 95% confidence intervals.
Discussion
The results of this study suggest that μ decreases significantly with increasing mass and that our decay function provides a better fit for articular pendulum data over a range of mass values. Stanton’s equation produced higher estimates of μ within our range of masses, however the estimates of the two functions appear to converge as mass increases. Given the equation for the viscous damping coefficient representing velocity-dependent energy loss (Eq. 7), c is expected to be dependent on mass. In this study, however, c appeared to be independent of mass.
Although the assumption that μ is independent of mass has been widely applied with the use of Stanton’s equation, our findings are consistent with those of Jones, who first described alterations in the μ of human IP joints with varied loading (Jones, 1934). Decreases in μ due to increasing load were also described by Walker (Walker et al., 1968), who attributed the trends to “boosted lubrication”.
c is a reflection of viscous damping, which is linearly proportional to the velocity of the rotation of the joint (Crisco et al., 2007). Synovial fluid is non-Newtonian, and could contribute to the apparent viscous damping. However, Charnley observed a linear decay in a disarticulated cadaver human ankle joint pendulum, suggesting that intra-articular ligaments, or the synovium, play a large role in viscous damping (Charnley, 1960; Kawano et al., 2003). In our study, both μL and μE were higher than those previously cited by Charnley (.005-.024), as well as other recent studies (0.0018-0.016) (Kawai et al., 2004; Kawano et al., 2003; Mori et al., 2002; Tanaka et al., 2004). This suggests that the capsular and ligamentous attachments may increase μE in addition to providing viscous damping to the joint. Our increased μE values may also be due to variations in cartilage surface asperity deformation and engagement occurring with loading. While the actual μ of the guinea pig articular surface is not known, we have previously published an estimated range of .064-0.11, calculated using a Stanton decay model and a 300g compressive load (Teeple et al., 2007).
Pendulum systems offer a simple, cost effective method of studying articular friction, but they do have limitations. First, the calculated values represent the entire joint surface interaction. Second, both decay models neglect aerodynamic drag and energy loss due to the other soft tissue structures surrounding the joint, which in turn will affect the estimate of μ and c. Thus, it is difficult to separate their effects from viscous damping parameters. Third, a constant linear value for both c and μ were assumed, but they may vary with joint position. Fourth, the limbs were frozen and thawed before testing which could potentially affect the properties of the synovial fluid. However, all samples underwent the same protocol, so any changes should be equivalent across all specimens. Finally, errors in joint radius measurement also translate to errors in predicting μ for both models. While the knees were obtained from 9 and 12 month old animal, we do not expect this to affect our results, as we have previously shown that there is no difference in μL for knees spanning 3 to 12 months (Teeple et al., 2008).
This study demonstrates that the exponential decay model provides an improved fit to the experimental data across a range of masses, and therefore appears to be a better method for estimating μ in the articular pendulum. Notably, the results of this study show that no suitable inter-study comparisons of articular pendulum μ values can be made without recognizing the loads used in each study, as μ is mass dependent for both models.
Acknowledgements
This publication was made possible by Grant Number P20-GM104937from NIH. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH. The authors would like to acknowledge RIH Orthopaedic Foundation, Lucy Lippitt Endowment, and University Orthopedics for their additional support.
Footnotes
Conflicts of Interest Statement
There are no conflicts to disclose.
References
- Charnley J. The lubrication of animal joints in relation to surgical reconstruction by arthroplasty. Annals of the Rheumatic Diseases. 1960;19(1):10–19. doi: 10.1136/ard.19.1.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchill DL, Incavo SJ, Johnson CC, Beynnon BD. The transepicondylar axis approximates the optimal flexion axis of the knee. Clinical Orthopaedics & Related Research. 1998;356(11):111–118. doi: 10.1097/00003086-199811000-00016. [DOI] [PubMed] [Google Scholar]
- Crisco JJ, Blume J, Teeple E, Fleming BC, Jay GD. Assuming exponential decay by incorporating viscous damping improves the prediction of the coefficient of friction in pendulum tests of whole articular joints. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 2007;221(3):325–333. doi: 10.1243/09544119JEIM248. [DOI] [PubMed] [Google Scholar]
- Dowson D, Jin Z-M. Micro-elastohydrodynamic lubrication of synovial joints. Engineering in Medicine. 1986;15(2):63–65. doi: 10.1243/emed_jour_1986_015_019_02. [DOI] [PubMed] [Google Scholar]
- Grood ES, Suntay WJ. A joint coordinate system for the clinical description of three-dimensional motions: application to the knee. Journal of Biomechanical Engineering. 1983;105(2):136–144. doi: 10.1115/1.3138397. [DOI] [PubMed] [Google Scholar]
- Jay GD, Harris DA, Cha C-J. Boundary lubrication by lubricin is mediated by o-linked beta(1-3) Gal-GalNAc oligosaccharides. Glycoconjugate Journal. 2001;18(10):807–815. doi: 10.1023/a:1021159619373. [DOI] [PubMed] [Google Scholar]
- Jay GD, Torres JR, Rhee DK, Helminen HJ, Hytinnen MM, Cha C-J, Elsaid K, Kim K-S, Cui Y, Warman ML. Association between friction and wear in diarthrodial joints lacking lubricin. Arthritis & Rheumatism. 2007;56(11):3662–3669. doi: 10.1002/art.22974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones E. Joint lubrication. The Lancet. 1934;223:1426–1427. [Google Scholar]
- Jones E. Joint lubrication. The Lancet. 1936;227:1043–1045. [Google Scholar]
- Kawai N, Tanaka E, Takata T, Miyauchi M, Tanaka M, Todoh M, van Eijden T, Tanne K. Influence of additive hyaluronic acid on the lubricating ability in the temporomandibular joint. Journal of Biomedical Materials Research, Part A. 2004;70(1):149–153. doi: 10.1002/jbm.a.30078. [DOI] [PubMed] [Google Scholar]
- Kawano T, Miura H, Mawatari T, Moro-Oka T, Nakanishi Y, Higaki H, Iwamoto Y. Mechanical effects of the intraarticular administration of high molecular weight hyaluronic acid plus phospholipid on synovial joint lubrication and prevention of articular cartilage degeneration in experimental osteoarthritis. Arthritis & Rheumatism. 2003;48(7):1923–1929. doi: 10.1002/art.11172. [DOI] [PubMed] [Google Scholar]
- Krishnan R, Kopacz M, Ateshian GA. Experimental verification of the role of interstitial fluid pressurization in cartilage lubrication. Journal of Orthopaedic Research. 2004;22(3):565–570. doi: 10.1016/j.orthres.2003.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan R, Park S, Eckstein F, Ateshian GA. Inhomogeneous cartilage properties enhance superficial interstitial fluid support and frictional properties, but do not provide a homogeneous state of stress. Journal of Biomechanical Engineering. 2003;125(5):569–577. doi: 10.1115/1.1610018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar P, Oka M, Toguchida J, Kobayashi M, Uchida E, Nakamura T, Tanaka K. Role of uppermost superficial surface layer of articular cartilage in the lubrication mechanism of joints. Journal of Anatomy. 2001;199(3):241–250. doi: 10.1046/j.1469-7580.2001.19930241.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Naito M, Moriyama S. Highly viscous sodium hyaluronate and joint lubrication. International Orthopaedics. 2002;26(2):116–121. doi: 10.1007/s00264-002-0330-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanton TE. Boundary lubrication in engineering practice. The Engineer. 1923;135:678–680. [Google Scholar]
- Tanaka E, Iwabe T, Dalla-Bona DA, Kawai N, van Eijden T, Tanaka M, Kitagawa S, Takata T, Tanne K. The effect of experimental cartilage damage and impairment and restoration of synovial lubrication on friction in the temporomandibular joint. Journal of Orofacial Pain. 2005;19(4):331–336. [PubMed] [Google Scholar]
- Tanaka E, Kawai N, Tanaka M, Todoh M, van Eijden T, Hanaoka K, Dalla-Bona DA, Takata T, Tanne K. The frictional coefficient of the temporomandibular joint and its dependency on the magnitude and duration of joint loading. Journal of Dental Research. 2004;83(5):404–407. doi: 10.1177/154405910408300510. [DOI] [PubMed] [Google Scholar]
- Teeple E, Elsaid KA, Fleming BC, Jay GD, Aslani K, Crisco JJ, Mechrefe AP. Coefficients of Friction, Lubricin, and Cartilage Damage in the Anterior Cruciate Ligament-Deficient Guinea Pig Knee. Journal of Orthopaedic Research. 2008;26:231–237. doi: 10.1002/jor.20492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teeple E, Fleming BC, Mechrefe AP, Crisco JJ, Brady MF, Jay GD. Frictional properties of hartley guinea pig knees with and without proteolytic disruption of the articular surfaces. Osteoarthritis & Cartilage/OARS, Osteoarthritis Research Society. 2007;15(3):309–315. doi: 10.1016/j.joca.2006.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker PS, Dowson D, Longfield MD, Wright V. ‘Boosted lubrication’ in synovial joints by fluid entrapment and enrichment. Annals of the Rheumatic Diseases. 1968;27(6):512–520. doi: 10.1136/ard.27.6.512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright V, Dowson D. Lubrication and cartilage. Journal of Anatomy. 1976;121(Pt 1):107. [PMC free article] [PubMed] [Google Scholar]