Abstract
About 1–2% of the babies are born with bicuspid aortic valves instead of the normal aortic valve with three leaflets. A significant portion of the patients with the congenital bicuspid valve morphology suffer from aortic valve stenosis and/or ascending aortic dilatation and dissection thus requiring surgical intervention when they are young adults. Patients with bicuspid aortic valves (BAVs) have also been found to develop valvular stenosis earlier than those with the normal aortic valve. This paper overviews current knowledge of BAVs, where several studies have suggested that the mechanical stresses induced on the valve leaflets and the abnormal flow development in the ascending aorta may be an important factor in the diseases of the valve and the aortic root. The long-term goals of the studies being performed in our laboratory are aimed towards potential stratification of bicuspid valve patients who may be at risk for developing these pathologies based on analyzing the hemodynamic environment of these valves using fluid-structure interaction (FSI) modeling. Patient-specific geometry of the normal tri-cuspid and bicuspid valves are reconstructed from real-time 3D ultrasound images and the dynamic analyses performed in order to determine the potential effects of mechanical stresses on the valve leaflet and aortic root pathology. This paper describes the details of the computational tools and discusses challenges with patient-specific modeling.
Introduction
About 1 – 2 percent of babies are born with bicuspid aortic valves (BAV), a congenital malformation, compared to the normal aortic valve with three leaflets (tricuspid aortic valve, TAV). BAV malformations are inherited, and involves the entire aortic root having a propensity for both valvular and ascending aortic complications (Fedak et al., 2002). Approximately 33% of the BAV population develops aortic stenosis, regurgitation, and endocarditis (Ward, 2000). In addition, these patients are also at risk of developing ascending aortic complications including dissection and aneurysm formation (Fedak et al. 2002). In the BAV subjects, the aortic root and ascending aortic dimensions have been found to be larger compared to matched subjects with normal aortic valves (Pachulski et al., 1991; Nistri et al., 1999; Cecconi et al., 2005). Santarpia et al. (2011) have reported an increase in the aortic stiffness and reduction of the aortic and left ventricular deformation properties in BAV patients. Widely varying geometry has been reported with BAV, including those with the fusion of two leaflets with or without the presence of raphe, a small strip of non-valvular tissue at the site of fusion. Sievers and Schmidtke (2007) have classified the BAV into three major types: purely bicuspid with no raphe, with 1 raphe and with two raphes. Schaefer et al. (2008) identified three morphologies of BAV: a fusion of right and left coronary cusps; right and non-coronary cusp fusion; and left and non-coronary cusps with a vast majority of the BAVs studied falling in the category the left-right fusion. They also reported that left-right fusion was more common in men and the sinuses were larger in this type of BAV.
Aortic valve calcification is one major cause for aortic valve replacement surgery. One suggested cause of this calcification is attributed to regions of stress concentration on the leaflets of the valves as they undergo complex deformation during the cardiac cycle (Thubrikar et al. 1986). Patients with BAV are more likely to develop calcific aortic stenosis compared to those with normal aortic valves and it has been suggested that the geometric variations in BAV compared to that of the normal TAV may be a factor for the same (Weinberg and Kaazempur Mofrad, 2008; Conti et al., 2010). Weinberg and Kaazempur Mofrad performed a multi-scale comparative study of TAV and BAV geometries at the organ, tissue, and cellular levels. Even though differences in the mechanics were observed at the organ level between the two geometries, no differences were observed in the cellular deformations between these two valves. They suggested that the differences in calcification between TAV and BAV may be due to factors other than geometric differences between the two valves. On the other hand, Conti et al. reported the presence of abnormal leaflet stress in BAV geometry and suggested that leaflet stress may play a role in tissue remodeling at the raphe region and in early leaflet degeneration.
Although it has been recognized that patients with BAV may also have congenital abnormalities affecting the aortic root, a number of studies have also suggested that the altered blood flow dynamics past the BAV may be an important factor in complications found in the ascending aortic root of these patients. In vitro experiments with cryopreserved aortic root with BAV along with flow simulations have demonstrated excessive folding and creasing of the leaflets during a cardiac cycle, extended areas of leaflet contact, significant morphologic stenosis, and asymmetrical flow pattern distal to the valve (Robicsek et al., 2004). This study has suggested that the abnormal flow patterns may be a factor in the ascending aortic dilatation and dissection. Time-resolved magnetic resonance imaging was employed to demonstrate restricted systolic conjoint cusp motion causing flow deflection in subjects with a BAV with right-left coronary cusp fusion (Della Corte et al., 2011). Hope et al. (2008) employed time-resolved 3D phase-contrast MR imaging to demonstrate pronounced helical flow and eccentric systolic jet in the ascending aorta in patients with BAV and suggested that elevated shear stresses could result in aneurysm formation in these patients.
Finite element (FE) structural analysis has been traditionally employed in the analysis of heart valve dynamics in order to compute the stress distribution on the leaflets particularly with the valve in the fully closed position in order to delineate the regions of abnormal stress concentrations and to correlate the same with common regions of calcification and structural failure. More recently dynamic FE analyses have been reported in order to compute the complex motion of the leaflets during a cardiac cycle and identify regions of stress concentrations on the valvular structure (Gnyaneshwar et al., 2002; Kim et al., 2008). Conti et al. (2010) have reported on a dynamic FE analysis of a right/left fusion BAV to demonstrate that the bicuspid valve opened asymmetrically with an elliptic orifice. They conclude that BAV geometry results in alterations in the leaflet dynamics, entailing abnormal leaflet stress and that the leaflet stress may play a role in tissue remodeling and early leaflet degeneration.
To assess the effect of flow past restricted cuspal geometry of the BAV on the aortic root and the ascending aorta, a computational fluid dynamic (CFD) or more realistically, a fluid-structure interaction (FSI) analysis is necessary. Even though a number of FSI analyses past heart valves have been reported (de Hart, 2003; Kunzelman et al., 2007), the analyses reported have been restricted to non-physiological leaflet material properties and flow regimes due to computational challenges. With respect to flow past a BAV, Della Corte et al. (2011) have recently reported that the restricted cuspal motion in right-left BAV (what we refer to as Type III), results in systolic flow deflection towards the right anterolateral ascending aorta from phase-contrast magnetic resonance (MR) imaging confirmed by CFD simulation. Hope et al. (2008) have demonstrated eccentric flow jet with prominent helical flow in the ascending aorta in a patient with a BAV and aortic coarctation employing phase-contrast MR imaging. These studies further reinforce the idea that significantly altered flow past BAV geometry into the ascending aorta may play a role in the pathology of the aortic wall.
With the advent of ultrasound, CT, and MR imaging modalities, and with advances in image processing techniques, it is now possible to obtain patient-specific morphologically realistic three-dimensional images of the organs of interest at various times in the cardiac cycle. Thus patient-specific mechanical analysis is being increasingly applied in biomechanics of the human circulation. Our laboratory has been involved in the dynamic analysis of heart valve dynamics towards delineation of the effect of mechanical stresses on the calcification of leaflets in the case of bioprosthetic valves (Kim et al., 2006; Kim et al., 2007; Kim et al., 2008) and in the flow induced-stresses on thrombus initiation with mechanical valve prostheses (Krishnan, 2006; Govindarajan et al., 2009). With respect to the bicuspid valve pathological problems, our hypothesis has been that BAVs with certain specific geometries result in regions of abnormal stresses on the leaflets and the aortic root during the valvular function. These abnormal stresses may be one of the important factors resulting in early calcification of the leaflets as well as ascending aortic pathology and hence such studies may potentially enable the stratification of BAV patients at risk. We describe below our efforts towards patient-specific BAV analysis to examine the above hypothesis, description of our methodology and preliminary results, and also the challenges associated with such an analysis.
FE Dynamic Analysis with simulated BAV geometry
In order to confirm our hypothesis that the geometrical variations in the BAV may be a dominant factor resulting in wide variations in the deformation characteristics and leaflet stresses, we initially performed a dynamic analysis with simulated BAV geometries (Jermihov et al., 2011). We reconstructed a simulated TAV with nominal dimensions based on values published in the literature. We modified the TAV geometry as needed to create three commonly occurring types of BAV geometry as reported by Sievers and Schmidtke (2007). The effect of a raphe was also simulated by increasing the stiffness in the region of fusion in one of the BAV geometries. We assumed a uniform thickness for the leaflet. The material for the leaflets were assumed to be an anisotropic Fung-type hyperelastic strain energy function based on the bi-axial testing data of fresh porcine aortic valve specimens (Huang, 2004). The aortic annulus was assumed to be rigid and a physiologically realistic pressure load was applied on the leaflets to simulate the opening and closing phases of the leaflets during a cardiac cycle. We employed the FE software ABAQUS/Explicit (HKS Inc., Pawtucket, RI) for its efficacy in solving dynamic contact simulations involving large deformation.
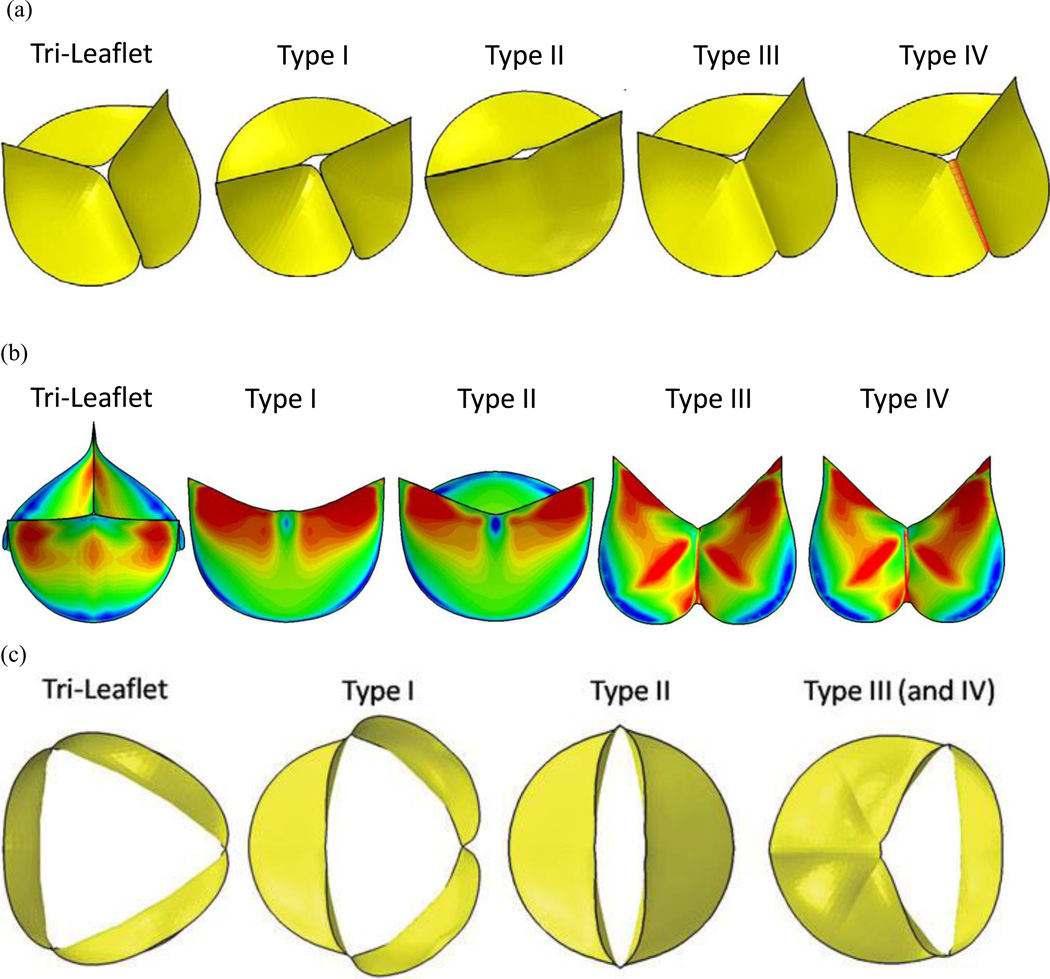
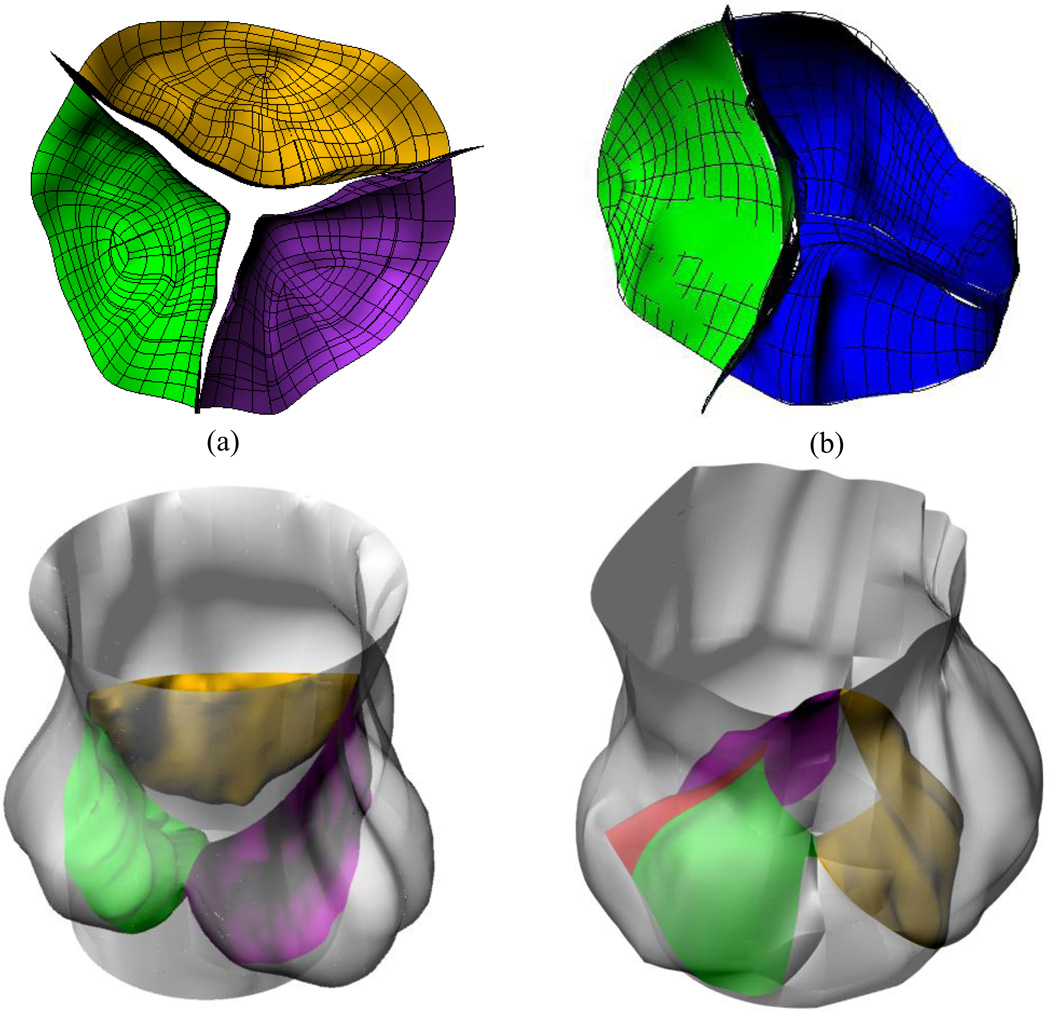
The geometry for the TAV and the three types of BAV employed in the study are shown in Figure 1a. Type I depicts one oversized leaflet and a fusion of two undersized leaflets. Type II, a purely bicuspid valve with two symmetric leaflets. Type III is a left-right fusion, with a second leaflet similar in shape to a normal TAV leaflets. BAV Type IV in this figure is similar to that of Type III except for the presence of the raphe. The maximum in plane principal stresses from our dynamic simulation during the fully closed position of the valve is shown in Figure 1b. The corresponding orifice opening of the various valve types in the fully open position is shown in Figure 1c. It can be observed that there is a wide variation in the in plane stress distribution on the leaflets based on the geometry of the BAV and the stresses on the leaflets of the BAV are significantly different from the TAV. Such differences on the leaflet stresses between the TAV and BAV have been confirmed by Conti et al. (2010). We repeated the dynamic analysis by increasing and decreasing the primary material parameter (effective Young’s modulus) for the leaflet by 25% and in both cases, our results did not show any significant differences compared to those with the originally specified magnitudes. This study confirmed that variations in geometry among the BAV types (Figure 1a) significantly affect the leaflet stresses compared to variations in material property of the leaflets. Hence, abnormal leaflet stresses with specific geometries among the BAV may be responsible for significant aortic valve degradation in many BAV patients. Furthermore, our study revealed that even though the presence of raphe resulted in local increase in leaflet stresses in the vicinity of the raphe, the overall deformation characteristics and the leaflet stress distribution pattern were not significantly affected (Jermihov et al., 2011).
Figure 1.
(a) Idealized bicuspid aortic valve geometries employed to study impact of geometry on stresses in valve leaflets (Jermihov et al., 2011) and the alterations in hemodynamics in the ascending aorta (Burken, 2012; Vigmostad et al., 2012). Type I depicts one oversized leaflet and a fusion of two undersized leaflets. Type II is two symmetric leaflets. Type III is a left-right fusion, with a second leaflet similar in shape to a normal TAV leaflets. Type IV employs the same geometry as type III, but with a raphe. (b) The maximum in plane principal stresses from our dynamic simulation during the fully closed position of the valve (c) The corresponding orifice opening of the various valve types in the fully open position. Reprinted from Cardiovascular Engineering and Technology, 2(1): 48–56, 2011 with kind permission from Springer Science and Business Media.
Aortic Root Flow Dynamics with Simulated BAV Geometry
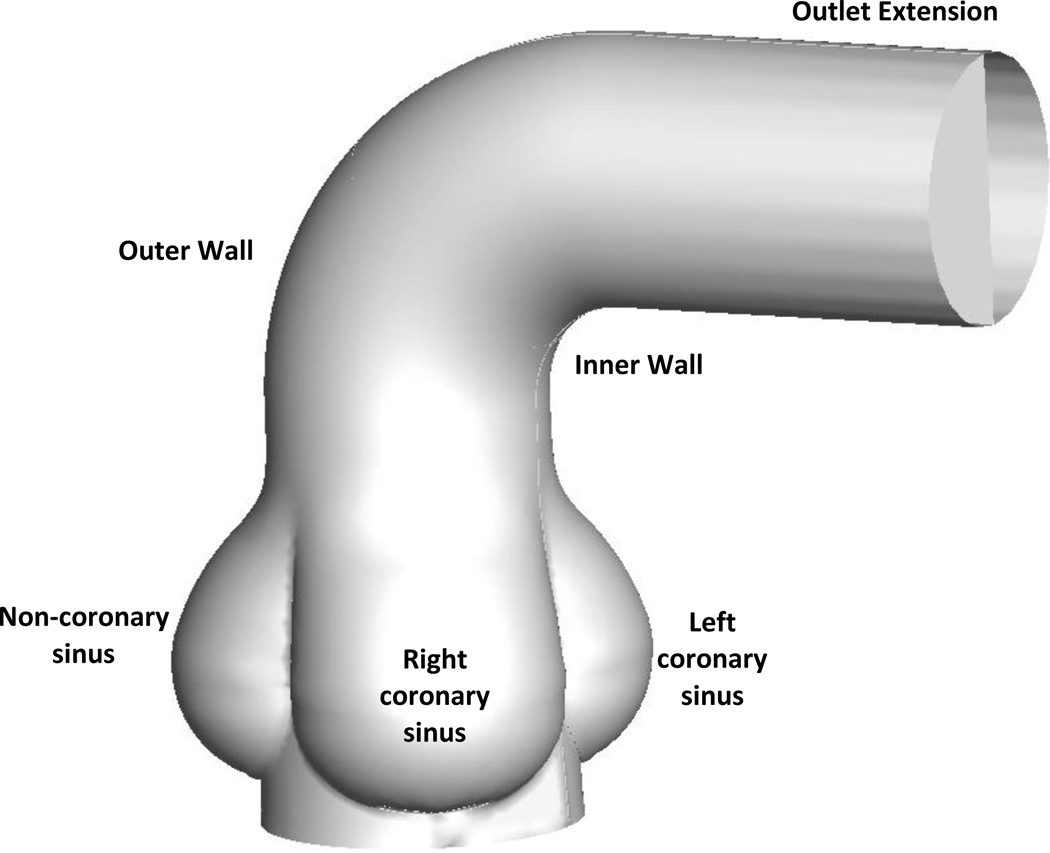
As can be observed from the predicted valve orifices in the fully open position shown in Figure 1c, the various types of BAV result in highly asymmetric non-circular orifices compared to central circular orifice for the TAV. The presence of asymmetric and non-circular orifices with BAV has been further confirmed by others (Robicsek et al., 2004; Hope et al., 2008; Della Corte et al., 2011). It can be anticipated that such varied orifice openings will result in a range of flow characteristics in the aortic root and the ascending aorta. In order to delineate important flow features emanating from the various simulated BAV geometries, we have performed a hemodynamic analysis using computational fluid dynamics (CFD). Towards this aim, we selected the normal TAV and four BAV geometries from the FE analysis (Type I, II, II rotated by 90° and type III) in the fully open position and incorporated a simulated aortic root and the curved segment of the ascending aorta as shown in Figure 2 (Burken, 2012; Vigmostad et al., 2012). The model shown in the figure includes the ascending aortic segment ending at the proximal aortic arch and an extension at the outlet has been included to minimize end effects. We assumed the aortic wall to be rigid and the leaflets stationary in the fully open position for the flow analysis. We assumed the fluid to be Newtonian with the viscosity coefficient representative of the whole human blood (3.5 cP) and assumed a uniform velocity at the inlet of 0.7 m/s (representing a peak systolic flow rate of 18 liters per minute across the valve) and employed an unsteady laminar flow simulation using FLUENT 12.1.4 (ANSYS, INC).
Figure 2.
The idealized aortic arch geometry included three sinuses and the ascending aorta. The valve geometry in the fully open position was placed within the aorta, and flow was computed at the fully open position. The model includes the simulated ascending aorta ending at the proximal aortic arch and an extension at the outlet has been added to minimize end effects.
The results show that there is a substantial difference in flow development amongst the various bicuspid valves, and an even more significant difference between any BAV and the tricuspid “control” model. This was quantified by examining wall shear stress, velocity profiles, and the dynamic pressure distribution in the ascending aorta. The effective orifice area (EOA) was quantified for each case, and while the EOA was similar for the various BAV cases, the flow was very different amongst the cases. Table 1 summarizes the EOA for the simulations.
Table 1.
The EOAs for all five cases in cm2
| TAV | BAV I | BAV II | BAV II-90 | BAV III | |
|---|---|---|---|---|---|
| EOA (cm2) | 3.59 | 1.77 | 1.84 | 1.84 | 1.60 |
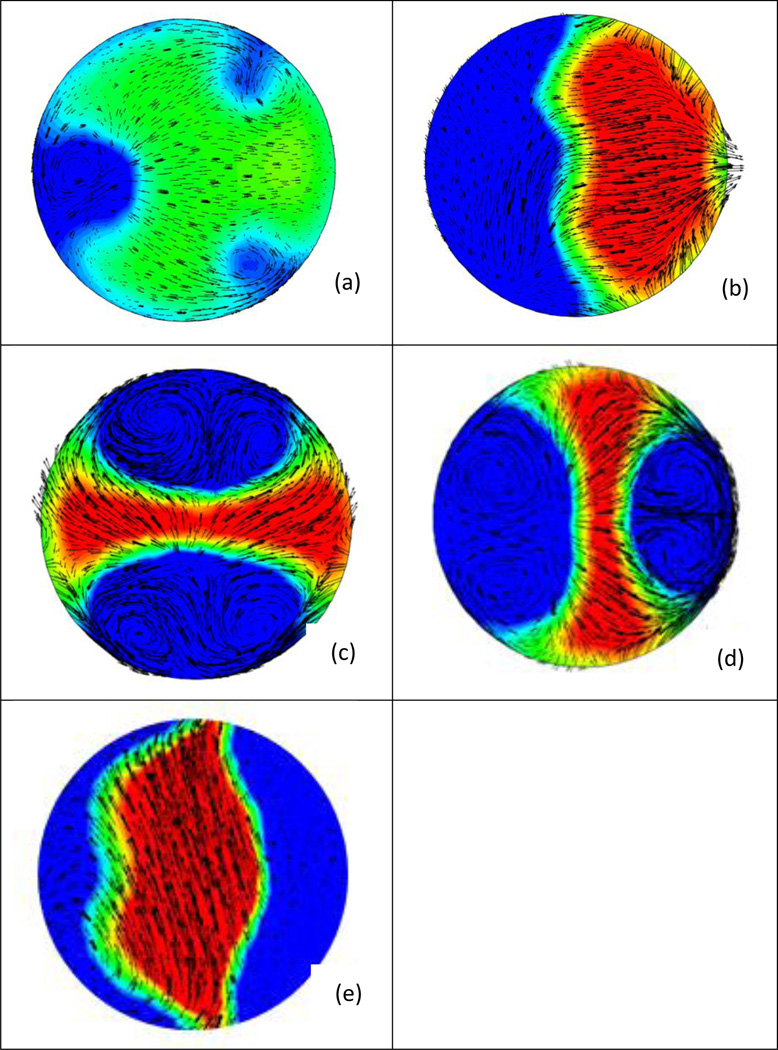
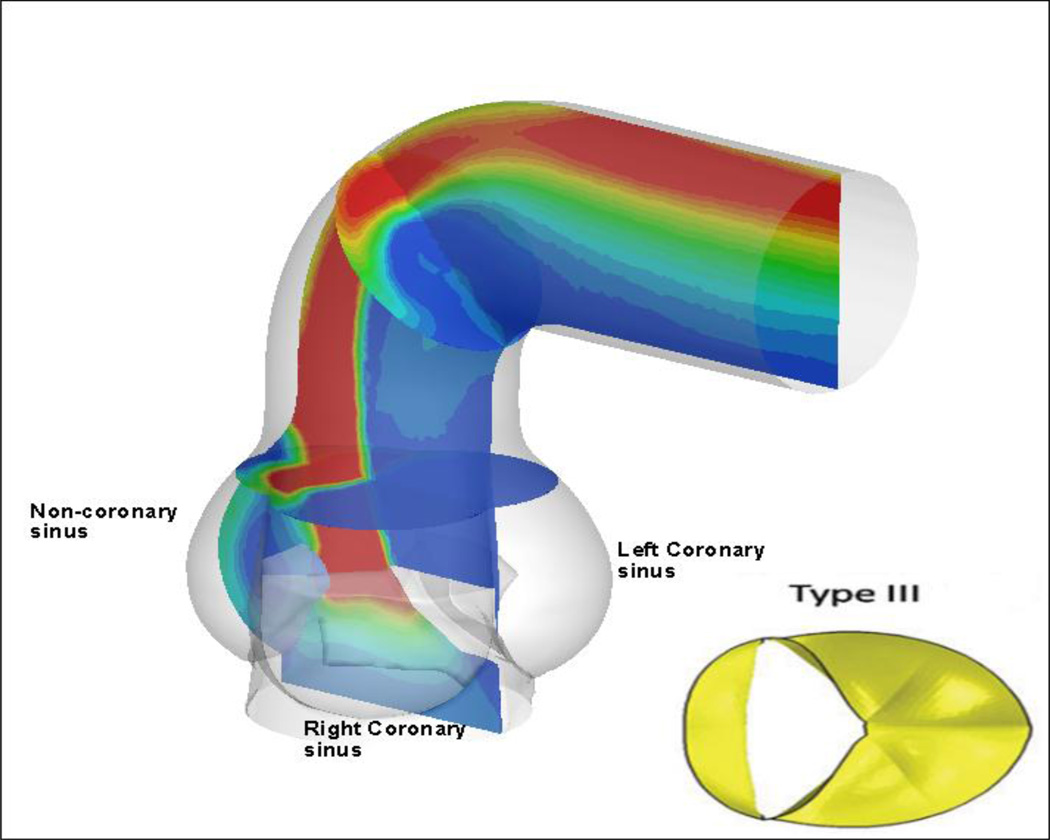
Figure 3 shows contours of axial velocity for the TAV and four BAV cases, where a slice at the Sinotubular junction has been made, and in-plane velocity is shown in vector form. The most common type of BAV, type III (Figure 3e) shows a strong eccentric jet, resulting from the fusion of the right and left coronary leaflets, thus shifting the flow to the outer wall. This is also visualized in Figure 4, where dynamic pressure is shown for BAV type III, at the centerline slice and two slices within the cross-section of the vessel (Burken, 2012; Vigmostad et al., 2012).
Figure 3.
Cross-sections of velocity (vectors show in-plane velocity while contours show axial velocity) taken distal to the valve at the sinutubular junction (STJ). (a) Tricuspid aortic valve (b) BAV Type 1 (c) BAV Type 2 and (d) Type 2 rotated 90 degrees, (e) BAV Type 3. Note the strong jet on the inner wall with type 1 BAV, and an eccentric jet in type 3 geometry. Type 2 (symmetric valve leaflets) results in strong helical flow, with two sets of counter-rotating vortices (Burken, 2012; Vigmostad et al., 2012).
Figure 4.
The most common BAV, a fusion of the right and left leaflets, results in a strong eccentric jet, which impacts the outer wall of the ascending aorta. Contours of dynamic pressure are shown (Burken, 2012; Vigmostad et al., 2012).
It should be emphasized that the two studies described above employed idealized geometries for the various types of the BAV. The results of the first study (Jermihov et al., 2011) showed that the magnitudes of the leaflet stresses varied widely with the variations in the simulated BAV geometry and the leaflet stresses in BAV were significantly larger in BAV compared to that in TAV. These results suggest that increased leaflet stresses with specific BAV geometry may contribute to the observed earlier leaflet calcification in patients with BAV compared to TAV patients. The fluid dynamic simulations past the fully open orifices into a simulated aortic root (Jermihov et al., 2011) also demonstrated that flow with eccentric jets and highly asymmetric ascending aortic wall shear stress distribution can be observed with simulated BAV geometry. The simulated TAV geometry ignores the variations in leaflet sizes in patient-specific TAVs and also the variations in the aortic sinuses and the ascending aorta with BAVs. In order to consider these variations in the assessment of the effect of mechanical stresses on the leaflet and ascending aortic pathology, patient-specific studies are required as described below.
Towards Patient-specific FE and FSI Analysis
Geometry
The reconstruction of morphologically realistic 3D geometry of the aortic and mitral valvular apparatus (root, leaflets, and the sinuses in the case of the aortic valve and the chordae tendinae and the papillary muscle attachment in the case of mitral valve) has now become possible with ultrasound and MR imaging modalities and with advances in the image processing techniques (Votta et al., 2008; Rim et al., 2011; Pouch et al., 2012). Rim (Rim et al., 2011) employed trans esophageal echocardiographic (TEE) image data to reconstruct the geometry of the mitral valve. Conti et al. have employed measurements from 2D MR images obtained from a number of subjects in order to reconstruct a typical 3D geometry of TAV and BAV for FE analysis (Conti et al., 2010).
We employ geometric reconstructions of the TAV and BAV from real-time 3D echocardiographic (rt3DE) data obtained in the Gorman Laboratories at the University of Pennsylvania for our dynamic analysis. Typical images of the reconstructed aortic valve leaflets (top row) and the aortic root (bottom row) for a patient-specific TAV and BAV with the leaflets in the fully closed position are shown in Figure 5. The images clearly demonstrate the asymmetric geometry of the aortic root and the leaflets with unequal sizes for both the TAV and BAV and dynamic analyses from such morphologically realistic geometries can be anticipated to result in a more realistic computation of the deformation and stress distribution on the valve leaflets and the root. Although geometry can now be obtained via relatively non-invasive imaging modalities, there is still an important limitation in the use of reconstructed images. Even though it is possible to obtain the detailed 3D geometry of the valvular apparatus, ultrasound imaging lacks sufficient resolution to provide information on the thickness of the leaflets or the aortic root. It is a common practice to assume a constant thickness for the aortic root and also for the leaflets. Variable thickness has been observed within the leaflets of aortic valves (Grande et al. 1998) and the lack of the thickness information in the reconstructed patient-specific geometry should be kept in mind. However, past studies from our group have shown that varying thickness uniformly by 10% does not result in substantial differences in the stress distribution on bioprosthetic heart valves (Kim et al., 2006)
Figure 5.
Examples of reconstructed (a) TAV and (b) BAV employed in the finite element analysis. In addition to the marked asymmetry of the leaflets as was shown in Figure 5, the complex geometry of the sinuses can be seen in this figure.
While non-invasive imaging modalities make patient-specific modeling a realistic possibility for future clinical use, the process of segmenting images and turning the resulting geometry into a body-fitted or geometrically descriptive mesh for computational analysis is quite time-consuming, and often a major bottleneck in performing such analyses (Dumont et al., 2004; Vigmostad and Udaykumar, 2011). Several groups have developed valuable tools which make segmentation of medical images simpler, and help expedite the meshing process (Steinman et al., 2003; Antiga et al., 2008; Taylor and Steinman, 2010). Recently, our group has begun working on true imaging-to-computation analysis algorithms, in which the mesh generation process is circumvented, through the use of level-set based segmentation tools which then double as a description of the geometry in our in-house levelset-based flow code (Krishnan et al., 2006; Dillard et al., 2012). With these types of tools, image-based computational dynamics will become more feasible for large cohorts of patients, and help expand our understanding of BAV anomalies.
Material properties
Even though patient-specific geometry of the valve can be obtained with reasonable accuracy as described above, it is not practical at present to anticipate obtaining information about the actual material property for the mechanical analysis. It is well known that biological soft tissues exhibit a multi-axial non-linear stress-strain relationship (Sacks and Sun, 2003) and experimental studies have also demonstrated that the leaflets are stiffer along the circumferential direction compared to the radial direction. Sun et al. (2005) and Huang (2004) have reported on anisotropic material property description for the aortic tissue leaflets based on bi-axial load-deformation data from pericardial bioprosthetic and fresh porcine aortic tissue respectively. Even though initial FE studies assumed a linear isotropic elastic material specification for the valvular structures, more recently, studies have incorporated a Fung-type constitutive model based on bi-axial experimental data from bovine pericardial tissue (Kim et al., 2006) or fresh porcine valve leaflet tissue (Jermihov et al., 2011). Though uniaxial force-deformation experimental data have been reported with excised human valve leaflet specimens, there is a lack of biaxial test data on fresh healthy human valve leaflet specimens. Furthermore, it can be anticipated that BAV leaflets will have altered material property compared to that of healthy TAV and there is lack of information on the force deformation behavior of BAV valve tissue along with those for the raphe that may be present in these valves. Hence, even though patient-specific geometry has been employed in the recently reported studies on the heart valve biomechanics, the material property specification still must rely upon sparsely available experimental data from either animal tissue or in rare cases, from excised human tissue. In the case of FSI analysis, the material properties of the blood also needs to be specified and due to the relatively high Reynolds number flows during the opening phase of the cardiac cycle, it is a common practice to assume the fluid to be Newtonian with the density and viscosity representative of whole human blood.
FE analysis
FE analysis of BAVs reported to date have employed either simulated geometry (Weinberg and Kaazempur Mofrad, 2008; Jermihov et al., 2011) or geometry generated from dimensions averaged from a number of 2D MR images from BAV patients with normal function, as assessed by echocardiography (Conti et al., 2010). The emphasis of Weinberg’s study was to explore the effect of the number of leaflets, a geometric factor, on the development of calcified aortic stenosis. They employed a multi-scale study starting from the stress analysis at the organ level and zooming into the area of interest at the tissue and subsequently cell scale. They demonstrate that the cellular deformations are not significantly different between TAV and BAV in the calcification-prone region. On the other hand, Conti et al. have reported that the BAV geometry per se entails abnormal leaflet stress in comparison to TAV geometry in the case of (what we refer to as) BAV type III (right/left leaflet fusion). The relative increase in the leaflet stresses with BAV geometry has been further confirmed by Jermihov, by employing simulated commonly occurring BAV geometrical variations.
We are employing 3D TAV and BAV geometry, including the sinuses up to the Sino-tubular junction (STJ) obtained from ultrasound imaging (Figure 5) for the structural analysis. These images are obtained employing real-time 3D ultrasound imaging at the University of Pennsylvania (Gorman Laboratories) and the details of the segmentation of the images are included in Pouch et al. (2012). Since the thickness of the structures are not available from the image data, we assumed the thicknesses of the leaflets, the annulus, and the sinuses to be 0.73, 2.3, and 2.0 mm respectively, based on measurements by Grande et al. (1998). We assumed the Fung-type material property specification for the leaflets based on biaxial tests of fresh porcine aortic valve leaflet tissue (Jermihov et al., 2011) and an isotropic, linear, elastic modulus of 2 MPa and a Poisson’s ratio of 0.3 for the root and the sinuses (Gnyaneshwar et al., 2002). The base of the annulus and the top of the STJ were fixed from motion along the axis (longitudinal direction). The difference between the ventricular and aortic pressures during the opening and closing phases of the cardiac cycle are applied on the appropriate leaflet surfaces based on published pressure-time curves in the dynamic FE analysis.
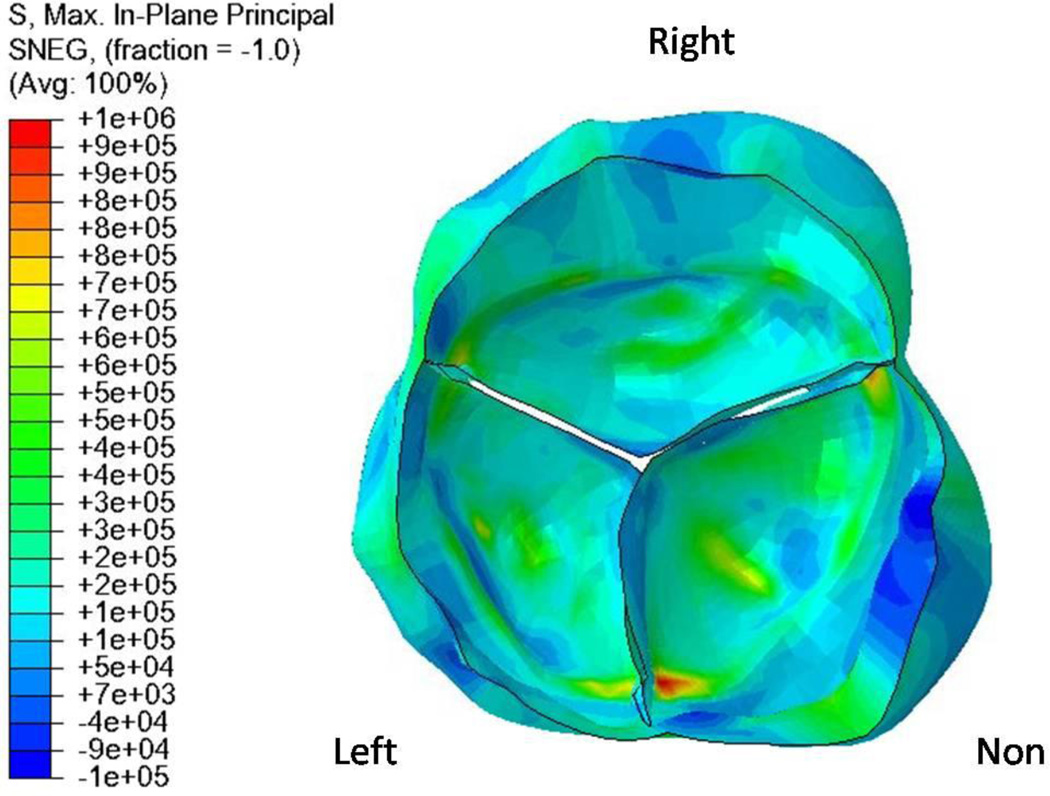
Preliminary results of the in-plane principal stress distribution on the leaflets for a patient-specific TAV are shown in Figure 6. Gnyaneshwar et al. (2002) have pointed out the importance of incorporating the deformation of the annulus on the computed stresses on the leaflets. The present study was performed with assumed elastic properties for the annulus and the sinuses in order to obtain a physiologically realistic dynamic simulation. The results clearly demonstrate the highly asymmetric stress distribution reflecting the asymmetric geometry, as compared to an assumed symmetric simulated geometry of the TAV. Also, note that the peak stress occurs in the non-coronary leaflet near the commissure, as has been reported in previous studies (Christie and Barratt-Boyes, 1991; Grande et al., 1998). The dynamic FE analysis done on a large number of human TAV geometry can be employed to determine the average magnitudes and variations of in-plane principal stresses that can be anticipated with healthy TAV. These results can then be compared with the computed stress distribution with patient-specific BAV analysis that will enable us to delineate the effect of variations in the BAV geometry with regions of abnormal in-plane stresses. A follow-up on these patients on the clinical outcomes can then be correlated with the results of regions of abnormal stress concentrations. Such studies may provide important information on specific BAV geometry that are susceptible towards calcification and may enable physicians to stratify patients at risk for development of valvular stenosis and develop appropriate treatment strategies.
Figure 6.
Typical results showing contours of maximum in-plane principal stresses, as computed from a patient-specific TAV model in the fully closed configuration. Note that the peak stress occurs in the non-coronary leaflet near the commissure, as has been reported in previous studies (Christie and Barratt-Boyes, 1991).
FSI analysis
The dynamic FE analysis described above yields important information about the stress distribution on the leaflets as well as on the aortic wall if included in the geometry. Such studies have been useful in determining a correlation between the regions of abnormal stresses and subsequent calcification or structural failure. However, in such an analysis, a uniform pressure load is applied on the valvular structures and hence the local fluid dynamically induced pressure and shear stress distribution are not included in the analysis. Furthermore, any alterations in the flow past the valve orifice in the case of BAV cannot be analyzed with the structural analysis alone. One alternative is to assume the walls to be rigid in the configuration at any particular time point in the cardiac cycle (e.g. valve in the fully open position) and perform a quasi-static CFD analysis to assess the altered flow past BAV geometry in the ascending aorta as described earlier. However, in order to the effect of local flow-induced stresses on the stress distribution on the valve structures, FSI analysis is necessary. FSI analyses of heart valve dynamics are complicated by the large differences in the material properties of the leaflets and the fluid as well as the complex three-dimensional motion of the leaflets resulting in numerical challenges.
A number of FSI studies on valve dynamics have been previously reported. De Hart and colleagues have reported on the FSI analysis of an aortic valve (De Hart et al., 2003). Due to the numerical challenges, this study was restricted to non-physiological material property specification for the leaflets and the analysis was also restricted to Reynolds number much lower than those anticipated for physiological flow regime. More recently, Kunzelmen and colleagues (Kunzelman et al., 2007; Einstein et al., 2010) reported on a 3D FSI simulation of the closing dynamics of a mitral valve. The leaflet was modeled assuming a neo-Hookean behavior, and was coupled to the flow computation, where blood was modeled as a compressible fluid using an artificial compressibility approach; however the bulk modulus of blood was modified by several orders of magnitude (to render it similar to that of air) for computational efficiency. While these previous simulations of bioprosthetic/native valves exist, the numerical challenges that accompany such computations have constrained the simulations to non-physiological parameter ranges and inadequate grid (Vigmostad et al., 2009; Vigmostad and Udaykumar, 2011).
To overcome limitations of previous studies, so that a full FSI solution can be achieved using physiologic Reynolds numbers, realistic material properties, and highly resolved grids, our group has developed in-house FSI algorithms. Our FSI algorithm employs a partitioned approach to coupling the fluid and structure, so that our previously developed FE models can be coupled with our in-house fixed Cartesian grid flow solver (Marella et al., 2005; Krishnan et al., 2006; Vigmostad et al., 2009; Vigmostad and Udaykumar, 2011). We have employed a fixed Cartesian grid flow solver in order to avoid the re-meshing that becomes necessary with the complex motion of the valve components, and employed an experimentally derived non-linear, anisotropic material property description for the valve leaflets, as previously used in our FE studies (Kim et al., 2007; Kim et al., 2008). Motion of the leaflets is computed using our FE algorithms, and the leaflets and their motion are represented in the flow domain using levelsets.
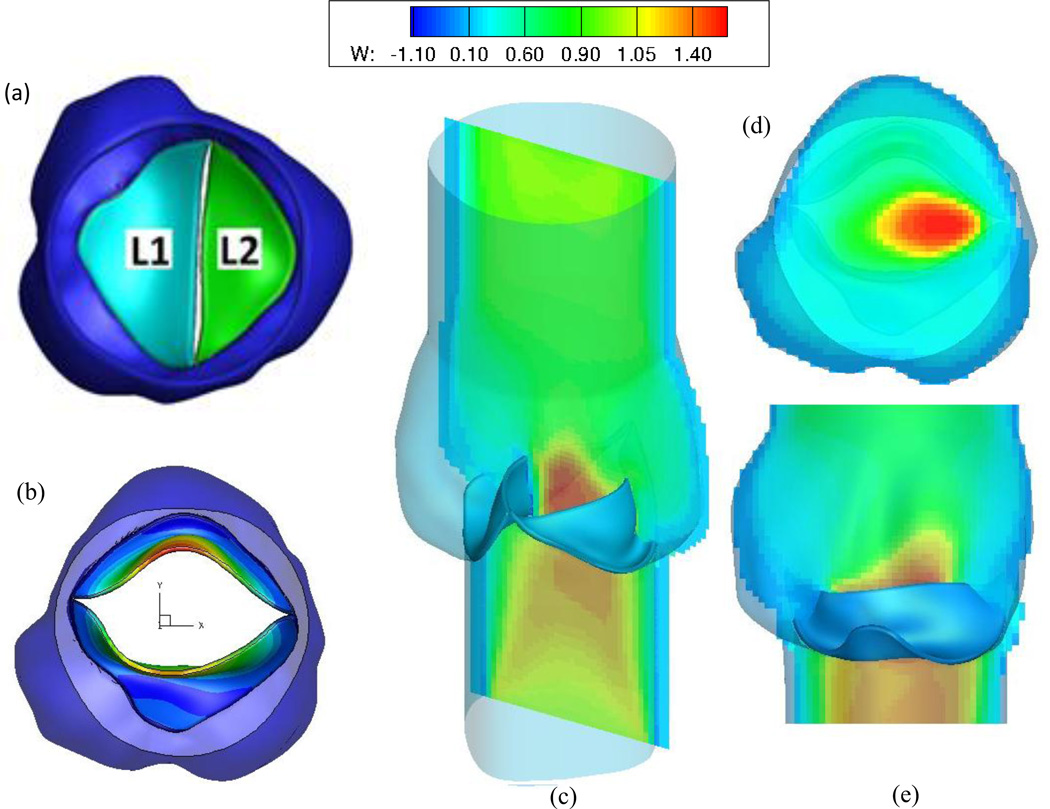
Our FSI algorithm strongly couples the fluid and structure using sub-iterations between the partitioned solvers, for a robust and stable solution to both the flow solver and FE solutions. At the interface, we have implemented an immersed interface-like approach (Lima et al., 2007; Vigmostad et al., 2009; Vigmostad and Udaykumar, 2011) to incorporate the dynamics of the moving leaflet on the fluid, as a source term in the momentum equation. We have validated the FSI algorithm with previously published results, and have recently used this approach to model a patient-specific bicuspid aortic valve during the opening phase of the cardiac cycle. Our preliminary results from this study are shown in Figure 7. The data was obtained from ultrasound imaging of a type II bicuspid aortic valve patient. Axial velocity contours show a skewed jet towards the left coronary region, and even in the fully open position, the leaflet cross-sectional area is substantially reduced from a tricuspid aortic valve.
Figure 7.
Preliminary results for a full FSI simulation of a patient-specific bicuspid aortic valve. (a) The original, closed configuration of the type II BAV plus aortic root, where L1 is adjacent to the non- and right-coronary sinuses, while L2 is attached to the left-coronary sinus. (b) The fully open position of the BAV, with contours of displacement. Note the relatively small EOA. (c) Axial flow contours (d) Axial flow at a slice within the aortic sinus (e) Flow along the center slice of the geometry, between the two open leaflets. Note the skewing of the jet, toward the left coronary sinus region.
Challenges and Future Directions
Apart from the challenges involved in the FSI algorithm development enumerated above in order to perform physiologically realistic and accurate simulations, additional difficulties in performing patient-specific analyses need to be kept in mind. With advances in imaging modalities and image processing techniques, morphologically realistic geometry of the organ of interest can be obtained as demonstrated in this work. However, the images obtained above do not provide accurate information on the thickness of the structures due to limitations in the image resolution and hence necessitates the assumption of uniform thickness. The effect of variation of the thickness on the deformation and stress distribution on the structures of interest are essentially neglected in these studies. The second major limitation is the lack of patient-specific material property information to be employed in the analysis. Biological soft tissues generally exhibit an anisotropic, non-linear stress-strain behavior and limited studies have been reported on the appropriate constitutive laws for the leaflets and the aortic wall tissue with bi-axial force deformation experiments with either animal or human tissue. Generally, simulations are limited to using the material property specification from published data since it is not practical to obtain patient-specific material properties. In addition, even the normal material behavior of the soft tissue can be anticipated to vary regionally and information is lacking on such variability even for the normal and healthy valve leaflets. With congenital malformations such as BAV, the leaflets may not have the same material property as in the case of normal TAV, even in the case of BAVs with echocardiographically assessed normal function. Even the aortic wall tissue in subjects with BAV may be significantly different in the presence of diseases such as Marfan’s syndrome or raphes on the leaflet. The FE and FSI analyses described above do not consider these effects and assume material property specifications from the limited published data.
In the presentation of the results, it is the usual practice to demonstrate mesh independence and also compare the results such as the magnitudes of computed stresses, local strains, or fluid velocity with previously published computational or experimental results for validation. Generally a correlation is also obtained with the simulation-predicated regions of stress concentrations with the common sites of calcification and tear found on the leaflets. With patient-specific studies, a direct correlation between the abnormal stresses computed in the simulations and subsequent alterations on the leaflets is possible. Towards this objective, a BAV patient-specific simulation can be performed at a given time and follow-up examinations can be performed on the patient to determine the location of any subsequent leaflet calcification. Performing such studies with a number of patients with varying BAV geometry with longitudinal follow–up data may potentially identify specific BAV geometric types that result in calcific aortic stenosis (CAS). If successful, such studies will result in our ability to stratify BAV patients at risk for CAS in order to improve their clinical treatment and management. Furthermore, even such a correlation does not yield information on the mechanism for the calcification process due to the increased stresses on the leaflets. In order to increase our understanding of this relationship, the detailed mechano-biology of the leaflet tissue at the microstructural level is necessary and a multi-scale simulation towards this end has been reported by (Weinberg and Kaazempur Mofrad, 2008). Further advances in multi-scale simulations including the modeling of the mechano-biology at the microstructural level is necessary for a mechanistic determination of the effect of induced leaflet stresses on CAS if any.
Acknowledgements
The partial support of this study with grants from NIH (HL 071814 and HL 109597) and by the Iowa Department of Economic Health (IDED) are gratefully acknowledged.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
We wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.
References
- Antiga L, Piccinelli M, et al. An image-based modeling framework for patient-specific computational hemodynamics. Med Biol Eng Comput. 2008;46(11):1097–1112. doi: 10.1007/s11517-008-0420-1. [DOI] [PubMed] [Google Scholar]
- Burken JA. Biomedical Engineering. The University of Iowa; 2012. Determining the Effect of Congenital Bicuspid Aortic Valves on Aortic Dissection Using Computational Fluid Dynamics. M.S. [Google Scholar]
- Cecconi M, Manfrin M, et al. Aortic dimensions in patients with bicuspid aortic valve without significant valve dysfunction. Am J Cardiol. 2005;95(2):292–294. doi: 10.1016/j.amjcard.2004.08.098. [DOI] [PubMed] [Google Scholar]
- Christie GW, Barratt Boyes BG. On stress reduction in bioprosthetic heart valve leaflets by the use of a flexible stent. J Card Surg. 1991;6(4):476–481. doi: 10.1111/j.1540-8191.1991.tb00348.x. [DOI] [PubMed] [Google Scholar]
- Conti CA, Della Corte A, et al. Biomechanical implications of the congenital bicuspid aortic valve: a finite element study of aortic root function from in vivo data. J Thorac Cardiovasc Surg. 2010;140(4):890–896. 896, e891–e892. doi: 10.1016/j.jtcvs.2010.01.016. [DOI] [PubMed] [Google Scholar]
- De Hart J, Peters GW, et al. A three-dimensional computational analysis of fluid-structure interaction in the aortic valve. J Biomech. 2003;36(1):103–112. doi: 10.1016/s0021-9290(02)00244-0. [DOI] [PubMed] [Google Scholar]
- de Hart J, Peters GW, Schreurs PJ, Baaijens FP. A three-dimensional computational analysis of fluid-structure interaction in the aortic valve. J Biomech. 2003;36(1):103–112. doi: 10.1016/s0021-9290(02)00244-0. [DOI] [PubMed] [Google Scholar]
- Della Corte A, Bancone C, et al. Restricted cusp motion in right-left type of bicuspid aortic valves: A new risk marker for aortopathy. J Thorac Cardiovasc Surg. 2011 doi: 10.1016/j.jtcvs.2011.10.014. [DOI] [PubMed] [Google Scholar]
- Dillard S, Udaykumar HS, et al. ASME 2012 Summer Bioengineering Conference. Fajardo, Puerto Rico: ASME; 2012. Image Based Modeling of Biotransport Through Complex Moving Geometries. [Google Scholar]
- Dumont K, Stijnen JM, et al. Validation of a fluid-structure interaction model of a heart valve using the dynamic mesh method in fluent. Comput Methods Biomech Biomed Engin. 2004;7(3):139–146. doi: 10.1080/10255840410001715222. [DOI] [PubMed] [Google Scholar]
- Einstein DR, Del Pin F, et al. Fluid-Structure Interactions of the Mitral Valve and Left Heart: Comprehensive Strategies, Past, Present and Future. Int J Numer Methods Eng. 2010;26(3–4):348–380. doi: 10.1002/cnm.1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fedak PW, Verma S, et al. Clinical and pathophysiological implications of a bicuspid aortic valve. Circulation. 2002;106(8):900–904. doi: 10.1161/01.cir.0000027905.26586.e8. [DOI] [PubMed] [Google Scholar]
- Gnyaneshwar R, Kumar RK, et al. Dynamic analysis of the aortic valve using a finite element model. Ann Thorac Surg. 2002;73(4):1122–1129. doi: 10.1016/s0003-4975(01)03588-3. [DOI] [PubMed] [Google Scholar]
- Govindarajan V, Udaykumar HS, et al. Impact of design parameters on bileaflet mechanical heart valve flow dynamics. J. Heart Valve Disease. 2009;18:535–545. [PMC free article] [PubMed] [Google Scholar]
- Grande KJ, Cochran RP, et al. Stress variations in the human aortic root and valve: the role of anatomic asymmetry. Ann Biomed Eng. 1998;26(4):534–545. doi: 10.1114/1.122. [DOI] [PubMed] [Google Scholar]
- Hope MD, Meadows AK, et al. Images in cardiovascular medicine. Evaluation of bicuspid aortic valve and aortic coarctation with 4D flow magnetic resonance imaging. Circulation. 2008;117(21):2818–2819. doi: 10.1161/CIRCULATIONAHA.107.760124. [DOI] [PubMed] [Google Scholar]
- Huang HY. Bioengineering. University of Pittsburgh; 2004. Micromechanical simulations of heart valve tissue. PhD. [Google Scholar]
- Jermihov PN, Jia L, et al. Effect of Geometry on the Leaflet Stresses in Simulated Models of Congenital Bicuspid Aortic Valves. Cardiovasc Eng Technol. 2011;2(1):48–56. doi: 10.1007/s13239-011-0035-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H, Chandran KB, et al. An experimentally derived stress resultant shell model for heart valve dynamic simulations. Ann Biomed Eng. 2007;35(1):30–44. doi: 10.1007/s10439-006-9203-8. [DOI] [PubMed] [Google Scholar]
- Kim H, Lu J, et al. Dynamic simulation pericardial bioprosthetic heart valve function. J Biomech Eng. 2006;128(5):717–724. doi: 10.1115/1.2244578. [DOI] [PubMed] [Google Scholar]
- Kim H, Lu J, et al. Dynamic simulation of bioprosthetic heart valves using a stress resultant shell model. Ann Biomed Eng. 2008;36(2):262–275. doi: 10.1007/s10439-007-9409-4. [DOI] [PubMed] [Google Scholar]
- Krishnan S, Udaykumar HS, et al. Two-dimensional dynamic simulation of platelet activation during mechanical heart valve closure. Annals of Biomedical Engineering. 2006;34(10):1519–1534. doi: 10.1007/s10439-006-9194-5. [DOI] [PubMed] [Google Scholar]
- Krishnan S, Udaykumar HS, et al. Two-dimensional dynamic simulation of platelet activation during mechanical heart valve closure. Ann Biomed Eng. 2006;34(10):1519–1534. doi: 10.1007/s10439-006-9194-5. [DOI] [PubMed] [Google Scholar]
- Krishnan S, Udaykumar HS, Marshall JS, Chandran KB. Dynamic analysis of platelet activation during mechanical heart valve operation. Annals of Biomedical Engineering. 2006;34:1519–1534. doi: 10.1007/s10439-006-9194-5. [DOI] [PubMed] [Google Scholar]
- Kunzelman KS, Einstein DR, et al. Fluid-structure interaction models of the mitral valve: function in normal and pathological states. Philos Trans R Soc Lond B Biol Sci. 2007;362(1484):1393–1406. doi: 10.1098/rstb.2007.2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lima R, Wada S, et al. World Congress on Medical Physics and Biomedical Engineering 2006. Springer; 2007. Velocity measurements of blood flow in a rectangular PDMS microchannel assessed by confocal micro-PIV system. [Google Scholar]
- Marella S, Krishnan S, et al. Sharp interface Cartesian grid method I: An easily implemented technique for 3D moving boundary computations. Journal of Computational Physics. 2005;210(1):1–31. [Google Scholar]
- Nistri S, Sorbo MD, et al. Aortic root dilatation in young men with normally functioning bicuspid aortic valves. Heart. 1999;82(1):19–22. doi: 10.1136/hrt.82.1.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pachulski RT, Weinberg AL, et al. Aortic aneurysm in patients with functionally normal or minimally stenotic bicuspid aortic valve. Am J Cardiol. 1991;67(8):781–782. doi: 10.1016/0002-9149(91)90544-u. [DOI] [PubMed] [Google Scholar]
- Pouch AM, Yushkevich PA, et al. Development of a semi-automated method for mitral valve modeling with medial axis representation using 3D ultrasound. Medical Physics. 2012;39(2):933–950. doi: 10.1118/1.3673773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rim Y, Laing ST, et al. Proceedings of the International Conference on Modeling, Simulation, and Visualization Methods. Las Vegas: 2011. Patient-specific computational evaluation of the mitral valve apparatus using three-dimensional echocardiography; pp. 89–94. [Google Scholar]
- Robicsek F, Thubrikar MJ, et al. The congenitally bicuspid aortic valve: how does it function? Why does it fail? Ann Thorac Surg. 2004;77(1):177–185. doi: 10.1016/s0003-4975(03)01249-9. [DOI] [PubMed] [Google Scholar]
- Sacks MS, Sun W. Multiaxial mechanical behavior of biological materials. Annu Rev Biomed Eng. 2003;5:251–284. doi: 10.1146/annurev.bioeng.5.011303.120714. [DOI] [PubMed] [Google Scholar]
- Schaefer BM, Lewin MB, et al. The bicuspid aortic valve: an integrated phenotypic classification of leaflet morphology and aortic root shape. Heart. 2008;94(12):1634–1638. doi: 10.1136/hrt.2007.132092. [DOI] [PubMed] [Google Scholar]
- Sievers HH, Schmidtke C. A classification system for the bicuspid aortic valve from 304 surgical specimens. J Thorac Cardiovasc Surg. 2007;133(5):1226–1233. doi: 10.1016/j.jtcvs.2007.01.039. [DOI] [PubMed] [Google Scholar]
- Steinman DA, Milner JS, et al. Image-based computational simulation of flow dynamics in a giant intracranial aneurysm. AJNR Am J Neuroradiol. 2003;24(4):559–566. [PMC free article] [PubMed] [Google Scholar]
- Sun W, Abad A, et al. Simulated bioprosthetic heart valve deformation under quasi-static loading. J Biomech Eng. 2005;127(6):905–914. doi: 10.1115/1.2049337. [DOI] [PubMed] [Google Scholar]
- Taylor CA, Steinman DA. Image-based modeling of blood flow and vessel wall dynamics: applications, methods and future directions: Sixth International Bio-Fluid Mechanics Symposium and Workshop, March 28–30, 2008 Pasadena, California. Ann Biomed Eng. 2010;38(3):1188–1203. doi: 10.1007/s10439-010-9901-0. [DOI] [PubMed] [Google Scholar]
- Vigmostad S, Udaykumar HS. Algorithms for Fluid–Structure Interaction. In: Chandran KB, Udaykumar HS, Reinhardt JM, editors. Image-based Computational Modeling in the Human Circulatory and Pulmonary Systems. Springer-Verlag Publications; 2011. [Google Scholar]
- Vigmostad S, Udaykumar HS, et al. Fluid-structure interaction methods in biological flows with special emphasis on heart valve dynamics. International Journal for Numerical Methods in Biomedical Engineering. 2009;26:435–470. [Google Scholar]
- Vigmostad SC, Burken JA, et al. 7th International Biofluid Mechanics Symposium. Dead Sea, Israel: Engineering Conferences International; 2012. Flow Development Past Bicuspid Aortic Valves and the Relationship to Ascending Aortic Pathology. [Google Scholar]
- Votta E, Caiani E, et al. Mitral valve finite-element modelling from ultrasound data: a pilot study for a new approach to understand mitral function and clinical scenarios. Philos Transact A Math Phys Eng Sci. 2008;366(1879):3411–3434. doi: 10.1098/rsta.2008.0095. [DOI] [PubMed] [Google Scholar]
- Ward C. Clinical significance of the bicuspid aortic valve. Heart. 2000;83(1):81–85. doi: 10.1136/heart.83.1.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberg EJ, Kaazempur Mofrad MR. A multiscale computational comparison of the bicuspid and tricuspid aortic valves in relation to calcific aortic stenosis. Journal of Biomechanics. 2008;41(16):3482–3487. doi: 10.1016/j.jbiomech.2008.08.006. [DOI] [PubMed] [Google Scholar]