Formalism for Hypercomplex Multidimensional NMR Employing Partial-Component Subsampling

Abstract

Multidimensional NMR spectroscopy typically employs phase-sensitive detection, which results in hypercomplex data (and spectra) when utilized in more than one dimension. Nonuniform sampling approaches have become commonplace in multidimensional NMR, enabling dramatic reductions in experiment time, increases in sensitivity and/or increases in resolution. In order to utilize nonuniform sampling optimally, it is necessary to characterize the relationship between the spectrum of a uniformly sampled data set and the spectrum of a subsampled data set. In this work we construct an algebra of hypercomplex numbers suitable for representing multidimensional NMR data along with partial-component nonuniform sampling (i.e. the hypercomplex components of data points are subsampled). This formalism leads to a modified DFT–convolution relationship involving a partial-component, hypercomplex point-spread function set. The framework presented here is essential for the continued development and appropriate characterization of partial-component nonuniform sampling.

Introduction

Ever since NMR was invented by Rabi et al. [1], and further developed by Bloch and Purcell et al. [2–4], scientists have continued to devise methods for enhancing sensitivity and resolution. Ernst and Anderson introduced the Fourier Transform NMR in the mid 1960s [5], which shortened experiment times and increased spectral sensitivity. Jean Jeener conceived of the first 2D experiment in 1971 and it was ultimately carried out by Ernst et al. in 1975 [6]. The long experiment times required by multidimensional NMR led to Bodenhausen and Ernst’s accordion experiment in 1981 [7], which launched the concept of nonuniform sampling (NUS) and further motivated the development of non-Fourier spectral reconstruction [8]. The next significant change in sampling strategy that impacted sensitivity came with the hypercomplex representation of phase-sensitive data by States et al. [9], which was later formalized by Delsuc [10]. Each hypercomplex entry in the multidimensional data array contains a set of real valued components. The component values give the magnitudes of the signal recorded at various phase angles.

Multidimensional NMR has incrementally evolved over the last several decades through the continued development of novel NUS schemes and non-Fourier reconstruction techniques (see [11] for review). One contributing factor to the improved understanding of NUS is the advent of rigorous, quantitative methods for characterizing NUS schemes [12–15] and reconstruction methods [8, 16–19]. Central to understanding these efforts has been the Discrete Fourier Transform (DFT)–Convolution Theorem, which states for complex-valued vectors a and b,

$$\mathcal{F}(\mathit{a}\circ \mathit{b})=\mathcal{F}(\mathit{a})\ast \mathcal{F}(\mathit{b}),$$ (1)

where is the DFT operator, ∘ is the Hadamard product (i.e. elementwise multiplication), and * is convolution. For a “data vector” a and a “sampling function” b, the DFT–Convolution Theorem states that the DFT of the sampling function ( (b)), often referred to as the point-spread function (PSF), relates the spectrum obtained by complete uniform sampling ( 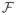(a)) to the spectrum obtained by subsampling ( 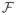(a ∘ b)). In particular, the sampling artifacts in the PSF enter into the subsampled spectrum by way of convolution with the uniformly sampled spectrum. It should be noted that while non-Fourier reconstruction methods are often designed to suppress sampling artifacts and generally achieve better sensitivity than the DFT of zero-augmented subsampled data, the PSF is still appropriate for the relative comparison of sampling schemes.

Until the recent introduction of random-phase detection (RPD, [20]), subsampling ignored the multi-component nature of hypercomplex data; samples included either all the components of a data value or none of them (we call this full-component sampling). In contrast, RPD, which is the first presentation of a partial-component sampling scheme, collects only one component from each data value. In general, partial-component subsampling of multidimensional, hypercomplex data can not be handled by the classic DFT–Convolution Theorem. This paper formalizes a modified DFT–Convolution Theorem to accommodate partial-component subsampling and serves as an extension of the work by Delsuc [10]. In addition, the derivation of the modified DFT-Convolution relationship provides a means for characterizing the sampling-induced spectral aliases that arise from any partial-component sampling scheme.

The derivation reveals the proper form of the PSF under partial-component subsampling. These results modernize the theoretical foundations of multidimensional NMR and provide a platform for quantifying the spectral sensitivity of the next generation of novel sampling schemes.

Methods

The following subsections introduce an algebra of hypercomplex numbers along with the DFT, convolution and Hadamard operators necessary to define a modified DFT–Convolution relationship suitable for analysis of partial-component, nonuniform sampling of hypercomplex, multidimensional NMR data. Note that the algebra developed here is quite different from the quaternion or octonion algebras commonly employed in other fields [21–23]; among other things, our multiplication is commutative.

An Algebra of Hypercomplex Numbers

Two fundamental properties of hypercomplex NMR data are:

• Applying a 90-degree phase shift in dimension i followed by a 90-degree phase shift in dimension j yields the same result as applying the two phase shifts in the opposite order.

• Applying a 180-degree phase shift in any dimension results simply in a change of sign.

The work of Delsuc [10] is extended by defining an algebra of hypercomplex numbers that satisfies the above properties.

Each dimension in a d-dimensional hypercomplex number system has real and imaginary components. A single real-valued unit, denoted by “1”, is common to all dimensions and is the identity element of the algebra, whereas each dimension k = 1, …, d has a unique imaginary unit u_k. The imaginary units are the generators of the algebra and, along with the identity element, can be used to construct a set of 2^d basis elements of the algebra. The particular set of basis elements or components (casually referred to as “phases” in NMR) employed here is defined as

$${\mathcal{P}}_d=\{{\phi }_1\cdots {\phi }_d\mid {\phi }_k\in \{1,u_k\}\},$$ (2)

where φ₁ ···φ_d is a product of units performed according to the multiplication rules:

$$\begin{array}{c}{u}_i{u}_j=u_j{u}_i,\\ u_i^2=-1.\end{array}$$ (3)

These rules express the fundamental properties of hypercomplex NMR noted at the top of this section, provided that multiplication by u_k is interpreted as a phase shift by 90 degrees in dimension k.

A value in the d-dimensional hypercomplex space ℍ_d is a weighted sum over the component set. For example, consider the three-dimensional case. The generators u₁, u₂ and u₃ produce the component set

$${\mathcal{P}}_3=\{1,u_1,u_2,u_3,u_1{u}_2,u_1{u}_3,u_2{u}_3,u_1{u}_2{u}_3\},$$ (4)

and a general member of the space ℍ₃ can be written as

$$x=a+{bu}_1+{cu}_2+{du}_3+{eu}_1{u}_2+{fu}_1{u}_3+{gu}_2{u}_3+{hu}_1{u}_2{u}_3,$$ (5)

where the coefficients a, b, …, h are real numbers. In the context of multidimensional NMR, the real unit along each dimension is typically referred to as “R” and the imaginary unit along each dimension is referred to as “I”. In this notation, for example, the component u₁u₃ from 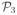is expressed as “IRI” and f above could be referred to as the “IRI” coefficient of x.

As a simpler example, the 1-dimensional hypercomplex space ℍ₁ has only one imaginary unit, u₁. Numbers in this space have only two components, R and I, and they can be written in the form x = a + bu₁. It’s easy to see that the multiplication operation defined in Equation (3) makes this space isomorphic to the usual complex numbers.

The exponential function is defined for hypercomplex numbers according to the usual Taylor series expansion. Using this formula one can show that the familiar properties of exponentials continue to hold: If x and y are hypercomplex numbers then e^x+y = e^x · e^y, and for any real number a and imaginary unit u_k we have e^au_k = cos(a) + u_k sin(a).

We will write “x{φ}” for the real-valued coefficient of the component φ ∈ 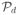appearing in x. Thus in Equation (5) above, f = x{u₁u₃}. It follows that a general member of ℍ_d can be written as

$$x=\sum _{\phi \in {\mathcal{P}}_d}x\{\phi \}·\phi .$$ (6)

A multidimensional array X of hypercomplex numbers is similarly expressed as

$$X=\sum _{\phi \in {\mathcal{P}}_d}X\{\phi \}·\phi ,$$ (7)

where X{φ} is now the real-valued array whose elements are the coefficients of the component φ. The hypercomplex element of X located at the indices k₁, …, k_d will be written as “X[k₁, …, k_d]”. This system of notation puts the square brackets and curly brackets on equal footing, emphasizing how indexing along dimension is similar to indexing along component.

DFT

Let $\mathit{t}\in {\mathbb{H}}_d^N$ be a hypercomplex vector of length N (the subscript on “ℍ” indicates the dimensionality of the phase-space and the superscript indicates the size of the vector). The hypercomplex DFT on dimension j of t is the length-N vector f defined by:

$$\mathit{f}[k]=\frac{1}{\sqrt{N}}\sum _{n=0}^{N-1}{e}^{-2\pi u_{j}kn/N}\mathit{t}[n].$$ (8)

This is the same as the usual formula for the DFT of a complex vector except that the ordinary imaginary unit i has been replaced with u_j. We write f = 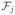(t), with the subscript j indicating the dimension on which 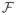acts.

The DFT operator 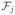is extended to multidimensional arrays by performing a single DFT on all the sub-vectors parallel to the j-th dimension. Thus, if T is a d-dimensional array of hypercomplex values then

$${\mathcal{F}}_j(T)[k_1,\dots ,k_d]=\frac{1}{\sqrt{N_j}}\sum _{n_j=0}^{N_j-1}{e}^{-2\pi u_j{k}_j{n}_j/N_j}T[k_1,\dots ,k_{j-1},n_j,k_{j+1},\dots ,k_d],$$ (9)

where N_j is the size of T ’s j-th dimension. Note that the dimension index j is used here in two different ways: It specifies the location of elements in T (i.e., k_j, n_j, and N_j) and also the hypercomplex unit in the exponential factor (i.e., u_j). By contrast, Equation (8) uses j only to select a hypercomplex unit, independently of the single dimension the vector f comprises.

A full DFT of a multidimensional hypercomplex data array involves performing a single transform in each of the dimensions: 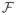(T) = 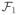(··· (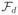T) ···). The order of the transforms is irrelevant because the u_j units commute; the series of subscripts has been omitted from the multidimensional Fourier operator on the left hand side to indicate that all dimensions have been transformed. Written out in full, this becomes

$$\mathcal{F}(T)[k_1,\dots ,k_d]=\frac{1}{\sqrt{N_1\cdots N_d}}\sum _{n_1=0}^{N_1-1}\cdots \sum _{n_d=0}^{N_{d-1}}{e}^{-2\pi (u_1{k}_1{n}_1/N_1+\cdots +u_d{k}_d{n}_d/N_d)}T[n_1,\dots ,n_d].$$ (10)

Convolution

Let $\mathit{f},\mathit{g}\in {\mathbb{H}}_d^N$ be hypercomplex vectors. The convolution of f and g (written as f * g) is the length-N vector h defined by:

$$\mathit{h}[k]=\frac{1}{\sqrt{N}}\sum _{n=0}^{N-1}\mathit{f}[n]·\mathit{g}[k-n].$$ (11)

The vectors f and g are treated as periodic, with element indices that fall out of the range {0, …, N − 1} wrapped back in range through the modulo operator. The hypercomplex convolution defined above differs from the classic complex-valued convolution only in that the multiplication operator (·) is now hypercomplex multiplication performed according to Equation (3).

Convolution is defined similarly for multidimensional, hypercomplex data sets. The sums run over all the dimensions:

$$(F\ast G)[k_1,\dots ,k_d]=\frac{1}{\sqrt{N_1\cdots N_d}}\sum _{n_1=0}^{N_1-1}\cdots \sum _{n_d=0}^{N_d-1}F[n_1,\dots ,n_d]·G[k_1-n_1,\dots ,k_d-n_d].$$ (12)

With these definitions, the DFT–Convolution theorem (Equation (1)) holds for hypercomplex vectors (if 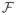is replaced by 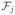) and for multidimensional arrays of hypercomplex values.

NMR Data and Sampling in Time/Phase

In the original NUS scheme, for each hypercomplex point in the data set, either all the components are sampled or none of them are (i.e. full-component sampling). This can be represented mathematically using the Hadamard operator. Let T be a fully sampled data set; then the NUS data set is specified by T ∘ S, where S is a multidimensional array of the same size as T whose elements are 1 (for the data points that are sampled) or 0 (for the points that are not). S is called the sampling function.

The Hadamard product will not suffice for the more general case of partial-component subsampling (e.g. RPD, in which each element of the array is sampled at exactly one of its components). To handle such schemes we introduce a modified Hadamard operator (⊙) and define partial-component subsampling as

$$T^{\prime }=T\odot S,$$ (13)

where the sampling function S is written as a hypercomplex array in which the coefficient values are 1 for the points and components that are sampled and 0 for those that are not. (It is worth emphasizing that the hypercomplex representation of S is for notational convenience only. The sampling function should be viewed not as a single array of hypercomplex values, but rather as a set of real valued arrays, with one array for each hypercomplex component. While it may be useful to store or refer to the set as a single hypercomplex array, it does not act mathematically as a hypercomplex array.) In the modified Hadamard product of two arrays, the values are multiplied element-wise and component-wise within elements. In other words, for each component φ

$$(T\odot S)\{\phi \}=T\{\phi \}\circ S\{\phi \},$$ (14)

and therefore

$$T^{\prime }\sum _{\phi \in {\mathcal{P}}_d}(T\{\phi \}\circ S\{\phi \})·\phi .$$ (15)

The modified Hadamard product on hypercomplex data arrays is thus a summation of real valued Hadamard products.

Unfortunately the classic DFT–Convolution relationship does not hold for the modified Hadamard operator. Instead, a separate relation holds for each component φ:

$$\mathcal{F}((T\odot S)\{\phi \})=\mathcal{F}(T\{\phi \})\ast \mathcal{F}(S\{\phi \}),$$ (16)

which results from applying Equation (1) to Equation (14). Multiplying each side by φ and adding leads, by way of Equation (7), to

$$\mathcal{F}(T^{\prime })=\mathcal{F}(T\odot S)=\sum _{\phi \in {\mathcal{P}}_d}\mathcal{F}(T\{\phi \}·\phi )\ast \mathcal{F}(S\{\phi \}).$$ (17)

This expresses the spectrum of a partial-component NUS data set, 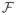(T′), in terms of a convolution between component-isolated spectra of the fully sampled data set, 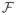(T {φ} · φ), and a component-isolated point-spread function, 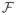(S{φ}). The latter is a member of the component-isolated PSF set

$$\text{PSF}(S)=\{\mathcal{F}(S\{\phi \})\mid \phi \in {\mathcal{P}}_d\}.$$ (18)

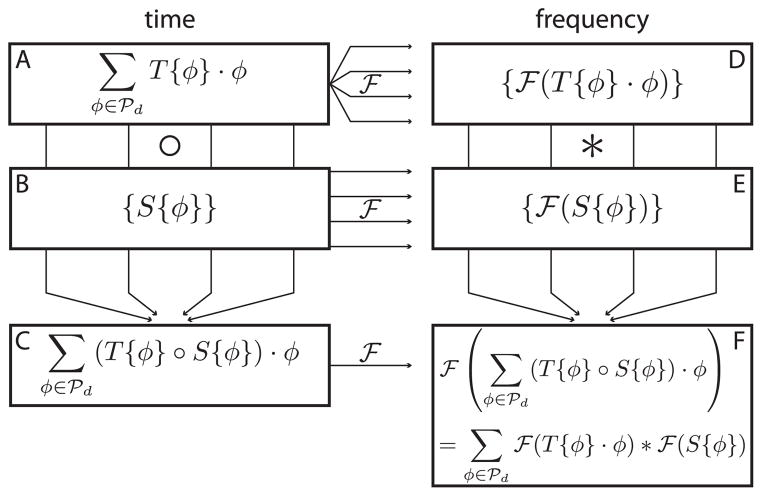
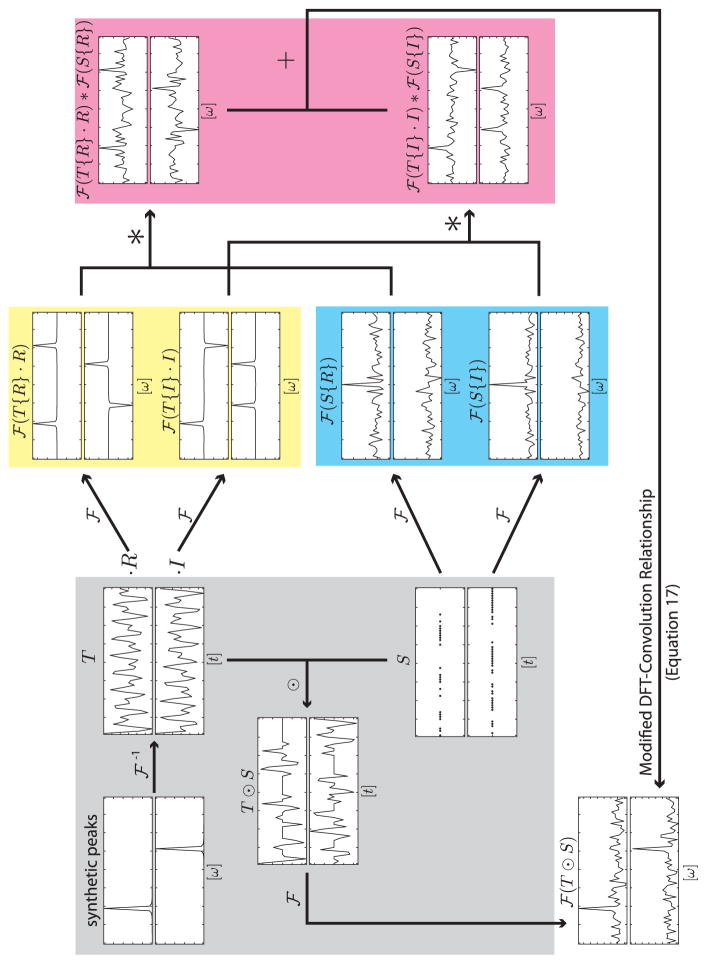
The relationships among the functional components of Equation (17) are shown in Figure 1; a visualization of these relationships is shown in Figure 2, in which a 1-dimensional spectrum containing a synthetic peak in the real component and another in the imaginary component is paired with RPD sampling. The component-isolated PSF set defined in Equation (18) is shown in the cyan box. The yellow box shows that the true peaks are aliased by the separation of T into its components. However, due to the change in sign, the convolution products in the magenta box show constructive interference at the true locations of the synthetic peaks (left of center in the real component, right of center in the imaginary component) and destructive interference at the aliased locations of the synthetic peaks (right of center in the real component, left of center in the imaginary component).

Figure 1. DFT–Convolution Theorem Modified for Partial-Component Subsampling.

Each hypercomplex component of the time-domain data (panel A) is subsampled by the corresponding component of the sampling function (panel B) according to the Hadamard product (∘) to produce zero-augmented, subsampled data (panel C). All quantities in the time domain (left column) are transformed to the frequency domain (right column) by the DFT (denoted by the horizontal arrows labeled with 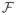). Each component of the time-domain data is isolated and processed by DFT, producing a set of hypercomplex spectra (indicated by the “one-to-many” grouping of arrows from panel A to panel D). Each of the real-valued sampling function components is processed by DFT to produce a set of hypercomplex PSFs (indicated by the set of disjoint arrows from panel B to panel E). The spectrum of the zero-augmented, subsampled data can be reached either by taking its DFT (indicated by the single arrow from panel C to panel F) or by pairwise convolving the set of uniformly sampled spectra with the PSF set and adding (indicated by the “many-to-one” grouping of arrows from panels D and E to panel F). The equivalence of these results (shown in panel F) is the modified DFT–Convolution relationship.

Figure 2. Illustration of Modified DFT–Convolution Relationship in 1D.

Each complex valued function involved in Equation (17) is shown with the real component in the top panel and the imaginary component in the bottom panel. All arrows are labeled with operators as defined in the text. As this figure serves a qualitative, not quantitative purpose, the numerical values on axes have been omitted to reduce visual clutter, but the scaling on the vertical axes within each real/imaginary plot pair is the same. The horizontal axes are labeled “[t]” for time domain data, which runs from 0 to 63, and “[ω]” for frequency domain data, which has 0Hz centered. The inputs (i.e. synthetic peak and sample schedule) are encompassed by a gray box along with their associated functions. The component-isolated DFTs of the time domain data are shown in the yellow box. The PSF set is shown in the cyan box. The convolution products are shown in the magenta box.

It is instructive to apply this analysis to the degenerate case of full-component subsampling. In this situation, for each point in the time domain either all the components are sampled or none of them are. Hence for each element of S, either all the component coefficients are 1 or all are 0. It follows that the component-isolated sampling functions S{φ} are all equal to a single real-valued sampling function S′, which then distributes out of the summation in Equation (17). The end result is

$$\mathcal{F}(T^{\prime })=\left(\sum _{\phi \in {\mathcal{P}}_d}\mathcal{F}(T\{\phi \}·\phi )\right)\ast \mathcal{F}(S^{\prime })=\mathcal{F}(T)\ast \mathcal{F}(S^{\prime }),$$ (19)

which agrees with Equation (1) as expected.

PSF Peak-to-sidelobe Ratio (PSR)

Let T be a multidimensional, hypercomplex array of time domain data and let S be the corresponding sampling function. In characterizing the aliasing artifacts present in the PSF, we observe that all of the component-isolated PSFs defined in Equation (18) enter into the summation of convolutions in Equation (17). Further, the components of the PSFs “mix” with the components of 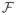(T) and are recombined through the summation to determine the components of 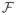(T ⊙ S). Given these interconnections, it is appropriate to measure the spectral aliasing in terms of the power of the PSF taken across all components:

$$\text{power}(\text{PSF})=\sum _{\phi \in {\mathcal{P}}_d}\sum _{{\phi }^{\prime }\in {\mathcal{P}}_d}{(\mathcal{F}(S\{\phi \})\{{\phi }^{\prime }\})}^2,$$ (20)

where the squaring is taken element-wise so that power(PSF) is a real-valued multidimensional array of the same size as S.

The PSF power gives an upper bound on the magnitude of spectral aliasing. Consider a subsampled data set and let φ₁ and φ₂ be two of the hypercomplex components. The φ₁ and φ₂ components of the data will necessarily be correlated with each other because they are subsets of the same fully sampled signal. The structure of S may be such that 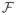(S{φ₁}) and 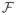(S{φ₂}) both have non-central peaks at the same location, but of opposite amplitudes. When convolved with 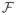(T {φ₁}) and 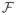(T {φ₂}) according to the right-hand side of Equation (17), it is possible for the aliased peaks to cancel out in the summation over the components and not appear in the final spectrum. Since the interference of sampling artifacts depends on the sampling function and on the structure of the time domain data, it is not possible to decouple the contributions in the general case. As such, we employ the PSF power and expect that alternative metrics may be developed in the future.

The PSF power shows the multidimensional distribution of artifacts and careful visual inspection may reveal features of a candidate sampling scheme. However, the conclusions may be subjective and difficult to automate. As a first-order approximation to sensitivity, the peak-to-sidelobe ratio (PSR, an adapted form of the sidelobe-to-peak ratio of Lustig et al. [24]) may be employed. PSR is defined as the ratio between (1) the central element of the PSF power (i.e. the element at zero frequency) and (2) the largest non-central element of the PSF power. The sampling function corresponding to complete sampling has a PSF power with a central element proportional to the square root of the number of sampled points; all the other elements of the PSF power are 0, leading to an infinite PSR. At lower sampling coverages, the central element is smaller and the structure embedded in the sampling function reveals itself as non-central peaks in the PSF, thereby reducing the PSR to a finite value. For example, the sampling function in Figure 2, has PSR=8.6.

Conclusion

Given a hypercomplex, multidimensional data array, a full-component sampling function may by expressed as a single real-valued array and the subsampled data is obtained with a Hadamard product. The classic DFT–Convolution Theorem is applicable and the hypercomplex DFT of the real-valued sampling function defines the PSF, which serves to characterize the sampling artifacts introduced in the NUS spectrum. A partial-component sampling function has a real-valued array for each component, and the subsampled data is obtained by taking the Hadamard product of each component of the sampling function with the corresponding component of the data array. The component-weighted summation of Hadamard products propagates through the classic DFT–Convolution Theorem, which leads to the central result of this paper.

While the modifications to the classic DFT–Convolution relationship necessary to accommodate partial-component subsampling may appear minor, their implications are significant. The component-weighted summation of convolutions on the right hand side of Equation (17) effectively superimposes the convolution products. Even though each of the component-isolated PSFs is completely determined by the sampling function, the extent to which their artifacts constructively or destructively mix is partially determined by the specific values of the time domain data being subsampled. In the general case, this “many-to-one” mapping can not be decoupled, thereby complicating metrics based solely on the PSF, as discussed in the PSR section above and demonstrated in Figure 2.

NMR spectroscopists have relied on the classic DFT–Convolution Theorem to govern the characterization of sampling artifacts since the inception of NUS. Subsampling schemes have evolved and have outgrown the underlying mathematical foundation. The derivations in this paper provide the formal foundation for a new generation of subsampling schemes, which is essential for proper characterization and optimization.

• We formalize a hypercomplex algebra suitable for multidimensional NMR data.

• The DFT–Convolution Theorem is modified to accommodate partial-component sampling.

• The point-spread function set indicates spectral sensitivity for nonuniform sampling.

• The framework is essential for development of partial-component nonuniform sampling.