Abstract
Thrombotic complications with mechanical circulatory support (MCS) devices remain a critical limitation to their long-term use. Device-induced shear forces may enhance the thrombotic potential of MCS devices through chronic activation of platelets, with a known dose–time response of the platelets to the accumulated stress experienced while flowing through the device–mandating complex, lifelong anticoagulation therapy. To enhance the thromboresistance of these devices for facilitating their long-term use, a universal predictive methodology entitled Device Thrombogenicity Emulation (DTE) was developed. DTE is aimed at optimizing the thromboresistance of any MCS device. It is designed to test device-mediated thrombogenicity, coupled with virtual design modifications, in an iterative approach. This disruptive technology combines in silico numerical simulations with in vitro measurements, by correlating device hemodynamics with platelet activity coagulation markers – before and after iterative design modifications aimed at achieving optimized thrombogenic performance. The design changes are first tested in the numerical domain, and the resultant device conditions are then emulated in a Hemodynamic Shearing Device (HSD) in which platelet activity is measured under device emulated conditions. As such, DTE can be easily incorporated during the device research and development phase – achieving minimization of the device thrombogenicity before prototypes are built and tested thereby reducing the ultimate cost of preclinical and clinical trials. The robust capability of this predictive technology is demonstrated here in various MCS devices. The presented examples indicate the potential of DTE for reducing device thrombogenicity to a level that may obviate or significantly reduce the extent of anticoagulation currently mandated for patients implanted with MCS devices for safe long-term clinical use.
1. Introduction
The advent of Mechanical Circulatory Support devices has provided life-saving solutions to patients with severe cardiovascular diseases. The REMATCH trial (Stevenson LW, 2004) was one of the first major studies to demonstrate that left ventricular assist devices (LVAD) are superior to drug therapy for advanced heart failure, paving the way for their use as long-term heart replacement therapy for patients ineligible for heart transplantation. Despite the success of this study the MCS arm demonstrated significant limitations with unacceptable complication rates (Portner et al., 2001), and strokes (Lazar et al., 2004). Second and third generation continuous-flow VADs that have emerged clinically in recent years have improved the clinical outcomes. However, in the recent HeartMate II VAD Destination-Therapy Trial patients still suffered 11% disabling stroke rate (Slaughter et al., 2009), attributed to the increased shear stress, offering the possibility that improved VAD design could prevent this problem in the future (Geisen et al., 2008). The AbioCor artificial heart, was developed as a possible solution to the chronic shortage in availability of human hearts for transplantation. In the pilot trial of the AbioCor TAH (ABIOMED, Inc), a high rate of thromboembolic complications made the clinical outcomes disappointing (Frazier et al., 2004) stemming from design and valvular issues. Mechanical Heart Valve (MHV) patients develop thromboembolic complications at a rate of 0.7% to 6.4% per patient year (Butchart et al., 2003; Butchart et al., 2001). In these patients, platelets are chronically activated (Edmunds, 1996; Edmunds et al., 1997). All these devices, as well as new emerging MCS devices, progressively share common limitations of thromboemebolism and hemolysis
The formation of thromboemboli in MCS devices is potentiated by contact with foreign surfaces and regional flow phenomena that stimulate blood clotting, in particular via activation of platelets. The nonphysiologic flow patterns generated in a device are considered as one of the major culprits in enhancing the hemostatic response. The well-known “Virchow's triad” of altered blood, surface, and flow, establishes the blood-artificial surface interaction problem as a multifactorial one. The flow component, perhaps the most complex part of the triad, combines all three, i.e. flow - local flow patterns play a substantial role in coagulation reactions, blood - platelet aggregation, and surface – local deposition on activated surfaces. It determines where a thrombus will form, its size and composition, and whether or not it will remain locally or embolize (Sorensen et al., 1999a, b). Thrombus and thrombo-emboli generated in cardiovascular devices are composed primarily of platelets, with less fibrin involvement than one would encounter in situations associated with low-shear thrombosis (Harker and Slichter, 1970).
Flow-induced shear platelet activation causes both aggregation and thrombin generation, showing consistent ‘dose’ and time response characteristics of equivalent chemical agonists (O'Brien and Salmon, 1990). A commonly used threshold for platelet activation under constant shear level was established by Hellums et al., (Hellums et al., 1987), forming the foundation for shear-induced platelet activation (SIPA). In prosthetic devices the pathological blood flow patterns related to pulsatility, eddy formation, and turbulence, may predominate the platelets response (Alveriadou et al., 1993; Folie and McIntire, 1989). The cumulative effect of varying flow stresses and exposure times along platelet trajectories was studied in stenoses and past MHV (Bluestein, 2004b, a; Bluestein et al., 2002; Bluestein et al., 1997; Bluestein et al., 2000; Cao and Rittgers, 1998).
In PHV and CVS devices portions of the flow cycle may become turbulent, (Bluestein et al., 1994; Bluestein et al., 2000), with elevated stresses within MHV hinges (Yoganathan et al., 1998). VADs induce changes to coagulation through activation of platelets (Rothenburger et al., 2002; Wilhelm et al., 2001) despite aggressive anticoagulant therapy, with flow patterns implicated in the underlying risk for their thromboembolism (Jin and Clark, 1993), especially cerebral embolism (e.g., rates ranging from 7.4% for the Heartmate I VAD to approx. 50% for the Novacor VAD system) (El-Banayosy et al., 2001). Platelet aggregates are the source of microembolic signals (MES) measured in patients with PHV (Grosset et al., 1996). A significant effect of valve hemodynamics on platelet activation for two differing valve designs (bileaflet. vs. monoleaflet) was also observed in patients (Laas et al., 2003).
The AbioCor TAH study indicated that while no evidence of significant hemolysis was observed in animal or human patients studies, (Dowling et al., 2004; Samuels et al., 2005), the majority of patients died of stroke related complications. Regretfully, very few data on flow-induced thrombogenic aspects are currently available (Charron et al., 1994). Several approaches for studying device-induced thrombogenicity were developed by a few groups (Paul et al., 1998),(Travis et al., 2002),(Jesty and Bluestein, 1999; Jesty et al., 2003). Jesty & Bluestein developed an innovative Platelet Activity State (PAS) assay, facilitating measurements of the thrombogenic potential induced by flow in devices. This technique was applied to in vitro measurements of flow-induced platelet activation in MHVs mounted in an LVAD (Yin et al., 2004), and in bioprosthetic and polymer valves (Yin et al., 2005), which are targeted for minimally invasive, percutaneous valve delivery (Feldman, 2006; Mesana, 2006) – the breakthrough technique with a huge promise for patients who cannot tolerate cardiothoracic surgery. The goal is for polymer valves, which are better suited for catheter-based stented delivery, to have thrombogenic potential comparable to the latter thereby obviating the need for mandatory anticoagulation therapy. Leakage gap width within bileaflet MHV pivots was demonstrated to have a significant effect on platelet damage (Travis et al., 2001). Thrombus formation was investigated in blood flow through orifices simulating these MHV hinges region using a thrombin-antithrombin-llI (TAT) assay (Fallon et al., 2006).
Vortex shedding was observed experimentally and computed numerically in the wake of MHV leaflets and in various MCS devices. Shed vortices were studied in the wake of MHVs (Bluestein et al., 2001; Bluestein et al., 2002; Reif et al., 1990) which promote hemostatic reaction by providing optimal mixing for platelet aggregation, increasing the procoagulant surfaces needed for the coagulation reactions to proceed, and dispersing the clotting factors in the process. Elevated turbulent stresses (1,200 to 2,000 dynes/cm2), which were measured in such wakes (Grigioni et al., 2001; Yoganathan et al., 1986), reiterated their role in activating platelets. Prior activation and the extrusion of platelets pseudopodia, potentially induced by the elevated shear stresses globally preceding vortex shedding, increases their effective hydrodynamic volume by several folds, resulting in an increased collision rate (Wurzinger et al., 1985). Numerical simulation in the wake of a MHV depicted the wake dynamics and complex behavior of vortex shedding (Huang et al., 1994), (Kelly et al., 1999; King et al., 1997; Krafczyk et al., 1998). First unsteady turbulent Reynolds Averaged (URANS) simulations using the transient turbulence Wilcox k-ω model (Bluestein et al., 2002; Bluestein et al., 2000) quantified stress histories of platelets along pertinent trajectories. Advanced URANS and Direct Numerical Simulations (DNS) included a damage accumulation in repeated passages past valves (Yared, 2006), and FSI simulation comparing the thrombogenic potential of ATS and St. Jude Medical MHVs (Dumont, 2007).
Few models for hemolysis have been developed over the years, e.g., as a function of mechanical energy dissipation (Bluestein and Mockros, 1969), or shear stress (Apel et al., 2001; Bludszuweit, 1995; Burgreen et al., 2001). In these predictive phenomenological models, that are adaptable to platelets, the normalized internal damage accumulates until a critical value of damage is reached, either as a function of the instantaneous stress level and the previous damage history, or as weight average damage accumulation over a number of cycles. In vitro hemolysis indices were investigated numerically over 3D device domains for the purpose of design optimization (Garon and Farinas, 2004), and by integrating hemolysis and platelet lysis indices along trajectories in the flow field of MHV (Goubergrits and Affeld, 2004). Several models examined the interaction of activated platelets with the blood field (Kuharsky and Fogelson, 2001; Sorensen et al., 1999a), and platelet deposition (Reininger et al., 1999; Worth Longest and Kleinstreuer, 2003). Such modeling efforts provide insight into the areas where platelets have a high probability for activation, leading to thrombus formation and thromboembolism.
2. Methods
The Device Thrombogenicity Emulation (DTE) Methodology and its Components
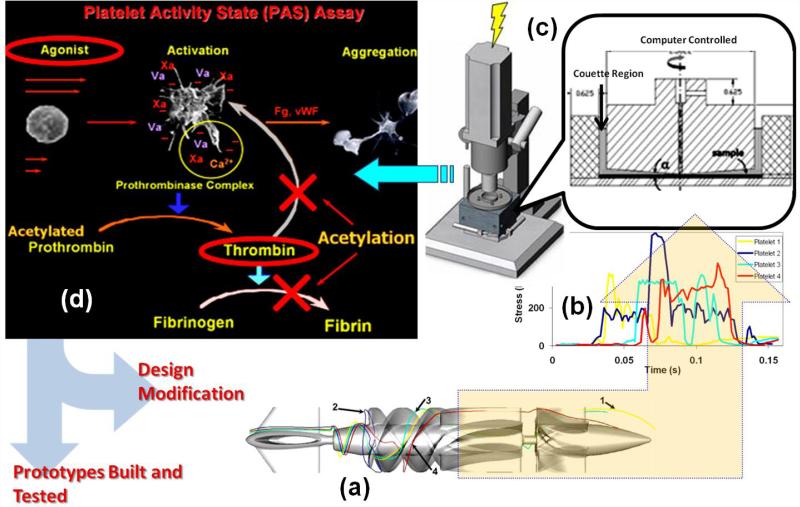
DTE is an iterative optimization process, summarized in a composite flow chart schematic (Fig. 1). Briefly: ‘hot spot’ platelet trajectories (extreme flow trajectories which expose platelets to the highest stress-loading conditions) are extracted from extensive advanced numerical simulations of the blood flow in the device. Those are resolved to quantify the stress loading waveforms, which are programmed into a hemodynamic shearing device (HSD) where the stress loading conditions within the device are emulated. Samples of gel filtered platelets exposed to these stress loading waveforms are removed from the HSD and assayed to measure thrombin generation rates, a surrogate marker for platelet activation, using the Platelet Activity State (PAS) assay (Jesty and Bluestein, 1999; Jesty et al., 2003). Designs may then be iteratively modified to reduce the thrombogenic potential, as computed in the virtual (modeling) domain, and the resultant stress loading waveforms programmed and further tested in the HSD. This iterative process involves changing design parameters specific to the device and repeating the numerical simulations of the blood flow through the redesigned device. When optimized thromboresistance is achieved via DTE. A prototype of the optimized device may then be built and tested to validate that optimization was achieved by comparing it to the baseline or predicate device design prior to optimization.
Fig. 1.
The DTE methodology iterative optimization flow chart: (a) ‘hot spot’ platelet trajectories extracted from the numerical simulation in the device (VAD in this case) are resolved to determine the (b) stress loading waveforms, which are programmed into the (c) HSD, where the stress loading conditions within the device are emulated. Samples are removed from the HSD and assayed to measure the thrombin generation rates using the (d) PAS assay. The procedure is reiterated by changing design parameters specific to the device and repeating the numerical simulation of the blood flow through the redesigned device. After the iterative process achieves a significant reduction in platelet activity, the iterations are stopped and an optimized prototype is built and tested.
The numerical simulations of blood flow through the devices (modeled as a two-phase fluid with the platelets suspended in plasma (Gosman and Ioannides, 1983)) combine Fluid structure Interaction (FSI) with Unsteady Reynolds Averaged Navier-Stokes (URANS) CFD. Highly resolved computational grids (currently up to 20 million elements) are generated as required for the two equation k-ω turbulence model (Wilcox, 1994). This simulation approach is further described in detail in our previous publications (Alemu et al., 2010; Xenos et al., 2010). Typical platelet trajectories in the flow field of a VAD and their corresponding stress-loading histories (computed with the combined effect of shear stress and exposure time (Alemu and Bluestein, 2007; Apel et al., 2001; Hellums, 1994) are shown (Fig. 1a&b). Currently up to 65,000 such histories are collapsed into a quantitative probability density function (PDF) which serves as the ‘thrombogenic footprint’ of the device (Alemu et al., 2010; Xenos et al., 2010)–mapping where the cumulative stress of each trajectory will end up in the distribution of the stress accumulation (SA) range characterizing the specific device. For improved thromboresistance it is desired that the dominant mode of the distribution be shifted to the lower SA range, i.e. a “leftward shift,” and as few trajectories as possible residing in the riskier higher SA range (where platelets are likely to activate).
The HSD (Fig. 1c) combines features of cone and plate, and Couette viscometers to dynamically expose a population of platelets to a uniform shear stress field of rapidly varying levels (Girdhar and Bluestein, 2008), which are programmed into the device according to the loading waveforms extracted from advanced numerical simulations of blood flow through a device (Fig. 1b). The PAS assay employs a modified prothrombinase method using a real-time chromogenic assay to measure thrombin formation–a universal marker of platelet activation. It quantifies the propensity of any blood recirculating device to induce thrombosis by measuring the contribution of the device to the induction of platelet activation and the hemostatic response (Jesty and Bluestein, 1999; Jesty et al., 2003). Thrombin formation is monitored as blood flows through device prototypes or within the HSD, and as the positive feedback loop is blocked in this assay (as well as the cleaving of the soluble fibrinogen into insoluble fibrin) the extent of measured thrombin generation is directly coupled to the prothrombinase activity, i.e., the platelet activation and aggregation induced by the agonist- flow induced shear stress (Fig. 1d).
For VAD recirculation experiments whole blood (120 ml) was obtained from healthy adult volunteers (n = 10) in accordance with Stony Brook University IRB regulations. Purified platelets (15×106/ml) or platelets and red cells (800×106/ml) were diluted in modified Tyrode's buffer. Timed samples (0, 10, 20, 30 min) were obtained from platelets or platelets + red cells exposed within the VAD flow loop and activation measured with the PAS assay as described above. The slope of normalized platelet activation was fitted to a linear model and reported as platelet activation rate (PAR). For the studies comparing the efficacy of VAD optimization to that of using anticoagulants reported below, platelets in buffer as previously described (Aspirin (ASA) treatment), or platelets in buffer with the addition of red blood cells (Dipyridamole treatment) were recirculated in the flow-loop through the non-optimized VAD ± ASA or Dipyridamole, both at a concentration of 20 μM; corresponding to plasma concentrations from low-dose formulations of both drugs. These in vitro dosages were equivalent to the maximal possible absorption of the metabolized drug in a subject's circulation.
We have previously applied the DTE methodology for optimizing the thrombogenic performance of various MCS and prosthetic heart valves, e.g., MHV (Xenos et al., 2010), polymer valves (Claiborne et al., 2011) and VADs (Girdhar et al., 2012). In the following section an example of utilizing DTE for achieving optimal thromboresistance in a VAD is demonstrated and also compared in vitro to the equivalent effect achieved by anti-thrombotic therapy.
3. Results
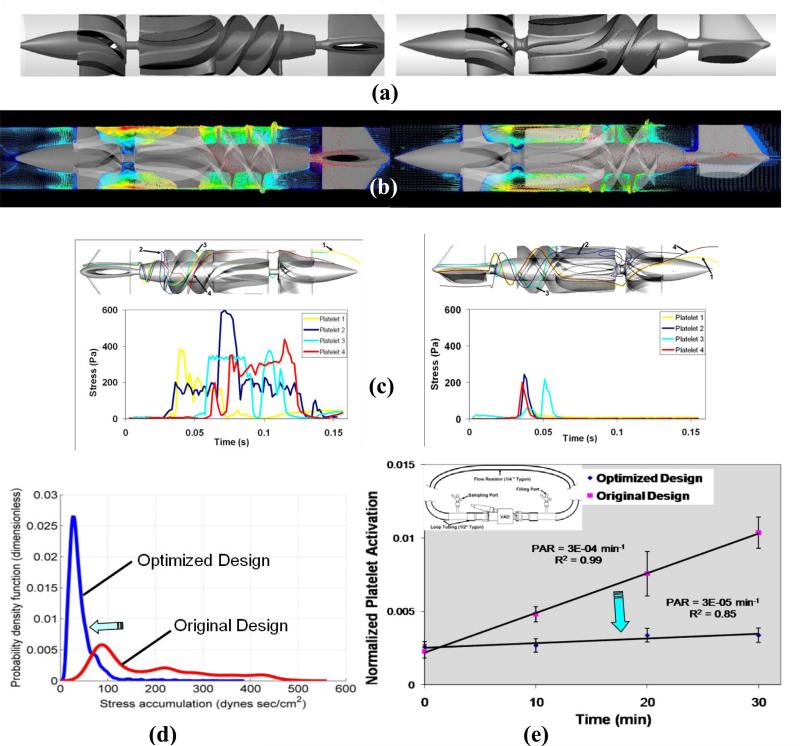
The efficacy of DTE was demonstrated in VADs by comparing two rotary blood pump prototypes (DeBakey Micromed vs Heart Assist 5, Micromed Inc., Houston, TX). Geometric features of the original VAD design (DeBakey Micromed) that were implicated in the thrombogenicity of this device were modified to create the optimized VAD design (Heart Assist 5). The design modifications included: the inlet flow straightener (4 blades reduced to 3), streamlined inlet hub and bearing taper, impeller region (blade leading edge and pitch angle, blade profiles), impeller-shroud gap and near wall region, and the impeller–diffuser interface. The original and optimized designs are shown in Fig. 2a. Numerical simulations (URANS FSI- 25 rotations at 9,000 rpm) were used to calculate the cumulative stresses along thousands of flow trajectories through both devices (before and after the optimization) and collapsed into PDFs – the ‘thrombogenic footprint’ of each device prototype. Following the specific design changes, the extensive numerical simulations conducted clearly indicate that the PDFs of the optimized design point to significantly reduced overall thrombogenicity, i.e. a marked shift to the left (lower stress accumulation values), (Fig. 2c). ‘Hot spot’ trajectories and the corresponding waveforms used for emulation in the HDS before (left) and after optimization (right) (Fig. 2 b) similarly show a significant reduction in the levels of dynamic loading stresses.
Fig. 2.
Optimization of a VAD using the DTE methodology: (a) The original Micromed DeBakey (left) and the optimized Heart Assist 5 (right) (b) The flow field with platelets dispersion patterns superimposed showing flow velocities and stresses in the device before (left) and after the optimization (right) (c) ‘Hot spot’ trajectories and the corresponding waveforms used for emulation in the HDS before (left) and after optimization (right) showing a very significant reduction in the loading stresses (d) PDF of the stress accumulation showing a very significant shift towards lower SA values for the optimized VAD (e) Comparative measurements of platelet activity in the VAD prototypes performed in a recirculation flow loop (CO=4 L/min) before and after the optimization, showing an order of magnitude reduction of the platelet activity rate (PAR = the slope of the platelet activation over 30 min. recirculation)
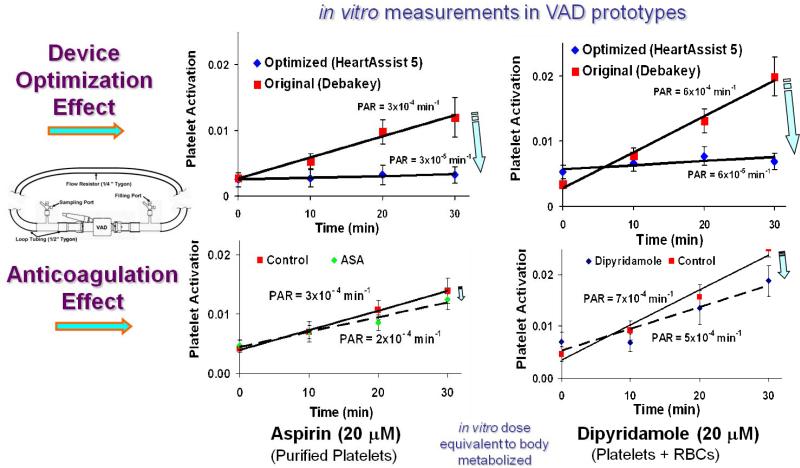
Comparative platelet activity measurements were performed in a recirculation flow loop with both pump prototypes (pre- and post-optimization) running under clinical operating conditions (speed – 9500 rpm, cardiac output 4 L/min, pressure rise – 80 mm Hg). The measurements showed that an order of magnitude lower platelet activity rate (PAR) was achieved for the optimized device (non-optimized VAD PAR=3×10-4, Optimized VAD PAR=3×10-5, p < 0.01). This clearly demonstrates the efficacy of the DTE methodology for attaining safe and cost-effective pre-clinical MCS thrombo-optimization.
In order to further examine the efficacy of the DTE optimization, we conducted a comparative study of the level of platelet activity reduction achieved via optimization alone to that achieved by the addition of conventional antithrombotic pharmacologic agents.. The effect of the reduction achieved by the optimization (with the optimized HA5 VAD) was compared to that achieved by Aspirin (ASA) and Dipyridamole, which were added to the non-optimized VAD operating in the recirculation flow loop under the same operating conditions described above. The non-optimized VAD, with no addition of the antithrombotic agents, served as the control for all cases studied. While a significant decrease in platelet activation rate (PAR) was observed for both the ASA and the Dipyridamole treatments, it was markedly less than that achieved via VAD optimization: approximately a third for the Aspirin (PAR reduced from 3×10-4 to 2×10-4) as compared to that achieved by the optimization (PAR reduced from 3×10-4 to 3×10-5), and similarly approximately a third for the Dipyridamole (PAR reduced from 7×10-4 to 5×10-4) as compared to approx. 90% reduction achieved by the optimization (PAR reduced from 6×10-4 to 6×10-5) (Fig 3).
Fig. 3.
Comparison of platelet activity reduction achieved by optimization to that achieved by two common antithrombotic agents – Aspirin (ASA) and Dipyridamole. Platelet Activation Rate (PAR) in the optimized (top) and non-optimized VAD+antocoagulation (bottom): platelets (left) and platelets + RBC (right). The non-optimized VAD is the control (red), optimization (blue) ASA (green) Dipyridamole (blue), correspondingly.
4. Discussion
The efficacy of DTE for optimizing the thromboresistance was demonstrated in a redesigned VAD. The marked reduction which was achieved in the platelet activation level (an order of magnitude) far exceeded that which was achieved by the addition of current clinical antithrombotic agents. The DTE methodology allows for a comprehensive evaluation of the thrombogenic potential of devices as a surrogate for initial animal or human testing. This system can identify “hot spot” regions within a device during distinct flow phases and compute flow trajectories and stress load histories within these regions. The programmable HSD which emulates the device conditions is universal, i.e., it is not device specific, thus serving as an ultimate test bed for evaluating almost any type of blood-contacting device design modifications before building costly prototypes.
The DTE methodology as described here for the optimization of a VAD, is based on the premise of allowing for accurate comparisons in both the in silico (numerical) and the experimental domains and correlating the two in order to predict the expected thrombogenic performance of the device. In our experimental studies we intentionally use an experimental model that differs in certain aspects from the physiologic scenario. We use purified blood platelets preferentially over whole blood or plasma experiments, as this enables us to isolate and measure the direct effect of pathological shear-induced damage on platelets and their capacity to generate thrombin. In this manner we can directly measure the most relevant coagulation marker (thrombin) which represents the contribution of activated platelets to the coagulation cascade and accurately reflects the flow-induced thrombogenicity of different device designs. It enables us to control and more sensitively measure subtle effects of the various experimental parameters involved in the thrombogenic potential of blood recirculating devices. Our group established the PAS validity over the years, in addition to its strong correlation to the more traditional platelet surface activation markers, e.g., P-selectin, while enabling near real-time measurements, which are crucial for recirculation experiments (Jesty et al., 2003).
Although currently DTE is primarily used to study MCS devices and prosthetic heart valves, in vitro assessment of hemodynamic shearing forces and subsequent platelet activation might be an efficient means of making iterative changes in other potentially thrombogenic cardiac and arterial devices, such as stents. In the case of stents, for example, because of the relative infrequency of thrombosis with current models of stents, demonstrating thrombogenicity reduction in clinical trials of newer stent platforms will likely require tens of thousands of patients. The DTE offers the ability to evaluate new stent designs by emulating their operating conditions. The system is operated under emulated shear stress loading conditions extracted from numerical simulations of blood flow in various device configurations in the circulation - under both normal and/or pathological blood flow conditions, and compared to other designs. The HSD may also be used to study the interaction between flowing platelets and cell-cultured endothelium. It may also be utilized to study the efficacy of various anticoagulation drug regimens under emulated normal and pathological physiological conditions. In this manner, the DTE methodology could allow expeditious assessment of iterative device designs with respect to platelet activation and thrombogenicity, in order to optimize their thromboresistance.
5. Conclusions
We have demonstrated a proof-of-concept applicability of our DTE methodology by comparing the thromboresistance of two continuous flow rotary VAD designs. Specifically, an order of magnitude lower Platelet Activity Rate (PAR) was measured in the optimized VAD design (HeartAssist 5™) as compared to the VAD before the optimization, correlating to a very significant overall shift in the mean stress accumulation (SA) to lower values as observed with the optimized design. The overall results of this analysis reflect a most significant design improvement, indicating that recipients of the optimized VAD may not require anticoagulation. Additionally it demonstrates that design changes may offer a more robust alternative to anti-platelet drugs such as Aspirin and Dipyridamole.
Acknowledgement
This study was funded by grants from the National Institute of Health: NIBIB Quantum Award Phase I R01 EB008004-01 (DB), and Quantum Award: Implementation Phase II-U01 EB012487-0 (DB).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
None of the authors has a conflict of interest.
References
- Alemu Y, Bluestein D. Flow-induced platelet activation and damage accumulation in a mechanical heart valve: numerical studies. Artif Organs. 2007;31:677–688. doi: 10.1111/j.1525-1594.2007.00446.x. [DOI] [PubMed] [Google Scholar]
- Alemu Y, Girdhar G, Xenos M, Sheriff J, Jesty J, Einav S, Bluestein D. Design Optimization of a Mechanical Heart Valve for Reducing Valve Thrombogenicity – a Case Study with ATS valve. ASAIO J. 2010 doi: 10.1097/MAT.0b013e3181e65bf9. doi: 10.1097/MAT.0b013e3181e65bf9. [DOI] [PubMed] [Google Scholar]
- Alveriadou B, Moake J, Turner N, Ruggeri Z, Folie B, Phillips M, Schreiber A, Hrinda M, McIntire L. Real-time analysis of shear dependent thrombus formation and its blockade by inhibitors of von Willebrand factor binding to platelets. Blood. 1993;81:1263–1276. [PubMed] [Google Scholar]
- Apel J, Paul R, Klaus S, Siess T, Reul H. Assessment of hemolysis related quantities in a microaxial blood pump by computational fluid dynamics. Artif Organs. 2001;25:341–347. doi: 10.1046/j.1525-1594.2001.025005341.x. [DOI] [PubMed] [Google Scholar]
- Bludszuweit C. Model for a general mechanical blood damage prediction. Artif Organs. 1995;19:583–589. doi: 10.1111/j.1525-1594.1995.tb02385.x. [DOI] [PubMed] [Google Scholar]
- Bluestein D. Research Approaches for Studying Flow Induced Thromboembolic Complications in Blood Recirculating Devices. Expert Rev. Medical Devices. 2004a;1:65–80. doi: 10.1586/17434440.1.1.65. [DOI] [PubMed] [Google Scholar]
- Bluestein D, Einav S, Hwang NH. A squeeze flow phenomenon at the closing of a bileaflet mechanical heart valve prosthesis. J Biomech. 1994;27:1369–1378. doi: 10.1016/0021-9290(94)90046-9. [DOI] [PubMed] [Google Scholar]
- Bluestein D, Einav S, Leondes C.T.e. Biomechanics systems techniques and applications: Cardiovascular techniques. CRC Press LLC; Boca Raton, FL: 2001. Techniques in the analysis of stability of pulsatile flow through heart valves. [Google Scholar]
- Bluestein D, Li YM, Krukenkamp IB. Free emboli formation in the wake of bi-leaflet mechanical heart valves and the effects of implantation techniques. J Biomech. 2002;35:1533–1540. doi: 10.1016/s0021-9290(02)00093-3. [DOI] [PubMed] [Google Scholar]
- Bluestein D, Niu L, Schoephoerster RT, Dewanjee MK. Fluid mechanics of arterial stenosis: relationship to the development of mural thrombus. Ann Biomed Eng. 1997;25:344–356. doi: 10.1007/BF02648048. [DOI] [PubMed] [Google Scholar]
- Bluestein D, Rambod E, Gharib M. Vortex shedding as a mechanism for free emboli formation in mechanical heart valves. J Biomech Eng. 2000;122:125–134. doi: 10.1115/1.429634. [DOI] [PubMed] [Google Scholar]
- Bluestein D, Yin W, Affeld K, Jesty J. Flow-Induced Platelet Activation in a Mechanical Heart Valve. J. Heart Valve Dis. 2004b;13:501–508. [PubMed] [Google Scholar]
- Bluestein M, Mockros LF. Hemolytic effects of energy dissipation in flowing blood. Med Biol Eng. 1969;7:1–16. doi: 10.1007/BF02474665. [DOI] [PubMed] [Google Scholar]
- Burgreen GW, Antaki JF, Wu ZJ, Holmes AJ. Computational fluid dynamics as a development tool for rotary blood pumps. Artif Organs. 2001;25:336–340. doi: 10.1046/j.1525-1594.2001.025005336.x. [DOI] [PubMed] [Google Scholar]
- Butchart EG, Ionescu A, Payne N, Giddings J, Grunkemeier GL, Fraser AG. A new scoring system to determine thromboembolic risk after heart valve replacement. Circulation. 2003;108(Suppl 1):II68–74. doi: 10.1161/01.cir.0000087383.62522.1e. [DOI] [PubMed] [Google Scholar]
- Butchart EG, Li HH, Payne N, Buchan K, Grunkemeier GL. Twenty years’ experience with the Medtronic Hall valve. J Thorac Cardiovasc Surg. 2001;121:1090–1100. doi: 10.1067/mtc.2001.113754. [DOI] [PubMed] [Google Scholar]
- Cao J, Rittgers SE. Particle motion within in vitro models of stenosed internal carotid and left anterior descending coronary arteries. Ann Biomed Eng. 1998;26:190–199. doi: 10.1114/1.131. [DOI] [PubMed] [Google Scholar]
- Charron M, Follansbee W, Ziady GM, Kormos RL. Assessment of biventricular cardiac function in patients with a Novacor left ventricular assist device. J Heart Lung Transplant. 1994;13:263–267. [PubMed] [Google Scholar]
- Claiborne TE, Girdhar G, Gallocher-Lowe S, Sheriff J, Kato YP, Pinchuk L, Schoephoerster RT, Jesty J, Bluestein D. Thrombogenic potential of Innovia polymer valves versus Carpentier-Edwards Perimount Magna aortic bioprosthetic valves. ASAIO J. 2011;57:26–31. doi: 10.1097/MAT.0b013e3181fcbd86. [DOI] [PubMed] [Google Scholar]
- Dowling RD, Gray LA, Jr., Etoch SW, Laks H, Marelli D, Samuels L, Entwistle J, Couper G, Vlahakes GJ, Frazier OH. Initial experience with the AbioCor implantable replacement heart system. J Thorac Cardiovasc Surg. 2004;127:131–141. doi: 10.1016/j.jtcvs.2003.07.023. [DOI] [PubMed] [Google Scholar]
- Dumont K, Vierendeels J, van Nooten G, Verdonck P, Bluestein D. Comparison of ATS Open Pivot Valve and St Jude Regent Valve using a CFD model based on fluid-structure interaction. J. Biomech. Eng. 2007 Accepted for publication. [Google Scholar]
- Edmunds LH., Jr. Is prosthetic valve thrombogenicity related to design or material? Tex Heart Inst J. 1996;23:24–27. [PMC free article] [PubMed] [Google Scholar]
- Edmunds LH, Jr., McKinlay S, Anderson JM, Callahan TH, Chesebro JH, Geiser EA, Makanani DM, McIntire LV, Meeker WQ, Naughton GK, Panza JA, Schoen FJ, Didisheim P. Directions for improvement of substitute heart valves: National Heart, Lung, and Blood Institute's Working Group report on heart valves. J Biomed Mater Res. 1997;38:263–266. doi: 10.1002/(sici)1097-4636(199723)38:3<263::aid-jbm11>3.0.co;2-c. [DOI] [PubMed] [Google Scholar]
- El-Banayosy A, Korfer R, Arusoglu L, Kizner L, Morshuis M, Milting H, Tenderich G, Fey O, Minami K. Device and patient management in a bridge-to-transplant setting. Ann Thorac Surg. 2001;71:S98–102. doi: 10.1016/s0003-4975(00)02618-7. discussion S114-105. [DOI] [PubMed] [Google Scholar]
- Fallon AM, Shah N, Marzec UM, Warnock JN, Yoganathan AP, Hanson SR. Flow and thrombosis at orifices simulating mechanical heart valve leakage regions. J Biomech Eng. 2006;128:30–39. doi: 10.1115/1.2133768. [DOI] [PubMed] [Google Scholar]
- Feldman T. Percutaneous valve repair and replacement: challenges encountered, challenges met, challenges ahead. Circulation. 2006;113:771–773. doi: 10.1161/CIRCULATIONAHA.105.605600. [DOI] [PubMed] [Google Scholar]
- Folie BJ, McIntire LV. Mathematical analysis of mural thrombogenesis. Concentration profiles of platelet-activating agents and effects of viscous shear flow. Biophys J. 1989;56:1121–1141. doi: 10.1016/S0006-3495(89)82760-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frazier OH, Dowling RD, Gray LA, Jr., Shah NA, Pool T, Gregoric I. The total artificial heart: where we stand. Cardiology. 2004;101:117–121. doi: 10.1159/000075992. [DOI] [PubMed] [Google Scholar]
- Garon A, Farinas M-I. Fast Three-dimensional Numerical Hemolysis Approximation. Artificial Organs. 2004;28:1016–1025. doi: 10.1111/j.1525-1594.2004.00026.x. [DOI] [PubMed] [Google Scholar]
- Geisen U, Heilmann C, Beyersdorf F, Benk C, Berchtold-Herz M, Schlensak C, Budde U, Zieger B. Non-surgical bleeding in patients with ventricular assist devices could be explained by acquired von Willebrand disease. European Journal of Cardio-Thoracic Surgery. 2008;33:679–684. doi: 10.1016/j.ejcts.2007.12.047. [DOI] [PubMed] [Google Scholar]
- Girdhar G, Bluestein D. Biological effects of dynamic shear stress in cardiovascular pathologies and devices. Expert Rev Med Devices. 2008;5:167–181. doi: 10.1586/17434440.5.2.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girdhar G, Xenos M, Alemu Y, Chiu WC, Lynch BE, Jesty J, Einav S, Slepian MJ, Bluestein D. Device thrombogenicity emulation: a novel method for optimizing mechanical circulatory support device thromboresistance. PLoS One. 2012;7:e32463. doi: 10.1371/journal.pone.0032463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosman AD, Ioannides E. Aspects of computer simulation of liquid-fuelled combustors. AIAA J Energy. 1983;7:482–490. [Google Scholar]
- Goubergrits L, Affeld K. Numerical estimation of blood damage in artificial organs. Artif Organs. 2004;28:499–507. doi: 10.1111/j.1525-1594.2004.07265.x. [DOI] [PubMed] [Google Scholar]
- Grigioni M, Daniele C, D'Avenio G, Barbaro V. The influence of the leaflets’ curvature on the flow field in two bileaflet prosthetic heart valves. J Biomech. 2001;34:613–621. doi: 10.1016/s0021-9290(00)00240-2. [DOI] [PubMed] [Google Scholar]
- Grosset DG, Georgiadis D, Kelman AW, Cowburn P, Stirling S, Lees KR, Faichney A, Mallinson A, Quin R, Bone I, Pettigrew L, Brodie E, MacKay T, Wheatley DJ. Detection of microemboli by transcranial Doppler ultrasound. Tex Heart Inst J. 1996;23:289–292. [PMC free article] [PubMed] [Google Scholar]
- Harker LA, Slichter SJ. Studies of platelet and fibrinogen kinetics in patients with prosthetic heart valves. N Engl J Med. 1970;283:1302–1305. doi: 10.1056/NEJM197012102832402. [DOI] [PubMed] [Google Scholar]
- Hellums J, Peterson D, Stathopoulos N, Moake J, Giorgio T. Studies on the mechanisms of shear-induced platelet activation. In: Hartman A, Kuschinsky W, editors. Cerebral ischemia and hemorhelogy. Springer and Verlag; New York: 1987. [Google Scholar]
- Hellums JD. 1993 Whitaker Lecture: biorheology in thrombosis research. Ann Biomed Eng. 1994;22:445–455. doi: 10.1007/BF02367081. [DOI] [PubMed] [Google Scholar]
- Huang ZJ, Merkle CL, Abdallah S, Tarbell JM. Numerical simulation of unsteady laminar flow through a tilting disk heart valve: prediction of vortex shedding. J Biomech. 1994;27:391–402. doi: 10.1016/0021-9290(94)90015-9. [DOI] [PubMed] [Google Scholar]
- Jesty J, Bluestein D. Acetylated prothrombin as a substrate in the measurement of the procoagulant activity of platelets: elimination of the feedback activation of platelets by thrombin. Anal Biochem. 1999;272:64–70. doi: 10.1006/abio.1999.4148. [DOI] [PubMed] [Google Scholar]
- Jesty J, Yin W, Perrotta P, Bluestein D. Platelet activation in a circulating flow loop: combined effects of shear stress and exposure time. Platelets. 2003;14:143–149. doi: 10.1080/0953710031000092839. [DOI] [PubMed] [Google Scholar]
- Jin W, Clark C. Experimental investigation of unsteady flow behaviour within a sac-type ventricular assist device (VAD). J Biomech. 1993;26:697–707. doi: 10.1016/0021-9290(93)90033-b. [DOI] [PubMed] [Google Scholar]
- Kelly SG, Verdonck PR, Vierendeels JA, Riemslagh K, Dick E, Van Nooten GG. A three-dimensional analysis of flow in the pivot regions of an ATS bileaflet valve. Int J Artif Organs. 1999;22:754–763. [PubMed] [Google Scholar]
- King MJ, David T, Fisher J. Three-dimensional study of the effect of two leaflet opening angles on the time-dependent flow through a bileaflet mechanical heart valve. Med Eng Phys. 1997;19:235–241. doi: 10.1016/s1350-4533(96)00066-5. [DOI] [PubMed] [Google Scholar]
- Krafczyk M, Cerrolaza M, Schulz M, Rank E. Analysis of 3D transient blood flow passing through an artificial aortic valve by Lattice-Boltzmann methods. J Biomech. 1998;31:453–462. doi: 10.1016/s0021-9290(98)00036-0. [DOI] [PubMed] [Google Scholar]
- Kuharsky AL, Fogelson AL. Surface-mediated control of blood coagulation: the role of binding site densities and platelet deposition. Biophys J. 2001;80:1050–1074. doi: 10.1016/S0006-3495(01)76085-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laas J, Kseibi S, Perthel M, Klingbeil A, El-Ayoubi L, Alken A. Impact of high intensity transient signals on the choice of mechanical aortic valve substitutes. Eur J Cardiothorac Surg. 2003;23:93–96. doi: 10.1016/s1010-7940(02)00677-2. [DOI] [PubMed] [Google Scholar]
- Lazar RM, Shapiro PA, Jaski BE, Parides MK, Bourge RC, Watson JT, Damme L, Dembitsky W, Hosenpud JD, Gupta L, Tierney A, Kraus T, Naka Y. Neurological events during long-term mechanical circulatory support for heart failure: the Randomized Evaluation of Mechanical Assistance for the Treatment of Congestive Heart Failure (REMATCH) experience. Circulation. 2004;109:2423–2427. doi: 10.1161/01.CIR.0000129414.95137.CD. [DOI] [PubMed] [Google Scholar]
- Mesana T. Percutaneous valve technology: an historical opportunity for cardiac surgeons. Curr Opin Cardiol. 2006;21:94. [Google Scholar]
- O'Brien JR, Salmon GP. An independent haemostatic mechanism: shear induced platelet aggregation. Adv Exp Med Biol. 1990;281:287–296. doi: 10.1007/978-1-4615-3806-6_30. [DOI] [PubMed] [Google Scholar]
- Paul R, Marseille O, Hintze E, Huber L, Schima H, Reul H, Rau G. In vitro thrombogenicity testing of artificial organs. Int J Artif Organs. 1998;21:548–552. [PubMed] [Google Scholar]
- Portner PM, Jansen PG, Oyer PE, Wheeldon DR, Ramasamy N. Improved outcomes with an implantable left ventricular assist system: a multicenter study. Ann Thorac Surg. 2001;71:205–209. doi: 10.1016/s0003-4975(00)02514-5. [DOI] [PubMed] [Google Scholar]
- Reif TH, Schulte TJ, Hwang NH. Estimation of the rotational undamped natural frequency of bileaflet cardiac valve prostheses. J Biomech Eng. 1990;112:327–332. doi: 10.1115/1.2891192. [DOI] [PubMed] [Google Scholar]
- Reininger CB, Lasser R, Rumitz M, Boger C, Schweiberer L. Computational analysis of platelet adhesion and aggregation under stagnation point flow conditions. Comput Biol Med. 1999;29:1–18. doi: 10.1016/s0010-4825(98)00039-0. [DOI] [PubMed] [Google Scholar]
- Rothenburger M, Wilhelm MJ, Hammel D, Schmidt C, Tjan TD, Bocker D, Scheld HH, Schmid C. Treatment of thrombus formation associated with the MicroMed DeBakey VAD using recombinant tissue plasminogen activator. Circulation. 2002;106:I189–192. [PubMed] [Google Scholar]
- Samuels LE, Holmes EC, Entwistle JC., 3rd Swan-Ganz monitoring of the AbioCor artificial heart. Ann Thorac Surg. 2005;80:1133. doi: 10.1016/j.athoracsur.2003.10.044. [DOI] [PubMed] [Google Scholar]
- Slaughter MS, Rogers JG, Milano CA, Russell SD, Conte JV, Feldman D, Sun B, Tatooles AJ, Delgado RM, 3rd, Long JW, Wozniak TC, Ghumman W, Farrar DJ, Frazier OH. Advanced heart failure treated with continuous-flow left ventricular assist device. N Engl J Med. 2009;361:2241–2251. doi: 10.1056/NEJMoa0909938. [DOI] [PubMed] [Google Scholar]
- Sorensen EN, Burgreen GW, Wagner WR, Antaki JF. Computational simulation of platelet deposition and activation: I. Model development and properties. Ann Biomed Eng. 1999a;27:436–448. doi: 10.1114/1.200. [DOI] [PubMed] [Google Scholar]
- Sorensen EN, Burgreen GW, Wagner WR, Antaki JF. Computational simulation of platelet deposition and activation: II. Results for Poiseuille flow over collagen. Ann Biomed Eng. 1999b;27:449–458. doi: 10.1114/1.201. [DOI] [PubMed] [Google Scholar]
- Stevenson LW ML, Desvigne-Nickens P, et al. Left ventricular assist device as destination for patients undergoing intravenous inotropic therapy: A subset analysis from REMATCH (Randomized Evaluation of Mechanical Assistance in Treatment of Chronic Heart Failure). Circulation. 2004;110:975–981. doi: 10.1161/01.CIR.0000139862.48167.23. [DOI] [PubMed] [Google Scholar]
- Travis BR, Leo HL, Shah PA, Frakes DH, Yoganathan AP. An analysis of turbulent shear stresses in leakage flow through a bileaflet mechanical prostheses. J Biomech Eng. 2002;124:155–165. doi: 10.1115/1.1448519. [DOI] [PubMed] [Google Scholar]
- Travis BR, Marzec UM, Leo HL, Momin T, Sanders C, Hanson SR, Yoganathan AP. Bileaflet aortic valve prosthesis pivot geometry influences platelet secretion and anionic phospholipid exposure. Ann Biomed Eng. 2001;29:657–664. doi: 10.1114/1.1385808. [DOI] [PubMed] [Google Scholar]
- Wilcox DC. Simulation of transition with a two-equation turbulence model. AIAA J. 1994;32:247–255. [Google Scholar]
- Wilhelm MJ, Hammel D, Schmid C, Stypmann J, Asfour B, Kemper D, Schmidt C, Morley D, Noon GP, Debakey ME, Scheld HH. Clinical experience with nine patients supported by the continuous flow Debakey VAD. J Heart Lung Transplant. 2001;20:201. doi: 10.1016/s1053-2498(00)00427-7. [DOI] [PubMed] [Google Scholar]
- Worth Longest P, Kleinstreuer C. Comparison of blood particle deposition models for non-parallel flow domains. J Biomech. 2003;36:421–430. doi: 10.1016/s0021-9290(02)00434-7. [DOI] [PubMed] [Google Scholar]
- Wurzinger LJ, Blasberg P, Schmid-Schonbein H. Towards a concept of thrombosis in accelerated flow: rheology, fluid dynamics, and biochemistry. Biorheology. 1985;22:437–450. doi: 10.3233/bir-1985-22507. [DOI] [PubMed] [Google Scholar]
- Xenos M, Girdhar G, Alemu Y, Jesty J, Slepian M, Einav S, Bluestein D. Device Thrombogenicity Emulator (DTE) - Design optimization methodology for cardiovascular devices: A study in two bileaflet MHV designs. J Biomech. 2010 doi: 10.1016/j.jbiomech.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yared A, Bluestein D. Flow induced platelet activation and damage accumulation in a mechanical heart valve – numerical studies. Artificial Organs. 2006 doi: 10.1111/j.1525-1594.2007.00446.x. Accepted for publication. [DOI] [PubMed] [Google Scholar]
- Yin W, Alemu Y, Affeld K, Jesty J, Bluestein D. Flow-induced platelet activation in bileaflet and monoleaflet mechanical heart valves. Ann Biomed Eng. 2004;32:1058–1066. doi: 10.1114/b:abme.0000036642.21895.3f. [DOI] [PubMed] [Google Scholar]
- Yin W, Gallocher S, Pinchuk L, Schoephoerster RT, Jesty J, Bluestein D. Flow Induced Platelet Activation in a St. Jude MHV, a Trileaflet Polymeric Heart Valve and a St. Jude Tissue Valve. Artificial Organs. 2005;29:826–831. doi: 10.1111/j.1525-1594.2005.29109.x. [DOI] [PubMed] [Google Scholar]
- Yoganathan AP, Ellis JT, Healy TM, Chatzimavroudis GP. Fluid dynamic studies for the year 2000. J Heart Valve Dis. 1998;7:130–139. [PubMed] [Google Scholar]
- Yoganathan AP, Woo YR, Sung HW. Turbulent shear stress measurements in the vicinity of aortic heart valve prostheses. J Biomech. 1986;19:433–442. doi: 10.1016/0021-9290(86)90020-5. [DOI] [PubMed] [Google Scholar]