Toward patient-specific simulations of cardiac valves: state-of-the-art and future directions

Abstract

Recent computational methods enabling patient-specific simulations of native and prosthetic heart valves are reviewed. Emphasis is placed on two critical components of such methods: 1) anatomically realistic finite element models for simulating the structural dynamics of heart valves; and 2) fluid structure interaction methods for simulating the performance of heart valves in a patient specific beating left ventricle. It is shown that the significant progress achieved in both fronts paves the way toward clinically relevant computational models that can simulate the performance of a range of heart valves, native and prosthetic, in a patient-specific left heart environment. The significant algorithmic and model validation challenges that need to be tackled in the future to realize this goal are also discussed.

1. Introduction

It is estimated that valvular heart disease (VHD) prevalence and incidence are relevant in industrialized countries (Iung and Vahanian, 2011), with associated dramatic socio-economic burden due to the need for surgical treatment and hospitalization, as well as to possible peri- and post-operative complications (Iribarne et al., 2012). A recent study performed in the United States on a population of almost 12,000 patients lead to estimate VHD prevalence in 2.5%, with a progressive increase with patients’ age, up to 13.2% after 75 years of age (Nkomo et al., 2006). Among heart valves, the aortic valve (AV) and the mitral valve (MV), i.e. the outflow and inflow valve of the left ventricle (LV), are the most frequently affected by pathologies requiring surgical intervention, mostly through replacement for the AV and through repair for the MV (Barnett and Ad, 2009; Gammie et al., 2009)

In the last two decades heart valve surgery has been characterized by major improvements, thanks to the advent of increasingly effective surgical repair techniques and advances in prosthetic heart valves. The most recent advance in this regard is represented by the introduction of percutaneous devices, such as transcatheter AV implants (TAVIs) and mitral annuloplasty devices (Feldman et al., 2011; Smith et al., 2011). The increasing sophistication of surgical solutions and the broad range of available heart valve prostheses necessitate the development of quantitative patient-specific computer simulation tools to aid surgical planning through the assessment of pre-operative scenarios and prediction of post-operative and/or post-implantation outcomes. Critical prerequisite for developing such tools, however, is the integration of state-of-the-art clinical imaging with biomechanical computational approaches.

Clinical imaging

In the assessment of valvular morphology, echocardiography is the imaging technique of choice, given its ease of use and comparatively low cost (Pennell et al., 2004). Real-time 3D echocardiography (RT3DE) allows to obtain detailed morphological and functional data on heart valves either non-invasively or with limited invasiveness. Trans-thoracic (TT) and trans-esophageal (TE) RT3DE are extremely valuable in the morphologic analysis of the MV, in the assessment of aortic stenosis and to elucidate the mechanism of aortic regurgitation; in particular, TE-RT3DE is recommended for guidance of interventional mitral valve procedures and of TAVI (Lang et al., 2012). On the other hand, multi-slice computed tomography (MSCT) and cardiac magnetic resonance (CMR) have been shown to provide higher reproducibility than echocardiography in the assessment of the AV annular dimensions (Jabbour et al., 2011). Hence, multimodality imaging is critical for improving the accuracy of AV measurements and reducing the chance for prosthesis sizing errors in patients considered for percutaneous AV procedures (Holmes et al., 2012).

Exploiting the features of these imaging technologies, different algorithms for the 3D image-based visualization of valvular apparatus have been recently proposed to improve the quantitative evaluation of valvular pathologies. Many efforts have focused on the development of algorithms for the automatic detection of MV substructures (Veronesi et al., 2008; Schneider et al., 2012), the 3D geometric reconstruction of the entire MV apparatus (Jassar et al., 2011; Vergnat et al., 2011; Voigt et al., 2011), and the dynamic modeling of the aorto-mitral coupling (Ionasec et al., 2009; Veronesi et al., 2009). Furthermore, Grbic and colleagues recently proposed a complete and modular model of the entire heart, comprising the four heart valves, estimating global valvular location and motion using automated learning-based algorithms on 4D CT images (Grbic et al., 2012).

Biomechanics and hemodynamics models

These models utilize a wide range of numerical methodologies to solve the equations of continuum mechanics in order to represent at some level the coupled interaction of blood flow with tissues and implanted devices. Depending on their degree of sophistication and anatomic realism, such models could yield the spatial and temporal variability of a range of clinically relevant quantities, such as wall shear stress, regions of blood stasis or turbulence, mechanical stresses in the tissues, etc. These models may be categorized in three broad classes:

1. mass-spring models (MSMs) describe a continuous structure as a cloud of discrete masses connected by a network of springs to compute the response of the structure to mechanical stimuli;

2. structural finite element models (FEMs) compute tissue field variables, e.g. stresses and strains, typically assuming that the effect of the surrounding blood can be simplistically described through prescribed pressures;

3. 3D fully-coupled fluid structure interaction (FSI) models explicitly account for the coupling between valves and surrounding blood flow, thus overcoming the inherent limitation of FEMs.

MSMs are widely adopted in computer graphics to achieve visual realism when representing moving deformable objects. With regard to biomedical applications, MSMs are used to build augmented reality systems for surgical training and to support surgical planning, thanks to their capability to provide real-time simulations. Examples include application of MSMs to laparoscopic procedures and breast surgery, where they allow for realistic and relatively simple simulation of tissue resection. MSMs have been applied to heart valve modeling only very recently by few researchers (Hammer et al., 2011a; Hammer et al., 2011b; Hammer et al., 2012). Despite the considerable potential of MSMs as real-time patient-specific simulation tools, their application to heart valve biomechanics is still in the embryonic stages.

On the contrary, FEM and FSI models have been increasingly adopted in the last two decades to study AV and MV biomechanics both for native and prosthetic valves (Figure 1). The former models are computationally more efficient as they can handle the complexity of anatomic geometries by decoupling the fluid and structural domains. For that FEMs have been able to tackle and provide powerful insights into clinically relevant patient-specific situations (Stevanella et al., 2011b; Mansi et al., 2012; Xu et al., 2012). 3D FSI models are computationally expensive and for that their application has, for the most part, been restricted to study native and prosthetic valves placed in simplified domains, e.g. straight axisymmetric aortic lumens (Griffith, 2012). More recently, attempts to investigate the coupled interaction of valves with the complex hemodynamic environment of the left ventricle in anatomic, patient-specific domains have also began to emerge (Le and Sotiropoulos, 2012a). With the advent of massively parallel computational platforms and continuous algorithmic advances (Taylor and Figueroa, 2009; Sotiropoulos, 2012), 3D FSI simulations of heart valves in patient-specific left heart anatomies are now well within reach. The clinical relevance of such models can be augmented by incorporating advances in clinical imaging and image processing to enable the detailed morphological description of heart valves. A fully patient-specific model should also include patient-specific tissue mechanical properties, which are not measurable in vivo. However, while these may change notably between healthy and pathological conditions, and between different pathological states (e.g. functional mitral regurgitation vs. myxomatous disease), within a well-defined clinical scenario inter-subject variations in mechanical properties may not be as relevant as those in morphological features of the valve and of its environment.

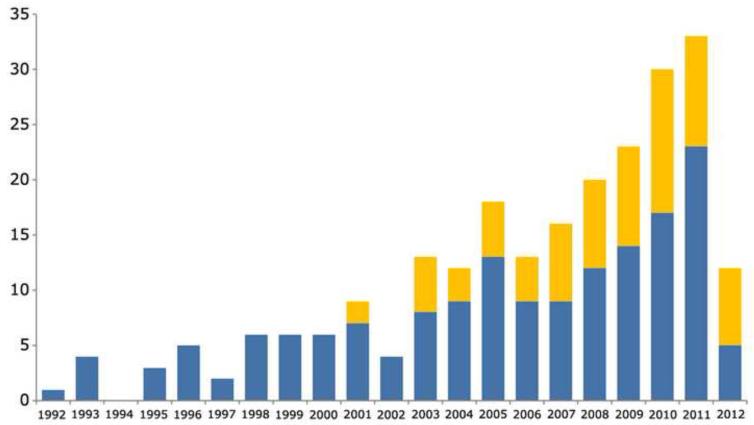
Figure 1.

Number of peer reviewed scientific manuscripts published per year, on the numerical modeling of native AV and MV biomechanics (blue), and on the fluid structure interaction modeling of prosthetic heart valves (orange). Source: Thomson Reuters ISI Web of Knowledge, updated July 2012.

In this review paper we seek to: provide a critical review of recent progress in image-based patient-specific FEM and FSI modeling of heart valves; present recent results from the application of these models to study heart valve pathophysiology and function; and discuss challenges and opportunities for developing the next generation of computational tools to aid the planning of heart valve surgery.

2. Previous work on heart valve patient-specific FEM modeling

For a computational model to evolve into a clinically relevant simulation tool it must be able to capture: heart valve morphology, mechanical properties, kinematic constraints and valve-blood interaction. In this section we review the state of the art in all of these four areas in the context of FEM models, which simplify the treatment of blood flow but employ sophisticated models for simulating valve morphology, structural properties and function.

2.1 Modelling valve morphology

The MV is composed of four principal substructures: mitral annulus (MA), anterior and posterior leaflets, chordae tendineae and two papillary muscles (PMs). In systole, their synergic action prevents from blood backflow from the LV to the left atrium: as LV pressure increases forcing leaflets closure, the annulus shrinks and the PMs contract, tightening the chordae tendineae, thus regulating leaflets dynamics and preventing from both leaflet prolapse and lack of coaptation.

The AV consists of three asymmetrical leaflets (right, left, non-coronary); this asymmetry persists in the contiguous structures within the aortic root, i.e. the interleaflet triangles, connecting the AV to the aorto-ventricular junction, the Valsalva sinuses and the proximal ascending aorta. As for the MV, also in the aortic root the interplay between the different substructures is crucial to AV function, i.e. to its wide and rapid opening during systole and closure during diastole.

The key features of the studies tackling patient-specific MV or AV morphological modelling for biomechanical simulations are summarized in Table 1.

Table 1.

Different approaches to heart valve patient-specific morphological reconstruction.

Study	Valve	LV	Data Source	Automation	Patient-Specific Features	Time-dependent boundaries
Votta 2008	MV	X	TT- RT3DE	Semi- automated	Leaflets extent and inclination MA profile PMs tips position	MA displacement
Wenk 2010	MV	√	CMR	Manual	Leaflets surface MA profile LV+PMs	MA + PMs motion from LV deformation
Stevanella 2011	MV	X	CMR	Manual	Leaflets extent and inclination MA profile PMs tips position	MA + PMs displacement
Mansi 2012	MV	X	TE- RT3DE	Fully automated	Leaflets surface+thickness MA profile PMs tips position	MA + PMs displacement
Xu 2012	MV	X	TE- RT3DE	Manual	Leaflets surface MA profile PMs tips position	Fixed boundaries
Pouch 2012	MV	X	TE- RT3DE	Semi- automated	Leaflets surface+thickness MA profile PMs tips position	Fixed boundaries
Wang 2012	MV	X	MSCT	Manual	Leaflets surface+thickness MA profile PMs tips position Chordal insertions	MA + PMs displacement
Sirois 2011	AV	X	MSCT	Manual	Ascending aorta Valsalva sinuses Coronary ostia	Fixed boundaries
Wang 2012	AV	√	MSCT	Semi- automated	LV + Ascending aorta Valsalva sinuses Coronary ostia	Fixed boundaries
Capelli 2012	AV	X	MSCT	Manual	Ascending aorta Valsalva sinuses Coronary ostia	Fixed boundaries

AV=aortic valve; MV=mitral valve; LV=left ventricle; MA=mitral annulus; PMs= papillary muscles; TT-RT3DE/TE-RT3DE = trans-thoracic/trans-esophageal real time 3D echocardiography; CMR=cardiac magnetic resonance; MSCT = multi-slice computed tomography.

MV studies differ by type of clinical imaging, i.e. ultrasound imaging (Votta et al., 2008; Xu et al., 2010; Mansi et al., 2012; Pouch et al., 2012), CMR (Wenk et al., 2010; Stevanella et al., 2011b) or MSCT (Wang and Sun, 2012), level of automation, and completeness of the morphological reconstruction. Regarding automation, the gold standard is likely represented by the works of (Pouch et al., 2012) and (Mansi et al., 2012), in which the detailed 3D description of the MA profile, PM tips position and leaflets configuration is obtained from RT3DE; however, while the latter used machine-learning algorithms to fully automate MV detection, the former required the manual initialization of the MA, but allowed to capture leaflet thickness distribution, which strongly affects the stress pattern on the leaflets. With regard to the completeness of MV reconstruction, the use of MSCT (Wang and Sun, 2012) made it possible for the first time to also account for the patient-specific description of the distribution of chordal origins on the PM tips and their insertions into the leaflets. On the other hand, only (Wenk et al., 2010), through the manual segmentation of a series of orthogonal short-axis and long-axis cine-CMR sequences, accounted for the patient-specific LV wall and thus described not only the position of PM tips but also the bulk of PMs.

Of note, the referenced AV models are not aimed at simulating the function of the native AV, but at analysing the deployment of TAVIs (Sirois et al., 2011; Capelli et al., 2012; Wang et al., 2012). MSCT scans are typically adopted to reconstruct aortic leaflets and root structures, thanks to their very high spatial resolution, using commercial image processing software allowing automated 3D reconstruction (Capelli et al., 2012; Wang et al., 2012) or custom-made software for manual segmentation (Sirois et al., 2011).

2.2 Modelling mechanical properties of tissues

Heart valve tissues are soft and hydrated with a composite and regionally-varying microstructure. As a result, when tested ex vivo they undergo large strains and show a heterogeneous, incompressible, non-linear and anisotropic mechanical behaviour. Up to now, patient-specific material properties of the heart valves have never been directly measured in vivo. In vivo properties were indirectly assessed only for the anterior mitral leaflet (AML) and only on ovine models; through inverse finite element modelling, (Krishnamurthy et al., 2009; Krishnamurthy et al., 2010) identified AML in vivo regional and time-dependent mechanical properties by fitting the time-varying position of radiopaque markers previously sewn on the AML and acquired via biplane fluoroscopy. They found the AML to have an almost linear and anisotropic response, with the elastic modulus in the two principal directions of the AML one order of magnitude higher than those measured ex vivo, and they showed that these features are due to the presence of active contractile elements in the AML tissue (Swanson et al., 2011). Based on those same data, (Kvitting et al., 2010) found that throughout the entire cardiac cycle the AML exhibits a complex pattern of 3D curvature, which was postulated to be related to the contractile properties of the AML.

Despite these recent findings, whose implications may be extended to humans, current MV patient-specific models account for material properties based on ex vivo mechanical tests performed on porcine (May-Newman and Yin, 1995) and human (Wang and Sun, 2012) MV leaflets, and porcine chordae (Kunzelman and Cochran, 1990). Based on these data, MV leaflet response was typically modelled using either linear orthotropic elastic or transversely isotropic hyperelastic properties, while recently (Wang and Sun, 2012) applied a more sophisticated constitutive model accounting for dispersed embedded fibre families (Gasser et al., 2006). Chordae tendineae were assumed linear elastic or isotropic hyperelastic (Table 2).

Table 2.

Material models used to describe heart valve mechanical response.

Study	Valve	Leaflets	Chordae	Valsalva sinuses / Ascending aorta	LV
Votta 2008	MV	Hyperelastic Transversely Isotropic	Hyperelastic isotropic	-	-
Wenk 2010	MV	Hyperelastic Transversely Isotropic	Hyperelastic isotropic	-	Hyperelastic Transversely Isotropic (passive+active)
Stevanella 2011	MV	Hyperelastic Transversely Isotropic	Hyperelastic isotropic	-	-
Mansi 2012	MV	Orthotropic Linear Elastic	Piece-wise linear elastic	-	-
Xu 2012	MV	Orthotropic Linear Elastic	Linear elastic	-	-
Pouch 2012	MV	Orthotropic Linear Elastic	Linear elastic	-	-
Wang 2012	MV	Hyperelastic Anisotropic	Hyperelastic isotropic	-	-
Sirois 2011	AV	Hyperelastic Anisotropic	-	Hyperelastic Anisotropic	-
Wang 2012	AV	Hyperelastic Anisotropic with distributed fibers	-	Hyperelastic Anisotropic with distributed fibers	Hyperelastic Anisotropic with distributed fibers
Capelli 2012	AV	Hyperelastic Isotropic	-	Hyperelastic Isotropic	-

Regarding the aortic root mechanical response, (Capelli et al., 2012) used a Mooney-Rivlin constitutive model, including aortic residual stresses, to replicate the behaviour of excised human dilated ascending aortic tissue (Okamoto et al., 2002), while (Sirois et al., 2011; Wang et al., 2012) used more complex strain-energy functions capturing tissue anisotropy, based on ex vivo data from human samples (Martin et al., 2011). LV passive response was modeled as non-linear anisotropic and (Wenk et al., 2010) accounted also for its active contraction through the constitutive model proposed by (Guccione et al., 1993).

2.3 Modelling of kinematic constraints

As previously mentioned, MV and AV annular dimensions and shape vary dynamically during the cardiac cycle, and simultaneously PMs change their position by contracting and relaxing, thus regulating chordal tension and MV leaflet motion. Patient-specific MA motion was first included in a biomechanical model by (Votta et al., 2008), who used an automated tracking algorithm based on optical flow and region-based matching techniques, starting from the manual initialization provided at end-diastole. However, PMs motion was not captured due to echocardiographic window limitations, and their time-dependent displacements were assumed from a geometrical criterion. This limitation was overcome by frame-by-frame manual identification of MA and PMs on CMR long-axis cut-planes (Stevanella et al., 2011b) or MSCT scans (Wang and Sun, 2012), and by automatic MA and PMs detection and tracking using machine-learning algorithms on TE-RT3DE images (Mansi et al., 2012); in these models, MA and PMs motion was imposed through kinematic boundary conditions, i.e. time-dependent nodal displacements. Differently, in (Wenk et al., 2010) the whole LV was modelled, and MA and PMs motion resulted from the LV wall response to the intracavitary pressure. The other MV models neglected MA and PMs dynamics. Similarly, the three AV models did not account for the dynamic changes of the aortic root boundaries (Table 1).

2.4 Accounting for valve-blood interaction

AV and MV transient opening and closure are mainly driven by the trans-valvular pressure drop; for this reason, in structural FEMs the effect of blood is modelled by applying pressure loads on valvular leaflets. In MV models, a measured (Wenk et al., 2010) or standard time-dependent transvalvular pressure is applied to the ventricular side of the leaflets. In AV models focused on TAVI deployment, native leaflets are not (Capelli et al., 2012; Wang et al., 2012) or barely loaded (Sirois et al., 2011), while the prosthetic valve is expanded either through controlled radial displacements (Wang et al., 2012) or pressure-driven inflation of a balloon (Capelli et al., 2012).

In general, heart valve function can be realistically captured through the mentioned approaches, but the local features of blood flow field can play a non-negligible role in specific applications (Lau et al., 2010). These include the analysis of LV filling through the MV and of aortic fluid dynamics associated with AV pathologies (e.g. bicuspid AV).

1. Previous work on 3D FSI numerical models

Patient-specific FSI modeling of heart valves requires coupling models that have the morphological and physiologic sophistication of the previous described FEMs with state-of-the-art computational fluid dynamic models (Sotiropoulos and Borazjani, 2009). Computational methods for FSI simulations can be divided into two broad categories: boundary-conforming methods and non-boundary conforming methods.

The most common boundary-conforming method is the so-called Arbitrary-Lagrangian-Eulerian (ALE) formulation, in which the computational mesh is deformed dynamically to always conform to the boundaries of the computational domain, say the leaflets of the AV. ALE methods can be used both with structured and unstructured grids but their usefulness is limited to problems with relatively simple geometries and moderate deformations. ALE methods have been applied to simulate, among others, FSI between blood flow through a compliant aorta (Fernandez and Moubachir, 2005) and through a mechanical bileaflet AV (Cheng et al., 2004).

Non-boundary conforming methods eliminate the need for the grid to conform to moving boundaries and as such are inherently applicable to cardiovascular flow problems. In such methods the fluid domain is discretized with a structured mesh while the solid surfaces are discretized with a set of Lagrangian grid nodes, which are used to track the motion of the solid within the fluid domain. The effect of the moving immersed body on the fluid is accounted for by adding, either explicitly or implicitly, body forces to the governing equations of motion. Depending on how they handle the fluid/solid interface, non-boundary conforming methods can be broadly classified as diffused-interface and sharp-interface methods.

In the first category belongs Peskin’s classical immersed boundary (IB) method (Peskin, 1972) in which the forces acting at the fluid/solid interface are distributed by a discrete delta-function and as a result the interface is no longer sharp but effectively diffused across few grid nodes. The original IB method is only first order accurate (Peskin, 1972) but a variant of the method that is formally second-order accurate and combines adaptive mesh refinement to increase resolution in the vicinity of immersed boundaries has also been proposed (Griffith et al., 2007). The method has been applied to simulate flow in the human heart (Peskin and Mcqueen, 1989) and more recently through aortic valves (Griffith, 2012). Another method in this category is the fictitious domain method (Glowinski et al., 1999), which has been extensively applied to heart valve simulations. The main difference between this approach and Peskin’s classical IB method is that it couples the solid/fluid interface together through a Lagrange multiplier (or local body force) (van Loon et al., 2006). The fictitious domain method had been applied to simulate flow in a 2D model of the native valve (De Hart et al., 2000) as well as in a 3D trileaflet heart valve at relatively low, non-physiological Reynolds number (peak systole Re=900) with symmetry assumption (De Hart et al., 2003a; De Hart et al., 2003b; De Hart et al., 2004). A major limitation of diffused interface methods is the computational cost associated with carrying out simulations at physiologic Reynolds numbers due to the large numbers of grid nodes required to accurately resolve the wall shear stress on diffused immersed boundaries (van Loon et al., 2006). For that reason such methods are more recently used in conjunction with local mesh refinement (Griffith et al., 2007).

To remedy the difficulties inherent with diffused interface methods, a class of sharp-interface immersed boundary methods has been developed which treat the immersed boundary as a sharp interface and account for its effect on the fluid with different ways. In the so-called cut-cell methods (Udaykumar et al., 1999) the shape of grid cells in the vicinity of the boundary is modified to produce a locally boundary-fitted mesh. Because of this feature, cut-cell methods are cumbersome to implement in 3D complex cardiovascular flows and for the most part their applicability has been restricted thus far to two-dimensional FSI problems, including 2D aortic valves (see (Vigmostad et al., 2010) for a recent review). An alternative sharp-interface formulation readily applicable to arbitrarily complex flow domains is the curvilinear immersed boundary (CURVIB) developed by Sotiropoulos and co-workers. The CURVIB method is a hybrid formulation, integrating structured curvilinear boundary fitted grids with the sharp-interface IB methodology of (Gilmanov and Sotiropoulos, 2005) — for example, the empty aorta is discretized with a boundary-conforming curvilinear mesh and the valve leaflets are treated as sharp, immersed boundaries within the background curvilinear mesh. In the same class of methods belong the unstructured IB methods developed by (Lohner et al., 2008) and (Appanaboyina et al., 2008), which instead of a structured, curvilinear background mesh employ an unstructured background grid with a sharp-interface IB approach to handle complex immersed boundaries. Such methods are inherently suited to be used for patient-specific FSI simulations of heart valves and other medical devices, such ventricular assist devices, different stents designs. The CURVIB method has been extensively applied to carry out the first pulsatile, physiologic flow simulations through bileaflet and trileaflet AVs at high numerical resolution (see (Sotiropoulos and Borazjani, 2009) for recent reviews). (Dasi et al., 2007), (Ge and Sotiropoulos, 2007) reported simulations for a bileaflet mechanical AV (BMAV) in a straight aorta and with leaflet motion prescribed from experimental measurements. (Borazjani et al., 2008) and (Borazjani et al., 2010) reported the first FSI simulations for a BMAV in a straight and a patient-specific anatomic aorta. (Ge and Sotiropoulos, 2010) applied the CURVIB method to simulate physiologic, pulsatile flow through a trileaflet AV with prescribed leaflet motion to explore the links between wall shear stress patterns and AV calcification.

A major issue in heart valve FSI simulations is the approach adopted to couple the fluid and structural domains. The most common and practical approach is to partition the system into two separate fluid and structure domains (Felippa et al., 2001; Nicosia et al., 2003; Ranga et al., 2006) and their interaction is accounted for through boundary conditions at the fluid-structure interface (Felippa et al., 2001; Borazjani et al., 2008). Depending on how these boundary conditions are applied (implicit vs. explicit) two types of coupling, loose and strong coupling (referred to as LC-FSI and SC-FSI, respectively) are possible. In LC-FSI algorithms the structural domain is updated once at each time step using the forces obtained from fluid calculation in the previous time step, which makes LC-FSI algorithms computationally expedient. Since the pressure gradient across the valve is large during the opening phase, the sensitivity of leaflet response to the flow fluctuation largely depends on its inertia. As the specific weight ratio between the leaflet material and blood approaches unity, the inertia of the leaflet is relatively low. Thus LC-FSI algorithms cannot predict correctly the leaflet displacement, leading to numerical instability (Borazjani et al., 2008). On the contrary, SC-FSI algorithms iterate in pseudo-time within each physical time step until both the fluid and structural equations converge to the next time step. Such methods are in general more robust and stable at the cost of higher computational time. They too may exhibit, however, numerical instabilities for problems with low mass ratio and could require special stabilization measures such as non-linear under-relaxation (Borazjani et al., 2008). Coarse grid SC-FSI simulations of mechanical heart valves have been reported, among others, by (Dumont et al., 2007) while high-resolution simulations have been reported by (Borazjani et al., 2008) and (De Tullio et al., 2009). (Vierendeels et al., 2008) used the SC-FSI method to simulate a 2D tissue valve and (De Hart et al., 2003b) used the LC-FSI method to simulate a 3D tissue valve with the symmetry assumption. Finally, we should note that a major challenge in tri-leaflet heart valve FSI simulations is the arbitrary coaptation between the leaflets of the valve during the closing phase. Most previous FSI methods have circumvented this problem by not allowing the valve to fully close. The first attempt to carry out 3D FSI for an AV with leaflet coaptation was reported recently by (Marom et al., 2012), who coupled a FEM commercial code with a commercial flow solver. Multi scale approach is also coupled with FSI approach to further investigate the effect of hemodynamics on the leaflet deformation at the cellular level (Weinberg and Kaazempur Mofrad, 2007).

4. New approaches and recent advances

In this section we present recent advances that pave the way toward fully realistic simulations of heart valves in patient-specific left heart models. We start by presenting recent advances in FEM modeling of the mitral valve followed by advances in FSI simulation of a BMAV driven by a beating, anatomic LV.

4.1 Patient specific structural analysis of healthy and prolapsed MVs

The modeling approach developed and initially tested few years ago (Votta et al., 2008) was applied to derive MV patient-specific models from TT-RT3DE in two small cohorts: five healthy volunteers (HMVs) and five patients affected by MV prolapse undergoing early surgery (PMVs). Analyses were aimed at testing the approach capability to discriminate between healthy and prolapsed MVs, as well as to capture the location and severity of the prolapse.

TT-RT3DE imaging was performed on all subjects. For PMVs only, intra-operative TE-RT3DE images were acquired; volumetric datasets were analyzed off-line using the MVQ software, part of the Q-Lab suite (Philips Medical Systems).

As in (Votta et al., 2008), TT-RT3DE data were processed to obtain patient-specific information on MV morphology at end-diastole (ED), when MV leaflets were assumed stress-free. Information consisted in: extent and orientation of MV leaflets, which were integrated into a general paradigm of free-edge profile (Kunzelman et al., 1994) and regional thickness (Stevanella et al., 2011b), MA profile, and PM tips position. A set of branched chordae was defined consistently with ex vivo findings on their regional distribution (Lam et al., 1970) and geometry (Kunzelman and Cochran, 1990). For PMVs only, specific chordae were eliminated or elongated, based on the clinical examination of TT-RT3DE data.

Through automated tracking (Votta et al., 2008), MA dynamics from ED to peak systole (PS) was obtained. Due to the impossibility to detect the PMs in every frame of interest, their motion was derived from in vivo data obtained in animal models (Dagum et al., 2000).

The mechanical response of all tissues was assumed non-linear elastic. Leaflet anisotropic response was modeled using the strain energy potential proposed by (May-Newman and Yin, 1998). Polynomial strain energy potentials, fitted to literature data (Kunzelman and Cochran, 1990), were used to model chordae tendineae response.

A physiological time-dependent transvalvular pressure drop, up to 120 mmHg, was applied on MV leaflets. MV function from ED to PS was simulated using the commercial numerical solver ABAQUS/Explicit 6.10-1 (SIMULIA, Dassault Systèmes) on a 12-core Intel Xeon (2.93 GHz) workstation.

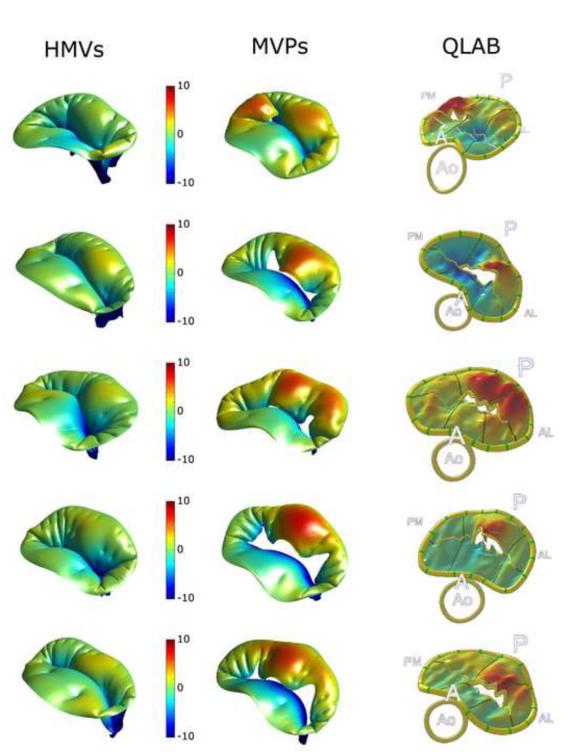
For HMVs, computed MV dynamics and coaptation were consistent with experimental findings: coaptation involved the leaflets rough zone, and was complete for pressures of 16-28 mmHg (Dagum et al., 2000). Still, a non-physiological bulging of the anterior leaflet was obtained in MV closed configuration, and its complex compound in vivo shape (Kvitting et al., 2010) was not reproduced; likely, this was a consequence of neglecting the ED compound shape and the systolic active stiffening of MV leaflets, which both drive their closed configuration (Stevanella et al., 2011a). For PMVs, at PS the local signed distance from the leaflets to the MV orifice was computed and compared to the corresponding ground truth datum obtained from Q-Lab image analyses (Figure 2). At a qualitative analysis, FEM simulations captured with good approximation the position and the extent of the prolapse regions and of the regurgitant areas; in two out of five PMVs, consistency with TT-RT3DE data was achieved after tuning the position of the elongated/ruptured chordae through preliminary simulations. Besides, the sensitivity of computed MV configuration at PS to the definition of chordae tendineae was recently underscored in (Mansi et al., 2012).

Figure 2.

Computed PS configuration for HMVs (left column) and PMVs (central column); color-coded contour maps represent the signed distance (mm) along the axial direction from the insertion on the annulus. For PMVs the comparison with ground truth data reconstructed from TE-RT3DE via Q-Lab is provided (right column).

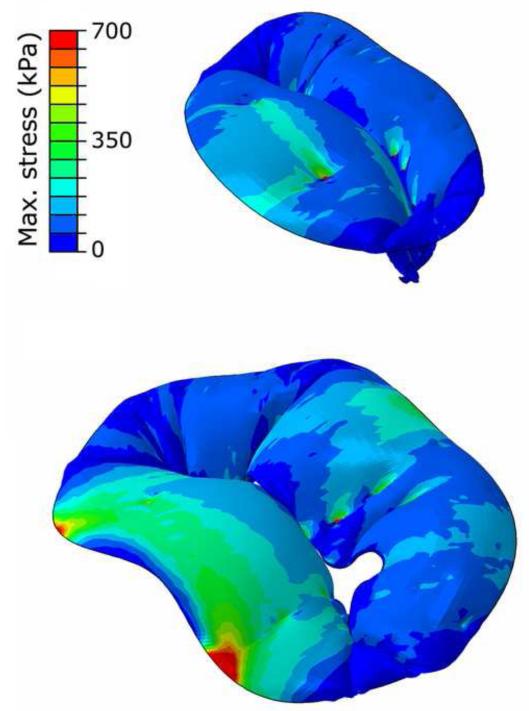
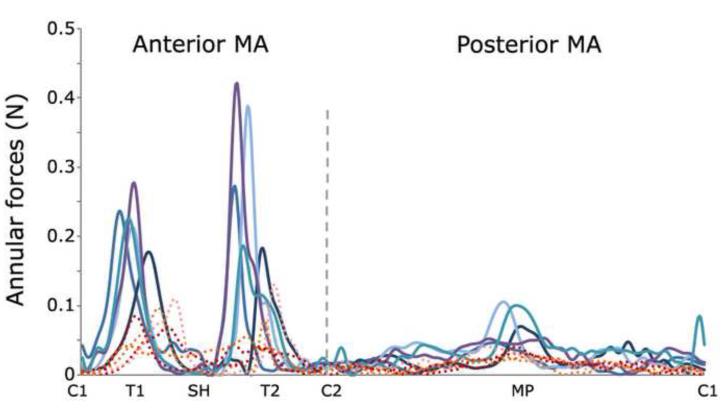
At PS tensions within MV sub-structures were notably different in PMVs and HMVs. In PMVs an abnormal stress increase was always computed in the annular region of the prolapsed cusps, and markedly higher peak stresses were detected next to the fibrous trigones (600-800 kPa vs. 200-350 kPa, Figure 3). MA forces maintained the same spatial distribution in the two cohorts, with extremely low values at the commissures and paracommissures, and peak values at the fibrous trigones. However, in PMVs forces averaged over the anterior and posterior portion of the MA increased with respect to HMVs, from 0.02-0.06 to 0.05-0.08 N and from 0.01-0.02 to 0.02-0.04 N, respectively (Figure 4). A similar increase was observed in PM forces, whose magnitude averaged over the two PMs was 3.47-5.77 N in HMVs, and increased up to 7.38-10.42 N in MVPs. Of note, the percentage increases in leaflets stresses, MA forces and PM forces observed for MVPs are comparable; this result reflects the contiguity of the three sub-structures, which transmit the mechanical loads due to ventricular pressure as in a closed loop.

Figure 3.

Leaflets maximum principal stresses. A representative example is provided for HMVs (top) and PMVs (bottom).

Figure 4.

Local annular forces magnitude. Dashed and continuous lines refer to HMVs and PMVs, respectively. C1, C2=commissures; T1,T2=trigones; SH=saddle horn, MP=posterior mid-point.

The number of subjects considered in the study is relatively small, thus any consideration on the implications of our results should be considered preliminary. Still, results gathered so far suggest that the proposed approach is robust, since it was able to reproduce with good approximation the biomechanics of valves with different dimensions, morphological peculiarities, and pathophisiologic conditions. For PMVs in particular, the main effects of the considered disease on MV systolic function were captured, showing a common pattern of biomechanical alterations, whose knowledge may help in identifying the most suitable surgical option to relieve the valve from excessive stresses. The main limitation on the way towards the application of this approach to surgical planning consists in its computational performance; simulations required about 6 h even on high-performance parallel hardware, and the tuning of the chordal apparatus, when needed, made the simulation process much longer. This limitation may be overcome by adopting less time-consuming but still reliable methods, such as co-rotated FEMs, which, thanks to the linearization of the equations to be solved, allow to simulate MV closure almost in real time (Mansi et al., 2012).

4.2 FSI simulation of a BMAV in patient-specific left ventricle

Previous FSI simulations of heart valves have been carried out in a stand-alone aorta with a prescribed inflow wave form. Recent findings, however, do suggest that the patient-specific flow in the LVOT is greatly affected by the dynamically deforming left ventricle during diastole (Nakamura et al., 2006; Hong et al., 2008). Computational methods for simulating the flow in anatomic LV models reconstructed from imaging modalities have recently been reported but in such models the heart valves have been omitted and their function has been approximated by prescribing appropriate flow wave forms at the MV and/or AV positions (Schenkel et al., 2009; Krittian et al., 2010). In this section, we summarize our recent FSI simulations of a BMAV implanted in an anatomic LVOT and driven by the dynamic motion of a beating LV (Le, 2011; Le and Sotiropoulos, 2012a; Le and Sotiropoulos, 2012b; Le et al., 2012).

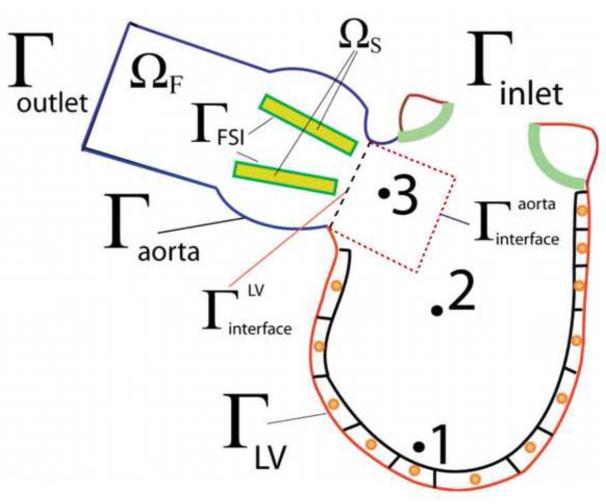
A conceptual sketch of our model is shown in Figure 5. The domain consists of two sub-domains: the LV and the aorta sub-domains, respectively. The numerical method used for the simulations is the FSI-CURVIB method described in detail in (Borazjani et al., 2008) enhanced with an overset Chimera grid approach to facilitate the accurate discretization of the LV/LVOT sub-domains. The LV moves with prescribed motion (see below) and is treated as a sharp interface immersed boundary. The LVOT and aorta are discretized by a curvilinear boundary fitted mesh and aortic wall is assumed to be rigid. The BMAV is treated as an immersed boundary in the aortic lumen and its motion is calculated via the strongly coupled FSI approach of (Borazjani et al., 2008). The details of the overall formulation can be found in (Le, 2011) and (Le and Sotiropoulos, 2012a).

Figure 5.

Schematic of the computational framework and the partition between the fluid and the solid domains. Γ_inlet and Γ_outlet are the inlet and outlet of the computational domain. Γ_aorta is the aortic portion of the domain where the no-slip boundary condition is applied. Γ_FSI is the interface between the BMAV leaflets and the blood flow, which is simulated via FSI. The Γ_LV represents the endocardium surface where the left ventricle beats. Reproduced with permission from Le and Sotiropoulos (2012a).

To simulate the LV motion, we animate an anatomic LV chamber geometry, reconstructed from MRI data of a healthy volunteer, by developing a lumped modeling approach. This approach, which is described in detail in (Le, 2011) and (Le and Sotiropoulos, 2012b), is broadly inspired by cardiac electro-physiology and yields global LV kinematics that are well within the physiological range. The long and short LV axes length of the left ventricle model are L = 80mm and DL = 47mm, respectively. The diameter of the aorta at the LVOT is D = 26.7 mm. No mitral valve is included in the model and thus the mitral orifice is set to be fully open during diastole and fully closed during systole. The effect of the MV is accounted for by imposing a physiologic flow wave form. The heart beat cycle T is chosen to correspond to a heart rate of 52 bpm, T = 1.15s. The simulation time step is Δt = 0.1074 ms and the computational mesh consists of 17.67 million grid nodes. The valve is a St. Jude Regent 23mmm implanted in the LVOT.

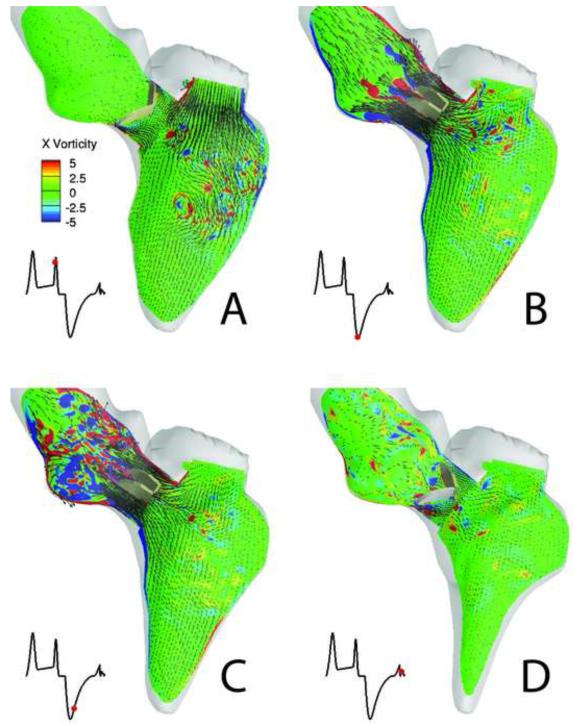
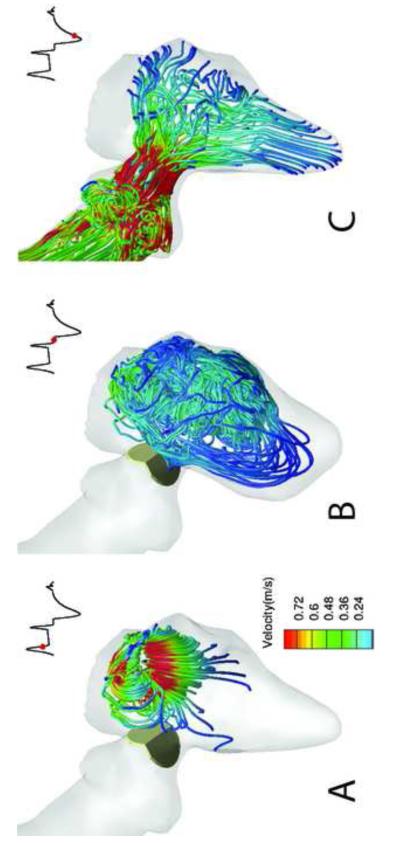
Sample simulated results spanning a time interval from early diastole, prior to valve opening, to late diastole, as the valve begins to close, are plotted In Figure 6. During early diastole (Figure 6a), the LV flow is dominated by small scale vortical structures following the breakdown of the E- and A-wave mitral vortex rings during systole (see (Le, 2011; Le and Sotiropoulos, 2012b; Le et al., 2012) for more details). The large scale flow direction in the LV rotates in the clockwise direction, guiding the blood flow into the LVOT as shown in Figure 6a. The systolic phase starts with the contraction of the LV causing the small scale flow structures to be ejected into the LVOT and the resulting accelerating flow through the LVOT to open the valve leaflets as shown in Figure 6b. Shear layer formation and roll-up phenomena are clearly observed in Figure 6b in the wake of the valve leaflets. These shear layers are broadly similar to those observed in previous simulations and experiments with a BMAV in a straight axi-symmetric aorta (Dasi et al., 2007). Our results do show, however, that in the anatomic case the shear-layer formation is impacted by interactions with small-scale flow structures that are advected by the accelerating systolic flow from the LV chamber past the valve leaflets. As the LV continues to contract, the vortical structures shed from the valve leaflets advance toward the aortic root and break up rapidly into a turbulent-like state past peak systole as seen in Figure 6c. At the end of systole, the LV slightly expands and the direction of the aortic flow is reversed driving the leaflets swiftly to the fully close position as shown in Figure 6d. The three-dimensional structure of the flow phenomena described above is illustrated in Figure 7, which shows the formation of the asymmetric, donut-shaped, mitral vortex ring at the end of the E-wave filling. The subsequent breakdown of this ring at late diastole and the intense stretching of vertical structures as the contracting LV directs the flow into the LVOT and opens the valve are shown in Figure 7b and 7c.

Figure 6.

Simulated FSI of a BMAV driven by a beating LV. Blood flow patterns at four instants during the cardiac cycle (A to D) visualized in terms of planar velocity vectors and out-of-plane vorticity contours at the symmetry plane of the BMAV. In each figure, the red dot in the inset marks the time instant in the cardiac cycle.

Figure 7.

Simulated FSI of a BMAV driven by a beating LV. 3D blood flow patterns at three instants during the cardiac cycle (A to C) are visualized in terms of instantaneous streamlines colored with velocity magnitude. In each figure, the red dot in the inset marks the time instant in the cardiac cycle. The red dot in the inset shows the time instance in the cardiac cycle.

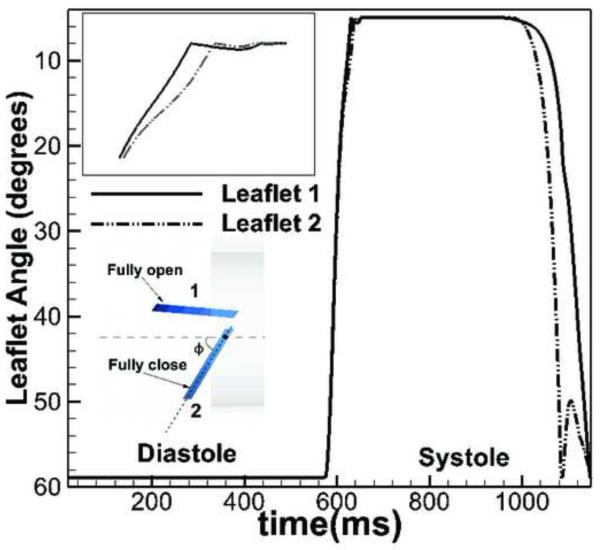
The calculated kinematics of the BMAV leaflets is shown in Figure 8 in terms of the temporal variation of the angle of each leaflet. Asymmetries between the motion of leaflet 1 and 2 are observed as the leaflets reach the fully open position and during the closing phase as seen in Figure 8. The large asymmetry of the leaflet kinematics is due to the three-dimensional anatomic geometry (see extensive discussion in (Borazjani et al., 2010)) giving rise to a highly three-dimensional retrograde flow into the LV through the valve leaflets as seen in Figure 6d. These findings clearly underscore the importance of patient-specific anatomic factors on heart valve performance and demonstrate the need for developing image-guided FSI computational models in order to obtain clinically relevant results.

Figure 8.

The kinematic (angle) of upper leaflet (1) and lower leaflet (2) over the whole cardiac cycle. The difference of two leaflet motion is most significant near the closing phase of the BMHV. The inset shows the definition of the opening angle with fully open and fully close position. Reproduced with permission from Le and Sotiropoulos (2012a).

Summary and conclusions

We reviewed recent advances in computational methods that pave the way for patient-specific simulations of native and prosthetic cardiac valves at physiologic conditions. Sophisticated FEMs have been developed for the mitral and aortic native valves, which can now yield clinically relevant insights into valvular morphology and function. Such models, however, are limited by the need to prescribe the hemodynamic loading across the valve. Patient specific FSI models, which in principle alleviate the above difficulties and can simulate valves in anatomic LV/LVOT models, have also been developed. The clinical relevance of these models, however, is limited by the fact that so far they have considered FSI for relatively simple bi-leaflet mechanical valves and simplified the treatment of the MV.

Advancing toward a computational framework that can simulate a range of cardiac valves, native and prosthetic, in patient-specific left heart models will require integrating the sophistication and clinical realism of FEMs with the computational power of FSI algorithms. A number of computational advances will be required to accomplish this goal, including: the development of robust and efficient FSI algorithms for tissues and compliant blood vessels; the integration of imaging modalities with FSI methods to obtain patient-specific geometry and kinematics of the left heart; the development and integration with FSI methods of efficient FEMs for simulating stents to enable simulation of TAVIs; and the integration of the aforementioned algorithmic advances into a powerful computational framework that can take advantage of massively parallel supercomputers. To ensure that the resulting computational framework will be clinically relevant and useful, the advances in computational modeling should proceed in tandem with carefully designed in vitro and in vivo experiments to yield data for validating the computational models.