Prediction of phenotypes of missense mutations in human proteins from biological assemblies

Abstract

Single nucleotide polymorphism (SNPs) are the most frequent variation in the human genome. Non-synonymous SNPs that lead to missense mutations can be neutral or deleterious, and several computational methods have been presented that predict the phenotype of human missense mutations. These methods employ sequence-based and structure-based features in various combinations, relying on different statistical distributions of these features for deleterious and neutral mutations. One structure-based feature that has not been studied significantly is the accessible surface area within biologically relevant oligomeric assemblies. These assemblies are different from the crystallographic asymmetric unit for more than half of X-ray crystal structures. We find that mutations in the core of proteins or in the interfaces in biological assemblies are significantly more likely to be disease-associated than those on the surface of the biological assemblies. For structures with more than one protein in the biological assembly (whether the same sequence or different), we find the accessible surface area from biological assemblies provides a statistically significant improvement in prediction over the accessible surface area of monomers from protein crystal structures (p=6e-5). When adding this information to sequence-based features such as the difference between wildtype and mutant position-specific profile scores, the improvement from biological assemblies is statistically significant but much smaller (p=0.018). Combining this information with sequence-based features in a support vector machine leads to 82% accuracy on a balanced data set of 50% disease-associated mutations from SwissVar and 50% neutral mutations from human/primate sequence differences in orthologous proteins.

Introduction

Single nucleotide polymorphisms (SNPs) are the most common form of genetic variation in humans.^1,2 Some SNPs are directly linked to disease through changes in protein sequence or changes in transcription and translation. Others may be in linkage with the actual causative mutation and not directly responsible for aberrant gene function. While effects on transcription or translation rates are currently difficult to predict, a number of groups have presented methods for the predicting of the phenotypes of missense mutations on proteins – those SNPs that change a single amino acid in a protein sequence. We recently benchmarked several of these, available as web servers or downloadable programs, including SIFT,^3–5 PolyPhen,^6–8 PMut,^9–11 SNPs3D,^12,13 PhD-SNP,¹⁴ and nsSNPAnalyzer,¹⁵ on a novel set of mutations in a single protein, human cystathionine beta synthase (CBS). We found that the top methods were PolyPhen, SIFT and nsSNPAnalyzer, which have similar performance rates on a mutation data set derived from functional complementation of cystathionine beta synthase deletion in yeast by human CBS.¹⁶

In our previous work, we analyzed some features often used in phenotype prediction including surface area in both monomeric proteins and biological assemblies, sequence conservation score, and values in position-specific scoring matrices (PSSMs). This was accomplished by deriving kernel density estimates for each feature for the deleterious and neutral mutations sets and then calculating the neutral probability and deleterious probability given a value of a certain feature. We evaluated the ability of these kernel classification functions to predict phenotypes on data limited to just two protein systems, CBS and the Lac repressor.¹⁷ The two systems behaved somewhat differently in the tests we performed, and thus we decided that a more comprehensive analysis was warranted.

With large data sets of deleterious and neutral mutations from a diverse set of proteins, in this paper we analyze the ability of various features to predict phenotypes. In most previous publications, the values of features associated with deleterious or neutral mutations are left largely unexplored. In this paper, we explore kernel density estimates and classification on several different features of sequences, sequence alignments of homologues and protein structures. Any feature may be analyzed in terms of a decision point or cutoff below which more mutations are deleterious and above which more mutations are neutral (or vice versa). Traditionally, such cutoffs for PSSM scores or accessible surface areas may be set across all data in the mutation sets, averaging across residue types. We show that different residue types have different optimal cutoffs for both sequence-based and structure-based scores.

Several other recent reports have discussed the effects of missense mutations on protein-protein interactions and biological assemblies. Zhang et al. investigated the molecular effect of three missense mutations on spermine synthase that were clinically linked to Snyder-Robinson syndrome.¹⁸ They revealed the effects of those three mutations on spermine synthases’s stability, flexibility and interactions by calculating single-point energies and pKa from molecular dynamics simulations. In a larger study from the same group, Teng et al. built homology models of three-dimensional structures of 264 protein-protein complexes with known nsSNPs at the interface, and investigated the effect of nsSNPs on the binding energy with the CHARMM force field and continuum electrostatic calculation.¹⁹ They found that disease-causing nsSNPs tend to destabilize the electrostatic component of protein-binding energy in contrast with nsSNPs that were not annotated to be disease-causing. More recently, David et al. analyzed the location of nsSNPs in terms of their location in the protein core, at protein-protein interfaces, and on the surface when not at an interface.²⁰ They found that compared to a chance distribution, disease SNPs are preferentially located at interfaces rather than in non-interface surface positions.

Given our previous results and the data of David et al., we were particularly interested in whether knowledge of the structure of biological assemblies from the PDB would improve phenotype prediction. This has been applied previously to a limited extent⁶ but not analyzed systematically. The PDB provides information on the “biological assembly” (BA) present (or hypothesized to be present) in each crystal structure in the archive. These biological assemblies either come from the authors of structures themselves or from the PISA web server²¹ and differ from the asymmetric unit in about 65% of X-ray crystallographic structures. The authors and PISA agree with each other only about 75% of the time, but we have found that in well-attested biological interactions (present in a large number of crystal forms for diverse members of single protein families) PISA provides somewhat higher accuracy than the authors do on average.²² In fact authors often deposit the asymmetric unit as the biological assembly, even when their publication on the structure shows a different assembly (Xu and Dunbrack, unpublished data). We have therefore used the PISA database to provide the structures of biological assemblies, and we have evaluated the ability of accessible surface areas from protein monomers and protein assemblies to predict the phenotypes of missense mutations. The biological assemblies improve phenotype predictions significantly for those mutations that are located in interfaces of biological assemblies. This is not a large proportion of all mutations and therefore the overall improvement in accuracy is not very large. It does indicate that knowing the correct structures of protein-protein interactions is important for predicting the correct phenotype of some mutations. We have also studied the impact of using multiple PDB entries and their biological assemblies for each mutant where these are available and show that the minimum surface area over several biological assemblies is a better predictor than the surface area from a single structure.

Methods

Data sets

We created a dataset, HumanDisease, from the SwissVar database (release 57.8 of 22-Sep-2009)² by removing unclassified variants, variants in very long proteins (sequences of more than 2000 amino acids), redundant variants, and variants that are not accessible by single-site nucleotide substitutions. We obtained non-human primate sequences from UniprotKB²³ and used PSI-BLAST^24,25 to identify likely primate orthologues of human proteins in the SwissVar data sets using a sequence identity cutoff of 90% between the human and primate sequences. To avoid misaligned amino acids near deletions, perhaps caused by missing exons, we selected mutations without insertions or deletions within 10 amino acids on either side of the mutation of amino acid differences in the PSI-BLAST alignments, and compiled them into a data set of human/primate sequence differences, PrimateMut. Only those 150 types of mutations that can occur by single-site nucleotide substitutions were included in HumanDisease and PrimateMut, although we did not directly check DNA sequences to see if this is how the sequence changes occurred. A total of 222 human proteins were present in both sets but only 29 mutations were at the same site in each of the sets. However, none of these were to the same mutant amino acid.

To define the structural dataset, we mapped the human mutation sites in the HumanDisease and PrimateMut data sets to known structures of human proteins in the PDB using SIFTS²⁶, which provides Uniprot sequence identifiers and sequence positions for residues in the PDB. The data sets are provided as Supplementary Tables S1 and S2 respectively.

We constructed two structural data sets, HumanDiseaseStr and PrimateMutStr, which contain mutation sites available in known structures. The data sets are provided as Supplementary Tables S3 and S4 respectively.

To produce an independent test set, we compared the SwissVar release 2012_03 of March 21, 2012 with that of release 57.8 of Sep. 22, 2009 used to derive datasets HumanDisease and PrimateMut. We selected the human-disease mutations contained in the new release but not contained in the previous release. In addition, we also searched all human proteins in Uniprot/SwissProt against primate sequences to obtain additional primate polymorphisms not contained in PrimateMut. The data sets are provided as Supplementary Tables S5 through S8.

Structure-based features

For wildtype position of each mutation, we used the program Naccess²⁷ to calculate the percent accessible surface area in all available biological assemblies and monomers containing the mutation site. For biological assemblies, we downloaded the XML file from PISA which contains symmetry operators for building the coordinates of these assemblies. These assemblies were built as described.²⁸

Sequence-based features

We used PSI-BLAST^24,25 to search human protein sequences against the database UniRef100²⁹ for two rounds with an E-value cutoff of 10 to calculate the Position-Specific Scoring Matrix (PSSM) score for the mutations. We obtained the PSSM score of the wildtype residues and the PSSM score of the mutant residues from the PSI-BLAST matrix output. For each query, we selected homologues from the PSI-BLAST output with sequence identity greater than 20% and input these proteins to the program BLASTCLUST²⁴ to cluster these sequences at a sequence identity threshold of 35%. A multiple sequence alignment of the sequences in the cluster containing the target human protein was created with the program Muscle.^30,31 Finally, the multiple sequence alignment was input to the program AL2CO³² to calculate the conservation score for each wildtype residue of human proteins.

Kernel density estimation and kernel classification

To investigate the properties of several sequence and structural features, we used one-dimensional kernel density estimates to calculate a probability density function of each feature for the deleterious mutation sets ( ph= D ) and the supposedly neutral phenotype data sets ( ph= N ). The nonparametric kernel density estimate using a Gaussian kernel function for a continuous variable can be written³³:

$$p(x\mid ph)=\frac{1}{n_{ph}h\sqrt{2\pi }}\sum _{i=1,n_{ph}}exp\left(\frac{-{(x-x_i)}^2}{2h^2}\right)$$ (1)

where h is a bandwidth parameter used to control the smoothing of the density estimate for n_ph data points. After calculating kernel density estimates for both the neutral ( N ) and deleterious ( D ) mutation set, we used Bayes' rule to calculate the kernel classification functions:

$$p(ph\mid x)=\frac{p(x\mid ph)p(ph)}{p(x\mid N)p(N)+p(x\mid D)p(D)}$$ (2)

for phenotype ph equal to either N or D . While in most cases we used balanced data to calculate p(x|ph) and p(ph|x), strictly this is not necessary, since we can set p(ph), p(N), and p(D)to 0.5 to artificially balance the mutations in the calculation of p(ph|x).

To optimize the bandwidth h , we employed a maximum-likelihood estimation procedure to maximize the probabilities of the phenotypes given the feature values using a tenfold cross-validation procedure. As a function of h , we maximized the value of the log likelihood:

$$L(h)=\sum _{i\in \{N\}}lnp(ph=N\mid x_i)+\sum _{j\in \{D\}}lnp(ph=D\mid x_j)$$ (3)

where the sums are taken over the set of neutral mutations {N} and the set of deleterious mutations {D} . The same value of h was used for both the neutral set and deleterious set density estimations.

Results

Data sets

We obtained disease-associated mutations from SwissVar² and neutral mutations from a comparison of human protein sequences with those of primates as described in the Methods section. We defined subsets of these mutations by identifying those residues in the disease set and primate set that were present in structures of human proteins in the Protein Data Bank. The four sets are detailed in Table I. As an independent testing set, we repeated this procedure in March 2012, and defined comparable “independent” data sets of mutations that do not contain any of the mutations in the original data sets.

Table I.

The number of proteins, mutations for each data set

Training data set			Independent data set
Data set	#Proteins	#Mutations	Data set	#Proteins	#Mutations
HumanDisease	2582	19056	HumanDisease_new	711	6154
PrimateMut	3153	22790	PrimateMut_new	2307	12176
HumanDiseaseStr	562	6938	HumanDiseaseStr_new	209	1405
PrimateMutStr	719	3575	PrimateMutStr_new	551	2346

The data sets are provided as Supplemental Tables S1 through S8.

Analysis of structure-based features

Information from protein structures can be helpful in predicting the phenotypes of missense mutations.¹² With actual structures of the proteins under consideration, rather than structures of homologues, detailed structural information such as hydrogen bonding, side-chain packing, and backbone conformations might be used in phenotype predictions. However, since most human proteins do not have known structures, other than through structure prediction from the structures of homologous proteins, we decided to test a simpler feature for its ability to predict phenotypes – the relative accessible surface area of the wildtype residues.

Such surface areas are usually calculated from the structure of the protein monomer from available crystal structures, or in some cases the full deposited coordinates in the PDB. However, for X-ray crystal structures, the standard PDB files contain the asymmetric units used by crystallographers to solve the structure. The more biologically relevant structures are the “biological assemblies” available from the PDB and from the PISA web server.²¹ We found previously that PISA’s biological assemblies are more likely to be correct and consistent than the author-deposited assemblies,²² so we calculated the relative surface accessibility from PISA’s most stable biological assembly. PISA’s first biological assembly is the same as the asymmetric unit for only about 35% of X-ray structures in the PDB. Thus, using the biological assembly rather than the asymmetric unit may make a large difference in predictions.

We analyzed the rate of deleterious and neutral mutations in various locations within the oligomers of various sizes. Using the criteria of David et al.²⁰, we defined the core residues of proteins as those that had surface accessibility < 5 Ų in protein monomers, while interface residues are those wildtype residues that had any atom contact < 5 Å from another protein in the biological assembly. The remaining residues comprised the residues on the surfaces of biological assemblies. The mutations for homodimers and heterodimers as well as homooligomers and heterooligomers (larger than dimers) were balanced so that data sets had 50% deleterious and 50% neutral mutations, and the numbers of deleterious and neutral mutations in each location were counted. The results are shown in Table II. Core residues are the most likely to be deleterious with rates from 65% to 77%, compared to a 50% rate for each oligomer data set. The deleterious rates in of residues in interfaces are also higher than 50%. They are higher in homooligomers than in homodimers, and higher still in heterodimers. In heterooligomers, they are higher in the heterodimeric interfaces than in the homodimeric interfaces. Conversely, the rates on the surfaces of biological assemblies – not in the core of single proteins or in interfaces – have deleterious rates considerably lower than 50%, ranging from 28.5% to 38% across the oligomer types.

Table II.

Rates of deleterious mutations in interfaces various biological assemblies

	Core		Interface		Surface of BA
Oligomer	Count	D (%)	Count	D (%)	Count	D (%)
Homodimer	502	71.9	253	55.7	771	34.1
Homooligomer	293	65.2	384	64.6	517	38.2
Heterodimer	192	77.1	152	67.8	368	28.5
Heterooligomer	221	72.9	474	58.9	489	29.4
Hetero-interfaces	--	--	356	61.2	--	--
Homo-interfaces	--	--	118	51.7	--	--

Mutations were balanced for each oligomer type (50% deleterious, 50% neutral), and rate of deleterious mutations was calculated for each location within the oligomers.

David et al. compared the structural location of disease-associated mutations and polymorphisms given in SwissVar.²⁰ They calculated the odds ratios for mutations to be in the core, in interfaces within biological assemblies, or on the surface of biological assemblies in terms of odds ratios. The odds ratio for being present in location i compared to location j for a particular set of mutations is

$$OR=\frac{x_i/(1-x_i)}{x_j/(1-x_j)}$$

We calculated the OR values for our data again using the same criteria for core, interface and surface used by David et al. Our data are compared to those of David et al. in Table III. Our results are either within or near the confidence intervals given by David et al.. Of most interest is that our neutral mutations from sequence differences between human proteins and primate orthologue human show an ratio of 0.70 for being in an interface compared being on the surface of biological assemblies. David et al showed a slight preference for the interface for their neutral mutations, probably because a larger percentage of SwissVar polymorphisms may in fact be somewhat deleterious.

Table III.

Odds ratios for location of mutations

	Core vs. noncore (95% CI)		Interface vs. surface (95% CI)		Core vs. interface (95% CI)
	Ref 20	Our data	Ref 20	Our data	Ref 20	Our data
Disease mutations	1.77 (1.62–1.93)	1.93 (1.87–2.00)	1.59 (1.44–1.76)	1.84 (1.73–1.95)	1.30 (1.17–1.44)	1.14 (1.07–1.21)
Primate mutations	0.67 (0.57–0.79)	0.56 (0.40–0.72)	1.15 (1.00–1.32)	0.70 (0.52–0.88)	0.61 (0.50–0.73)	0.71 (0.63–0.79)

The data in Tables II and III indicate that data on the location of mutations may provide a suitable feature for prediction of missense mutations. Whether an amino acid is in the core is determined by its accessible surface area in individual protein chains, and whether a mutation is in the interface or on the surface is related to its accessible surface area in biological assemblies.

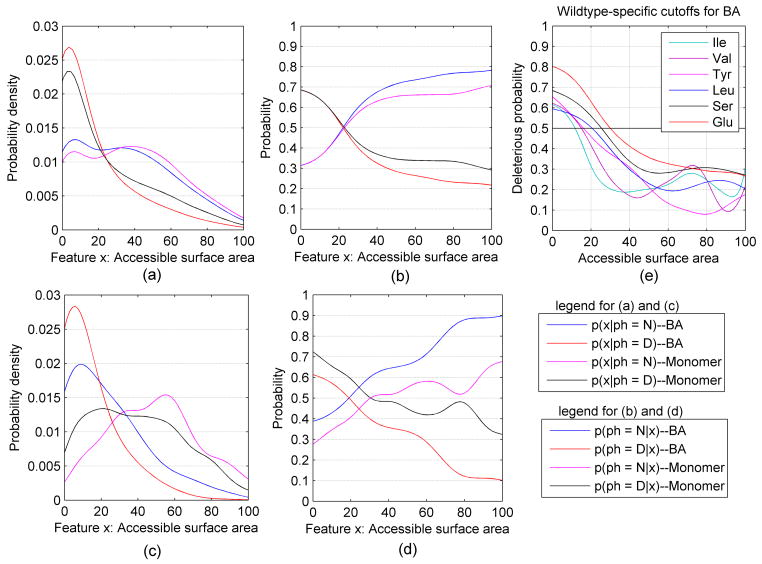
For the mutations in HumanDiseaseStr and PrimateMutStr whose wildtype residues were present in one or more structures in the PDB, we calculated kernel density estimates of the surface areas calculated from the protein monomers and from the biological assemblies from PISA from the structures with highest resolution. The structure data consisted of 6938 disease-associated mutations and 3575 human-primate mutations. The kernel density estimates for the neutral (N) and deleterious (D) mutations are shown in Figure 1a for both the relative surface accessibility (RSA) of the biological assemblies (BAs) from PISA and for protein monomers. For both the monomers and biological assemblies, the density of RSA for the deleterious mutation is highest at 0% RSA and decreases steadily at higher RSAs (the slight increase in density from 0% to 10% RSA is likely a boundary artifact, since there are no data points below 0%). The density of the RSA for the neutral mutations has peaks at 0% and 35–40%, with density spread relatively evenly from 0% to 60%. As expected, the biological assembly RSA densities are shifted to lower values compared to the monomer RSA density, since some residues are buried upon formation of complexes with other proteins or with ligands but the shift is larger for the deleterious mutations than for the neutral mutations.

Figure 1.

Kernel density and classification curves for relative accessible surface area (RSA). (a) Density of RSA for wildtype residues in PrimateMutStr (N) and HumanDiseaseStr (D) in biological assemblies (BA) and in monomers. (b) Classification curves for RSAs of biological assemblies and monomers. (c) Density of RSA for wildtype residues that change surface area on formation of the biological assembly from the monomers. (d) Classification curves for RSAs for wildtype residues that change surface area on formation of the biological assembly from the monomers. (e) The probability of deleterious mutations for several different amino acid types from the RSA in biological assemblies.

Setting P(N) = P(D) = 0.5 to calculate the probability of each phenotype given the feature value, the resulting kernel classification functions are shown in Figure 1b. When residues are completely buried in either the monomer or the biological assembly, its chance of being a deleterious mutation is about the same at roughly 70%. Being fully accessible in the biological assembly confers an 80% chance of being neutral, while being fully accessible in the monomer confers a 70% chance of being neutral. Thus, having a high relative surface accessibility in the biological assembly is more predictive of being a neutral mutation than having the same surface accessibility in the monomer. This is because a certain fraction of the residues that are accessible in the monomers move to much lower RSAs in the biological assemblies and mutation of these residues in protein-protein or protein-ligand interfaces is often deleterious. For both monomer RSAs and biological assembly RSAs, an RSA of about 22% provides an equal chance of being deleterious or neutral.

Only those residues that have lower surface accessibility in the biological assembly can be affected by considering the structure of the biological assemblies. In our structure mutation set, 20% (2090/10513) of the mutations have different surface area in the biological assemblies compared to the monomers. Of these 2090, a total of 76.3% (1594/2090) of these mutations are deleterious, compared to 66.0% of the entire structure data set, indicating that mutating a residue with biologically relevant interactions in protein complexes affects its phenotype. Figure 1c and 1d show the kernel density estimates and kernel classification curves respectively for the mutations with different surface area in biological assemblies and monomers. In Figure 1d, setting P(D) = P(N) = 0.5 to calculate the classification probability, the curves in Figures 1c and 1d are quite different than those in Figures 1a and 1b. The cross points are now an RSA value of 19% for the biological assemblies and 32% for the monomer surface areas.

To explore whether these classification curves and the cutoffs used to assign phenotypes (the point where the classification curves cross each other) might depend on residue type, we calculated the surface area probability density curves separately for each wildtype residue and for each mutant residue type. When the overall numbers of neutral and deleterious mutations are balanced, the numbers for each specific residue type are not. The rates of deleterious mutations for each residue type are given in Table IV for the structure-based data sets. They vary quite significantly; for example, 82% of Cys wildtype mutations are deleterious, while only 26% of Val mutations are deleterious in an overall balanced data set. Cys residues are highly likely to be involved in specific interactions either in disulfides or with ions. We found that of the deleterious Cys mutations, there are 62% were involved in disulfide bonds and 22% were involved in ion interactions for a total of 84%.

Table IV.

Rates of deleterious mutations for each residue type from an overall balanced data set.

Wildtype residue					Mutant residue
	Structure set		Full set			Structure set		Full set
	Count	P(D)	Count	P(D)		Count	P(D)	Count	P(D)
C	236	82	1136	74	W	118	89	784	88
W	91	81	433	77	C	268	81	1540	80
G	482	75	3095	75	P	352	73	2249	66
R	785	65	4576	68	F	182	65	1044	59
Y	190	63	886	65	Y	206	65	948	67
P	333	62	1865	60	R	685	55	3605	56
D	374	55	1670	57	H	352	54	1740	57
F	179	55	944	51	D	319	52	1508	56
L	417	55	2466	55	G	327	52	1754	47
A	448	51	2860	43	L	451	52	2304	54
E	413	47	1764	51	Q	317	52	1642	54
H	234	44	1175	44	S	599	48	3297	45
S	451	42	2801	39	K	331	47	1556	53
M	230	39	1270	36	E	286	44	1502	48
N	285	39	1452	39	N	297	44	1568	45
Q	298	37	1254	35	M	216	43	1298	45
T	471	32	2258	35	T	433	42	2505	39
I	417	31	2062	28	V	547	39	3125	38
K	302	29	1371	33	I	404	30	2076	29
V	514	26	2774	33	A	460	29	2067	25
All	7150	50	38112	50	All	7150	50	38112	50

Table IV demonstrates that P(N) and P(D) for individual residue types are not equal, even in an overall balanced mutation dataset. However, an unbalanced dataset will affect the performance of kernel density classification. To calculate residue specific classification curves, we set P(N) = P(D) = 0.5 for the structure-based data sets. Figure 1e shows the deleterious classification curves of surface area in the biological assemblies for different wildtype residues, demonstrating that different RSA cutoffs for deleterious/neutral calls should benefit phenotype predictions. Table V provides the residue-specific cutoffs for both monomer and biological assembly surface areas.

Table V.

Residue-specific cutoffs and global cutoff for dPSSM, biological assembly surface area, and monomer surface area

Biological assembly surface area*				Monomer surface area*			dPSSM score
Wildtype	Cutoff	Mutant	Cutoff	Wildtype	Cutoff	Mutant	Cutoff	Wildtype	Cutoff	Mutant	Cutoff
I	11.7	L	12.8	F	10.9	L	10.9	V	2.4	I	2.4
M	12.3	T	17.5	Y	11.7	M	13.8	A	2.8	M	2.6
C	13.2	I	18.0	I	12.5	W	14.5	K	2.8	N	2.9
V	15.0	W	18.1	M	12.5	V	15.0	E	3.0	P	3.1
F	15.1	Y	19.1	V	15.5	I	15.8	I	3.0	K	3.2
A	15.5	N	21.0	C	17.2	F	17.7	Q	3.0	V	3.2
Y	16.0	R	21.1	H	17.6	G	20.2	S	3.0	T	3.3
H	17.7	M	21.2	A	19.0	R	21.9	T	3.1	Q	3.5
L	20.5	F	21.8	Q	21.9	Y	22.0	L	3.3	E	3.6
N	22.2	S	22.3	L	22.1	H	22.3	M	3.6	A	3.8
R	22.8	V	22.4	T	22.2	T	23.0	R	3.9	F	3.8
Q	23.0	H	22.5	R	23.0	N	23.7	N	4.0	H	3.9
T	24.1	A	23.3	S	25.8	S	24.2	D	4.5	D	3.9
S	25.4	C	24.5	K	26.6	P	25.0	F	4.9	R	4.5
K	27.0	D	24.6	W	27.0	Q	25.0	Y	5.2	L	4.6
G	27.4	Q	24.8	G	27.2	D	26.1	G	5.3	S	4.7
P	28.0	P	25.0	N	27.5	A	27.5	H	5.5	G	5.2
W	29.0	G	25.9	P	28.2	K	27.8	P	7.1	Y	5.9
E	30.0	K	26.0	D	30.5	E	30.8	C	7.4	C	6.0
D	31.8	E	28.9	E	33.2	C	34.8	W	9.1	W	6.0
Global cutoff		22.1		Global cutoff		22.9		Global cutoff		3.7

^*Surface area in Ų.

The classification functions can be used to make predictions of phenotype given the value of a feature from which the true positive rate (TPR), true negative rate (TNR), positive predictive value (PPV), negative predictive value (NPV), overall accuracy (ACC) and balanced accuracy (BACC) can be calculated. The true positive rate is the fraction of actual deleterious mutants which are predicted to be deleterious (“positive”). The positive predictive value is the fraction of deleterious predictions which are actually deleterious. Accuracy is simply the total percentage of the predictions that are correct, while balanced accuracy is equal to (TPR+TNR)/2. The latter provides a better assessment of prediction accuracy when the data set used for evaluation is unbalanced (different numbers of positive and negative data points). When the number of positive and negative points are equal, ACC is equal to BACC.

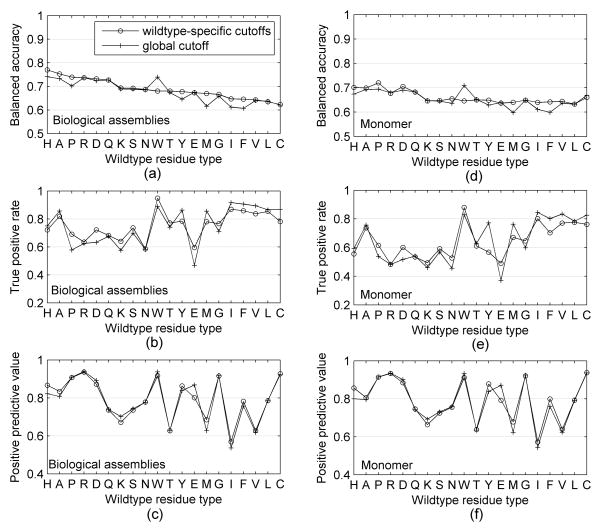
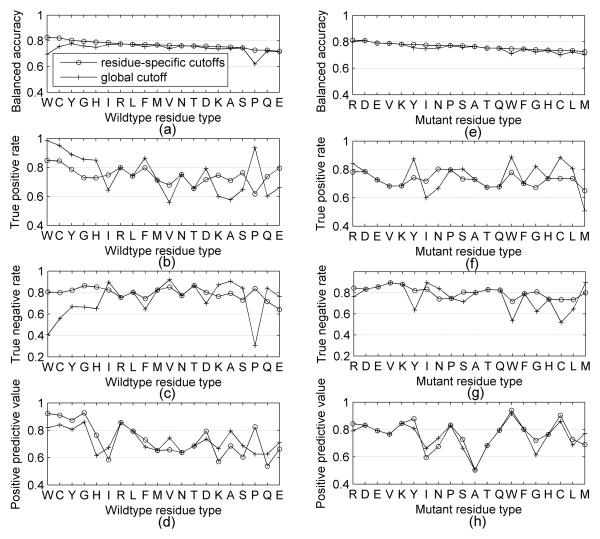
The results for the global and residue-specific cutoffs are shown in Figure 2. All of the wildtype-specific cutoffs achieve a better balanced accuracy than the global cutoffs for biological assemblies excluding Trp (see Figure 2a), especially for wildtype residues Met (improved 5.4%), Pro (improved 4%) and Phe (improved 4%). We also found wildtype residue types Asp, Glu and Pro have the largest variations of TPR, while the wildtype-specific accessibility cutoffs have much closer positive predictive value with the global accessibility cutoff for biological assembly, as shown in Figures 2b and 2c. Figure 2d shows that the wildtype-specific cutoffs achieve a better balanced accuracy than the global cutoffs for monomer surface areas except for Trp and Cys, and especially for wildtype residue Met (improved 4%) and Phe (improved 4%). For monomer protein, we found the same wildtype residue types Asp, Glu and Pro have the largest variations of TPR as that of biological assemblies, and the positive predictive value is close for wildtype-specific cutoffs and global cutoffs, as shown in Figure 2e and 2f. We also observed that the wildtype-specific cutoffs and global cutoff of biological assembly RSAs produced better balanced accuracy, true positive rate and positive predictive value than that of monomer structures.

Figure 2.

Performance of wildtype-specific and global accessibility cutoffs for biological assemblies and monomers.

We also compared the performance of mutant-specific cutoffs with the performance of the global cutoff. As we expected, the balanced accuracy of mutant-specific cutoffs of biological assembly is better than that of global cutoff excluding mutant residue types Cys and Trp, especially for the mutant residue type Glu (improved 2.4%) and Leu (improved 1.4%. The balanced accuracy of mutant-specific cutoffs of monomer is also better than that of global cutoff excluding mutant residue types Cys and Trp, especially for the mutant residue type Glu (improved 2.4%) and Leu (improved 1.4%).

With the structure-based classification curves in hand, we can predict the phenotypes for mutations in the data set and calculate the accuracy measures, TPR, TNR, PPV, NPV, ACC and balanced accuracy (BACC). These are given in the first section of Table VI for the case where we use a single biological unit or monomer from the structure with highest resolution for each mutation. For global accessibility cutoff, the biological assemblies provide higher true positive rate, positive predictive value, negative predictive value, overall accuracy and balanced accuracy than monomer. These differences are not large because only 20% of the mutations have different surface areas in the biological assemblies and the monomers, and only a proportion of these produce different predictions using the RSAs from the two sources. For wildtype-specific accessibility cutoff, the biological assemblies also provide higher TPR, PPV, NPV, ACC and BACC than monomer, compared with the global cutoff. The wildtype-specific cutoffs achieves a better performance than the global cutoffs for biological assemblies and monomer.

Table VI.

The performance of PSSM and surface area terms using kernel density classification functions

	Features	TPR	TNR	PPV	NPV	ACC	BACC
Surface area from highest resolution biological assembly	Global cutoff for BA surface area	73.0	62.2	78.9	54.2	69.3	67.6
	Global cutoff for monomer surface area	62.7	67.0	78.7	48.1	64.2	64.9
	Wildtype-specific cutoffs for BA	74.2	63.6	79.8	55.9	70.6	68.9
	Wildtype-specific cutoffs for Monomer	62.9	69.0	79.8	48.9	65.0	66.0
Surface area from multiple biological assemblies	Single BA surface area	72.3	65.4	79.5	55.9	69.9	68.8
	Single monomer surface area	66.4	67.8	79.3	52.1	66.9	67.1
	Minimal BA surface area	75.9	63.5	79.4	58.7	71.6	69.7
	Minimal monomer surface area	66.8	67.1	79.0	52.1	66.9	67.0
	Maximal BA surface area	67.4	67.6	79.4	52.8	67.5	67.5
	Maximal monomer surface area	64.6	67.4	78.6	50.7	65.6	66.0
	Averaged BA surface area	74.5	64.6	79.6	57.7	71.0	69.5
	Averaged monomer surface area	67.7	67.1	79.3	52.8	67.5	67.4
Surface area from homo and hetero biological assemblies	Surface area in homo BA	78.2	61.5	80.0	59.0	72.6	69.9
	Surface area in homo monomer	72.4	64.0	79.8	54.2	69.6	68.2
	Surface area in hetero BA	77.2	61.0	79.5	57.6	71.7	69.1
	Surface area in hetero monomer	72.0	63.3	79.4	53.5	69.1	67.6
PSSM scores	Wildtype residue PSSM score	70.7	71.4	67.4	74.5	71.1	71.1
	Mutant residue PSSM score	66.8	79.6	73.3	74.2	73.8	73.2
	dPSSM (Wildtype – mutant PSSM)	76.0	79.0	75.2	79.8	77.7	77.5
	Best of six kernel probabilities	70.4	84.4	79.0	77.3	78.0	77.4
dPSSM from data set balanced for each wildtype amino acid type	Global dPSSM cutoff	73.4	75.5	75.0	73.9	-	74.4
	Wildtype-specific dPSSM cutoffs	73.4	79.3	78.0	74.9	-	76.3
dPSSM from data set balanced for each mutant amino acid type	Global dPSSM cutoff	74.5	77.4	76.7	75.2	-	75.9
	Mutant-specific dPSSM cutoffs	72.8	80.8	79.1	74.8	-	76.8

“BA” = biological assembly

The best method in each section for each accuracy measure is shown in bold italic type.

Utilizing multiple biological assemblies

Many human proteins are present in multiple PDB entries, sometimes with different binding partners and ligands and sometimes in different oligomeric states due to the constructs used or crystallization conditions. PISA’s biological assemblies are in some sense hypothetical, based on an empirically parameterized scoring function optimized to give the best tradeoff of sensitivity and specificity. We therefore sought to determine whether there is any advantage in using accessible surface area information from multiple PDB entries.

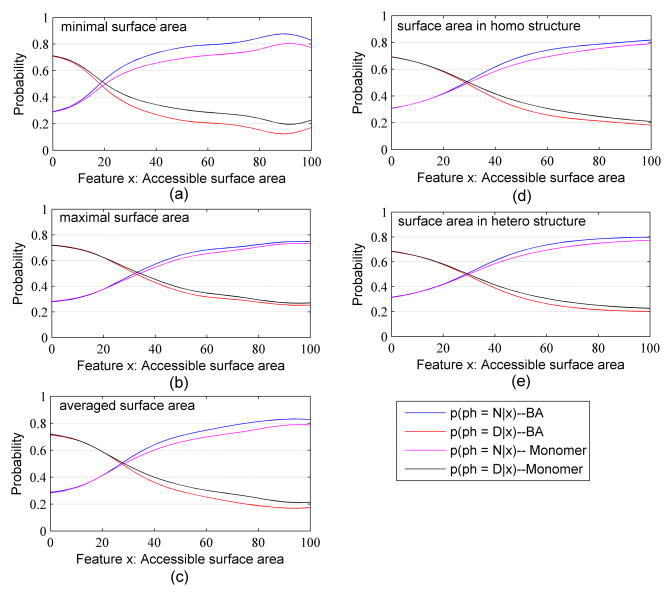
From the 10,513 mutations represented in structures, we created a set of 6,382 mutations (2,234 primate polymorphisms and 4,148 human disease mutations) that can be found in more than one PDB structure. Setting P(N) = P(D) = 0.5 in Equation 2, we calculated optimized kernel densities and classification curves for these mutations using: 1) the surface area of the wildtype residue from the single biological assembly of the highest resolution structure as before; 2) the surface area from the monomer of the highest resolution structure as before; 3) the minimum value of the surface areas of the residue from all available biological assembly; 4) the minimum value from all monomers; 5) the maximum value from all BAs; 6) the maximum value from all monomers; 7) the average value over all BAs; 8) the average value over all monomers. The kernel density estimates and kernel classification functions are shown in Figure 3a, 3b and 3c, and the accuracy results for phenotype prediction are given in the second section of Table VI.

Figure 3.

Kernel classification curves for the (a) minimal; (b) maximal; (c) average; (d) single heterooligomer structure of highest resolution; (e) single homooligomer surface area of highest resolution.

The various accuracy measures exhibit different behaviors for the different sources of the relative surface accessibilities. The minimal surface area over multiple biological assemblies is better for predicting the phenotype of the deleterious mutations with higher TPR value (75.9%) than the average BA surface area (74.5%) or the maximum BA surface area (67.4%). Each of these values for the BAs is higher than the equivalent value for the monomers by several percent. For the PPV, the average and minimum surface areas perform nearly equivalently and the biological assembly values are only slightly better (0.3–0.4%) than each of the monomer values. For the TNR values, by contrast, the monomer results are better than each of the biological assembly results by 1–4%. The average and minimum surface area results are the best and nearly the same. The NPV results resemble the TPR results with the highest value coming from the minimal surface areas and large increases for the BA surface areas over the corresponding monomer surface areas.

Many proteins interact with other proteins as they carry out their biological functions. There are structures of many of these interactions in the PDB for human proteins. We therefore investigated whether heterooligomeric structures would perform differently than homooligomeric (or monomeric) structures. For each mutation present in the coordinates of at least one heterooligomeric structure and one homooligomeric structure, we chose one structure of highest resolution from each. This resulted in 2357 human-disease mutations and 1200 primate polymorphisms. Setting P(N) = P(D) = 0.5 in Equation 2, we calculated the predictive accuracy of the kernel classification curves from the surface areas in the single highest resolution hetero and homo structure. The kernel classification curves for homooligomeric and heterooligomeric surface areas are shown in Figure 3d and 3e respectively. The curves are relatively similar, showing the advantage of using the biological assembly surface areas over the monomer surface areas in both cases. The cross point is slightly different between monomer and biological assembly for the homooligomeric structures.

The kernel density classification results are given in Table VI. The surface areas from the homooligomeric biological assemblies are a little higher in balanced accuracy by 0.8% than the surface areas in the heterooligomeric biological assemblies. The reason may be that mutations in homooligomeric interfaces may be more disruptive, since most such interfaces are symmetric. Thus, a single mutation affects two residues in an interface, not just one as it would do in a heterodimeric interaction. As we showed earlier, the minimum value over all available biological assemblies, both heterooligomeric and homooligomeric, results in higher prediction accuracy.

Analysis of sequence-based features

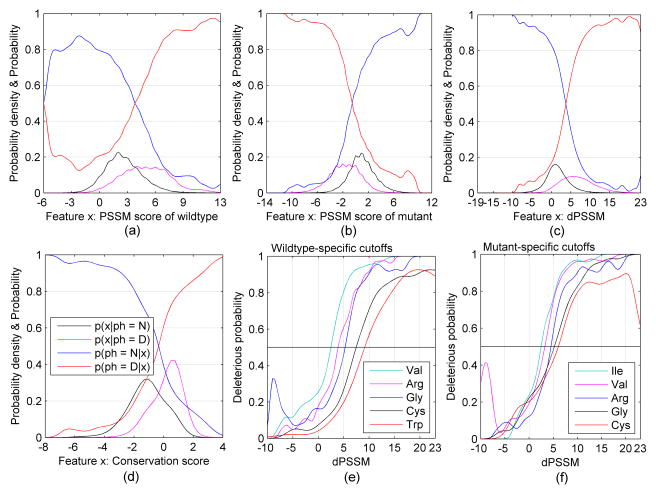
For sequence-based features, we can use a larger data set since we do not require an existing protein structure. The data set consisted of 19056 human disease mutations and 22790 primate mutations. In Figure 4, we explore several sequence-based features – PSSM score of the wildtype residue (Figure 4a), PSSM score of the mutant residue (Figure 4b), the difference in these two PSSM scores (“dPSSM”, Figure 4c), and a conservation score³² (Figure 4d). In each case, the probability density of the feature (deleterious=black and neutral=magenta) and the classification functions (deleterious=red and neutral=blue) are shown. In order to avoid the effect of an unbalanced dataset, the classification curves in Figures 4a–4d are based on setting p(N) = p(D) = 0.5 in Equation 2.

Figure 4.

The kernel curves for three types of PSSM score and conservation score. The curves p(x | ph) are probability density estimates for the feature x. The curves p(ph | x) are kernel classification functions for the feature x.

In Figure 4a–4d, the results are not divided by residue type. To explore whether these classification curves and the cutoffs used to assign phenotypes (the point where the classification curves cross each other) might depend on residue type, we calculated the dPSSM probability density curves separately for each wildtype residue and for each mutant residue type. When the overall numbers of neutral and deleterious mutations are balanced, the numbers for each specific residue type are not. The rates of deleterious mutations for each residue type are given in Table IV for the full data sets. They vary quite significantly; for example, 77% of Trp wildtype mutations are deleterious, while only 28% of Ile mutations are.

Setting p(N) = p(D) = 0.5 in Equation 2 and then using Equation 1 and 2 to calculate p(ph= D|x), we calculated the residue-specific curves shown in Figures 4e and 4f for wildtype and mutant residue types respectively. The curves cross p=0.5 at different points for different residue types. For example, for Val, the deleterious/neutral cutoff is at a PSSM difference of about 2.4, while for Trp, the cutoff is at 9.1. For the mutant residues, the cutoff for Ile is 2.4 while for Cys it is 6.0. The cutoffs for all wildtype and mutant residues as well as the global cutoffs are given in Table V.

The last section of Table VI shows the performance of the PSSM score of the wildtype residue, the PSSM score of the mutant residue, and the PSSM score difference (dPSSM). The mutant residue PSSMs performs a little better than wildtype residue PSSMs, while as expected the difference in PSSM scores performs better than either PSSM score alone with a total accuracy of 77.7% and balanced accuracy of 77.5%, compared to the random prediction rate of 50% from the balanced data sets.

For each mutation in the balanced mutation set, we assigned a predicted phenotype based on the highest one of the six probabilities: p(D | pssm _ wt ) , p(N | pssm _ wt ) , p(D | pssm _ mut), p(N | pssm _ mut), p(D | pssm _ diff ) and p(N | pssm _ diff ) . Table VI also shows the result of this approach (“Best of six kernel probabilities”). The true negative rate and the positive predictive value obtained from the consensus of six kernel probabilities is higher than those of the individual scores, and the overall accuracy (78.0%) is a little better than that of the PSSM difference alone; however, the balanced accuracy (77.4%) is a little worse than that of PSSM difference alone.

Since the kernel classification curves in Figures 4e and 4f showed that different residue types would have different cutoffs for phenotype predictions, we analyzed the predictive accuracy of classification curves for each residue type. For each wildtype or mutant residue, we used kernel density estimates to calculate the optimal bandwidth, the neutral and deleterious probability densities and the neutral and deleterious classification probabilities given dPSSM since dPSSM gets the best performance among those three types of PSSM score.

Figure 5a, 5b, 5c and 5d show the performance of global and wildtype-specific cutoff for the dPSSM score using balanced accuracy, true positive rate, true negative rate and positive predictive value respectively. In balanced accuracy, the wildtype-specific cutoffs are better than the global cutoff for 15 out of 20 residue types, while they are the same for 5 residue types since those residue types have the same cutoff. Especially, for Pro and Trp, the wild-type-specific cutoffs improve the results by 11% and 13%. Figures 5b and 5c demonstrates that residue-specific cutoffs improve the true negative rate much more than the true positive rate. Figure 5d shows that the wildtype residues which have better positive predictive value also have a better true negative rate. In general, the true positive value decreases for the wildtype residues whose residue-specific cutoffs are larger than the global dPSSM cutoff, while the positive predictive value increases for the wildtype residues whose residue-specific cutoffs are larger than the global dPSSM cutoff .

Figure 5.

Performance of global and residue-specific cutoff for dPSSM scores.

Similarly, Figures 5e, 5f, 5g and 5h compare the results for mutant-specific cutoffs with the global cutoff for the dPSSM score for balanced accuracy, true positive rate, true negative rate and positive predictive value respectively. The mutant-specific cutoffs are better for 10 residue types, while they are the same as the global cutoffs for the other 10 residue types. For Trp and Pro, the mutant-specific cutoffs improve the results by 4% and 3%. Again, the true positive rate increases for the mutant residues whose residue-specific cutoffs are less than the global dPSSM cutoff, while the positive predictive value increases for the mutant residues whose residue-specific cutoffs are larger than the global dPSSM cutoff.

Table V gives the values of the cutoffs for the dPSSM scores for each mutant residue type. We created separate data sets that are balanced for every wildtype and mutant residue type and used global dPSSM cutoff and residue-specific dPSSM cutoff to classify the mutations in these two datasets. The results in Table VI show that the mutant-specific cutoffs get slightly better balanced accuracy than that of wildtype-specific cutoffs, and both of them got a higher true negative rate, positive predictive value, the overall accuracy and balanced accuracy than those of global cutoff. Since the training data set and the testing data set are balanced, the overall accuracy is equal to the balanced accuracy.

Support vector machines for combining sequence- and structure-based features

In the previous sections, we assessed the prediction performance of two sequence-based features and two structure-based features. In order to train a support vector machine (SVM) model on a combination of these features, we created a randomly balanced mutation set which contains 7136 mutations (3568 neutral mutations and 3568 deleterious mutations). With this data set, we assessed various combinations of features with tenfold cross validation to obtain unbiased assessments of the ability of SVMs to predict phenotype from the sequence-based and structural features. Table VII gives the results of combining these features with SVMs.

Table VII.

The performance of SVMs on balanced data sets

Feature	TPR	TNR	PPV	NPV	BACC
Surface area of monomer	63.9	65.4	64.9	64.5	64.7
Surface area of BA	73.5	62.2	66.1	70.1	67.9
Surface area of BA and monomer	75.5	60.0	65.4	71.0	67.8
BA surface area & PSSM score	73.7	80.2	78.9	75.4	77.0
BA surface area & conservation score	79.9	72.4	74.3	78.3	76.1
PSSM score & conservation score	83.6	76.6	78.1	82.4	80.1
BA surface area & PSSM score & conservation score	82.9	80.2	80.7	82.4	81.5
Two sequence and two structural features	83.0	80.5	81.0	82.6	81.7
Same four features on balanced independent testing dataset	82.7	78.3	79.2	81.9	80.5

All results except the last line are based on 10-fold cross-validation (training on 90% and testing on the remaining 10%, and performing this procedure for each 10% of the data). The last line provides results trained on all the mutations in the cross-validation set but tested on an independent data set.

The results in Table VII show that combining all four features (monomer and biological surface area, dPSSM score and conservation score) results in the highest ten-fold cross-validation balanced accuracy (81.7%), compared to various subsets of these four features. We tested an SVM trained on this entire data set on a balanced independent data set of deleterious and neutral mutations not contained in the training data set. The results show that the model performs approximately as well on the independent data as it does on the training data (through cross validation), although TPR and NPV are somewhat higher on the independent data set and the TNR and PPV are better for the cross validation data set.

To evaluate the statistical significance of the differences in performance between the various combinations of features in Table VII, we calculated p-values by using Fisher's exact test. The results are shown in Table VIII. As expected from the accuracy results in Table VII, any feature set containing sequence information (with or without structure) is better than feature sets containing only structural information with p-values better than 1e-26. The more interesting results are that the p-value of biological assembly surface area and monomer surface area is 5.8e-05, demonstrating that the difference in performance (an improvement of 3.2% of balanced accuracy) is statistically significant. Adding the structural information (biological assembly and monomer surface areas) to the sequence-based information (dPSSM and conservation scores) results in a small but statistically significant improvement in prediction rates (p-values of 0.035 and 0.018 for either BA or BA+monomer surface areas together).

Table VIII.

p-values of the difference in performance between feature sets

	Monomer	BA	BA+ monomer	BA+ dPSSM	BA+ cons	dPSSM+ cons	BA+ dPSSM+cons	BA+monomer +dPSSM+cons
Monomer	-	5.8E-05	9.8E-05	5.1E-59	2.3E-50	7.1E-95	1.1E-114	3.5E-117
BA	5.8E-05	-	0.90	3.9E-34	1.1E-27	2.5E-62	1.4E-78	1.2E-80
BA+monomer	9.8E-05	0.90	-	8.4E-35	2.8E-28	3.1E-63	1.4E-79	1.1E-81
BA+dPSSM	5.1E-59	3.9E-34	8.4E-35	-	0.21	7.2E-06	3.8E-11	6.5E-12
BA+cons	2.3E-50	1.1E-27	2.8E-28	0.21	-	7.9E-09	3.0E-15	3.6E-16
dPSSM+cons	7.1E-95	2.5E-62	3.1E-63	7.2E-06	7.9E-09	-	0.035	0.018
BA+dPSSM+cons	1.1E-114	1.4E-78	1.4E-79	3.8E-11	3.0E-15	0.035	-	0.81
BA+monomer+dPSSM+cons	3.5E-117	1.2E-80	1.1E-81	6.5E-12	3.6E-16	0.018	0.81	-

“cons” = conservation score; “BA” = biological assembly accessible surface area; “monomer” = monomer accessible surface area

Discussion

Our goal in this study was not to develop a new method for prediction of phenotypes but to explore some common features used in these methods in greater depth, in particular the role of biological assemblies in phenotype prediction.

Like many other groups, we chose to use the SwissVar disease-associated mutations as the source of our deleterious data set.² The main reason is the sheer size and diversity of the SwissVar data set. From our earlier studies,¹⁶ it was evident that extrapolating from data on one or two protein systems (like the large Lac repressor data set) would not necessarily provide accurate predictions on large, diverse data like missense polymorphisms across the human proteome. For the residue-specific calculations in our study, these data sets would not have been large enough. However, it should be kept in mind that our results are for a mixture of monogenic and polygenic disease mutations.

Any feature that will be useful in phenotype prediction must have a different statistical distribution for neutral mutations than for deleterious mutations. In a very limited number of previous reports, the distributions of feature values for neutral and deleterious mutation data sets are given and compared. For instance, Yue et al. gave the overall rates of various structure features in their neutral and deleterious data sets.¹² For example. in their data, 82% of disease mutations were buried in protein structures, while only 40% of neutral mutations were. Bao and Cui also studied the predictive power of individual features used in their nsSNPAnalyzer program.³⁴

The closest approach to the one shown here in analyzing predictive features was performed by Ferrer-Costa et al., who provided histograms of various feature values for both deleterious and neutral variants.^9,10 Their data showing overlapping but shifted distributions of PSSM scores, residue volumes, and other features. However, histograms using non-overlapping bins are inherently noisy and statistically biased. The kernel density estimates used in this paper provide smooth and statistically unbiased density estimates. Separate kernel density estimates for the deleterious and neutral mutations can be readily turned into kernel classification functions that provide the probability of each phenotype as a function of the feature values. The predictive properties of different features can be easily visualized and compared.

Employing kernel density estimates and kernel classification functions, we investigated the properties of some commonly used sequence-based features, including PSSM scores and conservation scores. We found that the behavior of these functions depends strongly on the wildtype and mutant amino acid types. This occurs in part because the rates of deleterious and neutral mutations vary significantly by residue type (Table IV). Thus in an overall balanced data set (P(N) = P(D) = 0.5), the values of P(N) and P(D) for each residue type are not balanced. This is expected – some residue types have very specific structural and functional roles that are not easily accomplished by other residue types (e.g., Cys, Trp, Gly, Pro). The genetic code and the kinds of errors that occur in DNA replication also have effects on what mutations occur with any frequency and which amino acid types are more susceptible to deleterious mutations because of large changes in biophysical properties. For some wildtype amino acid types the residue-specific dPSSM scores are much better than the global dPSSM scores are, and the same holds for the mutant amino acid types. For many residue types, the results are quite similar and the overall improvement in prediction accuracy is modest – from 74.4% correct predictions to 76.3% correct predictions with wildtype-specific cutoffs and from 75.9% correct predictions to 76.8% correct predictions with mutant-specific cutoffs (Table VI).

We found previously that for the Lac repressor data, surface areas calculated from the structure of the homodimer bound to DNA were much more predictive than surface areas calculated from the monomeric protein.¹⁶ Other groups have also used biological assemblies given by PQS,³⁵ including Ferrer-Costa et al.,⁹ Yue and Moult,¹² and Sunyaev et al.⁷ The MuD server allows users to choose from among the biological assemblies given by different PDB entries for interpretation and visualization of mutations,³⁶ although they did not study the predictive effects of using the biological assemblies compared to monomers.

We were therefore very interested to find out whether this would hold true with a diverse set of proteins and structures in the PDB. In general, the surface areas in the biological assemblies are more predictive than the surface areas in monomers derived from PDB structures. However, the mutations that are actually affected by interactions in the biological assemblies are a minority of all mutations in our data sets. Only 20% of the 10,513 mutations in our structure data set change surface area at all and only 12% by more than 5 Ų on going from monomer to biological assembly. An improvement in predictive accuracy on these mutations results in a statistically significant (p-value = 0.00006) increase in overall balanced accuracy from 64.9% to 67.6% (Table VI).

We went to some length to determine whether we could exploit the biological assemblies further using residue-specific cutoffs and multiple biological assemblies. Using residue-specific cutoffs raises this value to 68.9% and using the minimum value over a number of biological assemblies it to 69.7%. Combining the surface areas from biological assemblies with sequence based features such as dPSSM and conservation scores shows a small but statistically significant improvement over using the sequence-based features alone, because the sequence-based features already exhibit fairly high accuracies when used alone.

Predicting phenotypes of mutations remains a challenging bioinformatics problem for a number of reasons. As mentioned earlier, mutations associated with polygenic diseases may be only mildly deleterious in their functional consequences, and therefore quite difficult to predict. Also many of the features that are available are highly correlated with other features, and each adds only marginally to the predictive ability of any machine-learning method. In a recent assessment of several methods on an approximately balanced data set (48% deleterious),³⁷ the best methods MutPred³⁸ and SNPS&GO³⁹ reached accuracies of about 74–82%, depending on the test set used. We hope that exploring these features in great depth a better understanding of associations between sequence and structural features and phenotype predictions may be possible.